测量平差 第三章
第三章监测网平差及基准点稳定性分析

剔除动点后,其余点构成统计量
F1
ˆF 2 ˆ02
ˆF
2
=
dFT
PFF fF
dF
当F1<F分析值,分析即结束,反之,继续 剔除动点,继续检验,直到原假设不再拒绝,
最后剩下的都是稳定的点。
• 当网中存在固定点时,采用这些固定点作 基准,应用经典平差;
• 当网中某些点具有相对的稳定性,它们相 互变动是随机的情况下,则用这些点作拟 稳点,用拟稳平差对成果进行分析;
• 当监测网所有网点具有微小的随机变动时, 自由网平差是一种有效的分析方法.
因此,要合理地确定监测网的参考系,首先要 确定哪些点是稳定的或相对稳定的点,哪些点是 不稳定的点。从20世纪70年代起,人们相继提出 了多种关于监测点稳定性分析方法,其中平均间 隙法是一种比较典型的方法。
m i=1
xi =0
xm
x
1 m
m i 1
xi
0, x为水准网的高程重心.
x =0说明水准网的自由网平差参考系是网的高程重心.
以测边网为例:自由网平差
x1
1
G
T
X=
0
- y10
0 1 x10
1 0 - y20
0 1 x20
…1 …0 … ym0
0 1 xm0
y1 xm
所以:对监测网进行稳定性分析,并 根据稳定性分析结果选择平差方法,确立 一个对变形分析比较有利的参考系,是变 形观测数据处理的一项重要任务。
§3—2 监测网的参考系及其平差
起算数据称为平差问题的基准:基准给出了控制网的位 置。
尺度和方位的定义 即控制网的参考系.
• 经典平差:采用选择固定基准的办法确定参考 系. (满足待估参数的求取要求) • 监测网平差:满足有多期复测的观测值估计的 位移 是一种“绝对的”或接近绝对的位移
误差理论与测量平差基础第三章 协方差传播律及权

X
0 1
,
X
0 2
,
,
X
0 n
也可写为:
dZ
f X1
dX1 0
f X
2
dX2 0
f X
n
0 dX n
KdX
因此只要对非线性函数求全微分,获得系数矩阵即 可应用协方差传播率
12
第三章 协方差传播率及权
6、多个观测向量非线性函数的方差—协方差矩阵
基本思想:a、利用泰勒级数展开,略去二次以上项,
为第l2ilj i组E观(li测 值E(l的i ))方(l j 差 E;(l j ))
为第i组观测值关于第j组观测值的协方差,协方差用 来描述第i个观测值与第j个观测值之间的相关程度。
3
第三章 协方差传播率及权
§3-2 协方差传播率
1、协方差传播律的作用 (图3-1示例)
计算观测向量函数的方差—协方差矩阵,从而评 定观测向量函数的精度。
20
第三章 协方差传播率及权
对上式求全微分,得
dZ1
f1 X 1
dX 1
f1 X 2
dX 2
f1 X n
dX n
dZ 2
f 2 X 1
dX 1
f 2 X 2
dX 2
f 2 X n
dX n
dZt
f t X 1
dX 1
f t X 2
dX 2
f t X n
dX n
21
第三章 协方差传播率及权
2、预备公式
E(C) C , E(CX ) CE(X ), E(X Y ) E(X ) E(Y )
E(X1 X 2 X n ) E(X1) E(X 2) E(X n )
测量平差[3]
![测量平差[3]](https://img.taocdn.com/s3/m/142d6d69561252d380eb6ecd.png)
第七章
间接平差
ˆ ˆ ˆ ˆ ˆ 线性化(变量代换法) v xi = x0 + mxi′ cosα − myi′ sin α − xi ˆ ˆ ˆ ˆ ˆ v yi = y0 + myi′ cosα + mxi′ sin α − yi
X
0 2
X
0 T 3
] = [100.078
100.099 101.266] ( m)
T
第七章
⎡− 1 1 ⎢ 0 −1 ⎢ ⎢− 1 0 V =⎢ 6,1 ⎢1 0 ⎢0 1 ⎢ ⎢0 0 ⎣ 0⎤ ⎡3⎤ ⎢3⎥ 1⎥ ⎥ ⎢ ⎥ ⎢11⎥ 1⎥ ˆ− ⎢ ⎥ ⎥x 0⎥ 3,1 ⎢ 0 ⎥ ⎢0⎥ 0⎥ ⎥ ⎢ ⎥ 1⎥ ⎢0⎥ ⎦ ⎣ ⎦
n×1
ˆ L = L +V
第七章
间接平差
例:选择独立、足够的参数
C = 2km P = diag [2 2 2 1 1 1]
T
1 0.023 1
2 1.114 1
3 1.142 1
4 0.079 2
5 0.099 2
6 1.210 2 h(m) S(km)
n=6, t=3, r=3
X = X
0
[
0 1
ΔZ BC 3 6 BC
ˆ v ΔX AB = X 1 − X A − ΔX AB ˆ v = X − Y − ΔY
ΔY AB 2 A AB
ˆ v ΔZ AB = X 3 − Z A − ΔZ AB ˆ v ΔX AC = X 4 − X A − ΔX AC ˆ v = X − Y − ΔY
ΔY AC 5 A AC
第七章
间接平差
在三角网平差中,通常选m个待定点的坐标平差值作为 待估参数,即t=2m 。 h 这样选,既足数,又独立, 而且容易写出参数与观测 值之间的函数关系。一般 地,角度观测值可由右图 表示,于是有:
测量平差第三章习题与答案

测量平差第三章思考题3.1 下列各式中的()1,2,3i L i =均为等精度独立观测值,其中误差为s ,试求X 的中误差: (1)()12312X LL L =++;(2)123L L X L =3.2 已知观测值1L ,2L 的中误差12s s s ==,120s =,设11225,2X L Y L L =+=-,12Z L L =,t X Y =+,试求X ,Y ,Z 和t 的中误差。
的中误差。
3.3 设有观测向量[]12331TL L L L =,其协方差阵为,其协方差阵为40003002L LD éùêú=êúêúëû分别求下列函数的的方差:分别求下列函数的的方差: (1)1133F L L =-; (2)2233F L L =3.4 设有同精度独立观测值向量[]12331TL LLL=的函数为113s i n s i n A BL Y S L =,22A B Y L a =-,式中A B a 和A B S 为无误差的已知值,测角误差1"s =,试求函数的方差12y s 、22y s及其协方差12y y s3.5 在图中△ABC 中测得A A s б,边长b b s ±,c c s ±,试求三角形面积的中误差ss 。
3.6 在水准测量中,设每站观测高差的中误差均为1mm ,今要求从已知点推算待定点的高程中误差不大于5cm ,问可以设多少站?,问可以设多少站? 3.7 有一角度测4个测回,得中误差为0.42〃,问再增加多少个测回其中误差为0.28〃?〃? 3.8 在相同观测条件下,应用水准测量测定了三角点A ,B ,C 之间的高差,设三角形的边长分别为S 1=10km ,S 2=8km ,S 3=4km ,令40km 的高差观测值权威单位权观测,试求各段观测高差之权及单位权中误差。
《测量平差》学习辅导

《测量平差》学习辅导第一章测量平差及其传播定律一、学习要点(一)内容:测量误差的概念、测量误差来源、分类;偶然误差概率特性;各种精度指标;真误差定义;协方差传播律;权与定权的常用方法;协因数传播律;权逆阵及其传播规律。
(二)基本要求:1.了解测量平差研究的对象和内容;2.掌握偶然误差的四个概率特性;3.了解精度指标与误差传播偶然误差的规律;4.了解权的定义与常用的定权方法;5.掌握协方差传播率。
(三)重点:偶然误差的规律性,协方差、协因数的概念、传播律及应用;权的概念及定权的常用方法。
(四)难点:协方差、协因数传播率二、复习题(一)名词解释1.偶然误差2.系统误差3.精度4.单位权中误差(二)问答题1.偶然误差有哪几个概率特性?2.权是怎样定义的,常用的定权方法有哪些?(三)计算题σ的量测中误差1.在1:500的图上,量得某两点间的距离d=23.4mm,dσ。
σ=±0.2mm,求该两点实地距离S及中误差s三、复习题参考答案 (一)名词解释1.偶然误差:在一定条件下做一系列的观测,如果观测误差从表面上看其数值和符号不存在任何确定的规律性,但就大量误差总体而言,具有统计性的规律,这种误差称为偶然误差。
2.系统误差:在一定条件下做一系列的观测,如果观测的误差在大小、符号上表现出系统性,或者为某一常数,或者按照一定的规律变化,这种带有系统性和方向性的误差称为系统误差。
3.精度:表示同一量的重复观测值之间密集或吻合的程度,即各种观测结果与其中数的接近程度。
4.单位权中误差:权等于1的中误差称为单位权中误差。
(二)问答题1.答:有四个概率特性:①在一定观测条件下,误差的绝对值有一定的限值,或者说超出一定限值的误差出现的概率为零;②绝对值较小的误差比绝对值较大的误差出现的概率大;③绝对值相等的正负误差出现的概率相同;④偶然误差的数学期望为零。
2.答:设i L (i=1,2,3,…,n ),他们的方差为2i σ,如选定任一常数0σ,则定义:22ip σσ=,称为观测值L i 的权。
第三章条件平差
独立三角网
自由三角网
自由测角网
附合三角网(测角)
• 例:
∆ቤተ መጻሕፍቲ ባይዱ
α ∆
当n=35、n=22、n=35+22时,其条件式个数各为多 少?有哪些类型?
图形条件(内角和条件):
B
b1
a2
c1 D c2 a1 b3 c3 a3 b2 C
A
圆周条件(水平条件):
b1
a2
c1 a1 a3 c3
c2 b2 b3
5.1.06、 5.1.07
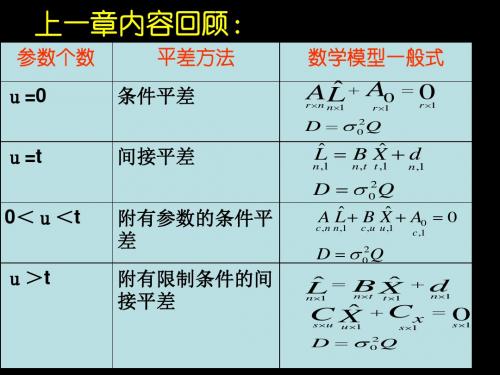
上节内容回顾:
改正数条件式 观测值的协方差阵 法方程
AV W 0
D P Q
2 0 1 2 0
r n n n
Naa K W 0 N aa AQ AT
r r n r
改正数方程
V P A K QA K
T
1 T
wr
T
• 则条件方程可写成:
ˆA 0 AL 0
• 以及改正数条件式:
W AL A0
AV W 0
这样一来,对于一个平差问题,我们能够得到 其数学模型:
AV W 0 D P Q
2 0 1 2 0
下面要解决的问题是: 由上述的数学模型来求改正数V。
不难发现,不能求得V的唯一解!!! 解决不唯一解的办法就是附加一个约束条件---“最小二乘估计” 即满足:
极条件(边长条件):
b1 a2
c1
a1 b3 c3
c2 b2 a3
极条件(边长条件)就是指由不同路线推算得到 的同一边长的长度应相等。
三角网的基本图形 1) 单三角形 2)大地四边形
3)中点多边形。
测量平差课后习题答案 张书毕

P点坐标的中误差为: x 0.17m, y 0.06m 将各点值代入函数得: X P 2462.66m,Y P 5842.59m p点坐标为x=2462.66 0.17m,y=5842.59 0.06m
10
.解答:
千米 =
AB
1 1 站 站 0.0075 3m s 0.08
向量 X 1 Y1 X 1
(1) 试求坐标差函数 X X 2 X 1 与 Y Y 2 Y1 的方差—协方差阵; (2) 求两点间边长 S X 2 Y 2 与坐标方位角T arctan(Y / X )的方差 —协方差阵。 解答: (1) 向量 X 1 Y1 X 1 Y 2 T 的协方差阵得
6
d x
.解答: 由题意可知:
S AB cos 1 cos TAB 3
S AB sin 1 sin TAB 3
'' sin 2
d 1
S AB sin 1 cos 2 cos TAB 3
'' sin 2 2
d 2
'' sin 2
1 1 f h H A h1 h2 H B 2 2
P
LL
5 8 1 1 协因数阵Q P LL LL 4 1 8 2 32 Q 0 5 Q D LL 0
2
1 8 5 2 1 1 1 2 4 2 4 8 1 2 5 5 8
2
4
.解答:
第 1 页/共 44 页
《测量平差》参考答案 Ch1---Ch4
2 1 0 P LL 1 3 1 0 1 2 Q P LL Q Q
《测量平差》课程教案

附件3
交通职业学院
课程教案
学年第学期
开课单位交通职业学院道桥系测量教研室
授课教师
职称
课程名称测量平差
课程性质职业能力课
教材名称《测量平差》
适用专业(方向)工程测量与监理
交通职业学院制
年9月8日
《课程教案》填写说明
一、用宋体、5号字填写,每项页面大小可按照规定格式自行添减。
二、一次课为一份教案(不包括封面)。
三、“课程性质”填基本素质课、职业能力课、素质拓展课;素质拓展课的“适用专业(方向)”填写“全校各专业”。
四、“开课单位”填学院、学系和教研室(无教研室只填学院和学系)。
五、授课类型指理论课、讨论课、实验、社会实践、实习或见习课、其他等。
六、“教学内容”应具体,而不应只填写教材章节名称或讲授主题的题目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2:若要在两已知点间布设一条附和水准路线,已 知每公里观测中误差等于±5.0mm,欲使平差后 线路中点高程中误差不大于±10mm,问该路线长 度最多可达几公里?
例3:设在测站A上(如图),已 知∠ABC=α,设无误差,而观 测角β1和β2的中误差为σ1=σ2= 1.4秒,协方差σ12=-1秒,就 角x的中误差σx
k10 k 20 K0 t1 k t0
2 DZZ Z K DXX K T tt tn nn nt
若有X的r个函数:
y1 y2 Y FX F0 r1 y r
可得:
2 DYY Y F DXX F T rr rn nn nr
应用协方差传播公式得
N x N
2 x
2
例题
已知某台经纬仪一测回的测角中误差为±6'',如 果要使各测回的平均值的中误差不超过±2'',则至少 应测多少测回? 解:由公式
2 x
2
N
可得
2 62 N 2 2 9 x 2
答:至少应测9测回
三、若干独立误差的联合影响
t ,1 t , n n ,1 t , r r ,1
DYY
DXY
求 DZZ
DZX
DZY
三、非线性函数的情况 设有观测值X的非线性函数:
Z f ( X ) f ( X 1 , X 2 , X n )
已知:
X [ X 1 , X 2 ,... X n ]T , DXX
n ,1 0 X 0 [ X 10 , X 2 ,... X n0 ]T n ,1
求:DZZ
将Z按台劳级数在X0处展开:
0 0 Z f ( X 10 , X 2 , X n )
f f f 0 0 0 ( )0 ( X 1 X 1 ) ( )0 ( X 2 X 2 ) ( )0 ( X n X n ) X 1 X 2 X n (二次以上项)
2 C
2 s
S2
2
2
0.84cm
2
§3-4权与定权的常用方法
一、权的定义
设Li (i 1,2,..., n), 它们的方差为 ,
2 i
如选定任一常数 0,则定义 :
2 0 pi 2 i
称为观测值Li的权。权与方差成反比。
1 2
D XX
2 X X 2 X X
1 n 2 n
2 X
nX2
2 Xn
若有X的t个函数:
z1 z2 Z KX K 0 t1 z t
1n
k2n ktn
k11 k12 k 21 k 22 K tn k t1 kt 2
解 法 一
(1)、列函数式, 由图知: X C X A S cos 0 , YC YA S sin 0 (2)、线性化
dX C cos dYC sin
dS 0
S
sin
2
dS 0
S
(3)、应用协方差传播公式可得坐标方差计算式
C
L2
α0
L1 B
s AC
s in L1 s0 s in L2
A
AC 0 (180 L1 L2 ) xC x A s AC cos AC yC y A s AC s in AC
XC,YC的中误差与L1,L2的中误差之间的关系是什么?
二.本章将要阐述的问题
hAB h1 h2 +hn
设水准测量中每一测站观测高差hi的精度相同, 其 方差均为 , 则具有N个测站的水准路线的总高差为
h h1 h2 ... hN
2 h2 h21 h22 h2n N 站
h
N 站
在平坦地区的水准测量中, 每公里的测站数大致相 2 等, 因此, 每公里观测高差的方差相等, 设其均为 km , 则S公里观测高差的方差和中误差分别为
(4).计算点位方差
2 C
S2
2
X Y sin cos
2
2
cos2
2
c
c
sin 2 0
2
0
2 s
2
0
0
2
s
2
2
S2
6000 .00 *10 0 .5
206265 2
2 2 h S km
h S km
ˆ ˆ h S km
其估值公式为
2 ˆ h S km ˆ2
例题
水准测量中若要求每公里观测高差中误差不超过 10mm,水准路线全长高差中误差不超过60mm, 则该 水准路线长度不应超过多少公里? 解:由公式
S
第三章 协方差传播律与权
在实际工作中,经常间接测量某些量,待求量通过间接测量 的方程式 y f ( x1 , x2 ,, xn ) 获得。通过测量获得量 x1 , x2 ,, xn 的数值后,即可由上面的函数关系计算出待 求量y 的数值。 本章将要讨论的问题是:测量数据的误差怎样作用于间接量 y,即给定测量数据的测量误差,现在提出这样一个问题: 观测值函数的精度如何评定?其中误差与观测值的中误差存 在怎样的关系?如何从后者得到前者?阐述这种关系的公式 称为协方差传播律。
2 h
2 km
可得
2 h 60 2 S 2 2 36 km 10
答:该水准路线长度不应超过36公里。
二、同精度独立观测算数平均值的精度
设L1,L2,…,Ln为一组等精度的独立观测值(方差均
为σ2) , 其算术平均值为
x
1 L1 L2 ... LN N
1 1 1 L1 L2 ... LN N N N
差的关系。
一、观测值线性函数的方差
设有n维观测向量X,其数学期望μ和协方差阵分别为:
设有n维观测向量X的函数Z为:Z=KX+K0,求DZZ=? 式中K为系数阵,K0为常数。 根据方差的定义得:
2 DZZ Z E Z EZ Z EZ
T
DZZ KDXX K
S2 2 cos 0 s 2 sin 2 0 Xc S2 2 2 2 2 sin 0 s 2 cos2 0 Yc
2 2
cos
d 0 d 0
2 Z
T
上式的纯量形式为:
2 2 2 2 2 DZZ Z k12 12 k 2 2 k n n 2k1k 2 12
2k1k3 13 2k1k n 1n 2k n -1k n n -1,n
当向量中的各分量两两独立时,它们之间的互协m
2
解 法 二
由C点纵、横向方差求点位方差 如图AC边上边长方差称为 s2 , 而在它的垂直方 纵向方差 向的方差称为横向方差 。 横向方差是由AC边的坐标 方位角α的方差引起的, 由图知
S S
2 2 u 2
2
2
2
2
点位方差为
f k0 f ( X 1 , X 2 , X ) ( ) 0 X i0 i 1 X i
n 0 0 0 n
Z [k 1 , k 2 , kn ] X k0 KX k0
n ,1
DZZ KDXX K
T
例4、根据极坐标法测设P点的坐标,设已知 点无误差,测角中误差为m,边长中误差ms, 试推导P点的点位中误差。
设若干独立误差的联合影响下观测结果的真误差为
z 1 2 n
由协方差传播律可得:
2 2 2 Z 12 2 n
2 Z 即, 观测结果的方差 ,等于各独立误差所对应的方
差之和
。
四、平面控制点的点位精度
如下图所示导线, A为已知点, α0为AB方向的方位 角 , β 为观测角 , 其方差为 ±4.0(″)2, 观测边长 S为 600.00 m, 其方差为0.5cm2, 试求C点的点位方差。
xe
dx
数学期望的传播规律:
常数c的数学期望为E(c)=c 随机变量X乘以常数c,则有 E CX CE X 随机变量X 1 , X 2 ,, X n 之和的数学期望为
E X 1 X 2 X n E X1 E X 2 E X n
一.常见问题举例
1.如图,观测了一个 三角形的三个内角 L1,L2,L3.将其闭合差 ω平均分配后的各角的 平差值为:
C L2
L3 A
L1 B
ˆ i Li 1 L 3
即:平差值是对过观测值计算得到的,如果已知观测 值的中误差,怎么求平差值中误差?
2.如图,在侧方交会中,已知A,B 两点的坐标(XA,YA)和(XB,YB),它们之 间的距离为S0,坐标方位角为α0,由 交会的观测角L1,L2求交会点的坐标:
二、多个观测值线性函数的协方差阵
设有观测向量n维X,其数学期望和协方差阵已知:
1 E ( X 1 ) 2 E ( X 2 ) X E( X ) n n
2 X1 2 X 2 X1 2 X X n 1 2 X X 2 X2
