数学建模历年赛题的分析
《2024年2016年全国大学生数学建模竞赛B题解题分析与总结》范文

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言2016年全国大学生数学建模竞赛B题是一道涉及复杂系统建模与优化的题目,要求参赛者针对实际问题进行数学建模、求解及分析。
本文将详细介绍该题目的背景、意义、解题思路及总结,以期为其他参赛者提供参考。
二、题目背景与意义本题以城市交通拥堵问题为背景,要求参赛者建立数学模型,对城市交通流量进行预测及优化。
该问题具有较高的现实意义,因为随着城市化进程的加速,交通拥堵已成为各大城市面临的重要问题。
通过数学建模,我们可以更好地理解交通拥堵的成因,为解决交通拥堵问题提供理论依据。
三、解题思路1. 问题分析首先,我们需要对题目进行深入分析,明确问题的背景、目标及约束条件。
本题主要涉及城市交通流量的预测及优化,需要考虑到交通网络的复杂性、交通流量的时变性、道路资源的有限性等因素。
2. 数学建模根据问题分析,我们可以建立相应的数学模型。
本题中,我们采用交通流理论及运筹学原理,建立了一个多因素影响的城市交通流量预测模型。
模型中考虑了道路类型、交通状况、天气等因素对交通流量的影响。
同时,为了优化交通流量,我们还建立了一个基于遗传算法的交通信号灯配时优化模型。
3. 模型求解在建立数学模型后,我们需要进行模型求解。
本题中,我们采用MATLAB软件进行模型求解。
首先,我们利用历史数据对预测模型进行训练,得到各因素对交通流量的影响程度。
然后,我们根据实时交通数据及天气数据,利用预测模型对未来一段时间内的交通流量进行预测。
最后,我们利用遗传算法对交通信号灯配时进行优化,以达到缓解交通拥堵的目的。
四、解题方法与技巧在解题过程中,我们需要掌握一些方法和技巧。
首先,我们要对题目进行深入分析,明确问题的本质及需求。
其次,我们要建立合理的数学模型,考虑到各种因素的影响。
在求解过程中,我们需要选择合适的算法及软件工具,以提高求解效率及准确性。
此外,我们还需要注重模型的验证与优化,确保模型的可靠性和实用性。
《2024年2016年全国大学生数学建模竞赛B题解题分析与总结》范文

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言全国大学生数学建模竞赛(CUMCM)是衡量各高校数学类学科学生学习与实践能力的标志性竞赛之一。
其中,B题以真实问题的复杂性吸引了广大参赛选手的关注。
本文将对B题的具体题目内容、解题过程、常见方法和误区进行分析,并结合实例对竞赛结果进行总结,以期为其他参赛同学提供一定的参考。
二、题目分析B题通常关注某一实际领域的复杂问题,涉及多个因素的综合考量。
其要求参赛者通过建立数学模型,解决实际问题。
具体问题包括某个地区的旅游经济预测和资源合理配置。
针对此问题,首先需要对旅游业的各项数据进行详细分析,然后构建适当的数学模型,并使用合适的数学工具和软件进行计算和模拟。
三、解题过程1. 数据收集与分析:收集该地区的历史旅游数据,包括游客数量、消费水平、旅游景点分布等。
同时,分析该地区的经济、文化、交通等影响旅游业的因素。
2. 模型构建:根据收集的数据和实际情况,选择合适的数学模型进行建模。
常见的模型包括时间序列预测模型(如ARIMA 模型)、多元回归模型等。
3. 模型求解与验证:利用数学软件(如MATLAB、SPSS等)对模型进行求解,并对模型的预测结果进行验证。
验证方法包括与历史数据进行对比、进行敏感性分析等。
4. 资源合理配置:根据预测结果和实际情况,制定合理的资源分配方案,如旅游景点的开发策略、交通设施的优化配置等。
四、常见方法与误区1. 常见方法:在建模过程中,应选择合适的数学模型和方法。
对于时间序列预测问题,常用的有ARIMA模型、指数平滑法等;对于多元回归问题,则需要考虑各因素之间的相互关系。
同时,还应充分利用计算机技术进行数据分析和模拟。
2. 误区提示:在建模过程中,要避免陷入一些常见的误区。
例如,过分追求模型的复杂性和精确度而忽视模型的实用性和可解释性;忽视数据的预处理和清洗工作;忽略模型的验证和修正等。
五、实例分析以某次B题竞赛的优秀解决方案为例,详细分析其解题过程和关键点。
美赛国赛数学建模试题的分析与体会

重庆邮电大学 数理学院
❖ 另外,为了能够选拔优秀队员参赛,我们每 年5月进行校内数学建模竞赛,通过校内竞赛 一方面我们可以让更多的人参与到数学建模 活动中 ,从而得到锻炼(400~500个队每 年),另一方面我们可以选拔相对优秀的队 员参加全国竞赛。这样,获得参加全国赛的 队员既有荣誉感,也有责任感。
谢 谢!
2020/2/6
重庆邮电大学 数理学院
2020/2/6
重庆邮电大学 数理学院
❖ 1994年: (A)山区修建公路的设计造价问题 (B)锁具的制造、销售和装箱问题
❖ 1995年: (A)飞机的安全飞行管理调度问题 (B)天车与冶炼炉的作业调度问题
2020/2/6
重庆邮电大学 数理学院
❖ 1996年: (A)最优捕鱼策略问题 (B)节水洗衣机的程序设计问题
2020/2/6
重庆邮电大学 数理学院
❖ 针对赛题数据量越来越“海”,我们有专门 的教练负责计算机软件应用的培训专题,主 要给学生讲解基本软件的应用知识,给学生 抛砖引玉似的讲解当前数学建模中常用软件, 主要让学生自己在课余熟悉软件的功能和操 作。这样,学生面对大数据时心里有底,需 求相应的软件求解。这样的训练结果是:参 赛学生应对复杂数据应对自如,不会因为数 据复杂二放弃该题。
2020/2/6
重庆邮电大学 数理学院
❖ 针对赛题实时性越来越“紧”,我们在培 训时希望同学们关注近期来重大问题,如 奥运、股市、物价、传染病、环境保护等 实时性问题,以便他们遇到这类问题时有 很好的心里准备,这样在心里上他们会有 一定的优势。这样的训练结果是:参赛学 生在书籍做到心中有数。
2020/2/6
2020/2/6
重庆邮电大学 数理学院
全国大学生数学建模竞赛D题解析

汇报人:
CONTENTS
PRT ONE
PRT TWO
竞赛名称:全国大学生数学建模竞 赛
竞赛目的:培养大学生数学建模能 力提高解决实际问题的能力
添加标题
添加标题
竞赛级别:国家级
添加标题
添加标题
竞赛影响:促进大学生数学建模技 术的发展选拔优秀人才
竞赛起始于XXXX年 每年举办一次 参赛对象为全国大学生 竞赛目的是提高大学生数学建模能力和科技创新能力
组建合适的团队分工明确
制定详细的计划合理安排时间
充分准备所需的知识和技能
准备阶段:研究 题目收集资料建 立模型
实施阶段:编程 实现模拟实验优 化模型
总结阶段:撰写 论文整理思路提 炼经验
反思阶段:总结 得失分析原因改 进策略
赛题分析:对竞赛题目进行深入剖析明确解题思路和要点 经验教训:总结竞赛过程中遇到的问题和不足提出改进措施 团队协作:评估团队成员在竞赛中的表现和贡献提出优化建议 未来规划:根据竞赛经验和教训制定个人和团队未来的学习和发展计划
模型验证:通过对比实际数据和模型预测结果对模型的准确性和可靠性进行评估和改进
数据清洗:去除异常值、缺失值和重复值 数据筛选:根据需求筛选有效数据 数据转换:对数据进行必要的转换以适应分析需求 数据可视化:通过图表、图像等形式直观展示数据
确定问题类型和目 标函数
确定算法的输入和 输出
设计算法的流程图 和伪代码
培养团队协作精神 提升大学生数学应用能力
促进学科交叉融合
为国家和社会培养创新型人 才
PRT THREE
题目背景:全国大学生数学建模竞赛D题 题目要求:分析D题所涉及的数学建模方法和技巧 题目内容:对D题进行解析包括问题分析、模型建立、求解过程等 题目难度:对D题的难度进行评估并给出解题建议
《2024年2016年全国大学生数学建模竞赛B题解题分析与总结》范文

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言2016年全国大学生数学建模竞赛(CUMCM)是面向全国各高校学生的大型数学建模类比赛。
在众多赛题中,B题以其复杂的实际问题背景和深入的应用数学知识引起了广泛关注。
本文旨在针对B题的解题过程进行详细分析,并做出相应的总结。
二、题目概述B题主要描述了一个实际生活中遇到的问题:基于网络平台的交通流量预测。
题目要求参赛者根据历史交通流量数据,分析交通流量的变化规律,并建立数学模型进行预测。
三、解题分析1. 数据收集与预处理首先,我们需要收集相关的历史交通流量数据。
这些数据可能包括时间、地点、交通流量等信息。
收集到的原始数据需要进行清洗和预处理,例如去除异常值、缺失值等,以获得更为准确的数据。
2. 建立数学模型根据数据的特点和问题需求,我们选择合适的数学模型进行建模。
考虑到交通流量与时间的关系较为密切,我们可以选择时间序列分析模型,如ARIMA模型等。
此外,考虑到不同地点之间的交通流量可能存在相互影响,我们还可以引入空间相关性分析,如空间自回归模型等。
3. 模型优化与验证建立数学模型后,我们需要对模型进行优化和验证。
这包括调整模型的参数、对模型进行诊断分析等。
我们可以通过对比模型的预测值与实际值,计算误差指标(如均方误差、平均绝对误差等)来评估模型的性能。
同时,我们还可以使用交叉验证等方法来验证模型的稳定性。
4. 模型应用与结果展示最后,我们将建立的数学模型应用于实际问题中,对未来的交通流量进行预测。
我们将预测结果以图表等形式进行展示,方便评委和观众理解。
同时,我们还可以对结果进行解释和讨论,说明模型的优点和局限性。
四、总结通过本文总结:经过详细的分析与探讨,针对2016年全国大学生数学建模竞赛B题,我们采取了有效的解决策略。
从数据收集与预处理到模型建立与优化,每一步都紧密联系实际,充分考虑了交通流量数据的特性和问题需求。
在建模过程中,我们选择了合适的时间序列分析模型和空间相关性分析模型,旨在捕捉交通流量的变化规律。
数学建模竞赛命题过程及题目分析

油位探针
油位探测 装置
油位探针
油
β
3m
地平线垂直线
(a)无偏转倾斜的正截面图 (b)横向偏转倾斜后正截面图
结合评奖对本科组选作A, B题的分析
• 本科组全国14108队参赛,送全国1393份论文,其中A题877 份(63%),B题516份(37%),其比例基本代表全部参赛 队的情况.
• 获一等奖的210 队中A题133队,B题77队.
• A题获一等奖的队多数集中在重点高校:
北京17队(北航5、北大3、北邮3、清华2)
图3 储油罐截面示意图
油
注油口
位
出油管
探
针 油浮子
1.2m
1.2m
油 α
0.4m 2.05m (a) 小椭圆油罐cm正面示意图
水平线
1.78m
Байду номын сангаас
(b) 小椭圆油罐截面示意图
图4 小椭圆型油罐形状及尺寸示意图
附件1 实验数据
流水 C进油 D油位高
号
量/L 度/mm
采集时间
说明
2010-08-20 (1)罐体无变位进油,罐内
11
50 159.02
10:32:18 油量初值262L;
12
100 176.14
2010-08-20 (2)C列进油量是每次加入 10:33:18 50L油后的累加值
13
150 192.59
2010-08-20 (3)D列是原罐内初始油量加入 10:34:18 相应油量后油位高度值。
全国大学生数学建模竞赛赛题综合评析
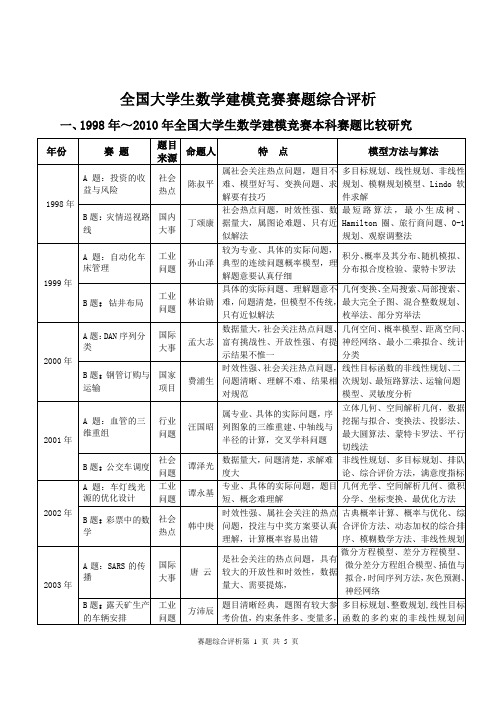
社会热点
叶其孝、周义仓
开放性强、社会关注性强,突出数据来源的可靠性、结论解释的合理性
数据收集与处理、问题的分析与假设,初等数学方法、一般统计方法、多目标规划、回归分析、综合评价方法、灰色预测
2009年
A题:制动器试验台的控制方法分析
工业问题
方沛辰、刘笑羽
问题具体、专业性强,要花时间读懂、理解清楚问题
出版社的资源配置
孟大志
艾滋病疗法的评价及疗效的预测
边馥萍
易拉罐形状和尺寸的最优设计(C题)
叶其孝
煤矿瓦斯和煤尘的监测与控制(D题)
韩中庚
2007年
中国人口增长预测
唐云
乘公交,看奥运
方沛辰、吴孟达
手机“套餐”优惠几何(C题)
韩中庚
体能测试时间安排(D题)
刘雨林
2008年
数码相机定位
谭永基
高等教育学费标准探讨
叶其孝、周义仓
地面搜索(C题)
肖华勇
NBA赛程的分析与评价(D题)
姜启源
2009年
制动器试验台的控制方法分析
方沛辰、刘笑羽
眼科病床的合理安排
吴孟达、毛紫阳
卫星和飞船的跟踪测控(C题)
周义仓
会议筹备(D题)
王宏健
2010年
储油罐的变位识别与罐容表标定
韩中庚
2010年上海世博会影响力的定量评估
杨力平
输油管的布置(C题)
1
6
8
付鹂
重庆大学
1
6
9
姜启源
清华大学
4
3
10
陈叔平
浙江大学、贵州大学
2
5
11
数学建模经典算法及试题分析

从网上找来的关于十大经典数学模型,看完之后感觉很有帮助,于是编辑了一下发到网上来,供数学建模爱好者们讨论学习,欢迎指导。
1、蒙特卡罗算法(该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,是比赛时必用的方法)2、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具)3、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo软件实现)4、图论算法(这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备)5、动态规划、回溯搜索、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法(这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用)7、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)8、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)9、数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用)10、图象处理算法(赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理)1、蒙特卡罗方法(MC)(Monte Carlo):蒙特卡罗(Monte Carlo)方法,或称计算机随机模拟方法,是一种基于“随机数”的计算方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、CUMCM历年赛题的分析
2、从问题的实际意义分析
从28个问题的实际意义方面分析,大体上可以分为工 业、农业、工程设计、交通运输、经济管理、生物医 学和社会事业等七个大类。
一、CUMCM历年赛题的分析
赛题的通用解题方法
3、从问题的解决方法上分析
从问题的解决方法上分析,涉及到的数学建模方 法有几何理论、组合概率、统计分析、优化方法、 图论、网络优化、层次分析、插值与拟合、差分方 法、微分方程、排队论、模糊数学、随机决策、多 目标决策、随机模拟、灰色系统理论、神经网络、 时间序列、综合评价方法、机理分析等方法。
1. CUMCM 的历年赛题浏览
2003年:(A)SARS的传播问题(集体) (B)露天矿生产的车辆安排问题(吉林大:方沛辰) (D)抢渡长江问题(华中农业大学:殷建肃)
2004年:(A)奥运会临时超市网点设计问题(北工大:孟大志) (B)电力市场的输电阻塞管理问题(浙大:刘康生) (C)酒后开车问题(清华大学:姜启源) (D)公务员的招聘问题(信息工程大学:韩中庚)
一、CUMCM历年赛题的分析
算法总计
3、从问题的解决方法上分析
用到插值拟合的问题有4个; 用到神经网络的4个; 用灰色系统理论的2个; 用到时间序列分析的至少2个; 用到综合评价方法的至少2个; 机理分析方法和随机模拟都多次用到; 其它的方法都至少用到一次。 大部分题目都可以用两种以上的方法来解决,即 综合性较强的题目有21个,占75%。
一、CUMCM历年赛题的分析
题型
4、从问题的题型上分析
(2)理论性较强的问题有12个,占46.2% : 94A,94B,95A,96A,97A,98B,99A,00B,01A, 02A,03A,04B; (3)实用性较强的问题有14个,占50% : 93A,94B,95B,96B,98B,99B,00B,01A,01B, 02B,03A,04B,05A,05B; (4)算法要求强的问题有6个,占21.4% : 95A,97B,99B,00A,00B,05B; (5)数据量较大的问题有10个,占35.7% : 00A,00B,01A,01B,02B,03A,04A,04B,05A, 05B.
一、CUMCM历年赛题的分析
1. CUMCM 的历年赛题浏览:
1996年:(A)最优捕鱼策略问题(北师大:刘来福) (B)节水洗衣机的程序设计问题(重大:付鹂)
1997年:(A)零件参数优化设计问题(清华:姜启源) (B)金刚石截断切割问题(复旦:谭永基等)
1998年:(A)投资的收益和风险问题(浙大:陈淑平) (B)灾情的巡视路线问题(上海海运学院:丁颂康)
一、CUMCM历年赛题的分析
赛题常用方法,优化和概率
3、从问题的解决方法上分析
用的最多的方法是优化方法和概率统计的方法. 用到优化方法的共有19个题,占总数的67.9%, 其中整数规划4个,线性规划4个,非线性规划14个 ,多目标规划4个。 用到概率统计方法的有15个题,占53.6%,几乎 是每年至少有一个题目用到概率统计的方法。 用到图论与网络优化方法的问题有4个; 用到层次分析方法的问题有3个;
2001年:(A)三维血管的重建问题(浙大:汪国昭) (B)公交车的优化调度问题(清华:谭泽光) (C)基金使用计划问题(东南大学:陈恩水)
2002年:(A)汽车车灯的优化设计问题(复旦:谭永基等) (B)彩票中的数学问题(信息工程大学:韩中庚) (D) 球队的赛程安排问题(清华:姜启源)
一、CUMCM历年赛题的分析
纵览14年的本科组28个题目(专科组还有9个题 目),我们可从问题的实际意义、解决问题的方法和 题型三个方面作一些简单的分析。
一、CUMCM历年赛题的分析
1. CUMCM 的历年赛题浏览:
1992年:(A)作物生长的施肥效果问题(北理工:叶其孝) (B)化学试验室的实验数据分解问题(复旦:谭永基)
一、CUMCM历年赛题的分析
4、从问题的题型上分析
(1)“即时性”较强的问题有10个,占35.7%:
1993B:足球队排名问题; 1998B:灾情巡视路线问题; 2000A:DNA序列分类问题; 2000B:钢管订购与运输问题; 2001B:公交车的调度问题; 2002B:彩票中的数学问题; 2003A:SARS的传播问题; 2004A:奥运会临时超市网点设计问题 2004B:电力市场的输电阻塞管理问题 2005A: 长江水质的评价和预测问题
工业类:电子通信、机械加工 与制造、机械设计与 控制等行业,共有8个
交通运输类:3个题,占 10.7%
题,占28.6%。
经济管理类:4个题,占
农业类:1个题,占3.6%。 14.3%
工程设计类: 3个题,占10.7%。生物医学类:4个题,占
有的问题属于交叉的,或者1是4.边3%缘的。
社会事业类: 5个题,占17.8%
1999年:(A)自动化机床控制管理问题(北大:孙山泽) (B)地质堪探钻井布局问题(郑州大学:林诒勋) (C)煤矸石堆积问题(太原理工大学:贾晓峰)
一、CUMCM历年赛题的分析
1. CUMCM 的历年赛题浏览:
2000年:(A)DNA序列的分类问题(北工大:孟大志) (B)钢管的订购和运输问题(武大:费甫生) (C)飞越北极问题(复旦大学:谭永基) (D)空洞探测问题(东北电力学院:关信)
1993年:(A)通讯中非线性交调的频率设计问题(北大:谢衷洁) (B)足球甲级联赛排名问题(清华:蔡大用)
1994年:(A)山区修建公路的设计造价问题(西电大:何大可) (B)锁具的制造、销售和装箱问题(复旦:谭永基等)
1995年:(A)飞机的安全飞行管理调度问题(复旦:谭永基等) (B)天车与冶炼炉的作业调度问题(浙大:刘内容:
1、 CUMCM的历年赛题分析; 2、数学建模竞赛的发展趋势; 3、参加数学建模竞赛的技巧;
一、CUMCM历年赛题的分析
随着数学建模竞赛的深入开展,竞赛的规模越 来越大,竞赛的水平也在不断地提高,竞赛水平的 提高主要体现在赛题水平的提高,而赛题的水平主 要体现在赛题的综合性、实用性、创新性、即时性, 以及多种解题方法的创造性、灵活性等,特别是给 参赛者留有很大的发挥创造的想象空间。
