二次函数中的相似三角形
二次函数与相似三角形问题(含答案 完美打印版)

综合题讲解 函数中因动点产生的相似三角形问题例题 如图1,已知抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B 。
⑴求抛物线的解析式;(用顶点式...求得抛物线的解析式为x x 41y 2+-=) ⑵若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;⑶连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似若存在,求出P 点的坐标;若不存在,说明理由。
分析:1.当给出四边形的两个顶点时应以两个顶点的连线.......为四边形的边和对角线来考虑问题以O 、C 、D 、B 四点为顶点的四边形为平行四边形要分类讨论:按OB 为边和对角线两种情况2. 函数中因动点产生的相似三角形问题一般有三个解题途径① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
y xEQ PC B OA 例题2:如图,已知抛物线y=ax 2+4ax+t (a >0)交x 轴于A 、B 两点,交y 轴于点C ,抛物线的对称轴交x 轴于点E ,点B 的坐标为(-1,0). (1)求抛物线的对称轴及点A 的坐标;(2)过点C 作x 轴的平行线交抛物线的对称轴于点P ,你能判断四边形ABCP 是什么四边形并证明你的结论;(3)连接CA 与抛物线的对称轴交于点D ,当∠APD=∠ACP 时,求抛物线的解析式.练习1、已知抛物线2y ax bx c =++经过5330P E ⎫⎪⎪⎝⎭,,,及原点(00)O ,.(1)求抛物线的解析式.(由一般式...得抛物线的解析式为225333y x x =-+) (2)过P 点作平行于x 轴的直线PC 交y 轴于C 点,在抛物线对称轴右侧且位于直线PC 下方的抛物线上,任取一点Q ,过点Q 作直线QA 平行于y 轴交x 轴于A 点,交直线PC 于B 点,直线QA 与直线PC 及两坐标轴围成矩形OABC .是否存在点Q ,使得OPC △与PQB △相似若存在,求出Q 点的坐标;若不存在,说明理由.(3)如果符合(2)中的Q 点在x 轴的上方,连结OQ ,矩形OABC 内的四个三角形OPC PQB OQP OQA ,,,△△△△之间存在怎样的关系为什么练习2、如图,四边形OABC 是一张放在平面直角坐标系中的矩形纸片,点A 在x 轴上,点C 在y 轴上,将边BC 折叠,使点B 落在边OA 的点D处。
二次函数中相似三角形存在性
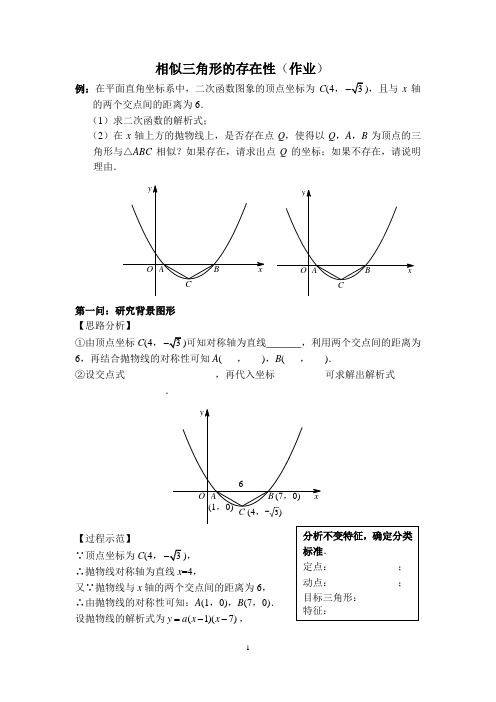
相似三角形的存在性(作业)例:在平面直角坐标系中,二次函数图象的顶点坐标为C(4,),且与x轴的两个交点间的距离为6.(1)求二次函数的解析式;(2)在x轴上方的抛物线上,是否存在点Q,使得以Q,A,B为顶点的三角形与△ABC相似?如果存在,请求出点Q的坐标;如果不存在,请说明理由.第一问:研究背景图形【思路分析】①由顶点坐标C(4,可知对称轴为直线_______,利用两个交点间的距离为6,再结合抛物线的对称性可知A(___,___),B(___,___).②设交点式__________________,再代入坐标__________可求解出解析式__________________.【过程示范】∵顶点坐标为C(4,又∵抛物线与x设抛物线的解析式为将C (4,代入可得,9a =,∴所求解析式为2y x x =. 第二问:整合信息、分析特征、设计方案 【思路分析】相似三角形存在性问题也是在存在性问题的框架下进行的:①分析特征:先研究定点、动点,其中_________为定点,点__为____________________的动点;则________为目标三角形.进一步研究此三角形,发现其中________________;构造辅助线:____________________________,能够计算出∠BAC =_____°,∠ACB =________°;再考虑研究△QAB ,固定线段为______,并且由于点Q 在x 轴上方的抛物线上,所以△QAB 为______(填“钝角”或“直角”)三角形.②画图求解:先考虑点Q 在抛物线对称轴右侧的情况,此时 ∠ABQ 为钝角,要想使△ABC 与△ABQ 相似,则需要∠ABQ =_____°,且_________.求解时,可根据∠ABQ =_____°,AB =BQ =_____来求出Q 点坐标.同理,考虑点Q 在抛物线对称轴左侧时的情况.③结果验证:考虑点Q 还要在抛物线上,将点Q 代入抛物线解析式验证.【过程示范】存在点Q 使得△QAB 与△ABC 相似.由抛物线对称性可知,AC =BC ,过点C 作CD ⊥x 轴于则AD =3,CD在Rt △ACD 中,tan ∠DAC, ∴∠BAC =∠ABC =30°,∠ACB =120°. ①当△ACB ∽△ABQ 时, ∠ABQ =120°且BQ =AB =6. 过点Q 作QE ⊥x 轴,垂足为E , 则在Rt △BQE 中,BQ =6,∠QBE =60°, ∴QE =BQ ·sin60°=6=BE =3, ∴E (10,0),Q 1(10,. 当x =10时,y= ∴点Q 1在抛物线上.②由抛物线的对称性可知,还存在AQ2=AB,此时△Q2AB∽△ACB,点Q2的坐标为(-2,.综上:Q1(10,,Q2(-2,.1.如图,已知抛物线y=x2-1与x轴交于A,B两点,与y轴交于点C,过点A作AP∥CB交抛物线于点P.(1)求A,B,C三点的坐标.(2)在x轴上方的抛物线上是否存在一点M,过点M作MG⊥x轴于点G,使以A,M,G为顶点的三角形与△PCA相似?若存在,请求出点M的坐标;若不存在,请说明理由.2.如图,抛物线y=ax2+b与x轴交于点A,B,且点A的坐标为(1,0),与y轴交于点C(0,1).(1)求抛物线的解析式,并求出点B的坐标.(2)过点B作BD∥CA交抛物线于点D,在x轴上点A的左侧是否存在点P,使以P,A,C为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由.3.如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求抛物线的解析式.(2)P是抛物线上一动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.【参考答案】例题示范: 第一问:① x =4,(1,0),(7,0)② y =a (x -1)(x -7),C (4,,2y x x =+ 第二问:①点A ,B ,C ,点Q ,在x 轴上方的抛物线上,△ABC ,CA =CB ,过点C 作CD ⊥AB 于点D ,30,120,AB ,钝角。
二次函数背景下的相似三角形存在性问题

二次函数背景下的相似三角形存在性问题
二次函数背景下的相似三角形存在性问题是中考数学常考的题型,在考试中一般出现在压轴题的位置,综合性强,难度略大。
这篇文章主要来讨论下二次函数背景下的相似三角形存在性问题的解题思路方法及应用举例。
【模型解读】
在坐标系中确定点,使得由该点及其他点构成的三角形与其他三角形相似,即为“相似三角形存在性问题”.
【相似判定】
判定1:三边对应成比例的两个三角形是相似三角形;
判定2:两边对应成比例且夹角相等的两个三角形是相似三角形;
判定3:有两组角对应相等的三角形是相似三角形.
以上也是坐标系中相似三角形存在性问题的方法来源,根据题目给的已知条件选择恰当的判定方法,解决问题.
【题型分析】
通常相似的两三角形有一个是已知的,而另一三角形中有1或2个动点,即可分为“单动点”类、“双动点”两类问题.
【思路总结】
根据相似三角形的做题经验,可以发现,判定1基本是不会用的,这里也一样不怎么用,对比判定2、3可以发现,都有角相等!
所以,要证相似的两个三角形必然有相等角,关键点也是先找到一组相等角.
然后再找:
思路1:两相等角的两边对应成比例;
思路2:还存在另一组角相等.
事实上,坐标系中在已知点的情况下,线段长度比角的大小更容易表示,因此选择方法可优先考虑思路1.
一、如何得到相等角?
二、如何构造两边成比例或者得到第二组角?
搞定这两个问题就可以了.
【例题】
【分析】
综上所述,点P的坐标为(3,2)或(3,9).
【总结】
【练习】
声明:文章图文来源网络,意在分享,仅限交流学习使用,如有分享不当或侵权,请联系删除。
二次函数几何-动点构造相似三角形(DOC)

二次函数中的动点相似三角形专题:相似三角形 突破口:寻找比例关系以及特殊角 函数中因动点产生的相似三角形问题一般有三个解题途径。
① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程。
例题1、如图1,已知抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B 。
⑴求抛物线的解析式;⑵若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;⑶连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似?若存在,求出P 点的坐标;若不存在,说明理由。
例题、解:⑴由题意可设抛物线的解析式为1)2x (a y 2+-= ∵抛物线过原点, ∴1)20(a 02+-= ∴41a -=. 抛物线的解析式为1)2x (41y 2+--=,即x x 41y 2+-=⑵如图1,当OB 为边即四边形OCDB 是平行四边形时,CD ∥=OB,由1)2x (4102+--=得4x ,0x 21==,∴B(4,0),OB =4. ∴D 点的横坐标为6将x =6代入1)2x (41y 2+--=,得y =-3, ∴D(6,-3);根据抛物线的对称性可知,在对称轴的左侧抛物线上存在点D,使得四边形ODCB 是平行四边形,此时D 点的坐标为(-2,-3),当OB 为对角线即四边形OCBD 是平行四边形时,D 点即为A 点,此时D 点的坐标为(2,1) ⑶如图2,由抛物线的对称性可知:AO =AB,∠AOB =∠ABO. 若△BOP 与△AOB 相似,必须有∠POB =∠BOA =∠BPO 设OP 交抛物线的对称轴于A′点,显然A′(2,-1) ∴直线OP 的解析式为x 21y -= 由x x 41x 212+-=-, 得6x ,0x 21== .∴P(6,-3)过P 作PE ⊥x 轴,在Rt △BEP 中,BE =2,PE =3, ∴PB =13≠4.∴PB≠OB,∴∠BOP≠∠BPO, ∴△PBO 与△BAO 不相似,同理可说明在对称轴左边的抛物线上也不存在符合条件的P 点. 所以在该抛物线上不存在点P ,使得△BOP 与△AOB 相似.例题2、在直角坐标系中,O 为坐标原点,点A 的坐标为(2,2),点C 是线段OA 上的一个动点(不运动至O ,A 两点),过点C 作CD ⊥x 轴,垂足为D ,以CD 为边在右侧作正方形CDEF. 连接AF 并延长交x 轴的正半轴于点B ,连接OF,设OD =t. ⑴ 求tan ∠FOB 的值;⑵用含t 的代数式表示△OAB 的面积S ;⑶是否存在点C, 使以B ,E ,F 为顶点的三角形与△OFE 相似,若存在,请求出所有满足要求的B 点的坐标;若不存在,请说明理由.(1)作AH ⊥x 轴于H ,交CF 于P ∵A(2,2) ∴AH=OH=2 ∴∠AOB=45° ∴CD=OD=DE=EF=t ∴1tan 22t FOB t ∠== ……………………3分 (2)∵CF ∥OB ∴△ACF ∽△AOB ∴AP CF AH OB = 即22t tOB-= ∴22t OB t =- ∴12(02)22OAB tS OB AH t t∆=⋅=<<- ………………6分 (3)要使△BEF 与△OFE 相似,∵∠FEO=∠FEB=90° ∴只要OE EF EB EF =或OE EF EF EB= 即:2BE t =或12EB t =① 当2BE t =时, 4BO t =, ∴242t t t=- ∴0t =(舍去)或32t = ∴B(6,0) ……………………8分② 当12EB t =时, (ⅰ) 当B 在E 的右侧时,52OB OE EB t =+=, ∴2522t t t =- ∴0t =(舍去)或65t = ∴B(3,0) …………………10分(ⅱ) 当B 在E 的左侧时,如图,32OB OE EB t =-=, ∴2322t t t =- ∴0t =(舍去)或23t = ∴B(1,0) ……………………12分举一反三1.如图,一次函数y =-2x 的图象与二次函数y =-x 2+3x 图象的对称轴交于点B .(1)写出点B 的坐标 ;(2)已知点P是二次函数y=-x2+3x图象在y轴右侧..部分上的一个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点. 若以CD为直角边的△PCD与△OCD相似,则点P的坐标为.。
二次函数与相似三角形
分析: ( 1) 第一步是基础知识,可由学生自己解决,只对个别不会的学生加以
辅导,可以由 B 号学生帮助解决 ( 2) 第二步要判断两个直角三角形相似, 可以证明夹着直角的四条边成
0)、B(0,3)两点,其顶点为 D. (1) 求该抛物线的解析式; (2) △ AOB 与△ BDE 是否相似?如果相似, 请予以证明; 如果不相似, 请 说明理由 .
分析: (1) 加强准确度练习 (2)此题与例题十分相似,尽量让学生自己解决,只对个别不会的
学生加以辅导,可以由 A 号学生帮助解决
六、小结
类似本节这类综合应用题,我们应注意什么问题?要怎样解决问题?
( 1.认真读题,写出所有可得的基本信息; 2.再次确认细节问题,比如点
的位置,字母的取值范围等; 3.划分成几个小的基本问题逐步解决 ;4.仔细
观察结论,想一想有无其它方法或更为简单的方法,为以后解题总结经
验。)
已知抛物线 y=ax2+bx+c 的顶点坐标为 (4,-1),与 y 轴交于点 C(0,3),O 是原
点.
(1)求这条抛物线的解析式;
作业布置
(2)设此抛物线与 x 轴的交点为 A ,B( A 在 B 的左边),问在 y 轴上是否
存在点 P,使以 O,B,P 为顶点的三角形与△ AOC 相似?若存在,请求出点 P
的坐标:若不存在,请说明理由 .
一般形式
例1
与坐标轴交点
顶点坐标 板书设计
相似判定方法
2023年中考数学压轴题专题04 二次函数与相似问题-【含答案】

专题4二次函数与相似问题函数中因动点产生的相似三角形问题一般有三个解题途径①求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
相似三角形常见的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A”型和“X”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形.(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.判定定理“两边及其夹角法”是常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来,按照对应边成比例,分AB DEAC DF=和AB DFAC DE=两种情况列方程.应用判定定理“两角法”解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等.应用判定定理“三边法”解题不多见,根据三边对应成比例列连比式解方程(组).还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.【例1】(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.(1)求该抛物线的表达式;(2)若PE∥x轴交AB于点E,求PD+PE的最大值;(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.【例2】.(2022•衡阳)如图,已知抛物线y=x2﹣x﹣2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图象记为“图象W”,图象W交y轴于点C.(1)写出图象W位于线段AB上方部分对应的函数关系式;(2)若直线y=﹣x+b与图象W有三个交点,请结合图象,直接写出b的值;(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图象W于点N,是否存在这样的点P,使△CMN与△OBC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【例3】.(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y 轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)求CP+PQ+QB的最小值;(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.【例4】(2022•玉林)如图,已知抛物线:y=﹣2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=,P是第一象限内抛物线上的任一点.(1)求抛物线的解析式;(2)若点D为线段OC的中点,则△POD能否是等边三角形?请说明理由;(3)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.1.(2020秋•兴城市期末)如图,抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,与y轴交于点C,D为第一象限抛物线上的动点,连接AC,BC,DA,DB,DB与AC相交于点E.(1)求抛物线的解析式;(2)如图1,设△ADE的面积为S1,△BCE的面积为S2,当S1=S2+5时,求点D的坐标;(3)如图2,过点C作CF∥x轴,点M是直线CF上的一点,MN⊥CF交抛物线于点N,是否存在以C,M,N为顶点的三角形与△BCO相似?若存在,请直接写出点M的坐标,若不存在,请说明理由.2.(2020秋•郴州期末)已知抛物线y=x2﹣3x+与x轴交于A,B两点(点A在点B的左边).(1)求A,B两点的坐标;(2)如图1,若点D是抛物线上在第四象限的点,连接DA并延长,交y轴于点P,过点D作DE⊥x轴于点E.当△APO与△ADE的面积比为=时.求点D的坐标;(3)如图2,抛物线与y轴相交于点F.若点Q是线段OF上的动点,过点Q作与x轴平行的直线交抛物线于M,N两点(点M在点N的左边).请问是否存在以Q,A,M为顶点的三角形与△QNA相似?若存在,求出点Q的坐标;若不存在,请说明理由.3.(2020秋•长垣市期末)如图1,抛物线y=x2+bx+c与x轴、y轴分别交于点B(6,0)和点C(0,﹣3).(1)求抛物线的解析式;(2)点P是直线BC下方抛物线上一动点,其横坐标为m,连接PB、PC,当△PBC的面积为时,求m 值;(3)如图2,点M是线段OB上的一个动点,过点M作x轴的垂线l分别与直线BC和抛物线交于D,E 两点,是否存在以C,D,E为顶点的三角形与△BDM相似,若存在,请直接写出点M的坐标;若不存在,请说明理由.4.(2021秋•邹城市期末)如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.(1)求A,B,C三点的坐标;(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.5.(2021秋•攸县期末)如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M和点N的坐标;②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;③是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.6.(2022•禹城市模拟)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.(1)求出抛物线的解析式;(2)P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M 为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;=S△ABC,直接写出点D (3)若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得S△DCA的坐标.7.(2022•祥云县模拟)如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),交y轴于点C(0,3),点M是该抛物线上第一象限内的一个动点,ME垂直x轴于点E,交线段BC于点D,MN∥x轴,交y轴于点N.(1)求抛物线y=ax2+bx+c的表达式;(2)若四边形MNOE是正方形,求该正方形的边长;(3)连结OD,AC,抛物线上是否存在点M,使得以C,O,D为顶点的三角形与△ABC相似,若存在,请求出点M的坐标,若不存在,请说明理由.8.(2022•松江区校级模拟)如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.(1)求抛物线的解析式以及顶点坐标;(2)连接BC,CD,DB,求∠CBD的正切值;(3)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BE,直线BE与对称轴交于点M,在(2)的条件下,点P是抛物线对称轴上的一点,是否存在点P使△CDB和△BMP相似,若存在,求点P坐标,若不存在,请说明理由.9.(2022•平江县一模)如图,抛物线y=ax2+bx+8与x轴交于A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求该抛物线的函数表达式;(2)点P是第一象限内抛物线上的动点,连接PB,PC,设四边形PBOC和△AOC的面积分别为S四边形PBOC ,记S=S四边形PBOC﹣S△AOC,求S最大值点P的坐标及S的最大值;和S△AOC(3)点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△BOC相似?若存在,求点M的坐标;若不存在,请说明理由.10.(2022•莱州市一模)如图①,在平面直角坐标系中,抛物线y=x2+c经过点A(4,3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,﹣2)且垂直于y轴的直线,连接PO.(1)求抛物线的表达式,并求出顶点B的坐标;(2)试证明:经过点O的⊙P与直线l相切;(3)如图②,已知点C的坐标为(1,2),是否存在点P,使得以点P,O及(2)中的切点为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.11.(2022•巩义市模拟)已知,二次函数y=ax2+bx﹣3的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于C点,点A的坐标为(﹣1,0),且OB=OC.(1)求二次函数的解析式;(2)当0≤x≤4时,求二次函数的最大值和最小值分别为多少?(3)设点C'与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC'与△POB相似,且PC 与PO是对应边?若存在,求出点P的坐标;若不存在,请说明理由.12.(2022•澄迈县模拟)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求该抛物线的函数表达式及顶点C的坐标;(2)设该抛物线上一动点P的横坐标为t.①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;③在图3中,若P是y轴左侧该抛物线上的动点,过点P作PM⊥x轴,垂足为M,是否存在点P使得以点P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.13.(2022•丰南区二模)如图①、②,在平面直角坐标系中,一边长为2的等边三角板CDE恰好与坐标系中的△OAB重合,现将三角板CDE绕边AB的中点G(G点也是DE的中点),按顺时针方向旋转180°到△C′ED的位置.(1)直接写出C′的坐标,并求经过O、A、C′三点的抛物线的解析式;(2)点P在第四象限的抛物线上,求△C′OP的最大面积;(3)如图③,⊙G是以AB为直径的圆,过B点作⊙G的切线与x轴相交于点F,抛物线上是否存在一点M,使得△BOF与△AOM相似?若存在,请求出点M的坐标;若不存在,请说明理由.14.(2022•莱芜区三模)如图,在平面直角坐标系中,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=x2+bx+c的图象经过A和点C(0,﹣3).(1)求二次函数的表达式;(2)如图1,平移线段AC,点A的对应点D落在二次函数在第一象限的图象上,点C的对应点E落在直线AB上,直接写出四边形ACED的形状,并求出此时点D的坐标;(3)如图2,在(2)的条件下,连接CD,交x轴于点M,点P为直线CD下方抛物线上一个动点,过点P作PF⊥x轴,交CD于点F,连接PC,是否存在点P,使得以点P,C,F为顶点的三角形与△COM相似?若存在,求出线段FP的长度;若不存在,请说明理由.15.(2022•临清市三模)如图,抛物线y=﹣x2+bx+c的顶点D坐标为(1,4),且与x轴相交于A,B两点(点A在点B的左侧,与y轴相交于点C,点E在x轴上方且在对称轴左侧的抛物线上运动,点F在抛物线上并且和点E关于抛物线的对称轴对称,作矩形EFGH,其中点G,H都在x轴上.(1)求抛物线解析式;(2)设点F横坐标为m,①用含有m的代数式表示点E的横坐标为(直接填空);②当矩形EFGH为正方形时,求点G的坐标;③连接AD,当EG与AD垂直时,求点G的坐标;(3)过顶点D作DM⊥x轴于点M,过点F作FP⊥AD于点P,直接写出△DFP与△DAM相似时,点F 的坐标.16.(2022•成都模拟)如图①,已知抛物线y=﹣(x﹣1)2+k交x轴于A,B两点,交y轴于点C,P是抛物线上的动点,且满足OB=3OA.(1)求抛物线的解析式;(2)若点P在第一象限,直线y=x+b经过点P且与直线BC交于点E,设点P的横坐标为t,当线段PE 的长度随着t的增大而减小时,求t的取值范围;(3)如图②,过点A作BC的平行线m,与抛物线交于另一点D.点P在直线m上方,点Q在线段AD 上,若△CPQ与△AOC相似,且点P与点O是对应点,求点P的坐标.17.(2022•东莞市校级一模)在平面直角坐标系xOy中,已知抛物线y=﹣x2+2kx+2k2+1与x轴的左交点为A,右交点为B,与y轴的交点为C,对称轴为直线l,对于抛物线上的两点(x1,y1),(x2,y2)(x1<k<x2),当x1+x2=2时,y1﹣y2=0恒成立.(1)求该抛物线的解析式;(2)点M是第二象限内直线AC上方的抛物线上的一点,过点M作MN⊥AC于点N,求线段MN的最大值,并求出此时点M的坐标;(3)点P是直线l右侧抛物线上的一点,PQ⊥l于点Q,AP交直线l于点F,是否存在这样的点P,使△PQF与△ACO相似?若存在,请求出点P的坐标,若不存在,请说明理由.18.(2022•碑林区校级模拟)如图,Rt△ABC中,∠ACB=90°,AB=8,AC=4,以AB所在直线为x轴建立平面直角坐标系,若C(0,2).(1)请直接写出A、B的坐标;(2)求经过A、B、C三点的抛物线表达式;(3)l为抛物线对称轴,P是直线l右侧抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△ABC全等,求满足条件的点P,点E的坐标.【例1】(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.(1)求该抛物线的表达式;(2)若PE∥x轴交AB于点E,求PD+PE的最大值;(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.【分析】(1)直接利用待定系数法,即可求出解析式;(2)先求出点C的坐标,然后证明Rt△DPE∽Rt△AOC,再由二次函数的最值性质,求出答案;(3)根据题意,可分为两种情况进行分析:当△AOC∽△APD时;当△AOC∽△DAP时;分别求出两种情况的点的坐标,即可得到答案.【解析】(1)将A(0,3)和B(,﹣)代入y=﹣x2+bx+c,,解得,∴该抛物线的解析式为y=﹣x2+2x+3;(2)设直线AB的解析式为y=kx+n,把A(0,3)和B(,﹣)代入,,解得,∴直线AB的解析式为y=﹣x+3,当y=0时,﹣x+3=0,解得:x=2,∴C点坐标为(2,0),∵PD⊥x轴,PE∥x轴,∴∠ACO=∠DEP,∴Rt△DPE∽Rt△AOC,∴,∴PE=PD,∴PD+PE=PD,设点P的坐标为(a,﹣a2+2a+3),则D点坐标为(a,﹣a+3),∴PD=(﹣a2+2a+3)﹣(﹣a+3)=﹣(a﹣)2+,∴PD+PE=﹣(a﹣)2+,∵﹣<0,∴当a=时,PD+PE有最大值为;(3)①当△AOC∽△APD时,∵PD⊥x轴,∠DPA=90°,∴点P纵坐标是3,横坐标x>0,即﹣x2+2x+3=3,解得x=2,∴点D的坐标为(2,0);∵PD⊥x轴,∴点P的横坐标为2,∴点P的纵坐标为:y=﹣22+2×2+3=3,∴点P的坐标为(2,3),点D的坐标为(2,0);②当△AOC∽△DAP时,此时∠APG=∠ACO,过点A作AG⊥PD于点G,∴△APG∽△ACO,∴,设点P的坐标为(m,﹣m2+2m+3),则D点坐标为(m,﹣m+3),则,解得:m=,∴D点坐标为(,1),P点坐标为(,),综上,点P的坐标为(2,3),点D的坐标为(2,0)或P点坐标为(,),D点坐标为(,1).【例2】(2022•衡阳)如图,已知抛物线y=x2﹣x﹣2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图象记为“图象W”,图象W交y轴于点C.(1)写出图象W位于线段AB上方部分对应的函数关系式;(2)若直线y=﹣x+b与图象W有三个交点,请结合图象,直接写出b的值;(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图象W于点N,是否存在这样的点P,使△CMN与△OBC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【分析】(1)令x=0和翻折的性质可得C(0,2),令y=0可得点A、B的坐标,利用待定系数法即可求出图象W的解析式;(2)利用数形结合找出当y=﹣x+b经过点C或者y=﹣x+b与y=x2﹣x﹣2相切时,直线y=﹣x+b与新图象恰好有三个不同的交点,①当直线y=﹣x+b经过点C(0,2)时,利用一次函数图象上点的坐标特征,即可求出b值;②当y=﹣x+b与y=x2﹣x﹣2相切时,联立一次函数解析式和抛物线解析式,利用根的判别式Δ=0,即可求出b值.综上即可得出结论;(3)先确定△BOC是等腰直角三角形,分三种情况:∠CNM=90°或∠MCN=90°,分别画图可得结论.【解析】(1)当x=0时,y=﹣2,∴C(0,2),当y=0时,x2﹣x﹣2=0,(x﹣2)(x+1)=0,∴x1=2,x2=﹣1,∴A(﹣1,0),B(2,0),设图象W的解析式为:y=a(x+1)(x﹣2),把C(0,2)代入得:﹣2a=2,∴a=﹣1,∴y=﹣(x+1)(x﹣2)=﹣x2+x+2,∴图象W位于线段AB上方部分对应的函数关系式为:y=﹣x2+x+2(﹣1<x<2);(2)由图象得直线y=﹣x+b与图象W有三个交点时,存在两种情况:①当直线y=﹣x+b过点C时,与图象W有三个交点,此时b=2;②当直线y=﹣x+b与图象W位于线段AB上方部分对应的函数图象相切时,如图1,﹣x+b=﹣x2+x+2,x2﹣2x+b﹣2=0,Δ=(﹣2)2﹣4×1×(b﹣2)=0,∴b=3,综上,b的值是2或3;(3)∵OB=OC=2,∠BOC=90°,∴△BOC是等腰直角三角形,如图2,CN∥OB,△CNM∽△BOC,∵PN∥y轴,∴P(1,0);如图3,CN∥OB,△CNM∽△BOC,当y=2时,x2﹣x﹣2=2,x2﹣x﹣4=0,∴x1=,x2=,∴P(,0);如图4,当∠MCN=90°时,△OBC∽△CMN,∴CN的解析式为:y=x+2,∴x+2=x2﹣x﹣2,∴x1=1+,x2=1﹣(舍),∴P(1+,0),综上,点P的坐标为(1,0)或(,0)或(1+,0).【例3】(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)求CP+PQ+QB的最小值;(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.【分析】(1)由y=﹣x2+3x+4可得A(﹣1,0),B(4,0),C(0,4);(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,可知四边形CC'QP是平行四边形,及得CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,而B,Q,C'共线,故此时CP+PQ+BQ最小,最小值为BC'+PQ的值,由勾股定理可得BC'=5,即得CP+PQ+BQ最小值为6;(3)由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣=,设Q(,t),则P(,t+1),M(0,t+1),N(,0),知BN=,QN=t,PM=,CM=|t﹣3|,①当=时,=,可解得Q(,)或(,);②当=时,=,得Q(,).【解析】(1)在y=﹣x2+3x+4中,令x=0得y=4,令y=0得x=﹣1或x=4,∴A(﹣1,0),B(4,0),C(0,4);(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,如图:∵CC'=PQ,CC'∥PQ,∴四边形CC'QP是平行四边形,∴CP=C'Q,∴CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,∵B,Q,C'共线,∴此时CP+PQ+BQ最小,最小值为BC'+PQ的值,∵C(0,4),CC'=PQ=1,∴C'(0,3),∵B(4,0),∴BC'==5,∴BC'+PQ=5+1=6,∴CP+PQ+BQ最小值为6;(3)如图:由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣=,设Q(,t),则P(,t+1),M(0,t+1),N(,0),∵B(4,0),C(0,4);∴BN=,QN=t,PM=,CM=|t﹣3|,∵∠CMP=∠QNB=90°,∴△CPM和△QBN相似,只需=或=,①当=时,=,解得t=或t=,∴Q(,)或(,);②当=时,=,解得t=或t=(舍去),∴Q(,),综上所述,Q的坐标是(,)或(,)或(,).【例4】(2022•玉林)如图,已知抛物线:y=﹣2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=,P是第一象限内抛物线上的任一点.(1)求抛物线的解析式;(2)若点D为线段OC的中点,则△POD能否是等边三角形?请说明理由;(3)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.【分析】(1)把点B(2,0)代入y=﹣2x2+bx+c中,再由对称轴是直线x=列方程,两个方程组成方程组可解答;(2)当△POD是等边三角形时,点P在OD的垂直平分线上,所以作OD的垂直平分线与抛物线的交点即为点P,计算OD≠PD,可知△POD不可能是等边三角形;(3)分种情况:①当PC∥x轴时,△CPM∽△BHM时,根据PH的长列方程可解答;②②如图3,△PCM ∽△BHM,过点P作PE⊥y轴于E,证明△PEC∽△COB,可得结论.【解析】(1)由题意得:,解得:,∴抛物线的解析式为:y=﹣2x2+2x+4;(2)△POD不可能是等边三角形,理由如下:如图1,取OD的中点E,过点E作EP∥x轴,交抛物线于点P,连接PD,PO,∵C(0,4),D是OD的中点,∴E(0,1),当y=1时,﹣2x2+2x+4=1,2x2﹣2x﹣3=0,解得:x1=,x2=(舍),∴P(,1),∴OD≠PD,∴△POD不可能是等边三角形;(3)设点P的坐标为(t,﹣2t2+2t+4),则OH=t,BH=2﹣t,分两种情况:①如图2,△CMP∽△BMH,∴∠PCM=∠OBC,∠BHM=∠CPM=90°,∴tan∠OBC=tan∠PCM,∴====2,∴PM=2PC=2t,MH=2BH=2(2﹣t),∵PH=PM+MH,∴2t+2(2﹣t)=﹣2t2+2t+4,解得:t1=0,t2=1,∴P(1,4);②如图3,△PCM∽△BHM,则∠PCM=∠BHM=90°,过点P作PE⊥y轴于E,∴∠PEC=∠BOC=∠PCM=90°,∴∠PCE+∠EPC=∠PCE+∠BCO=90°,∴∠BCO=∠EPC,∴△PEC∽△COB,∴=,∴=,解得:t1=0(舍),t2=,∴P(,);综上,点P的坐标为(1,4)或(,).1.(2020秋•兴城市期末)如图,抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,与y轴交于点C,D为第一象限抛物线上的动点,连接AC,BC,DA,DB,DB与AC相交于点E.(1)求抛物线的解析式;(2)如图1,设△ADE的面积为S1,△BCE的面积为S2,当S1=S2+5时,求点D的坐标;(3)如图2,过点C作CF∥x轴,点M是直线CF上的一点,MN⊥CF交抛物线于点N,是否存在以C,M,N为顶点的三角形与△BCO相似?若存在,请直接写出点M的坐标,若不存在,请说明理由.【分析】(1)运用待定系数法将A(4,0),B(﹣1,0)代入y=ax2+bx+4,解方程组即可求得答案;(2)根据题意,当S1=S2+5,即S△ABD=S△ABC+5,设D(x,y),表示出△ABD和△ABC的面积,列方程求解即可;(3)分情况讨论,列出三角形相似的三种情况,画出相应图形,设M(m,4),则N(m,﹣m2+3m+4),运用相似三角形性质,建立方程求解即可.【解析】(1)∵抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,∴,解得:,∴y=﹣x2+3x+4;(2)∵抛物线y=﹣x2+3x+4与y轴交于点C,令x=0,则y=4,∴C(0,4),∵S1=S2+5,∴S1+S△AEB=S2+S△AEB+5,=S△ABC+5,即S△ABD∵A(4,0),B(﹣1,0),∴AB=5,设D(x,y),∴×5×y=×5×4+5,∴y=6,∴﹣x2+3x+4=6,解得:x1=1,x2=2,∴D1(1,6),D2(2,6);(3)设M(m,4),则N(m,﹣m2+3m+4),①如图2,△BOC∽△NMC,则=,∴=,解得:m=0(舍去),m=,经检验,m=是原方程的解,∴M(,4);②如图3,△BOC∽△CMN,则=,∴=,解得:m=0(舍去),m=﹣1,经检验,m=﹣1是原方程的解,∴M(﹣1,4);③如图4,△BOC∽△NMC,则=,∴=,解得:m=0(舍去),m=,经检验,m=是原方程的解,∴M(,4);④如图5,△BOC∽△CMN,则=,∴=,解得:m=0(舍去),m=7,经检验,m=7是原方程的解,∴M(7,4);综上所述,点M的坐标为(,4)或(﹣1,4)或(,4)或(7,4).2.(2020秋•郴州期末)已知抛物线y=x2﹣3x+与x轴交于A,B两点(点A在点B的左边).(1)求A,B两点的坐标;(2)如图1,若点D是抛物线上在第四象限的点,连接DA并延长,交y轴于点P,过点D作DE⊥x轴于点E.当△APO与△ADE的面积比为=时.求点D的坐标;(3)如图2,抛物线与y轴相交于点F.若点Q是线段OF上的动点,过点Q作与x轴平行的直线交抛物线于M,N两点(点M在点N的左边).请问是否存在以Q,A,M为顶点的三角形与△QNA相似?若存在,求出点Q的坐标;若不存在,请说明理由.【分析】(1)在抛物线解析式中,令y=0则可求得A、B的坐标;(2)证明△AOP∽△AED,根据相似三角形面积的比等于对应边的比的平方列比例式可得AE=2,从而得点D的横坐标为3,代入抛物线的解析式可得点D的坐标;(3)如图2所示,若以Q,A,M为顶点的三角形与△QNA相似,有两种情况,但是∠QAM与∠QAN不可能相等,所以最后只存在一种情况:△AQM∽△NQA,列比例式可得结论.【解析】(1)当y=0时,x2﹣3x+=0,解得:x1=1,x2=5,∴A(1,0),B(5,0);(2)∵DE⊥x轴,∴∠AED=90°,∴∠AOP=∠AED=90°,∵∠OAP=∠DAE,∴△AOP∽△AED,∴==,∴=,∵OA=1,∴AE=2,∴OE=3,当x=3时,y=﹣3×3+=﹣2,∴D(3,﹣2);(3)如图2,设Q(0,m),当x=0时,y=,∴F(0,),∵点Q是线段OF上的动点,∴0≤m≤,当y=m时,x2﹣3x+=m,x2﹣6x+5﹣2m=0,x=3,∴x1=3+,x2=3﹣,∴QM=3﹣,QN=3+,在Rt△AOQ中,由勾股定理得:AQ=,∵∠AQM=∠AQN,∴当△AQM和△AQN相似只存在一种情况:△AQM∽△NQA,∴,∴AQ2=NQ•QM,即1+m2=(3+)(3﹣),解得:m1=﹣1+,m2=﹣1﹣(舍),∴Q(0,﹣1+).3.(2020秋•长垣市期末)如图1,抛物线y=x2+bx+c与x轴、y轴分别交于点B(6,0)和点C(0,﹣3).(1)求抛物线的解析式;(2)点P是直线BC下方抛物线上一动点,其横坐标为m,连接PB、PC,当△PBC的面积为时,求m 值;(3)如图2,点M是线段OB上的一个动点,过点M作x轴的垂线l分别与直线BC和抛物线交于D,E 两点,是否存在以C,D,E为顶点的三角形与△BDM相似,若存在,请直接写出点M的坐标;若不存在,请说明理由.【分析】(1)根据点A、B的坐标,利用待定系数法即可求出该抛物线的函数关系式;(2)根据点P是直线BC下方抛物线上一动点,其横坐标为m,表示PH的长,根据三角形的面积列方程解出即可得出结论;(3)先根据两三角形相似判断出∠CED=∠BMD=90°或∠DCE=∠DMB=90°,进而分两种情况讨论即可得出结论.【解析】(1)把点B(6,0)和点C(0,﹣3)代入得:,解得:,∴抛物线的解析式为;(2)设直线BC的解析式为:y=ax+n,由点B(6,0)和C(0,﹣3)得:,解得:,∴直线BC的解析式为,如图1,过点P作y轴的平行线交BC于点H,∵点P的坐标为(m,),PH∥y轴,∴点H的坐标为(m,),∴PH=y H﹣y P=﹣()=﹣,x B﹣x C=6﹣0=6,=PH×6=(﹣)×6=﹣=,∵S△PBC解得:m1=1,m2=5,∴m值为1或5;(3)如图2,∵∠CDE=∠BDM,△CDE与△BDM相似,∴∠CED=∠BMD=90°或∠DCE=∠DMB=90°,设M(x,0),①当∠CED=∠BDM=90°,∴CE∥AB,∵C(0,﹣3),∴点E的纵坐标为﹣3,∵点E在抛物线上,∴x2﹣x﹣3=﹣3.∴x=0(舍)或x=5,∴M(5,0);②当∠DCE=∠DMB=90°,∵OB=6,OC=3,∴BC==3,由(2)知直线BC的关系式为y=x﹣3,∴OM=x,BM=6﹣x,DM=3﹣x,由(2)同理得ED=﹣+3x,∵DM∥OC,∴,即,∴CD=,∴BD=BC﹣CD=﹣x,∵△ECD∽△BMD,∴,即=,∴=x(3﹣x)2,x(6﹣x)(1﹣x)=0,x1=0(舍),x2=6(舍),x3=1,∴M(1,0);综上所述:点M的坐标为(5,0)或(1,0).4.(2021秋•邹城市期末)如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.(1)求A,B,C三点的坐标;(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.【分析】(1)将抛物线配方后可得顶点A的坐标,将抛物线和一次函数的解析式联立方程组,解出可得B 和C的坐标;(2)先根据两点的距离计算AB、BC、AC的长,根据勾股定理的逆定理可得:∠ABC=90°,最后根据两边的比相等且夹角为90度得两三角形相似;(3)存在,设M(x,0),则P(x,x2+2x),表示OM=|x|,PM=|x2+2x|,分两种情况:有=或=,根据比例式代入可得对应x的值,计算点P的坐标即可.【解答】(1)解:y=x2+2x=(x+1)2﹣1,∴顶点A(﹣1,﹣1);由,解得:或∴B(﹣2,0),C(1,3);(2)证明:∵A(﹣1,﹣1),B(﹣2,0),C(1,3),∴AB==,BC==3,AC==2,∴AB2+BC2=AC2,==,∴∠ABC=90°,∵OD=1,CD=3,∴=,∴,∠ABC=∠ODC=90°,∴△ODC∽△ABC;(3)存在这样的P点,设M(x,0),则P(x,x2+2x),∴OM=|x|,PM=|x2+2x|,当以O,P,M为顶点的三角形与△ABC相似时,有=或=,由(2)知:AB=,CB=3,①当=时,则=,当P在第二象限时,x<0,x2+2x>0,∴,解得:x1=0(舍),x2=﹣,当P在第三象限时,x<0,x2+2x<0,∴=,解得:x1=0(舍),x2=﹣,②当=时,则=3,同理代入可得:x=﹣5或x=1(舍),综上所述,存在这样的点P,坐标为(﹣,﹣)或(﹣,)或(﹣5,15).5.(2021秋•攸县期末)如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M和点N的坐标;②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;③是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.【分析】(1)①函数的对称轴为:x=﹣=,故点M(,),即可求解;②设抛物线与x轴左侧的交点为R(﹣1,0),则点A与R关于抛物线的对称轴对称,连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,即可求解;③四边形MNPD为菱形,首先PD=MN,即(﹣2x2+2x+4)﹣(﹣2x+4)=,解得:x=或(舍去),故点P(,1),而PN==≠MN,即可求解;(2)分∠DBP为直角、∠BDP为直角两种情况,分别求解即可.【解析】(1)①函数的对称轴为:x=﹣=,故点M(,),当x=时,y=﹣2x+4=3,故点N(,3);②设抛物线与x轴左侧的交点为R(﹣1,0),则点A与R关于抛物线的对称轴对称,连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,将R、B的坐标代入一次函数表达式:y=kx+b并解得:直线RB的表达式为:y=4x+4,当x=时,y=6,故点Q(,6);③不存在,理由:设点P(x,﹣2x+4),则点D(x,﹣2x2+2x+4),MN=﹣3=,四边形MNPD为菱形,首先PD=MN,即(﹣2x2+2x+4)﹣(﹣2x+4)=,解得:x=或(舍去),故点P(,1),而PN==≠MN,故不存在点P,使四边形MNPD为菱形;(2)当点P的横坐标为1时,则其坐标为:(1,2),此时点A、B的坐标分别为:(2,0)、(0,4),①当∠DBP为直角时,以B、P、D为顶点的三角形与△AOB相似,则∠BAO=∠BDP=α,tan∠BAO==2=tanα,则sinα=,PA=,PB=AB﹣PA=2﹣=,则PD==,故点D(1,);②当∠BDP为直角时,以B、P、D为顶点的三角形与△AOB相似,则BD∥x轴,则点B、D关于抛物线的对称轴对称,故点D(1,4),综上,点D的坐标为:(1,4)或(1,),将点A、B、D的坐标代入抛物线表达式:y=ax2+bx+c并解得:y=﹣2x2+2x+4或y=﹣x2+3x+4.6.(2022•禹城市模拟)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.(1)求出抛物线的解析式;(2)P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M 为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;=S△ABC,直接写出点D (3)若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得S△DCA的坐标.。
初中数学中考复习——二次函数相似三角形

AD AB
1 3
,AE=2cm,
1.如图,△ABC中,AB>AC,D、E两点 分别在边AC,AB上,且DE与BC 不平行. 请填上一个你认为合适的条件,使
△ADE∽△ABC:∠1=∠B 或∠2=∠C .
2.如图,下列条件不能判断△ADB∽△ABC 的是( D )
A.∠ABD=∠ACB B.AB2=AD﹒AC C.∠ADB=∠ABC D. AD DB
ABE =CBE
Q BC CD ,CDE CBE ABE 又Q AEB CED ,VAEB : VCED
(2)解 :Q BC 4, CD 4
QVቤተ መጻሕፍቲ ባይዱEB : VCED
CE CD 即CE 4
AE AB
12
CE 2
5.如图,D是△ABC 的AB边上一点,连结
DC,且 AC2 AB • ,AD△ADC与△ACB
(一)平行线分线段成比例定理
1.两条直线被一组平行线所截,所得的 对应线段 成比例 .
2.平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段 _成__比__例__.
如图,AB∥CD∥EF,AF与BE相交于
点G,且AG=2,GD=1,DF=5,求
BC CE
的值=_3_:_5_____.
Rt△DCE的面积为S3,则S1 = S2+S3(用
“>”、“=”、“<”填空);
(2)写出图中的三对相似三角形,并选择其中一
对进行证明.
解:(2)图中的三对相似三角形 △BCD∽△CFB △BCD∽△DEC △DEC∽△CFB
证明:∵四边形ABCD、BFED是矩形 ∴∠F=∠BCD,BD∥EF
∴∠DBC=∠BCF ∴△BCD∽△CFB
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案

中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数中的相似三角形
例1(2011绵阳):已知抛物线y = x2 -2x +m -1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B.
(1)求m的值;
(2)过A作x轴的平行线,交抛物线于点C,求证△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线C’,且与x轴的左半轴交于E点,与y轴交于F点。
如图,请在抛物线C’上求点P,使得△EFP是以EF为直角边的直角三角形.
例1图例1(1)(2)图例1(3)图
例2:如图,抛物线y = ax2 +bx + 1与x轴交于两点A(-1,0)、B(1,0)与y轴交于点C.(1)求抛物线的解析式;
(2)过点B作BD∥CA与抛物线交于点D,求四边形ACBD的面积;
(3)在x轴下方的抛物线上是否存在点M,过M作MN⊥x轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由.
例2(1)(2)图例2(3)图
例3:已知,如图,二次函数y = ax2 - 2ax + c(a ≠ 0)的图象与y轴交于点C(0,4),与x 轴交于点A、B,点A的坐标为(4,0).
(1)求该二次函数的关系式并写出它的对称轴和顶点坐标;
(2)点Q是线段AB上的动点,过点Q作QE∥AC交BC于点E,连接CQ,当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标(2,0).问:是否存在这样的直线l.使△ODF是等腰三角形?若存在,请求出点P坐标;若不存在,请说明理由.
思考:在(1)中抛物线的对称轴上是否存在点M,使△BCM是直角三角形?若存在,请直接写出点M坐标;若不存在,请说明理由.
例3(1)(2)图例3(3)图
例3思考。
