《相遇问题》PPT课件青岛版小学数学
合集下载
课件PPT《相遇问题》

03
04
我已经掌握了相遇问题的基本 概念和公式,能够解决简单的 相遇问题。
我已经掌握了相遇问题的基本 概念和公式,能够解决简单的 相遇问题。
我已经掌握了相遇问题的基本 概念和公式,能够解决简单的 相遇问题。
我已经掌握了相遇问题的基本 概念和公式,能够解决简单的 相遇问题。
预告下节课内容
下节课我们将学习追及问题,探讨两 个物体在同一路线上同向而行,速度 快的物体追上速度慢的物体的问题。
解决这类问题通常需要综合运 用速度叠加原理、相遇时间计 算公式以及逻辑推理等方法。
通过分析问题的本质和建立数 学模型,可以逐步推导出问题 的答案。
05
火车过桥与错车中的相遇问题
火车过桥时间计算
桥长+车长=速度×时间 (桥长+车长)÷速度=时间
(桥长+车长)÷时间=速度
两列火车错车时间计算
(甲车长+乙车长)÷速度和=错车时间 速度和×错车时间=甲车长+乙车长
顺流而下与逆流而上相遇时间计算
当两个物体在同向流动的水中 相遇时,顺流而下的物体会比 逆流而上的物体更快地相遇。
相遇时间可以通过以下公式计 算:相遇时间 = 路程和 / (顺 流速度 + 逆流速度)。
其中,顺流速度 = 船速 + 水 速,逆流速度 = 船速 - 水速。
复杂流水行船相遇问题解析
在复杂的流水行船相遇问题中, 可能需要考虑多个物体的速度、 水流速度以及它们之间的相对 位置等因素。
02
直线相遇问题
同向而行求相遇时间
02
01
03
速度差×相遇时间=路程差 路程差÷速度差=相遇时间 路程差÷相遇时间=速度差
相向而行求路程和
2023年青岛版数学四年级上册16相遇问题优选课件
西
东
(140 + 150)×5 = 290 × 5 = 1450(米)
?米 140 ×5 + 150×5 = 700 + 750 = 1450(米)
答:两个工程队一共铺设管道 1450 米。 返回
两队分别从两头同时施工,8个月开通。这条隧道长多少米?
150×8 + 120×8 = 1200+960 = 2160(米)
大货车平均每小 时行驶65千米。
小货车平均每小 时行驶75千米。
?千米
返回
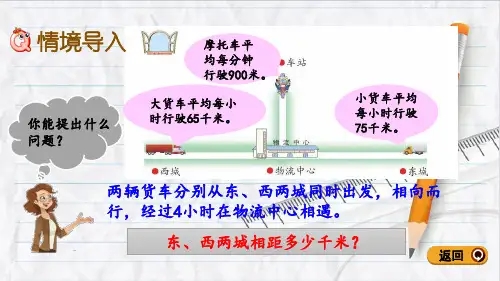
两辆货车分别从东、西两城同时出发,相向而行, 经过4小时在物流中心相遇,大货车平均每小时行 驶65千米。小货车平均每小时行驶75千米。东、 西两城相距多少千米?
每小时65千米
4小时相遇
每小时75千米
?千米
返回
两辆货车分别从东、西两城同时出发,相向而行,经过4小 时在物流中心相遇,大货车平均每小时行驶65千米。小货车 平均每小时行驶75千米。东、西两城相距多少千米?
(150 + 120)×8 = 270 × 8 = 2160(米)
答:这条隧道长2160米。
返回
两人同时打印一份稿件,甲的打字速度是80字/分,乙的 打字速度是65字/分。甲1小时比乙多录入多少个字?
80×60 - 65×60 = 4800-3900 = 900(个)
(80 - 65)×60 = 15 × 60 = 900(个)
?千米
110 ×5 + 100×5 = 550 + 500 = 1050(千米)
答:东、西两地相距1050千米。
返回
甲、乙两个工程队从同一地点分别向东、西两个方向铺设
管道。甲队每天铺设管道140米,乙队每天铺设管道150米。
2016-2017年新青岛版数学四年级上册相遇问题(公开课课件)

解决问题
同时、相对 相距、相遇
小丽和小明两人同时从东、西两地相对出发,
小明每分钟走 100 米,小丽每分钟走 50 米,4分 钟后两人相遇,请问东、西两地相距多少米?
100米
100米
100米
100米
50米 50米 50米 50米
பைடு நூலகம்
两列火车同时从甲、乙两站 向对 开出,客车每小时行60千米,
货车每小时行50千米,经过5小时 后两车相遇,甲、乙两站相距多
思考题:
小军与小华从同一地点背向而行,小军每 分钟走120米,小华每分钟走80米,5分钟后 两人都走到了家,请问小军与小华两人的家 相距多少米?
回忆你这节课有什么收获?
少千米?
五(一)班举办联欢会,装饰展
示栏,分配小红和小丽两名同学折纸鹤, 小亮折彩色纸花,小红平均每小时折20只
纸鹤,小丽平均每小时折25只纸鹤,小亮
平均每小时折18朵彩色纸花。 请问2小时后他们两个同学共折纸鹤多 少只?
思考题:
甲、乙两辆车同时从A、B两地相对开出, 已知甲车每小时行驶45千米,乙车每小时行 驶50千米,3小时后两车正好相距90千米。AB 两地之间距离多少千米?
同时、相对 相距、相遇
小丽和小明两人同时从东、西两地相对出发,
小明每分钟走 100 米,小丽每分钟走 50 米,4分 钟后两人相遇,请问东、西两地相距多少米?
100米
100米
100米
100米
50米 50米 50米 50米
பைடு நூலகம்
两列火车同时从甲、乙两站 向对 开出,客车每小时行60千米,
货车每小时行50千米,经过5小时 后两车相遇,甲、乙两站相距多
思考题:
小军与小华从同一地点背向而行,小军每 分钟走120米,小华每分钟走80米,5分钟后 两人都走到了家,请问小军与小华两人的家 相距多少米?
回忆你这节课有什么收获?
少千米?
五(一)班举办联欢会,装饰展
示栏,分配小红和小丽两名同学折纸鹤, 小亮折彩色纸花,小红平均每小时折20只
纸鹤,小丽平均每小时折25只纸鹤,小亮
平均每小时折18朵彩色纸花。 请问2小时后他们两个同学共折纸鹤多 少只?
思考题:
甲、乙两辆车同时从A、B两地相对开出, 已知甲车每小时行驶45千米,乙车每小时行 驶50千米,3小时后两车正好相距90千米。AB 两地之间距离多少千米?
青岛版数学六年级上册比例法解决相遇问题(课件)

3.甲、乙两人同时从A、B两地出发相向而行,甲的速度是乙的速度的1.5 倍,到达对方的出发点后立刻返回,如果第一次相遇点和第二次相遇点相 距40千米,那么A、B两地相距多少千米?
4.甲、乙两车同时从A地开往B地,甲车到达B地后立即返回在离B地45千 米处与乙车相遇。甲乙两车的速度比是3:2,求AB两地相距多少千米?
课后练习
1.A、B两地之间有一条公路,大客车从A到B需要6小时,小客车要4小时。 两车同时从A、B两地出发相向而行,在离中点24千米的地方相遇,求A、 B两地的距离。
2.甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,丙每分钟走80米, 甲、乙从A、丙从B同时出发相向而行,丙遇到乙后,经过10分钟遇到了 甲,求A、B之间的距离。
60米和50米,甲从B地,乙和丙从A地同时出发相向而行, 途中甲遇到乙后10分钟又遇到丙,求A、B两地的距离。
(四)两人多次相遇问题
相遇1次,两人走的路程和为1个全程;
相遇2次,两人走的路程和为3个全程;
相遇3次,两人走的路程和为5个全程;
相遇4次,两人走的路程和为7个全程;
……,
……;
相遇N次,两人走的路程和为2N-1个全程。
练习2:快车、慢车分别从A、B两地,同时出发,相向
而行。已知快车、慢车的速度比是5:4,相遇时距两地的 中点24千米。相遇后,两车继续前行,当慢车行驶到两 地中点时,快车行驶了多少千米?
(三)多人相遇问题
例题4:甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,
丙每分钟走80米,甲、乙从A、丙从B同时出发相向而行,丙遇 到乙后,经过10分钟遇到了甲,求A、B之间的距离。
例题5:甲、乙两人同时从A、B两地出发相向而行,甲的速度
(五上)数学PPT课件-4.4 解决问题——相遇问题 ︳青岛版 (16张)

解:设孙老师平均每分钟划x米。
450×7+7x=5600 3150+7x=5600 7x=5600-3150 x=2450÷7 x=350
答:孙老师平均每分钟划350米。
孙老师和胡老师同时从桃花源出发回澧县,孙 老师坐大巴,胡老师开车,经过1.5小时后,孙 老师落后胡老师15千米,孙老师坐大巴每小时 行70千米,胡老师每小时行多少千米?
方法一: 0.25x+3.6x=38.5 方法二:(0.25+3.6)x=38.5
3.85x=38.5
3.85x答:大约8:30胡老师能接到孙老师。
孙老师在桃花溪泛舟,遇到了相向而行的胡 老师,我们的出发点之间大约相距5600米, 过了7分钟相遇,胡老师平均每分钟划450米, 孙老师平均每分钟划多少米?
•
2.但与此同时,诗歌批评庸俗化的趋 势越来 越明显 ,不少 诗歌批 评为了 应酬需 要,违 心而作 ,学术 含量可 疑,甚 至堕落 为诗人 小圈子 里击鼓 传花的 游戏道 具。这 类批评 对诗歌 创作来 说类同 饮鸩止 渴,还 不如索 性没有 的好。
•
3.批评文章却写得天花乱坠,一再上 演“皇 帝的新 衣”闹 剧。这 些批评 牵强附 会、肆 意升华 ,外延 无限扩 张,乃 至另起 炉灶, 使批评 成为原 创式的 畅想, 早已失 去了与 原作品 的联系 。
亲爱的同学们,再见!
•
4.评庸俗化表现为概念代替文本,行 为代替 写作。 较之个 体性的 埋头创 作,不 少诗人 似乎更 喜欢混 个脸熟 ,在这 样的背 景和语 境下, 诗歌批 评基本 沦为诗 人间的 交际和 应酬。 哪怕是 纷纷攘 攘的流 派或主 义之争 ,也往 往是你 方唱罢 我登场 ,名目 噱头不 少,却 未见得 与文学 和读者 有何关 系。
450×7+7x=5600 3150+7x=5600 7x=5600-3150 x=2450÷7 x=350
答:孙老师平均每分钟划350米。
孙老师和胡老师同时从桃花源出发回澧县,孙 老师坐大巴,胡老师开车,经过1.5小时后,孙 老师落后胡老师15千米,孙老师坐大巴每小时 行70千米,胡老师每小时行多少千米?
方法一: 0.25x+3.6x=38.5 方法二:(0.25+3.6)x=38.5
3.85x=38.5
3.85x答:大约8:30胡老师能接到孙老师。
孙老师在桃花溪泛舟,遇到了相向而行的胡 老师,我们的出发点之间大约相距5600米, 过了7分钟相遇,胡老师平均每分钟划450米, 孙老师平均每分钟划多少米?
•
2.但与此同时,诗歌批评庸俗化的趋 势越来 越明显 ,不少 诗歌批 评为了 应酬需 要,违 心而作 ,学术 含量可 疑,甚 至堕落 为诗人 小圈子 里击鼓 传花的 游戏道 具。这 类批评 对诗歌 创作来 说类同 饮鸩止 渴,还 不如索 性没有 的好。
•
3.批评文章却写得天花乱坠,一再上 演“皇 帝的新 衣”闹 剧。这 些批评 牵强附 会、肆 意升华 ,外延 无限扩 张,乃 至另起 炉灶, 使批评 成为原 创式的 畅想, 早已失 去了与 原作品 的联系 。
亲爱的同学们,再见!
•
4.评庸俗化表现为概念代替文本,行 为代替 写作。 较之个 体性的 埋头创 作,不 少诗人 似乎更 喜欢混 个脸熟 ,在这 样的背 景和语 境下, 诗歌批 评基本 沦为诗 人间的 交际和 应酬。 哪怕是 纷纷攘 攘的流 派或主 义之争 ,也往 往是你 方唱罢 我登场 ,名目 噱头不 少,却 未见得 与文学 和读者 有何关 系。
完整版《相遇问题》PPT之一.ppt

60千米
50千米
甲地
乙地
8
精品文档
救护车和小轿车同时从甲乙两地相对开出, 救护车每小时行驶60千米,小轿车每小时行 驶50千米,经过4小时相遇甲乙两地相距多少 千米?
60千米
50千米
甲地
乙地
9
精品文档
救护车和小轿车同时从甲乙两地相对开出, 救护车每小时行驶60千米,小轿车每小时行 驶50千米,经过4小时相遇甲乙两地相距多少 千米?
60千米
50千米
甲地
乙地
10
精品文档
救护车和小轿车同时从甲乙两地相对开出, 救护车每小时行驶60千米,小轿车每小时行 驶50千米,经过4小时相遇甲乙两地相距多少 千米?
60千米
50千米
甲地
乙地
11
精品文档
救护车和小轿车同时从甲乙两地相对开出, 救护车每小时行驶60千米,小轿车每小时行 驶50千米,经过4小时相遇甲乙两地相距多少 千米?
60千米
50千米
甲地
乙地
14
精品文档
救护车和小轿车同时从甲乙两地相对开出, 救护车每小时行驶60千米,小轿车每小时行 驶50千米,经过4小时相遇甲乙两地相距多少 千米?
60千米
50千米
甲地
乙地
15
精品文档
救护车和小轿车同时从甲乙两地相对开出, 救护车每小时行驶60千米,小轿车每小时行 驶50千米,经过4小时相遇甲乙两地相距多少 千米?
60千米
50千米
甲地
乙地
28
精品文档
救护车和小轿车同时从甲乙两地相对开出, 救护车每小时行驶60千米,小轿车每小时行 驶50千米,经过4小时相遇甲乙两地相距多少 千米?
2017新青岛版四年级上册-快捷的物流运输-相遇问题.ppt
路程
7200(米)
每小时行驶的千米数×行驶时间 = 65 × 4 =
路程
260(千米)
路程和距离的区别
• 距离
距离
路程
每分钟行驶的米数× 900 ×
时间
8
= = = =
路程
7200(米)
每小时行驶的千米数× 65 ×
时间
4
路程
260(千米)
速度 × 时间
900 × 8
= = = =
路程
7200(米)
东城
你能用线段图整理条件和问题吗?
两辆货车分别从东、西两城同时出发,相向而行,经过4小 时在物流中心相遇。东、西两城相距多少千米?
每小时65千米 西城 物流中心 ?千米 4小时相遇 每小时75千米 东城
路程和
速度和
总结
大货车平均每小 时行驶65千米。 小货车平均每小 时行驶75千米。
模拟演示
同时出发 相向而行, 两辆货车分别从东、西两城 同时出发、 经过4小时在物流中心相遇. 东、西两城相距多少千米?
大货车平均每小 每小时65千米 时行驶65千米。 小货车平均每小 每小时75 75 千米 时行驶 千米。
西城
物流中心 ?千米
摩托车平均 每分钟行驶 900米。 大货车平均 每小时行驶 65千米。 小货车平均 每小时行驶 75千米。
车站到物流中心相距 多少米? 西城与物流中心相距 多少千米?东城呢? 东、西两城相距多少 千米?
●摩托车从车站出发经过8分钟到达物流中心。 ●两辆货车分别从东、西两城同时出发,相向 而行,经过4小时在物流中心相遇。
小强和小丽同时从自己家里出发,向对方走去。 小强每分走65米,小丽每分走50米。经过4分,两人 相遇。他们两家相距多少米?
青岛版小学数学《相遇问题》课件
西城 物流中心 ?千米 东城
65+75
65+75
65+75
65+75
(65 + 75)× 4 = 140 × 4 = 560(千米)
返回
答:东、西两城相距560千米。
练习
70×6+60×6
(70+60)×6
练习
110 ×5 + 100×5
(110 + 100)×5
= 550 + 500 = 1050(千米)
相 遇 问 题
车站到物流中心相距 多少米?
东、西两城相距多少 西城与物流中心相距多 千米? 少千米?
东城与物流中心相距 多少千米?
东、西两城相距多少 千米?
两辆货车分别从东、西 两城 同时出发 , 相向而行, 经过4小时在物流中心相遇 。 东、西两城相距多少千米?
两辆货车分别从东、西两城同时出发,相向而行,大货车平 均每小时行驶65千米,小货车平均每小时行驶75千米,经过 4小时在物流中心相遇。 东、西两城相距多少千米?
两工程队共同修一段路 两个人共同打字 两个人共同做一批零件 ……
实际问题
建立模型
模型应用Βιβλιοθήκη = 210 × 5 = 1050(千米)
答:东、西两地相距 1050 千米。
练习
150×8+120×8
(150+120)×8
练习
90×35+110×35
(90+110)×35
路程① + 路程②=总路程 速度和 × 相遇时间=总路程
两个人共同走一段路 两辆汽车共同开一段路 两列火车 两艘船 ……
65千米/时 物流中心 西城 ?千米 东城 75千米/时
65+75
65+75
65+75
65+75
(65 + 75)× 4 = 140 × 4 = 560(千米)
返回
答:东、西两城相距560千米。
练习
70×6+60×6
(70+60)×6
练习
110 ×5 + 100×5
(110 + 100)×5
= 550 + 500 = 1050(千米)
相 遇 问 题
车站到物流中心相距 多少米?
东、西两城相距多少 西城与物流中心相距多 千米? 少千米?
东城与物流中心相距 多少千米?
东、西两城相距多少 千米?
两辆货车分别从东、西 两城 同时出发 , 相向而行, 经过4小时在物流中心相遇 。 东、西两城相距多少千米?
两辆货车分别从东、西两城同时出发,相向而行,大货车平 均每小时行驶65千米,小货车平均每小时行驶75千米,经过 4小时在物流中心相遇。 东、西两城相距多少千米?
两工程队共同修一段路 两个人共同打字 两个人共同做一批零件 ……
实际问题
建立模型
模型应用Βιβλιοθήκη = 210 × 5 = 1050(千米)
答:东、西两地相距 1050 千米。
练习
150×8+120×8
(150+120)×8
练习
90×35+110×35
(90+110)×35
路程① + 路程②=总路程 速度和 × 相遇时间=总路程
两个人共同走一段路 两辆汽车共同开一段路 两列火车 两艘船 ……
65千米/时 物流中心 西城 ?千米 东城 75千米/时
《相遇问题》教学PPT
(2)挖一条长165米的隧道,由甲、乙两个工程队从两端同时施工。甲队每天 向前挖6米,乙队每天向前挖5米。挖通这条隧道需要多少天?
解:挖通这条隧道需要x天。 6x+5x=165
(3)要录入一份5700字的文件,由于时间紧急,安排甲、乙两名打字员同时 开始录入。甲每分录入100个字,乙每分录入90个字,录完这份文件需要用多
长时间;90x=5700
例、如图:A、B两人在周长是400米的环形跑道上 跑步,如果两人从同一地点出发背向而行,已知A每 分钟行30米/分,B每分行20米/分.问多少分钟后他俩 第一次相遇?
B A
解:速度和:30+20=50(米/分)
400÷50=8(分钟) 答:8分钟后他俩第一次相遇。
50÷100=0.5(时) 路程÷速度(和)=时间 答:他们出发后0.5小时相遇,
一、只列式不计算
(1)北京和呼和浩特相距660千米。一列火车从呼和浩特开出,每时行驶 48千米;另一列火车从北京开出,每时行驶72千米。两列火车同时开出,相向 而行,经过几时相遇?
解:解设x小时两车相遇 48x+72x=660
+ = 小张行驶的 路程
小王行驶的 路程
总路程
速40度× x
速60度× x
50千米
小张用的时间=小王用的时间
小张 40千米/时
相遇点
小王 60千米/时
+ = 小张行驶的
小王行驶的
路程
解:设x小时相遇.
路程
总路程
40x + 60x
100 x x
=50
=50 =0.5
答:他们出发后0.5小时相遇。
方法二: 60+40=100(千米) 两人1小时行的路程,即两人的速度和
解:挖通这条隧道需要x天。 6x+5x=165
(3)要录入一份5700字的文件,由于时间紧急,安排甲、乙两名打字员同时 开始录入。甲每分录入100个字,乙每分录入90个字,录完这份文件需要用多
长时间;90x=5700
例、如图:A、B两人在周长是400米的环形跑道上 跑步,如果两人从同一地点出发背向而行,已知A每 分钟行30米/分,B每分行20米/分.问多少分钟后他俩 第一次相遇?
B A
解:速度和:30+20=50(米/分)
400÷50=8(分钟) 答:8分钟后他俩第一次相遇。
50÷100=0.5(时) 路程÷速度(和)=时间 答:他们出发后0.5小时相遇,
一、只列式不计算
(1)北京和呼和浩特相距660千米。一列火车从呼和浩特开出,每时行驶 48千米;另一列火车从北京开出,每时行驶72千米。两列火车同时开出,相向 而行,经过几时相遇?
解:解设x小时两车相遇 48x+72x=660
+ = 小张行驶的 路程
小王行驶的 路程
总路程
速40度× x
速60度× x
50千米
小张用的时间=小王用的时间
小张 40千米/时
相遇点
小王 60千米/时
+ = 小张行驶的
小王行驶的
路程
解:设x小时相遇.
路程
总路程
40x + 60x
100 x x
=50
=50 =0.5
答:他们出发后0.5小时相遇。
方法二: 60+40=100(千米) 两人1小时行的路程,即两人的速度和
《相遇问题》课件ppt
多个物体在不同时间、不同方向相遇:需要综合考虑时间 和空间因素,建立更为复杂的数学模型。
三维空间中的相遇问题
物体在三维空间中相遇,需要考虑垂直和水平方向的距离:需要使用三维坐标系 和向 Nhomakorabea计算方法。
考虑空气阻力、重力等因素:三维空间中物体的运动还受到重力和空气阻力的影 响,因此需要综合考虑这些因素。
物理方法
总结词
利用物理学的原理和方法来求解相遇问题
详细描述
物理方法通常涉及到速度、加速度等物理概念。通过对物体的运动过程进行分析 ,建立相关的物理方程,从而求解相遇问题。在某些情况下,还可以使用动能定 理、动量定理等物理定理来简化问题的求解
03
相遇问题的实际应用
追及问题
总结词
在直线运动中,两人或多个物体同时从不同位置出发,在相 对运动中不断靠近或远离的问题。
总结词
在环形的跑道上,多个人或物体同时从不同位置出发,不断追逐相遇的问题。
详细描述
环型跑道问题需要考虑不同方向上的相对运动,需要分析每圈运动中各物体的相 对位置和速度变化,列出方程求解。
火车相遇问题
总结词
两列火车同时从不同的火车站出发,在相对运动中相遇的问 题。
详细描述
火车相遇问题需要考虑火车自身的长度和速度,同时还需要 考虑两列火车相对速度的变化。需要分析运动过程,列出方 程求解。
解决方法和思路
解析法
通过对相遇问题的数学模型进行解析,得出解决问题的公式和方法。
综合法
通过画图、分析运动过程、找出等量关系等方法,综合解决相遇问题。
经典例题解析
两辆汽车相向而行,在一条直线上,已知两车之间的距离和 两车行驶的速度,求两车相遇的时间。
两艘船同时出发,相向而行,在一条直线上,已知两船之间 的距离和两船行驶的速度,求两船相遇的时间和相遇的位置 。
三维空间中的相遇问题
物体在三维空间中相遇,需要考虑垂直和水平方向的距离:需要使用三维坐标系 和向 Nhomakorabea计算方法。
考虑空气阻力、重力等因素:三维空间中物体的运动还受到重力和空气阻力的影 响,因此需要综合考虑这些因素。
物理方法
总结词
利用物理学的原理和方法来求解相遇问题
详细描述
物理方法通常涉及到速度、加速度等物理概念。通过对物体的运动过程进行分析 ,建立相关的物理方程,从而求解相遇问题。在某些情况下,还可以使用动能定 理、动量定理等物理定理来简化问题的求解
03
相遇问题的实际应用
追及问题
总结词
在直线运动中,两人或多个物体同时从不同位置出发,在相 对运动中不断靠近或远离的问题。
总结词
在环形的跑道上,多个人或物体同时从不同位置出发,不断追逐相遇的问题。
详细描述
环型跑道问题需要考虑不同方向上的相对运动,需要分析每圈运动中各物体的相 对位置和速度变化,列出方程求解。
火车相遇问题
总结词
两列火车同时从不同的火车站出发,在相对运动中相遇的问 题。
详细描述
火车相遇问题需要考虑火车自身的长度和速度,同时还需要 考虑两列火车相对速度的变化。需要分析运动过程,列出方 程求解。
解决方法和思路
解析法
通过对相遇问题的数学模型进行解析,得出解决问题的公式和方法。
综合法
通过画图、分析运动过程、找出等量关系等方法,综合解决相遇问题。
经典例题解析
两辆汽车相向而行,在一条直线上,已知两车之间的距离和 两车行驶的速度,求两车相遇的时间。
两艘船同时出发,相向而行,在一条直线上,已知两船之间 的距离和两船行驶的速度,求两船相遇的时间和相遇的位置 。
