基本不等式(完整版)
基本不等式全部公式

基本不等式全部公式1.三角不等式:对于任意实数a和b,有,a+b,≤,a,+,b2. Cauchy-Schwarz 不等式:对于任意实数 a1, a2,...,an 和 b1, b2,...,bn,有(a1b1 + a2b2 + ... + anbn)² ≤ (a₁² + a₂² + ... + an²)(b₁² + b₂² + ... + bn²)3. 二次平均不等式:对于任意非负实数 x1, x2,...,xn,有√((x₁² + x₂² + ... + xn²)/n) ≥ ((x₁ + x₂ + ... + xn)/n)4. 广义平均不等式:对于任意非负实数 x1, x2,...,xn 和实数 p ≠ 0,有(x₁ᵖ + x₂ᵖ + ... + xnᵖ)/n ≥ ((x₁ + x₂ + ... + xn)/n)ᵖ5. AM-GM 不等式:对于任意非负实数 x₁, x₂,...,xn,有(x₁x₂...xn)^(1/n) ≤ (x₁ + x₂ + ... + xn)/n6. Jensen 不等式:设 f 是凸函数,则对于非负实数 x₁, x₂, (x)和非负实数权重 w₁, w₂,...,wn,有f(w₁x₁ + w₂x₂ + ... + wnxn) ≥ w₁f(x₁) + w₂f(x₂) + ... +wnfn(xn)7. Hessemberg 不等式:对于非负实数 x₁, x₂,...,xn,有(x₁ + t)ⁿ ≤ x₁ⁿ + nx₁ⁿ⁻¹t + n(n-1)x₁ⁿ⁻²t²/2 + ... + tⁿ8. Bernoulli 不等式:对于实数x ≥ -1 和正整数 n,有(1+x)ⁿ ≥ 1 + nx9. Muirhead 不等式:对于非负实数 a₁, a₂,...,an 和 b₁,b₂,...,bn 满足 a₁ + a₂ + ... + an = b₁ + b₂ + ... + bn,有a₁ᵖ₁a₂ᵖ₂...anᵖₙ + permutations ≥ b₁ᵖ₁b₂ᵖ₂...bnᵖₙ + permutations10. 反柯西不等式:对于任意非负实数 a₁, a₂,...,an,有(a₁/a₂ + a₂/a₃ + ... + an-₁/an + an/a₁) ≥ n以上是一些常见的基本不等式公式。
最新基本不等式完整版(非常全面)

基本不等式专题辅导一、知识点总结1、基本不等式原始形式(1)若R b a ∈,,则ab b a 222≥+(2)若R b a ∈,,则222b a ab +≤2、基本不等式一般形式(均值不等式)若*,R b a ∈,则ab b a 2≥+3、基本不等式的两个重要变形 (1)若*,R b a ∈,则ab ba ≥+2(2)若*,R b a ∈,则22⎪⎭⎫ ⎝⎛+≤b a ab总结:当两个正数的积为定植时,它们的和有最小值;当两个正数的和为定植时,它们的积有最小值;特别说明:以上不等式中,当且仅当b a =时取“=”4、求最值的条件:“一正,二定,三相等”5、常用结论 (1)若0x >,则12x x+≥ (当且仅当1x =时取“=”) (2)若0x <,则12x x+≤- (当且仅当1x =-时取“=”) (3)若0>ab ,则2≥+ab b a (当且仅当b a =时取“=”)(4)若R b a ∈,,则2)2(222b a b a ab +≤+≤ (5)若*,R b a ∈,则2211122b a b a ab ba +≤+≤≤+特别说明:以上不等式中,当且仅当b a =时取“=” 6、柯西不等式(1)若,,,a b c d R ∈,则22222()()()a b c d ac bd ++≥+ (2)若123123,,,,,a a a b b b R ∈,则有:22222221231123112233()()()a a a b b b a b a b a b ++++≥++(3)设1212,,,,,,n n a a a b b ⋅⋅⋅⋅⋅⋅与b 是两组实数,则有 222(a a a ++⋅⋅⋅+)222)b b b ++⋅⋅⋅+(2()a b a b a b ≥++⋅⋅⋅+二、题型分析题型一:利用基本不等式证明不等式1、设b a ,均为正数,证明不等式:ab ≥ba 112+2、已知cb a ,,为两两不相等的实数,求证:ca bc ab c b a ++>++2223、已知1a b c ++=,求证:22213a b c ++≥ 4、已知,,a b c R+∈,且1a b c ++=,求证:abc c b a 8)1)(1)(1(≥---5、已知,,a b c R+∈,且1a b c ++=,求证:1111118a b c ⎛⎫⎛⎫⎛⎫---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭6、(2013年新课标Ⅱ卷数学(理)选修4—5:不等式选讲 设,,a b c 均为正数,且1a b c ++=,证明:(Ⅰ)13ab bc ca ++≤; (Ⅱ)2221a b c b c a++≥.7、(2013年江苏卷(数学)选修4—5:不等式选讲 已知0>≥b a ,求证:b a ab b a 223322-≥-题型二:利用不等式求函数值域1、求下列函数的值域 (1)22213x x y += (2))4(x x y -=(3))0(1>+=x x x y (4))0(1<+=x xx y题型三:利用不等式求最值 (一)(凑项)1、已知2>x ,求函数42442-+-=x x y 的最小值;变式1:已知2>x ,求函数4242-+=x x y 的最小值;变式2:已知2<x ,求函数4242-+=x x y 的最大值;练习:1、已知54x >,求函数14245y x x =-+-的最小值;2、已知54x <,求函数14245y x x =-+-的最大值;题型四:利用不等式求最值 (二)(凑系数)1、当时,求(82)y x x =-的最大值;变式1:当时,求4(82)y x x =-的最大值;变式2:设230<<x ,求函数)23(4x x y -=的最大值。
基本不等式完整版

基本不等式完整版一、知识点总结1.基本不等式原始形式:若 $a,b\in\mathbb{R}$,则 $a^2+b^2\geq 2ab$。
2.基本不等式一般形式(均值不等式):若 $a,b\in\mathbb{R^*}$,则 $a+b\geq 2\sqrt{ab}$。
3.基本不等式的两个重要变形:1)若 $a,b\in\mathbb{R^*}$,则 $\frac{a+b}{2}\geq \sqrt{ab}$。
2)若 $a,b\in\mathbb{R^*}$,则 $ab\leq\left(\frac{a+b}{2}\right)^2$。
总结:当两个正数的积为定值时,它们的和有最小值;当两个正数的和为定值时,它们的积有最小值。
特别说明:以上不等式中,当且仅当 $a=b$ 时取“=”。
4.求最值的条件:“一正,二定,三相等”。
5.常用结论:1)若 $x>0$,则 $x+\frac{1}{x}\geq 2$(当且仅当$x=1$ 时取“=”)。
2)若 $x<0$,则 $x+\frac{1}{x}\leq -2$(当且仅当 $x=-1$ 时取“=”)。
3)若 $a,b>0$,则 $\frac{a}{b}+\frac{b}{a}\geq 2$(当且仅当 $a=b$ 时取“=”)。
4)若 $a,b>0$,则 $ab\leq \left(\frac{a+b}{2}\right)^2\leq \frac{a^2+b^2}{2}$。
5)若 $a,b\in\mathbb{R^*}$,则 $\frac{1}{a+b}\leq\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\leq\frac{1}{2}\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}$。
特别说明:以上不等式中,当且仅当 $a=b$ 时取“=”。
6.柯西不等式:1)若 $a,b,c,d\in\mathbb{R}$,则$(a^2+b^2)(c^2+d^2)\geq (ac+bd)^2$。
基本不等式完整版(非常全面)[整理]
![基本不等式完整版(非常全面)[整理]](https://img.taocdn.com/s3/m/9348b628cd1755270722192e453610661ed95ab5.png)
基本不等式完整版(非常全面)[整理]
基本不等式可以指几乎所有组成分析和数学的基础。
它可以使许多不同的数学问题变
得更容易理解,因此使用它们进行计算是极其重要的。
基本不等式包括了三类不等式:大
小不等式,加法不等式和乘法不等式。
以下是一些基本的不等式定义。
1、大小不等式:大小不等式表示一个数与另一个数之间的存在或缺失的关系。
例如,如果A > B,则表示A大于B,而A ≤ B表示A小于或等于B,A ≠ B表示A与B之间存
在某种不同。
2、加法不等式:加法不等式表示两个数相加时的结果。
例如,A + B > C的意思是A
与B的和大于C,A + B ≤ C的意思是A与B的和小于或等于C,A + B = C的意思是A
与B的和等于C。
一般地,一个数与另一个数之间的关系可以用不等式来表示,但也可以用不等式来表
示多个数之间的关系:
1、省略不等式:3x + 2y = 4z,这表示3x + 2y至少等于4z的意思。
基本不等式可以用来处理大量数学问题,比如解一元不等式、求函数的极值以及进行
多元函数分析等。
它们对于熟悉数学理论和解决数学问题都极其重要。
(完整版)基本不等式及其应用

基本不等式及其应用1.ab ≤a +b2(1)基本不等式成立的条件:a ≥0,b ≥0; (2)等号成立的条件:当且仅当a =b 时取等号.2.几个重要的不等式(1)a 2+b 2≥2ab (a ,b ∈R ); (2)b a +ab ≥2(a ,b 同号). (3)ab ≤⎝⎛⎭⎪⎫a +b 22(a ,b ∈R ); (4)a 2+b 22≥⎝ ⎛⎭⎪⎫a +b 22(a ,b ∈R ). 以上不等式等号成立的条件均为a =b .3.算术平均数与几何平均数(1)设a ≥0,b ≥0,则a ,b 的算术平均数为a +b2,几何平均数为ab .(2)基本不等式可叙述为两个非负数的算术平均数不小于它们的几何平均数;也可以叙述为两个正数的等差中项不小于它们正的等比中项.4.利用基本不等式求最值问题 已知x >0,y >0,则(1)若x +y =s (和为定值),则当x =y 时,积xy 取得最大值s 24; (2)若xy =p (积为定值),则当x =y 时,和x +y 取得最小值2p .选择题:设x >0,y >0,且x +y =18,则xy 的最大值为( )A .80B .77C .81D .82解析 ∵x >0,y >0,∴x +y 2≥xy ,即xy ≤(x +y2)2=81,当且仅当x =y =9时,(xy )max =81若正数x ,y 满足4x 2+9y 2+3xy =30,则xy 的最大值是( ) A.43 B.53 C .2 D.54解析 由x >0,y >0,得4x 2+9y 2+3xy ≥2·(2x )·(3y )+3xy (当且仅当2x =3y 时等号成立),∴12xy +3xy ≤30,即xy ≤2,∴xy 的最大值为2若2x +2y =1,则x +y 的取值范围是( )A .[0,2]B .[-2,0]C .[-2,+∞)D .(-∞,-2] 解析 22x +y ≤2x +2y =1,∴2x +y ≤14,即2x +y ≤2-2,∴x +y ≤-2若实数x ,y 满足xy >0,则x x +y +2yx +2y的最大值为( ) A .2- 2 B .2+ 2 C .4+2 2 D .4-2 2 解析x x +y+2y x +2y=x (x +2y )+2y (x +y )(x +y )(x +2y )=x 2+4xy +2y 2x 2+3xy +2y 2=1+xy x 2+3xy +2y 2=1+1x y +3+2y x≤1+13+2=4-22,当且仅当x y =2yx ,即x 2=2y 2时取等号若函数()f x =x +1x -2(x >2)在x =a 处取最小值,则a 等于( ) A .1+ 2 B .1+ 3 C .3 D .4 解析 当x >2时,x -2>0,f (x )=(x -2)+1x -2+2≥2(x -2)×1x -2+2=4,当且仅当x -2=1x -2(x >2),即x =3时取等号,即当f (x )取得最小值时,x =3,即a =3已知x ,y ∈(0,+∞),2x -3=(12)y ,若1x +my (m >0)的最小值为3,则m 等于( ) A .2 B .2 2 C .3 D .4解析 由2x -3=(12)y 得x +y =3,1x +m y =13(x +y )(1x +m y )=13(1+m +y x +mx y )≥13(1+m +2m ),(当且仅当y x =mx y 时取等号),∴13(1+m +2m )=3,解得m =4已知直线ax +by +c -1=0(b ,c >0)经过圆x 2+y 2-2y -5=0的圆心,则4b +1c 的最小值是( )A .9B .8C .4D .2解析 圆x 2+y 2-2y -5=0化成标准方程,得x 2+(y -1)2=6,∴圆心为C (0,1) ∵直线ax +by +c -1=0经过圆心C ,∴a ×0+b ×1+c -1=0,即b +c =1 ∴4b +1c =(b +c )(4b +1c )=4c b +b c +5 ∵b ,c >0,∴4c b +bc ≥24c b ·b c =4,当且仅当4c b =b c 时等号成立.由此可得b =2c ,且b +c =1,即b =23,c =13时,4b +1c 取得最小值9已知各项均为正数的等比数列{a n }满足a 7=a 6+2a 5,若存在两项a m ,a n 使得a m a n =4a 1,则1m +4n 的最小值为( )A.32B.53C.94D.256解析 由各项均为正数的等比数列{a n }满足a 7=a 6+2a 5,可得a 1q 6=a 1q 5+2a 1q 4, ∴q 2-q -2=0,解得q =2或q =-1(舍去)a m a n =4a 1,∴q m +n -2=16,∴2m +n -2=24,∴m +n =6 ∴1m +4n =16(m +n )(1m +4n )=16(5+n m +4m n )≥16(5+2n m ·4m n )=32当且仅当n m =4m n 时,等号成立,故1m +4n 的最小值等于32在等差数列{a n }中,a n >0,且a 1+a 2+…+a 10=30,则a 5a 6的最大值是( ) A .3 B .6 C .9 D .36解析 ∵a 1+a 2+…+a 10=30,∴5(a 1+a 10)=30,即a 1+a 10=a 5+a 6=6,∵a 5+a 6≥2a 5a 6,∴6≥2a 5a 6,即a 5a 6≤9,当且仅当a 5=a 6时取等号,∴a 5a 6的最大值为9若实数a ,b 满足1a +2b =ab ,则ab 的最小值为( )A.2 B .2 C .2 2 D .4 解析 依题意知a >0,b >0,则1a +2b ≥22ab =22ab,当且仅当1a =2b ,即b =2a 时,“=”成立.∵1a +2b =ab ,∴ab ≥22ab ,即ab ≥22,∴ab 的最小值为2 2已知a >0,b >0,a ,b 的等比中项是1,且m =b +1a ,n =a +1b ,则m +n 的最小值是( ) A .3 B .4 C .5 D .6解析 由题意知:ab =1,∴m =b +1a =2b ,n =a +1b =2a ,∴m +n =2(a +b )≥4ab =4若a ,b 都是正数,则⎝ ⎛⎭⎪⎫1+b a ·⎝ ⎛⎭⎪⎫1+4a b 的最小值为( ) A .7 B .8 C .9 D .10 解析 ∵a ,b 都是正数,∴⎝ ⎛⎭⎪⎫1+b a ⎝ ⎛⎭⎪⎫1+4a b =5+b a +4a b ≥5+2b a ·4ab =9,当且仅当b =2a >0时取等号已知a >0,b >0,若不等式3a +1b ≥ma +3b 恒成立,则m 的最大值为( )A .9B .12C .18D .24 解析 由3a +1b ≥m a +3b ,得m ≤(a +3b )(3a +1b )=9b a +ab +6又9b a +ab +6≥29+6=12,∴m ≤12,∴m 的最大值为12已知a >0,b >0,a +b =1a +1b ,则1a +2b 的最小值为( )A .4B .22C .8D .16 解析 由a >0,b >0,a +b =1a +1b =a +b ab ,得ab =1,则1a +2b ≥21a ·2b =2 2.当且仅当1a =2b ,即a =22,b 2时等号成立已知a >0,b >0,a +b =2,则y =1a +4b 的最小值是( ) A.72 B .4 C.92 D .5 解析 依题意,得1a +4b =12(1a +4b )·(a +b )=12[5+(b a +4a b )]≥12(5+2b a ·4a b )=92,当且仅当⎩⎪⎨⎪⎧a +b =2,b a =4ab ,a >0,b >0,即a =23,b =43时取等号,即1a +4b 的最小值是92若log 4(3a +4b )=log 2ab ,则a +b 的最小值是( )A .6+2 3B .7+2 3C .6+4 3D .7+4 3解析由题意得⎩⎪⎨⎪⎧ab >0,ab ≥0,3a +4b >0,∴⎩⎨⎧a >0,b >0.又log 4(3a +4b )=log 2ab ,∴log 4(3a +4b )=log 4ab ,∴3a +4b =ab ,故4a +3b =1. ∴a +b =(a +b )(4a +3b )=7+3a b +4ba ≥7+23ab ·4b a =7+43,当且仅当3a b =4b a 时取等号若正数a ,b 满足1a +1b =1,则1a -1+9b -1的最小值是( )A .1B .6C .9D .16解析 ∵正数a ,b 满足1a +1b =1,∴b =a a -1>0,解得a >1,同理可得b >1,∴1a -1+9b -1=1a -1+9a a -1-1=1a -1+9(a -1)≥21a -1·9(a -1)=6,当且仅当1a -1=9(a -1),即a =43时等号成立,∴最小值为6设()f x =ln x,0<a <b ,若p =f (ab ),q =f ⎝⎛⎭⎪⎫a +b 2,r =12(f (a )+f (b )),则下列关系式中正确的是( ) A .q =r <p B .q =r >p C .p =r <q D .p =r >q 解析 ∵0<a <b ,∴a +b2>ab ,又∵f (x )=ln x 在(0,+∞)上为增函数,故f ⎝⎛⎭⎪⎫a +b 2>f (ab ),即q >p .又r =12(f (a )+f (b ))=12(ln a +ln b )=12ln a +12ln b =ln(ab )12=f (ab )=p ,故p =r <q已知函数()f x =x +px -1(p 为常数,且p >0),若f (x )在(1,+∞)上的最小值为4,则实数p 的值为( ) A .1 B .2 C.94 D.74 解析 由题意得x -1>0,f (x )=x -1+px -1+1≥2p +1,当且仅当x =p +1时取等号, ∵f (x )在(1,+∞)上的最小值为4,∴2p +1=4,解得p =94填空题:已知x ,y ∈R +,且x +4y =1,则xy 的最大值为________解析 1=x +4y ≥24xy =4xy ,∴xy ≤(14)2=116,当且仅当x =4y =12,即⎩⎪⎨⎪⎧x =12y =18时,(xy )max =116已知实数m ,n 满足m ·n >0,m +n =-1,则1m +1n 的最大值为________解析 ∵m ·n >0,m +n =-1,∴m <0,n <0,∴1m +1n =-(m +n )⎝ ⎛⎭⎪⎫1m +1n =-⎝ ⎛⎭⎪⎫2+n m +m n ≤-2-2n m ·mn=-4,当且仅当m =n =-12时,1m +1n 取得最大值-4已知x <54,则()f x =4x -2+14x -5的最大值为________解析 ∵x <54,∴5-4x >0,则f (x )=4x -2+14x -5=-(5-4x +15-4x )+3≤-2+3=1.当且仅当5-4x =15-4x ,即x =1时,等号成立.故f (x )=4x -2+14x -5的最大值为1函数y =x 2+2x -1(x >1)的最小值为________解析 y =x 2+2x -1=(x 2-2x +1)+(2x -2)+3x -1=(x -1)2+2(x -1)+3x -1=(x -1)+3x -1+2≥23+2当且仅当(x -1)=3(x -1),即x =3+1时,等号成立函数y =x -1x +3+x -1的最大值为________解析 令t =x -1≥0,则x =t 2+1,∴y =t t 2+1+3+t =tt 2+t +4当t =0,即x =1时,y =0;当t >0,即x >1时,y =1t +4t +1, ∵t +4t ≥24=4(当且仅当t =2时取等号),∴y =1t +4t +1≤15,即y 的最大值为15(当t =2,即x =5时y 取得最大值).若正数x ,y 满足x +3y =5xy ,则3x +4y 的最小值是________解析 由x +3y =5xy 可得15y +35x =1,∴3x +4y =(3x +4y )(15y +35x )=95+45+3x 5y +12y 5x ≥135+125=5已知x >0,y >0,x +3y +xy =9,则x +3y 的最小值为________ 解析 由已知得x =9-3y1+y ,∵x >0,y >0,∴y <3,∴x +3y =9-3y 1+y +3y =3y 2+91+y=3(1+y )2-6(1+y )+121+y=121+y+(3y +3)-6≥2121+y ·(3y +3)-6=6, 当且仅当121+y=3y +3,即y =1,x =3时,(x +3y )min =6已知函数()f x =x 2+ax +11x +1(a ∈R ),若对于任意x ∈N +,()f x ≥3恒成立,则a 的取值范围是______解析 对任意x ∈N +,f (x )≥3恒成立,即x 2+ax +11x +1≥3恒成立,即知a ≥-(x +8x )+3设g(x)=x+8x,x∈N+,则g(2)=6,g(3)=173∵g(2)>g(3),∴g(x)min=173,∴-(x+8x)+3≤-83,∴a≥-83,故a的取值范围是[-83,+∞)已知x>0,y>0,且1x+2y=1,则x+y的最小值是________解析∵x>0,y>0,∴x+y=(x+y)(1x+2y)=3+yx+2xy≥3+22(当且仅当y=2x时取等号),∴当x=2+1,y=2+2时,(x+y)min=3+2 2函数y=1-2x-3x(x<0)的最小值为________解析∵x<0,∴y=1-2x-3x=1+(-2x)+(-3x)≥1+2(-2x)·3-x=1+26,当且仅当x=-62时取等号,故y的最小值为1+2 6若关于x的方程9x+(4+a)3x+4=0有解,则实数a的取值范围是________解析分离变量得-(4+a)=3x+43x≥4,得a≤-8设a+b=2,b>0,则12|a|+|a|b取最小值时,a的值为________解析∵a+b=2,∴12|a|+|a|b=24|a|+|a|b=a+b4|a|+|a|b=a4|a|+b4|a|+|a|b≥a4|a|+2b4|a|×|a|b=a4|a|+1,当且仅当b4|a|=|a|b时等号成立又a+b=2,b>0,∴当b=-2a,a=-2时,12|a|+|a|b取得最小值若当x>-3时,不等式a≤x+2x+3恒成立,则a的取值范围是________解析设f(x)=x+2x+3=(x+3)+2x+3-3,∵x>-3,所以x+3>0,故f(x)≥2(x+3)×2x+3-3=22-3,当且仅当x=2-3时等号成立,∴a的取值范围是(-∞,22-3]若对于任意x >0,xx 2+3x +1≤a 恒成立,则a 的取值范围是________解析 xx 2+3x +1=13+x +1x ,∵x >0,∴x +1x ≥2(当且仅当x =1时取等号),则13+x +1x ≤13+2=15,即x x 2+3x +1的最大值为15,故a ≥15.解答题:已知x >0,y >0,且2x +5y =20. (1)求u =lg x +lg y 的最大值; (2)求1x +1y 的最小值.解 (1)∵x >0,y >0,∴由基本不等式,得2x +5y ≥210xy . ∵2x +5y =20,∴210xy ≤20,xy ≤10,当且仅当2x =5y 时,等号成立.因此有⎩⎪⎨⎪⎧ 2x +5y =20,2x =5y ,解得⎩⎪⎨⎪⎧x =5,y =2,此时xy 有最大值10.∴u =lg x +lg y =lg(xy )≤lg10=1,∴当x =5,y =2时,u =lg x +lg y 有最大值1. (2)∵x >0,y >0,∴1x +1y =⎝ ⎛⎭⎪⎫1x +1y ·2x +5y 20=120⎝ ⎛⎭⎪⎫7+5y x +2x y ≥120⎝⎛⎭⎪⎫7+25y x ·2x y =7+21020, 当且仅当5y x =2xy 时,等号成立.由⎩⎨⎧2x +5y =20,5y x =2xy ,解得⎩⎨⎧x =1010-203,y =20-4103.∴1x +1y 的最小值为7+21020专项能力提升设x ,y 均为正实数,且32+x +32+y=1,则xy 的最小值为( ) A .4 B .4 3 C .9 D .16解析 由32+x +32+y=1得xy =8+x +y , ∵x ,y 均为正实数,∴xy =8+x +y ≥8+2xy (当且仅当x =y 时等号成立), 即xy -2xy -8≥0,解得xy ≥4,即xy ≥16,∴xy 的最小值为16设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0,则当xy z 取得最大值时,2x +1y -2z 的最大值为( ) A .0 B .1 C.94 D .3 解析 由已知得z =x 2-3xy +4y 2,(*)则xyz =xyx 2-3xy +4y2=1x y +4y x -3≤1,当且仅当x =2y 时取等号,把x =2y 代入(*)式,得z =2y 2,∴2x +1y -2z =1y +1y -1y 2=-⎝ ⎛⎭⎪⎫1y -12+1≤1已知m >0,a 1>a 2>0,则使得m 2+1m ≥|a i x -2|(i =1,2)恒成立的x 的取值范围是( )A .[0,2a 1]B .[0,2a 2]C .[0,4a 1]D .[0,4a 2]解析 ∵m 2+1m =m +1m ≥2(当且仅当m =1时等号成立),∴要使不等式恒成立, 则2≥|a i x -2|(i =1,2)恒成立,即-2≤a i x -2≤2,∴0≤a i x ≤4, ∵a 1>a 2>0,∴⎩⎪⎨⎪⎧0≤x ≤4a 1,0≤x ≤4a 2,即0≤x ≤4a 1,∴使不等式恒成立的x 的取值范围是[0,4a 1]已知x ,y ∈R 且满足x 2+2xy +4y 2=6,则z =x 2+4y 2的取值范围为________ 解析 ∵2xy =6-(x 2+4y 2),而2xy ≤x 2+4y 22,∴6-(x 2+4y 2)≤x 2+4y 22, ∴x 2+4y 2≥4(当且仅当x =2y 时取等号).又∵(x +2y )2=6+2xy ≥0,即2xy ≥-6,∴z =x 2+4y 2=6-2xy ≤12(当且仅当x =-2y 时取等号) 综上可知4≤x 2+4y 2≤1211设a >0,b >0,若3是3a 与3b 的等比中项,则1a +1b 的最小值为________解析 由题意知3a ·3b =3,即3a +b =3,∴a +b =1,∵a >0,b >0,∴1a +1b =⎝ ⎛⎭⎪⎫1a +1b (a +b )=2+b a +a b ≥2+2b a ·a b =4,当且仅当a =b =12时,等号成立点(a ,b )为第一象限内的点,且在圆(x +1)2+(y +1)2=8上,则ab 的最大值为________解析 由题意知a >0,b >0,且(a +1)2+(b +1)2=8,化简得a 2+b 2+2(a +b )=6,则6≥2ab +4ab (当且仅当a =b 时取等号),令t =ab (t >0),则t 2+2t -3≤0,解得0<t ≤1,则0<ab ≤1,∴ab 的最大值为1.正数a ,b 满足1a +9b =1,若不等式a +b ≥-x 2+4x +18-m 对任意实数x 恒成立,则实数m 的取值范围是________解析 ∵a >0,b >0,1a +9b =1,∴a +b =(a +b )⎝ ⎛⎭⎪⎫1a +9b =10+b a +9a b ≥10+29=16,由题意,得16≥-x 2+4x +18-m ,即x 2-4x -2≥-m 对任意实数x 恒成立,而x 2-4x -2=(x -2)2-6,∴x 2-4x -2的最小值为-6,∴-6≥-m ,即m ≥6.。
基本不等式完整版(非常全面)
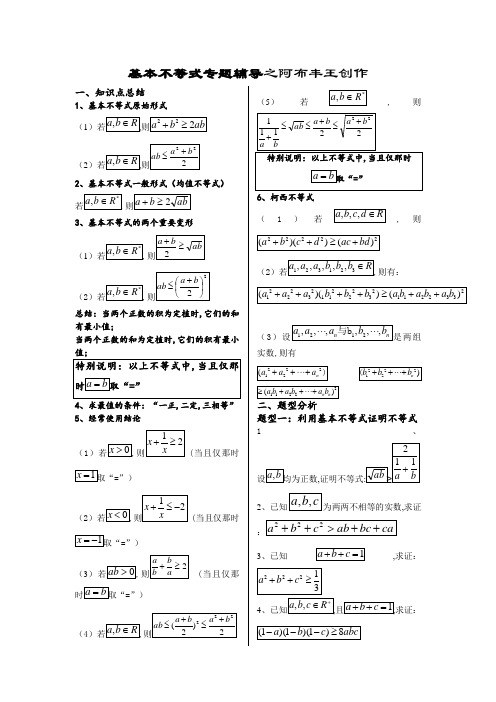
基本不等式专题辅导之阿布丰王创作一、知识点总结1、基本不等式原始形式(1(22、基本不等式一般形式(均值不等式)3、基本不等式的两个重要变形(1(2总结:当两个正数的积为定植时,它们的和有最小值;当两个正数的和为定植时,它们的积有最小4、求最值的条件:“一正,二定,三相等”5、经常使用结论(1当且仅那时=”)(2当且仅那时=”)(3当且仅那=”)(4(5)若,则6、柯西不等式 (1)若,则(2则有:(3两组实数,则有题型一:利用基本不等式证明不等式1、,2,求证3、已知,求证:45、已知,,a b c R +∈,且1a b c ++=,求证:1111118a b c ⎛⎫⎛⎫⎛⎫---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭6、(2013年新课标Ⅱ卷数学(理)选修4—5:不等式选讲设,,a b c 均为正数,且1a b c ++=,证明: (Ⅰ)13ab bc ca ++≤; (Ⅱ)2221a b c b c a++≥.7、(2013年江苏卷(数学)选修4—5:不等式选讲 已知>≥b a ,求证:b a ab b a 223322-≥-题型二:利用不等式求函数值域1、求下列函数的值域(1)22213x x y +=(2))4(x x y -= (3))0(1>+=x x x y(4))0(1<+=x x x y题型三:利用不等式求最值 (一)(凑项)1、已知2>x ,求函数42442-+-=x x y 的最小值;变式1:已知2>x ,求函数4242-+=x x y 的最小值;变式2:已知2<x ,求函数4242-+=x x y 的最年夜值;练习:1、已知54x >,求函数14245y x x =-+-的最小值;2、已知54x <,求函数14245y x x =-+-的最年夜值;题型四:利用不等式求最值 (二)(凑系数)1、那时,求(82)y x x =-的最年夜值;变式14(82)y x x =-的最年夜值;变式2:设230<<x ,求函数)23(4x x y -=的最年夜值.202<<x ,y x x =-()63的最年夜值;变式40<<x ,)28(x x y -=的最年夜值;3、求函数)2521(2512<<-+-=x x x y 的最年夜值;(提示:平方,利用基本不等式) 数)41143(41134<<-+-=x x x y 的最年夜值;题型五:巧用“1”的代换求最值问题1最小值;法一: 法二:变式1:已知,求变式2最小值;变式3:已求.变式4:值;变式5: (1)值;(2)若且,求变式6:使得题型六:分离换元法求最值(了解)1、求函数的值域;变式:2、示:换元法)变式:题型七:基本不等式的综合应用1小值2、(2009天津)已知,求变式1:(2010求关值;变式2:(2012湖北武汉诊断)已知,那时像恒过定点,若点在直线,3、已知,,求变式1:变式2:(2010山东)已知值;(提示:通分或三角换元)变式3:(2011浙江)已知年夜值;4、(2013年山东(理))取得最年夜值时值为()()A(提示:代入换元,利用基本不等式以及函数求最值)变式:设是正数,满足题型八:利用基本不等式求参数范围1、(2012且,最小值;2、已知且,4)(提示:分离参数,换元法)变式:已若,题型九:利用柯西不等式求最值1、二维柯西不等式若,则2、二维形式的柯西不等式的变式3、二维形式的柯西不等式的向量形式4、三维柯西不等式则有:5,。
高中数学:基本不等式(含答案)

高中数学:必修5 基本不等式一、基础知识1.重要不等式:a 2+b 2≥2ab (a ,b ∈R )一般地,对于任意实数a ,b ,有a 2+b 2≥2ab ,当且仅当______________时,等号成立.2.基本不等式如果a >0,b >0,那么2a bab +≤,当且仅当______________时,等号成立. 其中,2a b+叫做正数a ,b 的算术平均数,ab 叫做正数a ,b 的几何平均数. 因此基本不等式也可叙述为:两个正数的算术平均数不小于它们的几何平均数.3.基本不等式的证明(1)代数法:方法一 因为a >0,b >0,所以我们可以用a ,b 分别代替重要不等式中的a ,b ,得22()()2a b a b +≥⋅,当且仅当a b =时,等号成立.即2a bab +≥( a >0,b >0),当且仅当a =b 时,等号成立. 方法二 因为2222()()2()0a b ab a b ab a b +-=+-=-≥, 所以20a b ab +-≥,即2a b ab +≥,所以2a bab +≤. 方法三 要证2a bab +≥,只要证2a b ab +≥,即证20a b ab +-≥,即证2()0a b -≥,显然2()0a b -≥总是成立的,当且仅当a =b 时,等号成立.(2)几何法:如图,AB 是圆的直径,C 是AB 上一点,AC =a ,BC =b ,过点C 作垂直于AB 的弦DE ,连接AD ,BD .易证Rt Rt ACD DCB △∽△,则CD 2=CA ·CB ,即CD =______________.这个圆的半径为2a b +,显然它大于或等于CD ,即2a bab +≥,当且仅当点C 与圆心重合,即a =b 时,等号成立.2a bab +≤的几何意义:半径不小于半弦.4.重要不等式和均值不等式的常用变形公式及推广公式(1)2b a a b +≥(a ,b 同号);2b aa b +≤-(a ,b 异号). (2)12a a +≥(a >0);12a a+≤-(a <0). (3)114a b a b +≥+(a >0,b >0);22a a b b≥-(a >0,b >0).(4)222a b ab +≤,2()2a b ab +≤,4ab ≤a 2+b 2+2ab ,2(a 2+b 2)≥(a +b )2(,)a b ∈R . (5)12212(,,,,2)nn n a a a a a a a n n n+++≥∈≥∈R N ,.(6)2121212111()()(,,,n n na a a n a a a a a a ++++++≥为正实数,且2)n n ≥∈N ,.5.均值不等式链若a >0,b >0,则2112a b a b+≤≤≤+,当且仅当a =b 时,等号成立.其中211a b +分别叫做a ,b 的调和平均数和平方平均数.6.最值定理已知x >0,y >0,则若x+y 为定值s ,则当且仅当x =y 时,积xy 有最大值24s (简记:和定积最大); 若xy 为定值t ,则当且仅当x =y 时,和x +y有最小值简记:积定和最小).参考答案:重难易错点:一、利用基本不等式判断不等式是否成立要判断不等式是否成立,关键是把握其运用基本不等式时能否严格遵循“一正、二定、三相等”这三个条件.例1.(1)设f (x )=ln x ,0<a <b ,若p =f ),q =()2a b f +,r =12(f (a )+f (b )),则下列关系式中正确的是 A .q =r <pB .p =r <qC .q =r >pD .p =r >q(2)给出下列不等式:①12x x +≥;②1||2x x+≥;③21(0)4x x x +>>;④1sin 2sin x x +≥;⑤若0<a <1<b ,则log a b +log b a ≤-2.其中正确的是______________. 【答案】(1)B ;(2)②⑤.【点析】基本不等式常用于有条件的不等关系的判断、比较代数式的大小等.一般地,结合所给代数式的特征,将所给条件进行转换(利用基本不等式可将整式和根式相互转化),使其中的不等关系明晰即可解决问题.二、利用基本不等式证明不等式利用基本不等式证明不等式的一般思路:先观察题中要证明的不等式的结构特征,若不能直接使用基本不等式证明,则考虑对代数式进行拆项、变形、配凑等,使之达到能使用基本不等式的形式;若题目中还有其他条件,则先观察已知条件和所证不等式之间的联系,当已知条件中含有“1”时,要注意“1”的代换.另外,解题时要时刻注意等号能否取到.例2.(1)已知a >0,b >0,c >0,求证:222a b c a b c b c a++≥++;(2)已知a >b ,ab =2,求证:224a b a b+≥-.观察a-b,a2+b2,可联想到通过加减2ab的方法配凑出(a-b)2,从而化为可使用基本不等式的形式,结合ab =2可使问题得到解决.三、利用基本不等式求最值(1例3.(1)已知f(x)=x+1x+2(x<0),则f(x)有A.最大值为4B.最小值为4 C.最小值为0 D.最大值为0(2)已知0<x<4,则x(4-x)取得最大值时x的值为A.0 B.2 C.4 D.16(3)已知函数f(x)=2x(x>0),若f(a+b)=16,则f(ab)的最大值为_______________;(4)已知a,b∈R,且ab=8,则|a+2b|的最小值是_______________.【答案】(1)D;(2)C;(3)16;(4)8.【点析】利用基本不等式求最值要牢记三个关键词:一正、二定、三相等,即①一正:各项必须为正;②二定:各项之和或各项之积为定值;③三相等:必须验证取等号时条件是否具备.(2使用基本不等式条件的可通过“变形”来转换,常见的变形技巧有:拆项、凑项、凑系数等.例4.(1)已知x>0,则函数y=231x xx++的最小值为_______________;(2)若x>1,则函数y=11xx+-的最小值为_______________;(3)若0<x<125,则函数y=x(12-5x)的最大值为_______________.(31”的替换,或构造不等式求解.例5.(1)已知a>0,b>0,a+b=1,则11a b+的最小值为_______________;(2)已知a>0,b>0,11a b+=2,则a+b的最小值为_______________;(3)若正实数x,y满足x+y+3=xy,则xy的最小值是_______________;(4)已知x >0,y >0,x +y +xy =3,则x +y 的最小值是_______________. 【答案】(1)4;(2)2;(3)9;(4)2.【点析】在构造不等式求最值时,既要掌握公式的正用,也要注意公式的逆用.例如,当a >0,b >0时,a 2+b 2≥2ab 逆用就是ab ≤222a b +;2a b+≥ab 逆用就是ab ≤2()2a b +等.还要注意“添项、拆项、凑系数”的技巧和等号成立的条件等.四、基本不等式在实际中的应用利用基本不等式解决应用问题的关键是构建模型,一般来说,都是从具体的几何图形,通过相关的关系建立关系式.在解题过程中尽量向模型2bax ab x+≥(a >0,b >0,x >0)上靠拢. 例6.如图,要规划一个矩形休闲广场,该休闲广场含有大小相等的左右两个矩形草坪(如图中阴影部分所示),且草坪所占面积为18 000 m 2,四周道路的宽度为10 m ,两个草坪之间的道路的宽度为5 m .试问,怎样确定该矩形休闲广场的长与宽的尺寸(单位:m ),能使矩形休闲广场所占面积最小?【答案】当矩形休闲广场的长为140 m ,宽为175 m 时,可使休闲广场的面积最小.【点析】本题容易出现的思维误区:①未能理清草坪边长与休闲广场边长之间的关系;②求出目标函数后不会运用基本不等式求最值,缺乏必要的配凑、转化变形能力,从而无法利用基本不等式求最值,或者不会利用基本不等式等号成立的条件求变量的取值.五、忽略等号成立的条件导致错误例7、函数22()2f x x =+的最小值为_______________.【错解】2222223211()22222x x f x x x x x +++===++≥+++,所以函数()f x 的最小值为2.【错因分析】错解中使用基本不等式时,等号成立的条件为22122x x +=+,即22x +=1,显然x 2≠-1,即等号无法取到,函数()f x 的最小值为2是不正确的. 【正解】()21222+++=x x x f ,令()()t t t g t x t 1,2,22+=≥+=.易知函数()tt t g 1+=在[)∞+,2上六、忽略等号成立的一致性导致错误例8、若x>0,y>0,且x+2y=1,则11x y+的最小值为_______________.基本不等式:基础习题强化1.已知01x <<,则(1)x x -取最大值时x 的值为A B C D 2.若实数,a b 满足323a b +=,则84a b +的最小值是A .B .4C .D .3.若0,0,x y >>且22x y +=,则21x y+的最小值是A .3BC .3D .924.若1a >,则211a a a -+-的最小值是A .2B .4C .1D .35.已知2212,202b m a a n b a -=+>=≠-()(),则m ,n 之间的大小关系是 A .m >nB .m <nC .m =nD .不能确定6.己知,a b 均为正实数,且直线60ax by +-=与直线()3250b x y --+=互相垂直,则23a b +的最小值为 A .12B .13C .24D .257.已知0a >,0b >,11a b a b +=+,则12a b+的最小值为A .4B .C .8D .168.若正数a ,b 满足3ab a b =++,则ab 的取值范围为________________. 9.已知,,a b c +∈R ,且3a b c ++=,则111a b c++的最小值是________________.10.若实数a ,b 满足12a b+=ab 的最小值为________________. 11.设230<<x ,则函数4(32)y x x =-的最大值为________________. 12.已知a >0,b >0,ab =8,则当a 的值为________________时,22log log (2)a b ⋅取得最大值.能力提升13.已知a ,b 都是正实数,且满足2a b ab +=,则2a b +的最小值为A .12B .10C .8D .614.已知1,1a b >>,且11111a b +=--,则4a b +的最小值为 A .13B .14C .15D .1615.已知不等式1)()9ax y x y++≥(对任意正实数x ,y 恒成立,则正实数a 的最小值为 A .8B .6C .4D .216.若正实数,a b 满足1a b +=,则A .11a b+有最大值4 B .ab 有最小值14C .a b +有最大值2D .22a b +有最小值2217.已知0,0a b >>,若不等式3103m a b a b--≤+恒成立,则m 的最大值为 A .4B .16C .9D .318.设实数x ,y 满足2102146x y x y x y +≤⎧⎪+≤⎨⎪+≥⎩,则xy 的最大值为A .252B .492C .12D .1419.已知a >0,b >0,c >0,且a +b +c =1,则111a b c++的最小值为_________________. 20.在4×+9×=60的两个中,分别填入一个自然数,使它们的倒数之和最小,则中应分别填入____________和____________.21.若a ,b ,c >0且(a +c )(a +b )=423-,则2a +b +c 的最小值为________________. 22.已知正实数a ,b 满足:1a b +=,则222a ba b a b +++的最大值是________________.其他23.某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图所示).设矩形的长为x 米,钢筋网的总长度为y 米. (1)列出y 与x 的函数关系式,并写出其定义域;(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?24.(1)求函数2710(1)1x x y x x ++=>-+的最小值;(2)已知正数a ,b 和正数x ,y ,若a +b =10,1a bx y+=,且x +y 的最小值是18,求a ,b 的值.25.已知函数2()21,f x x ax a a =--+∈R .(1)若2a =,试求函数()(0)f x y x x=>的最小值; (2)对于任意的[0,2]x ∈,不等式()f x a ≤成立,试求a 的取值范围.26.(天津文理)已知a ,b ∈R ,且360a b -+=,则128ab+的最小值为_______________. 27.(江苏)在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,120ABC ∠=︒,ABC ∠的平分线交AC于点D ,且1BD =,则4a c +的最小值为_______________.28.(山东理)若0a b >>,且1ab =,则下列不等式成立的是A .()21log 2aba ab b +<<+ B .()21log 2a b a b a b<+<+ C .()21log 2a b a a b b +<+<D .()21log 2a ba b a b +<+< 29.(天津文理)若,a b ∈R ,0ab >,则4441a b ab++的最小值为________________.30.(江苏)某公司一年购买某种货物600吨,每次购买x 吨,运费为6万元/次,一年的总存储费用为4x 万元.要使一年的总运费与总存储费用之和最小,则x 的值是________________. 31.(山东文)若直线1(0,0)x ya b a b+=>>过点(1,2),则2a b +的最小值为________________.【参考答案】1.【答案】B 2.【答案】C 3.【答案】D 4.【答案】D 5.【答案】A 6.【答案】D 7.【答案】B8.【答案】[)+∞,9 9.【答案】3 10.【答案】 11.【答案】9212.【答案】4 13.【答案】C 14.【答案】B 15.【答案】C 16.【答案】C 17.【答案】B 18.【答案】A19.【答案】9 20.【答案】6 4 21.【答案】2 22.23.【答案】(1)9003(0150)y x x x=+-<<;(2)长为30米,宽为15米时,所用的钢筋网的总长度最小. 24.【答案】(1)9;(2)28a b =⎧⎨=⎩或82a b =⎧⎨=⎩. 25.【答案】(1)2-;(2)3[,)4+∞.26.【答案】0.25 27.【答案】9 28.【答案】B 29.【答案】4 30.【答案】30 31.【答案】8。
基本不等式公式五个

基本不等式公式五个1. 基本不等式原始形式。
- 对于任意实数a,b,有a^2+b^2≥slant2ab,当且仅当a = b时等号成立。
- 证明:(a - b)^2=a^2-2ab + b^2≥slant0,移项可得a^2+b^2≥slant2ab。
2. 基本不等式的变形一(均值不等式)- 对于正实数a,b,有(a + b)/(2)≥slant√(ab),当且仅当a = b时等号成立。
- 证明:由a^2+b^2≥slant2ab,令A=√(a),B=√(b)(a,b>0),则A^2+B^2≥slant2AB,即a + b≥slant2√(ab),所以(a + b)/(2)≥slant√(ab)。
3. 基本不等式的变形二(推广到三个正数)- 对于正实数a,b,c,有a^3+b^3+c^3≥slant3abc,当且仅当a = b = c时等号成立。
- 证明:a^3+b^3+c^3-3abc=(a + b + c)(a^2+b^2+c^2-ab - bc - ca)- 而a^2+b^2+c^2-ab - bc - ca=(1)/(2)[(a - b)^2+(b - c)^2+(c - a)^2]≥slant0,当且仅当a = b = c时等号成立。
- 又因为a,b,c>0,所以a^3+b^3+c^3≥slant3abc。
4. 基本不等式的变形三(三个正数的均值不等式)- 对于正实数a,b,c,有(a + b + c)/(3)≥slantsqrt[3]{abc},当且仅当a = b = c时等号成立。
- 证明:由a^3+b^3+c^3≥slant3abc,令A=sqrt[3]{a},B=sqrt[3]{b},C=sqrt[3]{c},则A^3+B^3+C^3≥slant3ABC,即a + b + c≥slant3sqrt[3]{abc},所以(a + b + c)/(3)≥slantsqrt[3]{abc}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2b+a≥2,ab>0; ab
a+b 3ab≤ 2 2,a,b∈R;
当且仅当 a=b 时 等号成立.
4a2+b2≥
a+b 2
2,a,b∈R
2
(5) 2 ab a b a2 b2 (a 0,b 0) .
11
2
2
ab
一、直接法
【例 1】以下结论,正确的是( ) A.y=x+ ≥4
B.ex+ >2
A. 2
B.2
C.2 2
D.4
解析:由1+2= ab知 a>0,b>0,所以 ab=1+2≥2 2 ,即 ab≥2 2,
ab
ab
ab
1=2,
ab 当且仅当 1+2=
即 a=4 2,b=2 4 2时取“=”,所以 ab 的最小值为 2 ab,
2.故选 C
ab
变式 1:若实数 x、y 满足 2x+2y=1,则 x+y 的取值范围是( )
证明: (a b)2 0 a2 2ab b2 0 a2 b2 2ab
推论: ab a2 b2 ( a,b R ). 2
2、如果 a 0 , b 0 ,则 a b 2 ab ,(当且仅当 a b 时取等号“=”).
推论: ab
(a b )2 ( a
a2 0 ,b 0 );
C.x(1﹣x)≤(
)2 =
D.sinx+
(0<x<π)的最小值是 2
解:A:当 x<0 时,不满足题意;B:
C:由基本不等式可得,x(1﹣x) 等号,故 C 符合题意; D:当 0<x<π时,0<sinx≤1,则 故选:C.
=2,不符合题意; = ,当且仅当 x=1﹣x 即 x= 时取
,等号取不到,故 D 不符合题意.
利用基本不等式求最值问题 已知 x>0,y>0,则: (1)如果积 xy 是定值 p,那么当且仅当 x=y 时,x+y 有最小值是 2 p.(简记:积定和最小) (2)如果和 x+y 是定值 p,那么当且仅当 x=y 时,xy 有最大值是p2.(简记:和定积最大)
4
4、几个重要的不等式
1a2+b2≥2ab,a,b∈R;
变式 2:函数 y=2﹣x﹣ (x>0)的最大值为
.
解析:y=2﹣x﹣ =2﹣(x+ )
=2﹣4=﹣2,当且仅当 x=2 时取等号.
所以函数 y=2﹣x﹣ (x>0)的最大值为﹣2.故答案为:﹣2. 转化符 号:若含变 量的项是负数,则提取 负号,将其转 化为正数,再利用“公式”求
最值.
【例 2】(2015·高考湖南卷)若实数 a,b 满足1+2= ab,则 ab 的最小值为( ) ab
A.(﹣∞,﹣2] B.[0,2]
C.[﹣2,+∞) D.[﹣2,0]
解析:由实数 x、y 满足 2x+2y=1,根据基本不等式得,
1=2x +2y≥2
,故 x+y≤﹣2.故选:A.
变式 2:已知 x 为正实数,且 x2+y2=1,则 x 1+y2的最大值为________. 2
解析:因为 x>0,所以 x 1+y2= 2
D.4
【例 5】设 a,b>0,a+b=5,则 a+1+ b+3的最大值为________.
答案:3 2 解 析 : 令 t = a+1 + b+3 , 则 t2 = a + 1 + b + 3 + 2 (a+1)(b+3) = 9 + 2 (a+1)(b+3)≤9+a+1+b+3=13+a+b=13+5=18,
1+y2 x2 2 2 ≤
2
x2+
1+y2 22
.又 x2+
1+y2 22
=
x2+y2 2
2
+1=3.所以 x 1+y2≤ 2×3=3 2,当且仅当 x2 =1+y2 ,即 x = 3时,等号成立.故
22
22 4
22
2
(x 1+y2)max=342.
【例 3】若 a,b 都是正数,且 a+b=1,则(a+1)(b+1)的最大值为( )
利用基本不等式求最值
——最全方法总结
主讲:陈鑫城
常用方法: 一、直接法 二、连续放缩 三、配凑法 四、常数代换法 五、整体换元 六、消元法 七、转化为不等式 八、拆(添)项 九、齐次化 十、确定主次元 十一、基本不等式与其他知识交汇
知识概要
1、如果 a,b R ,那么 a2 b2 2ab (当且仅当 a b 时取等号“=”).
A.
B.2
C.
D.4
解析:由题意,可知:(a+1)(b+1)≤(Βιβλιοθήκη )2=( )2= .故选:C.
【例 4】若实数 x,y 满足 x+y=8,则 x2+y2 的最小值是( )
A.8
B.32
C.16
解:因为
,当且仅当 x=y 时等号成立,
因为 x+y=8,所以
,
所以 x2+y2≥32, 故 x2+y2 的最小值是 32, 故选:B .
当且仅当 a+1=b+3 时取等号,此时 a=7,b=3. 22
所以 tmax= 18=3 2. 乘方:若目标函数 带有根号,则先乘 方后配凑为和为定 值.
【例 6】已知实数 a,b 满足 ab>0,则
A.2﹣
B.2+
﹣
的最大值为( )
C.3﹣2
D.3+2
解:∵ab>0,
则﹣
=
=
=
=3
,
当且仅当
时取等号,此时取得最大值为 3
b2
(a b )2
.
2
2
2
3、基本不等式 ab≤a+b 2
(1)设 a>0,b>0,则 a,b 的算术平均数为a+b,几何平均数为 ab,基本不等式可叙述为: 2
两个正数的算术平均数不小于它们的几何平均数. (2)基本不等式成立的条件:a>0,b>0. (3)等号成立的条件:当且仅当 a=b 时取等号. ◆注:在利用基本不等式求最值时,要紧扣“一正、二定、三相等”的条件.“一正”是说 每个项都必须为正值,“二定”是说各个项的和(或积)必须为定值.“三相等”是说各项的 值相等时,等号成立.多次使用均值不等式解决同一问题时,要保持每次等号成立条件的 一致性和不等号方向的 一致性.
变式 1:已知函数 f(x)=4x+a(x>0,a>0)在 x=3 时取得最小值,则 a=__________. x
解析:因为 x >0,a>0,所以 f(x)=4x +a≥2 4x·a=4 a,当且仅当 4x=a,即 4x2=a
x
x
x
时,f(x)取得最小值.又因为 f(x)在 x=3 时取得最小值,所以 a=4×32=36.
.
故选:C.
二、连续放缩
利用基本不等式求函数或代数式的最值时一定要注意验证等号是否成立,特别是当连 续多次使用基本不等式时,一定要注意每次是否能保证等号成立,并且注意取等号的条件 的一致性,因此在利用基本不等式处理问题时,列出等号成立的条件不仅是解题的必要步 骤,也是检验转换是否有误的一种方法。
