多元Logistic回归分析
多元线性回归logistic回归
20
（四）自变量的筛选
基本思路：尽可能将回归效果显著的自变量选入方程 中，作用不显著的自变量排除在外。 （1）全局择优法（all possible subsets selection）： （2）逐步选择法
前进法（Forward selection） 后退法（Backward elimination） 逐步法（Stepwise）
Sum of Square s
1
Re g re ssi o n
13 3.71 1
df Me an Square
4
33 .4 28
F
S i g.
8.278 .000a
Re si dua l
88 .8 41
22
4.03 8
To tal
22 2.55 2
26
a. P redict ors: (Const ant ), 总 胆 固醇 x1, 胰 岛 素x3, 糖 化 血红 蛋 白 x4, 甘 油 三脂 x2
β0为回归方程的常数项（constant)，表示各自变量均为0时y的平 均值；
m为自变量的个数； β1、β2、βm为偏回归系数（Partial regression coefficient）
意义：如β1 表示在X2、X3 …… Xm固定条件下，X1 每增减 一个单位对Y 的效应（Y 增减β个单位）。 e为去除m个自变量对Y影响后的随机误差，称残差（residual)。
Sig. .047 .701 .099 .036 .016
将总胆固醇(X1) 剔除。 注意：通常每次只剔除关系最弱的一个因素。
对于同一资料，不同自变量的t值可以相互比较，t的绝对
值越大，或P越小，说明该自变量对Y所起的作用越大。
二元、多元logistic回归分析
二元logistic回归分析1.理论Logistic回归模型：设因变量为Y，自变量为x1，x2，...，xn。
事件发生与不发生的概率比Pi /（1-pi）被称为事件发生比。
后对事件发生比做对数变换，能得到logistic回归的线性模式：ln（pi /（1-pi））=β+β1x1+...βnxn采用最大似然比法或者迭代法对参数的估计，参数通过似然比检验和Wold 检验。
二元logistic回归是指因变量为二分类变量时的回归分析。
在建立回归模型时，目标的取值范围在0-1之间。
常因变量为二分类数据自变量可以是连续型随机变量和分类数据图1数据类型2.重新编码操作步骤首先将数据导入spss中，数据情况如下图所示，首先先对变量进行重新编码处理。
图2数据情况第一步、点击转换、重新编码为相同的变量。
图3数据编码第一步第二步：进入图中变量框后，将需要处理的变量放入变量放入框中，后点击旧值和新值，在旧值中输入原有值，后在新值中输入新值，点击添加、继续。
图4数据编码第二步3.二元logistic回归分析操作步骤第一步：点击分析、回归、二元logistic。
图5二元logistic回归分析第一步第二步：进入图中对话框后将因变量、自变量放入对应变量框中，点击分类、进入定义分类变量框后。
将协变量框中的分类变量放入分类协变量框中（一般情况除二分类或有序分类数据不需哑变量设置），并进行哑变量的设置，点击继续。
图6第二步第三步：点击选项，勾选霍斯默-莱梅肖拟合优度、Exp(B)的置信区间、迭代历史记录。
点击继续、确定。
图7选项勾选4.二元logistic回归分析结果二元logistic回归分析的个案摘要、因变量编码、分类变量编码结果。
图8分类变量编码迭代历史记录、分类表、方程中的变量、未包括在方程中的变量结果。
图9块0：起始块迭代历史记录、模型中的Omnibus检验、模型摘要、霍斯默-莱梅肖检验。
图10块1：方法=输入分类表、方差中的变量结果。
(整理)多项分类Logistic回归分析的功能与意义1.
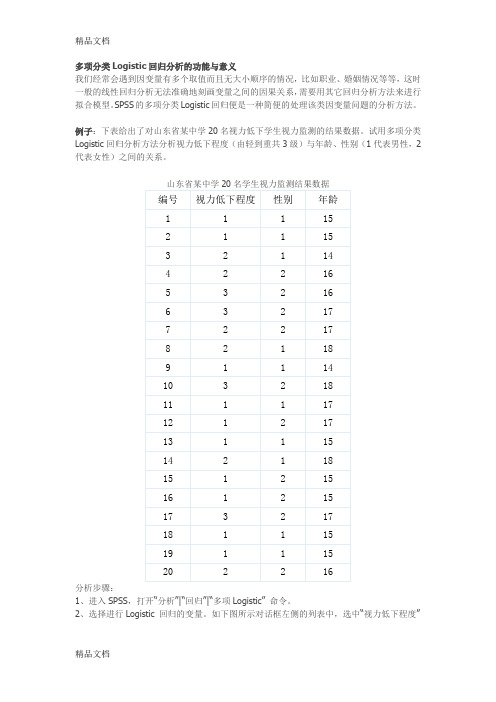
多项分类Logistic回归分析的功能与意义我们经常会遇到因变量有多个取值而且无大小顺序的情况，比如职业、婚姻情况等等，这时一般的线性回归分析无法准确地刻画变量之间的因果关系，需要用其它回归分析方法来进行拟合模型。
SPSS的多项分类Logistic回归便是一种简便的处理该类因变量问题的分析方法。
例子：下表给出了对山东省某中学20名视力低下学生视力监测的结果数据。
试用多项分类Logistic回归分析方法分析视力低下程度（由轻到重共3级）与年龄、性别（1代表男性，2代表女性）之间的关系。
并单击向右的箭头按钮使之进入“因变量”列表框，选择“性别”使之进入“因子”列表框，选择“年龄”使之进入“协变量”列表框。
还是以教程“blankloan.sav"数据为例，研究银行客户贷款是否违约（拖欠）的问题，数据如下所示：上面的数据是大约700个申请贷款的客户，我们需要进行随机抽样，来进行二元Logistic 回归分析，上图中的“0”表示没有拖欠贷款，“1”表示拖欠贷款，接下来，步骤如下：1：设置随机抽样的随机种子，如下图所示：选择“设置起点”选择“固定值”即可，本人感觉200万的容量已经足够了，就采用的默认值，点击确定，返回原界面、2：进行“转换”—计算变量“生成一个变量（validate)，进入如下界面：在数字表达式中，输入公式：rv.bernoulli（0.7），这个表达式的意思为：返回概率为0.7的bernoulli分布随机值如果在0.7的概率下能够成功，那么就为1，失败的话，就为"0"为了保持数据分析的有效性，对于样本中“违约”变量取缺失值的部分，validate变量也取缺失值，所以，需要设置一个“选择条件”点击“如果”按钮，进入如下界面：如果“违约”变量中，确实存在缺失值，那么当使用"missing”函数的时候，它的返回值应该为“1”或者为“true"，为了剔除”缺失值“所以，结果必须等于“0“也就是不存在缺失值的现象点击”继续“按钮，返回原界面，如下所示：将是“是否曾经违约”作为“因变量”拖入因变量选框，分别将其他8个变量拖入“协变量”选框内，在方法中，选择：forward.LR方法将生成的新变量“validate" 拖入"选择变量“框内，并点击”规则“设置相应的规则内容，如下所示：设置validate 值为1，此处我们只将取值为1的记录纳入模型建立过程，其它值（例如：0）将用来做结论的验证或者预测分析，当然你可以反推，采用0作为取值记录点击继续，返回，再点击“分类”按钮，进入如下页面在所有的8个自变量中，只有“教育水平”这个变量能够作为“分类协变量” 因为其它变量都没有做分类，本例中，教育水平分为：初中，高中，大专，本科，研究生等等, 参考类别选择：“最后一个”在对比中选择“指示符”点击继续按钮，返回再点击—“保存”按钮，进入界面：在“预测值"中选择”概率，在“影响”中选择“Cook距离” 在“残差”中选择“学生化”点击继续，返回，再点击“选项”按钮，进入如下界面：分析结果如下：1：在“案例处理汇总”中可以看出：选定的案例489个，未选定的案例361个，这个结果是根据设定的validate = 1得到的，在“因变量编码”中可以看出“违约”的两种结果“是”或者“否” 分别用值“1“和“0”代替，在“分类变量编码”中教育水平分为5类，如果选中“为完成高中，高中，大专，大学等，其中的任何一个，那么就取值为1，未选中的为0，如果四个都未被选中，那么就是”研究生“ 频率分别代表了处在某个教育水平的个数，总和应该为489个1：在“分类表”中可以看出：预测有360个是“否”（未违约）有129个是“是”（违约）2：在“方程中的变量”表中可以看出：最初是对“常数项”记性赋值，B为-1.026，标准误差为：0.103那么wald =( B/S.E)²=(-1.026/0.103)² = 99.2248, 跟表中的“100.029几乎接近，是因为我对数据进行的向下舍入的关系，所以数据会稍微偏小，B和Exp(B) 是对数关系，将B进行对数抓换后，可以得到：Exp(B) = e^-1.026 = 0.358, 其中自由度为1，sig为0.000，非常显著1：从“不在方程中的变量”可以看出，最初模型，只有“常数项”被纳入了模型，其它变量都不在最初模型内表中分别给出了，得分，df , Sig三个值, 而其中得分（Score)计算公式如下：（公式中（Xi- X¯) 少了一个平方）下面来举例说明这个计算过程：(“年龄”自变量的得分为例）从“分类表”中可以看出：有129人违约，违约记为“1”则违约总和为129，选定案例总和为489那么：y¯ = 129/489 = 0.2638036809816x¯ = 16951 / 489 = 34.664621676892所以：∑(Xi-x¯)² = 30074.9979y¯（1-y¯）=0.2638036809816 *（1-0.2638036809816 ）=0.19421129888216 则：y¯（1-y¯）* ∑(Xi-x¯)² =0.19421129888216 * 30074.9979 = 5 840.9044060372 则：[∑Xi(yi - y¯）]^2 = 43570.8所以：=43570.8 / 5 840.9044060372 =7.4595982010876 = 7.46 （四舍五入）计算过程采用的是在EXCEL 里面计算出来的，截图如下所示：从“不在方程的变量中”可以看出，年龄的“得分”为7.46，刚好跟计算结果吻合！！答案得到验证~1:从“块1” 中可以看出：采用的是：向前步进的方法，在“模型系数的综合检验”表中可以看出：所有的SIG 几乎都为“0”而且随着模型的逐渐步进，卡方值越来越大，说明模型越来越显著，在第4步后，终止，根据设定的显著性值和自由度，可以算出卡方临界值，公式为：=CHIINV(显著性值,自由度) ，放入excel就可以得到结果2：在“模型汇总“中可以看出：Cox&SnellR方和Nagelkerke R方拟合效果都不太理想，最终理想模型也才：0.305 和0.446，最大似然平方的对数值都比较大，明显是显著的似然数对数计算公式为：计算过程太费时间了，我就不举例说明计算过程了Cox&SnellR方的计算值是根据：1：先拟合不包含待检验因素的Logistic模型，求对数似然函数值INL0 （指只包含“常数项”的检验）2：再拟合包含待检验因素的Logistic模型，求新的对数似然函数值InLB （包含自变量的检验）再根据公式：即可算出：Cox&SnellR方的值！提示：将Hosmer 和Lemeshow 检验和“随机性表” 结合一起来分析1：从 Hosmer 和Lemeshow 检验表中，可以看出：经过4次迭代后，最终的卡方统计量为：11.919，而临界值为：CHINV(0.05,8) = 15.507卡方统计量< 临界值，从SIG 角度来看：0.155 > 0.05 , 说明模型能够很好的拟合整体，不存在显著的差异。
多元线性回归logistic回归
X12
…
X1p
Y1
2
X21
X22
…
X2p
Y2
┆
┆
┆
…
┆
┆
n
Xn1
Xn2
…
Xnp
Yn
Y为定量变量——Linear Regression Y为二项分类变量——Binary Logistic Regression Y为多项分类变量——Multinomial Logistic Regression Y为有序分类变量——Ordinal Logistic Regression Y为生存时间与生存结局——Cox Regression
1
(Constant) 6.500 2.396
2.713 .012
甘 油 三 脂 x2 .402
.154
.354 2.612 .016
糖 化 血 红 蛋 白 .x6463
.230
.413 2.880 .008
胰 岛 素 x3
-.287
.112
-.360 -2.570 .017
a.Dep end ent Variable: 血 糖 y
将总胆固醇(X1) 剔除。 注意：通常每次只剔除关系最弱的一个因素。
对于同一资料，不同自变量的t值可以相互比较，t的绝对
值越大，或P越小，说明该自变量对Y所起的作用越大。
多元线性回归logistic回归
14
重新建立不包含提出因素的回归方程
C oe ffi ci e na ts
Un s tan dardiz eSdtan da rdi z e d C oe ffici e n ts C oe ffici e n ts
由上表得到如下多元线性回归方程：
多元logistics回归结果解读
多元logistic回归是一种用于研究多个自变量对因变量影响的统计方法。
通过多元logistic回归分析，我们可以了解自变量对因变量的贡献程度，并确定哪些自变量对因变量有显著影响。
在解读多元logistic回归结果时，需要注意以下几点：
系数解读：在多元logistic回归模型中，每个自变量的系数表示该变量对因变量的贡献程度。
系数的符号表示了影响的方向，正号表示正相关，负号表示负相关。
系数的绝对值表示影响的大小，绝对值越大，影响越大。
OR值解读：在多元logistic回归模型中，每个自变量的OR值表示该变量对因变量发生概率的影响程度。
OR值的范围在0到无穷大之间，值越大表示该自变量对因变量的影响越大。
显著性检验：在多元logistic回归模型中，每个自变量都需要进行显著性检验。
如果某个自变量的p值小于预设的显著性水平（如0.05），则认为该自变量对因变量有显著影响。
模型评估：在多元logistic回归分析结束后，需要对模型进行评估。
常用的评价指标包括模型的拟合优度、预测准确率等。
如果模型的评估结果良好，则认为模型可用于预测或解释实际问题。
总之，多元logistic回归结果解读需要综合考虑系数的符号、绝对值、OR值、显著性检验和模型评估等多个方面。
通过深入了解自变量对因变量的贡献程度和影响方式，可以帮助我们更好地理解数据，并进行科学决策。
7-多元Logistic-回归分析解析
什么是哑变量？
一个含有g个类的分类型变量可以构造g个哑变量。
29
如何用SAS程序构造哑变量？ data d2； set d1； array a{3} student teacher worker； do i=1 to 3； a{i}=( x 1= i ) ； end； run；
data d2； set d1；
INTERCPT 1 3.7180 0.6387 33.8853
0.0001
.
.
BIRTHWT 1 -0.00397 0.000588 45.6092
0.0001 -0.702480 206.996
1、因变量bpd对自变量birthwt 的logistic回归模型是：
2、自变量birthwt 的回归系数在统计意义上不等于0 (p=0.0001)，因此，OR=0.996在统计意义上不等于1。 OR=0.996 说明新生儿出生体重每增加一个单位(g)，患 BPD病的机会就会减少大约0.4% 。即患bpd病的概率 随新生儿出生体重的增加而下降。
• 按因变量取值个数:
• 二值logistic回归分析
• 多值logistic回归分析
• 按自变量个数:
• 一元logistic回归分析
• 多元logistic回归分析
9
第二节 Logistic 回归分析的数学模型
(1) 二值一元logistic回归模型: 令y是1,0变量，x是任
意变量，p=p(y=1|x) ，那么，二值变量y关于 变量x的一元logistic 回归 模型是:
Analysis of Maximum Likelihood Estimates
Parameter Standard Wald
《多元Logistic回归》课件
交叉验证是一种评估模型泛化能力的手段，通过将数据集 分成训练集和验证集，反复训练和验证模型，以获得更可 靠的评估结果。常用的交叉验证方法有k-fold交叉验证、 留出交叉验证等。
03
多元Logistic回归的实现步 骤
数据预处理：特征选择、缺失值处理等
特征选择
选择与目标变量相关的特征，去除无关 或冗余特征，提高模型的预测性能。
多元Logistic回归与一元Logistic回归的区别
一元Logistic回归只涉及一个自变量，而多元 Logistic回归涉及多个自变量。
多元Logistic回归能够同时处理多个特征，更准确 地描述数据的复杂关系，提高预测精度。
多元Logistic回归需要更多的数据和计算资源，因 为需要迭代计算每个特征与因变量言 • 多元Logistic回归的原理 • 多元Logistic回归的实现步骤 • 多元Logistic回归的优缺点 • 多元Logistic回归的案例分析 • 总结与展望
01
引言
多元Logistic回归的定义
多元Logistic回归是一种用于处理分 类问题的统计方法，它通过将多个自 变量与因变量之间的关系转换为概率 形式，从而对因变量进行预测。
结果。
它能够提供每个类别的预测概率 ，这在某些情况下非常有用，例 如在医学诊断中确定疾病的风险
。
多元Logistic回归在处理分类问 题时具有较高的预测精度和稳定
性。
缺点
多元Logistic回归对数据的分布 假设较为严格，通常要求数据 呈正态分布或近似正态分布。
它还假设自变量与因变量之间 存在线性关系，这在某些情况 下可能不成立，导致模型的预
案例三：用户点击率预测
总结词
用户点击率预测是多元Logistic回归在互联 网广告领域的典型应用，通过分析用户行为 和广告特征，预测用户是否会点击广告。
Logistic回归分析
Logistic 回归分析Logistic 回归分析是与线性回归分析方法非常相似的一种多元统计方法。
适用于因变量的取值仅有两个（即二分类变量，一般用1和0表示）的情况，如发病与未发病、阳性与阴性、死亡与生存、治愈与未治愈、暴露与未暴露等，对于这类数据如果采用线性回归方法则效果很不理想，此时用Logistic 回归分析则可以很好的解决问题。
一、Logistic 回归模型设Y 是一个二分类变量，取值只可能为1和0，另外有影响Y 取值的n 个自变量12,,...,n X X X ，记12(1|,,...,)n P P Y X X X ==表示在n 个自变量的作用下Y 取值为1的概率，则Logistic 回归模型为：[]0112211exp (...)n n P X X X ββββ=+-++++它可以化成如下的线性形式：01122ln ...1n n P X X X P ββββ⎛⎫=++++ ⎪-⎝⎭通常用最大似然估计法估计模型中的参数。
二、Logistic 回归模型的检验与变量筛选根据R Square 的值评价模型的拟合效果。
变量筛选的原理与普通的回归分析方法是一样的，不再重复。
三、Logistic 回归的应用（1）可以进行危险因素分析计算结果各关于各变量系数的Wald 统计量和Sig 水平就直接反映了因素i X 对因变量Y 的危险性或重要性的大小。
（2）预测与判别Logistic回归是一个概率模型，可以利用它预测某事件发生的概率。
当然也可以进行判别分析，而且可以给出概率，并且对数据的要求不是很高。
四、SPSS操作方法1．选择菜单2．概率预测值和分类预测结果作为变量保存其它使用默认选项即可。
例：试对临床422名病人的资料进行分析，研究急性肾衰竭患者死亡的危险因素和统计规律。
Logistic回归分析.sav解：在SPSS中采用Logistic回归全变量方式分析得到：（1）模型的拟合优度为0.755。
stata多元logistic回归结果解读
stata多元logistic回归结果解读【实用版】目录一、多元 logistic 回归的概念与原理二、多元 logistic 回归模型的建立三、多元 logistic 回归结果的解读四、实际案例应用与分析五、总结正文一、多元 logistic 回归的概念与原理多元 logistic 回归是一种用于分析多分类变量与二元变量之间关系的统计分析方法。
它可以对多个自变量与因变量之间的关系进行同时分析，适用于研究多个因素对某一现象的影响。
logistic 回归是一种分类回归方法，它将二元变量（如成功/失败、是/否等）与多个自变量之间的关系建模为逻辑斯蒂函数，从而预测因变量的概率。
二、多元 logistic 回归模型的建立在建立多元 logistic 回归模型时，首先需要将数据整理成合适的格式。
模型中，因变量为二元变量（通常用 0 和 1 表示），自变量为多元变量（可以是分类变量或连续变量）。
然后，通过添加截距项，构建多元logistic 回归模型。
在 Stata 软件中，可以使用命令“logit”来实现多元 logistic 回归分析。
三、多元 logistic 回归结果的解读多元 logistic 回归的结果主要包括系数、标准误、z 值、p 值、OR 值等。
其中，系数表示自变量对因变量的影响程度，正系数表示正相关，负系数表示负相关；标准误表示系数的估计误差；z 值表示系数除以标准误的值，用于检验系数的显著性；p 值表示假设检验的结果，一般小于0.05 认为显著；OR 值表示风险比，表示一个自变量对因变量的影响程度。
四、实际案例应用与分析假设我们研究一个城市居民的出行选择行为，希望了解影响居民选择不同交通方式的因素。
我们可以建立一个多元 logistic 回归模型，将居民的出行方式作为因变量（二元变量），交通方式的类型、出行距离、出行时间等因素作为自变量。
通过分析模型结果，我们可以得到各个因素对居民出行选择行为的影响程度，从而制定更有针对性的交通政策。
多元Logistic回归分析
P2=
P2 = p(y=2) =P2-P1
P3= p(y≤3 | x) = 1 - P2 累积概率模型
P3 = p(y=3) =1-P2 独立概率模型
12
第三节 Logistic回归分析方法步骤
1、估计参数 ---- 最大似然法 2、检验参数的显著性
H0: βj=0 vs H1: βj≠0 3、检验模型的显著性
注意：对于二值Logistic回归模型，Y=0的模型是：
p = p(y=0|x1,…,xk ) = 1 - p(y=1|x1,,xk)
10
Logistic 回归模型的另外一种形式 它给出变量z=logit(p)关于x 的线性函数。
11
(3) 多值logistic回归模型:
例如，当y取值1,2,3时，logistic回归模型是：
and
Criterion
Only
Covariates Chi-Square for Covariates
AIC
148.262
146.686
.
SC
147.648
145.458
.
-2 LOG L
146.262
142.686
3.576 with 1 DF (p=0.0586)
Score
.
.
4.224 with 1 DF (p=0.0399)
• 二分类变量： o 生存与死亡 o 有病与无病 o 有效与无效 o 感染与未感染
• 多分类有序变量： o 疾病程度（轻度、中度、重度） o 治愈效果（治愈、显效、好转、无效）
• 多分类无序变量： o 手术方法（A、B、C） o 就诊医院（甲、乙、丙、丁）
stata多元logistic回归结果解读
stata多元logistic回归结果解读【原创版】目录一、什么是多元 logistic 回归二、多元 logistic 回归的结果解读1.Odds ratio（风险比）2.显著性水平（sig.）3.系数估计4.模型整体检验三、实例分析四、总结正文一、什么是多元 logistic 回归多元 logistic 回归是一种用于分析多自变量与二分类因变量之间关系的统计模型。
它可以帮助我们了解各个自变量对因变量的影响程度以及预测概率。
在 Stata 中，我们可以使用 logistic 回归命令进行分析，例如：logit depvar indepvar1 indepvar2...，其中 depvar 表示因变量，indepvar1、indepvar2 等表示自变量。
二、多元 logistic 回归的结果解读1.Odds ratio（风险比）Odds ratio（风险比）是一种衡量自变量对因变量影响程度的指标。
它表示当某个自变量取某一值时，事件发生的概率与该自变量取另一值时事件发生概率的比值。
在 Stata 结果中，我们可以看到每个自变量的 OR 值，正值表示该自变量与因变量正相关，负值表示负相关，接近 1 表示关系较弱。
2.显著性水平（sig.）显著性水平是用来判断自变量对因变量影响是否显著的指标。
在Stata 结果中，我们可以看到每个自变量的 sig.值。
一般而言，sig.值小于 0.05，我们认为该自变量对因变量的影响是显著的；sig.值大于等于 0.05，我们认为该自变量对因变量的影响不显著。
3.系数估计系数估计表示自变量对因变量的影响程度。
在 Stata 结果中，我们可以看到每个自变量的系数估计值。
系数值越大，表示该自变量对因变量的影响越大；系数值越小，表示影响越小。
4.模型整体检验模型整体检验可以帮助我们判断模型是否整体上显著。
在 Stata 中，我们可以使用 logistic 命令进行模型整体检验，例如：logit depvar indepvar1 indepvar2..., test(1)。
多元logistic回归分析2017
则四个格子所对应的概率分别是：
p1
p( y
1|
x
1)
exp( ) 1 exp( )
；
p2
p( y
1|
x
0)
exp( ) 1 exp( )
1
p1
p( y
0|
x
1)
1
1
exp(
)
；1
p2
p( y
0|
x
0)
1
1
exp( )
则似然函数为：
L [ exp( ) ]a[ exp( ) ]b[
15
例、口服避孕药（OC）与心肌梗死（MI）关系的病例对照研究结果
病例（MI） 对照
合计
服用 OC
39
24
63
未服 OC
114
154
268
合计
153
178
331
Logistic 回归分 析结果
16
表 15-1 为吸烟、饮酒与食管癌关系的病例-对照研究调查 资料，试进行 logistic 回归分析。
logistic回归模型的参数估计常采用最大似然估计。其基本 思想是先建立似然函数与对数似然函数，求使对数似然函 数最大时的参数值，其估计值即为最大似然估计值。
在病例-对照研究中，假设变量 y 取值 1 和 0 分别表示对象患
病和不患病；变量 x 取值 1 和 0 表示具有和不具有某种危险因 素；具体调查数据见下表：
其中， 0 为常数项， 1, 2 ,, m 为偏回归系数。
（15.1）
4
设 Z 0 1 X1 2 X 2 m X m ，则 Z 与 P 之间关系的
logistic 曲线如下图所示 。
如何用spss17.0进行二元和多元logistic回归分析
如何用spss17.0进行二元和多元logistic回归分析一、二元logistic回归分析二元logistic回归分析的前提为因变量是可以转化为0、1的二分变量，如：死亡或者生存，男性或者女性，有或无，Yes或No，是或否的情况。
下面以医学中不同类型脑梗塞与年龄和性别之间的相互关系来进行二元logistic回归分析。
（一）数据准备和SPSS选项设置第一步，原始数据的转化：如图1-1所示，其中脑梗塞可以分为ICAS、ECAS和NCAS三种，但现在我们仅考虑性别和年龄与ICAS的关系，因此将分组数据ICAS、ECAS和NCAS转化为1、0分类，是ICAS赋值为1，否赋值为0。
年龄为数值变量，可直接输入到spss中，而性别需要转化为（1、0）分类变量输入到spss当中，假设男性为1，女性为0，但在后续分析中系统会将1，0置换（下面还会介绍），因此为方便期间我们这里先将男女赋值置换，即男性为“0”，女性为“1”。
图 1-1第二步：打开“二值Logistic 回归分析”对话框：沿着主菜单的“分析（Analyze）→回归（Regression）→二元logistic（Binary Logistic）”的路径（图1-2）打开二值Logistic 回归分析选项框（图1-3）。
如图1-3左侧对话框中有许多变量，但在单因素方差分析中与ICAS 显著相关的为性别、年龄、有无高血压，有无糖尿病等（P<0.05），因此我们这里选择以性别和年龄为例进行分析。
在图1-3中，因为我们要分析性别和年龄与ICAS的相关程度，因此将ICAS选入因变量（Dependent）中，而将性别和年龄选入协变量（Covariates）框中，在协变量下方的“方法（Method）”一栏中，共有七个选项。
采用第一种方法，即系统默认的强迫回归方法（进入“Enter”）。
接下来我们将对分类（Categorical），保存（Save），选项（Options）按照如图1-4、1-5、1-6中所示进行设置。
多元回归分析与Logistic回归分析的应用研究的开题报告
多元回归分析与Logistic回归分析的应用研究的开题报告一、研究背景及意义随着社会经济的快速发展，人民生活水平不断提高，需求日益复杂多样。
各个行业也面临着挑战和机遇。
在经济研究领域，多元回归分析和Logistic回归分析是两种常用的分析方法，它们对于对人们在实际生活和工作中进行数据分析和决策具有积极的推动作用。
多元回归分析是一种很常用的统计分析方法，它在社会科学领域有广泛的应用。
多元回归分析是在研究两个或两个以上自变量与因变量的关系时使用的，它可以解决多个变量之间的共线性问题，同时能够测定变量之间的相关性和影响力。
而Logistic回归分析则是一种分类算法，在预测二元分类变量时应用广泛。
它能够通过建立数学模型来预测某一个事件的发生概率，并给出相应的概率值。
这种算法广泛应用于人口普查、医学、金融以及市场营销等领域。
因此，本文旨在对多元回归分析和Logistic回归分析的应用进行研究，以期提升分析方法的效率和准确性，并为实际决策提供科学依据。
二、研究内容与目标本文将从以下两个方面进行研究：1. 多元回归分析的应用研究（1）研究多元回归分析的基本概念和方法，以及其在社会科学领域的应用。
（2）以某公司的销售数据为例，运用多元回归分析法，探究产品销售量与价格、广告费用等自变量之间的关系，分析自变量的线性关系以及各自变量的影响大小。
2. Logistic回归分析的应用研究（1）研究Logistic回归分析的基本概念和方法，以及其在分类预测领域的应用。
（2）以一个银行的信用评级为例，运用Logistic回归分析法，预测客户违约的概率，设置相应的阈值，以提高贷款风险管理的能力。
三、研究方法与步骤在本文中，将使用如下的研究方法:1.文献综述法：通过查阅相关文献，深入了解多元回归分析和Logistic回归分析的基本概念、方法以及应用领域。
2.数据分析法：通过实际案例应用多元回归分析和Logistic回归分析，分析数据之间的相互关系，总结规律，得出结论。
多元logistic回归结果
多元logistic回归结果多元logistic回归分析是一种非常常见的统计分析方法，主要用于预测一个因变量的概率取值，而这个概率取值是由多个自变量共同决定的。
这种方法不仅能够应用于学术研究，在商业领域也非常广泛。
那么，在进行多元logistic回归分析时，其结果都有哪些含义呢？本篇文章将从不同角度对结果进行解读。
首先，从变量系数的角度看，多元logistic回归分析结果能够提供每个自变量对因变量影响的指向。
具体而言，回归系数的符号表示该变量的影响方向，正号表示该变量对因变量有积极的影响，负号表示该变量对因变量有负面的影响。
另外，系数的大小也表明了变量对结果的影响程度，系数越大，说明该变量对结果的影响越强。
需要注意的是，由于多元logistic回归是一种联合分析方法，不同变量之间可能存在复杂的交互作用关系，因此，在考虑单个变量对模型的贡献时，也需要关注其他变量的影响因素。
其次，从拟合度的角度看，多元logistic回归结果能够提供模型的总体拟合度。
一般情况下，多元logistic回归模型会给出一个拟合度指标，例如R²值或对数似然比（log-likelihood），该指标可以表征模型拟合数据的程度。
一般而言，R²值越高，表明模型对数据的拟合程度越好，但同时也需要考虑模型的过拟合或欠拟合问题。
对数似然比是一种基于统计假设检验的拟合度指标，可以通过比较模型对数似然值与基准模型对数似然值之间的差异来衡量模型拟合程度。
这种方法更加严谨，但需要对模型假设进行一定的测试。
此外，从预测能力的角度看，多元logistic回归结果还能提供模型的预测能力。
在实际应用中，多元logistic回归分析通常会将数据集分为训练集和测试集，先用训练集来拟合模型，再用未知的测试集来进行模型的预测效果测试。
在测试中，常见的预测评估指标包括准确率、召回率和F1分数等。
准确率可以表征模型对样本分类的准确程度，召回率可以表征模型对正样本的捕捉能力，F1分数是准确率和召回率的加权平均值。
多元Logistic回归
95% C onfidence Interv al for Exp(B)
Exp(B) Lo wer Bou ndUpper Bou nd
.269 .926
. 1.855
.
.127 .479
. 1.061
.
.569 1.791
. 3.244
.
.520 .726
. 1.887
.
.268 .367
. 1.105
有以下模型：
如方果程希相望减比即较可l得bn 和到P P c相两Y Y 应组 函，a c 数则。直 接将c 上 述两2x 1 1 2pxp
例题：
研究不同学校和不同课程计划对学生学习方式偏好
的影响，得到数据如下表。试进行logistic回归分
析学。校 课程计划
学生偏好的学习方式
.
1.009 1.434
. 3.221
.
模型结果的解释
变量“school1”回归系数为负值， 显著不为零，表明：自修与上课两种 学习方式相比，学校1的学生比学校3 的学生更容易选择上课
学校2与学校3的学生的选择则没什么
Lnp 0.5931.134school10.076school20.618program 自 修 Parameter Estimates
b. This p arameter is set to zero becau se it is redundan t.
单击此处添加副标题
结束
202X/XX/XX 汇报人姓名
Байду номын сангаас
Variable”框
OK
三．Analyze →Regression → Multinomial Logistic 打开Multinomial Logistic
stata多元logistic回归结果解读
stata多元logistic回归结果解读摘要：一、多元logistic 回归简介1.logistic 回归的定义2.logistic 回归与线性回归的区别3.多元logistic 回归的应用场景二、stata 软件进行多元logistic 回归分析1.安装并打开stata 软件2.输入数据并定义变量3.进行多元logistic 回归分析三、解读多元logistic 回归结果1.结果概述2.系数解释3.OR 值和P 值解读4.模型检验和其他统计指标四、结论与建议1.根据结果进行因素分析2.对未来研究的展望正文：一、多元logistic 回归简介Logistic 回归是一种广义的线性回归分析模型，主要用于处理二分类变量（如患病与未患病）的问题。
与线性回归相比，logistic 回归的输出结果是概率，更符合实际情况。
多元logistic 回归是在logistic 回归的基础上，增加自变量个数，以考虑多个因素对二分类变量的影响。
多元logistic 回归广泛应用于数据挖掘、疾病自动诊断、经济预测等领域。
例如，在探讨引发疾病的危险因素时，可以根据危险因素预测疾病发生的概率。
以胃癌病情分析为例，可以选择两组人群（胃癌组和非胃癌组），根据他们的体征和生活方式等自变量，通过多元logistic 回归分析，得到危险因素的权重，从而了解哪些因素是胃癌的危险因素。
同时，可以根据该权值预测一个人患癌症的可能性。
二、stata 软件进行多元logistic 回归分析要使用stata 软件进行多元logistic 回归分析，首先需要安装并打开stata 软件。
然后，输入数据并定义变量。
将因变量设为二分类变量（如患病与未患病），自变量可以包括连续变量和分类变量。
接下来，在stata 命令窗口中输入“logistic”命令，进行多元logistic 回归分析。
三、解读多元logistic 回归结果在多元logistic 回归分析完成后，stata 会生成一系列结果。
多元有序logistic回归模型_条件__解释说明
多元有序logistic回归模型条件解释说明1. 引言1.1 概述本篇文章旨在介绍多元有序logistic回归模型，并深入探讨其条件和解释说明。
随着数据科学和机器学习的发展，logistic回归作为一种广泛应用于分类问题的经典算法之一，已被广泛研究和运用。
然而，针对多元分类问题中存在有序等级的情况，传统的二元logistic回归无法满足需求。
因此，多元有序logistic回归模型应运而生，可以更好地处理具有有序等级的分类变量。
1.2 文章结构本文将从以下几个方面对多元有序logistic回归模型进行详细阐述：首先，在"2. 多元有序logistic回归模型"部分将介绍该模型的基本概念、原理及其在实际场景中的应用。
接下来，在"3. 条件"部分将讨论条件定义和分类，并重点探究条件对多元有序logistic回归模型的影响，并提供实际案例分析以加深理解。
在"4. 解释说明"部分，我们将介绍如何解读模型结果、参数估计意义以及验证结果和评价指标等重要内容。
最后，在"5. 结论"部分将对整个研究进行总结和发现的归纳，并提出未来研究的建议和展望。
1.3 目的本文的目的是系统介绍多元有序logistic回归模型，深入剖析其条件和解释说明。
通过阅读本文，读者将能够理解多元有序logistic回归模型在处理具有有序等级分类变量时的优势和应用场景，并且学会如何正确解读模型结果，理解参数估计意义，并通过验证结果和评价指标对模型进行评估。
最终，本文旨在为数据科学从业者提供一个全面、清晰和实用的参考指南，以便更好地运用多元有序logistic 回归模型来解决实际问题。
2. 多元有序logistic回归模型:2.1 模型介绍:多元有序logistic回归模型是一种用于预测有序分类结果的统计模型。
它通过将多个有序分类作为目标变量，并基于一组自变量进行建模，来分析目标变量与自变量之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9
(2) 二值多元logistic回归模型： 令y是1,0变量，x1,x2,…,xk是任意k个变量； p=p(y=1|x1,x2,…,xk)，那么，变量y关于变量x1,x2,…,xk 的k元logistic回归模型是：
• 按因变量取值个数：
o 二值logistic回归分析
o 多值logistic回归分析
• 按自变量个数：
o 一元logistic回归分析
o 多元logistic回归分析
8
第二节 Logistic 回归分析的数学模型
(1) 二值一元logistic回归模型： 令y是1,0变量，x是任
意变量，p=p(y=1|x) ，那么，二值变量y关于 变量x的一元logistic 回归 模型是：
15
The LOGISTIC Procedure Data Set: WORK.EG7_1A Response Variable: Y Response Levels: 2 Number of Observations: 4 Weight Variable: WT Sum of Weights: 295 Link Function: Logit
注意：对于二值Logistic回归模型，Y=0的模型是：
p = p(y=0|x1,…,xk ) = 1 - p(y=1|x1,…,xk)
10
Logistic 回归模型的另外一种形式 它给出变量z=logit(p)关于x 的线性函数。
11
(3) 多值logistic回归模型:
例如，当y取值1,2,3时，logistic回归模型是：
Response Profile
Ordered
Total
Value
Y Count
Weight
1
1
2
20.00000
2
0
2 275.00000
16
Model Fitting Information and Testing Global Null Hypothesis BETA=0
Intercept
Intercept
P1 = p(y=1) = P1 P1=
P2=
P2 = p(y=2) =P2-P1
P3= p(y≤3 | x) = 1 - P2 累积概率模型
P3 = p(y=3) =1-P2 独立概率模型
12
第三节 Logistic回归分析方法步骤
1、估计参数 ---- 最大似然法 2、检验参数的显著性
H0: βj=0 vs H1: βj≠0 3、检验模型的显著性
1、什么是Logistic 回归分析？ 研究因变量y取某个值的概率变量p与 自变量x的依存关系。 p=p(y=1|x)=f(x)
7
2ogistic回归分析
o 非条件logistic回归分析（成组数据）
o 条件logistic回归分析（配对病例-对照数据）
效等不同的效果?
是回归分析问题: Y=f(x)
5
如何解决这样的问题？
不能直接分析 变量y与x的关系
y取某个值的概 率变量p与x 的 关系
Logistic回归模型
y=f(x) y=1,0 x任意
p=p(y=1|x)=f(x) 0≤p≤1, x任意
存在，且不唯一
6
第一节 Logistic 回归分析的概念
2
回忆：
回归分析的分类
一个 因变 量y
连续型因变量 (y) --- 线性回归分析 分类型因变量 (y) ---Logistic 回归分析 生存时间因变量 (t) ---生存风险回归分析 时间序列因变量 (t) ---时间序列分析
多个因变量 (y1,y2…yk)
路径分析 结构方程模型分析
3
医学研究中经常遇到分类型变量
H0: β1=…=βk=0 vs H1: βj≠0 4、解释参数的实际意义
13
例1、自变量是二值分类型变量 某医院为了研究导致手术切口感染的原因，收集了295例手术 者情况，其中，手术时间小于或等于5小时的有242例，感染者 13例；手术时间大于5小时的有53例，感染者7例。试建立手术 切口感染(y)关于手术时间(x)的logistic回归模型。
• 二分类变量： o 生存与死亡 o 有病与无病 o 有效与无效 o 感染与未感染
• 多分类有序变量： o 疾病程度（轻度、中度、重度） o 治愈效果（治愈、显效、好转、无效）
• 多分类无序变量： o 手术方法（A、B、C） o 就诊医院（甲、乙、丙、丁）
4
医学研究者经常关心的问题
• 哪些因素导致了人群中有的人患胃癌而有的人不患胃癌? • 哪些因素导致了手术后有的人感染，而有的人不感染？ • 哪些因素导致了某种治疗方法出现治愈、显效、好转、无
and
Criterion
Only
Covariates Chi-Square for Covariates
AIC
148.262
146.686
.
SC
147.648
145.458
.
-2 LOG L
146.262
142.686
3.576 with 1 DF (p=0.0586)
Score
.
.
4.224 with 1 DF (p=0.0399)
第七章
多元Logistic 回归分析
Multiple Logistic Regression Analysis
1
主要内容
➢ Logistic 回归分析的基本概念 ➢ Logistic 回归分析的数学模型 ➢ Logistic 回归模型的建立和检验 ➢ Logistic 回归系数的解释 ➢ 配对病例-对照数据的logistic回归分析
>
0 (≤
7
4163
46
25239
53
242
14
data eg7_1a; input y x wt @@; cards;
11 7 1 0 13 0 1 46 0 0 229 ; run; proc logistic descending ;
model y=x ; weight wt; run;
SAS程序
Analysis of Maximum Likelihood Estimates
Parameter Standard Wald
Pr > Standardized
Variable DF Estimate Error Chi-Square Chi-Square Estimate