互斥事件习题
概率与统计习题集(蓝皮2960)
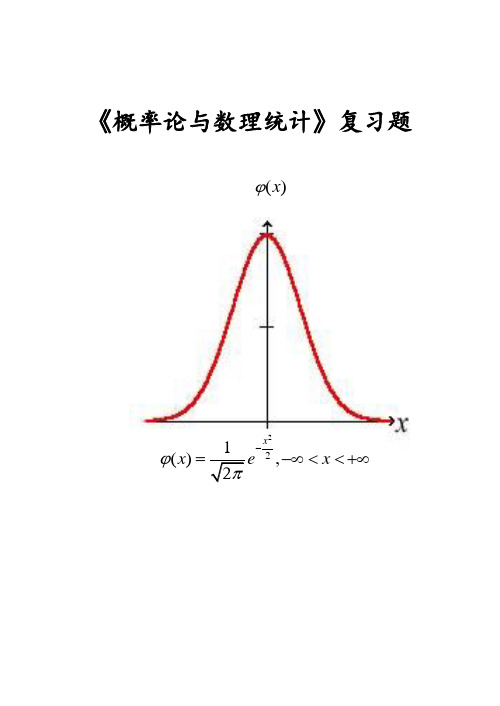
《概率论与数理统计》复习题()xϕ221(),xx e xϕ-=-∞<<+∞1习题一一、填空题:1. 设事件,A B 互斥且()0.1,()0.3P A P A B =+=,则()_______P B = 2. 设()0.2,()0.3,()0.4,P A P B P A B ==⋃=则()_______P A B ⋃= 3. 将10个球随机地放入10个盒子中去,则至少有一个盒子空着的概率为___________ 4. 若在区间(0,1)内任取两个数,记A =“两数之积小于41”,=B “两数之和大于21”,则=⋃)(B A P 5.随机地向半圆:00)y a <<>内掷一点,点落在半圆内任何区域的概率与该区域的面积成正比,则原点和该点的连线与x 轴的夹角小于4π的概率为__________ 6. 将三个球随机地放入4个杯子中去,则杯中球的最多个数为1的概率为_______7. 设对于随机事件A 、B 、C ,有41)()()(===C P B P A P ,81)(=AC P ,0)()(==BC P AB P , 则C B A 、、三个事件至少有一个发生的概率为________8. 设A 、B 为随机事件,3.0)(,7.0)(=-=B A P A P ,则______)(=AB P9.若2.0)(,5.0)(,6.0)(===AB P B P A P ,则_____)(_____,)(_____,)(____,)(=⋃===B A P B A P B A P B A P 10.在n 阶行列式det(ij a )的展开式中任取一项,若此项不含元素11a 的概率为20001999,则此行列式的阶数n = 。
11.箱中盛有a 个白球和b 个黑球,从中任意地接连取1+k )1(b a k +≤+个球,如果每次取出后不放回,则1+k 次取出的是白球的概率为_________ 二、选择题:1.设,,A B C 是任意三个事件,则下列命题正确的是( ) (A )()A B B A B ⋃-=- (B )()A B B A -⋃= (C )()()A B C A B C ⋃-=⋃- (D )A B AB AB ⋃=⋃2.设随机事件,,A B C 两两互斥,且()0.2P A =,()0.3P B =,()0.4P C =,则[()]P A B C ⋃-=( )(A )0.3 (B )0.5 (C )0.1 (D )0.443.对于任意两个随机事件A和B,有()P A B -=( ) (A)()()P A P B - (B)()()()P A P B P AB -+2(C)()()P A P AB - (D)()()()P A P B P AB +-4.设B 、C 分别是将一枚筛子连掷两次后出现的点数,则方程20x Bx C ++=有实根的概率为( )(A )136(B )536(C )1736(D )19365.设c B A P b B P a A P =+==)(,)(,)(,则=)(B A P [ ] (A )b a - (B )b c - (C ))1(b a - (D )a b -6.若1(),2P A =1()2P B =,则下列等式成立的是( )(A )()1P A B ⋃= (B) 1()4P AB =(C) 1()2P AB = (D)()()P AB P AB =7.以A 表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件A 为(A )“甲种产品滞销,乙种产品畅销”; (B )“甲、乙两种产品均畅销” (C )“甲种产品滞销”; (D )“甲种产品滞销或乙种产品畅销”。
独立又互斥的事件例子

独立又互斥的事件例子独立事件和互斥事件是概率论中的两个重要概念,它们在实际生活中也有很多应用。
独立事件指的是两个或多个事件之间没有任何关联,一个事件的发生不会影响另一个事件的发生;而互斥事件则是指两个或多个事件之间是互相排斥的,一个事件的发生会排除另一个事件的发生。
下面我将列举一些独立事件和互斥事件的例子。
独立事件:1. 抛硬币,正面朝上的概率是1/2,每次抛硬币的结果是独立的。
2. 摇骰子,每个点数出现的概率是1/6,每次摇骰子的结果是独立的。
3. 抽奖,每个人中奖的概率是相同的,每次抽奖的结果是独立的。
4. 打牌,每个人的牌是随机分配的,每次打牌的结果是独立的。
5. 看电影,每个人对电影的评价是独立的,一个人的评价不会影响另一个人的评价。
6. 购买彩票,每个号码中奖的概率是相同的,每次购买彩票的结果是独立的。
7. 看天气预报,每天的天气预报是独立的,前一天的天气预报不会影响后一天的天气预报。
8. 看病,每个人的病情是独立的,一个人的病情不会影响另一个人的病情。
9. 赌博,每个人的赌注是独立的,一个人的输赢不会影响另一个人的输赢。
10. 交通事故,每个车辆的事故发生概率是独立的,一个车辆的事故不会影响另一个车辆的事故。
互斥事件:1. 抛硬币,正面和反面是互斥事件,一个硬币只能有一个面朝上。
2. 摇骰子,每个点数是互斥事件,一个骰子只能有一个点数。
3. 抽奖,中奖和不中奖是互斥事件,一个人只能中一次奖。
4. 打牌,赢和输是互斥事件,一个人只能赢或输。
5. 看电影,喜欢和不喜欢是互斥事件,一个人只能有一个评价。
6. 购买彩票,中奖和不中奖是互斥事件,一个号码只能中一次奖。
7. 看病,治愈和未治愈是互斥事件,一个人只能有一个结果。
8. 赌博,赢和输是互斥事件,一个人只能赢或输。
9. 选课,选A课和选B课是互斥事件,一个人只能选一门课。
10. 考试,及格和不及格是互斥事件,一个人只能有一个成绩。
§2 2.3 第2课时 互斥事件习题课

6 7 P = 1− = . 1 20 10
(2)为了取出2人分别表演独唱和朗诵, (2)为了取出2人分别表演独唱和朗诵,抽取并观察第一 为了取出 张卡片后,又放回箱子中, 张卡片后,又放回箱子中,充分混合后再从中抽取第二 张卡片, 张卡片,求: i)独唱和朗诵由同一个人表演的概率; 独唱和朗诵由同一个人表演的概率;
判断下列给出的每对事件, 判断下列给出的每对事件,(ⅰ)是否为互斥事件,(ⅱ) 是否为互斥事件, 是否为对立事件,并说明道理. 从扑克牌40 40张 红桃、 是否为对立事件,并说明道理. 从扑克牌40张(红桃、黑 方块、梅花点数从1 10各10张 任取一张. 桃、方块、梅花点数从1-10各10张)中,任取一张. 抽出红桃” 抽出黑桃” (1)“抽出红桃”与“抽出黑桃”; 抽出红色牌” 抽出黑色牌” (2)“抽出红色牌”与“抽出黑色牌”; 抽出的牌点数为5的倍数” (3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于 9”. (1)是互斥事件,不是对立事件; (1)是互斥事件,不是对立事件; 是互斥事件 (2)既是互斥事件,又是对立事件; (2)既是互斥事件,又是对立事件; 既是互斥事件 (3)不是互斥事件,当然不可能是对立事件. (3)不是互斥事件,当然不可能是对立事件. 不是互斥事件
两个互斥事件的概率公式 预备概念:事件“ 预备概念:事件“A+B”表示A和B至少有一个发生的 B”表示A 表示 事件. 事件. 概括:在一个随机试验中,如果事件A 概括:在一个随机试验中,如果事件A和B是互斥事件 那么: P(A+B)=P(A)+P(B) 那么: 公式推广:若随机事件A 两两为互斥事件, 公式推广:若随机事件A1,A2……An两两为互斥事件, 则有
2.设M = { 1,2,3,4,5}, 任取x, y ∈M,x ≠ y. 求: + y恰为 的倍数的概率; (1)x 3 (2)xy恰为 的倍数的概率. 3
高中会考概率习题(含答案)

1. 一个射手进行一次射击,试判断下面四个事件A 、B 、C 、D 中有哪些是互斥事件事件A :命中的环数大于8;事件B :命中的环数大于5; 事件C :命中的环数小于4;事件D :命中的环数小于6.2. 某市派出甲、乙两支球队参加全省足球冠军赛.甲乙两队夺取冠军的概率分别是73和41.试求该市足球队夺得全省足球冠军的概率.3. 下列说法中正确的是A .事件A 、B 中至少有一个发生的概率一定比A 、B 中恰有一个发生的概率大B .事件A 、B 同时发生的概率一定比事件A 、B 恰有一个发生的概率小C .互斥事件一定是对立事件,对立事件不一定是互斥事件D .互斥事件不一定是对立事件,对立事件一定是互斥事件 4. 在放有5个红球、4个黑球、3个白球的袋中,任意取出3个球,分别求出3个全是同色球的概率5. 某单位36人的血型类别是:A 型12人,B 型10人,AB 型8人,O 型6人.现从这36人中任选2人,求此2人血型不同的概率.6. 在一只袋子中装有7个红玻璃球,3个绿玻璃球.从中无放回地任意抽取两次,每次只取一个.试求: (1)取得两个红球的概率; (2)取得两个绿球的概率;(3)取得两个同颜色的球的概率;(4)至少取得一个红球的概率.7. 将4名教师分配到3种中学任教,每所中学至少1名教师,则不同的分配方案共有A .12种B .24种C .36种D .48种8. 从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有A .140种B .120种C .35种D .34种9. 某人射击一次击中的概率为,经过3次射击,此人至少有两次击中目标的概率为A .81125B .54125C .36125D .2712510. (HARD)某班新年联欢会原定的5个节目已排成节目单, 开演前又增加了两个新节目.如果将这两个新节目插入原节目单中, 那么不同插法的种数为A .42B .96C .124D .4811.(HARD)在一次足球预选赛中,某小组共有5个球队进行双循环赛(每两队之间赛两场),已知胜一场得3分,平一场得1分,负一场的0分. 积分多的前两名可出线(积分相等则要要比净胜球数或进球总数). 赛完后一个队的积分可出现的不同情况种数为A.22 B.23 C.24 D.2512.(HARD) 4位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道题中任选一题作答,选甲题答对得100分,答错得-100分;选乙题答对得90分,答错得-90分。
小学数学概率练习题

小学数学概率练习题题目一:概率基础1. 掷一个骰子,问出现偶数的概率是多少?2. 一袋中有5个红球、3个蓝球和2个黄球,从中任意取出一个球,问取出红球的概率是多少?3. 一张扑克牌从52张牌中随机抽取一张,问抽到一张黑桃的概率是多少?题目二:事件概率计算1. 班级有30个男生和20个女生,从中随机抽取一名学生,问抽到女生的概率是多少?2. 有三个红色球和两个蓝色球,从中任意取出两个球,问取出两个红色球的概率是多少?3. 一副扑克牌中去掉所有的黑桃,剩下的牌共有39张,从中抽取一张牌,问抽到一张红桃的概率是多少?题目三:条件概率1. 一袋中有5个红球、3个蓝球和2个黄球,从中任意取出一个球,已知取出的球是红球,问这个球原本是黄球的概率是多少?2. 一盒中有10个苹果,其中3个是有虫子的,从中任意取出一个苹果,已知取出的苹果有虫子,问这个苹果原本是好的概率是多少?3. 有两个袋子,一个袋子中有3个红球和2个蓝球,另一个袋子中有4个红球和1个蓝球,先随机选择一个袋子,再从袋子中随机取出一个球,已知取出的球是红球,问这个球来自第一个袋子的概率是多少?题目四:互斥事件概率1. 掷两个骰子,问至少一个骰子出现1点的概率是多少?2. 有一副扑克牌,从中抽取一张牌,问抽到红桃或红心的概率是多少?3. 某班级有20名男生和30名女生,从班级中随机选择一名学生,问选择到男生或高年级学生的概率是多少?题目五:独立事件概率1. 一副扑克牌中任选两张牌,问两张牌都是红色的概率是多少?2. 一袋中有4个红球和5个蓝球,从中随机取出一个球,不放回,再从中取出一个球,问两次取出的球都是红球的概率是多少?3. 有两个盒子,一个盒子中有4个红球和2个蓝球,另一个盒子中有3个红球和3个蓝球,分别从两个盒子中随机取出一个球,问两次取出的球颜色相同的概率是多少?这些题目涵盖了概率基础知识、事件概率计算、条件概率、互斥事件概率和独立事件概率等内容。
互斥事件、相互独立事件的概率单元练习题

§11.2 互斥事件、相互独立事件的概率一、选择题:一、选择题:1.若1)(=+B A P ,则事件A A 与与B B 的关系是(的关系是(的关系是( ))A .A A 、、B B 是互斥事件是互斥事件是互斥事件 B B B..A A 、、B B 是对立事件是对立事件是对立事件C .A A 、、B B 不是互斥事件不是互斥事件不是互斥事件D D D.以上都不对.以上都不对.以上都不对2.两个事件对立是这两个事件互斥的( ))A .充分但不是必要条件.充分但不是必要条件B B.必要但不是充分条件.必要但不是充分条件.必要但不是充分条件C .充分必要条件.充分必要条件D D.既不充分又不必要条件.既不充分又不必要条件.既不充分又不必要条件3.今有光盘驱动器50个,其中一级品45个,二级品5个,从中任取3个,出现二级品的概率为(现二级品的概率为( ))A .35035C CB B..350352515C C C C ++ C C..3503451C C -D D..3501452524515C C C C C + 4.打靶时,甲每打10次可中靶8次,乙每打10次可中靶7次,若两人同时射一个目标,则他们都中靶的概率是(一个目标,则他们都中靶的概率是( ))A .1514B B..2512C C..43D D..53 5.某产品分甲、乙、丙三级,其中乙、丙两级均属次品若生产中出现乙级品的概率为0.030.03,,丙级品的概率为0.010.01,,则对成品抽查一件抽得正品的概率为( ))A .0.99B B..0.98C .0.97D D..0.966.甲盒中有200个螺杆,其中有160个A 型的,乙盒中有240个上螺母,其中有180个A 型的,现从甲、乙两盒中各任取一个,则能配成A 型的螺栓概率为( )). A .201 B.1615 C C..53 D .2019 7.流星穿过大气层落在地面上的概率为0.0020.002,则流星数量为,则流星数量为10个的流星群穿过大气层有4个落在地面上的概率约为(个落在地面上的概率约为( ))A .51032.3-´B .81032.3-´C .51064.6-´D .81064.6-´8.有10门炮同时向目标各发射一发炮弹,如果每门炮的命中率都是0.10.1,则目,则目标被击中的概率约为(标被击中的概率约为( )). 则乘客期待电车首先停靠的概率等于 .18.A 、B 、C 、D 、E 五人分四本不同的书,每人至多分一本,求:(1)A 不分甲书,B 不分乙书的概率. (2)甲书不分给A 、B ,乙书不分给C 的概率. 19.19.从从1,2,3,…,,…,100100这100个数中,随机取出两个数,求其积是3的倍数的概率概率2020.两台机床加工同样的零件,第一台出废品的概率是.两台机床加工同样的零件,第一台出废品的概率是0.03 0.03 ,第二台出废品的,第二台出废品的概率是0.02 0.02 .加工出来的零件堆放在一起.若第一台加工的零件是第二台加工.加工出来的零件堆放在一起.若第一台加工的零件是第二台加工的零件的2倍,求任意取出的零件是合格品的概率.21.21.学校文艺队每个成员,唱歌、跳舞至少会一门.已知会唱歌的有学校文艺队每个成员,唱歌、跳舞至少会一门.已知会唱歌的有5人,会跳舞的有7人现从中选3人,至少要有一人既会唱歌又会跳舞的概率是2116 ,求该队的人数.队的人数.22.22.对贮油器进行对贮油器进行8次独立射击,若第一次命中只能使汽油流出而不燃烧,第二次命中才能使汽油燃烧起来.每次射击命中目标的概率为0.20.2,求汽油燃烧起来,求汽油燃烧起来的概率.的概率.某商场经销某商品,顾客可采用一次性付款或分期付款购买 0 元 元的概率 43,甲、丙,甲、丙 两人都做错的概率是1,乙、丙两人都做对的概率是1。
高中概率问题练习题及讲解

高中概率问题练习题及讲解1. 掷骰子问题- 题目:一个均匀的六面骰子被掷两次,求两次掷出的点数之和为7的概率。
- 解析:首先确定所有可能的结果总数,即6*6=36种。
然后找出两次掷骰子点数和为7的组合,它们是(1,6)、(2,5)、(3,4)、(4,3)、(5,2)和(6,1),共6种。
因此,所求概率为6/36,简化后为1/6。
2. 抽卡片问题- 题目:从一副没有大小王的52张扑克牌中随机抽取一张,求抽到黑桃A的概率。
- 解析:一副标准扑克牌中有13张黑桃,其中只有1张是黑桃A。
因此,抽到黑桃A的概率为1/52。
3. 独立事件问题- 题目:如果一个事件A发生的概率是0.3,另一个事件B发生的概率是0.5,且A和B是相互独立的,求A和B同时发生的概率。
- 解析:独立事件同时发生的概率等于各自发生概率的乘积。
因此,A和B同时发生的概率为0.3*0.5=0.15。
4. 互斥事件问题- 题目:如果事件A和事件B是互斥的,且它们发生的概率分别为0.4和0.3,求至少有一个事件发生的概率。
- 解析:互斥事件至少有一个发生的概率等于它们各自发生概率的和,减去它们同时发生的概率(如果有的话)。
由于A和B互斥,它们不可能同时发生,所以同时发生的概率为0。
因此,至少有一个事件发生的概率为0.4+0.3=0.7。
5. 条件概率问题- 题目:已知事件A发生的概率为0.5,事件B在A发生条件下发生的概率为0.7,求事件B发生的概率。
- 解析:事件B发生的总概率等于事件A发生且B发生的概率加上事件A不发生且B发生的概率。
由于A和B在A发生条件下是相关的,我们只能计算A发生且B发生的概率,即0.5*0.7=0.35。
事件A不发生且B发生的概率需要额外信息才能计算。
6. 全概率公式问题- 题目:如果事件A1、A2、A3是两两互斥的事件,它们发生的概率分别为p1、p2、p3,且它们的并集概率为1,求事件B在这些条件下发生的概率,已知B在A1、A2、A3条件下发生的概率分别为p(B|A1)、p(B|A2)、p(B|A3)。
9.1.2概率与统计练习题

件B'∪D',依据互斥事件的概率加法公式,有P(B'∪D')=P(B')+P(D')=0
.29+0.35=0.64. ②(法一)由于A,AB型血不能输给B型血的人,所以“任找一人,其
考点整合 基础训练 典例导练 考径避陷 方法技巧 名校押题
1~6 6~9 10~12
血不能输给张三”为事件A'∪C',依据互斥事件的概率加法公式, 有P(A'∪C')=P(C')+P(A')=0.28+0.08=0.36.
①任找一人,其血可以输给张三的概率是多少? ②任找一人,其血不能输给张三的概率是多少? (2)一个箱子内有9张票,其号码分别为1,2,…,8,9,从中任取出2张,其 号码至少有一个为奇数的概率是多少? 【分析】(1)分析的是互斥事件,那么直接用公式可解决.
例题备选
(2)“至少有一个为奇数”的对立事件是“都为偶数”,那么可以 用对立事件的概率来解决. 【解析】(1)①对任一人,其血型为A,B,AB,O的事件分别记为A',B', C',D'.由已知,有P(A')=0.28,P(B')=0.29,P(C')=0.08,P(D')=0.35.因为B, O型血可以输给张三,所以“任找一人,其血可以输给张三”为事
2.特别地,若事件B与事件A互为对立事件,则A∪B为必然 事件,P(A∪B)=1.再由加法公式得P(A)=1-P(B). 3.若事件A与B互斥,则P(A∪B)=P(A)+P(B)(推广情况:如果 A1、A2、…、An彼此至斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
互斥事件习题篇一:互斥对立事件练习题互斥对立事件练习题 1.把红、黑、蓝、白4张纸牌随机地分发给甲、乙、丙、丁4个人, 每人分得1张,事件“甲分得1张红牌”与事件“乙分得1张红牌”是( C ) A.对立事件B.不可能事件 C.互斥但不对立事件 D.以上答案都不对 2.1人在打靶中连续射击2次,事件“至少有1次中靶” 的对立事件是( C ) A.至多有1次中靶 B.2次都中靶 B. C.2次都不中靶 C.只有1次中靶 3.1人在打靶中连续射击2次,事件“2次都中靶” 的对立事件是( B ) A.2次都不中靶 B.至多有1次中靶 C.至少有1次中靶 D.只有1次中靶 4.产品中有正品4件,次品3件,从中任取2件,其中事件:①恰有一件次品和恰有2件次品;②至少有1件次品和全都是次品;③至少有1件正品和至少有一件次品;④至少有1件次品和全是正品。
4组中互斥事件的组数是 ( B) A.1组 B. 2组 C.3组D. 4组 5.某人在打靶中连续射击2次,事件“至少有一次中靶”的互斥事件是( C ) A.至多有一次中靶 B.两次都中靶C.两次都不中靶D.只有一次中靶 6.从装有红球、白球和黑球各2个的口袋内一次取出2个球,给出以下事件:①两球都不是白球;②两球中恰有一白球;③两球中至少有一个白球.其中与事件“两球都为白球”互斥而非对立的事件是( A ) A.①② B.①③ C.②③ D.①②③ 7.一个人连续射击2次,则下列各事件中,与事件“恰中一次”互斥但不对立的事件是( D ) A.至多射中一次B.至少射中一次 C.第一次射中 D.两次都不中8.抛掷一个骰子,记A为事件“落地时向上的数是奇数”, B为事件“落地时向上的数是偶数”,事件A与B是 ( C ). (A)互斥但不对立事件(B)对立但不互斥事件(C)对立事件(D)不是互斥事件 9.在下列结论中,正确的为 ( B) A.若A与B是两互斥事件,则A?B是必然事件. B.若A与B是对立事件,则A?B是必然事件 . C.若A与B是互斥事件,则A?B是不可能事件. D.若A与B是对立事件,则A?B不可能是必然事件. 10. 在下列结论中正确的为( B) ①互斥事件一定是对立事件;②对立事件不一定是互斥事件③互斥事件不一定是对立事件;④对立事件一定是互斥事件 A.①② B.③④ C.②③ D.②④ 11.从装有5个红球和3个白球的口袋内任取3个球,那么下列各对事件中,互斥而不对立的是( D ) A.至少有一个红球与都是红球 B.至少有一个红球与都是白球 C.至少有一个红球与至少有一个白球D.恰有一个红球与恰有两个红球 12.从装有4个黑球和3个白球的口袋内任取3个球,下列事件①恰有1个白球和全是白球;②至少有1个白球和全是黑球;③至少有1个白球和至少有2个白球;④至少有1个白球和至少有1个黑球;其中互为对立事件的是(B ) A.① B.②C.③ D.④篇二:互斥对立事件知识点+练习题一、知识点复习 1.事件的包含关系如果事件A 发生,则事件B______.则称事件B______事件 A. 2.相等事件若______且______,那么事件A与事件B相等. 3.并(和)事件若某事件发生当且仅当___________,则称此事件为事件A与B的并事件(或称和事件)记作:A∪B. 4.交(积)事件若某事件发生当且仅当_________,则称此事件为事件A与B的交事件(或称积事件)记作:A∩B. 5.互斥事件若A∩B为_________,即A∩B=______,那么称事件A与事件B________. 6.对立事件____________________对立事件.例如:某同学在高考中数学考了150分,与这同学在高考中考得130分,这两个事件是________. 7.互斥事件概率加法公式当事件A与B互斥时,满足加法公式:P(A∪B)=P(A)+P(B);若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)=________,于是有P(A)=________. 例如:投掷骰子六点向上的概率为1/6,投得向上点数不为六点的概率为:________. 8. 如果事件A与事件B互斥,则____________________;如果事件A与事件B对立,则________________________。
二、练习题 1.在一对事件A,B中,若事件A 是必然事件,事件B是不可能事件,那么A和B() A.是互斥事件,不是对立事件 B.是对立事件,但不是互斥事件 C.是互斥事件,也是对立事件 D.既不是对立事件,也不是互斥事件 2.把红、黑、蓝、白4张纸牌随机地分发给甲、乙、丙、丁4个人,每人分得1件,事件“甲分得红牌”与事件“乙分得红牌”是( ) A.对立事件 B.不可能事件 C.互斥但不对立事件D.以上答案都不对 3.给出以下结论:①互斥事件一定对立②对立事件一定互斥③互斥事件不一定对立④事件A与B的和事件的概率一定大于事件A的概率⑤事件A与B互斥,则有P(A)=1-P(B) 其中正确命题的个数为( ) A.0个 B.1个 C.2个 D.3个4、某县城有甲、乙两种报纸供居民订阅,记事件A为“只订甲报”,事件B为“至少订一种报纸”,事件C为“至多订一种报纸”,事件D为“不订甲报”,事件E为“一种报纸也不订”.判断下列事件是不是互斥事件;如果是,再判断它们是不是对立事件: (1)A与C;(2)B与E;(3)B与D;(4)B与C;(5)C与E.5.某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.判断下列每对事件是事件的运算不是互斥事件,如果是,再判断它们是不是对立事件. (1)恰有1名男生与恰有2名男生; (2)至少1名男生与全是男生; (3)至少1名男生与全是女生; (4)至少1名男生与至少1名女生. 6、抛掷一枚骰子,下列事件: A={出现奇数点},B={出现偶数点},C={点数小于3},D={点数大于2},E={点数是3的倍数}.则:(1)A∩B=________,B∩C=________. (2)A∪B =________,B+C=________. (3)记为事件H的对立事件,则=_______,∩C =_____,∪C=_____, +=______. 7.某校组织一个夏令营,在高一(1)班抽一部分学生参加,记事件A为抽到高一(1)班的运动员,事件B为抽到高一(1)班数学竞赛小组成员,事件C为抽到高一(1)班英语竞赛小组成员.说明下列式子所表示的事件:(1)A∪B (2)A∩C(3)A∪(B∩C) 8、某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算这个射手在一次射击中: (1)射中10环或7环的概率; (2)没有射中10环的概率; (3)不够7环的概率. (4)该射手射击两次中第一次射中10环,第二次射中8环的概率; (5)该射手射击两次中有一次射中10环,一次射中8环的概率;篇三:互斥事件、相互独立事件的概率单元练习题11.2 互斥事件、相互独立事件的概率一、选择题: 1.若P(A?B)?1 ,则事件A 与B 的关系是() A.A 、B 是互斥事件 B.A 、B 是对立事件 C.A 、B 不是互斥事件 D.以上都不对 2.两个事件对立是这两个事件互斥的() A.充分但不是必要条件B.必要但不是充分条件 C.充分必要条件D.既不充分又不必要条件 3.今有光盘驱动器50个,其中一级品45个,二级品5个,从中任取3个,出现二级品的概率为() 3133121C5C5?C52?C5C45C5C45?C52C45A.3 B.C.1?3D. 33C50C50C50C50 4.打靶时,甲每打10次可中靶8次,乙每打10次可中靶7次,若两人同时射一个目标,则他们都中靶的概率是()A.141233B.C. D. 152545 5.某产品分甲、乙、丙三级,其中乙、丙两级均属次品若生产中出现乙级品的概率为0.03,丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为() A.0.99 B.0.98 C.0.97 D.0.96 6.甲盒中有200个螺杆,其中有160个A型的,乙盒中有240个上螺母,其中有180个A 型的,现从甲、乙两盒中各任取一个,则能配成A型的螺栓概率为(). A.115319B. C.D. 2016520 7.流星穿过大气层落在地面上的概率为0.002,则流星数量为10个的流星群穿过大气层有4个落在地面上的概率约为() A.3.32?10?5 B.3.32?10?8 C.6.64?10?5D.6.64?10?8 8.有10门炮同时向目标各发射一发炮弹,如果每门炮的命中率都是0.1,则目标被击中的概率约为()A.0.45 B.0.55 C.0.65 D.0.75 9.某人参加一次,若五道题中解对四题则为及格,已知他的解题正确率为 3 ,则他及格的概率是(). 5 A.24381010571053 B. C. D. 3125312531253125 二、填空题 10.乘客在某电车站等待26路或16路电车,该站停靠16,22,26,31四路电车假定各路电车停靠的频率一样,则乘客期待电车首先停靠的概率等于 . 11.今有一批球票,按票价分类如下:10元票5张,20元票3张,50元票2张,从这10张票中随机抽出3张,票价和为70元的概率是____________. 12.某市派出甲、乙两支球队参加全省足球冠军赛甲乙两队夺取冠军的概率分别31是和.则该市足球队夺得全省冠军的概率是_________. 74 13.从甲、乙、丙三种零件中各取1件组成某产品,所用三零件必须是正品,所得产品才是合格品.已知三种零件的次品率分别为2%,3%,5%,则产品的次品率是______. 14.两台独立在两地工作的雷达,每台雷达发现飞行目标的概率分别为0.9和0.85,则有仅有1台雷达发现飞行目标的概率为___________. 15.一袋中有8个白球,4个红球;另一袋中,有6个白球,6个红球.从每袋中任取一个球,则取得颜色相同的球的概率是_________. 16.如图10-12,靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成,射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.35、0.30、0.25,求不命中靶的概率为____________.三、解答题 17.某同学参加科普知识竞赛,需回答3个问题.竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响. (1)求这名同学得300分的概率;(2)求这名同学至少得300分的概率. 18.A、B、C、D、E五人分四本不同的书,每人至多分一本,求:(1)A不分甲书,B不分乙书的概率. (2)甲书不分给A、B,乙书不分给C的概率. 19.从1,2,3,…,100这100个数中,随机取出两个数,求其积是3的倍数的概率 20.两台机床加工同样的零件,第一台出废品的概率是0.03 ,第二台出废品的概率是0.02 .加工出来的零件堆放在一起.若第一台加工的零件是第二台加工的零件的2倍,求任意取出的零件是合格品的概率. 21.文艺队每个成员,唱歌、跳舞至少会一门.已知会唱歌的有5人,会跳16舞的有7人现从中选3人,至少要有一人既会唱歌又会跳舞的概率是,求该21 队的人数. 22.对贮油器进行8次独立射击,若第一次命中只能使汽油流出而不燃烧,第二次命中才能使汽油燃烧起来.每次射击命中目标的概率为0.2,求汽油燃烧起来的概率. 23.如图,已知电路中4个开关闭合的概率都是概率.1 ,且是互相独立的,求灯亮的 2 24.根据以往资料统计,顾客采用一次性付款的概率是06,经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元(Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率;(Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率 25.甲、乙、丙三人分别独立解一道题,已知甲做对这道题的概率是两人都做错的概率是3,甲、丙 411,乙、丙两人都做对的概率是。
