河南省郑州市枫杨外国语学校2019-2020学年八年级下学期第一次月考数学试题(word无答案)
人教版初中数学八年级下册第一次月考试卷(河南省郑州市

2018-2019学年河南省郑州市中原区枫杨外国语中学八年级(下)开学数学试卷一、选择题(每题3分,共30分)1.(3分)下列运算错误的是()A.B.C.D.2.(3分)已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是()A.20或16B.20C.16D.以上答案均不对3.(3分)下列三角形,①有两个角等于60°;②有一个角等于60°的等腰三角形;③一腰上的中线也是这条腰上的高的等腰三角形,其中能判定是等边三角形的个数是()A.3个B.2个C.1个D.0个4.(3分)在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在所给的下列条件中能判断△ABC不是直角三角形的是()A.∠A=∠C﹣∠B B.a2=c2﹣b2C.a=k,b=k,c=k(k>0)D.a:b:c=2:3:45.(3分)如图所示,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为()A.45°B.55°C.60°D.65°6.(3分)如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在()A.△ABC三条中线的交点处B.△ABC三条角平分线的交点处C.△ABC三条高线的交点处D.△ABC三条边的垂直平分线的交点处7.(3分)如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于()A.1:1:1B.1:2:3C.2:3:4D.3:4:58.(3分)给出下面5个式子:①3>0;②4x+3y≠0;③x=3;④x﹣1;⑤x+2≤3,其中不等式有()A.2个B.3个C.4个D.5个9.(3分)已知不等式2x﹣a≤0的正整数解恰好是1,2,3,4,5,那么a的取值范围是()A.a>10B.10≤a≤12C.10<a≤12D.10≤a<12 10.(3分)如图是小李销售某种食品的总利润y元与销售量x千克的函数图象(总利润=总销售额﹣总成本).由于目前销售不佳,小李想了两个解决方案:方案(1)是不改变食品售价,减少总成本;方案(2)是不改变总成本,提高食品售价.下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是()A.②,③B.①,③C.①,④D.④,②二、填空题(每题3分,共18分)11.(3分)如图,已知CA=CB,则数轴上点A所表示的数是.12.(3分)已知:点A(﹣1,a)、B(1,b)在函数y=﹣2x+m的图象上,则a b (在横线上填写“>”或“=”或“<”).13.(3分)已知正比例函数y=kx(k是常数,k≠0),当﹣3≤x≤1时,对应的y的取值范围是﹣1≤y≤,且y随x的减小而减小,则k的值为.14.(3分)如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D =∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是cm.15.(3分)如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为.16.(3分)如图,等边三角形ABC中,AB=8,BD⊥AC于点D,点E、F分别是BC、DC 上的动点,沿EF所在直线折叠△CEF,使点C落在BD上的点C′处,当△BEC′是直角三角形时,BC′的值为.三、解答题(共7小题)17.(8分)计算:(1)(2).18.(6分)郑州市开展了“中学生阳光体育运动”,小明和小亮在课外活动中,报名参加了短跑训练小组.在5次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.(1)请根据图中信息,分别计算他们的平均数、极差和方差填入表格:(2)若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?19.(8分)(1)解不等式,并求出它的正整数解;(2)已知关于x,y的方程组的解满足不等式x+y<3,求实数a的取值范围.20.(6分)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.21.(8分)一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中AB所示;慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段OC所示,根据图象进行以下研究.解读信息:(1)甲,乙两地之间的距离为km;(2)线段AB的解析式为;线段OC的解析式为;问题解决:(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象.22.(8分)为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.(1)参加此次研学旅行活动的老师和学生各有多少人?(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为辆;(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.23.(8分)操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:(1)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②说明理由.(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由.2018-2019学年河南省郑州市中原区枫杨外国语中学八年级(下)开学数学试卷参考答案与试题解析一、选择题(每题3分,共30分)1.(3分)下列运算错误的是()A.B.C.D.【分析】根据二次根式的加减法对A进行判断;根据二次根式的乘法法法则对B进行判断;根据二次根式的除法法法则对C进行判断;根据二次根式的性质对D进行判断.【解答】解:A、与不是同类二次根式,不能合并,所以A选项的计算错误;B、==,所以B选项的计算正确;C、÷==,所以C选项的计算正确;D、(﹣)2=2,所以D选项的计算正确.故选:A.【点评】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.2.(3分)已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是()A.20或16B.20C.16D.以上答案均不对【分析】根据非负数的意义列出关于x、y的方程并求出x、y的值,再根据x是腰长和底边长两种情况讨论求解.【解答】解:根据题意得,解得,(1)若4是腰长,则三角形的三边长为:4、4、8,不能组成三角形;(2)若4是底边长,则三角形的三边长为:4、8、8,能组成三角形,周长为4+8+8=20.故选:B.【点评】本题考查了等腰三角形的性质、非负数的性质及三角形三边关系;解题主要利用了非负数的性质,分情况讨论求解时要注意利用三角形的三边关系对三边能否组成三角形做出判断.根据题意列出方程是正确解答本题的关键.3.(3分)下列三角形,①有两个角等于60°;②有一个角等于60°的等腰三角形;③一腰上的中线也是这条腰上的高的等腰三角形,其中能判定是等边三角形的个数是()A.3个B.2个C.1个D.0个【分析】根据等边三角形的判定判断即可.【解答】解:①两个角为60度,则第三个角也是60度,则其是等边三角形,故正确;②这是等边三角形的判定2,故正确;③根据等边三角形三线合一性质,故正确.所以都正确.故选:A.【点评】本题考查了对等边三角形的判定定理的应用,注意:等边三角形的判定定理有:①三边都相等的三角形是等边三角形,②三角都相等的三角形是等边三角形,③有一个角等于60°的等腰三角形是等边三角形.4.(3分)在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在所给的下列条件中能判断△ABC不是直角三角形的是()A.∠A=∠C﹣∠B B.a2=c2﹣b2C.a=k,b=k,c=k(k>0)D.a:b:c=2:3:4【分析】利用直角三角形的定义和勾股定理的逆定理逐项判断即可.【解答】解:A、由条件可得∠A+∠B=∠C,且∠A+∠B+∠C=180°,可求得∠C=90°,故△ABC为直角三角形;B、由条件可得a2+b2=c2,满足勾股定理的逆定理,故△ABC是直角三角形;C、由条件有a2+b2=k2+(k)2=3k2=(k)2=c2,满足勾股定理的逆定理,故△ABC是直角三角形;D、设a=2x,则b=3x,c=4x,由a2+b2=(2x)2+(3x)2=13x2≠(4x)2=c2,不满足勾股定理的逆定理,故△ABC不是直角三角形;故选:D.【点评】本题主要考查直角三角形的判定方法,掌握判定直角三角形的方法是解题的关键,可以利用定义也可以利用勾股定理的逆定理.5.(3分)如图所示,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为()A.45°B.55°C.60°D.65°【分析】根据内角和定理求得∠BAC=95°,由中垂线性质知DA=DC,即∠DAC=∠C =30°,从而得出答案.【解答】解:在△ABC中,∵∠B=55°,∠C=30°,∴∠BAC=180°﹣∠B﹣∠C=95°,由作图可知MN为AC的中垂线,∴DA=DC,∴∠DAC=∠C=30°,∴∠BAD=∠BAC﹣∠DAC=65°,故选:D.【点评】本题主要考查作图﹣基本作图,熟练掌握中垂线的作图和性质是解题的关键.6.(3分)如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在()A.△ABC三条中线的交点处B.△ABC三条角平分线的交点处C.△ABC三条高线的交点处D.△ABC三条边的垂直平分线的交点处【分析】要求到三小区的距离相等,首先思考到A小区、B小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上,同理到B小区、C 小区的距离相等的点在线段BC的垂直平分线上,于是到三个小区的距离相等的点应是其交点,又因为三角形三边的垂直平分线相交于一点,所以答案可得.【解答】解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.则超市应建在△ABC三条边的垂直平分线的交点处.故选:D.【点评】本题主要考查线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等;此题是一道实际应用题,做题时,可分别考虑,先满足到两个小区的距离相等,再满足到另两个小区的距离相等,交点即可得到.7.(3分)如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于()A.1:1:1B.1:2:3C.2:3:4D.3:4:5【分析】利用角平分线上的一点到角两边的距离相等的性质,可知三个三角形高相等,底分别是20,30,40,所以面积之比就是2:3:4.【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,∵点O是内心,∴OE=OF=OD,∴S△ABO:S△BCO:S△CAO=•AB•OE:•BC•OF:•AC•OD=AB:BC:AC=2:3:4,故选:C.【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式.做题时应用了三个三角形的高时相等的,这点式非常重要的.8.(3分)给出下面5个式子:①3>0;②4x+3y≠0;③x=3;④x﹣1;⑤x+2≤3,其中不等式有()A.2个B.3个C.4个D.5个【分析】主要依据不等式的定义﹣﹣﹣﹣﹣用“>”、“≥”、“<”、“≤”、“≠”等不等号表示不相等关系的式子是不等式来判断.【解答】解:①3>0;②4x+3y≠0;⑤x+2≤3是不等式,故选:B.【点评】本题考查不等式的识别,一般地,用不等号表示不相等关系的式子叫做不等式.解答此类题关键是要识别常见不等号:><≤≥≠.9.(3分)已知不等式2x﹣a≤0的正整数解恰好是1,2,3,4,5,那么a的取值范围是()A.a>10B.10≤a≤12C.10<a≤12D.10≤a<12【分析】先求出不等式的解集,再根据正整数解恰好是1,2,3,4,5,逆推a的取值范围.【解答】解:解不等式2x﹣a≤0得:x≤a.根据题意得:5≤a<6,解得:10≤a<12.故选:D.【点评】本题考查了一元一次不等式的整数解,解答此题要先求出不等式的解集,再根据整数解的情况确定a的取值范围.本题要求熟练掌握不等式及不等式的解法,准确的理解整数解在不等式解集中的意义,并会逆推式子中有关字母的取值范围.10.(3分)如图是小李销售某种食品的总利润y元与销售量x千克的函数图象(总利润=总销售额﹣总成本).由于目前销售不佳,小李想了两个解决方案:方案(1)是不改变食品售价,减少总成本;方案(2)是不改变总成本,提高食品售价.下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是()A.②,③B.①,③C.①,④D.④,②【分析】逐条分析4个图象的变化得知:①售价不变,总成本减少;②售价不变,总成本增加;③总成本不变,售价增加;④总成本不变,售价减少,对照制定的两个方案即可得出结论.【解答】解:①根据函数图象可知,斜率不变,与y轴交点上移,即售价不变,总成本减少;②根据函数图象可知,斜率不变,与y轴交点下移,即售价不变,总成本增加;③根据函数图象可知,斜率变大,与y轴交点不变,即总成本不变,售价增加;④根据函数图象可知,斜率变小,与y轴交点不变,即总成本不变,售价减少.表示方案(1)的图象为①,表示方案(2)的图象为③.故选:B.【点评】本题考查了一次函数的应用,解题的关键是根据函数的性质分析4个图象.本题属于基础题,难度不大,解决该题型题目时,根据一次函数的性质分析图象是关键.二、填空题(每题3分,共18分)11.(3分)如图,已知CA=CB,则数轴上点A所表示的数是1﹣.【分析】首先在直角三角形中,利用勾股定理可以求出线段CB的长度,得出CA的长度,求出点A与原点的距离,即可得出数轴上点A所表示的数.【解答】解:根据题意,由勾股定理得:CB==,∴CA=CB=,∴A到原点的距离是﹣1,∵A在原点左侧,∴点A所表示的数是1﹣,故答案为:1﹣.【点评】此题主要考查了实数与数轴之间的对应关系、勾股定理;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.12.(3分)已知:点A(﹣1,a)、B(1,b)在函数y=﹣2x+m的图象上,则a>b(在横线上填写“>”或“=”或“<”).【分析】根据一次函数y=kx+b的性质,当k<0时,y将随x的增大而减小,即可得出a,b的大小关系即可.【解答】解;∵k=﹣2<0,∴y将随x的增大而减小,∵﹣1<1,∴a>b.故答案为:>.【点评】此题主要考查了一次函数的增减性,比较简单.解答此题的关键是熟知一次函数y=kx+b(k≠0)的增减性,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.13.(3分)已知正比例函数y=kx(k是常数,k≠0),当﹣3≤x≤1时,对应的y的取值范围是﹣1≤y≤,且y随x的减小而减小,则k的值为.【分析】由一次函数的性质,进行运算求解.【解答】解:易知k>0时,y随x的减少而减少,∴当x=﹣3时,y=﹣1,代入正比例函数y=kx得:﹣1=﹣3k解得k=,故答案为:.【点评】此题考查一次函数的性质,要注意根据一次函数图象的性质来分析.14.(3分)如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D =∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是8cm.【分析】作出辅助线后根据等边三角形的判定得出△BDM为等边三角形,△EFD为等边三角形,从而得出BN的长,进而求出答案.【解答】解:延长DE交BC于M,延长AE交BC于N,∵AB=AC,AE平分∠BAC,∴AN⊥BC,BN=CN,∵∠DBC=∠D=60°,∴△BDM为等边三角形,∴BD=DM=BM=5,∵DE=3,∴EM=2,∵△BDM为等边三角形,∴∠DMB=60°,∵AN⊥BC,∴∠ENM=90°,∴∠NEM=30°,∴NM=1,∴BN=4,∴BC=2BN=8(cm),故答案为8.【点评】此题主要考查了等腰三角形的性质和等边三角形的性质,能求出MN的长是解决问题的关键.15.(3分)如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为2a+3b.【分析】由题意可知:AC=AB=a+b,由于DE是线段AC的垂直平分线,∠BAC=36°,所以易证AE=CE=BC=b,从可知△ABC的周长;【解答】解:∵AB=AC,BE=a,AE=b,∴AC=AB=a+b,∵DE是线段AC的垂直平分线,∴AE=CE=b,∴∠ECA=∠BAC=36°,∵∠BAC=36°,∴∠ABC=∠ACB=72°,∴∠BCE=∠ACB﹣∠ECA=36°,∴∠BEC=180°﹣∠ABC﹣∠ECB=72°,∴CE=BC=b,∴△ABC的周长为:AB+AC+BC=2a+3b故答案为:2a+3b.【点评】本题考查线段垂直平分线的性质,解题的关键是利用等腰三角形的性质以及垂直平分线的性质得出AE=CE=BC,本题属于中等题型.16.(3分)如图,等边三角形ABC中,AB=8,BD⊥AC于点D,点E、F分别是BC、DC 上的动点,沿EF所在直线折叠△CEF,使点C落在BD上的点C′处,当△BEC′是直角三角形时,BC′的值为8﹣8或.【分析】由等边三角形的性质可得∠DBC=30°,分∠BEC'=90°,∠BC'E=90°两种情况讨论,由直角三角形的性质可求BC'的长.【解答】解:∵△ABC是等边三角形,BD⊥AC,∴∠DBC=30°∵折叠∴CE=C'E,若∠BEC'=90°,且∠C'BE=30°∴BE=C'E,BC'=2C'E,且BE+CE=BC=8∴CE+CE=8∴CE=4﹣4=C'E∴BC'=8﹣8若∠BC'E=90°,∠C'BE=30°,∴BE=2C'E,BC'=C'E,且BE+CE=BC=8∴CE==C'E∴BC'=故答案为:8﹣8或【点评】本题考查了翻折变换,等边三角形的性质,折叠的性质,熟练运用折叠的性质是本题的关键.三、解答题(共7小题)17.(8分)计算:(1)(2).【分析】(1)先把各二次根式化为最简二次根式得到原式=4+3﹣2+4,然后合并同类二次根式;(2)根据二次根式的除法法则得到原式=5﹣6+4,然后分别进行除法运算,再化简后合并即可.【解答】解:(1)原式=4+3﹣2+4=7+2;(2)原式=5﹣6+4=5﹣6+4=20﹣18+4=2+4.【点评】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.18.(6分)郑州市开展了“中学生阳光体育运动”,小明和小亮在课外活动中,报名参加了短跑训练小组.在5次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.(1)请根据图中信息,分别计算他们的平均数、极差和方差填入表格:(2)若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?【分析】(1)根据平均数、方差的定义及算法,即可解答;(2)根据方差的意义和各自的得分分别进行分析即可.【解答】解:(1)小明的平均数是:(13.3+13.4+13.3+13.2+13.3)=13.3;极差是:13.4﹣13.2=0.2;小亮的平均数是:(13.2+13.4+13.1+13.5+13.3)=13.3;方差是:[(13.2﹣13.3)2+(13.4﹣13.3)2+(13.1﹣13.3)2+(13.5﹣13.3)2+(13.3﹣13.3)2]=0.02;(2)小明同学的成绩较为稳定,但是他的最高成绩没有小亮高,爆发力不够,有待提高.而小亮同学爆发力还行,但是成绩不稳定,需加强.【点评】此题考查了读折线统计图的能力以及平均数,方差的意义.平均数平均数表示一组数据的平均程度;方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法.19.(8分)(1)解不等式,并求出它的正整数解;(2)已知关于x,y的方程组的解满足不等式x+y<3,求实数a的取值范围.【分析】(1)首先解不等式,然后确定不等式的解集中的正整数值即可;(2)首先解关于x,y的方程组,求得x,y的值,代入x+y<3,即可得到一个关于a的不等式,求得a的值.【解答】解:(1)去分母,得:3(x﹣2)≤2(7﹣x),去括号,得:3x﹣6≤14﹣2x,移项、合并同类项得:5x≤20,系数化成1得:x≤4.故原不等式的正整数解是:1,2,3,4.(2),①+②得:3x=6a+3,解得:x=2a+1,代入①得:y=2a﹣2,∵x+y<3,∴2a+1+2a﹣2<3,即4a<4,解得:a<1.【点评】考查了一元一次不等式的整数解,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.20.(6分)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.【分析】要求∠EDF的度数,只需求出∠BDE和∠FDC的度数即可,由FD⊥BC,得∠FDC=90°;而∠BDE在Rt△BDE中,故只需求出∠B的度数.因∠B=∠C,只需求出∠C的度数即可.因∠AFD是△CDF的外角,∠AFD=158°∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°.【解答】解:∵FD⊥BC,所以∠FDC=90°,∵∠AFD=∠C+∠FDC,∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°,∴∠B=∠C=68°.∵DE⊥AB,∵∠DEB=90°,∴∠BDE=90°﹣∠B=22°.又∵∠BDE+∠EDF+∠FDC=180°,∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣22°﹣90°=68°.【点评】考查三角形内角和定理,外角性质,垂直定义等知识.21.(8分)一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中AB所示;慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段OC所示,根据图象进行以下研究.解读信息:(1)甲,乙两地之间的距离为450km;(2)线段AB的解析式为y1=450﹣150x(0≤x≤3);线段OC的解析式为y2=75x (0≤x≤6);问题解决:(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象.【分析】(1)利用A点坐标为(0,450),可以得出甲,乙两地之间的距离;(2)利用A点坐标为(0,450),B点坐标为(3,0),代入y1=kx+b求出即可,利用线段OC解析式为y2=ax求出a即可;(3)利用(2)中所求得出,y=|y1﹣y2|进而求出函数解析式,得出图象即可.【解答】解:(1)根据左图可以得出:甲、乙两地之间的距离为450km;故答案为:450km;(2)问题解决:线段AB的解析式为:y1=kx+b,根据A点坐标为(0,450),B点坐标为(3,0),得出:,解得:故y1=450﹣150x(0≤x≤3);将(6,450)代入y2=ax求出即可:y2=75x,故线段OC的解析式为y2=75x(0≤x≤6);(3)根据(2)得出:y=|y1﹣y2|=|450﹣150x﹣75x|=,∵y1=450﹣150x(0≤x≤3);y2=75x,∴D(2,150),利用函数解析式y=450﹣225x(0≤x≤2),当x=0,y=450,x=2,y=0,画出线段AE,利用函数解析式y=225x﹣450(2≤x<3),当x=2,y=0,x=3,y=225,画出线段EF,利用函数解析式y=75x(3≤x≤6),当x=3,y=225,x=6,y=450,画出线段FC,求出端点,画出图象,其图象为折线图AE﹣EF﹣FC.【点评】此题主要考查了一次函数的应用和待定系数法求解析式,根据已知图象上的点得出函数解析式以及利用分段函数分析是解题关键.22.(8分)为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.(1)参加此次研学旅行活动的老师和学生各有多少人?(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为8辆;(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.【分析】(1)设出老师有x名,学生有y名,得出二元一次方程组,解出即可;(2)根据汽车总数不能小于=(取整为8)辆,即可求出;(3)设租用x辆乙种客车,则甲种客车数为:(8﹣x)辆,由题意得出400x+300(8﹣x)≤3100,得出x取值范围,分析得出即可.【解答】解:(1)设老师有x名,学生有y名.依题意,列方程组为,解之得:,答:老师有16名,学生有284名;(2)∵每辆客车上至少要有2名老师,∴汽车总数不能大于8辆;又要保证300名师生有车坐,汽车总数不能小于=(取整为8)辆,综合起来可知汽车总数为8辆;故答案为:8;(3)设租用x辆乙种客车,则甲种客车数为:(8﹣x)辆,∵车总费用不超过3100元,∴400x+300(8﹣x)≤3100,解得:x≤7,为使300名师生都有座,∴42x+30(8﹣x)≥300,解得:x≥5,∴5≤x≤7(x为整数),∴共有3种租车方案:方案一:租用甲种客车3辆,乙种客车5辆,租车费用为2900元;方案二:租用甲种客车2辆,乙种客车6辆,租车费用为3000元;方案三:租用甲种客车1辆,乙种客车7辆,租车费用为3100元;故最节省费用的租车方案是:租用甲种客车3辆,乙种客车5辆.【点评】此题主要考查了二元一次方程组的应用与一次不等式的综合应用,由题意得出租用x辆甲种客车与租车费用的不等式关系是解决问题的关键.23.(8分)操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB 于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:(1)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②说明理由.(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由.【分析】(1)连接PC,通过证明△PCD≌△PBE,得出PD=PE.(2)分为点C与点E重合、、CE=1、E在CB的延长线上四种情况进行说明.【解答】解:(1)由图①可猜想PD=PE,再在图②中构造全等三角形来说明.即PD =PE.理由如下:连接PC,因为△ABC是等腰直角三角形,P是AB的中点,∴CP=PB,CP⊥AB,∠ACP=∠ACB=45°.∴∠ACP=∠B=45°.又∵∠DPC+∠CPE=∠BPE+∠CPE,∴∠DPC=∠BPE.∴△PCD≌△PBE.∴PD=PE.(2)△PBE是等腰三角形,①当PE=PB时,此时点C与点E重合,CE=0;②当BP=BE时,E在线段BC上,;E在CB的延长线上,;③当EP=EB时,CE=1.【点评】本题考查了全等三角形的判定与性质及等腰三角形的性质;此题是分类讨论题,应分情况进行论证,不能漏解.。
河南省郑州市八中2019—2020学年八年级下学期第一次月考数学试题

【分析】
根据一次函数图象的位置进行判断,从函数图象来看,就是确定直线y=kx+b是否在在x轴上(或下)方.
【详解】
根据图象可知:
①当x<3时,一次函数y1=kx+b的图象在x轴上方,故y1>0;
②当x<3时,一次函数y2=x+a的图象一部分在x轴上方,一部分在x轴下方,故y2>0或y2=0或y2<0;
选项A错误,∵ , ∴ (如果x>y,z<0,那么xz<yz);
选项B正确,∵ ∴ (如果x>y,z>0,那么xz>yz);
选项C错误,∵ 则 ,∴ (如果x>y,而z为任意实数或整式,那么x+z>y+z);
选项D错误,∵ ∴ (如果x>y,而z为任意实数或整式,那么x+z>y+z).
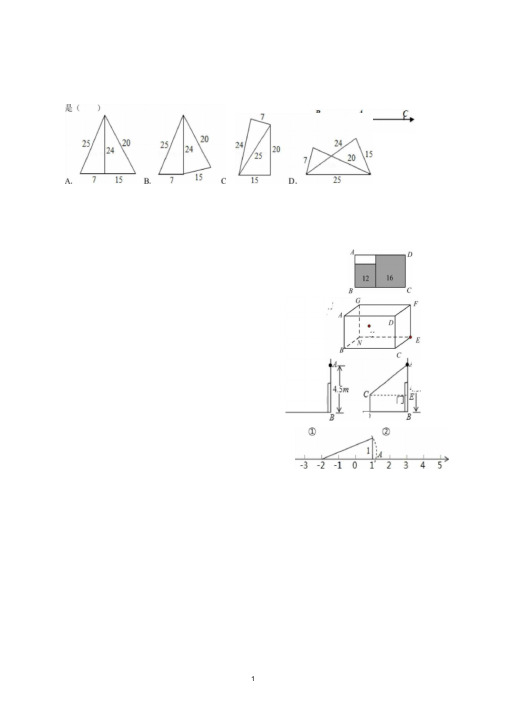
故选B
【点睛】
A. B. C. D.
二、填空题
11.用适当的符号表示 的平方是非负数:________.
12.如图,在 中, ,分别以A、C为圆心,大于AC的一半的长度为半径画弧,四弧交于两点M、N,作直线MN,交 于点 ,交 于点 .已知∠C=32°,则∠BAE的度数为________度.
13.如图, 平分 于 于 , 若 ,则 _______.
① ;
② .
17.解不等 式组,并把解集在数轴上表示出来.
18.如图,有两个长度相等的滑梯 和 ,左边滑梯的高度 与右边滑梯水平方向的长度 相等,判断两滑梯倾斜角 和 之间的数量关系?请说明理由.
19.如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,BN和CM有什么数量关系?请说明理由.
八年级下学期第一次月考数学试卷(含参考答案)

八年级下学期第一次月考数学试卷(含参考答案)(满分150分;时间:120分钟)学校:___________班级:___________姓名:___________考号:___________第I卷(选择题共40分)一.单选题.(共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个最符合题目要求。
1.下列各曲线是根据不同的函数绘制而成的,其中是中心对称图形的是( )2.若a<b<0,则下列条件一定成立的是( )A.ab<0B.a+b>0C.ac<bcD.a+c<b+c3.下列各式由左边到右边的变形中,是因式分解的为( )A.a2-16+3a=(a-4)(a+4)+3aB.10x2-5x=5x(2x-1)C.x2-4x+4=x(x-4)+4D.a(m+n)=am+an4.不等式x>4的解集在数轴上表示正确的是( )A. B. C. D.5.在平面直角坐标系中,已知点A的坐标为(1,4),如果将点A向右平移2个单位长度得到点A’,则点A’的坐标为( )A.(1,2)B.(1,6)C.(-1,4)D.(3,4)6.多项式12a3b-8ab2c的公因式是( )A.4a2B.4abC.2a2D.4abc7.下列多项式能用平方差公式进行因式分解的是( )A.x2-1B.x2+4C.x+9D.x2-6x8.下列多项式能直接用完全平方公式进行因式分解的是( )A.9x2-16y2B.4x2-4x+1C.x2+xy+y2D.9-3x+x29.如图,将△ABC绕点A逆时针旋转角a(0°<a<180°)得到△MDE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25,则旋转角a的度数是( )A.70°B.60°C.50°D.40°(第9题图) (第10题图)10.如图,将点A 1(1,1)向上平移1个单位,再向右平移2个单位,得到点A 2;将点A 2向上平移2个单位,再向右平移4个单位,得到点A 3;将点A 3向上平移4个单位,再向右平移8个单位,得到点A 4……按这个规律平移得到点A n ,则点A 2024的横坐标为( )A.22024B.22004-1C.22023-1D.2203+1第II 卷(非选择题 共110分)二.填空题:(每题4分,共24分)11.用适当的符号表示下列关系:a 是正数 .12.因式分解:a 2+4a= .13.若m>n ,则m -n 0(填">"或"="或"<").14.若一次函数y=kx+b 的图象如图所示,则关于x 的不等式kx+b<0的解集是 .(第14题图) (第15题图) (第16题图)15.如图,将周长为10cm 的△ABC 沿 BC 方向平移得到△DEF ,连接AD ,四边形ABFD 的周长为15cm ,则平移的距离为 cm.16.如图,长方形ABCD 中,AB=5,BC=12,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B’处,当△CEB'为直角三角形时,BE 的长为 .三.解答题(共10小题,86分)17.(4分)解下列不等式,并把不等式的解集在数轴上表示出来:-x -1≤3x -518.(6分)解不等式组{x -3(x -1)>11+3x 2>x -1,并写出它的所有非负整数解.19.(每题3分,共18分)因式分解:(1)8m 2n+2mn (2)-15a ³b 2+9a 2b 2-3ab 3 (3)4a 2-1(4)a 2-4ab+4b 2 (5)3x 3-12x (6)mx 2+2m 2x+m 320.(6分)先分解因式,再求值:2x(a-2)-y(2-a),其中a=2,x=1.5,y=-2.21.(6分)在如图所示的平面直角坐标系中,已知点4(1,2),B(3,1).(1)C点的坐标为.(2)将三角形ABC先向下平移4个单位,在向左平移3个单位,得到三角形A1B1C1,画出三角A1B1C1:(3)三角形A1B1C1的面积为。
郑州枫杨外国语2019-2020学年八年级数学上期月考试卷及答案
二、填空题(共10小题,毎题3分,共30分)IL阿的平方根足 _______________ .12.已知I;旦+3与2a - )5 λ⅛ m的平方根.^m=__________ .13-已知:直⅛∆ΛBC'的三边分别为ii, b, C t且周长为9,斜边为4,则∆ΛBC'的面积_____________________ ■14. ^AHCιp, J5=15, JC=I3, ∣茁MD= 12,则^ABC的周长是_____________________ .15・已⅛∏m, n分别为5 - √7的整数部分和小数部分,R 2m-n= _____________ *16.已⅛l∣7 - 3ιn∣+ (n ^ 5)2 = 3m - 7 - 4√w-3 ,则m+2n 的平方根为_____________ .17.若√3,456 =1.859, √34.56 =5.879. WIJ √3456(X) = _______ .18.?? b<0*化简J-a" —a—―― = _ J19.如图,在IUMEC中,ZACB = 90o,Z⅛ = 30o+AC=I t且AC⅛直线1上,将^AiiC绕点A顺时针施转到位H(I)r 可衍到点此时砒=2;将位置①的三角形绕点巴顺时针旋转到位国②,可衍到点此时= 2+√3 :将位賈②的三角形绕点尸2顺时针旋转到位■③・可得到点咛此时4F3= 3 + √3 ;……20. _________________ 在Rt∆ABC'中,ZACB-90'∖ AC=K. BCrb点D为射线BC上一点*甞∆ABD为等腰三角形时、∆ABD 的周丘为____ • 三、解答题(共7小题)21.计篦<8分)(1) 3 _—+(2__ J24 *(5分)实数口、/>、亡在数轴上的位i%⅛ll图,化简:y∕a^-∖a + h∖ + ^(c-<i)~ +∣Λ + c。
郑州市2019-2020学年下学期阶段性学业检测题 八年级数学 及答案

知识像烛光,能照亮一个人,也能照亮无数的人。
--培根郑州市2019-2020 学年下学期阶段性学业检测题八年级数学(满分100 分,考试时间90 分钟)一、选择题(每小题3 分,共30 分)1. “垃圾分类,从我做起”,以下四幅图案分别代表四类可回收垃圾,其中是中心对称图形的图案是()A.塑料B.旧衣物C.金属D.玻璃2. 若x<y,则下列不等式中不成立的是()A.x-1<y-1 B.3x<3y C.xyD.-2x<-2y 2 23. 下列各式由左边到右边的变形中,是因式分解的是()4. 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是()A.AE =DF B.∠A=∠D C.∠B=∠C D.AB =DC第4 题图第6 题图5. “新冠肺炎”知识竞赛共20 道题,每答对一题得10 分,答错或不答都扣5分,小颖得分不低于90 分.设她答对了x 道题,根据题意可列出的不等式为()A.10x-5(20-x)≥90 B.10x-5(20-x)>90C.10x-(20-x)≥90 D.10x-(20-x)>906. 如图,直线l1,l2,l3 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有()A.1 处B.2 处C.3 处D.4 处7. 如图,一个从边长为 30 cm 的正方形材料中剪出的垫片(图中的角度均为 90°),现测得 FG =5 cm ,则这个剪出的图形的周长是( ) A .135 cm B .130 cm C .125 cm D .120 cm第 7 题图 第 8 题图8. 如图,△ABC 中,点 E ,F ,G 分别在 BC ,AC ,AB 上,AE 与 BF 交于点 O ,且点 O 在 CG 上,根据尺规作图的痕迹,判断下列说法不正确的是( ) A .AE ,BF 是△ABC 的角平分线 B .点 O 到△ABC 三边的距离相等 C .CG 也是△ABC 的一条角平分线 D .AO =BO =CO9. “已知:△ABC 中,AB =AC ,求证:∠B <90°.”下面是用反证法证明这个问题的四个步骤:①∴∠A +∠B +∠C >180°,这与“三角形内角和为 180°”矛盾; ②因此假设不成立,∴∠B <90°; ③假设在△ABC 中,∠B ≥90°; ④由 AB =AC ,得∠B =∠C ≥90°,即∠B +∠C ≥180°. 这四个步骤正确的顺序应是( ) A .③④①② B .③④②① C .①②③④ D .④③①② 10. 如图,Rt △AOB 中,∠AOB =90°,OA =3,OB =4,将△AOB 沿 x 轴依次以三角形三个顶点为旋转中心顺时针旋转,分别得图②,图③,则旋转到图⑩时 直角顶点的坐标是( )A .(28,4)B .(36,0)C .(39,0)D .( 91 , 3 3 )2 2二、填空题(每小题3 分,共15 分)11. 某药品说明书上标明该药品保存的温度应是(10±4)℃,设该药品合适的保存温度为t℃,则t 的取值范围是.12. 请你写出一个原命题与它的逆命题都是真命题的命题:.13. 如图,△ABC 中,∠BAC=108°,E,G 分别为AB,AC 中点,且DE⊥AB,FG⊥AC,则∠DAF=.14. 关于x 的不等式-2x+a≥3 的解集如图所示,则a 的值是.15. 在直角坐标系中,O 为坐标原点,已知点A(1,2),点P 是y 轴正半轴上的一点,且△AOP 为等腰三角形,则点P 的坐标为.三、解答题(本大题共7 小题,共55 分)16. (6 分)小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:⎨⎪ (1)请将以上方框中数字序号位置应有的内容填写在下面的相应位置; ① ;② ;③ ;④ . ( 2 ) 如 果 点 C 的 坐 标 为 (1 , 3) , 那 么 不 等 式 kx +b ≤k 1x +b 1 的 解 集 为 .⎧2x + 1 < 3x 17. (7 分)解不等式组 ⎪=1 x <2 ⎩ 2,并求出最大整数解.18. (8 分)已知 a ,b ,c 分别是△ABC 的三边长.(1)分解因式:①ac -bc = ;②-a 2+2ab -b 2= ; (2)若 ac -bc =-a 2+2ab -b 2,试判断△ABC 的形状,并说明理由.19. (8 分)如图,8×7 的正方形网格中,点 A (2,0),点 B (3,2),点 C (4,2),请解答下列问题:(1)将△ABO 向右平移 4 个单位长度得到△A 1B 1O 1,请画出△A 1B 1O 1 并写 出点 A 1 的坐标; (2)将△ABO 绕点 C (4,2)顺时针旋转 90°得到△A 2B 2O 2,请画出△A 2B 2O 2并写出点 A 2 的坐标; (3)将△A 1B 1O 1 绕点 Q 旋转 90°可以和△A 2B 2O 2 完全重合,请直接写出点 Q 的坐标.20. (8 分)如图,△ABC 中,AB=AC,点D,E 分别在边AB,AC 上,且AD=AE,连接BE,CD,交点为F.(1)求证:∠ABE=∠ACD;(2)求证:过点A,F 的直线垂直平分线段BC.21. (8 分)某图书借阅室提供两种租书方式:一种是零星租书,每册收费1 元;另一种是会员租书,会员卡费用为每季度10 元,租书费每册0.5 元,小亮经常来租书,若每季度租书数量为x 册.(1)写出零星租书方式每季度应付金额y1(元)与租书数量x(册)之间的函数关系式;(2)写出会员卡租书方式每季度应付金额y2(元)与租书数量x(册)之间的函数关系式;(3)请分析小亮选取哪种租书方式更合算?22. (10 分)(1)如图1,O 是等边三角形ABC 内一点,连接OA,OB,OC,且OA=3,OB=4,OC=5,将△BAO 绕点B 顺时针旋转后得到△BCD,连接OD.填空:①旋转角为°;②线段OD 的长是;③∠BDC= °;(2)如图2,O 是△ABC 内一点,且∠ABC=90°,BA=BC.连接OA,OB,OC,将△BAO 绕点B 顺时针旋转后得到△BCD,连接OD.当OA,OB,OC 满足什么条件时,∠BDC=135°?请说明理由.⎨郑州市 2019-2020 学年下学期阶段性学业检测题八年级数学一、选择题1 2 3 4 5 6 7 8 9 10 C D B D A D B D A B二、填空题 11. 6≤t ≤14 12. 略 13. 36° 14. 115. (0,4),(0, 5 ),(0, 5)4三、解答题16. (1)① kx + b = 0 ;② ⎧ k 1 x + b 1 = y;③ kx + b >0 ;④ kx + b <0 ⎩k 2 x + b 2 = y(2)x ≥117. 不等式组的解集为 1<x <4,最大整数解为 3 18. (1)①c (a -b );②-(a -b )2(2)△ABC 为等腰三角形,理由略. 19. (1)图略,A 1 的坐标为(6,0);(2)图略,A 2 的坐标为(2,4); (3)点 Q 的坐标为(6,4). 20. (1)证明略;(2)证明略.21. (1)y 1=x ;(2)y 2=10+0.5x ; (3)当 0<x <20 时,选取零星租书方式更合算;当 x =20 时,选取零星租书和会员租书方式一样合算; 当 x >20 时,选取会员租书方式更合算22. (1)①60;②4;③150;(2)当 OC 2=OA 2+2OB 2 时,∠BDC =135°,理由略.。
河南省郑州市枫杨外国语学校2019-2020学年八年级下学期第一次月考数学试题

河南省郑州市枫杨外国语学校2019-2020学年八年级下学期第一次月考数学试题学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 下列式子:(1)4>0;(2)2x+3y<0;(3)x=3;(4)x≠y;(5)x+y;(6)x+3≤7中,不等式的个数有()A.2个B.3个C.4个D.5个2. 若关于 x 的不等式组的解集是 x<3,则 a 的取值范围是()A.a>3 B.a≥3C.a<3 D.a≤33. 不等式组的解集在数轴上表示正确的是()A.B.C.D.4. 下列不等式变形错误的是()A.若 a>b,则 1﹣a<1﹣b B.若 a<b,则 ax2≤bx2C.若 ac>bc,则 a>bD.若 m>n,则>5. 已知不等式组无解,则 a 的取值范围是()A.a ³ 3B.a ³ -3 C.a≤3D.a≤-36. 若关于x,y的二元一次方程组的解满足,则a的取值范围是A.B.C.D.7. 关于的不等式的正整数解是1、2、3,那么的取值范围是()A.B.C.D.8. 如图,已知直线过点,过点的直线交轴于点,则关于的不等式组的解集为()A.B.C.D.9. 下列不等式组是一元一次不等式组的是()C.D.A.B.10. 下列等式从左到右的变形属于因式分解的是()A.a2﹣2a+1=(a﹣1)2B.a(a+1)(a﹣1)=a3﹣aC.6x2y3=2x2?3y3D.11. 把因式分解,结果正确的是()A.B.C.D.12. 若多项式可因式分解成,其中、、均为整数,则之值为何?()A.B.C.D.13. 多项式:①16x2﹣8x;②(x﹣1)2﹣4(x﹣1)+4;③(x+1)4﹣4x(x+1)2+4x2;④﹣4x2﹣1+4x 分解因式后,结果中含有相同因式的是()A.①和②B.③和④C.①和④D.②和③14. 把多项式 3(x﹣y)2+2(y﹣x)3分解因式结果正确的是()A.(x﹣y)2(3﹣2x﹣2y)B.(x﹣y)2(3﹣2x+2y)C.(x﹣y)2(3+2x﹣2y)D.(y﹣x)2(3+2x﹣2y)15. 下列因式分解正确的是()A.x4﹣2x2+4=(x2﹣2)2B.3x2﹣9y+3=3(x2﹣3)C.x2n﹣x n=x n(x+1)(x﹣1)D.4x2+8ax+4a2=4(x+a)216. 若△ABC 的边长为 a、b、c,且满足 a2+b2+c2=ab+bc+ca,则△ABC 的形状是()A.等腰三角形B.等边三角形C.任意三角形D.不能确定17. 多项式x2y(a-b)-xy(b-a)+y(a-b)提公因式后,另一个因式为()A.B.C.D.18. 下列多项式能用公式法分解因式的有()①x2﹣2x﹣1;②﹣x+1;③﹣a2﹣b2;④﹣a2+b2;⑤x2﹣4xy+4y2;⑥m2﹣m+1A.1 个B.2 个C.3 个D.4 个19. 小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:,,2,,,,分别对应下列六个字:华、我、爱、美、游、中,现将因式分解,结果呈现的密码信息可能是()A.爱我中华B.我游中华C.中华美D.我爱美20. 多项式 x2﹣10xy+25y2+2(x﹣5y)﹣8 分解因式的结果是()A.(x﹣5y+1)(x﹣5y﹣8)B.(x﹣5y+4)(x﹣5y﹣2)C.(x﹣5y﹣4)(x﹣5y﹣2)D.(x﹣5y﹣4)(x﹣5y+2)二、填空题21. 已知(m+4)x|m|﹣3+6>0 是关于 x 的一元一次不等式,则 m 的值为_____.22. 若 4x2﹣(k﹣1)x+9 能用完全平方公式因式分解,则 k 的值为_____.23. 已知ab=﹣2,a﹣b=3,则a3b﹣2a2b2+ab3的值为_______.24. 已知 x2﹣x﹣1=0,则 2018+2x﹣x3的值是_____.25. 如果(2a+2b+1)(2a+2b﹣1)=3,那么 a+b 的值为_____.三、解答题26. 解一元一次不等式组:27. 因式分解:(1)(2)28. 五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.(1)求甲、乙两种商品每件的进价分别是多少元?(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.。
2019-2020学年河南省郑州外国语中学八年级下学期期中数学试卷 (含部分答案)

2019-2020学年河南省郑州外国语中学八年级第二学期期中数学试卷一、选择题(共10小题).1.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.2.下列各命题中,属于真命题的是()A.若m>n,则<B.若m﹣n>0,则m>nC.若m﹣m=0,则m=n=0D.若m>n,则>13.已知实数a,b满足|a﹣2|+(b﹣4)2=0,则以a,b的值为两边的等腰三角形的周长是()A.10B.8或10C.8D.以上都不对4.在正方形网格中,△ABC的位置如图所示,且顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个项点距离相等的点是()A.点E B.点F C.点G D.点H5.如图,A、B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2B.3C.4D.56.如图,已知△ABC的面积为16,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是()A.12B.8C.6D.47.在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F 作EF⊥BC于点E,则BE的长为()A.1B.C.D.8.下列各式从左到右因式分解正确的是()A.2x﹣6y+2=2(x﹣3y)B.x2﹣2x+1=x(x﹣2)+1C.x2﹣4=(x﹣2)2D.x3﹣x=x(x+1)(x﹣1)9.不等式组的最大整数解是()A.﹣1B.﹣2C.3D.410.如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC绕点C顺时针旋转得△CEF,当E落在AB边上时,连接BF,取BF的中点D,连接ED,则ED的长是()A.2B.4C.6D.4二、填空题(每小题3分,共15分)11.若a的3倍与2的差是负数,则可列出不等式.12.若有意义,则x的取值范围是.13.如图,在四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为.14.如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE ∥BC.△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有.15.如图,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE.交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,DE 的长为.三、解答题(共55分)16.解方程和不等式组(1)+=﹣1(2)17.先化简,再求值:(﹣)÷,然后从﹣2<a≤2的范围内选取一个合适的整数作为a的值代入求值.18.如图,Rt△ABC的三个顶点的坐标分别为A(﹣3,2)、B(0,4)、C(0,2).(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C.平移△ABC,若A对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;(2)若将△A1B1C绕某一点旋转得到△A2B2C2,请直接写出旋转中心的坐标为.(3)在x轴上找一点P,使得直线CP将△ABC的面积分为1:2,直接写出P点的坐标为.19.如图,直线l1:y=x+与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).(1)a=,k=;(2)直接写出关于x的不等式x+≥kx>0的解集;(3)若点B在x轴上,MB=MA,直接写出点B的坐标.(4)在x轴上是否存在一点N,使得NM﹣NA的值最大,若不存在,请说明理由;若存在,请直接写出点N的坐标.20.阅读理解:对于一些次数较高或者是比较复杂的式子进行因式分解时,换元法是一种常用的方法,下面是某同学用换元法对多项式(a2﹣2a﹣1)(a2﹣2a+3)+4进行因式分解的过程.解:设a2﹣2a=A,原式=(A﹣1)(A+3)+4(第一步)=A2+2A+1(第二步)=(A+1)2(第三步)=(a2﹣2a+1)2(第四步)回答下列问题:(1)该同学第二步到第三步运用了因式分解的(填代号).A.提取公因式B.平方差公式C.两数和的完全平方公式D.两数差的完全平方公式(2)按照“因式分解,必须进行到每一个多项式因式都不能再分解为止”的要求,该多项式分解因式的最后结果为.(3)请你模仿以上方法,求方程(x2﹣4x﹣3)(x2﹣4x+11)+49=0的解.21.在防疫新冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用2000元购进医用口罩若干个,第二次又用2000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25倍,购进的数量比第一次少200个.(1)求第一次和第二次分别购进的医用口罩数量为多少个?(2)药店第一次购进口罩后,先以每个3元的价格出售,卖出了a个后购进第二批同款罩,由于进价提高了,药店将口罩的售价也提升至每个3.5元继续销售卖出了b个后,两次共收入4800元.因当地医院医疗物资紧缺,药店决定将剩余的口罩全部捐赠给医院.请问药店捐赠口罩至少有多少个?22.如图,在等边三角形ABC中,AB=12cm,动点P从点A出发以1cm/s的速度沿AC 匀速运动,动点Q同时从点B出发以同样的速度沿CB的延长线方向匀速运动,当点P 到达点C时,点P,Q同时停止运动.设运动时间为ts,过点P作PE⊥AB于点E,连接PQ交AB于点D.(1)当t为何值时,△CPQ为直角三角形?(2)求DE的长.(3)取线段BC的中点M,连接PM,将△CPM沿直线PM翻折,得到△C′PM,连接AC′,当t=时,AC′的值最小,最小值为.参考答案一、选择题(每小题3分,共30分)1.A;2.B;3.A;4.B;5.B;6.B;7.C;8.D;9.A;10.A;二、填空题(每小题3分,共15分)11.3a﹣2<0;12.x≠﹣;13.3;14.②③④;15.,4,4;。
郑州市2019-2020八年级下学期第一次月考考试试题

学校_____________________ 班级____________ 姓名_________________ 考场 __________考号__________________密封线…………………………………………………………………………………………………………………………………………………………郑州市2019-2020学年下学期第一次月考试卷 八年级英语 (考试时间:90分钟,满分100分) 命题人:刘园园 审题人:殷巍 第I 卷(选择题,共65分) 一、听力理解(20小题,每小题1分,共20分) 第一节 听下面5段对话。
每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳答案,并将其标号填入题前括号内。
每段对话读两遍。
( )1. What will the man do at once? A. Take some medicine. B. See a doctor. C. Drink more water. ( )2. What did Ben play in P. E. class? A. Soccer B. Basketball C. V olleyball ( )3. What will Jack do tomorrow? A. He'll help the old people B. He'll clean up the street. C. He'll give out food. ( )4. What does the boy want the girl to fix up? A. His bike. B. His watch. C. His computer. ( )5. What does Father want Lisa to do? A. To give the dog a bath. B. To have a walk with him. C. To take the dog for a walk 第二节 听下面几段对话或独白。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省郑州市枫杨外国语学校2019-2020学年八年级下学期第一次
月考数学试题(word 无答案)
一、单选题
(★) 1 . 下列式子:
(1)4>0;(2)2x+3y <0;(3)x=3;(4)x≠y;(5)x+y ;(6)x+3≤7中,不等式的个数有( ) A .2个 B .3个 C .4个 D .5个
(★) 2 . 若关于 x 的不等式组 的解集是 x <3,则 a 的取值范围是()
A .a >3
B .a≥3
C .a <3
D .a≤3
(★) 3 . 不等式组 的解集在数轴上表示正确的是()
A .
B .
C .
D .
(★) 4 . 下列不等式变形错误的是()
A .若 a >b ,则 1﹣a <1﹣b
B .若 a <b ,则 ax 2≤bx 2
C .若 ac >bc ,则 a >b
D .若 m >n ,则
>
(★) 5 . 已知不等式组 无解,则 a 的取值范围是()
A .a ³ 3
B .a ³ -3
C .a≤3
D .a≤-3
(★★) 6 . 若关于x ,y 的二元一次方程组 的解满足 ,则a 的取值范围是
A .
B .
C .
D .
(★★) 7 . 关于的不等式的正整数解是1、2、3,那么的取值范围是()A.B.C.D.
(★★) 8 . 如图,已知直线过点,过点的直线交轴于点,则关于的不等式组的解集为()
A.B.C.D.
(★) 9 . 下列不等式组是一元一次不等式组的是()
A.B.C.D.
(★) 10 . 下列等式从左到右的变形属于因式分解的是()
A.a2﹣2a+1=(a﹣1)2B.a(a+1)(a﹣1)=a3﹣a
C.6x2y3=2x2•3y3D.
(★★) 11 . 把因式分解,结果正确的是()
A.B.
C.D.
(★) 12 . 若多项式可因式分解成,其中、、均为整数,则之值为何?()
A.B.C.D.
(★) 13 . 多项式:①16x 2﹣8x;②(x﹣1)2﹣4(x﹣1)+4;③(x+1)4﹣4x(x+1)2+4x 2;
④﹣4x 2﹣1+4x 分解因式后,结果中含有相同因式的是()
A.①和②B.③和④C.①和④D.②和③
(★) 14 . 把多项式 3(x﹣y)2+2(y﹣x)3分解因式结果正确的是()
A.(x﹣y)2(3﹣2x﹣2y)B.(x﹣y)2(3﹣2x+2y)
C.(x﹣y)2(3+2x﹣2y)D.(y﹣x)2(3+2x﹣2y)
(★) 15 . 下列因式分解正确的是()
A.x4﹣2x2+4=(x2﹣2)2B.3x2﹣9y+3=3(x2﹣3)
C.x2n﹣x n=x n(x+1)(x﹣1)D.4x2+8ax+4a2=4(x+a)2
(★) 16 . 若△ABC 的边长为 a、b、c,且满足 a 2+b 2+c 2=ab+bc+ca,则△ABC 的形状是()A.等腰三角形B.等边三角形C.任意三角形D.不能确定
(★★) 17 . 多项式 x 2 y( a- b)- xy( b- a)+ y( a- b)提公因式后,另一个因式为()A.B.C.D.
(★) 18 . 下列多项式能用公式法分解因式的有()①x 2﹣2x﹣1;② ﹣x+1;③﹣a 2﹣b 2;
④﹣a 2+b 2;⑤x 2﹣4xy+4y 2;⑥m 2﹣m+1
A.1 个B.2 个C.3 个D.4 个
(★) 19 . 小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:,,2,,,,分别对应下列六个字:华、我、爱、美、游、中,现将
因式分解,结果呈现的密码信息可能是()
A.爱我中华B.我游中华C.中华美D.我爱美
(★) 20 . 多项式 x 2﹣10xy+25y 2+2(x﹣5y)﹣8 分解因式的结果是()
A.(x﹣5y+1)(x﹣5y﹣8)B.(x﹣5y+4)(x﹣5y﹣2)
C.(x﹣5y﹣4)(x﹣5y﹣2)D.(x﹣5y﹣4)(x﹣5y+2)
二、填空题
(★) 21 . 已知(m+4)x |m|﹣3+6>0 是关于 x 的一元一次不等式,则 m 的值为_____.
(★) 22 . 若 4x 2﹣(k﹣1)x+9 能用完全平方公式因式分解,则 k 的值为_____.
(★★) 23 . 已知ab=﹣2,a﹣b=3,则a 3b﹣2a 2b 2+ab 3的值为_______.
(★★) 24 . 已知 x 2﹣x﹣1=0,则 2018+2x﹣x 3的值是_____.
(★) 25 . 如果(2a+2b+1)(2a+2b﹣1)=3,那么 a+b 的值为_____.
三、解答题
(★) 26 . 解一元一次不等式组:
(★) 27 . 因式分解:(1)
(2)
(★★) 28 . 五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.。
