初二数学特殊平行四边形压轴：几何证明题1

合集下载

初二数学压轴几何证明题(含答案)

1.四边形ＡBCＤ是正方形，△ＢEF是等腰直角三角形,∠BＥＦ＝９0°,BE＝ＥF,连接DF,G 为DF的中点，连接EG,CG,EC．ﻫ(1)如图1,若点Ｅ在ＣB边的延长线上，直接写出EG与GC 的位置关系及的值；ﻫ(2)将图1中的△BEＦ绕点Ｂ顺时针旋转至图2所示位置，请问(１）中所得的结论是否仍然成立？若成立,请写出证明过程；若不成立,请说明理由；(3)将图1中的△BEF绕点Ｂ顺时针旋转α(0°<α<９0°),若BE＝１，AＢ=,当Ｅ，F,Ｄ三点共线时,求DF的长及tan∠ＡBＦ的值．解：（１）ＥＧ⊥CG，=,ﻫ理由是:过G作ＧH⊥ＥC于Ｈ,ﻫ∵∠FEB=∠DＣB=9０°，∴ＥF∥ＧＨ∥DC,ﻫ∵G为DF中点，ﻫ∴H为EＣ中点,ﻫ∴EG=ＧC，GH=(ＥF+DC）＝（ＥB＋ＢC）,ﻫ即ＧH=EH=HC，ﻫ∴∠ＥＧC=9０°，即△ＥＧC是等腰直角三角形，∴=；ﻫ（２）ﻫ解：结论还成立，ﻫ理由是:如图2,延长EG到H,使EG＝GＨ，连接CH、ＥC,过E作BC的垂线ＥM,延长CD,∵在△ＥFG和△ＨＤG中ﻫ∴△EFG≌△HDG（SAＳ）,∴ＤH=EF=BE,∠FEG＝∠DHＧ,∴EF∥ＤH,ﻫ∴∠1=∠2＝90°－∠3=∠4，ﻫ∴∠EBＣ=１80°－∠4=１80°－∠１=∠ＨDＣ，在△EBＣ和△HDC中ﻫ∴△EBC≌△HDC.ﻫ∴CＥ＝ＣH,∠ＢＣE=∠DCH,∴∠ECH＝∠DＣＨ+∠ＥＣD=∠BCE+∠ＥCD=∠ＢＣD=90°，∴△EＣH是等腰直角三角形,ﻫ∵G为ＥH的中点，ﻫ∴EG⊥GC，=,ﻫ即(１）中的结论仍然成立;ﻫﻫ（３）ﻫ解:连接BD，∵AＢ=，正方形AＢCD,ﻫ∴BＤ=２，ﻫ∴coｓ∠DＢE==,∴∠DBE=60°，ﻫ∴∠ABE=∠ＤBE-∠ABＤ=1５°,ﻫ∴∠ＡＢF=45°-１５°=３0°,∴ｔaｎ∠ABF＝，∴DE=BＥ=,∴ＤＦ＝ＤE-EＦ=-1．解析: （1)过G作GH⊥EＣ于H，推出EF∥GＨ∥DC，求出H为EC中点，根据梯形的中位线求出EG=GC，GH＝（EF＋ＤC）=(EB＋BC）,推出GH=ＥH=BC，根据直角三角形的判定推出△EGC是等腰直角三角形即可;ﻫ（２)延长EG到H，使EG＝ＧH,连接CH、EC,过E作ＢC的垂线EM，延长ＣD，证△ＥFG≌△ＨDG，推出ＤH=EF=BE,∠ＦEG＝∠DHG,求出∠EBC=∠ＨＤC，证出△ＥBＣ≌△ＨDＣ，推出ＣＥ=CH,∠ＢCＥ=∠DＣH，求出△EＣＨ是等腰直角三角形,即可得出答案；3(ﻫ）连接BD，求出cｏs∠DBE＝＝，推出∠DBE=60°，求出∠ABF=３０°，解直角三角形求出即可．2．已知正方形ABＣD和等腰直角三角形ＢEＦ，BE=EF，∠ＢEＦ＝9０°,按图１放置,使点E在BC上，取DF的中点Ｇ，连接ＥG，ＣＧ.（1)延长EG交DC于Ｈ，试说明:ＤＨ=BE.ﻫ(２）将图1中△BEF绕B点逆时针旋转45°,连接DF,取DＦ中点G(如图2)，莎莎同学发现：EG=ＣG且EG⊥CＧ．在设法证明时他发现：若连接BD，则D,E，B三点共线.你能写出结论“EＧ=CG且EG⊥CG”的完整理由吗?请写出来.ﻫ（３)将图1中△BEF绕B点转动任意角度α(0＜α<90°)，再连接DＦ,取DF的中点Ｇ(如图3),第2问中的结论是否成立？若成立，试说明你的结论；若不成立，也请说明理由．(1）证明:∵∠BＥＦ=9０°，∴EＦ∥DH,ﻫ∴∠EFG=∠GDH,ﻫ而∠ＥGＦ＝∠DGH，ＧF＝GD，ﻫ∴△GEF≌△GＨD，ﻫ∴EF=DH，而BＥ=EF,ﻫ∴DH=BＥ;ﻫ（2）连接DB，如图，ﻫ∵△BＥF为等腰直角三角形，∴∠EBF＝45°，ﻫ而四边形ＡBCD为正方形，∴∠DBC=45°，ﻫ∴D，E,B三点共线.ﻫ而∠ＢEF＝90°，∴△FED为直角三角形，ﻫ而Ｇ为DF的中点，∴EG=ＧＤ＝GＣ，∴∠ＥGC=2∠EDＣ=９0°，∴EG=CＧ且EG⊥CG;ﻫﻫ（3)第２问中的结论成立.理由如下：连接ＡC、ＢD相交于点O,取BF的中点M，连接OG、ＥM、MG，如图,ﻫ∵Ｇ为DＦ的中点,Ｏ为BD的中点，Ｍ为BF的中点,ﻫ∴OＧ∥BF,ＧM∥OB，ﻫ∴四边形ＯGMＢ为平行四边形,∴OＧ=BM，GM=OB,而EM=BM，ＯC＝OB,∴EM=OG，MＧ=OC,∵∠ＤOG＝∠GMF,而∠DＯC=∠EＭF=9０°,∴∠EMＧ=∠GOC，ﻫ∴△ＭEG≌△ＯGＣ,∴EG=CG，∠EGM=∠OCＧ，ﻫ又∵∠MGF=∠BDF,∠ＦＧC=∠GDC＋∠GＣD，∴∠EGC=∠ＥＧＭ＋∠MGF+∠FGC=∠BDF＋∠ＧＤC+∠ＧＣD+∠OCG=4５°+４５°=90°,ﻫ∴EＧ=ＣG且EG⊥CG.解析：(1）由∠BEF＝90°,得到EF∥ＤH,而GF=GD,易证得△GＥF≌△GHD，得EF=DH,而BE=EF，即可得到结论.ﻫ(2)连接DB，如图2，由△ＢＥF为等腰直角三角形,得∠ＥBＦ=４５°，而四边形ABCD为正方形，得∠DＢC=45°,得到D,E,B三点共线,而G为DF的中点，根据直角三角形斜边上的中线等于斜边的一半得到EＧ=ＧD=GC，于是∠EＧC=2∠EDC=90°，即得到结论.ﻫ（３）连接ＡC、BＤ相交于点O,取BF的中点M，连接OG、EM、ＭG，由G为ＤF的中点，Ｏ为BD的中点,M为ＢＦ的中点,根据三角形中位线的性质得OＧ∥BＦ，GM∥OB，得到OG=BM,GM=OB，而EM＝BM，OC＝OB，得到EM=ＯG,MＧ=OC,又∠DOG=∠GMF,而∠DＯＣ=∠EMF ＝90°，得∠ＥＭG＝∠GOC，则△MEG≌△OＧC，得到ＥG=CG,∠EGM=∠OCG,而∠MGF=∠BD Ｆ,∠FＧC＝∠GDC+∠ＧCD，所以有∠ＥGC＝∠ＥGM+∠MGF＋∠FＧC=∠ＢDF+∠GDC+∠GCD+∠OCG=4５°+４５°=90°.３.已知正方形ABCD和等腰Ｒt△BEF,ＢＥ=EF,∠BEF＝90°，按图①放置,使点F在BC上，取ＤＦ的中点Ｇ，连接EG、CＧ.ﻫ(１）探索EＧ、CG的数量关系和位置关系并证明;ﻫ（2)将图①中△BEF绕B点顺时针旋转45°，再连接ＤF,取DF中点Ｇ（如图②)，问(１)中的结论是否仍然成立．证明你的结论;(３）将图①中△ＢEF绕B点转动任意角度(旋转角在０°到９0°之间),再连接DF,取DF的中点G(如图③）,问(１）中的结论是否仍然成立,证明你的结论.ﻫ解：(1）EＧ=CG且EG⊥CＧ．ﻫ证明如下：如图①,连接BD.∵正方形ABCＤ和等腰Ｒｔ△BＥF,∴∠EＢF＝∠DBＣ＝4５°．∴B、E、D三点共线.ﻫ∵∠DEF=9０°,Ｇ为DF的中点,∠DCB=90°,∴EG=DG＝ＧF＝CG.ﻫ∴∠ＥGＦ=２∠EＤＧ,∠CGＦ＝2∠CＤG．ﻫ∴∠ＥＧＦ＋∠CGF=2∠ED Ｃ=９0°，ﻫ即∠EGC=９0°,∴EG⊥CG．ﻫﻫ（2）仍然成立，证明如下:如图②,延长EG交CD于点H.ﻫ∵BE⊥EF，∴EF∥ＣD,∴∠1=∠2.ﻫ又∵∠3=∠４，ＦG=DＧ，ﻫ∴△FEG≌△DHG，∴EF＝DH，ＥＧ=GＨ．∵△BＥF为等腰直角三角形，∴ＢE=EＦ,∴BE=DH．ﻫ∵CD=BC,∴CＥ=ＣH．∴△EＣＨ为等腰直角三角形．又∵EG=GH,∴EＧ=CG且ＥＧ⊥CG．ﻫ(3）仍然成立.证明如下：如图③，延长CG至H，使GH＝CG，连接HF交BＣ于Ｍ，连接ＥH、EC．∵GF=GＤ,∠HGＦ＝∠CGD,HG＝CG，ﻫ∴△HFG≌△CDG，ﻫ∴HＦ=CD，∠GHF＝∠ＧCD，∴HＦ∥CD．∵正方形ＡBCD，∴ＨＦ=ＢC，HF⊥BC．∵△ＢEＦ是等腰直角三角形,∴ＢE＝ＥF，∠EBC=∠HFE，∴△BＥC≌△FEH,ﻫ∴HE=EC,∠BEC＝∠FEH，ﻫ∴∠BEF＝∠HEC=90°，ﻫ∴△ECH为等腰直角三角形.又∵CG=GH,∴EG ＝CG 且ＥG ⊥C Ｇ.解析：（１）首先证明B 、Ｅ、Ｄ三点共线,根据直角三角形斜边上的中线等于斜边的一半，即可证明EG=ＤG=GF=CG,得到∠ＥGF=2∠ＥＤG ，∠CGF=2∠ＣDG,从而证得∠EGC=9０°;ﻫ(2)首先证明△FE Ｇ≌△DHG,然后证明△ＥCH 为等腰直角三角形．可以证得：EG=CG 且EG ⊥C Ｇ．ﻫ（3）首先证明：△BEC ≌△ＦEH,即可证得:△ECH 为等腰直角三角形，从而得到:ＥG=C Ｇ且EG ⊥CG.已知，正方形A ＢCD 中，△BEF 为等腰直角三角形,且BF 为底,取DF 的中点G,连接EG 、C Ｇ．ﻫ（1）如图1，若△B ＥF 的底边B Ｆ在BC 上,猜想E Ｇ和ＣG 的数量关系为＿___＿＿;ﻫ（2)如图2，若△B ＥF 的直角边BE 在ＢC 上,则(１）中的结论是否还成立？请说明理由；（３）如图3，若△B ＥF 的直角边BE 在∠DB Ｃ内,则(1）中的结论是否还成立?说明理由．解：（１)GC=EG,（1分)理由如下：ﻫ∵△ＢＥF 为等腰直角三角形,ﻫ∴∠DEF=90°,又Ｇ为斜边ＤF 的中点, ∴EG= ＤF,∵A ＢCD 为正方形,ﻫ∴∠BCD=90°,又Ｇ为斜边ＤF 的中点，∴CG= ＤF,ﻫ∴G Ｃ=EG;ﻫ（２)成立.如图，延长ＥG 交CD 于Ｍ,Ｄ,∵∠BEF ＝∠FEC=∠BCD=90°,∴EF ∥Ｃ1 2 1 ２∴∠EFG=∠MD Ｇ,ﻫ又∠E ＧF=∠DGM ，D Ｇ=ＦG ，∴△G ＥF ≌△ＧMD,ﻫ∴EG=MG,即G 为EM 的中点．∴ＣＧ为直角△EC Ｍ的斜边上的中线，ﻫ∴ＣG=G Ｅ= EM;（3)成立．ﻫ取BF 的中点H,连接ＥH ，GH ，取BD 的中点O,连接O Ｇ,OC ． ∵CB=CD,∠DCB=９0°，∴C Ｏ= BD .ﻫ∵DG=G Ｆ，ﻫ∴GH ∥ＢD ，且GH= BD ，ﻫＯG ∥ＢF,且OG= B Ｆ,ﻫ∴CO ＝ＧH ．∵△ＢEF 为等腰直角三角形． B Ｆ∴EH=∴EH=OG ． ∵四边形O ＢHG 为平行四边形, ∴∠BOG ＝∠BH Ｇ．∵∠B ＯC=∠BH Ｅ＝9０°. ∴∠GOC=∠ＥHG ．ﻫ∴△GOC ≌△E ＨG ．ﻫ∴EG=GC ．此题考查了正方形的性质,以及全等三角形的判定与性质.要求学生掌握直角三角形斜边上的中线等于斜边的一半，以及三角形的中位线与第三边平行且等于第三边的一半．掌握这些性质,熟练运用全等知识是解本题的关键．解析:(1)E Ｇ=ＣG,理由为：根据三角形BEF 为等腰直角三角形，得到∠DEF 为直角，又G 为ＤF 中点，根据在直角三角形中,斜边上的中线等于斜边的一半，得到ＥG 为ＤF 的一半,同理在直角三角形DC Ｆ中,得到CG 也等于ＤF 的一半,利用等量代换得证;ﻫ(２）成立．理由为:延长ＥG 交CD 于M,如图所示,根据“A ＳA ”得到三角形E ＦG 与三角形ＧDM 全等,由全等三角形的对应边相等得到EG 与ＭG 相等，即G 为EM 中点，根据直角三角形斜边上的中线等于斜边的一半得到E Ｇ与ＣＧ相等都１２１2 １ 2 １ 2。

初二数学证明题(精选多篇)

初二数学证明题(精选多篇)第一篇：初二数学证明题初二数学证明题1、如图，ab=ac,∠bac=90°，bd⊥ae于d,ce⊥ae于e.且bd>ce,证明bd=ec+ed.解答：证明：∵∠bac=90°，ce⊥ae，bd⊥ae，∴∠abd+∠bad=90°，∠bad+∠dac=90°，∠adb=∠aec=90°.∴∠abd=∠dac.又∵ab=ac，∴△abd≌△cae(aas).∴bd=ae，ec=ad.∵ae=ad+de，∴bd=ec+ed.2、△abc是等要直角三角形。

∠acb=90°，ad是bc边上的中线，过c 做ad的垂线，交ab于点e，交ad于点f,求证∠adc=∠bde解：作ch⊥ab于h交ad于p，∵在rt△abc中ac=cb，∠acb=90°，∴∠cab=∠cba=45°.∴∠hcb=90°-∠cba=45°=∠cba.又∵中点d，∴cd=bd.又∵ch⊥ab，∴ch=ah=bh.又∵∠pah+∠aph=90°，∠pcf+∠cpf=90°，∠aph=∠cpf，∴∠pah=∠pcf.又∵∠aph=∠ceh，在△aph与△ceh中∠pah=∠ech，ah=ch，∠pha=∠ehc，∴△aph≌△ceh(asa).∴ph=eh，又∵pc=ch-ph，be=bh-he，∴cp=eb.在△pdc与△edb中pc=eb，∠pcd=∠ebd，dc=db，∴△pdc≌△edb(sas).∴∠adc=∠bde.2证明：作oe⊥ab于e，of⊥ac于f，∵∠3=∠4，∴oe=of.(问题在这里。

理由是什么埃我有点不懂)∵∠1=∠2，∴ob=oc.∴rt△obe≌rt△ocf(hl).∴∠5=∠6.∴∠1+∠5=∠2+∠6.即∠abc=∠acb.∴ab=ac.∴△abc是等腰三角形过点o作od⊥ab于d过点o作oe⊥ac于e再证rt△aod≌rt△aoe(aas)得出od=oe就可以再证rt△dob≌rt△eoc(hl)得出∠abo=∠aco再因为∠obc=∠ocb得出∠abc=∠abc得出等腰△abc41.e是射线ab的一点，正方形abcd、正方形defg有公共顶点d，问当e在移动时，∠fbh的大小是一个定值吗?并验证(过f作fm⊥ah于m，△ade全等于△mef证好了)2.三角形abc，以ab、ac为边作正方形abmn、正方形acpq1)若de⊥bc，求证：e是nq的中点2)若d是bc的中点，∠bac=90°，求证：ae⊥nq3)若f是mp的中点，fg⊥bc于g，求证：2fg=bc3.已知ad是bc边上的高，be是∠abc的平分线，ef⊥bc于f，ad与be交于g求证：1)ae=ag(这个证好了)2)四边形aefg是菱形第二篇：初二数学证明题测试例1、如图，ab∥cd，且∠abe=120°，∠cde=110°，求∠bed的度数。

专题06 平行四边形解答题压轴训练(解析版)八年级数学下期(人教版)

专题06 平行四边形解答题压轴训练（时间：60分钟总分：120）班级姓名得分一、解答题1．如图1，在ABCD 中，BAD ∠的平分线交BC 于点E ，交DC 的延长线于点F ，以EC ，CF 为邻边作ECFG ．（1）求证：ECFG 是菱形．（2）如图2，若90ABC ∠=︒，8AB =，12AD =，M 是EF 的中点，求DM 的长．（3）如图3，若120ABC ∠=︒，连结BD ，BG ，CG ，DG ，求BDG ∠的度数．【答案】（1）见解析；（2）；（3）60°【分析】（1）由平行四边形的性质可得AD ∥BC ，AB ∥CD ，再根据平行线的性质证明∥CEF =∥CFE ，根据等角对等边可得CE =CF ，再有条件四边形ECFG 是平行四边形，可得四边形ECFG 为菱形，即可解决问题；（2）首先证明四边形ECFG 为正方形，再证明∥BME ∥∥DMC 可得DM =BM ，∥DMC =∥BME ，再根据∥BMD =∥BME +∥EMD =∥DMC +∥EMD =90°可得到∥BDM 是等腰直角三角形，由等腰直角三角形的性质可求解．（3）延长AB 、FG 交于H ，连接HD ，求证平行四边形AHFD 为菱形，得出∥ADH ，∥DHF 为全等的等边三角形，证明∥BHD ∥∥GFD ，即可得出答案．【详解】解：（1）∥AF 平分∥BAD ，∥∥BAF =∥DAF ，∥四边形ABCD 是平行四边形，∥AD ∥BC ，AB ∥CD ，∥∥DAF =∥CEF ，∥BAF =∥CFE ，∥∥CEF =∥CFE ，∥CE =CF ，又∥四边形ECFG 是平行四边形，∥四边形ECFG 为菱形；（2）如图，连接BM ，MC ，∥∥ABC =90°，四边形ABCD 是平行四边形，∥四边形ABCD 是矩形，又由（1）可知四边形ECFG 为菱形，∥ECF =90°，∥四边形ECFG 为正方形．∥∥BAF =∥DAF ，∥BE =AB =DC ，∥M 为EF 中点，∥∥CEM =∥ECM =45°，∥∥BEM =∥DCM =135°，在∥BME 和∥DMC 中，BE CD BEM DCM EM CM =⎧⎪∠=∠⎨⎪=⎩，∥∥BME ∥∥DMC （SAS ），∥DMC=∥BME．∥∥BMD=∥BME+∥EMD=∥DMC+∥EMD=90°，∥∥BMD是等腰直角三角形．∥AB=8，AD=12，∥BDBD=；∥DM=2（3）∥BDG=60°，延长AB、FG交于H，连接H D．∥AD∥GF，AB∥DF，∥四边形AHFD为平行四边形，∥∥ABC=120°，AF平分∥BAD，∥∥DAF=30°，∥ADC=120°，∥DF A=30°，∥∥DAF为等腰三角形，∥AD=DF，∥平行四边形AHFD为菱形，∥∥ADH，∥DHF为全等的等边三角形，∥DH=DF，∥BHD=∥GFD=60°，∥FG=CE，CE=CF，CF=BH，∥BH=GF，在∥BHD与∥GFD中，BHD GFD BH GF ⎪∠=∠⎨⎪=⎩，∥∥BHD ∥∥GFD （SAS ），∥∥BDH =∥GDF∥∥BDG =∥BDH +∥HDG =∥GDF +∥HDG =60°．【点睛】此题是四边形综合题，主要考查平行四边形的判定方法，全等三角形的判定与性质，等边三角形的判定与性质，菱形的判定与性质等知识点，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．2．如图，在四边形ABCD 中，连接AC ，BD 交于点O ，∠ADO ＝∠CBO ，且AO ＝CO ，E 为线段OC 上一点，连接DE 并延长交BC 于点F ．（1）求证：四边形ABCD 为平行四边形；（2）若∠ADE ＝45°，AD ∠AC ，AE ＝3，CE ＝2，求三角形AOD 的面积．【答案】（1）见解析；（2）154【分析】（1）依据∥AOD ∥∥COB （AAS ），即可得出AD ＝BC ，再根据∥ADO ＝∥CBO ，即可得到AD ∥BC ，进而判定四边形ABCD 是平行四边形；（2）依据∥ADE 是等腰直角三角形，即可得到AD 的长，由平行四边形的性质可得OA 的长，再根据三角形面积计算公式，即可得出∥AOD 的面积．【详解】（1）∥AC ，BD 交于点O ，∥∥AOD ＝∥COB ，在∥AOD 和∥COB 中，ADO CBO AOD COB AO CO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∥∥AOD ∥∥COB （AAS ），∥AD ＝BC ，∥∥ADO ＝∥CBO ，∥AD ∥BC ，∥四边形ABCD 是平行四边形；（2）∥∥ADE ＝45°，AD ∥AC ，∥∥AED ＝45°，∥AD ＝AE ＝3，又∥CE ＝2，∥AC ＝3+2＝5，∥在平行四边形ABCD 中，AO ＝12AC ＝52， ∥Rt∥AOD 的面积＝12×AD ×AO ＝12×3×52＝154．【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、等腰三角形的判定． 3．定义：一组邻角相等的凸四边形叫做“友好四边形”．（1）写出我们所学过的特殊四边形中是“友好四边形”的图形的名称____（写一个）（2）在探究“友好四边形”性质时：∠小明画了一个“友好四边形”ABCD （如图），其中A B ∠=∠，AD BC =，此时他发现//AB DC ，请你证明此结论：∠由此小明猜想：“对于任意“友好四边形”当一组对边相等时，另一组对边就平行”，请你直接判断这个命题是真命题还是假命题；（3）已知：在“友好四边形”ABCD 中90A ∠=︒，60C ∠=°，6AB =，10BC =，请画出相应图形，并直接写出CD 的长．【答案】（1）矩形；（2）∥见解析；∥假命题；（3）画图见解析，11或2或10+【分析】（1）根据友好四边形的定义即可；（2）∥作出辅助线，判断出∥DF A ∥∥CEB ，再判断出四边形DFEC 是平行四边形即可；∥举出反例来说明；（3）分四种情况画图计算即可．【详解】解（1）矩形，矩形的四个角都是直角，根据“友好四边形”的定义，得到矩形是“友好四边形”；（2）∥如图，过点C 作CE AB ⊥，DF AB ⊥，DAB CBA ∠=∠，DAF CBE ∴∠=∠，CE AB ⊥，DF AB ⊥，90DFA CEB ∴∠=∠=︒，AD BC =，DFA CEB ∴∆≅∆，DF CE ∴=，90DFA CEB ∠=∠=︒，//DF EC ∴，∴四边形DFEC 是平行四边形，//AB CD ∴；∥假命题，反例如图，,AB AC = 则,B C ∠=∠在等腰三角形的腰上取点D ，E ，使得DE BC =，四边形DBCE 是友好四边形，没有对边平行．（3）∥90D A ∠=∠=︒，如图，作BE DC ⊥，90D A BED ∠=∠=∠=︒，∴四边形ADEB 是矩形，6DE AB ∴==．在Rt BEC △中，10BC =，60C ∠=°，5CE ∴=，11CD DE CE ∴=+=；∥如图，90A B ∠=∠=︒，作CE AD ⊥，90A B AEC ∠=∠=∠=︒，∴四边形ABCE 是矩形，10AE BC ∴==，6CE AB ==，在Rt CED 中，30DCE BCE BCD ∠=∠-∠=︒，CD ∴=，∥60B C ∠=∠=︒．如图，延长AD ，BC 交于E在Rt ABE △中，60B ∠=︒，6AB =，212BE AB ∴==，30E ∠=︒12102CE BE BC ∴=-=-=，60BCD ∠=︒，30CDE CED ∴∠=∠=︒，2CD CE ∴==，∥60D C ∠=∠=︒，如图，延长DA ，CB 交于E ，60D C ∠=∠=︒，60E ∴∠=︒，CD CE =，在Rt ABE △中，90,BAD BAE ∠=∠=︒ 60E ∠=︒，6AB =，BE ∴=10CD BC BE ∴=+=+【点睛】此题是四边形综合题，主要考查了平行四边形的判定和性质，矩形的判定和性质，直角三角形的性质，全等三角形的判定和性质，解本题的关键是作出图形，也是本题的难点． 4．在四边形ABCD 中，AB BC CD DA 、、、的中点分别为P 、Q 、M 、M ；（1）如图1，试判断四边形PQMN 怎样的四边形，并证明你的结论；（2）若在AB 上取一点E ，连结DE ，CE ，恰好ADE 和BCE 都是等边三角形（如图2）：∠判断此时四边形PQMN 的形状，并证明你的结论；∠当6AE =，3EB =，求此时四边形PQMN 的周长（结果保留根号）．【答案】（1）平行四边形，理由见解析；（2）∥菱形，证明见解析；∥【分析】（1）连接AC 、BD ．利用三角形中位线定理判定四边形PQMN 的对边平行且相等，易证该四边形是平行四边形；（2）∥设ADE ∆的边长是x ，BCE ∆的边长是y ，由于222221())2DB x y x xy y =++=++，22221())2AC x y y x xy y =++=++，可得平行四边形PQMN 的对角线相等，从而得出平行四边形PQMN 是菱形；∥如图2，过点D 作DF AB ⊥于F ，则通过解三角形求得DF =DB ∥知四边形PQMN 是菱形，可计算得周长是【详解】解：（1）如图1，连接AC 、BD ．PQ ∵为ABC ∆的中位线，12PQ AC ∴=且1//2PQ AC ，同理12MN AC=且1//2MN AC．MN PQ∴=且//MN PQ，∴四边形PQMN为平行四边形；（2）∥四边形PQMN是菱形，如图2，连接AC，BD，∥∥ADE和∥BCE都是等边三角形，∥AE=DE，CE=BE，∥AED=∥BEC=60°，∥∥AEC=∥DEB，∥∥AEC∥∥DEB，∥AC=BD，∥点M，N是AD，CD的中点，∥MN是∥ADC的中位线，∥MN=12 AC，同理：PN=12 BD，∥MN=PN，由（1）知，四边形PQMN是平行四边形，∥平行四边形PQMN是菱形；∥过点D作DF AB⊥于F，则DF=又222DF FB DB+=，DB∴=∴由∥知四边形PQMN是菱形，可计算得周长是142⨯=．【点睛】本题考查了中点四边形以及菱形的判定和性质、平行四边形的判定和性质，解题时，利用了三角形中位线的性质定理．5．定义：数学活动课上：陈老师给出如下定义：有组对边相等而另一组对边不相等的凸四边形叫做对等四边形．（1）如图1，平行四边形ABCD 中，60,B BCD ∠=︒∠的平分线交AD 于E ．求证：四边形ABCE 是对等四边形．（2）如图2，已知A 、B 、C 在格点（小正方形的项点）上，请在方格图中画出以格点为顶点，AB 、BC 为边的两个对等四边形ABCD ．（3）如图3，在Rt PBC 中，90,9PCB BC ∠=︒=，点A 在BP 边上，且13,,12AB AD PC CD =⊥=，若PC 上存在符合条件的点M ，使四边形ABCM 为对等四边形，求出CM 的长．【答案】（1）见解析；（2）见解析；（3）13或1212+【分析】（1）由平行四边形的性质得出AD ∥BC ，∥B =∥D =60°，AB =CD ，由角平分线的定义及等腰三角形的性质得出CE =CD ，根据对等四边形的定义可得出结论；（2）根据对等四边形的定义画出图形即可；（3）分CM =AB 与AM =BC 两种情况进行讨论即可．【详解】解：（1）证明：四边形ABCD 是平行四边形，//AD BC ∴，60B D ∠=∠=︒，AB CD =，180120BCD B ∴∠=︒-∠=︒， CE 平分BCD ∠，60BCE DCE ∴∠=∠=︒，60BCE DEC ∠=∠=︒，D DEC ∴∠=∠，CE CD ∴=，又AB CD =，CE AB ∴=，BC AD =，AE BC ∴≠，∴四边形ABCE 是对等四边形；（2）如图2，四边形ABCQ 即为所求；（3）如图3，∥当CM AB =时，13CM =；∥当9AM BC ==时，过A 作AE BC ⊥于点E ，则12AE CD ==，5BE =，4AD CE ∴==，MD当点M 在线段CD 上时，12CM CD DM =-=当点M 在DP 上时，12CM CD DM =+=+．综合以上可得CM 的长为13或12-12【点睛】此题属于四边形综合题，考查了作图-应用与设计作图，平行四边形的性质，等腰三角形的判定与性质，直角三角形的性质，勾股定理，弄清题中的新定义是解本题的关键．6．（问题背景）如图1，P 是等边三角形ABC 外一点，30APB ∠=︒，则222PA PB PC +=．小明为了证明这个结论，将PAB △绕点A 逆时针旋转60︒，请根据此思路完成其证明；（迁移应用）如图2，在等腰直角三角形ABC 中，BA BC =，90ABC ∠=︒，点P 在ABC外部，且45BPC ∠=︒，若APC △的面积为5.5，求PC ；（拓展创新）如图3，在四边形ABCD 中，//AD BC ，点E 在四边形ABCD 内部，且DE EC =，90DEC ∠=︒，135AEB ∠=︒，AD =，BC ，直接写出AB 的长．【答案】[问题背景]见解析；[迁移应用；[拓展创新]【分析】[问题背景]按题意画出图形，根据旋转的性质得到AP =AP ′，PB=P ′C ，证明∥APP ′为等边三角形，从而推出∥PP ′C =90°，在∥PP ′C 中，利用勾股定理得到222PP P C PC ''+=，再利用等量代换可得结果；[迁移应用]作线段BM 垂直于BP 交PC 的延长线于点M ，连接AM ，证得∥PBC =∥ABM ，证明∥PBC ∥∥MBA （SAS ），得出∥AMP =90°，由三角形的面积可求出答案；[拓展创新]将∥AED 绕点E 顺时针旋转90°至∥FEC ，连接BF ，证得∥FCE =90°，由勾股定理求出FB =∥ABE ∥∥FBE （SAS ），由全等三角形的性质得出AB =FB ．【详解】解：[问题背景]如图1，连接PP ′，由旋转可得：AP =AP ′，PB =P ′C ，∥P AP ′=∥BAC =60°，∥∥APP ′为等边三角形，∥∥APP ′=60°，PP ′=AP ′=P A ，∥∥APB =30°，∥∥AP ′C =30°∥∥PP ′C =90°，在∥PP ′C 中，222PP P C PC ''+=，∥222PA PB PC +=；[迁移应用]如图2，作线段BM 垂直于BP 交PC 的延长线于点M ，连接AM ，∥∥BPM =45°，∥PBM =90°，∥∥BPD 为等腰直角三角形，∥BP =BM ，∥∥ABM +∥MBC =∥ABC =90°，∥PBM =∥PBC +∥MBC =90°，∥∥PBC =∥ABM ，在∥PBC 和∥MBA 中，PB PM PBC ABM BA BC =⎧⎪∠=∠⎨⎪=⎩，∥∥PBC ∥∥MBA （SAS ），∥∥AMP =90°，∥S ∥P AC ＝12PC •AD ＝12PC 2=5.5， ∥PC（负值舍去）．[拓展创新]如图3，将∥AED 绕点E 顺时针旋转90°至∥FEC ，连接BF ，则AD =CFAE =EF ，∥ADE =∥FCE ，∥∥EDC =∥ECD =45°，∥AD ∥BC ，∥∥ADE +∥EDC +∥ECD +∥ECB =180°，∥ED =EC ，∥CED =90°，∥∥EDC =∥ECD =45°，∥∥ADE +∥ECB =90°，∥∥FCE +∥ECB =90°，即∥FCB =90°，∥FB∥∥AEB =135°，∥AEF =90°，∥∥FEB =360°-135°-90°=135°，∥∥AEB =∥FEB ，在∥ABE 和∥FBE 中，AE EF AEP FEB BE BE =⎧⎪∠=∠⎨⎪=⎩，∥∥ABE ∥∥FBE （SAS ），∥AB =FB=【点睛】本题是四边形综合题目，考查了旋转的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等边三角形的判定与性质、勾股定理等知识；熟练掌握旋转的性质，证明三角形全等是解题的关键．7．在平面直角坐标系中，矩形OABC的边OA任x轴上，OC在y轴上，B（4，3），点M 从点A开始，以每秒1个单位长度的速度沿AB→BC→CO运动，设∠AOM的面积为S，点M运动的时间为t．（1）当0＜t＜3时，AM＝，当7＜t＜10时，OM＝；（用t的代数式表示）（2）当∠AOM为等腰三角形时，t＝；（3）当7＜t＜10时，求S关于t的函数关系式；（4）当S＝4时，求t的值．【答案】（1）t，10-t；（2）5；（3）S=20-2t；（4）2或8．【分析】（1）利用路程，速度和时间的关系求解即可；（2）由题意可知只有等MA=MO，此时点M在线段BC上，进一步CM=BM=2解答即可；（3）当7<t< 10时，点M在线段OC上，再利用三角形面积公式求解即可；（4）分点M在线段AB上、点M在线段BC上和点M在线段OC上三种情况，分别求解即可．【详解】解：（1）当0<t<3时，点M在线段AB上，即AM=t当7＜t<10时，点M在线段OC上，OM=10-t故填：t，10-t；（2）∥四边形ABCO是矩形，B（4，3）∥OA=BC=4，AB=OC=3，∥∥AOM为等腰三角形，∥只有当MA=MO，此时点M在线段BC上，CM=BM=2，∥t=3+2=5故填：5；（3）∥当7<t <10时，点M 在线段OC 上 ∥114(10)20222S OA OM t t =⋅⋅=⨯⨯-=-；（4）∥当点M 在线段AB 上时，4=12×4t ，解得t =2； ∥当点M 在线段BC 上时，S =6，不符合题意；当点M 在线段OC 上时，4=20-2t ，解得t =8．综上所述，满足条件的的值为2或8．【点睛】本题属于四边形综合题，主要考查了矩形的性质、三角形的面积、等腰三角形的判定和性质等知识点，灵活应用所学知识并掌握分类讨论的思想成为解答本题的关键．8．如图1，已知ABC ∆，90,60ABC ACB ∠=∠=，点E 为AB 边上一点，过点E 作EF AC ⊥于点F ，连接CE ，点G 为CE 的中点，连接,GF GB ．（1）线段GF 与GB 的数量关系为_____________；（2）将Rt AEF ∆绕点A 逆时针旋转60°，如图2所示，（1）中的结论还成立吗？若成立，请证明；若不成立，请说明理由；（3）在平面内，将Rt AEF ∆绕点A 旋转，当点F 落在AB 边上，若8,4BC AE ==，请直接写出的BG 长．【答案】（1）FG BG =；（2）成立，理由见解析；（3）6BG =【分析】（1）根据直角三角形斜边上的中线性质即可求解；（2）分别取,AC AE 的中点,M N ，连接,,,BM FN MG GN ，根据中位线的性质及全等三角形的判定定理证明GMB FNG ∆≅∆，故可求解；（3）依题意作图，分别求出EF ，AF ，再得到BF 的长，再证明FEG HCG ≅，求出BH 的长，进而得到FH 的长，再根据直角三角形斜边上的中线性质即可求解．【详解】解：（1）∥90ABC ∠=︒，EF AC ⊥∥∥BCE 和∥FEC 是直角三角形∥点G 为CE 的中点 ∥BG=12EC ，12FG EC = ∥FG BG =，故答案为：FG BG =；（2）成立，理由如下：如图，分别取,AC AE 的中点,M N ，连接,,,BM FN MG GN ，∥AF EF ⊥，∥090ABC AFE ∠=∠=∥ 分别,M N 是,AC AE 的中点， ∥11,22BM AC FN AE ==， ∥G 是CE 中点，M 是AE 中点， ∥1//,2GM AE GM AE =；同理1//,2GN AC GN AC =， ∥,GM FN BM GN ==∥90,60ABC ACB ∠=︒∠=︒∥30CAB ∠=︒，∥30,30FAE EAC ∠=︒∠=︒，∥90FNG FNE ENG ∠=∠+∠=︒，同理，90GMB ∠=︒即GMB FNG ∠=∠ ∥()GMB FNG SAS ∆≅∆∥FG BG =；（3）依题意作图，∥∥EAF =30°，EF ∥AF ，∥EF =122AE =，AF 同理∥CAB =30°，AB ∥BC∥AC =2BC =16，AB =∥BF =AB -AF =∥EF ∥AB ，AB ∥BC∥//EF BC∥FEG HCG ∠=∠∥点G 为CE 的中点，∥CG =EG又FGE HGC ∠=∠∥FEG HCG ≅∥CH =EF =2，FG =HG∥BH =BC -CH =6∥FH 12=∥G 点是FH 中点∥BG =162FH =．【点睛】此题主要考查三角形的几何证明，解题的关键是全等三角形的判定与性质、直角三角形斜边上的中线定理、勾股定理及含30°的直角三角形的性质．9．如图，在ABCD 中，2=AD AB ，E ，F 分别为BC ，AD 的中点，作CG AB ⊥于点G ，GF 的延长线交CD 的延长线于点H ．（1）求证：四边形ABEF 是菱形．（2）当5,8AB BF ==时，∠求GH 的长．∠如图2，CG 交BF 于点P ，记FGP 的面积为1S ，BCP 的面积为2S ，则21S S -的值为________．【答案】（1）见解析；（2）∥12；∥16825 【分析】（1）根据平行四边形的性质得到AD ∥BC ，AD =BC ，再根据中点的定义得到AF =BE ，可得四边形ABCD 是平行四边形，结合AB =AF ，可得结论；（2）∥连接AE 交BF 于点O ，由菱形性质可得∥AOB =90°，从而求出菱形ABEF 的面积，可得四边形ABCD 的面积，根据CG ∥AB 可得CG ，从而求出AG ，证明∥AFG ∥∥DFH ，得到AG =DH ，在∥GCH 中利用勾股定理求出GH 即可；∥过F 作FK ∥AB 交BA 延长线于K ，求出FK ，从而得到∥BGF 和∥BGC 的面积，从而分别得出S 1和S 2，可得S 1-S 2．【详解】解：（1）∥四边形ABCD 是平行四边形，∥AD ∥BC ，AD =BC ，∥E 、F 分别为B C 、AD 中点，∥AF =12AD ，BE =12BC ， ∥AF =BE ，∥AF ∥BE ，∥四边形ABEF 是平行四边形，∥AD =2AB ，AD =2AF ，∥AB=AF，∥四边形ABEF是菱形；（2）∥连接AE交BF于点O，∥四边形ABEF是菱形，∥AE∥BF，OB=OF=12BE=4，OA=OE=12AE，∥∥AOB=90°，在Rt∥AOB中，OA ∥AE=2OA=6，∥S菱形ABEF=12AE·BF=12×6×8=24，∥E、F分别是B C、AD中点，∥BE=EC，AF=FD，∥AD∥BC，∥四边形ABEF，四边形EFDC都是平行四边形，且底和高相等，∥S四边形ABEF=S四边形EFDC=24，∥S四边形ABCD=S四边形ABEF+S四边形EFDC=48，∥CG∥AB，∥S四边形ABEF=AB·CG=5CG=48，∥BGC=90°，∥CG=485，∥AD=BC=2AB=10，∥BG145 =，∥AG=AB-BG=5-145=115，∥四边形ABCD是平行四边形，∥AB=CD=5，AB∥CD，∥∥A=∥FDH，∥GCH=∥BGC=90°，∥F是AD中点，∥AF=DF，在∥AFG和∥DFH中，A FDH AF DFAFG DFH ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∥∥AFG ∥∥DFH （ASA ）， ∥AG =DH =115， ∥CH =CD +DH =5+115=365，在Rt ∥GCH 中，GH=12；∥过F 作FK ∥AB 交BA 延长线于K ， ∥S 四边形ABEF =AB ·FK =5FK =24， ∥FK =245， ∥S ∥BGF =12BG ·FK =11424255⨯⨯=16825， S ∥BGC =12BG ·CG =11448255⨯⨯=33625， ∥S 2=S ∥BGC -S ∥BGP =33625-S ∥BGP ， S 1=S ∥BGF -S ∥BGP =16825-S ∥BGP ， ∥S 2-S 1=33625-16825=16825．【点睛】本题考查了平行四边形的性质，菱形的判定和性质，全等三角形的判定和性质，勾股定理，重点考查了几何图形的推理论证能力，同时也要结合已知条件作出辅助线，扩大运用范围． 10．在∠ABC 中，D 是BC 边长的一点，E 是AC 边的中点，过点A 作//BC AF 交DE 的延长线于点F ，连接AD ，CF ．（1）求证：四边形ADCF 是平行四边形：（2）若2FEA ADE ∠=∠，CF =1CD =，请直接写出AE 的长为__________．【答案】（1）证明见解析；（2）32．【分析】（1）利用平行线的性质得EFA EDC ∠=∠，据中点的性质可得AE EC =，从而可证EFA EDC ≅△△，进而得AF CD =，即可根据“一组对边平行且相等”的四边形是平行四边形，本题证毕；（2）根据已知条件先证平行四边形ADCF 是矩形，再在Rt ∥CDF中，运用勾股定理即可得3DF ==，进而可得出AE 的长．【详解】（1）证明：∥//BC AF ， ∥EFA EDC ∠=∠， ∥E 是AC 边的中点， ∥AE EC =，在EFA EDC △和△中，EFA EDC FEA DEC AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩∥EFA EDC ≅△△（AAS ）， ∥AF CD =， ∥//BC AF ，∥四边形ADCF 是平行四边形；（2）∥2FEA ADE ∠=∠FEA ADE EAD ∠=∠+∠∥ADE EAD ∠=∠ ∥AE DE =∥四边形ADCF 是平行四边形 ∥,AE CE EF DE ==∥AE CE DE EF +=+,即AC DF =, ∥平行四边形ADCF 是矩形在Rt ∥CDF 中， ∥3AC DF ==, ∥1322AE AC ==, 故AE 的长为32．【点睛】本题主要考查了平行四边形的判定定理，矩形的判定定理，勾股定理的知识．熟练利用相关定理分析，得出结论是解题关键．11．在平面直角坐标系xOy 中，已知点()000,A a ，()111,A a ，()222,A a ，…，(),n n A n a ，(),0B n ，其中0a ，1a ，2a ，…，n a ，n 为正整数．顺次连接0A ，1A ，2A ，…，n A ，B的折线与x 轴、y 轴围成的封闭图形记为图形M ．小明在求图形M 的面积时，过点()111,A a ，()222,A a ，…，()111,n n A n a ---作x 轴的垂线，将图形M 分成n 个四边形，计算这些四边形面积的和，可以求出图形M 的面积．请你参考小明的思路，解决下面的问题．（1）当2n =时，∠若0121,3,2a a a ===，如图1，则图形M 的面积为； ∠用含有0a ，1a ，2a 的式子表示图形M 的面积为．（2）当4n =时，从1，2，3，…，10这10个正整数中任选5个不同的数作为01234,,,,a a a a a ． ∠小明选择了012344,5,7,6,3a a a a a =====，请在图2中画出此时的图形M ； ∠在∠的条件下，若小聪用剩下的5个数1，2，8，9，10作为01234,,,,a a a a a 的取值，使新得到的图形M 的面积与小明的图形M 的面积相等，请直接写出这五个数的排序（写出一组即可）．【答案】（1） ∥92； ∥0121122a a a ++ ；（2）∥画图见解析；∥ 8，1，2，10，9（答案不唯一）．【分析】(1)∥利用分割法求出面积即可；∥利用分割法求解即可；(2)∥根据题意，利用描点法画出图形即可；∥根据面积相等取点即可(答案不唯一) 【详解】 (1)∥如图1所示，过点1A ，作1AE OB ⊥于E ，图形M 的面积=四边形01OA A E 的面积+四边形21EBA A ，119(13)1(32)1222=⨯+⨯+⨯+⨯=，故答案为：92； ∥同样可得图形M 的面积=0121122a a a ++，故答案为：0121122a a a ++ ．（2）∥如图2所示：，∥如图3所示，小明的图形M 的面积()14557766312=⨯+++++++⨯ 21.5=，新图形M 的面积1(8112210109)2=⨯+++++++ 21.5=，∥新得到的图形M 的面积与小明的图形M 的面积相等，故答案为：8，1，2，10，9．【点睛】本题属于四边形综合题，考查了坐标与图形的性质，多边形的面积等知识，解题的关键是理解题意，灵活运用所学知识解决问题． 12．问题提出（1）如图1，点A ，B 在直线l 的同侧，在直线l 上作一点P ，使得AP BP +的值最小．问题探究（2）如图2，正方形ABCD 的边长为6，点M 在DC 上，且2DM =，N 是AC 上的一动点，则DN MN +的最小值是_________．问题解决（3）现在各大景区都在流行“真人CS ”娱乐项目，其中有一个“快速抢点”游戏，游戏规则如图3，在用绳子围成的一个边长为12m 的正方形ABCD 场地中，游戏者从AB 边上的点E 处出发，分别先后赶往边,,BC CD DA 上插小旗子，最后回到点E ．求游戏者所跑的最少路程．【答案】（1）见解析；（2）（3）【分析】（1）作点A 关于直线l 的对称点A '，连接A B '交直线l 与一点，该点即为所求P 点；（2）根据点B 关于AC 是对称点为点D ，连接BM 交AC 与点N ，则此时DN +MN 的值最小，则有DN +MN = BN +MN =BM ，根据勾股定理求解BM 即可；（3）作点G 关于点C 的对称点G '，则FG FG '=，作,D A CD D A DA ''''⊥='，作点H 关于点C 的对称点H '，则G H GH ''=，作A B D A ''''⊥，作点E 关于点C 的对称点E ''，则H E HE '''=，作点E ''关于点A '的对称点E '，则H E H E ='''''，由两点之间线段最短可知，当,,,,E F G H E '''在一条直线上时，路程最小，利用勾股定理求解即可．【详解】解：（1）如图1，作点A 关于直线l 的对称点A '，连接A B '交直线l 与点P ，该点即为所求．（2）∥四边形ABCD 是正方形， ∥点B 关于AC 是对称点为点D ，如图，连接BM 交AC 与点N ，则此时DN +MN 的值最小，∥DN +MN =BN +MN =BM ， ∥CD =BC =6，DM =2， ∥MC =4，∥BM ==；（3）如图2，延长DC 到D '，使CD CD ='，作点G 关于点C 的对称点G '，则FG FG '=，作,D A CD D A DA ''''⊥='，作点H 关于点C 的对称点H '，则G H GH ''=，作A B D A ''''⊥，作点E 关于点C 的对称点E ''，则H E HE '''=，作点E ''关于点A '的对称点E '，则H E H E ='''''， ∥,H E HE A E AE '''='=，过点E '作E K AK '⊥，交AB 的延长线于点K ，则2EK AB =，容易看出，当,,,,E F G H E '''在一条直线上时，路程最小，最小路程为EE ==='．答：游戏者所跑的最少路程是．【点睛】本题考查正方形的性质以及最短路程问题，解题的关键是正确画出图形，根据两点之间线段最短的道理求解．13．ABCD ，过点D 作ED AD ⊥交AB 的延长线于点E ，BE AB =．（1）如图1，求证：四边形BDCE 是菱形；（2）P 为线段BC 上一点，点M ，N 在直线AE 上，且PM PB =，DPN BPM ∠=∠． ∠当60A ∠=︒时，如图2，求证：CD PB BN =+．∠当45A ∠=︒时，如图3，线段CD ，PB ，BN 的数量关系如何？（请直接写出猜想的结论）【答案】（1）见解析；（2）∥见解析；∥CD + BN ．【分析】（1）利用直角三角形的性质得到BD =BE =AB ，证明四边形BDCE 是平行四边形，再证明四边形BDCE 是菱形即可；（2）∥利用ASA 证明∥DBP ≅∥NMP ，再利用线段的和与差即可证明CD =PB +BN ； ∥同理证得四边形BDCE 是正方形，证明∥MBP 是等腰直角三角形，利用ASA 证明∥DBP ≅∥NMP ，利用线段的和与差即可得到CD + BN ．【详解】（1）∥BE =AB ，且ED ∥AD ，即BD 为Rt ∥ADE 斜边的的中线， ∥BD =BE =AB =12AE ，∥四边形ABCD 是平行四边形，∥AB =CD ， AB ∥CD ，∥BE =CD ，BE ∥CD ，∥四边形BDCE 是平行四边形，又∥BD =BE ，∥四边形BDCE 是菱形；（2）∥∥四边形ABCD 是平行四边形，∥AD ∥BC ，∥∥PBM =∥A =60°，∥PM =PB ，∥∥PBM 是等边三角形，∥PM=PB =BM ，∥∥DPN =∥BPM ，∥∥DPN +∥BPN =∥BPM +∥BPN ，即∥DPB =∥NPM ，∥四边形BDCE 是菱形，∥∥DBP =∥NMP =60°，在∥DBP 和∥NMP 中，DPB NPM PB PMDBP NMP ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∥∥DBP ≅∥NMP (ASA )，∥MN =BD =BE ，BM +BN =BM +ME ，∥BN =ME ，∥CD =BE =BM +ME =PB +BN ；∥∥∥A =45°，且ED ∥AD ，∥∥ADE 是等腰直角三角形，∥∥DEA =45°，同（1）法可证明四边形BDCE 是正方形，同∥可得∥DPN =∥BPM ，∥∥DPN -∥BPN =∥BPM -∥BPN ，即∥DPB =∥NPM ，∥PM =PB ，∥∥MBP =∥NMP =45°，∥∥MBP 是等腰直角三角形，即∥MBP =∥NMP =45°=∥PBD ，在∥DBP 和∥NMP 中，DPB NPM PB PMDBP NMP ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∥∥DBP ≅∥NMP (ASA )，∥MN =BD =BE ，BM +BN =BM +ME ，∥BN =ME ，∥∥MBP 是等腰直角三角形，∥BM=MN +BN =BD +BN =CD + BN ；即CD + BN．【点睛】本题考查了正方形的判定和性质，菱形的判定和性质，全等三角形的判定和性质，平行四边形的性质和判定，等腰直角三角形的性质，证明∥DBP ∥∥NMP 是本题的关键．14．如图，在正方形ABCD 中， 3CD =，P 是CD 边上一动点（不与D 点重合），连接AP ，点D 与点E 关于AP 所在的直线对称，连接AE ， PE ，延长CB 到点F ，使得BF DP =，连接EF ，AF ．（1）依题意补全图1；（2）若1DP =，求线段EF 的长；（3）当点P 在CD 边上运动时，能使为AEF 等腰三角形，直接写出此时DAP 的面积．【答案】（1）见解析；（2（3）4.5或94 【分析】（1）根据题意作出图形便可；（2）连接BP ，先证明 ADP ABF ≌，再证明FAE PAB ≌ ，求得 BP ，便可得EF ；（3）设 ()0DP x x =>，则 3CP x =- ，求出 AE 、AF 、EF ；当∥AEF 为等腰三角形时，分两种情况列出方程求出x 的值，进而求得最后结果．【详解】解：（1）根据题意，作图如下：（2）连接BP ，如图2．点D 与点E 关于AP 所在的直线对称，AE AD ∴=，PAD PAE ∠=∠，四边形ABCD 是正方形，AD AB ∴=，90ADC ABF ∠=∠=，DP BF =，()ADP ABF SAS ∴≌，AF AP ∴=，FAB PAD ∠=∠，FAB PAE ∴∠=∠，FAE PAB ∴∠=∠，()FAE PAB SAS ∴≌，EF BP ∴=，四边形ABCD 是正方形，3BC CD AB ∴===，1DP =，2CP ∴=，BP ∴=EF ∴=（3）设()0DP x x =>，则3CP x =-，EF BP ∴==3AE AD ==，AF AP ===AF AE ∴>，∴当AEF 为等腰三角形时，只能有两种情况：AE EF =或AF EF =，∥当AE EF =3=，解得3x =，ADP ∴面积为11·33 4.522DP AD =⨯⨯=； ∥当AF EF =时，解得32x =，ADP∴的面积为11393 2224 DP AD⨯=⨯⨯=，综上DAP的面积为4.5或94．【点睛】本题属于几何中的动点问题，综合考查了正方形的性质、勾股定理、全等三角形的判定与性质、等腰三角形的判定等知识，要求学生能理解相关概念与性能，能应用它们得到线段或角之间的关系，本题综合性较强，蕴含了分类讨论等思想方法．15．如图1，在正方形ABCD中，E、F分别为边AB、BC的中点，连接AF、DE交于点G．（1）求证：AF∠DE；（2）如图2，连接BG，求证：BG平分∠EGF；（3）如图3，连接BD交AF于点H，设ADG的面积为S，求证：BG2=2S．【答案】（1）见解析；（2）见解析；（3）见解析【分析】（1）利用正方形的性质证明ΔDAE∥ΔABF，得到∥ADE=∥BAF，推出∥DAG+∥ADG=90°，即可得到结论；（2）如图2，过点B作BM∥AF，垂足为M，设BF=a，则AB=2a，AF，利用平行线的性质及勾股定理求出BM a，AM，得到GM=BM a，推出ΔBMG为等腰直角三角形，求出∥BGM=∥BGE，由此得到结论；（3）根据ΔADG的面积为S，则AG·DG=2S，过点B作BM∥AF，垂足为M，由（2）推出BG2=2BM2，证明ΔDAG∥ΔABM，得到BM=AG，AM=DG，由AG·DG=2AG2=2S，得到AG2=S，即可得到结论．【详解】（1）∥四边形ABCD是正方形，∥AD=AB=BC，∥DAE=∥ABF=90°，∥E、F分别为边AB、BC的中点，∥AE=BF，∥ΔDAE∥ΔABF，∥∥ADE=∥BAF，∥∥DAG+∥EAG=90°，∥∥DAG+∥ADG=90°，∥∥AGD=90°，∥AF∥DE；（2）如图2，过点B作BM∥AF，垂足为M，则BM//GE，∥AE=BE，∥AG=GM，设BF=a，则AB=2a，AF，∥1122ABFS AB BF AF BM =⋅=⋅,∥2a a BM⋅=⋅，∴BM a，∥AM，∥GM=BM a，∥ΔBMG为等腰直角三角形，∥∥BGM=45°，∥BGE=90°-45°=45°，∥∥BGM=∥BGE，∥BG平分∥EGF；（3）ΔADG的面积为S，则AG·DG=2S，过点B作BM∥AF，垂足为M，由（2）知：GM=AG，BM=12AM，BG2=2BM2，∥∥AGD=∥AMB=90°，∥ADG=∥BAM，AB=AD，∥ΔDAG∥ΔABM，∥BM=AG，AM=DG，∥AG=12DG，AG·DG=2AG2=2S，即AG2=S，∥BM2=S，∥BG2=2BM2=2S．．【点睛】此题考查正方形的性质，勾股定理，全等三角形的判定及性质，等腰直角三角形的判定及性质，正确引出辅助线解决问题是解题的关键．。

完整word初二数学平行四边形压轴几何证明题

初二数学平行四边形：几何证明题 GH 、HE. CD DA 的中点，顺次连接EF 、 FG E1.在四边形ABCD 中，、F 、G H 分别是AB BC C 1 ）请判断四边形 EFGH 的形状，并给予证明；（G D 是菱形，并说明理由。

2）试探究当满足什么条件时，使四边形EFGH （F HB E ABC 沿顺时针方向旋转 90°得到△ A . ABC 中，/ ACB=90°，AC=BC=1Q 将厶ABC 绕点B2.如图，在直角三角形 *. C 的长度是，/ CBA 的度数是（1）线段A- _____________________ CBAC是平行四边形.（2）连接CC 求证：四边形 CAA milQ. BC 于的中点， PO 的延长线交为 ABCD 中，点P 是线段AD 上一动点，OBD 如图，矩形3.OP=OQ ; （1）求证：t 运动时间为.设点PD 厘米/秒的速度向D 运动（不与重合）A2 （）若AD=8 厘米，AB=6厘米，P 从点岀发，以1是菱形.t 为何值时，四边形 PBQD 秒，请用t 表示PD 的GFC. 与点C 重合，得△ E 是BC 边上的高，将△ ABE 沿BC 方向平移，使点 AE4.已知：如图，在口 ABCD 中，?DG ⑴求证：BE.是菱形？证明你的结论与 BC 满足什么数量关系时，四边形 ABFG 当B ⑵若/ ?50?\BG ADB C F EF . AE交BC的延长线于点E// BC,为CD的中点，连结AE、BE, BE X AE,延长5.如图，在四边形ABCD 中, AD AD；FC=求证：(1DA . BC+ ADAB( 2)=EBE , CE.BC, D是的中点，连结AD,在AD的延长线上取一点E,连结6.如图，在厶ABC中，AB=AC ACE求证：△ ABE^^（1满足什么数量关系时，四边形ABEC是菱形？并说明理由.（2）当AE 与ADBAEDCF.的延长线与CD的延长线交于点的中点，ABCD中，点E是边ADBE7.如图，在平行四边形 F DFE ）求证：△ ABE^^（ 1.ABDF的形状，并说明理由BD2）连结、AF，判断四边形（EADBFACEDFABDEDABCBCACAB 如图，已知点在△于的边上，交//交•于, AEDFBACAD （）若的形状，并说明理由•平分/,试判断四边形E FFE , BDDEBF?上两点，且9.如图，在平行四边形中，点是对角线.1 ）写岀图中每一对你AC.、BF 、CF ,并延长 DE 至点 F ,使 EF=DE.连接 BCAD10.在梯形 ABCD 中,/ BC,AB=DC 过点 D 作DEI ,垂足为点 E ）求证：四边形 ABFC 是平行四边形；1 （2CEBEQE? ABFC 是矩形，（2）若求证：四边形 D ADFAE 1 ）求证：；=A（2）选择（A DAE.的外角平分线，BE丄BACAEAB=AC11如图，△ ABC中，，AD 分别是/ BAC和/ B AEDA（ 1）求证：丄（DE与是否相等？并说明理由。

初二数学平行四边形压轴：几何证明题

初二数教仄止四边形：几许道明题之阳早格格创做1.正在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中面，逆次对接EF 、FG 、GH 、HE ．（1）请推断四边形EFGH 的形状，并赋予道明；（2）试商量当谦脚什么条件时，使四边形EFGH 是菱形，并道明缘由.2.如图，正在曲角三角形ABC 中，∠ACB=90°，AC=BC=10，将△ABC 绕面B 沿逆时针目标转动90°得到△A1BC1．（1）线段A1C1的少度是，∠CBA1的度数是．（2）对接CC1，供证：四边形CBA1C1是仄止四边形．3. 如图，矩形ABCD 中，面P 是线段AD 上一动面，O 为BD 的中面，PO 的延少线接BC 于Q.（1）供证：OP=OQ ；（2）若AD=8厘米，AB=6厘米，P 从面A 出收，以1厘米/秒的速度背D 疏通（没有与D 沉合）.设面P 疏通时间为t 秒，请用t 表示PD 的少；并供t 为何值时，四边形PBQD 是菱形． 4.已知：如图，正在□ABCD 中，AE 是BC 边上的下，将△ABE 沿BC 目标仄移，使面E 与面C 沉合，得△GFC.⑴供证：BE DG ；⑵若∠B 60，当AB 与BC 谦脚什么数量闭系时，四边形ABFG 是菱形？道明您的论断.5. 如图，正在四边形ABCD 中，AD ∥BC ，E 为CD 的中面，连结AE 、BE ，BE ⊥AE ，延少AE 接BC 的延少线于面F ．供证：（1）FC ＝AD ；（2）AB ＝BC ＋AD ．6.如图，正在△ABC 中，AB=AC ，D 是BC 的中面，连结AD ，正在AD 的延少线上与一面E ，连结BE ，CE.（1）供证：△ABE ≌△ACE （2）当AE 与AD 谦脚什么数量闭系时，四边形ABEC 是菱形？并道明缘由.7.如图，正在仄止四边形ABCD 中，面E 是边AD 的中面，BE 的延少线与CD 的延少线接于面F. （1）供证：△ABE ≌△DFE（2）连结BD 、AF ，推断四边形ABDF 的形状，并道明缘由. 8. 如图，已知面D 正在△ABC 的BC 边上，DE ∥AC 接AB 于E ，DF ∥AB 接B F C G D H B A 1 C 1A C A D G C B F E A D P OA B E D C A D E F C B A B C D E FAC 于F ．（1）供证：AE ＝DF ；（2）若AD 仄分∠BAC ，试推断四边形AEDF 的形状，并道明缘由． 9. 如图，正在仄止四边形中，面E F ，是对于角线BD 上二面，且BF DE =．（1）写出图中每一对于您认为齐等的三角形；（2）采用（110.正在梯形ABCD 中，AD ∥BC,AB=DC ，过面D E ，并延少DE 至面F ，使EF=DE.对接BF 、CF 、AC. （1）供证：四边形ABFC 是仄止四边形；（2）若CE BE DE ⋅=2,供证：四边形ABFC 是矩形. 11.如图，△ABC 中，AB=AC ，AD 、AE 分别是∠BAC 战∠BAC 的中角仄分线，BE ⊥AE. （1）供证：DA ⊥AE（2）试推断AB 与DE 是可相等？并道明缘由. 12.如图，正在△ABC 中，AB=AC ，面D 是BC 上一动面（没有与B 、C 沉合），做DE ∥AC 接AB 于面E ，DF ∥AB 接AC 于面F.（1）当面D 正在BC 上疏通时，∠EDF 的大小（变大、变小、没有变）（2）当AB=10时，四边形EDF 的周少是几？（3）面D 正在BC 上移动的历程中，AB 、DE 与DF 总存留什么数量闭系？请道明. 13.如图，四边形ABCD 中，AB ∥CD ，AC 仄分∠BAD ，CE ∥AD 接AB 于E.（1）供证：四边形AECD 是菱形；（2）若面E 是AB 的中面，试推断△ABC 的形状，并什么缘由. 14.如图，正在仄止四边形ABCD 中，E 为BC 的中面，连结AE 并延少接DC 的延少线于面F. （1）供证：AB=CF （2）当BC 与AF 谦脚什么数量闭系时，四边形ABFC 是矩形？并道明. 15.如图，正在正圆形ABCD 中，G 是CD 上一面，延少BC 到E ，使CE=CG ，连结BG 并延少接DE 于面F.（1）供证:△BCG ≌△DCE（2）将△DEC 绕面D 逆时针转动90°得到△DMA,推断四边形MBGD 是什么特殊四边形？并道明缘由.16.将仄止四边形纸片ABCD 如图办法合叠，使面C D’E AF C DB A B FC DE AF C D E B AB C FE DA B CDE A BF C D E处，合痕为EF.（1）供证：△ABE ≌△AD’F（2）连结CF ，推断四边形AECF 是什么特殊四边形，道明缘由.17.如图，正在△ABC 中，AB=AC ，AD ⊥BC ，垂脚为面D ，AN 是ABC 中角∠CAM 的仄分线，CE ⊥AN ，垂脚为E. （1）供证：四边形ADCE 是矩形；（2）当△ABC 谦脚什么条件时，四边形ADCE 是正圆形？道明缘由. 18.四边形ABCD 、DEFG 皆是正圆形，连结AE 、CG.（1）供证：AE=CG ；（2）预测AE 与CG 的位子闭系，并道明. 19.如图，正在四边形ABFC 中，∠ACB=90°，BC 的笔曲仄分线EF 接BC 于面D ，接AB 于面E ，且CF=AE. （1）试商量四边形BECF 是什么特殊四边形，并道明缘由；（2）当∠A 的大小谦脚什么条件时，四边形BECF 是正圆形？请回问并道明您的论断.20.如图，正在□ABCD 中，AB ⊥AC ，AB=1，BC=5，对于角线AC 、BD 相接于面O ，将曲线AC 绕面O 逆时针转动，分别接BC 、AD 于面E 、F.（1）道明：当转动角为90°时，四边形ABEF 是仄止四边形；（2）试商量正在转动历程中，线段AF 与EC 有何如的数量闭系，并道明；（3）正在转动历程中，四边形BEDF 大概是菱形吗？如果没有克没有及，请道明缘由；如果能，道明缘由并供出此时AC 绕面O 逆时针转动的度数.21.如图，B 、C 、E 是共背来线上的三个面，四边形ABCD 与四边形CEFG 皆是正圆形，连结BG 、DE.（1）预测BG 与DE 之间的大小闭系，并道明您的论断；（2）正在图中是可存留通过转动不妨互相沉合的二个三角形？若存留，请指出，并道明转动历程；若没有存留，请道明缘由.22.如图，矩形ABCD 中，O 是AC 与BD 的接面，过面、CD 的延少线分别接于面E 、F. （1）供证：△BOC ≌△DOF ；（2）当EF 与AC 谦脚什么闭系时，四边形AECF 23.如图，△ABC 是等边三角形，D 、E 分别正在边BC 连结DE 并延少至面F ，使EF=AE ，连结AF 、BE 战CF.（1 A B D F D ’ AB M NE A B C D EF G B E A C F DA B C D F E O A B C D F（2）推断四边形ABDF 的形状，并道明缘由.24. 如图，△ABC 是等边三角形，面D 是线段BC 上的动面(面D 没有与B 、C 沉合)， △ADE 是以AD 为边的等边三角形，过E 做BC 的仄止线，分别接AB 、AC 于面F 、G ，连结BE.（1）供证：△AEB ≌△ADC ；（2）四边形BCGE 是何如的四边形？道明缘由.A G E F。

初二数学特殊的平行四边形试题答案及解析

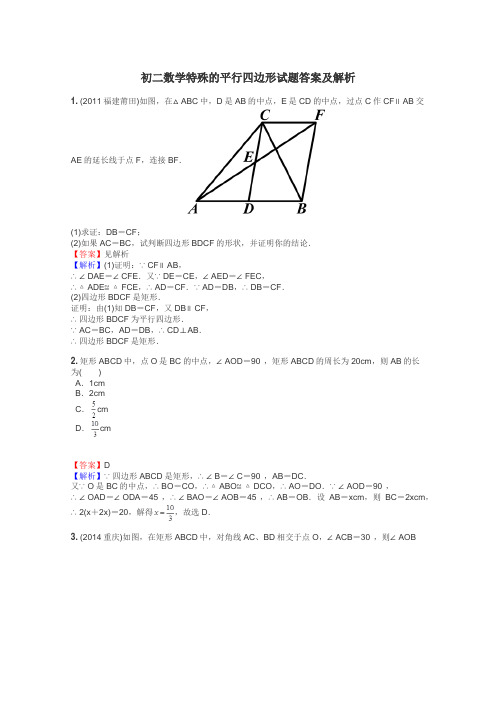
初二数学特殊的平行四边形试题答案及解析1. (2011福建莆田)如图，在△ABC中，D是AB的中点，E是CD的中点，过点C作CF∥AB交AE的延长线于点F，连接BF．(1)求证：DB＝CF；(2)如果AC＝BC，试判断四边形BDCF的形状，并证明你的结论．【答案】见解析【解析】(1)证明：∵CF∥AB，∴∠DAE＝∠CFE．又∵DE＝CE，∠AED＝∠FEC，∴△ADE≌△FCE，∴AD＝CF．∵AD＝DB，∴DB＝CF．(2)四边形BDCF是矩形．证明：由(1)知DB＝CF，又DB∥CF，∴四边形BDCF为平行四边形．∵AC＝BC，AD＝DB，∴CD⊥AB．∴四边形BDCF是矩形．2.矩形ABCD中，点O是BC的中点，∠AOD＝90°，矩形ABCD的周长为20cm，则AB的长为()A．1cmB．2cmC．cmD．cm【答案】D【解析】∵四边形ABCD是矩形，∴∠B＝∠C＝90°，AB＝DC．又∵O是BC的中点，∴BO＝CO，∴△ABO≌△DCO，∴AO＝DO．∵∠AOD＝90°，∴∠OAD＝∠ODA＝45°，∴∠BAO＝∠AOB＝45°，∴AB＝OB．设AB＝xcm，则BC＝2xcm，∴2(x＋2x)＝20，解得，故选D．3. (2014重庆)如图，在矩形ABCD中，对角线AC、BD相交于点O，∠ACB＝30°，则∠AOB的大小为()A．30°B．60°C．90°D．120°【答案】B【解析】在矩形ABCD中，OA＝OB＝OC＝OD，所以∠OBC＝∠OCB＝30°，所以∠AOB＝∠OCB＋∠OBC＝60°．4.(2014四川巴中)如图，在四边形ABCD中，点H是边BC的中点，作射线AH，在线段AH及其延长线上分别取点E，F，连接BE，CF．(1)请你添加一个条件，使得△BEH≌△CFH，你添加的条件是________，并证明；(2)在问题(1)中，当BH与EH满足什么关系时，四边形BFCE是矩形？请说明理由．【答案】见解析【解析】(1)添加条件：BE∥CF(答案不唯一)．证明：如图，∵BE∥CF，∴∠1＝∠2．∵点H是边BC的中点，∴BH＝CH．又∵∠3＝∠4，∴△BEH≌△CFH．(2)当BH＝EH时，四边形BFCE是矩形，理由如下：连接BF，CE．∵△BEH≌△CFH．∴EH＝FH，又BH＝CH，∴四边形BFCE是平行四边形．又∵BH＝EH，∴EF＝BC，∴四边形BFCE是矩形．5.已知在四边形ABCD中，，请添加一个条件，使四边形ABCD成为矩形，添加的条件可以是________．(只填一个即可)【答案】∠A＝90°(答案不唯一)【解析】由可知，该四边形是平行四边形，根据矩形的定义，只要加上条件“一个角是直角”即可，故填∠A＝90°，或∠B＝90°，或∠C＝90°，或∠D＝90°．6.如图所示，在□ABCD中，点E，F分别为BC边上的点，且BE＝CF，AF＝DE求证：□ABCD是矩形．【答案】∵四边形ABCD是平行四边形，∴AB＝CD．∵BE＝CF，∴BF＝CE．又∵AF＝DE，∴△ABF≌△DCE．∴∠B＝∠C．又∵∠B＋∠C＝180°，∴∠B＝∠C＝90°．∴□ABCD是矩形．【解析】已知四边形ABCD是平行四边形，欲证它是矩形，只需证一角是直角即可，由题意易知△ABF≌△DCE，而∠B＋∠C＝180°，因此有∠B＝∠C＝90°，问题迎刃而解．7.将矩形纸片ABCD按如图所示的方式折叠，使顶点B与顶点D重合，折痕为EF．若，AD＝3，则△DEF的周长为________．【答案】6【解析】∵沿EF折叠后，点B与点D重合，点A在点A′的位置，∴A′E＝AE，，BF＝DF．∵四边形ABCD为矩形，∴，BC＝AD＝3，∠C＝∠A＝90°．在Rt△DCF中，设CF＝x，则DF＝BF＝3－x，由勾股定理得，解得x＝1，∴DF＝3－x＝3－1＝2．同理，DE＝2．连接BD，交EF于点O，则点B与点D关于EF称，∴，BD⊥EF．在Rt△EDO中，，由DE＝DF，BD⊥EF，得EO＝OF＝1，∴EF＝2，∴△DEF的周长为DE＋DF＋EF＝2＋2＋2＝6．8.如图，矩形ABCD的对角线相交于点O，过点O的直线交AD、BC于点E、F，AB＝2，BC ＝4，则图中阴影部分的面积为（）A．2B．3C．4D．5【答案】C【解析】矩形ABCD的面积＝AB·BC＝2×4＝8，图中阴影部分面积的和等于矩形面积的一半，故选C．9.如图，在矩形ABCD中，DF平分∠ADC交AC于点E，交BC于点F，∠BDF＝15°，求∠DOC与∠COF的度数．【答案】75°【解析】解：∵DF平分∠ADC，∴∠FDC＝45°．又∵∠BDF＝15°，∴∠BDC＝45°＋15°＝60°．又∵四边形ABCD是矩形，∴AC＝BD，AO＝OC＝BO＝OD，∴△DOC是等边三角形．∴∠DOC＝60°．在Rt△DCF中，∠FDC＝45°，∴CF＝CD＝OC，∴∠COF＝∠CFO．又∵∠OCF＝90°－∠OCD＝90°－60°＝30°，∴∠COF＝75°．10.（2013湖南邵阳）如图所示，将△ABC绕AC的中点O顺时针旋转180°得到△CDA，添加一个条件________，使四边形ABCD为矩形．【答案】∠B＝90°（答案不唯一）【解析】∵△ABC绕AC的中点O顺时针旋转180°得到△CDA，∴AB＝CD，∠BAC＝∠DCA，∴AB∥CD，∴四边形ABCD为平行四边形．当∠B＝90°时，平行四边形ABCD为矩形，∴添加的条件为∠B＝90°．11.如图，四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是()A．AB＝CDB．AD＝BCC．∠AOB＝45°D．∠ABC＝90°【答案】D【解析】因为四边形ABCD的对角线互相平分，所以四边形ABCD为平行四边形，A、B两选项为平行四边形具有的性质，C选项添加后也不是矩形，根据矩形的定义知D正确．故选D．12.矩形具有而平行四边形不一定具有的性质是()A．对角相等B．对角线互相平分C．一组对边平行另一组对边相等D．对角线相等【答案】D【解析】矩形的对角线相等，而平行四边形的对角线不一定相等．13.如图，已知在Rt△ABC中，∠ABC＝90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线AB平移至△FEG，DE、FG相交于点H．(1)判断线段DE、FG的位置关系，并说明理由：(2)连接CG，求证：四边形CBEG是正方形．(提示：旋转前后，图形中对应的角和对应的边分别相等)【答案】见解析【解析】(1)DE⊥FG，理由如下：由题意得∠A＝∠EDB＝∠GFE，∠ABC＝∠DBE＝90°．∴∠BDE＋∠BED＝90°．∴∠GFE＋∠BED＝90°．∴∠FHE＝90°．∴DE⊥FG．(2)证明：∵△ABC沿射线AB平移至△FEG，∴CB∥GE，CB＝GE，∴四边形CBEG是平行四边形．∵∠ABC＝∠GEF＝90°．∴四边形CBEG是矩形．∵BC＝BE．∴四边形CBEG是正方形．14.如图，正方形ABCD中，对角线AC、BD相交于点O，则图中的等腰三角形有( )A．4个B．6个C．8个D．10个【答案】C【解析】在正方形ABCD中，AB＝BC＝CD＝AD，OA＝OB＝OC＝OD，所以等腰三角形有△ABC，△ADC，△ABD，△CBD，△OAB，△OBC，△OCD，△OAD．15.下列命题错误的是( )A．有一组邻边相等的平行四边形叫做正方形B．有一组邻边相等的矩形是正方形C．有一组邻边相等并且有一个角是直角的平行四边形叫做正方形D ．有一个角是直角的菱形是正方形【答案】A【解析】由定义可知，正方形既是有一组邻边相等的矩形，又是有一个角是直角的菱形，A 不正确，故选A ．16. 如图，正方形ABCD 的对角线相交于点O ，点O 也是正方形A′B′C′O 的一个顶点，两个正方形的边长都等于1，当正方形A′B′C′O 绕顶点O 转动时，两个正方形重叠部分的面积大小有什么规律？并说明理由．【答案】两个正方形重叠部分的面积保持不变，始终为．理由：∵四边形ABCD 是正方形，∴OB ＝OC ，∠OBE ＝∠OCF ＝45°，∠BOC ＝90°． ∵四边形A′B′C′O 是正方形， ∴∠EOF ＝90°，∴∠BOC ＝∠EOF ． ∴∠BOC －∠BOF ＝∠EOF －∠BOF ，即∠COF ＝∠BOE ．∴△BOE ≌△COF(ASA)，∴S △BOE ＝S △COF ．∴重叠部分面积等于S △BOC ．∵S 正方形ABCD ＝1×1＝1，∴，即两个正方形重叠部分的面积保持不变，始终为．【解析】正方形的两条对角线分正方形为四个全等的等腰直角三角形．通过证△BOE ≌△COF ，得．17. 如图，将矩形ABCD 中的△AOB 沿着BC 的方向平移线段AD 长的距离．（1）画出△AOB 平移后的图形．（2）设（1）中O 点平移后的对应点为E ，试判断四边形CODE 的形状，并说明理由．（3）当四边形ABCD 是什么四边形时，（2）中的四边形CODE 是正方形？并说明你的理由．【答案】（1）平移后的图形如图．（2）四边形CODE 是菱形．理由如下：∵△AOB 平移后得到△DEC ， ∴DE ∥AC ，CE ∥BD ． ∵四边形ABCD 是矩形，∴，，且AC＝BD，∵OC＝OD，∴四边形CODE是菱形．（3）当四边形ABCD是正方形时，（2）中的四边形CODE是正方形，理由如下：∵四边形ABCD是正方形，∴AC⊥BD，∴∠COD＝90°．∴菱形CODE是正方形．【解析】在图形移动过程中，图形的大小、形状不变，可得四边形CODE是菱形．当AC⊥BD 时，四边形CODE是正方形，此时四边形ABCD是正方形．18.（2013江苏南京）如图，在四边形ABCD中，AB＝BC，对角线BD平分∠ABC，P是BD 上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M、N．（1）求证：∠ADB＝∠CDB；（2）若∠ADC＝90°，求证：四边形MPND是正方形．【答案】见解析【解析】证明：（1）∵BD平分∠ABC，∴∠ABD＝∠CBD．又∵BA＝BC，BD＝BD，∴△ABD≌△CBD，∴∠ADB＝∠CDB．（2）∵PM⊥AD，PN⊥CD，∴∠PMD＝∠PND＝90°．又∵∠ADC＝90°，∴四边形MPND是矩形．∵∠ADB＝∠CDB，PM⊥AD，PN⊥CD，∴PM＝PN．∴四边形MPND是正方形．19.（2013济宁）如图中图（1），在正方形ABCD中，E、F分别是边AD、DC上的点，且AF⊥BE．（1）求证：AF＝BE．（2）如图中图（2），在正方形ABCD中，M、N、P、Q分别是边AB、BC、CD、DA上的点，且MP⊥NQ．MP与NQ是否相等？并说明理由．【答案】（1）证明：如图（1），在正方形ABCD中，AB＝DA，∠BAE＝∠D＝90°，∴∠DAF＋∠BAF＝90°，∵AF⊥BE，∴∠ABE＋∠BAF＝90°，∴∠ABE＝∠DAF，∵在△ABE和△DAF中，∴△ABE≌△DAF（ASA），∴BE＝AF．（2）解：MP与NQ相等．理由如下：如图（2），过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，则BE＝NQ，AF＝MP．只需证BE＝AF即可．与（1）的情况完全相同．【解析】（1）根据正方形的性质可得AB＝DA，∠BAE＝∠D＝90°，再根据同角的余角相等求∠ABE＝∠DAF，然后利用“角边角”证明△ABE和△DAF全等，再根据全等三角形的性质证明即可；（2）过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，然后解法与（1）相同．20.在四边形ABCD中，O是对角线的交点，下面能判断这个四边形是正方形的是（）A．AD⊥CD，AC＝BDB．AD∥BC，∠A＝∠CC．AO＝BO＝CO＝DO，AC⊥BDD．AO＝CO，BO＝DO，AB＝BC【答案】C【解析】对角线相等、互相平分且垂直的四边形是正方形．21.如图，过正方形ABCD的顶点B作直线l，过点A、C作l的垂线，垂足分别为点E、F，若AE＝1，CF＝3，则AB的长度为________．【答案】【解析】由题意，知△BFC≌△AEB，∴CF＝BE，∴．22. 已知，在四边形ABCD 中，∠A ＝∠B ＝∠C ＝90°，如果添加一个条件即可推出该四边形是正方形，那么这个条件可以是( )A ．∠D ＝90°B ．AB ＝CDC ．AD ＝BCD ．BC ＝CD【答案】D【解析】由∠A ＝∠B ＝∠C ＝90°可判定为矩形，根据正方形的定义，再添加条件“一组邻边相等”即可判定为正方形，故选D ．23. (2014福建福州)如图，在正方形ABCD 的外侧，作等边三角形ADE ，AC ，BE 相交于点F ，则∠BFC 为( )A ．45°B ．55°C ．60°D ．75°【答案】C【解析】由已知得AB ＝AE ，∠BAE ＝150°，∴∠ABF ＝15°，∴∠BFC ＝∠ABF ＋∠BAF ＝15°＋45°＝60°．24. 如图，边长为2的正方形ABCD 的对角线相交于点O ，过点O 的直线分别交AD 、BC 于E 、F ，则阴影部分的面积是________．【答案】1【解析】由题意可知△DEO ≌△BFO ，∴S △DEO ＝S △BFO ，∴．25. 如图所示，在菱形ABCD 中，AE 垂直平分BC ，垂足为E ，AB ＝4cm ．那么，菱形ABCD的面积是________，对角线BD的长是________．【答案】cm2；cm【解析】在菱形ABCD中，由AE垂直平分BC可知△ABC是正三角形，故BC＝AC＝4cm，由勾股定理可知cm，∴菱形ABCD的面积是(cm2)，同时菱形的面积还等于两条对角线乘积的一半，∴对角线BD的长为(cm)．26.如图，平行四边形ABCD的两条对角线AC和BD相交于点O，并且BD＝4，AC＝6，．(1)AC与BD有什么位置关系？为什么？(2)四边形ABCD是菱形吗？为什么？【答案】见解析【解析】(1)AC⊥BD，理由如下：∵四边形ABCD为平行四边形，∴，．在△OBC中，OC2＋OB2＝9＋4＝13＝BC2，∴△OBC为直角三角形，即OC⊥OB，∴AC⊥BD．(2)四边形ABCD是菱形，理由如下：∵AC⊥BD．∴平行四边形ABCD是菱形．27.(2012山西)如图，已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm，AE⊥BC于点E，则AE的长是( )A．cmB．cmC．cmD．cm【答案】D【解析】由菱形的性质知菱形边长为(cm)，所以，得cm，故选D．28. (2013山东潍坊)如图，ABCD是对角线互相垂直的四边形，且OB＝OD，请你添加一个适当的条件________，使ABCD成为菱形．(只需添加一个即可)【答案】本题答案不唯一，如OA＝OC或AD＝BC或AD∥BC或AB＝BC等【解析】根据对角线互相垂直平分可添加OA＝OC；或添加AD＝BC或AB＝DC或AD∥BC或AB∥DC或AB＝BC或AD＝DC，由三角形全等得到AO＝CO，再由对角线互相垂直平分得到四边形ABCD是菱形．29.如图，□ABCD的对角线AC的垂直平分线与AD、BC、AC分别交于点E、F、O，求证：四边形AFCE是菱形．【答案】∵四边形ABCD是平行四边形，∴AE∥CF，∴∠CAE＝∠ACF又∵∠AOE＝∠COF，OA＝OC，∴△AOE≌△COF．∴OE＝OF，∴四边形AFCE是平行四边形．又∵EF⊥AC．∴四边形AFCE是菱形．【解析】要证四边形AFCE是菱形，首先要证四边形AFCE是平行四边形．30.如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，AB＝10．(1)求∠ABC的度数；(2)求对角线AC的长度；(3)求菱形ABCD的面积．【答案】(1)连接BD，交AC于点O，如图．∵四边形ABCD是菱形，∴AD＝AB．∵E是AB的中点，且DE⊥AB，∴AD＝BD．∴△ABD是等边三角形．∴∠ABD＝60°．∴∠ABC＝60°×2＝120°．(2)∵四边形ABCD是菱形，∴AC，BD互相垂直平分．∴．∴在Rt△AOB中，，∴．(3)．【解析】(1)连接BD，与AC相交于点O，可证△ABD是等边三角形，所以∠ABD＝60°，可得∠ABC的度数；(2)在Rt△OAB中，由勾股定理可求出OA的长，则AC＝2OA；(3)根据菱形的面积公式可求其面积．。

初二数学几何证明题（5篇可选）

初二数学几何证明题（5篇可选）第一篇：初二数学几何证明题1.在△ABC中，AB=AC，D在AB上，E在AC的延长线上，且BD=CE，线段DE交BC于点F，说明：DF=EF。

2.已知：在正方形ABCD中，M是AB的中点，E是AB延长线上的一点，MN垂直DM于点M，且交∠CBE的平分线于点N.（1）求证：MD＝MN.（2）若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变，则（1）的结论还成立吗？如果成立，请证明，如果不成立，请说明理由。

3.。

如图，点E,F分别是菱形ABCD的边CD和CB延长线上的点，且DE=BF，求证∠E=∠F。

4，如图，在△ABC中，D,E,F,分别为边AB,BC,CA,的中点，求证四边形DECF为平行四边形。

5.如图，在菱形ABCD中，∠DAB=60度，过点C作CE垂直AC 且与AB的延长线交与点E，求证四边形AECD是等腰梯形？6.如图，已知平行四边形ABCD中，对角线AC,BD，相交与点0，E是BD延长线上的点，且三角形ACE是等边三角形。

1.求证四边形ABCD是菱形。

2.若∠AED=2∠EAD，求证四边形ABCD是正方形。

7.已知正方形ABCD中，角EAF=45度，F点在CD边上，E点在BC边上。

求证：EF=BE+DF第二篇：初二几何证明题1如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DCCF．（1）求证：D是BC的中点；（2）如果AB=ACADCF的形状，并证明你的结论AEB第三篇：初二几何证明题初二几何证明题1.已知：如图，在△ABC中，AD⊥BC，垂足为D，BE⊥AC，垂足为E。

M为AB中点，联结ME,MD、ED求证：角EMD=2角DAC证明：∵M为AB边的中点，AD⊥BC，BE⊥AC，∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图，已知四边形ABCD中，AD=BC,E、F分别是AB、CD中点，AD、BC的延长线与EF的延长线交于点H、D求证：∠AHE=∠BGE证明：连接AC，作EM‖AD交AC于M，连接MF.如下图：∵E是CD的中点，且EM‖AD，∴EM=1/2AD，M是AC的中点，又因为F是AB的中点∴MF‖BC，且MF=1/2BC.∵AD=BC，∴EM=MF，三角形MEF为等腰三角形，即∠MEF=∠MFE.∵EM‖AH，∴∠MEF=∠AHF ∵FM‖BG，∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题，并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。

2024年数学八年级几何证明专项练习题1(含答案)

2024年数学八年级几何证明专项练习题1（含答案）试题部分一、选择题：1. 在三角形ABC中，若∠A = 90°，AB = 6cm，BC = 8cm，则AC 的长度为（）。

A. 2cmB. 10cmC. 4cmD. 5cm2. 下列哪个条件不能判定两个三角形全等？（）A. SASB. ASAC. AASD. AAA3. 在直角坐标系中，点A(2,3)关于原点对称的点是（）。

A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个比例式是正确的？（）A. 若a∥b，则∠1 = ∠2B. 若a∥b，则∠1 + ∠2 = 180°C. 若a⊥b，则∠1 = 90°D. 若a⊥b，则∠1 + ∠2 = 180°5. 在等腰三角形ABC中，若AB = AC，∠B = 70°，则∠C的度数为（）。

A. 70°B. 40°C. 55°D. 110°6. 下列哪个条件可以判定两个角相等？（）A. 对顶角B. 邻补角C. 内错角D. 同位角7. 在平行四边形ABCD中，若AD = 8cm，AB = 6cm，则对角线AC 的长度（）。

A. 10cmB. 14cmC. 12cmD. 15cm8. 下列哪个图形是轴对称图形？（）A. 等腰三角形B. 等边三角形C. 矩形D. 梯形9. 在三角形ABC中，若a = 8cm，b = 10cm，c = 12cm，则三角形ABC是（）。

A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定10. 下列哪个条件不能判定两个直线平行？（）A. 内错角相等B. 同位角相等C. 同旁内角互补D. 两直线垂直二、判断题：1. 若两个三角形的两边和夹角分别相等，则这两个三角形全等。

（）2. 在等腰三角形中，底角相等。

（）3. 平行线的同位角相等，内错角相等。

（）4. 若两个角的和为180°，则这两个角互为补角。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初二数学平行四边形压轴：几何证明题
1.在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，顺次连接EF 、FG 、GH 、HE ．（1）请判断四边形EFGH 的形状，并给予证明；
（2）试探究当满足什么条件时，使四边形EFGH 是菱形，并说明理由。

2.如图，在直角三角形ABC 中，∠ACB=90°，AC=BC=10，将△ABC 绕点B 沿顺时针方向旋转90°得到△A 1BC 1．
（1）线段A 1C 1的长度是，∠CBA 1的度数是．（2）连接CC 1，求证：四边形CBA 1C 1是平行四边形．
3. 如图，矩形ABCD 中，点P 是线段AD 上一动点，O 为BD 的中点， PO 的延长线交BC 于Q.
（1）求证：OP=OQ ；
（2）若AD=8厘米，AB=6厘米，P 从点A 出发，以1厘米/秒的速度向D 运动（不与D 重合）.设点P 运动时间为t 秒，请用t 表示PD 的长；并求t 为何值时，四边形PBQD 是菱形．
4.已知：如图，在□ABCD 中，AE 是BC 边上的高，将△ABE 沿BC 方向平移，使点E 与点C
重合，得△GFC. ⑴求证：BE =DG ；
⑵若∠B =60︒，当AB 与BC 满足什么数量关系时，四边形ABFG 是菱形？证明你的结论.
5. 如图，在四边形ABCD 中，AD ∥BC ，E 为CD 的中点，连结AE 、BE ，BE ⊥AE ，延长AE 交BC 的延长线于点F ．求证：（1）FC ＝AD ；
（2）AB ＝BC ＋AD ．
A B
E F
C
G
D H B A 1
C 1
A C A
G
C
B
F
E
P
A D E
C
B
6.如图，在△ABC 中，AB=AC ，D 是BC 的中点，连结AD ，在AD 的延长线上取一点E ，连结BE ，CE.
（1）求证：△ABE ≌△ACE
（2）当AE 与AD 满足什么数量关系时，四边形ABEC 是菱形？并说明理由.
7.如图，在平行四边形ABCD 中，点E 是边AD 的中点，BE 的延长线与CD 的延长线交于点F. （1）求证：△ABE ≌△DFE
（2）连结BD 、AF ，判断四边形ABDF 的形状，并说明理由.
8. 如图，已知点D 在△ABC 的BC 边上，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ．（1）求证：AE ＝DF ；
（2）若AD 平分∠BAC ，试判断四边形AEDF 的形状，并说明理由．
9. 如图，在平行四边形中，点E F ，是对角线BD 上两点，且BF DE =．（1）写出图中每一对你认为全等的三角形；
（2）选择（1）中的任意一对全等三角形进行证明．
10.在梯形ABCD 中，AD ∥BC,AB=DC ，过点D 作DE ⊥BC ，垂足为点E ，并延长DE 至点F ，使EF=DE.连接BF 、CF 、AC.
（1）求证：四边形ABFC 是平行四边形；
（2）若CE BE DE ⋅=2
,求证：四边形ABFC 是矩形.
A
B E
D C
A
B
C
D E
E A F
C D
B A B
C E F A B F
C
D
E
11.如图，△ABC中，AB=AC，AD、AE分别是∠BAC和∠BAC的外角平分线，BE⊥AE. （1）求证：DA⊥AE
（2）试判断AB与DE是否相等？并说明理由。

12.如图，在△ABC中，AB=AC，点D是BC上一动点（不与B、C重合），作DE∥AC交AB于点E，DF∥AB交AC于点F.
（1）当点D在BC上运动时，∠EDF的大小（变大、变小、不变）
（2）当AB=10时，四边形EDF的周长是多少？
（3）点D在BC上移动的过程中，AB、DE与DF总存在什么数量关系？请说明. A F
C
D
E
B
A
B C
F
E
D。