第三章 群速度色散
相速度和群速度
群速度色散效应
由(7)式,不同的波长会有不同的群速度,波长越大,群速度越大。 early time late time
群速度色散的计算
单位:
Thank You !
单击此处添加副标题
Add your company slogan
汇报人姓名
群速度与波长的关系
相速度色散和群速度色散
群速度色散
在介质中由于不同频率的光的相速度也不一样,于是波包的形状会发生变化,这就是群速度色散,也称之为群速弥散. 相速度色散是色散的一阶效应,而群速度色散是色散的二阶效应。
相速度色散
由于不同频率的光在同一介质中的折射率是不一样的,于是不同频率的光的相速度也不一样,这就是相速度色散。
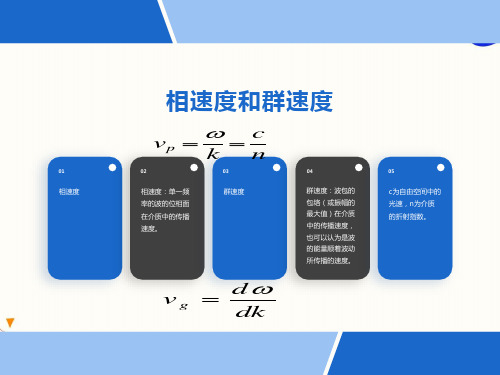
相速度和群速度
ቤተ መጻሕፍቲ ባይዱ
图中,波形传播的速度为群速度。 群速度和相速度的示意图 图中,包络面的移动速度为群速度 包络面
群速度的计算
群速度与频率的关系
由(4)式 当 时,有 时,有 正常色散 反常色散
01
因此,一般情况下(正常色散),群速度小于相速度。
分析:
02
当
时,有
03
当
无色散
吸收带
在吸收带附近长波一边的折射率比短波的大. 在吸收带内,n是无法测量的.
群速度色散

TFWHM 2(ln 2)1 2T0 1.665T0
沿光纤长度方向任一点z处的振幅为
U z,T
T02
T0
i2z
12
exp
2
T2
T02 i2 z
高斯脉冲在传输过程中其形状保持不变,但宽度T1随z增加,变为
T1
T0 1 z
LD
2
1
2
可以看出,尽管入射脉冲是不带啁啾的(无相位调制),但经光纤传 输后变成了啁啾脉冲,这一点通过把U(z,T)写成下面的形式就能清楚 地看出。
光纤不起太重要的作用,只是起传输光脉冲
的作用。T0>100ps & P0<1mW
2 L<< LNL LLD
×
脉冲变化由GVD决定,它作用引起脉冲展宽。
T0~1ps & P0<<1W
3. L LNL L<<LD ×
非线性起主要作用,SPM致脉冲频谱展宽 T0>100ps & P0>1W
4 L≥ LNL L≥LD
T t z e
T0
T0
同时,利用下面的定义引入归一化振幅U
A(z,t) P0 e(z 2)U (z, )
入射脉冲峰值功率
利用以上方程,U(z,τ)满足方程
=±1,取决于β2的符号
i U sgn(2 ) 2U ez | U |2 U
z
2LD 2 LNL
LD
T02
| 2
|
色散长度
LNL
双曲正割脉冲
这种脉冲的光场形式为
U
(0,T
)
sech
T T0
exp
iCT 2 2T02
沪科版八年级物理上册第3章第四节 光的色散

知1-讲
1. 光的色散现象:白光通过三棱镜后被分解为红、橙、黄、 绿、蓝、靛、紫七种颜色的光,这种现象叫做光的色散 现象。
2. 光的色散现象说明白光是由各种色光混合而成的。 3. 光的色散的原理——光的折射:由各种色光混合成的白
光经过三棱镜时发生折射,由于各种色光的偏折程度不 同,所以各种色光分散开,呈现彩色光带。
知1-练
1. [中考•抚顺,多选]中华文化源远流长,下列诗词涉及光 学知识,对其解释正确的是( AD ) A. “起舞弄清影”,影子是由光沿直线传播形成的 B. “明镜可鉴形”,明镜成像是因为光发生了折射 C. “潭清疑水浅”,潭水看起来浅是因为光发生了反射 D. “瀑水喷成虹”,彩虹是光的色散现象
知3-讲
方法点拨
知3-讲
逆向思维 决定
已知:透过物体色光的颜色 透明物体的颜色;物
决定 体反射色光的颜色 不透明物体的颜色。
确定 逆向思维:透明物体的颜色 透过色光的颜色;不
确定 透明物体的颜色 反射色光的颜色。
知3-练
例 3 太阳光透过玻璃后照在白纸上,白纸上呈现红色, 则玻璃是__红____色的,一块棉布几乎将所有色光全 部吸收,则这块棉布是___黑___色的。 解题秘方:透明物体的颜色由其透过的色光决定; 不透明物体的颜色由其反射的色光决定。
第三章 光的世界
第四节 光的色散
1 课时讲解 色散现象
色光混合 物体的颜色
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
知识点 1 色散现象
知1-讲
知1-讲
知识拓展 太阳光通过三棱镜时,不同色光向三棱镜底边偏折
的程度不同,紫光向三棱镜底边偏折的程度最大,红光向 三棱镜底边偏折的程度最小,导致彩色光带的出现。
正常色散介质中群速度与相速度的相对关系

正常色散介质中群速度与相速度的相对关系
光的传播速度在不同介质中会发生改变,这种现象被称为光在介质中的折射,其中光传播的速度,在正常色散介质中群速度与相速度有一定的关系。
在正常色散介质中,介质中的光速度与频率之间呈现线性关系,也就是说在相同介质中,频率越高,光速度也越高。
根据自然的光学原理,光在介质中的传输速度是由群速度和相速度组成的。
群速度和相速度在正常色散介质中是有一定的关系的。
群速度表示的是光信号在介质中整体传播的速度,而相速度则是光的电场和磁场在介质中传播的速度。
在正常的色散介质中,群速度通常要大于相速度,也就是说,在介质中传输光信号的速度整体上要快于电场和磁场的传输速度。
这可以通过正常色散介质中材料的复合折射率来解释。
光的相位速度与群速度之间的差异是由折射率的频率依赖性造成的。
在正常色散材料中,较高频率的光会快速折射并且离开表面,而较低频率的光则会被材料捕获和重新释放,从而形成相对较慢的群速度。
在光纤通讯系统中,光速度和光的传输性能至关重要。
对于正常色散介质,光信号传播的快慢由材料的折射率决定,因此了解群速度和相速度之间的相对关系对于光纤通讯系统的设计和优化非常重要。
总之,在正常色散介质中,群速度和相速度之间存在一定程度的相对关系。
群速度比相速度更高,这是由于复合折射率的频率依赖性造成的。
这种相对关系在光学系统的优化中非常重要,因为光速和光的传输性能通常是光学系统设计和优化的关键因素之一。
单模光纤中群速度色散和自相位调制所致啁啾的相互作用关系

三
co 丽 A D : v 一  ̄O V = G =
图 2为 。D v与 的 关 系 曲线 , 斯 脉 冲 沿 光 纤 传 播 时 , 不 同的 位 置 有 不 同 的斜 率 , 有 不 同 的 啁 啾 高 在 即
vD
:
一
等一 1 +
2g ( s n
丁
( ) 6
( ) 7
在 反 常 色 散 区 , 卢< O则 ( ) 变 为 : 令 。 6式
“IvD 一 一 G
T[ + ( z 。 1 ≠) 3 ]
上 D
( ) 7
( ) 对 于 高 斯 脉 冲 , 一 个 脉 冲 中 Z 近 似 为 常 数 , v和 T/ 为 一 直 线 , 1为 反 常 色 散 区 7式 每 D T。 图 c D T/ 的关 系 , 吣v和 T。 其频 率 啁 啾 为 负 啁啾 , 啾 的 传 输 特 性 由 KcD 定 : 啁 v决
( 1 )
式 s ()士 ,据 V 参 的 号 定L= 午为 散 度L 一 为 线 长 ・ 中g 一 1 GD 数 符 确 , = n 根 。 色 长 , 非 性 度 :
在 方 程 () , 7 , 虑 线 性 色 散 介 质 中脉 冲 传输 时 GVD 效 应 , ( ,) 满 足 的 微 分 方 程 为 1 中 令 =0 考 “ z f所
No v. 2 2 00 VoI 33 . N o. 6
文 章 编 号 : 0 O 1 3 ( 0 2 0 —6 70 1 0一 68 2 0)602—5
单 模 光 纤 中群 速 度 色 散 和 自相 位 调 制 所 致 啁 啾 的 相 互 作 用关 系 。
贾 维 国 , 洪 祥 宋晓 琴 乌 ,
第三章(2)光的吸收、色散、散射全解

性质以及周围介质等关系比较复杂。这种散射称 为米氏散射。 例1、白云由大气中的水汽组成,颗粒较大,它产 生的散射与波长关系不大,所以呈白色,属于米 氏散射。 例2、吸烟时,从点燃的烟头冒出的烟是蓝色的, 而从嘴里吐出的烟是白色的。这是由于烟头冒出 的烟颗粒很小,遵守瑞利散射定律,对蓝光散射 厉害。而从嘴里吐出的烟中,含有颗粒较大的蒸 汽团,属于米氏散射,散射光呈白色。
瑞利群速公式
Vg V p λ
dVp dλ
在真空中 V p ( λ ) c
Vg V p c
dV p c dn 2 d n d
dV p c dn 2 >0 d n d
c 在介质中 V p n
dn 在正常色散区 0 dλ
由瑞利群 速公式
Vg V p
dn 2B 3 将上式对求导得: D dλ λ
2、反常色散
在发生强烈吸收的波段,折射率n 随波长的增 加而增大,即dn /d0 。这种现象称为反常色散。
n
P
Q R
S
T
可见光
吸收带
石英的色散曲线
上图反映了物质在吸收区普遍遵从的色散规律。 在吸收区以外仍是正常色散,只是A、B、C等常量 的具体数值并不一定相同。
I
式中负号表示随吸收 层厚度增加光能量减小
O
x x dx x
若x = 0时光强为I0,x = L时光强为I
由积分
II0L 源自I 0 dx II 得: ln I αL 0
αL
朗伯定律
I I 0e
2、比尔定律 实验表明,当光通过透明溶液时,溶液对光 的吸收与溶液的性质及浓度有关,若不考虑溶剂 对光的吸收,稀溶液的吸收系数与溶质在溶液中 的浓度 (书上称质量分数C)成正比。
波包(群速相速)和色散

一波包维基百科,自由的百科全书跳转到:导航搜索汉汉▼一个正在传播中,非色散的波包。
在物理学里,一个波包是一群平面波在空间的一个小区域内的叠和。
这些平面波都有不同的波数、波长、相位、波幅,都分别地建设性干涉于空间的一个小区域。
依据不同的演化方程,在传播的时候,波包的包络线(素描波包轮廓的曲线)可能会保持不变(没有色散,如图右),或者包络线会改变(有色散)。
在量子力学里,波包有个特别的意思:波包被铨释为粒子的概率波,而在任何位置,任何时间,概率波波幅的绝对值的平方,就是在那个位置,那个时间,找到粒子的概率密度。
在这方面,它的功能类似波函数。
类似在经典力学里的哈密顿表述,在量子力学里,应用薛定谔方程,我们可以追溯一个量子系统随着时间的演化。
波包是薛定谔方程的数学解答。
在某些区域内,波包所囊括的面积的平方,可以铨释为找到粒子处于那区域的概率密度。
采用坐标表现,波包的位置给出了粒子的位置。
波包越狭窄,粒子的位置越明确,而动量的分布越扩散。
这位置的明确性和动量的明确性,两者之间的轻重取舍是海森堡不确定原理的一个标准例子。
目录隐藏1 背景 2 波包计算范例 3 参考文献 4 参阅编辑背景早在十七世纪,牛顿就已创始地建议光的粒子观:光的移动是以离散的束包形式,称为光微粒。
可是,在许多实验中,光表现出了波动行为。
这使科学家们渐渐地倾向于波动观,认为光是一种传播于介质中的波动。
特别著名的一个实验是英国科学家托马斯杨在1801 年设计与研究成功的双缝实验。
这实验试图解答光到底是粒子还是波动的问题。
从这实验观测到的干涉图案给予光的粒子观一个致命的打击。
大多数的科学家从此接受了光的波动观。
在20 世纪初期,科学家开始发现经典力学内在的许多严重的问题,许多实验的结果,都无法用经典理论来解释。
一直到1930 年代,光的粒子性,才真正地被物理学家广泛接纳。
在这段时间,量子力学如火如荼的发展,造成了许多理论上的突破。
许多深奥的实验结果,都能够得到圆满合理的解释。
群速度色散对二维异步OCDMA系统误码率的影响

p = ・一
I
,
, (-) ( R2 1 N 1 , W, ) + 一£ p I
。
扎
2
N _I
( ( 2・-- R I 一ZJ W -
p
—
。 +
、v( - R2,- r W, 一Z 三] J
一) ” ( 号 2 )
式 中 : 为光地 址码矩 阵 的行数 , 为列 数 ,
, 。
‰ 亍 卜b/ 2b 2 R , IWJ / R W  ̄ (
( L ) 程描 述 : NS 方
a A
+ = 一
, ( , 一_. 一) 】 ( 1 N ̄、W/ b 卜 号 } 3 ) -  ̄/( R , 州 +I R  ̄/ c ・ / )
其中, b为光 纤 的输 出光脉 冲和输 入光 脉 冲 F M 比值 。 WH
统性 能进 行研 究 。
2 理 论分 析 .
O D A系统采用的光地址码序列是~组 ( , ) CM 0 1 序列 , 其主要的设计参数为( , ,。A ) F 码字长 FKA, 为
度 , 0 1 序列的切普总数 ; 即( ,) K为码字重量 , 0 1 码序列中“ ” 即( ,) 1 的总数; 。 自 A 为 相关; A 为互相关。 本文
码分 多址 系统误码 率与传输距 离的关 系曲线和 与 用户数 关 系曲线 。数 值 结果表 明, 群速度 色散会 严重影 响二 维光
码 分 多 址 系统 的 性 能 。
关键词 : 群速度 色散 ; 二维光正交码 ; 维 O D 二 平步 C MA 中图分 类号 :N 5 T 22 文献标 识码 : A 文章编 号 :0 8— 7 5 2 1 )6一 1 0 10 3 1 (0 1 0 叭 7— 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Phase velocity and Group velocity
• 相速定义为与行波场保持固定相位的观 察者前进的速度。沿光纤轴传播的单色 波可以描述为
E(x,t) E0 coskx t
kx t const. vphase / k
• 群速定义为与群传播包络保持固定相位 的观察者前进的速度。
vg dk / d1
Using k= n()/c0, calculate: dk /d = (n + dn/d) / c0 vg c0 /n dn/d) = (c0 /n) / (1 + /n dn/d )
Finally:
vg
v phase
/
1
n
dn
d
So the group velocity equals the phase velocity when dn/d =
0.8
D
z/L = 4
D
0.6
0.4
T1 / T0 1 z / LD 2
0.2
0.0-6
-4
-2
0
2
4
6
T/T 0
24
GVD致脉冲啁啾
T
2sgn2 z / LD 1 z / LD 2T02
T
• 线性频率啁啾(横过脉冲的频率变化是线性的);
• 在正常色散区, > 0, 上或正啁啾(脉冲前沿红移,后 沿蓝移);在反常色散区, < 0,下或负啁啾(脉冲前 沿蓝移,后沿蓝红移);
E%tot (x,t) E%0 exp i(k1x 1t) E%0 exp i(k2x 2t)
Let
kave k1 k2 / 2 and k k1 k2 / 2
Similiarly, ave 1 ቤተ መጻሕፍቲ ባይዱ2 / 2 and 1 2 / 2
So: E%tot (x,t) E%0 exp i(kave x kx avet t)
Taking the real part yields the product of a rapidly varying
cosine (ave ) and a slowly varying cosine ().
16
When two light waves of different frequency interfere, they produce beats
T1 T0
1
C 2 z
T02
2
2z
T02
2
2C > 0时,脉冲单调展宽; 2C < 0时,脉冲先压缩再 展宽,最小脉宽和达到最小脉宽的光纤长度表达式 :
T1min
T0 , 1 C2
C zmin 1 C2 LD
26
GVD 对超Gaussian脉冲的影响
超Gaussian脉冲
A(0,T
)
exp
Az,T
1
2
A~0,exp
i 2
2 2
i 6
3 3
iT d
Where
A~0,
A0,T
expiT
d
22
GVD 对Gaussian脉冲的影响
Consider the propagation of an initial Gaussian pulse,
A0,T
A0
exp
T2 2T02
After propagating a distance z, the pulse evolved into the following form
Note that fiber folks define GVD as the negative of ours.
Sophisticated cladding structures, i.e., index profiles have been designed and optimized to produce a waveguide dispersion that modifies the bulk material dispersion
18
Group velocity is not equal to phase velocity
if the medium is dispersive (i.e., n varies)
For
our
example,
vg
k
c0k1 c0k2 n1k1 n2k2
where k1 and k2 are the k-vectors in vacuum.
•如何归一化?
每一个量分别选取一把参考尺子去度量。一 般来说,脉冲宽度用初始脉宽去度量;传播距离 用色散长度去度量;脉冲振幅用初始功率的平方 根去度量。
3
非线性Schrodinger方程的归一化
i A z
i
2
A
2
2
2A T 2
A2A
设入射脉冲的初始宽度和峰值功率分别为T0和 P0,定义色散长度LD和非线性长度LNL:
则NLS方程变换成如下归一化形式:
i U
sgn2 2U
2 2
N 2ez U
2U
式中N2 = LD/LNL , N是孤子阶数。
5
色散长度与非线性长度
•定义:
LD T02 / 2 , LNL 1/P0
其中T0和P0分别为入射脉冲的初始宽度和峰值 功率。
• 意义:
LD: GVD开始起作用的长度; LNL:非线性效应开始起的长度
LD T02 / 2 , LNL 1/P0
引入下列归一化变量
T /T0, A z, P0ez/2U z,
NLS方程变换成如下归一化形式:
i U z
sgn2 2U
2LD 2
ez LNL
U
2U
4
非线性Schrodinger方程的归一化
如果进一步引入归一化传播距离:
z / LD
E%tot (x, t) E%0 exp(i1t) E%0 exp(i2t)
Let
ave
1
2
2
and 1 2
2
So: E%tot (x, t) E%0 exp i(avet t) E%0 exp i(avet t) E%0 exp(iavet)[exp(it) exp(it)] 2E%0 exp(iavet) cos(t)
第三章 群速度色散
文双春 唐志祥
2009年3月17日星期二
1
Contents
• 非线性Schrodinger方程的归一化 • 色散致脉冲展宽 • GVD对啁啾脉冲的影响 • 高阶色散效应 • GVD对光通信系统的限制
2
非线性Schrodinger方程的归一化
•为什么归一化?
简洁 便于比较相对重要性 标准
12
Questions
• Does dispersion affect the propagation of a plane wave?
• A wave packet (pulse) comprises of a number of plane waves with different frequencies. What is the frequency of the pulse? What is the velocity of the pulse?
0.4
0.3
2T 0
0.2
0.1
0.0
-6
-4
-2
0
2
4
6
T
21
色散致脉冲展宽的解析研究方法
Starting equation:
A z
i2
2
2A T2
3
6
3A T3
This equation can be easily solved by Fourier
transformation. The solution is
17
Group velocity
Light wave beats (continued): Etot(x,t) = 2E0 cos(kavex–avet) cos(kx–t)
This is a rapidly oscillating wave [cos(kavex–avet)] with a slowly varying amplitude [2E0 cos(kx–t)] The phase velocity comes from the rapidly varying part: v = ave / kave What about the other velocity? Define the "group velocity:" vg /k In general, we define the group velocity as: vg d /dk
If n1 n2 n,
vg
c0 n
k1 k1
k2 k2
c0 n
phase
velocity
If n1 n2 ,
vg c
19
Calculating the Group velocity
vg d /dk
Now, is the same in or out of the medium, but k = k0 n, where k0 is the k-vector in vacuum, and n is what depends on the medium.So it's easier to think of as the independent variable:
“Angular dispersion”
dn/dl
Dispersion also disperses a pulse in time:
