数据库 关系运算(关系代数)
关系代数表达式总结-数据库
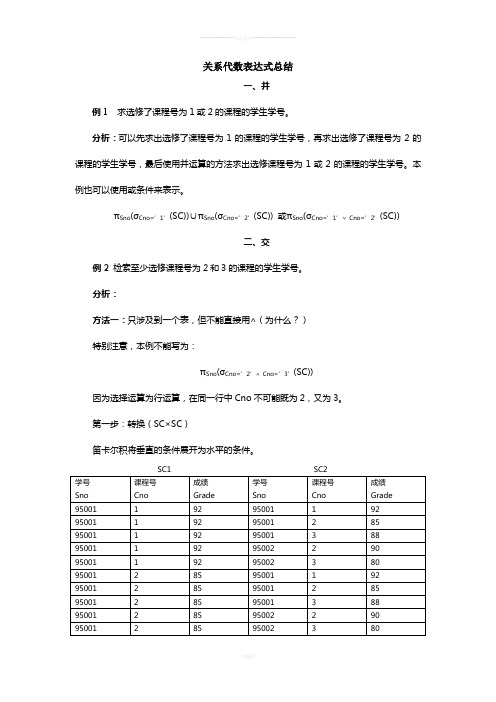
关系代数表达式总结一、并例1 求选修了课程号为1或2的课程的学生学号。
分析：可以先求出选修了课程号为1的课程的学生学号，再求出选修了课程号为2的课程的学生学号，最后使用并运算的方法求出选修课程号为1或2的课程的学生学号。
本例也可以使用或条件来表示。
πSno(σCno=’1’(SC))∪πSno(σCno=’2’(SC)) 或πSno(σCno=’1’∨Cno=’2’(SC))二、交例2 检索至少选修课程号为2和3的课程的学生学号。
分析：方法一：只涉及到一个表，但不能直接用∧（为什么？）特别注意，本例不能写为：πSno(σCno=’2’∧Cno=’3’(SC))因为选择运算为行运算，在同一行中Cno不可能既为2，又为3。
第一步：转换（SC×SC）笛卡尔积将垂直的条件展开为水平的条件。
选修课程号为2和3的学生：σ1=4∧2=’2’∧5=’3’(SC×SC)最后取出学生的学号：π1(σ1=4∧2=’2’∧5=’3’(SC×SC))方法二：πSno(σCno=’2’(SC))∩πSno(σCno=’3’(SC))三、差例3 将学生信息(‘95001’,’李勇’，‘男’，20，‘CS’)从Student表删除。
分析：可以将这行数据看成由一个元组构成的表，将Student表与该表进行差运算。
因此，该删除操作可表示为：Student-{‘95001’,’李勇’，‘男’，20，‘CS’}注意：但是当查询涉及到否定或全部值时，上述形式就不能表达了，就要用到差操作或除操作。
例4 求没有选修课程号为2的课程的学生学号。
分析：可以认为是在全部学号中去掉选修课程号为2的课程的学生学号，就得出没有选修课程号为2的学生学号。
由于在并、交、差运算中，参加运算的关系要求是兼容的，故应当先投影，再进行差运算。
πSno(Student)- πSno(σCno=’2’(SC))特别注意，本题不能写为：πSno(σCno≠’2’(SC))。
第四章 数据库设计基础——关系运算
3. 交（Intersection） ）
R和S
具有相同的目n 相应的属性取自同一个域
R∩S
仍为n目关系，由既属于R又属于S的元组组成 R∩S = { t|t ∈ R∧t ∈S } R∩S = R –(R-S）
An Introduction to Database System
交 (续) 续
An Introduction to Database System
(c)
An Introduction to Database System
1. 选择（Selection） 选择（ ）
1) 选择又称为限制（Restriction） 2) 选择运算符的含义 在关系R中选择满足给定条件的诸元组 σF(R) = {t|t∈R∧F(t)= '真'} F：选择条件，是一个逻辑表达式，基本形式为：
学生-课程数据库: 学生关系Student、课程关系Course和选修关系SC
Student
学号 Sno 200215121 200215122 200215123 200215125 姓名 Sname 李勇 刘晨 王敏 张立 性别 Ssex 男 女 女 男 (a) 年龄 Sage 20 19 18 19 所在系 Sdept CS IS MA IS
An Introduction to Database System
(b)
专门的关系运算(续 专门的关系运算 续)
SC
学号 Sno 200215121 200215121 200215121 200215122 200215122 课程号 Cno 1 2 3 2 3 成绩 Grade 92 85 88 90 80
200215121 200215121 200215122 200215122
数据库关系运算
第3章 关系运算及关系系统
除法的性质：
（1） R÷S的结果属性是由属于R但不属于S的所有属性
构成的。
（2） R÷S的任一元组都是R中某元组的一部分。 （3） R（X，Y）÷S（Y，Z）≡R（X，Y）÷πY（S）
或构造临时关系T={P2，P4}， 再求
πE＃， P＃（EP）÷T
第3章 关系运算及关系系统
⑧ 检索参与全部项目职工姓名。
πEN（（（πE＃， P＃（EP））÷πP＃（P）） πE＃， P＃（EP）÷πP＃（σE＃=′E3′（EP）） E）
⑨ 检索参与项目包含职工E3参与项目的职工号，
或参与项目不包含职工E3所参与项目的职工号及姓名。
第3章 关系运算及关系系统
R÷S=πX（R）－πX（（πX（R）×S）－R）
（4） R÷S的计算过程如下：
① T=πX（R）;
② W=（T×S）－R;
③ V=πX（W）;
④ R÷S=T－V。
【例3.3】 给定关系R和S， 求R÷S。
第3章 关系运算及关系系统
图3.5 除法操作举例
第3章 关系运算及关系系统
然连接。 为了保留更多信息， 还有外连接、 半连接、 外部并-----扩充的关系代数运算。
第3章 关系运算及关系系统
1． 外连接（Outer join） 两个关系 R和 S 作自然连接时， 两个关系
公共属性上值不相等的元组无法进入连接后的
新关系， 造成R和S中部分元组值被舍弃。 有时希望这些该舍弃的元组继续保留在新关系 中-----外连接。
图3.7
S
SC运算结果
数据库关系代数运算例题
数据库关系代数运算例题摘要：1.关系代数简介2.数据库关系代数运算例题详解a.并运算b.交运算c.差运算d.笛卡尔积运算e.投影运算f.选择运算g.连接运算3.总结与展望正文：一、关系代数简介关系代数是一种对关系数据库进行操作的数学理论。
它利用基本的集合运算和关系运算对关系数据库中的数据进行查询、插入、更新和删除等操作。
关系代数的基本运算包括并、交、差、笛卡尔积、投影、选择和连接等。
二、数据库关系代数运算例题详解1.并运算例题1：给定关系R和S，求R并S的结果。
解：设R={1, 2, 3, 4}, S={3, 4, 5, 6}，则R并S={1, 2, 3, 4, 5, 6}。
2.交运算例题2：给定关系R和S，求R交S的结果。
解：设R={1, 2, 3, 4}, S={3, 4, 5, 6}，则R交S={3, 4}。
3.差运算例题3：给定关系R和S，求R差S的结果。
解：设R={1, 2, 3, 4}, S={3, 4, 5, 6}，则R差S={1, 2}。
4.笛卡尔积运算例题4：给定关系R和S，求R与S的笛卡尔积。
解：设R={1, 2}, S={a, b}，则R与S的笛卡尔积为{（1, a），（1, b），（2, a），（2, b）}。
5.投影运算例题5：给定关系T，求T中属性A的投影。
解：设T={（1, 2, 3），（2, 3, 4），（3, 4, 5）}，则T中属性A的投影为{（1，3），（2，3），（3，5）}。
6.选择运算例题6：给定关系T，求满足条件“属性B大于2”的选择结果。
解：设T={（1, 2, 3），（2, 3, 4），（3, 4, 5）}，则满足条件“属性B大于2”的选择结果为{（2，3，4），（3，4，5）}。
7.连接运算例题7：给定关系R和S，求R与S的连接结果。
解：设R={（1, 2），（3, 4）}，S={（2, 3），（4, 5）}，则R与S的连接结果为{（1，2，3），（3，4，5）}。
关系数据库关系代数运算
• 是一种抽象的查询语言
SQL
• 介于关系代数和关系演算之间 • 集DDL、DML和DCL一身的关系数据语言
2.2 关系数据结构的形式化定义
关系模型建立在集合代数基础上，从集合论角度讨论 关系的形式化定义
定义1：域(Domain)－形式化表示为D
• 一组具有相同数据类型的值的集合，如整数、实数等。定义
张三 女
802
李四 男
803
王五 男
804
赵六 女
805
钱七 男
01
19
01
20
01
20
02
20
02
19
专业号 01 02 03
专业名 信息 数学 计算机
关系间的引用
例2 学生、课程、学生与课程之间的多对多联系
学生（学号，姓名，性别，专业号，年龄） 课程（课程号，课程名，学分） 选修（学号，课程号，成绩）
外码说明
关系R和S不一定是不同的关系 目标关系S的主码Ks 和参照关系的外码F必
须定义在同一个（或一组）域上 关于取名
外码并不一定要与相应的主码同名 当外码与相应的主码属于不同关系时，往往取
相同的名字，以便于识别
参照完整性举例
例１：学生实体与专业实体间的关系： 外码 学生（学号，姓名，性别，专业号，年龄） 专业（专业号，专业名）
04
90
04
88
关系间的引用
例3 学生实体及其内部的领导联系(一对多)
学生（学号，姓名，性别，专业号，年龄，班长）
学号
801 802 803 804 805
姓名
张三 李四 王五 赵六 钱七
性别
女 男 男 女 男
数据库关系代数运算例题
数据库关系代数运算例题
下面是一个关系代数运算的例题：
已知有两个关系表格R和S，分别包含以下字段：
R(A, B, C)
S(C, D)
问题1: 求R和S的笛卡尔积。
解答1: 笛卡尔积可以利用关系代数的乘积运算来表示。
乘积运算使用 ×符号表示，即 R × S。
问题2: 求R和S的并集。
解答2: 并集可以利用关系代数的并运算来表示。
并运算使用∪符号表示，即 R ∪ S。
问题3: 求R和S的交集。
解答3: 交集可以利用关系代数的交运算来表示。
交运算使用∩ 符号表示，即R ∩ S。
问题4: 求R和S的差集。
解答4: 差集可以利用关系代数的差运算来表示。
差运算使用 - 符号表示，即 R - S。
问题5: 求R关于字段A的投影。
解答5: 投影可以利用关系代数的投影运算来表示。
投影运算使用π 符号表示，即π(A)(R)。
问题6: 求R关于字段A的选择条件为A=1的选择。
解答6: 选择可以利用关系代数的选择运算来表示。
选择运算使用σ 符号表示，即σ(A=1)(R)。
问题7: 求R和S的连接条件为R.C=S.C的自然连接。
解答7: 自然连接可以利用关系代数的连接运算来表示。
连接运算使用⨝符号表示，并在连接条件上加上等式。
即 R ⨝(R.C=S.C) S。
第三章-关系代数与关系运算
第三章关系代数与关系运算关系数据语言有三类：1．关系代数语言2．关系演算语言（元组关系演算语言、域关系演算语言）3．具有关系代数和关系演算双重特点的语言如SQL一．关系代数关系代数：一种抽象的查询语言，是关系数据操纵语言的一种传统表达方式。
用对关系的运算来表达查询。
运算：将一定的运算符作用于一定的运算对象上，得到预期的运算结果运算三要素：运算符、运算对象、运算结果关系代数的运算对象和结果都是：关系关系代数运算符（四类）：集合运算符、专门的关系运算符、算术比较符和逻辑运算符集合运算符：并（U）、差（—）、交（∩）传统的集合运算符——从关系的“水平“方向即行的角度来进行专门的关系运算符：广义笛卡尔积（ⅹ）、选择（σ）、投影（π）、连接、除专门关系运算符不仅涉及行而且涉及列比较运算符：>、<、=、≥、≤、≠逻辑运算符：￢∧∨用来辅助专门的关系运算符二．传统的集合运算符传统集合运算符是二目运算符设关系R和S具有相同的目n(即n个属性),且相应的属性取自同一个域1．并（Union）记作：RUS={t|t∈R∨t∈S}结果仍是n目关系，由属于R或S的元组组成。
例：（a）（b）2.差关系R与S的差记作：R-S={t|t∈R∧t∈S} 结果仍是n目，由属于R而不属于S的所有元组组成。
如图E3.交关系R与S的交记作：R∩S = { t | t∈R∧t∈S }结果仍是n目，由即属于R又属于S的所有元组组成。
如图D 可以用差来表示R∩S=R-(R-S)4．广义笛卡尔积两个分别为n目和m目的关系R和S的广义笛卡尔积是一个（m+n）列的元组的集合。
元组的前n列是关系R的一个元组，后m列是关系S的一个元组。
若R有k1个元组，S有k2个元组，那么关系R与S的广义笛卡尔积有k1 x k2个元组，记作R×S = { t r t s | t r∈R∧t s∈S } 结果是m+n目如图例总结：集合运算符主要研究的是元组，即对表中的行进行研究、操作。
数据库关系代数运算例题
数据库关系代数运算例题（原创版）目录1.数据库关系代数概念2.关系代数运算分类3.关系代数运算例题a.并运算b.交运算c.差运算d.笛卡尔积e.投影运算f.选择运算g.连接运算h.自然连接正文一、数据库关系代数概念数据库关系代数是一种操作数据库中关系的数学方法，它可以在关系数据库中进行数据查询和数据处理。
关系代数基于数学集合代数概念，将数据库中的表看作是关系，通过对关系的操作实现对数据的操作。
二、关系代数运算分类关系代数运算主要分为以下几类：1.并运算：对两个关系进行并操作，返回一个新关系，包含属于任意一个关系的元组。
2.交运算：对两个关系进行交操作，返回一个新关系，包含既属于第一个关系又属于第二个关系的元组。
3.差运算：对两个关系进行差操作，返回一个新关系，包含属于第一个关系但不属于第二个关系的元组。
4.笛卡尔积：对两个关系进行笛卡尔积操作，返回一个新关系，包含所有可能的元组组合。
5.投影运算：对一个关系进行投影操作，返回一个新关系，包含原关系中的部分属性列。
6.选择运算：对一个关系进行选择操作，返回一个新关系，包含满足给定条件的元组。
7.连接运算：对两个关系进行连接操作，返回一个新关系，包含满足连接条件的元组。
8.自然连接：对两个关系进行自然连接操作，返回一个新关系，包含满足自然连接条件的元组。
三、关系代数运算例题1.并运算例题：设有学生表（学号，姓名，性别）和课程表（课程号，课程名），求所有学生的信息。
解答：使用并运算，将学生表和课程表进行并操作，得到一个新关系，包含所有学生的信息以及课程信息。
2.交运算例题：设有学生表（学号，姓名，性别）和成绩表（学号，成绩），求学生的姓名和成绩。
解答：使用交运算，将学生表和成绩表进行交操作，得到一个新关系，包含学生的姓名和成绩。
设有学生表（学号，姓名，性别）和课程表（课程号，课程名），求学生的信息，但不包括选修“数据库原理”课程的学生。
解答：使用差运算，将学生表和课程表进行差操作，得到一个新关系，包含不属于选修“数据库原理”课程的学生的信息。
数据库关系代数运算例题
数据库关系代数运算例题数据库关系代数是一种基于集合论和逻辑学的数学形式化表达数据库操作的方法。
它主要包括六种基本运算：选择（Selection）、投影（Projection）、并集（Union）、交集（Intersection）、差集（Difference）和连接（Join），以及补集（Complement）等附加运算。
这些运算可以用来描述和操作关系模型中的数据。
以下是一些数据库关系代数运算的例子：1. 选择（Selection）：通过设置条件来选择满足条件的元组。
比如，假设有一个关系R，包含属性A和B，选择满足A=1的元组可以表示为σ(A=1)(R)。
2. 投影（Projection）：通过选择部分属性来创建一个新的关系。
比如，假设有一个关系R，包含属性A、B和C，投影出包含属性A和B的新关系可以表示为π(A,B)(R)。
3. 并集（Union）：将两个具有相同属性的关系合并成一个新的关系。
比如，假设有两个关系R和S，它们包含相同属性A、B和C，将它们的并集可以表示为R ∪ S。
4. 交集（Intersection）：找到两个具有相同属性的关系中共有的元组，创建一个新的关系。
比如，假设有两个关系R和S，它们包含相同属性A、B和C，将它们的交集可以表示为R ∩ S。
5. 差集（Difference）：找到一个关系中有而另一个关系中没有的元组，创建一个新的关系。
比如，假设有两个关系R和S，它们包含相同属性A、B和C，将它们的差集可以表示为R - S。
6. 连接（Join）：通过匹配两个关系中的元组来创建一个新的关系。
比如，假设有两个关系R和S，它们包含属性A和B，通过匹配满足R.A=S.A的元组可以表示为R ⨝ S。
7. 补集（Complement）：找到一个关系中没有出现在另一个关系中的元组，创建一个新的关系。
这些数据库关系代数运算可以通过组合使用来执行复杂的查询操作。
它们提供了一种简洁和形式化的方法来描述和操作关系模型中的数据，方便开发人员进行数据库查询和数据处理。
数据库系统-关系代数
数据库系统-关系代数
关系代数是一种抽象的查询语言，是关系数据操纵语言的一种传统表达方式，它是利用对关系的运算来表达查询的。
任何运算都是将一定的运算符作用于一定的运算对象上，得到预期的运算结果。
关系代数的运算对象是关系，运算结果亦为关系。
在关系代数中，有5种基本运算，它们是并（U）、差（—）、投影、选择、笛卡尔积（X），其他运算如交、连接和除，均可通过这5种基本运算来表达。
1. 并运算：结果为二者元组之和去除重复行。
2. 交运算：结果为二者重复行。
3. 差运算：前者去除二者重复行。
4. 笛卡尔积：从数学角度理解，就是将集合A和集合B中所有有序对元素集合。
在数据库系统中，表示得是对两个关系R 和S进行操作，产生的关系中元组个数为两个关系中元组个数之积。
5. 投影：关系R上的投影是从R中选择出若干属性列组成新的关系。
6. 选择：选择又称为限制（Restriction）。
7. 自然连接：结果列数为二者属性列数之和减去重复列，行数为二者同名属性列其值相同时的结果元组。
此外，关系代数还有许多等价表示，如常考的关系代数是笛
卡尔积、选择、投影组合与自然连接的等价表示等。
数据库中的关系代数与关系演算
数据库中的关系代数与关系演算数据库涵盖的范围广泛，其运用的逻辑学与数学原理也十分严谨。
数据库中的关系代数与关系演算两个部分，是数据库分析与设计的重要内容。
本文将讨论它们的定义、方法及应用。
一、关系代数1.1 定义关系代数是一种数学形式，是一种用来描述数据库系统中数据操作的一种标准化语言。
关系代数理论分为两部分：关系代数和关系演算。
关系代数关注的是数据在层次结构中的使用。
1.2 方法关系代数的操作一般基于及定理。
关系代数的符号及运算有选择（selection）、投影（projection）、并（union）、差（difference）、乘积（product）、联接（join）以及除（division）等符号。
通过这些操作符，可以对单个关系进行处理。
一个关系实例可以看做是一个记录的集合，而这些记录也叫作元组。
1.3 应用关系代数的应用可以用于Web数据挖掘，企业数据分析，以及管理信息系统等方面。
在大多数的数据库软件中，关系代数已经内置在了SQL语言之中。
二、关系演算2.1 定义关系演算是关系完备性理论的一种重要语言，指对关系上的操作以及使用代数符号表示的过程。
关系演算是由图灵等科学家提出的一种用来处理关系数据的操作。
这种操作是从一个关系中提取出需要的信息来处理数据的。
2.2 方法关系演算有两种基本形式，分别是元组关系演算和域关系演算。
元组关系演算是指通过运算符来生成新的元组。
而域关系演算则是指通过运算符来生成新的属性值。
2.3 应用关系演算的应用包含多个方面，如关系数据库的设计，数据库查询语言的设计等。
在关系数据库中，使用关系演算的方法可以实现对数据的查询和管理，保证数据的一致性。
在现代信息技术中，关系演算也逐渐开始应用于生产及服务领域。
三、关系代数与关系演算的联系与区别关系代数和关系演算是两个相互补充、相互影响的部分。
它们的相同点在于都是面向关系的运算，都是关系数据库的理论基础。
而它们不同的地方则是，关系代数强调的是关系运算，即加、减、交、差等运算。
数据库关系代数运算例题
数据库关系代数运算例题关系代数是一种用于操作关系数据库的形式化查询语言。
它包括一组基本运算符，如选择、投影、并、差、笛卡尔积和连接等，通过这些运算符可以对关系进行操作和组合，从而实现复杂的查询。
下面我将给出一些关系代数运算的例题，以便更好地理解和应用这些运算符。
1. 选择运算符（σ）：假设有一个关系表R，包含属性A、B和C，我们希望选择满足条件A=1的元组。
则选择运算可以表示为，σ(A=1)(R)。
2. 投影运算符（π）：假设有一个关系表R，包含属性A、B和C，我们希望只保留属性A和B，可以使用投影运算符进行处理，π(A,B)(R)。
3. 并运算符（∪）：假设有两个关系表R和S，具有相同的属性集合，我们希望将两个表中的元组合并成一个表，可以使用并运算符，R∪S。
4. 差运算符（-）：假设有两个关系表R和S，我们希望从R中删除与S中相同的元组，可以使用差运算符，R-S。
5. 笛卡尔积运算符（×）：假设有两个关系表R和S，我们希望将两个表中的元组进行组合，生成一个新的表，可以使用笛卡尔积运算符，R×S。
6. 连接运算符（⋈）：假设有两个关系表R和S，具有一个共同的属性A，我们希望根据属性A将两个表中的元组进行连接，可以使用连接运算符，R⋈S。
以上是关系代数的一些基本运算符和例题，通过这些运算符的组合和应用，可以实现复杂的查询和操作。
在实际应用中，还可以使用更多的运算符和技巧来处理更复杂的问题。
关系代数是数据库领域重要的概念和工具，对于数据库的设计和查询优化都具有重要的意义。
关系运算----关系代数
R − S = {t | t ∈ R ∧ t ∉ S} 式中“－”为差运算符，t 为元组变量，结果 R-S 为一个新的与 R、S 同类的关系，该 关系是由属于 R 而且不属于 S 的元组构成的集合，即在 R 中减去与 S 中相同的那些元组。
c1
d1
a1
b1
c2
d2
a3
b3
c1
d1
a3
b3
c2
d2
图 2.12 关系 P1×R、P2×R 和 P3×R
3. 关系的联结——广义笛卡尔乘积运算
查询常常需要由多个关系生成一个新的关系。为了有效处理这种情况，引入广义笛卡尔 乘积运算。
设有关系 R、S，其中关系 R 有 r 个属性分量、m 个元组，关系 S 有 s 个属性分量、n 个元组，则二者的广义笛卡尔乘积(Cartesian Product)运算定义为：
2. 关系元组选定——选择运算
为了完成关系元组的选择，引入选择运算。 选择(Selection)也是一元关系运算，用于选取某个关系上我们感兴趣的某些行(满足一定 的条件的行)，并且将它们组成一个新的关系。
Sn
Sa
刘刚
21
Class 2003A
王建
22
张华
21
李倩
20
2003A 2003A 2003A
A
B
C
a1
b1
c1
a1
b2
c2
a1
b2
c2
a2
b2
c1
a2
b2
c1
a2
b2
数据库关系代数
R S {trts | tr R ts S}
RS
AB
C
a1 b1 c1
a1 b2 c2
a2 b2 c1
a1 b3 c2
码．
( Sno
Cno = ‘1’
(SC))
2)在学以生上号S码-C．数据Sno库( 中C，no查= ‘询1’选v 修Cno了=‘13’号课程或3号课程的
(SC))
Sno( Cno = ‘1’ (SC)) U
( Sno
Cno = ‘1’
(SC))
关系代数：综合应用
2)查询选修了２号课程的学生的学号
19
IS
95004 张立 男
19
IS
Sno Sname Ssex Sage Sdept
95002 刘晨 女
19
IS
95003 王敏 女
18
MA
95004 张立 男
19
IS
关系代数：投影
定义：从关系R中选择出满足条件F的若 干属性列并组成新的关系，列选
F(R) {t[A] | t R}
A2，…，An中的一部分，则A称为属性列或域列 t[A]=(t[Ai1]，t[Ai2]，…，t[Aik])表示元组t在属性列A上
诸分量的集合
A 则表示{A1，A2，…，An}中去掉{Ai1，Ai2，…，Aik}
后剩余的属性组
传统的集合运算 若R和S是同类关系(即它们都具有n个属性且相应属性
第四步：判断包含关系
数据库之关系运算
数据库之关系运算 关系操作的特点是操作对象和操作结果都是集合，⽽⾮关系数据模型的数据操作⽅式则为⼀次⼀个记录的⽅式。
关系数据代数语⾔、关系演算语⾔和具有关系代数和关系演算双重特点的语⾔（例如SQL）。
关系演算语⾔包含元组关系演算语⾔（例如Aplha、Quel）和域关系演算语⾔（例如QBE）。
关系代数语⾔、元组关系演算和域关系演算是抽象查询语⾔，它与具体的DBMS中实现的实际语⾔并不⼀样，但是可以⽤它评估实际系统中的查询语⾔能⼒的标准。
关系代数运算符有4类：集合运算符（∩交、∪并、- 差、× 笛卡尔积）、⽐较运算符（> ⼤于、≥ ⼤于等于、< ⼩于、≤ ⼩于等于 ≠ 不等于、= 等于）、逻辑运算符（¬ ⾮、ν与、Λ或）、专门的关系运算符（σ选择、÷ 除、π投影、⋈连接） 基本关系代数涵盖有五种：并、差、笛卡尔积、选择、投影，其他的都可以由这五种推出来如：各种连接。
以MySQL运⾏结果为例： ⾸先建⽴数据库 create database mydb； 在建⽴两个表格emp与dept详情如下：CREATE TABLE emp(empno INT,ename VARCHAR(50),job VARCHAR(50),mgr INT,hiredate DATE,sal DECIMAL(7,2),comm decimal(7,2),deptno INT) ;INSERT INTO emp values(7369,'SMITH','CLERK',7902,'1980-12-17',800,NULL,20);INSERT INTO emp values(7499,'ALLEN','SALESMAN',7698,'1981-02-20',1600,300,30);INSERT INTO emp values(7521,'WARD','SALESMAN',7698,'1981-02-22',1250,500,30);INSERT INTO emp values(7566,'JONES','MANAGER',7839,'1981-04-02',2975,NULL,20);INSERT INTO emp values(7654,'MARTIN','SALESMAN',7698,'1981-09-28',1250,1400,30);INSERT INTO emp values(7698,'BLAKE','MANAGER',7839,'1981-05-01',2850,NULL,30);INSERT INTO emp values(7782,'CLARK','MANAGER',7839,'1981-06-09',2450,NULL,10);INSERT INTO emp values(7788,'SCOTT','ANALYST',7566,'1987-04-19',3000,NULL,20);INSERT INTO emp values(7839,'KING','PRESIDENT',NULL,'1981-11-17',5000,NULL,10);INSERT INTO emp values(7844,'TURNER','SALESMAN',7698,'1981-09-08',1500,0,30);INSERT INTO emp values(7876,'ADAMS','CLERK',7788,'1987-05-23',1100,NULL,20);INSERT INTO emp values(7900,'JAMES','CLERK',7698,'1981-12-03',950,NULL,30);INSERT INTO emp values(7902,'FORD','ANALYST',7566,'1981-12-03',3000,NULL,20);INSERT INTO emp values(7934,'MILLER','CLERK',7782,'1982-01-23',1300,NULL,10);CREATE TABLE dept(deptno INT,dname varchar(14),loc varchar(13))INSERT INTO dept values(10, 'ACCOUNTING', 'NEW YORK');INSERT INTO dept values(20, 'RESEARCH', 'DALLAS');INSERT INTO dept values(30, 'SALES', 'CHICAGO');INSERT INTO dept values(40, 'OPERATIONS', 'BOSTON');1、并在MySQL中体现为合并结果集union（需要注意的是t1和t2的约束是相同的）去除重复列：select * from t1 union select * from t2；不去除重复列：select * from t1 union all select * from t2；2、笛卡尔积（以emp和dept表位例，其中emp有14条记录、dept中有4条记录形成的记录14*4=56条）select * from emp,dept;只有部分截图3 内连接（inner）在MySQL中不加限定条件的时候select * from emp inner join dept;结果与笛卡尔积是⼀样的。
自考数据库系统原理 第四章 关系运算 课后习题答案
自考数据库系统原理第四章关系运算课后习题答案2009-09-15 10:454.1 名词解释(1)关系模型：用二维表格结构表示实体集，外键表示实体间联系的数据模型称为关系模型。
(2)关系模式：关系模式实际上就是记录类型。
它的定义包括：模式名，属性名，值域名以及模式的主键。
关系模式不涉及到物理存储方面拿枋觯 鼋鍪嵌允 萏匦缘拿枋觥?(3)关系实例：元组的集合称为关系和实例，一个关系即一张二维表格。
(4)属性：实体的一个特征。
在关系模型中，字段称为属性。
(5)域：在关系中，每一个属性都有一个取值范围，称为属性的值域，简称域。
(6)元组：在关系中，记录称为元组。
元组对应表中的一行；表示一个实体。
(7)超键：在关系中能唯一标识元组的属性集称为关系模式的超键。
(8)候选键：不含有多余属性的超键称为候选键。
(9)主键：用户选作元组标识的一个候选键为主键。
（单独出现，要先解释“候选键”）(10)外键：某个关系的主键相应的属性在另一关系中出现，此时该主键在就是另一关系的外键，如有两个关系S和SC,其中S#是关系S的主键，相应的属性S#在关系SC中也出现，此时S#就是关系SC的外键。
(11)实体完整性规则：这条规则要求关系中元组在组成主键的属性上不能有空值。
如果出现空值，那么主键值就起不了唯一标识元组的作用。
(12)参照完整性规则：这条规则要求“不引用不存在的实体”。
其形式定义如下：如果属性集K是关系模式R1的主键，K也是关系模式R2的外键，那么R2的关系中， K的取值只允许有两种可能，或者为空值，或者等于R1关系中某个主键值。
这条规则在使用时有三点应注意： 1)外键和相应的主键可以不同名，只要定义在相同值域上即可。
2)R1和R2也可以是同一个关系模式，表示了属性之间的联系。
3)外键值是否允许空应视具体问题而定。
(13)过程性语言：在编程时必须给出获得结果的操作步骤，即“干什么”和“怎么干”。
如Pascal和C语言等。
数据库关系代数
并、差、笛卡儿积、投影、选择是关系代数的5种基本的运算,其他运算，即交、连接、除都可以通过基本的运算推导运算出。
1、并，设有两个关系R和S，它们具有相同的结构，R和S的并是由属于R或属于S的元组组成的集合；2、差，R和S的差是由属于R但不属于S的元组组成的集合；3、笛卡尔积，两个集合X和Y的笛卡尓积，又称直积，表示为X 与Y相乘，第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员；4、选择，从关系中找出满足给定条件的那些元组称为选择；其中的条件是以逻辑表达式给出的，值为真的元组将被选取；5、投影，从关系模式中挑选若干属性组成新的关系称为投影。
数据库系统（二）--关系型数据库之关系代数关系型数据库-关系操作集合1、基本的关系操作关系模型中常用的关系操作包括查询(Query)操作和插入(Insert)、删除(Delete)、修改(Update)操作两大部分。
查询操作分为：选择、投影、连接、除、并、差、交、笛卡尔积等；五种基本操作：选择、投影、并、差、笛卡尔积；关系操作的特点是集合操作方式，即操作的对象和结果都是集合、这种操作方式也称为一次一集合的方式。
2、关系数据语言的分类关系操作是通过关系语言来实现的。
关系语言的特点是高度非过程化，即：（1）用户不必请求数据库管理员为其建立特殊的存取路径，存取路径的选择由 DBMS 的优化机制来完成；（2）用户也不必求助于循环和递归来完成数据的重复操作。
关系操作的能力可以用两种方式来表示：代数方式和逻辑方式。
关系代数、元组关系演算和域关系演算均是抽象的查询语言。
结构化查询语言SQL充分体现了关系数据语言的特点和优点，是关于数据库的标准语言。
关系数据语言可以分为三类：关系代数语言、关系演算语言以及兼具两者双重特点的语言。
三类语言的共同特点是语言具有完备的表达能力，是非过程化的集合操作语言，功能强，能够独立使用也可以嵌入高级语言中使用。
3、关系代数操作包含三大要素：操作对象、操作符、操作结果。
数据库关系代数表达式
数据库关系代数表达式数据库关系代数表达式：1. 什么是数据库关系代数表达式？Solid State Drives（SSDs）是一种快速读写和存储用的计算机存储介质，它使用关系代数表达式（RELATION ALGEBRA）来表达多个表之间的关系。
它使用关系运算符来反映数据间的逻辑关系，有助于在数据库中的查询操作的效率和可靠性。
2. 关系代数表达式的基础上概念数据库关系代数表达式的基本概念，主要包括关系（relation）、运算符（operators）、连接（joins）、窗口函数（window functions）和子查询等。
（1）关系（relation）：关系代数的核心概念是关系，关系也就是数据表，比如学生表、课程表等，每一行数据都可以看作是表的一个实例。
（2）运算符（operators）：运算符用于对关系中的行数据作选择、连接、聚合等操作，常见的运算符有并集 union 、交集 intersect 、差集difference 、选择 selection 、投影 projection 、笛卡尔积 cartesian product 、条件 join 。
（3）连接（joins）：连接是两个或多个关系之间的链接方式，包括内连接 inner join、左外连接 left outer join、右外连接 right outer join和全外连接full outer join等。
（4）窗口函数（window functions）：窗口函数是一种特殊的运算符，它能够把一行数据拆分成多行，并对每一行的数据进行计算，窗口函数可用于实现排序、聚合、求平均值等操作。
（5）子查询（subqueries）：子查询是SQL语句中的一种特殊查询，它可以将一个查询语句的结果作为另一个查询语句的输入，它也可以把表中一行数据或列数据嵌入另一个查询语句中。
3. 数据库关系代数表达式的应用（1）查询和更新操作：数据库关系代数可以实现快速查询和更新操作，可大大提高查询效率和可靠性。
数据库关系代数
关系代数是关系数据库系统查询语言的理论基础一、关系代数的9种操作：关系代数中包括了：并、交、差、乘、选择、投影、联接、除、自然联接等操作。
五个基本操作：并(∪)、差(-)、笛卡尔积(×)、投影(σ)、选择(π)四个组合操作：交(∩)、联接(等值联接)、自然联接(R S)、除法(÷)注2：等值连接表示先做笛卡尔积(×)之后，对相应列进行选择或等值关联后的结果(仅筛选行、不筛选列)注2：自然连接表示两个关系中若有相同名称的属性，则自动作为关联条件，且仅列出一列二、关系代数表达式：由关系代数运算经有限次复合而成的式子称为关系代数表达式。
这种表达式的运算结果仍然是一个关系。
可以用关系代数表达式表示对数据库的查询和更新操作。
三、举例说明：设教学数据库中有3个关系：学生关系S(SNO, SNAME,AGE,SEX)学习关系SC(SNO,O,GRADE)课程关系C(O,AME,TEACHER)(1) 检索学习课程号为C2的学生学号与成绩------------------------------------SELECT SNO,GRADEFROM SCWHERE O='C2'------------------------------------π SNO, GRADE (σ O='C2' (SC))************************************(2) 检索学习课程号为C2的学生学号与XX------------------------------------SELECT SC.SNO,S.SNAMEFROM SC,SWHERE SC.SNO=S.SNOAND SC.O='C2'------------------------------------π SNO,SNAME (σ O='C2' (S SC))此查询涉及S和SC，先进行自然连接，然后再执行选择投影操作。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
BC
b2 c2 b3 c2 b2 c1 b2 c2 b3 c2 b2 c1 b2 c2 b3 c2 b2 c1
关系代数
• 概述 • 传统的集合运算 • 专门的关系运算
.
专门的关系运算
• 选择 • 投影 • 连接 •除
.
1. 选择（Selection）
• 1) 选择又称为限制（Restriction） • 2) 选择运算符的含义
第六讲 关系代数理论
关系数据库模型（3）
.
关系数据库
1. 关系数据模型概述 2. 关系数据模型的结构 3. 关系数据模型的完整性规则 4. 关系代数 5. 关系演算
.
关系模型
1. 关系数据模型的数据结构 2. 关系数据模型的操纵（运算） 3. 关系数据模型的完整性约束
.
关系数据操作
• 关系数据模型的操作
.
含义 运算符 含义
集 ∪并
比 ＞ 大于
合 -差
较 ≥ 大于等于
运 算
符
∩ ×
交
运
广义笛 卡尔积
算 符
＜ 小于
≤
小于等于 等于
＝ 不等于
.
≠
概述(续)
表 关系代数运算符（续）
运算符 含义 运算符 含义
专门的 关系
运算符
σ 选择 π 投影
连接
÷除
逻辑运 非 算符 ∧ 与
– 在关系R中选择满足给定条件的诸元组 σF(R) = {t|tR∧F(t)= '真'}
– F：选择条件，是一个逻辑表达式，基本形式为： [( ] X1θY1 [ )][φ [( ] X2θY2 [ )]]…
• θ：比较运算符（＞，≥，＜，≤，＝或<>） • X1，Y1等：属性名、常量、简单函数；属性名也可以用它
R-S
.
ABC a1 b1 c1
3. 交（Intersection）
• R和S
– 具有相同的目n – 相应的属性取自同一个域
• R∩S
– 仍为n目关系，由既属于R又属于S的元组组 成 R∩S = { t|t R∧t S } R∩S = R .–(R-S）
交 (续)
ABC
R a1 b1 c1 a1 b2 c2 a2 b2 c1 ABC
• R∪S
– 仍为n目关系，由属于R或属于S的元组组成 R∪S = { t|t R∨t S }
.
并(续)
ABC
R a1 b1 c1 a1 b2 c2 a2 b2 c1 ABC
S a1 b2 c2 a1 b3 c2
ABC R∪S a1 b1 c1
a1 b2 c2 a1 b3 c2 a2 b2 c1
a2 b2 c1 .
2. 差（Difference）
• R和S
– 具有相同的目n – 相应的属性取自同一个域
•R-S
– 仍为n目关系，由属于R而不属于S的所有元组 组成
R -S = { t|tR∧tS }
.
差(续)
ABC R a1 b1 c1
a1 b2 c2 a2 b2 c1 ABC S a1 b2 c2 a1 b3 c2 a2 b2 c1
.
概述(续)
2．关系代数运算的三个要素
运算对象：关系 运算结果：关系 运算符：四类
.
概述(续)
– 集合运算符
• 将关系看成元组的集合 • 运算是从关系的“水平”方向即行的角度来进行
– 专门的关系运算符
• 不仅涉及行而且涉及列
– 算术比较符
• 辅助专门的关系运算符进行操作
– 逻辑运算符
• 辅助专门的关系运算符进行操作
S a1 b2 c2
ABC
R ∩ S a1 b2 c2 a2 b2 c1
a1 b3 c2
a2 b2 c1 .
4. 广义笛卡尔积（Extended Cartesian Product）
•R
– n目关系，k1个元组
•S
– m目关系，k2个元组
• R×S
– 列：（n+m）列的元组的集合
• 元组的前n列是关系R的一个元组 • 后m列是关系S的一个元组
– 行：k1×k2个元组
• R×S = {tr ts |tr R. ∧ tsS }
广义笛卡尔积 (续)
ABC R a1 b1 c1
a1 b2 c2 a2 b2 c1
ABC S a1 b2 c2
a1 b3 c2 a2 b2 c1
A B CA
a1 b1 c1 a1 a1 b1 c1 a1 a1 b1 c1 a2 R × S a1 b2 c2 a1 a1 b2 c2 a1 a1 b2 c2 a2 a2 b2 c1 a1 a2 b2 c1 a1 a2 b2 c1 a2
– 查询
• 选择、投影、连接、除、并、交、差
– 数据更新
• 插入、删除、修改
.
关系代数
• 概述 • 传统的集合运算 • 专门的关系运算
.
概述
1. 关系代数 2. 运算的三要素 3. 关系代数运算的三个要素 4. 关系代数运算的分类 5. 表示记号
.
概述
1.关系代数 一种抽象的查询语言
用对关系的运算来表达查询
Zx={t[Z]|t R，t[X]=x} 它表示R中属性组X上值为x的诸元组在Z上分量的集合。
.
关系代数
• 概述 • 传统的集合运算 • 专门的关系运算
.
传统的集合运算
•并 •差 •交 • 广义笛卡尔积
.
1. 并（Union）
• R和S
– 具有相同的目n（即两个关系都有n个属性） – 相应的属性取自同一个域
.
概述(续)
（2） A，t[A]， A
若A={Ai1，Ai2，…，Aik}，其中Ai1，Ai2，…，Aik 是A1，A2，…，An中的一部分，则A称为属性列或 域列。t[A]=(t[Ai1]，t[Ai2]，…，t[Aik])表示元组t在 属性列A上诸分量的集合。A则表示{A1，A2，…， An}中去掉{Ai1，Ai2，…，Aik}后剩余的属性组。
∨或
.
概述(续)
4．关系代数运算的分类
传统的集合运算
并、差、交、广义笛卡尔积
专门的关系运算
选择、投影、连接、除
.
概述(续)
5．表示记号
（1） R，tR，t[Ai] 设关系模式为R(A1，A2，…，An) 它的一个关系设为R。tR表示t是R的一个元组t[Ai]
则表示元组t中相应于属性Ai的一个分量
.
概述(续)
– （3） tr ts R为n目关系，S为m目关系。tr R，tsS， tr ts称为元组的连接。它是一个n + m列的元 组，前n个分量为R中的一个n元组，后m个 分量为S中的一个m元组。
.
概述(续)
– 4）象集Zx
给定一个关系R（X，Z），X和Z为属性组。当t[X]=x时， x在R中的象集（Images Set）为：