spss数据正态分布检验
SPSS学习系列19. 正态性检验
19. 正态性检验实际中，经常需要检验数据是否服从正态分布。
一、Kolmogorov-Smirnov(K - S) 单样本检验这是一种分布拟合优度检验，即将一个变量的累积分布函数与特定分布进行比较。
有数据文件：对“数学成绩”“英语成绩”做正态性检验。
1.【分析】——【非参数检验】——【单样本】，打开“单样本非参数检验”窗口，【目标】界面勾选“自动比较观察数据和假设数据”2.【字段】界面，勾选“使用定制字段分配”，将要检验的变量“数学成绩”“英语成绩”选入【检验字段】框，3. 【设置】界面，选择“自定义检验”，勾选“检验观察分布和假设分布（Kolmogorov-Smimov检验）”点【选项】，打开“Kolmogorov-Smimov检验选项”子窗口，选择“正态分布”，勾选“使用样本数据”，点【确定】回到原窗口，点【运行】得到结果说明：样本量大于50用Kolmogorov-Smirnov检验，样本量小于50用Shapiro-Wilk检验；原假设H0：服从正态分布；H1：不服从正态分布。
P值<0.05, 拒绝原假设H0；P值>0.05, 接受原假设H0, 即服从正态分布；本例中，“数学成绩”、“英语成绩”的P值都>0.05, 故服从正态分布。
双击上面结果可以看到更详细的检验结果：注：类似的操作也可以检验数据是否服从“二项、均匀、指数、泊松”等分布。
二、用“旧对话框”进行上述检验1.【分析】——【非参数检验】——【旧对话框】——【1-样本K-S】，打开“单样本Kolmogorov-Smirnov检验”窗口，将要检验的变量选入【检验变量列表】框，【检验分布】勾选“常规”，2.点【精确】，打开“精确检验”窗口，勾选“精确”，“仅渐进法”——只计算检验统计量的渐近分布的近似概率值，而不计算确切概率，适用用样本量较大，P值远离α=0.05，节省计算时间，否则可能结果偏差较大；“Monte Carlo”——利用模拟抽样方法求得P值的近似无偏估计，适合大样本数据，节省计算时间；“精确”——计算精确的概率值（P值）。
SPSS统计分析1：正态分布检验.
正态分布检验一、正态检验的必要性[1]当对样本是否服从正态分布存在疑虑时，应先进行正态检验；如果有充分的理论依据或根据以往积累的信息可以确认总体服从正态分布时，不必进行正态检验。
当然，在正态分布存疑的情况下，也就不能采用基于正态分布前提的参数检验方法，而应采用非参数检验。
二、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。
如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。
如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。
Q-Q图为佳，效率较高。
以上两种方法以3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。
4、箱式图判断方法：观测离群值和中位数。
5、茎叶图类似与直方图，但实质不同。
三、计算法1、峰度（Kurtosis）和偏度（Skewness）（1）概念解释峰度是描述总体中所有取值分布形态陡缓程度的统计量。
这个统计量需要与正态分布相比较，峰度为0表示该总体数据分布与正态分布的陡缓程度相同；峰度大于0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；峰度小于0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。
峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。
峰度的具体计算公式为：注：SD就是标准差σ。
峰度原始定义不减3，在SPSS中为分析方便减3后与0作比较。
偏度与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性。
这个统计量同样需要与正态分布相比较，偏度为0表示其数据分布形态与正态分布的偏斜程度相同；偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏，即有一条长尾巴拖在右边，数据右端有较多的极端值；偏度小于0表示其数据分布形态与正态分布相比为负偏或左偏，即有一条长尾拖在左边，数据左端有较多的极端值。
spss-数据正态分布检验-Q
spss 数据正态分布检验 Q-Q图学习交流 2009-02-08 14:40 阅读1378 评论9字号：大中小把自己学习spss的一点理解拿出来晒一晒，要是不对大家可以留言啊，一定要讨论啊。
要观察某一属性的一组数据是否符合正态分布，可以有两种方法（目前我知道这两种，并且这两种方法只是直观观察，不是定量的正态分布检验）：1：在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。
具体如下：Analyze-----Descriptive Statistics-----Frequenc ies，打开频数统计对话框，在Statistics里可以选择获得各种描述性的统计量，如：均值、方差、分位数、峰度、标准差等各种描述性统计量。
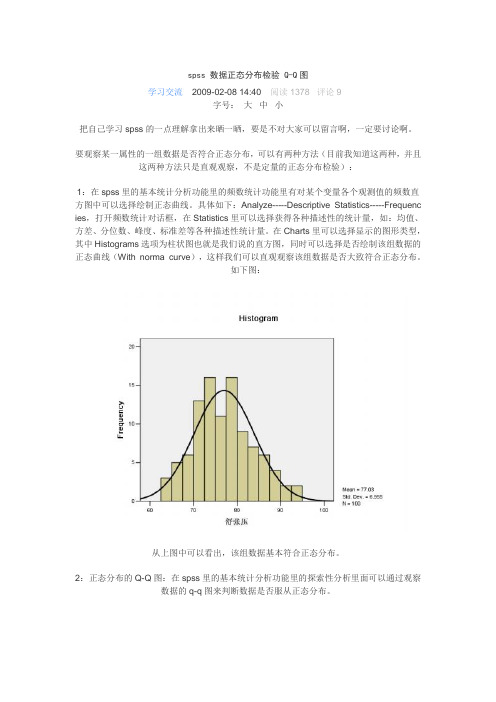
在Charts里可以选择显示的图形类型，其中Histograms选项为柱状图也就是我们说的直方图，同时可以选择是否绘制该组数据的正态曲线（With norma curve），这样我们可以直观观察该组数据是否大致符合正态分布。
如下图：从上图中可以看出，该组数据基本符合正态分布。
2：正态分布的Q-Q图：在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。
具体步骤如下：Analyze-----Descriptive Statistics-----Explore打开对话框，选择Plots选项，选择Normality plots with tests选项，可以绘制该组数据的q-q图。
图的横坐标为改变量的观测值，纵坐标为分位数。
若该组数据服从正态分布，则图中的点应该靠近图中直线。
纵坐标为分位数，是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i 个数据的位置，n为样本容量。
若该数组服从正态分布则其q-q图应该与理论的q-q图（也就是图中的直线）基本符合。
对于理论的标准正态分布，其q-q图为y=x直线。
spss判断是否符合正态分布
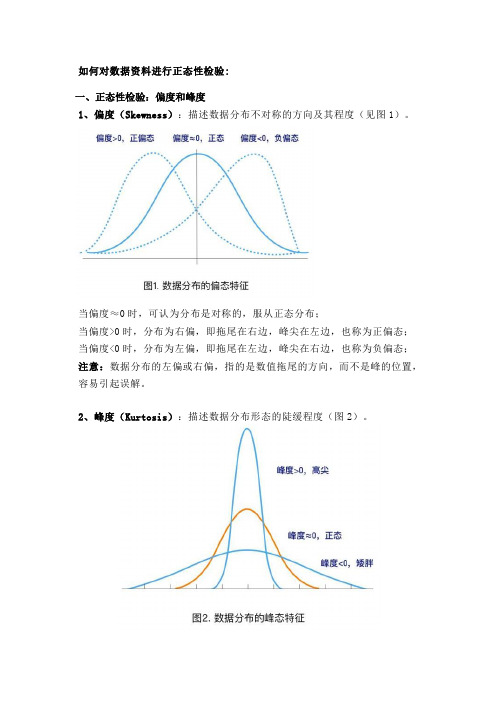
如何对数据资料进行正态性检验:一、正态性检验：偏度和峰度1、偏度（Skewness）：描述数据分布不对称的方向及其程度（见图1）。
当偏度≈0时，可认为分布是对称的，服从正态分布；当偏度>0时，分布为右偏，即拖尾在右边，峰尖在左边，也称为正偏态；当偏度<0时，分布为左偏，即拖尾在左边，峰尖在右边，也称为负偏态；注意：数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置，容易引起误解。
2、峰度（Kurtosis）：描述数据分布形态的陡缓程度（图2）。
当峰度≈0时，可认为分布的峰态合适，服从正态分布（不胖不瘦）；当峰度>0时，分布的峰态陡峭（高尖）；当峰度<0时，分布的峰态平缓（矮胖）；利用偏度和峰度进行正态性检验时，可以同时计算其相应的Z评分（Z-score），即：偏度Z-score=偏度值/标准误，峰度Z-score=峰度值/标准误。
在α=0.05的检验水平下，若Z-score在±1.96之间，则可认为资料服从正态分布。
了解偏度和峰度这两个统计量的含义很重要，在对数据进行正态转换时，需要将其作为参考，选择合适的转换方法。
3、SPSS操作方法以分析某人群BMI的分布特征为例。
(1) 方法一选择Analyze → Descriptive Statistics → Frequencies将BMI选入Variable(s)框中→点击Statistics →在Distribution框中勾选Skewness和Kurtosis(2) 方法二选择Analyze → Descriptive Statistics → Descriptives将BMI选入Variable(s)框中→点击Options →在Distribution框中勾选Skewness和Kurtosis4、结果解读在结果输出的Descriptives部分，对变量BMI进行了基本的统计描述，同时给出了其分布的偏度值0.194（标准误0.181），Z-score = 0.194/0.181 = 1.072，峰度值0.373（标准误0.360），Z-score = 0.373/0.360 = 1.036。
SPSS统计分析1：正态分布检验
正态分布检验一、正态检验的必要性[1]当对样本是否服从正态分布存在疑虑时，应先进行正态检验；如果有充分的理论依据或根据以往积累的信息可以确认总体服从正态分布时，不必进行正态检验。
当然，在正态分布存疑的情况下，也就不能采用基于正态分布前提的参数检验方法，而应采用非参数检验。
二、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。
如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。
如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳，效率较高。
3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。
4、箱式图判断方法：观测离群值和中位数。
5、茎叶图类似与直方图，但实质不同。
三、计算法1、峰度（Kurtosis）和偏度（Skewness）（1）概念解释峰度是描述总体中所有取值分布形态陡缓程度的统计量。
这个统计量需要与正态分布相比较，峰度为0表示该总体数据分布与正态分布的陡缓程度相同；峰度大于0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；峰度小于0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。
峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。
峰度的具体计算公式为：注：SD就是标准差σ。
峰度原始定义不减3，在SPSS中为分析方便减3后与0作比较。
偏度与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性。
这个统计量同样需要与正态分布相比较，偏度为0表示其数据分布形态与正态分布的偏斜程度相同；偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏，即有一条长尾巴拖在右边，数据右端有较多的极端值；偏度小于0表示其数据分布形态与正态分布相比为负偏或左偏，即有一条长尾拖在左边，数据左端有较多的极端值。
spss_数据正态分布检验方法及意义
spss 数据正态分布检验方法及意义判读要观察某一属性的一组数据是否符合正态分布，可以有两种方法（目前我知道这两种，并且这两种方法只是直观观察，不是定量的正态分布检验）：1：在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。
具体如下：Analyze-----Descriptive S tatistics-----Frequencies，打开频数统计对话框，在Statistics里可以选择获得各种描述性的统计量，如：均值、方差、分位数、峰度、标准差等各种描述性统计量。
在Charts里可以选择显示的图形类型，其中Histograms选项为柱状图也就是我们说的直方图，同时可以选择是否绘制该组数据的正态曲线（With nor ma curve），这样我们可以直观观察该组数据是否大致符合正态分布。
如下图：从上图中可以看出，该组数据基本符合正态分布。
2：正态分布的Q-Q图：在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。
具体步骤如下：Analyze-----Descriptive Statistics-----Explore打开对话框，选择Plots选项，选择Normality plots with tests选项，可以绘制该组数据的q-q 图。
图的横坐标为改变量的观测值，纵坐标为分位数。
若该组数据服从正态分布，则图中的点应该靠近图中直线。
纵坐标为分位数，是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置，n为样本容量。
若该数组服从正态分布则其q-q图应该与理论的q-q图（也就是图中的直线）基本符合。
对于理论的标准正态分布，其q-q图为y=x直线。
非标准正态分布的斜率为样本标准差，截距为样本均值。
如下图：如何在spss中进行正态分布检验1(转)(2009-07-22 11:11:57)标签：杂谈一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。
SPSS学习笔记-正态性检验
如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。
如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。
如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳，效率较高。
3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。
4、箱式图判断方法：观测离群值和中位数。
5、茎叶图类似与直方图，但实质不同。
二、计算法1、偏度系数（Skewness）和峰度系数（Kurtosis）计算公式：g1表示偏度，g2表示峰度，通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96，即p>0.05的结论时，才可以认为该组资料服从正态分布。
由公式可见，部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验（D检验）和Shapiro- Wilk（W检验）。
SAS中规定：当样本含量n≤2000时，结果以Shapiro – Wilk（W检验）为准，当样本含量n >2000时，结果以Kolmogorov – Smirnov（D检验）为准。
SPSS中则这样规定：（1）如果指定的是非整数权重，则在加权样本大小位于3和50之间时，计算Shapiro-Wilk统计量。
对于无权重或整数权重，在加权样本大小位于3和5000之间时，计算该统计量。
由此可见，部分SPSS教材里面关于“Shapiro – Wilk适用于样本量3-50之间的数据”的说法是在是理解片面，误人子弟。
（2）单样本Kolmogorov-Smirnov检验可用于检验变量（例如income）是否为正态分布。
spss正态分布检验方法
spss正态分布检验方法SPSS正态分布检验方法。
SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学、生物医学、教育研究等领域。
在数据分析过程中，正态分布检验是一项重要的统计方法，用于检验数据是否符合正态分布。
本文将介绍在SPSS中进行正态分布检验的方法及步骤。
SPSS正态分布检验方法主要包括两种统计检验，Shapiro-Wilk 检验和Kolmogorov-Smirnov检验。
Shapiro-Wilk检验是一种较为常用的正态性检验方法，适用于样本量较小（通常小于50）的情况。
在SPSS中，进行Shapiro-Wilk检验的步骤如下：1. 打开SPSS软件，导入需要进行正态分布检验的数据文件。
2. 选择“分析”菜单中的“描述统计”选项，然后在弹出的对话框中选择“探索性数据分析”。
3. 在“探索性数据分析”对话框中，将需要进行正态性检验的变量移动到“因子”框中。
4. 点击“统计”按钮，在弹出的对话框中勾选“Shapiro-Wil k”复选框。
5. 点击“确定”按钮，SPSS将输出Shapiro-Wilk检验的结果，包括统计量W和显著性水平。
Kolmogorov-Smirnov检验适用于样本量较大的情况，其原理是通过比较累积分布函数来检验数据是否符合正态分布。
在SPSS中进行Kolmogorov-Smirnov检验的步骤如下：1. 打开SPSS软件，导入需要进行正态分布检验的数据文件。
2. 选择“分析”菜单中的“非参数检验”选项，然后在弹出的对话框中选择“单样本K-S检验”。
3. 在“单样本K-S检验”对话框中，将需要进行正态性检验的变量移动到“测试变量列表”框中。
4. 点击“确定”按钮，SPSS将输出Kolmogorov-Smirnov检验的结果，包括统计量D和显著性水平。
在进行正态分布检验时，需要注意以下几点：1. 正态性检验是基于样本数据进行的统计推断，结果受样本量的影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
s p s s数据正态分布检验Newly compiled on November 23, 2020spss数据正态分布检验一、Z检验第一步：录入数据。
1．命名“变量视图”；2．“数据视图”中输入数据；第二步：进行分析。
第三步：设置变量；第四步：得到结果：二、相关系数检验在一项研究中，一个学生想检查生活意义和心理健康是否相关。
同意参与这项研究的30个学生测量了生活意义和心理健康。
生活意义的得分范围是10-70分（更高的得分表示更强的生活意义），心理健康的得分范围是5-35分（更高的得分表示更健康的心理状态）。
在研究中基本的兴趣问题也可以用研究问题的方式表示，例如例题：生活意义和心理健康相关吗相关系数数据的例子ParticipantMeaninginLifeWell-being ParticipantMeaninginLifeWell-being13519 26527 31419 43535 56534 63334 75435 82028 92512 105821 113018 123725 135119 145025 153029 167031 172512 185520 196131 205325 216032 223512 233528 245020 253924 266834 275628 281912 295635 306035说明：变量participant包含在数据中，但不用输入SPSS。
在spss中输入数据及分析步骤1：生成变量1．打开spss。
2．点击“变量视图”标签。
在spss中将生成两个变量，一个是生活意义，另一个是心理健康。
变量分别被命名为meaning和wellbeing。
3．在“变量视图”窗口前两行分别输入变量名称meaning和wellbeing。
步骤2：输入数据1．点击“数据视图”，变量meaning和wellbeing出现在数据视图前两列。
2．将两个变量的数据分别输入。
如图。
步骤3：分析数据1．从菜单栏中选择“分析>相关>双变量>……” 打开“双变量”对话框，变量meaning 和wellbeing 出现在对话框的左边。
2．选择变量meaning 和wellbeing ，点击向右箭头按钮（），把变量移到“变量”框中。
3．点击“确定”。
步骤4：解释结果二元相关性的输出结果显示如下：相关性wellbei ngmeaningwellbei ng Pearson 相关性1 .549**显着性（双侧）.002N 30 30meaning Pearson 相关性.549** 1显着性（双侧） .002N 30 30**.在.01水平（双侧）上显着相关。
SPSS 生成了一个输出表，标记为“相关性”，其中包括我们研究问题的答案，即变量meaning 和wellbeing 之间是否相关。
注意在表格中meaning 和wellbeing 出现了两次，一次在行，一次在列（这表明SPSS 生成的表格中出现了冗余）。
相关系数值和原假设检验的p 值位于同样的结果在相关性生活意义和心相关性显着，变量meaning和wellbeing相交处。
表格中显示meaning和wellbeing的相关性是，相应的p值是小于，原假设被拒绝，在meaning和wellbeing的总体中存在正相关（相关系数右边的两个星号暗示了在水平上相关性是统计显着的，因为p值为小于）。
剩下的两个单元格显示了1的相关性，一个完美的正相关。
即变量meaning和wellbeing自身与自身的相关性。
三、独立样本T检验例题：临床心理学家想调查认知行为治疗和精神分析治疗对抑郁症的相对有效性。
30名患有抑郁症的病人随机分配接受两个疗法。
其中15人接受行为治疗，另外15人接受精神分析治疗，经过两个月的治疗后，记录下每个病人抑郁症得分。
在本研究中，自变量是治疗方法（认知行为治疗与精神分析治疗），因变量是抑郁症，较高的分数表示更高的抑郁水平（抑郁水平的分数变化范围为10~70)。
在研究中基本的兴趣问题也可以用研究问题的方式表示，例如：“在接受认知行为治疗与精神分析治疗的病人中，抑郁症水平的均值是否存在差异呢”T检验用来检验两组数据的均值。
所以，零假设假设两组数据的均值相等：原假设指出两组的抑郁症分数均值在总体上是相等的：H0：μ精神分析=μ认知行为对立假设指出两组的抑郁症分数均值在总体上是不等的：H1：μ精神分析≠μ认知行为数据在下表列出了30个参与者的数据。
接受精神分析治疗的参与者标记为“1”，接受认知行为治疗的标记为“2”。
独立样本t检验例子的数据Participant Therapy Depression Participant Therapy Depression1 1 57 162 472 1 61 17 2 423 1 67 18 2 594 1 63 19 2 376 1 55 21 2 427 1 45 22 2 388 1 62 23 2 499 1 41 24 2 6110 l 36 25 2 4311 1 55 26 2 4712 1 57 27 2 4913 1 70 28 2 3714 l 62 29 2 4115 1 58 30 2 48说明：变量participant包含在数据中，但不用输入SPSS。
步骤1：生成变量1．打开SPSS。
2．点击【变量视图】标签。
在SPSS中将生成两个变最，一个是不同治疗方法的组别(自变量)，另一个是抑郁症分数(因变量)。
这些变量将各自被命名为therapy(治疗方法)和depression(抑郁症)。
3．在【变量视图】窗口前两行分别输入变量名称therapy和depression(详见图表)4．为变量therapy建立变量值标签，1=“精神分析治疗”，2=“认知行为治疗”。
步骤2：输入数据1．点击【数据视图】标签。
变量therapy和depression出现在【数据视图】窗口的前两列。
2．参照图表6-1，为每个参与者输入两个变量的数据。
对第一个参与者，为变量therapy和depression分别输人数值1和57。
依次输入全部30个参与者的数据。
对therapy，注意到前15个参与者为1（精神分析治疗），后15个参与者为步骤3：分析数据1．从菜单栏中选择【分析>比较均值>独立样本T检验】（见图）。
打开【独立样本T检验】对话框，变量therapy和depression出现在对话框的左边。
2．选择因变量depression，点击向右箭头按钮（）把变量移到【检验变量】框。
3．选择自变量therapy，点击向右箭头按钮（）把变量移到【分组变量】框中。
在【分组变量】框中，两个在括号内的问号出现在therapy的右边（见图）。
这些问号表示原先的数字分配到两个治疗样本中（也就是l、2）。
这些数字需要通过点击【定义组】来输入。
4．点击【定义组】。
5．【定义组】对话框被打开，在【组1】（表示精神分析治疗样本的数字）的右边输入“1”，并且在“组2”（表示认知行为治疗样本的数字）的右边输入“２”。
6．点击【继续】。
7．点击【确定】。
结果显示在【查看】窗口中。
步骤4：解释结果组统计量表输出的第一个表格显示每个治疗组的描述统计量，包括样本量、平均值、标准差和标准误差。
注意到认知行为治疗样本的抑郁分数均值（均值=）比精神分析治疗样本（均值=）的低。
我们稍后将会考虑这两组之间的差异对具有统计显着性而言是否足够大。
独立样本检验表第二个表格“独立样本检验表”显示在“均值相等的t检验”之后的“假设方差相等”栏中的结果。
方差方程的Levene检验“方差方程的Levene检验”检验两个治疗组的总体方差是否相等，这是独立样本t检验的一个假设。
SPSS使用个由Levene开发的方法来检验总体相等的假设。
Levene检验的原假设和对立假设是：H0：σ2精神分析=σ2认知行为（两组的总体方差相等）H1：σ2精神分析≠σ2认知行为（两组的总体方差不相等）T检验四、相依样本T检验在对某种程度上相关的两个样本的均值进行比较时，我们可以使用相依样本t检验（也称为配对样本t检验，重复测量t检验，匹配样本t检验等）。
在相依样本t检验中．两个样本可能包含同一个人在两个不同时刻进行侧量或者两个有联系的人分别测量的结果（例如，双胞胎的IQ，妻子与丈夫的沟通质量）。
准确定义相依样本t检验的关健在于记住两样本间要在某方面存在自然联系．下面给出一个相依样本t检验的例子。
一个国家选举机构的工作人员负责通过民意调查来决定经济和国家安全哪个议题对于选民更重要。
有25个选民被调查以确定两个议题的重要性等级，每个议题用1-7的等级表示（1=一点也不重要，7=极其重要）。
自变量是投票议题（经济、国家安全），（因）变量是重要性等级。
在研究中，基本的兴趣问题也可以用研究问题的方式表示，例如，“对选民来说经济重要性等级和国家安全是否存在不同”数据步骤1：生成变量1．打开spss。
2．点击【变量视图】标签。
在spss中将生成的两个变量，分别用于经济等级和国家安全。
两个变量分别命名为economy和security。
3．在【变量视图】窗口前两行分别输入变量名称economy和security。
（见图）。
步骤2：输入数据1．点击【数据视图】标签。
变量economy和security出现在【数据视图】窗口的两列。
2．为每个参与者输入两个变量的数据。
对第一个参与者，为变量economy和security分别输入等级5和7。
依次输入全部25个参与者的数据。
步骤3：分析数据1．从菜单栏中选择【分析>比较均值>配对样本T检验】。
打开【配对样本T检验】对话框，变量economy和security出现在对话框的左边。
2．选择因变量economy和security，点击向右箭头按钮（）把变量移到【成对变量】框中。
3．点击【确定】。
在spss中运行相依样本t检验程序，结果显示在“查看”视窗中。
步骤4：解释结果成对样本统计量输出的第一个表格“成对样本统计量”显示了economy和security的描述统计量、包括样本量、平均值、标准差和标准误差。
请注意，经济的平均重要性等级（均值=）比国家安全（均值=）的高。
我们稍后将会考虑这两个平均等级之间的差异（对）是否大到足以具有统计显着性。
成对样本相关系数表格“成对样本相关系数”除了提到这个相关性等于25个参与者对于经济和国家安全的等级之间的皮尔逊相关系数外，对于解释配对样本t检验不是重要的。
成对样本检验表格“成对样本检验”为我们的研究问题提供了答案，就是经济和国家安全的重要性等级间是否存在差异。
原假设的检验是以t的形式显示的，这里五、χ2独立性检验(一)双因素卡方检验双因素卡方检验法常用来检验两个因素是否互相独立。