Matlab第4章 解数值计算
matlab入门经典教程--第四章数值计算

m a t l a b入门经典教程--第四章数值计算-CAL-FENGHAI.-(YICAI)-Company One1第四章数值计算4.1引言本章将花较大的篇幅讨论若干常见数值计算问题:线性分析、一元和多元函数分析、微积分、数据分析、以及常微分方程(初值和边值问题)求解等。
但与一般数值计算教科书不同,本章的讨论重点是:如何利用现有的世界顶级数值计算资源MATLAB。
至于数学描述,本章将遵循“最低限度自封闭”的原则处理,以最简明的方式阐述理论数学、数值数学和MATLAB计算指令之间的内在联系及区别。
对于那些熟悉其他高级语言(如FORTRAN,Pascal,C++)的读者来说,通过本章,MATLAB卓越的数组处理能力、浩瀚而灵活的M函数指令、丰富而友善的图形显示指令将使他们体验到解题视野的豁然开朗,感受到摆脱烦琐编程后的眉眼舒展。
对于那些经过大学基本数学教程的读者来说,通过本章,MATLAB精良完善的计算指令,自然易读的程序将使他们感悟“教程”数学的基础地位和局限性,看到从“理想化”简单算例通向科学研究和工程设计实际问题的一条途径。
对于那些熟悉MATLAB基本指令的读者来说,通过本章,围绕基本数值问题展开的内容将使他们体会到各别指令的运用场合和内在关系,获得综合运用不同指令解决具体问题的思路和借鉴。
由于MATLAB的基本运算单元是数组,所以本章内容将从矩阵分析、线性代数的数值计算开始。
然后再介绍函数零点、极值的求取,数值微积分,数理统计和分析,拟合和插值,Fourier分析,和一般常微分方程初值、边值问题。
本章的最后讨论稀疏矩阵的处理,因为这只有在大型问题中,才须特别处理。
从总体上讲,本章各节之间没有依从关系,即读者没有必要从头到尾系统阅读本章内容。
读者完全可以根据需要阅读有关节次。
除特别说明外,每节中的例题指令是独立完整的,因此读者可以很容易地在自己机器上实践。
MATLAB从版升级到版后,本章内容的变化如下:MATLAB从版起,其矩阵和特征值计算指令不再以LINPACK和EISPACK库为基础,而建筑在计算速度更快、运行更可靠的LAPACK和ARPACK程序库的新基础上。
MATLAB-第4章

v
i 1
n
2 i
。
max { vi } 。
1 ≤i ≤n
设 A 是一个 m ×n 的矩阵,矩阵的 3 种常用范数如下。 1-范数: A 1 max { aij } 。
1 ≤ j ≤n i 1 m
2-范数: A 2 1 ,其中 λ 1 为 A'A 最大特征值。 ∞-范数: A max { aij } 。
【例4.6】先建立5 × 5矩阵A,然后将A的第一行元素乘以1, 第二行乘以2,…,第五行乘以5。 用一个对角矩阵左乘一个矩阵时,相当于用对角阵的第一个 元素乘以该矩阵的第一行,用对角阵的第二个元素乘以该 矩阵的第二行……依此类推,因此,只需按要求构造一个 对角矩阵D,并用D左乘A即可。命令如下: A=[1:5;2:6;3:7;4:8;5:9] D=diag(1:5); D*A %用D左乘A,对A的每行乘以一个指定常数
(2)构造对角矩阵 设V为具有m个元素的向量,diag(V,k)的功能是产生一个 n × n(n = m + k|)对角阵,其第k条对角线的元素即为 向量V的元素。 例如: diag(1:3,-1) ans = 0 0 0 0 1 0 0 0 0 2 0 0 0 0 3 0 省略k时,相当于k为0,其主对角线元素即为向量V的元素。
2.矩阵的秩与迹 (1)矩阵的秩 rank(A) (2)矩阵的迹 矩阵的迹即矩阵的对角线元素之和。 trace(A)。
3.向量和矩阵的范数
设向量 V = (v1 ,v2 ,…,vn ),向量的 3 种常用范数如下。 1-范数: V 2-范数: V ? -范数: V
1
vi 。
i 1
n
2
3.矩阵的转置 所谓转置,即把源矩阵的第一行变成目标矩阵第一列,第二 行变成第二列……依此类推。显然,一个m行n列的矩阵 经过转置运算后,变成一个n行m列的矩阵。MATLAB中, 转置运算符是单撇号(')。
实验四MATLAB数值计算与符号计算

实验四 MATLAB数值计算与符号计算一、实验目的1.掌握数据插值和曲线拟合的方法2.掌握求数值导数和数值积分的方法3.掌握代数方程数值求解的方法4.掌握常微分方程数值求解的方法5.掌握求解优化问题的方法6.掌握求符号极限、导数和积分的方法7.掌握代数方程符号求解的方法8.掌握常微分方程符号求解的方法二、实验原理1.数据插值a) 一维数据插值 Y1=interp1(X,Y,X1,’method’)b) 二维数据插值 Z1=interp2(X,Y,Z,X1,Y1,’method’)2.曲线拟合[P,S]=polyfit(X,Y,m)3.符号对象的建立(1)符号量名=sym(符号字符串):建立单个的符号变量或常量;(2)syms arg1 arg2,…,argn:建立n个符号变量或常量。
4.基本符号运算(1)基本四则运算:+,-,*,\,^(2)分子与分母的提取:[n,d]=numden(s)(3)因式分解与展开:factor(s),expand(s)(4)化简:simplify, simple(s)5.符号函数及其应用(1)求极限:limit(f,x,a)(2)求导数:diff(f,x,a);(3)求积分:int(f,v)三、实验内容1.按下表用3次样条方法插值计算0~900范围内整数点的正弦值和0~750范围内整数点的正切值,然后用5次多项式拟合方法计算相同的函数值,并将两种计算结果进行比较。
x2=0:75;y1=sin(pi.*x1./180);y2=tan(pi.*x2./180);;a=interp1(x1,y1,45,'cublic')b=interp1(x1,y1,45,'cublic')p1=polyfit(x1,y1,5)p2=polyfit(x2,y2,5)c1=polyval(p1,x1);c2=polyval(p2,x2);subplot(2,1,1);plot(x1,c1,':o',x1,y1,'r');subplot(2,1,2);plot(x2,c2,':o',x2,y2,'r');10203040506070802.(1)求函数33()sin cos f x x x =+在点,,,6432x ππππ=的数值导数。
matlab课后习题答案第四章
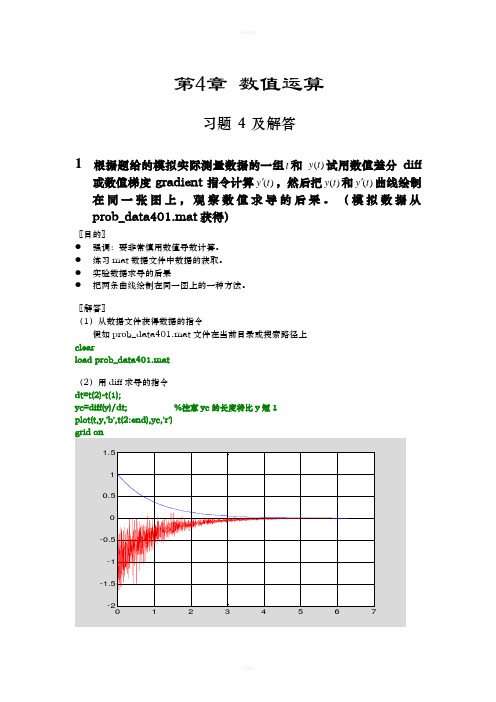
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
MATLAB实验四_求微分方程的解

参数说明
[T,Y] = solver(odefun,tspan,y0)
odefun 为显式常微分方程,可以用命令 inline 定义,或 在函数文件中定义,然后通过函数句柄调用。
dy 2 2 y 2 x 2x 求初值问题 的数值解,求解范 例: dx 围为 [0,0.5] y( 0 ) 1
dsolve的输出个数只能为一个 或 与方程个数相等。
只有很少一部分微分方程(组)能求出解析解。 大部分微分方程(组)只能利用数值方法求数值解。
Matlab函数数值求解
[T,Y] = solver(odefun,tspan,y0)
其中 y0 为初值条件,tspan为求解区间;Matlab在数值求解 时自动对求解区间进行分割,T (列向量) 中返回的是分割点 的值(自变量),Y (数组) 中返回的是这些分割点上的近似解, 其列数等于因变量的个数。
数学实验
实验四
求微分方程的解
问题背景和实验目的
自牛顿发明微积分以来,微分方程在描述事物运 动规律上已发挥了重要的作用。实际应用问题通过 数学建模所得到的方程,绝大多数是微分方程。 由于实际应用的需要,人们必须求解微分方程。 然而能够求得解析解的微分方程十分有限,绝大多 数微分方程需要利用数值方法来近似求解。 本实验主要研究如何用 Matlab 来计算微分方程 (组)的数值解,并重点介绍一个求解微分方程的 基本数值解法--Euler折线法。
Runge-Kutta 方法
Euler 法与 R-K法误差比较
Matlab 解初值问题
用 Maltab自带函数 解初值问题 求解析解:dsolve 求数值解:
ode45、ode23、 ode113、ode23t、ode15s、 ode23s、ode23tb
MATLAB数值计算-第4章-方程求根

MATLAB数值计算(读书日记及程序编写)第四章方程求根 (2)第四章 方程求根#二分法 求2的值转化成方程02-2=x最慢的方法是取初值1001=x 02-21>x ,取502=x这样得到也可以x0=a, x1=x0+h, 进行扫描,若f(x0)*f(x1)<0, 则扫描成功,有根区间为[x0,x1],否则继续扫描,如果出现x1>b ,表面扫描失败,再缩小步长h, 再次扫描。
>> format long %让显示的值为M=2,a=1,b=2,k=0;while b-a>epsx=(a+b)/2;if x^2>Mb=xelsea=xendk=k+1end执行后得到的值为:k =50b =1.414213562373095k =51b =1.414213562373095k =52最后得到的值就是Matlab 能表达的最接近的值。
#牛顿法求解f(x)=0的牛顿法是在f(x)画一条切线,确定切线与x 轴的焦点,通过迭代 )(x f )f(x -n n 1'=+n n x x 对于平方根的问题,牛顿法简洁有效,换成f(x)=x^2-M, )(x f n '=2x 这样⎪⎪⎭⎫ ⎝⎛+==+n n n n x M x M x x 212x -x -n 2n 1 该算法就是反复求x 和M/x 的平均值,Matlab 的程序为:format long %让显示的值为xprev=2; %取的不等于初值x 的一个值,让判断能继续x=100; %取的初值为3while abs(x-xprev)>eps*abs(x)xprev=x;x=0.5*(x+2/x)endx = 1.833333333333333x = 1.462121212121212x = 1.414998429894803x = 1.414213780047198x = 1.414213562373112x = 1.414213562373095x = 1.414213562373095可见6步很快就收敛然而,若f(x)不具有连续的、有界的一阶、二阶导数,牛顿法的收敛将变得很慢。
MATLAB教程4

4.4
ቤተ መጻሕፍቲ ባይዱ拟合与插值
说明:interp1仅是 插值指令的一种, 还有interp2 、 interp3等。
ys=interp1(x,y,xs,’method’); 其中:(1) x,y是测量数据对; (2) xs是需要内插的点所构成的向量。 (3) method是指所使用的内插方法。 插值算法: ‘nearest’,‘linear’,‘spline’,‘cubic’
f ( x) g ( x) f ( x) / g ( x)
杨惠--《matlab语言及应用》--第四章
4.3 多项式计算
3.
功能:按数组运算规则计算多项式的值。 多项式值的计算: 其中x可以是标量和数组。
y=polyval(p,x); y=polyvalm(p,x);
功能:按矩阵运算规 则计算多项式的值。 其中x必须为方阵。
conv(p1,p2)
3、多项式除法运算
[Q,r]=deconv(p1,p2)
p1=conv(p2,Q)+r
例题开讲
f ( x) 3x 5 5 x 4 2 x 3 7 x 2 5 x 6 g ( x) 3x 2 5 x 3
已知
求: (1) f ( x) g ( x) (2) f ( x) g ( x)
4.4 拟合与插值
1)最邻近插值方法(nearest)
插值点的值与其最邻近的点的函数值相等。
*
*
*
*
*
4.4 拟合与插值
2)线性插值方法( linear )
插值点的值在前,后两个数据点所构 成的直线上。
*
*
*
*
*
4.4
拟合与插值
数值分析第四章外推法计算数值微分MATLAB计算实验报告

数值分析第四章外推法计算数值微分MATLAB计算实验报告数值分析MATLAB计算实验报告姓名班级学号⼀、实验名称⽤MATLAB编程实现数值微分的外推法计算。
⼆、实验⽬的1.掌握数值微分和定义和外推法的计算过程;2.了解数值微分外推法的计算⽅法并且编写出与其算法对应的MATLAB程序代码;3.体会利⽤MATLAB软件进⾏数值计算。
三、实验内容⽤外推法计算f(x)=x2e?x在x=0.5的导数。
四、算法描述1.命名函数。
2.如果输⼊未知数少于四个,默认精度10^-33.描述T表矩阵坐标4.依次赋值计算 T表第⼀列5.根据数值微分计算公式求出T表矩阵的值6.若达到精度则运算结束,若未达到循环计算7.输出T表,得出的值就是导数值五、实验结果六、实验结果分析此实验通过MATLAB实现外推法数值微分计算,得到相应的数据,⽅便对数据进⾏分析。
从结果可以看出,当步长h=0.025时⽤中点微分公式只有3位有效数字,外推⼀次达到5位有效数字,外推两次达到9位有效数字。
七、附录(程序)function g=waituifa(fname,x,h,e)if nargin<4,e=1e-3;end;i=1;j=1;G(1,1)=(feval(fname,x+h)-feval(fname,x-h))/(2*h);G(i+1,1)=(feval(fname,x+h/2)-feval(fname,x-h/2))/h;G(i+1,j+1)=(4^j*G(i+1,j)-G(i,j))/(4^j-1);while abs(G(i+1,i+1)-G(i+1,i))>ei=i+1;G(i+1,1)=(feval(fname,x+h/2^i)-feval(fname,x-h/2^i))/(2*h/2^i); for j=1:iG(i+1,j+1)=((4^j)*G(i+1,j)-G(i,j))/(4^j-1);endendGg=G(i+1,i+1);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
trapz(x,y) 给出采样点(x, y)所连接折线下的面积,即函数y在自变量 区间x上的近似积分。而cumtrapz(x, y)的计算结果Sct是一个与y同样 大小的数组,Sct(k)是的 x ( k ) 近似值。
x (1)
y( x )dx
•在对计算数值积分精度没有严格要求的场合,trapz和cumtrapz是两 条比较方便易用的指令。这两条指令所的数值积分的精度与积分区间 分割的稀密程度有关。采样点数愈多,积分精度愈高,但精度无法定 量控制
aBmn [a bij ]mn
B AH
(bkj ) R i (bkj ) I (a jk ) R i (a jk ) I
【例 4.2-1】
数 学 含 义
Amn Bmn [aij bij ]mn
MATLAB表达 A+B, A-B a+B, a-B A*B a*B A'
a Bmn [a]mn [bij ]mn [a bij ]mn
Cmn [cij ]mn aij ml bij ln l aik bkj A ml Bln k 1 mn
第四章 数值计算
4.1 数值微积分 4.2 矩阵和代数方程 4.3 多项式运算和卷积
4.1 数值微积分
4.1.1 近似数值极限及导数
4.1.2 数值求和与近似数值积分
4.1.3 计算精度可控的数值积分
4.1.4 函数极值的数值求解
4.1.5 常微分方程的数值解
4.1.1 近似数值极限及导数
MATLAB提供了与“求导”概念 有关的“求差分”指令: dx=diff(X) FX = gradient(F) [FX,FY] = gradient(F)
i 1
i 1 m
j
Sct=cumtrapz(x, y)
采用梯形法沿列方向求函数y关于自变量x 的累计积分
〖说明〗 假如X是 (m n) 的数组,那末sum(X)的计算结果Sx是一个 (1 n) 的数组,其中Sx(k),就是X第k列全体元素的和。而cumsum(X)的计 算结果Scs仍是 (m n) 数组,它第( i, k)元素,就是X数组第k列前i个元素
MATLAB数值计算中,没有专门求 极限和导数的指令。原因是:有限 精度。但这不意味:数值计算不能 应用于与“导数”等函数邻域概念 有关的问题。事实上,数值计算是 解各类微分方程的最主要途径。
求(两点前向)差分 求一元(函数)梯度(三点中心差分) 求二元(函数)梯度
〖说明〗 •当X是向量时,dx = X(2:n) - X(1:n-1);当X是矩阵时,dx = X(2:n, : ) - X(1:n-1, : )。注意:dx的长度 •当F是向量时,FX(1) = F(2) - F(1),FX(end) = F(end) - F(end-1), FX(2:end-1) = ( F(3:end) - F(1:end-2) )/2。梯度采用“内点中心差 分”计算。注意:Fx的长度与F相同。 •当F是矩阵时,FX, FY是与F同样大小的矩阵。FX的每行给出F相应行元素 间的“梯度”;FY的每列给出F相应列元素间的“梯度”。
输入量options用于配置优化参数。在没有特殊需求情况下, 一般不必自行设置。 输出量exitflag若给出大于0的数,说明成功搜索到极值点。 输出量output给出具体的优化算法和迭代次数。 注意:7.x版“泛函”指令不能通过输入量传递优化函数中的 参数。 求一元函数极小值时,数值计算获得的区间收敛容差不会比
eps 更好。 求多元函数极小值时,数值计算的精度极限是 x
f ( x) eps
【例4.1-8】 【例4.1-9】
x
eps ,
4.1.5 常微分方程的数值解
MATLAB为解决常微分方程初值问题提供一组配套齐全、结构严整的指令
[t,Y] = ode45(odefun,tspan,y0) 采用4阶Runge-Kutta数值积分法解微分方程 〖说明〗 第一输入量odefun是待解微分方程的函数文件句柄。该函数文件的输出必须是 待解函数的一阶导数。不管原问题是不是一阶微分方程组,当使用ode45求解时 ,必须转化成(假设由n个方程组成)一阶微分方程组形式 y f ( y, t ) 式中y是 (n 1) 向量。 tspan常被赋成二元向量 [t 0 , t f ] ,此时tspan用来定义求数值解的时间区间。 输入量y0是一阶微分方程组的 (n 1) 初值列向量。 输出量t是所求数值解的自变量数据列向量(假定其数据长度为 N ),而Y则是
【例4.1-1】 【例4.1-2】 【例4.1-3】
4.1.2 数值求和与近似数值积分
Sx=sum(X) Scs=cumsum(X) St=trapz(x, y) 采用梯形法沿列方向求函数y关于自变量x 的积分 列方向求和 Sx(k ) X mn (i, k ) 沿列方向求累计和 Scs( j, k ) Xmn (i, k )
【例 4.1-5】
4.1.3 计算精度可控的数值积分
S1=quad(fun,a,b,tol) 采用递推自适应Simpson法计算积分 S1=quadl(fun,a,b,tol) 采用递推自适应 Lobatto法求数值积分 S2=dblquad(fun,xmin,xmax,ymin,ymax,tol) 二重(闭型)数值积分指令 S3=triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol) 三重(闭型)数值积分指令 〖说明〗 被积函数fun ,可以是字符串、内联对象、匿名函数和M函数文件的函 数句柄。被积函数的自变量一般采用字母x 。在此提醒读者注意:编写 被积函数时,要遵循“数组运算”规则。 对于一重积分指令quad, quadl,其积分下限、上限由输入量a、b传递。 而多重积分指令dblquad, triplequad的由内向外的积分限分别由输入量 xmin, xmax, ymin, ymax, zmin, zmax传递。 •输入宗量tol是个标量,用来控制绝对误差。缺省时,积分的绝对精度为
106
。
【例 4.1-6】
【例 4.1-7】
4.1.4 函数极值的数值求解
[x,fval,exitflag,output]=fminbnd(fun,x1,x2,options) 求一元函数在区间(x1, x2)中极小值 [x,fval,exitflag,output]=fminsearch(fun,x0,options) 单纯形法求多元函数极值点 〖说明〗 •第一输入量fun是待解目标函数,该目标函数可以采用字符串、内联对象、 匿名函数和M函数文件的函数句柄等不同形式表达。fminsearch被优化目 标函数fun中的多元自变量应采用单一变量名的向量形式表达(见例4.18)。 •fminbnd的第二、三个输入量x1, x2分别表示被研究区间的左、右边界。 输出量x, fval分别是极值点和相应的目标函数极值。 •fminsearch的第二个输入宗量x0可以是一个搜索起点的向量或一组搜索起 点的矩阵。当采用单个搜索起点时,输出量x也是一个单点(向量)。当 采用多个搜索起点(矩阵)时,输出量x就给出多个搜索结果(矩阵), 该矩阵的每一列代表一个候选极值点。这些搜索到的候选极值点按目标函 数值递增次序排列。极值点x(:,1) 对应的目标函数极小值由fval给出。
( N n) 矩阵。输出量Y行中第k列Y(:,k),就是向量y第k分量的解。
【例 4.1-10】
4.2 矩阵和代数方阵运算和特征参数 矩阵的变换和特征值分解 线性方程的解 一般代数方程的解
4.2.1
矩阵运算和特征参数
术 语 矩阵 加减 标量与矩阵 加减 矩阵 乘积 标量与矩阵 相乘 矩阵的转置
