第十二章排队论运筹学上海电力学院,施泉生
运筹学排队论

3 .排队问题的特征
• 总体来源
• 排队纪律(服务顺序)
• 服务员数量(通道)
15
第十五页,课件共有25页
3.1 总体来源
• 分析排队问题所用方法取决于潜在顾客数量
是否有限。
潜在顾客数量
有限顾客源
无限顾客源
例如:公司只有
三台机器时,需
要维修的数量
例如:排队等候
公共汽车的乘客
人
收银员
电影院售票窗口人
售票员
第六页,课件共有25页
Where the Time Goes ?
人一生中平均要花费---6个月 停在红灯前
8个月 打开邮寄广告
1年 寻找放置不当的物品
五年排队等
2年 回电话不成功
4年 做家务
待
5年 排队等待
6年 饮食
第七页,课件共有25页
为什么会出现排队现象?
顾客
顾客离开
顾客排队
服务设施
假定每小时平均有4位顾客到达,服务人员为每
位顾客的平均服务时间为15分钟。如果顾客到达的间
隔时间正好是15分钟,而服务人员为每位顾客的服务时
间也正好是15分钟,那么,就只需要一名服务人员,顾
客也根本用不着等待。
在以下情况将出现排队现象:
平均到达率高于平均服务率
顾客到达的间隔时间不一样(随机)
服务时间不一样(随机)
第八页,课件共有25页
8
普通能力
到达数量
时 间
• 排队问题并不是系统的固定状态,它与系统设计与管理的控制
有很大关系。如快餐店只允许很短的队长,也可为特定的顾客
留出特定的时间段;也可以通过使用更快的服务人员、机器或
《运筹学排队论》课件

合理分配服务器资源,以提高系统的吞吐量 和响应时间。
最优服务策略问题
总结词
研究如何制定最优的服务策略,以最大化系 统的性能指标。
服务顺序策略
确定服务器的服务顺序,以最小化顾客的等 待时间和平均逗留时间。
服务中断策略
在服务器出现故障时,选择最优的服务中断 策略,以最小化对顾客的影响。
服务时间分布策略
等待队长
指在某一时刻,正在等待服务的顾客总数。
逗留时间与等待时间
逗留时间
指顾客从到达系统到离开系统所经过的时间 。包括接受服务和等待的时间。
等待时间
指顾客到达系统后到开始接受服务所经过的 时间。
忙期与空闲期
要点一
忙期
指系统连续有顾客到达并接受服务的时间段。在这个时间 段内,系统内的顾客数可能会超过系统的容量。
03
02
交通运输
分析铁路、公路、航空等交通系统 的调度和运输效率。
计算机科学
研究计算机网络、云计算、分布式 系统的性能和优化。
04
排队论的基本概念
服务器
提供服务的设施或 人员。
等待时间
顾客到达后到开始 接受服务所需的时 间。
顾客
需要接受服务的对 象。
队列
顾客按到达顺序等 待服务的排列。
服务时间
顾客接受服务所需 的时间。
《运筹学排队论》ppt课件
目录
• 排队论简介 • 排队系统的组成 • 排队模型的分类 • 排队模型的性能指标 • 排队论的优化问题 • 排队论的发展趋势与展望
01
排队论简介
排队论的定义与背景
1
排队论(Queueing Theory)是运筹学的一个重 要分支,主要研究排队系统(Queueing Systems)的行为特性。
运筹学概论(施泉生)

运筹学与其他学科的关系
运 筹 学 与 管 理 科 学 (Management Science MS)关 系:管理科学涵盖的领域比运筹 学更宽一些。可以说,运筹学是 管理科学最重要的组成部分。
运筹学与其他学科的关系
运筹学与系统科学、系统分析、 工业工程的关系:系统科学、系统 分析、工业工程等学科研究的内容 比运筹学窄一些。
运筹学研究的特点
科学性 (1)它是在科学方法论的指导下通 过一系列规范化步骤进行的;
(2)它是广泛利用多种学科的科学 技术知识进行的研究。运筹学研究不 仅仅涉及数学,还要涉及经济科学、 系统科学、工程物理科学等其他学科。
运筹学研究的特点
实践性
运筹学以实际问题为分析对象, 通过鉴别问题的性质、系统的目标 以及系统内主要变量之间的关系, 利用数学方法达到对系统进行最优 化的目的。更为重要的是分析获得 的结果要能被实践检验,并被用来 指导实际系统的运行。
运筹学研究的特点
系统性
运筹学用系统的观点来分析 一个组织(或系统),它着眼于整 个系统而不是一个局部,通过协调 各组成部分之间的关系和利害冲突, 使整个系统达到最优状态。
运筹学研究的特点
综合性
运筹学研究是一种综合性的 研究,它涉及问题的方方面面,应 用多学科的知识,因此,要由一个 各方面的专家组成的小组来完成。
1939年由曼彻斯特大学物理学 家、英国战斗机司令部顾问、战后 获得诺贝尔奖金的P.M.S.Blackett为 首,组织了一个小组,代号 “Blackett马戏团”。这个小组包括 三名心理学家、两名数学家、两名 应用数学家、一名天文物理学家、 一名普通物理学家、一名海军军官、 一名陆军军官、一名测量员。
运筹学-排队论

(接受服务)
5
二、排队系统的组成和特征
1、输入过程
输入即指顾客到达排队系统,可能有以下不同情况。
(1)顾客源的组成
有限的 无限的
(2)顾客到来的方式
一个一个的 成批的
(3)顾客相继到达的间隔时间
确定型的 随机型的
(4)顾客的到来
相互独立的 关联的
(5)输入过程
平稳的,或称对时间是齐次的 非平稳的
6
14
9、其他常用数量指标
s —— 系统中并联服务台的数目;
—— 平均到达率;
1/
—— 平均到达间隔。
—— 平均服务率;
1/ —— 平均服务时间。
—— 服务强度,
每个服务台单位时间内的平均服务时间;
一般有 s ;当s=1时:
15
对于损失制和混合制的排队系统,顾客在到达服务系统时, 若系统容量已满,则自行消失。这就是说,到达的顾客不 一定全部进入系统,为此引入:
例如:某排队问题为
M / M / s / ∞ / ∞ /FCFS
则表示顾客到达间隔时间为负指数分布(泊松流);服务时 间为负指数分布;有s(s>1)个服务台;系统等待空间容量无 限(等待制);顾客源无限,采用先到先服务规则。 可简记为: M / M / s
12
四、排队系统的参数(分析结果)
1、队长(Ls) 指在系统中的顾客数,期望值 2、排队长(Lq) 指系统中排队等候服务的顾客数
13
5、忙期 指从顾客到达空闲服务机构起到服务机构再次空 闲止 这段时间长度,即服务机构连续繁忙的时间长度。 6、系统的状态n:指系统中的顾客数。 7、系统状态的概率Pn(t):指时刻t、系统状态为n的概率。 一般为关于t的微分方程、关于n的差分方程。 8、稳定状态:t→时,t=0时的系统不稳定状态将消失, 系统的状态概率分布不再随时间变化,即 limPn(t)→Pn。
运筹学课排队论应用教学观察

运筹学课排队论应用教学观察运筹学是一门应用数学学科,旨在寻求最优解决问题的方法与技巧。
在运筹学中,排队论是其中的一个重要分支,它涉及到排队系统中的效率、等待时间以及资源利用率等方面的问题。
近年来,越来越多的学校引入运筹学课程,并将排队论应用于教学中。
本文将对运筹学课排队论应用于教学的观察进行分析和讨论。
一、排队论的基本概念与模型在介绍运筹学课排队论的应用之前,我们先对排队论的基本概念与模型进行简要介绍。
排队论主要研究排队系统中的各种性能指标,如队长、等待时间、服务效率等。
其中,常见的模型包括单队列模型、多队列模型以及网络模型等。
二、运筹学课排队论应用的教学观察运筹学课排队论的应用教学观察可以从以下几个方面进行观察:1. 培养学生问题分析与解决能力通过运筹学课排队论的应用教学,学生需要掌握排队系统的建模与求解方法。
这要求学生具备较强的问题分析与解决能力,能够将实际问题抽象成数学模型,并运用排队论的知识进行分析和求解。
2. 增强学生的团队合作与协作能力在排队论应用教学中,学生通常需组成小组共同完成课程设计或实践项目。
这要求学生加强团队合作与协作能力,每个小组成员需要分工合作、协调资源,共同解决排队系统中的实际问题。
3. 提高学生的数学建模能力运筹学课排队论的应用教学要求学生具备较强的数学建模能力。
学生需要将实际中的问题转化为数学模型,并通过数学方法进行求解。
这对于学生的数学思维能力、抽象建模能力以及数学工具的熟练程度提出了较高的要求。
4. 增加学生对实际问题的理解与应用能力运筹学课排队论的应用教学将数学理论与实际问题相结合,帮助学生更好地理解与应用数学知识。
通过实际问题的分析与解决,学生能够更好地理解排队论的概念与模型,并将其应用于实际情境中。
5. 培养学生的动手实践能力在运筹学课排队论的应用教学中,学生通常需要进行实践性项目,如实地观察与数据采集、模型构建与求解等。
这有助于培养学生的动手实践能力,提升他们在实际问题中的应用能力。
运筹学——排队论
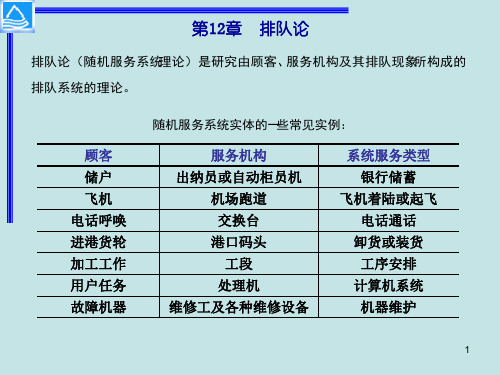
1 对于泊松流, λ表示单位时间内平均到 达的顾客数,因此, 就表示
λ
相继顾客到达的平均间 隔时间,这与 E[T ] =
1
λ
的意义正好相符。
18
服务时间v的分布 对一顾客的服务时间(也即在忙期相继离开系统的两顾客的间隔时间) 有时也服从负指数分布。这时设它的分布函数和密度函数分别为 Fv (t ) = 1 − e − µt , v的期望值 E (v) = 1 f v (t ) = µe − µt
期望值和方差相等,是泊松分布的一个重要特征,可以由此对一个 经验分布是否是泊松分布进行初步的识别。
16
3、负指数分布(negtive exponential distribution)
随机变量T的概率密度若是 λe −λt , t ≥ 0 fT (t ) = 0, t < 0 则称T服从负指数分布。T 分布函数是 1 − e −λt , t ≥ 0 FT (t ) = 0, t < 0 E[T ] = 1
∞
∑ P (t , t + ∆t ) = o( ∆t )
n=2 n
15
通过建立Pn (t )与Pn (t + ∆t )之间的关系方程并求解,得到
( λ t ) n − λt Pn (t ) = e n! t > 0, n = 0,1,2,L
Pn (t ) = Pn (0, t )表示长为t的时间区间内到达n个顾客的概率,并称随机变量 N (t )服从泊松分布,其数学期望和方差分别为 E[ N (t )] = λt Var[ N (t )] = λt
第12章 12章
排队论
排队论(随机服务系统理论)是研究由顾客、服务机构及其排队现象所构成的 排队系统的理论。
运筹学 排队论

S个服务台,一个队列的排队系统
排队系统类型:
服务台1
顾客到达 服务完成后离开
服务台2 服务台s
服务完成后离开
服务完成后离开
S个服务台, S个队列的排队系统
排队系统类型:顾客到达来自服务台1服务台s
离开
多服务台串联排队系统
排队系统类型:
聚 (输入)
服务机构
散 (输出)
随机聚散服务系统
随机性——顾客到达情况与顾客 接受服务的时间是随机的。 一般来说,排队论所研究的排队 系统中,顾客相继到达时间间隔 和服务时间这两个量中至少有一 个是随机的,因此,排队论又称 随机服务理论。
列车在系统中的平均停留时间
W=L/= 2/2=1(小时)
系统中等待编组的列车平均数
Lq=L-= 2-2/3=4/3(列) 列车在系统中的平均等待编组时间
Wq = Lq/ =(4/3)/(1/2)=2/3(小时)
记列车平均延误(由于站内2股道均 被占用而不能进站)时间为W0 则W0 = WP{N>2}=W{1-P0-P1-P2}
n:当系统处于状态n 时,整个系统的 平均服务率(单位时间内可以服务完 的平均顾客数);
当n为常数时记为;当每个服 务台的平均服务率为常数时,记每个 服务台的服务率为,则当n s 时, 有n=s。因此,顾客相继到达的平 均时间间隔为1/ ,平均服务时间为 1/ ,令= / s,则为系统的服 务强度。
W=E(T) :顾客在系统中的平均逗
留时间;
Tq:顾客在系统中的排队等待时间; Wq=E(Tq):顾客在系统中的平均
排队等待时间。
排队论研究的基本问题:
通过研究主要数量指标在瞬时或平稳 状态下的概率分布及数字特征,了解 系统运行的基本特征。 统计推断问题:建立适当的排队模型 是排队论研究的第一步,建立模型过 程中,系统是否达到平稳状态的检验; 顾客相继到达时间间隔相互独立性的 检验,服务时间的分布及有关参数的 确定等。
运筹学学生(大型作业1学分)(上海电力学院)任务书资料

上海电力学院课程设计(大型作业)任务书(2012/2013 学年第1学期)课题名称运筹学大型作业课题代码141303501,141303513院(系)经济与管理学院专业信息管理与信息系统2011级班级2011131学生时间2013.1.14-18老师签名:赵文会,曹金龙教研室主任(系主任)签名:《运筹学》大型作业任务书一、内容1、基础训练——熟悉计算机软件Winqsb的子菜单和Lindo软件求解线性规划问题。
能用Winqsb软件求解运筹学中的常见数学模型。
完成以下内容:2、综合训练:劳动力资源分配问题的见面。
(见附录1)二、目的通过大型作业教学,培养学生利用所学的运筹学知识,根据具体的问题,进行综合分析、计算、评价的能力,以全面理解运筹学的思想和方法并能用于实际工作。
三、要求:1、总体要求全面结合运筹学的内容,根据自己对问题的理解,通过分析,建立合理的运筹学模型,能利用计算机软件Winqsb求出最优解,并能根据自己的理解给出合理分析。
2、形式要求所用的运筹学内容应先有简明阐述,再与具体问题相结合的结论。
整个作业力求全面、丰富,应用资料注明来源。
打印成稿。
四、组织形式基础训练单独完成;每人交一份打印稿作业(正反打印)。
综合训练分组进行,每小组4人(含4人),小组完成时必须有明确的分工,必须有总负责人(总负责人也必须有自己的局部内容)。
综合训练部分小组提交一份打印稿作业。
任务书与大作业封面要在综合训练部分作业中。
注:小组完成的,应根据各人完成的具体工作,在大型作业的成品上注明,并按顺序排名。
五、考核形式大型作业的所有内容在1月18日结束之前交稿,教师可根据评阅情况的需要,指定部分作品进行答辩质疑与交流。
六、成绩评定1、大作业的总评成绩由三部分组成:基础训练+综合训练报告质量+平时表现(出席和答辩表现),具体比例为:40:30:30成绩由任课老师根据完成质量进行评定,以优\良\中\及格\不及格计分。
2.答辩表述要求答辩,如果由个人完成时由个人全面阐述,小组完成时应由一人总述(总述人也应有自己的局部内容),各成员陈述自己完成部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排队系统的符号表示:
“Kendall”记号:X / Y/ Z / W
其中:X表示顾客相继到达的时间间隔 分布;
Y表示服务时间的分布;
Z表示服务台个数;
W表示系统的容量,即可容纳的 最多顾客数。
例 12-1 M /M/ 1 /
M表示顾客相继到达的时间 间隔服从负指数分布; M表示服 务时间为负指数分布;单个服务 台;系统容量为无限(等待制) 的排队模型 。
混合制排队系统:
• 逗留时间(等待时间与服务时间 之和)有限。例:用高射炮射击 飞机,当敌机飞越射击有效区域 的时间为t时,若这个时间内未被 击落,也就不可能再被击落了。
损失制和等待制可看成是混
合制的特殊情形,如记s为系统 中服务台个数,则当k=s时,混 合制即为损失制;当k=时,即 成为等待制。
{Xn}的分布A(t)常见的有:
o 定常分布(D):顾客相继到达的 时间间隔为确定的。如产品通过传 送带进入包装箱就是定常分布。
o 最简流(或称Poisson)(M):顾客 相继到达的时间间隔{Xn}为独立的, 同为负指数分布,其密度函数为:
a(t)=
e- t 0
t0 t<0
❖ 排队及排队规则
➢ 排队
排队的不一定是人,也可以是物。如生 产线上的原材料,半成品等待加工;因 故障而停止运行的机器设备在等待修理; 码头上的船只等待装货或卸货;要下降 的飞机因跑道不空而在空中盘旋等。
当然,进行服务的也不一定是人,可 以是跑道,自动售货机,公共汽车等。
顾客——要求服务的对象。
服务员——提供服务的服务者(也称 服务机构)。
顾客、服务员的含义是广义的。
排队系统类型:
顾客到达
服务完成后离开
服务台
单服务台排队系统
排队系统类型:
服务台1
顾客到达
服务台2
服务完成后离开
服务台s
S个服务台,一个队列的排队系统
排队系统类型:
服务完成后离开
服务台1
顾客到达
Hale Waihona Puke 服务完成后离开服务台2
服务完成后离开
服务台s
S个服务台, S个队列的排队系统
例 12-2 M /M/ S / K
表示顾客到达的时间间隔服从负 指数分布; 服务时间为负指数分布; S个服务台;系统容量为K的排队模 型。
当 K= S 时为损失制排队模型;
当 K= 时为等待制排队模型。
o 具有优先权的服务(PS)。服务 台根据顾客的优先权的不同进行 服务。如病危的病人应优先治疗; 重要的信息应优先处理;出价高 的顾客应优先考虑。
❖ 服务机制
包括:服务员的数量及其连 接方式(串联还是并联);顾客 是单个还是成批接受服务;服务 时间的分布。记某服务台的服务 时间为V,其分布函数为B(t),密度 函数为b(t),则常见的分布有:
➢ 排队规则
当顾客到达时,若所有服务 台都被占有且又允许排队,则该 顾客将进入队列等待。服务台对 顾客进行服务所遵循的规则通常 有:
o 先来先服务(FCFS)
o 后来先服务(LCFS)。在许多库 存系统中就会出现这种情况,如 钢板存入仓库后,需要时总是从 最上面取出;又如在情报系统中, 后来到达的信息往往更重要,首 先要加以分析和利用。
o 有限排队——排队系统中顾客数 是有限的。
o 无限排队——顾客数是无限,队 列可以排到无限长(等待制排队 系统)。
有限排队还可以分成:
▪ 损失制排队系统:排队空间为零 的系统,即不允许排队。(顾客 到达时,服务台占满,顾客自动 离开,不再回来)(电话系统)
▪ 混合制排队系统:是等待制与损 失制结合,即允许排队,但不允 许队列无限长。
排队系统类型:
顾客到达
服务台1
离开
服务台s
多服务台串联排队系统
排队系统类型:
聚
散
服务机构
(输入)
(输出)
随机聚散服务系统
随机性——顾客到达情况与顾客 接受服务的时间是随机的。
一般来说,排队论所研究的排队 系统中,顾客相继到达时间间隔 和服务时间这两个量中至少有一 个是随机的,因此,排队论又称 随机服务理论。
混合制排队系统:
• 队长有限。即系统等待空间是有 限的。例:最多只能容纳K个顾客 在系统中,当新顾客到达时,若 系统中的顾客数(又称为队长) 小于K,则可进入系统排队或接受 服务;否则,便离开系统,并不 再回来。如水库的库容是有限的, 旅馆的床位是有限的。
混合制排队系统:
• 等待时间有限。即顾客在系统中 等待时间不超过某一给定的长度T, 当等待时间超过T时,顾客将自动 离开,不再回来。如易损失的电 子元件的库存问题,超过一定存 储时间的元器件被自动认为失效。
排队系统的描述 实际中的排队 系统各不相同,但概括起来都由 三个基本部分组成:输入过程, 排队及排队规则和服务机构。
❖ 输入过程
➢ 顾客总体(顾客源)数:可能是 有限,也可能是无限。
河流上游流入水库的水量可认为是 无限的;车间内停机待修的机器显 然是有限的。
➢ 到达方式:是单个到达还是成批到 达。库存问题中,若把进来的货看 成顾客,则为成批到达的例子。
➢ 顾客(单个或成批)相继到达的时 间间隔分布:这是刻划输入过程的 最重要内容。令T0=0,Tn表示第n顾 客到达的时刻,则有T0T1 T2….. Tn …… 记Xn= Tn –Tn-1 n=1,2,…, 则Xn是第n顾客与第n-1顾客到达的 时间间隔。
一般假定{Xn}是独立同分布,并记 分布函数为A(t)。
➢ 定长分布(D):每个顾客接受的 服务时间是一个确定的常数。
➢ 负指数分布(M):每个顾客接 受的服务时间相互独立,具有相 同的负指数分布:
b(t)= e- t t0
0
t<0
其中>0为一常数。
➢ K阶爱尔朗分布(En):
b(t)=
k(kt)k-1
(K-1)!
=
e- kt
当k=1时即为负指数分布;k 30,近似
第十二章 排队论
1引 言
2
排队论是研究排队系统(又称
随机服务系统)的数学理论和方法,
是运筹学的一个重要分支。
3 有形排队现象:进餐馆就餐,到图 书馆借书,车站等车,去医院看病, 售票处售票,到工具房领物品等现象。
4
无形排队现象:如几个旅客同时打电话 订车票;如果有一人正在通话,其他人 只得在各自的电话机前等待,他们分散 在不同的地方,形成一个无形的队列在 等待通电话。
