2021年高考数学二轮复习专题四《三角函数》综合练习题

合集下载

2021年高考数学二轮复习三角函数的图像与性质训练题理

2021年高考数学二轮复习三角函数的图像与性质训练题理1．(xx·浙江高考)函数f(x)＝sin xcos x ＋32cos 2x 的最小正周期和振幅分别是( )A ．π，1B ．π，2C ．2π，1D ．2π，22．(xx·浙江高考)已知函数f(x)＝Acos(ωx＋φ)(A>0，ω>0，φ∈R)，则“f(x)是奇函数”是“φ＝π2”的( ) A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．(xx·福建质检)函数f(x)＝x 2cos x 的图像大致是( )4．三角形ABC 是锐角三角形，若角θ终边上一点P 的坐标为(sin A －cos B ，cos A －sin C)，则sin θ|sin θ|＋cos θ|cos θ|＋tan θ|tan θ|的值是( )A ．1B ．－1C ．3D ．45．(xx·济南模拟)若函数f(x)＝2sin ⎝⎛⎭⎪⎫π6x ＋π3(－2<x<10)的图像与x 轴交于点A ，过点A 的直线l 与函数的图像交于B ，C 两点，则(＋)·＝( )A ．－32B ．－16C ．16D ．326．(xx·济南模拟)如图是函数y ＝Asin(ωx＋φ) 在区间⎣⎢⎡⎦⎥⎤－π6，5π6上的图像．为了得到这个函数的图像，只需将y ＝sin x(x ∈R)的图像上所有的点( )A ．向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变B ．向左平移π3个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变C ．向左平移π6个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变D ．向左平移π6个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变7．设α∈⎝ ⎛⎭⎪⎫0，π4，若tan ⎝⎛⎭⎪⎫α＋π4＝2cos 2α，则α＝________.8．(xx·荆州市质检)函数y ＝sin(ωx＋φ)(ω>0,0<φ<π)的最小正周期为π，且函数图像关于点⎝ ⎛⎭⎪⎫－3π8，0对称，则函数的解析式为________________． 9.已知函数f(x)＝Atan(ωx＋φ)⎝⎛⎭⎪⎫ω>0，|φ|<π2，y ＝f(x)的部分图像如图，则f ⎝ ⎛⎭⎪⎫π24＝________.10．(xx·安徽高考)设函数f(x)＝sin x ＋sin ⎝⎛⎭⎪⎫x ＋π3.(1)求f(x)的最小值，并求使f(x)取得最小值的x 的集合；(2)不画图，说明函数y ＝f(x)的图像可由y ＝sin x 的图像经过怎样的变化得到． 11．(xx·长春市调研)函数f(x)＝Asin(ωx＋φ) 的部分图像如图所示． (1)求函数y ＝f(x)的解析式；(2)当x ∈⎣⎢⎡⎦⎥⎤－π，－π6时，求f(x)的取值范围．12．(xx·辽宁省五校模拟)已知角α的顶点在原点，始边与x 轴的正半轴重合，终边经过点P(－3，3)．(1)求sin 2α－ta n α的值；(2)若函数f(x)＝cos(x －α)cos α－sin(x －α)sin α，求函数y ＝3f ⎝ ⎛⎭⎪⎫π2－2x －2f 2(x)在区间⎣⎢⎡⎦⎥⎤0，π2上的值域．1．选A 由f(x)＝sin xcos x ＋32cos 2x ＝12sin 2x ＋32cos 2x ＝sin ⎝⎛⎭⎪⎫2x ＋π3，得最小正周期为π，振幅为1.2．选B 若f(x)是奇函数，则φ＝π2＋kπ(k∈Z)，且当φ＝π2时，f(x)为奇函数．3．选B 因为f(－x)＝(－x)2cos(－x)＝x 2cos x ＝f(x)，所以函数f(x)为偶函数，排除C 、D ；又f ⎝ ⎛⎭⎪⎫π3＝⎝ ⎛⎭⎪⎫π32cos π3＝π218>0，所以排除A.4．选 B 因为三角形ABC 是锐角三角形，所以A ＋B>90°，即A>90°－B ，则sin A>sin(90°－B)＝cos B ，sin A －cos B>0，同理cos A －sin C<0，所以点P 在第四象限，sin θ|sin θ|＋cos θ|cos θ|＋tan θ|tan θ|＝－1＋1－1＝－1.5．选D 由f(x)＝0解得x ＝4，即A(4,0)，过点A 的直线l 与函数的图像交于B ，C 两点，根据对称性可知，A 是BC 的中点，如图，所以＋＝2，所以(＋)·＝2·＝2||2＝2×42＝32.6．选A 由题意知，A ＝1；由2πω＝5π6＋π6，得ω＝2；由2×π3－π62＋φ＝π2＋2kπ(k∈Z)，0<φ<π2，得φ＝π3，故y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3.只要把函数y ＝sin x 的图像向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变，即可得y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3的图像．7．解析：∵tan ⎝ ⎛⎭⎪⎫α＋π4＝2cos 2α，∴sin ⎝ ⎛⎭⎪⎫α＋π4cos ⎝⎛⎭⎪⎫α＋π4＝2(cos 2α－sin 2α)，整理得sin α＋cos αcos α－sin α＝2(cos α＋sin α)(cos α－sin α)．因为α∈⎝⎛⎭⎪⎫0，π4，所以sin α＋cos α≠0.因此(cos α－sin α)2＝12，即sin 2α＝12.由α∈⎝ ⎛⎭⎪⎫0，π4，得2α∈⎝⎛⎭⎪⎫0，π2，所以2α＝π6，即α＝π12.答案：π128．解析：由题意知最小正周期T ＝π＝2πω，∴ω＝2,2×⎝ ⎛⎭⎪⎫－3π8＋φ＝kπ(k∈Z)， ∴φ＝kπ＋3π4(k ∈Z)．又0<φ<π，∴φ＝3π4，∴y ＝sin ⎝ ⎛⎭⎪⎫2x ＋3π4. 答案：y ＝sin ⎝⎛⎭⎪⎫2x ＋3π49．解析：由图像可知，此正切函数的半周期等于3π8－π8＝2π8＝π4，即周期为π2，所以ω＝2.由题意可知，图像过定点⎝⎛⎭⎪⎫3π8，0，所以0＝Atan2×3π8＋φ，即3π4＋φ＝kπ(k∈Z)，所以φ＝kπ－3π4(k ∈Z)，又|φ|<π2，所以φ＝π4.再由图像过定点(0,1)，可得A＝1.综上可知，f(x)＝tan ⎝ ⎛⎭⎪⎫2x ＋π4.故有f ⎝ ⎛⎭⎪⎫π24＝tan ⎝ ⎛⎭⎪⎫2×π24＋π4＝tan π3＝ 3.答案： 310．解：(1)因为f(x)＝sin x ＋12sin x ＋32cos x ＝32sin x ＋32cos x ＝3sin ⎝ ⎛⎭⎪⎫x ＋π6，所以当x ＋π6＝2kπ－π2，即x ＝2kπ－2π3(k ∈Z)时，f(x)取最小值－ 3.此时x 的取值集合为(2)先将y ＝sin x 的图像上所有点的纵坐标伸长到原来的3倍(横坐标不变)，得y ＝3sin x 的图像；再将y ＝3sin x 的图像上所有的点向左平移π6个单位长度，得y ＝f(x)的图像．11．解：(1)由图像得A ＝1，T 4＝2π3－π6＝π2，所以T ＝2π，则ω＝1.将⎝ ⎛⎭⎪⎫π6，1代入得1＝sin ⎝ ⎛⎭⎪⎫π6＋φ，而－π2<φ<π2，所以φ＝π3.因此函数f(x)＝sin ⎝⎛⎭⎪⎫x ＋π3.(2)由于x ∈⎣⎢⎡⎦⎥⎤－π，－π6，－2π3≤x＋π3≤π6，所以－1≤sin ⎝⎛⎭⎪⎫x ＋π3≤12，所以f(x)的取值范围是⎣⎢⎡⎦⎥⎤－1，12.12．解：(1)∵角α的终边经过点P(－3，3)， ∴sin α＝12，cos α＝－32，tan α＝－33.∴sin 2α－tan α＝2sin αcos α－tan α ＝－32＋33＝－36. (2)∵f(x)＝cos(x －α)cos α－sin(x －α)sin α＝cos x ，x ∈R ， ∴y ＝3cos ⎝ ⎛⎭⎪⎫π2－2x －2cos 2x ＝3sin 2x －1－cos 2x ＝2sin ⎝ ⎛⎭⎪⎫2x －π6－1.∵0≤x≤π2，∴－π6≤2x－π6≤5π6.∴－12≤sin ⎝ ⎛⎭⎪⎫2x －π6≤1.∴－2≤2sin ⎝⎛⎭⎪⎫2x －π6－1≤1. 故函数y ＝3f ⎝ ⎛⎭⎪⎫π2－2x －2f 2(x)在区间⎣⎢⎡⎦⎥⎤0，π2上的值域为[－2,1]．35673 8B59 譙<24064 5E00 帀tBd40222 9D1E 鴞< H b33525 82F5 苵。

2021年高考数学二轮复习三角函数解答题专题训练(含解析)

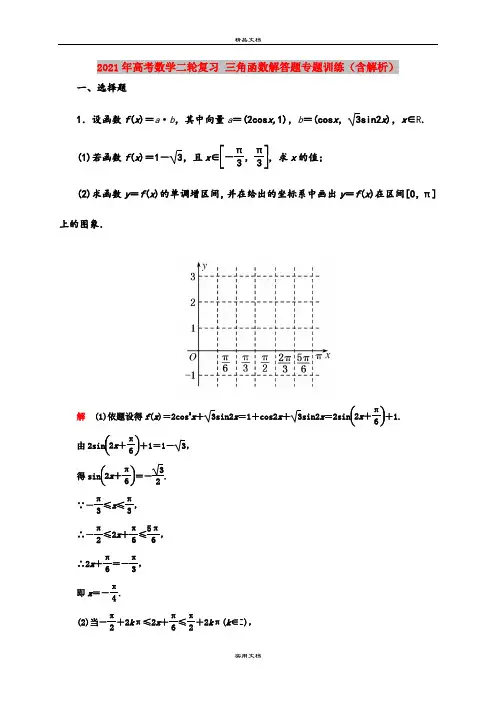
2021年高考数学二轮复习三角函数解答题专题训练（含解析）一、选择题1．设函数f (x )＝a ·b ，其中向量a ＝(2cos x,1)，b ＝(cos x ，3sin2x )，x ∈R . (1)若函数f (x )＝1－3，且x ∈⎣⎢⎡⎦⎥⎤－π3，π3，求x 的值；(2)求函数y ＝f (x )的单调增区间，并在给出的坐标系中画出y ＝f (x )在区间[0，π]上的图象．解 (1)依题设得f (x )＝2cos 2x ＋3sin2x ＝1＋cos2x ＋3sin2x ＝2sin ⎝⎛⎭⎪⎫2x ＋π6＋1. 由2sin ⎝ ⎛⎭⎪⎫2x ＋π6＋1＝1－3，得sin ⎝⎛⎭⎪⎫2x ＋π6＝－32. ∵－π3≤x ≤π3，∴－π2≤2x ＋π6≤5π6，∴2x ＋π6＝－π3，即x ＝－π4.(2)当－π2＋2k π≤2x ＋π6≤π2＋2k π(k ∈Z )，即－π3＋k π≤x ≤π6＋k π(k ∈Z )时，函数y ＝f (x )单调递增，即函数y ＝f (x )的单调增区间为⎣⎢⎡⎦⎥⎤－π3＋k π，π6＋k π(k ∈Z )，在[0，π]上列表如下：x 0 π6 π3 π2 2π3 5π6 π y232－12图象为：2．已知向量a ＝(cos x ＋3sin x ，3sin x )，b ＝(cos x －3sin x ，2cos x )，函数f (x )＝a ·b －cos2x .(1)求函数f (x )的值域；(2)若f (θ)＝15，θ∈⎣⎢⎡⎦⎥⎤π6，π3，求sin2θ的值．解 (1)f (x )＝a ·b －cos2x＝(cos x ＋3sin x )(cos x －3sin x )＋3sin x ·2cos x －cos2x ＝cos 2x －3sin 2x ＋23sin x cos x －cos2x ＝cos 2x －sin 2x －2sin 2x ＋23sin x cos x －cos2x ＝cos2x ＋3sin2x －1 ＝2sin ⎝⎛⎭⎪⎫2x ＋π6－1，所以f (x )的值域为[－3,1]．(2)由(1)知f (θ)＝2sin ⎝ ⎛⎭⎪⎫2θ＋π6－1，由题设2sin ⎝⎛⎭⎪⎫2θ＋π6－1＝15，即sin ⎝⎛⎭⎪⎫2θ＋π6＝35. ∵θ∈⎣⎢⎡⎦⎥⎤π6，π3， ∴2θ＋π6∈⎣⎢⎡⎦⎥⎤π2，5π6，∴cos ⎝⎛⎭⎪⎫2θ＋π6＝－45， ∴sin2θ＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2θ＋π6－π6＝sin ⎝ ⎛⎭⎪⎫2θ＋π6cos π6－cos ⎝ ⎛⎭⎪⎫2θ＋π6sin π6＝35×32－⎝ ⎛⎭⎪⎫－45×12＝33＋410. 3．已知函数f (x )＝A sin(ωx ＋φ)其中x ∈R ，A >0，ω>0，－π2<φ<π2的部分图象如图所示．(1)求函数f (x )的解析式；(2)已知函数f (x )的图象上的三点M ，N ，P 的横坐标分别为－1,1,5，求sin ∠MNP 的值．解 (1)由图可知，A ＝1，最小正周期T ＝4×2＝8. 由T ＝2πω＝8，得ω＝π4. 又f (1)＝sin ⎝ ⎛⎭⎪⎫π4＋φ＝1，且－π2<φ<π2，∴π4＋φ＝π2.解得φ＝π4， ∴f (x )＝sin ⎝ ⎛⎭⎪⎫π4x ＋π4.(2)∵f (－1)＝0，f (1)＝1，f (5)＝sin ⎝ ⎛⎭⎪⎫5π4＋π4＝－1，∴M (－1,0)，N (1,1)，P (5，－1)． ∴|MN |＝5，|PN |＝20，|MP |＝37. 由余弦定理得cos ∠MNP ＝5＋20－3725×20＝－35.∵∠MNP ∈(0，π)， ∴sin ∠MNP ＝45.4．已知m ＝(2cos x ＋23sin x,1)，n ＝(cos x ，－y )，且m ⊥n . (1)将y 表示为x 的函数f (x )，并求f (x )的单调增区间；(2)已知a ，b ，c 分别为△ABC 的三个内角A ，B ，C 对应的边长，若f ⎝ ⎛⎭⎪⎫A 2＝3，且a ＝2，b ＋c ＝4，求△ABC 的面积．解 (1)由m ⊥n ，得m ·n ＝2cos 2x ＋23sin x cos x －y ＝0，即y ＝2cos 2x ＋23sin x cos x ＝cos2x ＋3sin2x ＋1 ＝2sin ⎝⎛⎭⎪⎫2x ＋π6＋1， ∴由－π2＋2k π≤2x ＋π6≤π2＋2k π，k ∈Z ，得－π3＋k π≤x ≤π6＋k π，k ∈Z ，即函数f (x )的增区间为⎣⎢⎡⎦⎥⎤－π3＋k π，π6＋k π，k ∈Z .(2)∵f ⎝ ⎛⎭⎪⎫A 2＝3，∴2sin ⎝⎛⎭⎪⎫A ＋π6＋1＝3.即sin ⎝⎛⎭⎪⎫A ＋π6＝1. ∴A ＋π6＝π2＋2k π，k ∈Z .又0<A <π， ∴A ＝π3，由余弦定理，得a 2＝b 2＋c 2－2bc cos A ，即4＝b 2＋c 2－bc ， ∴4＝(b ＋c )2－3bc ，又b ＋c ＝4， ∴bc ＝4，∴S △ABC ＝12bc sin A ＝12×4×32＝ 3.5．已知函数f (x )＝3sinωx ＋φ2cosωx ＋φ2＋sin2ωx ＋φ2⎝ ⎛⎭⎪⎫其中ω>0，0<φ<π2.其图象的两个相邻对称中心的距离为π2，且过点⎝ ⎛⎭⎪⎫π3，1. (1)求函数f (x )的解析式；(2)在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，a ＝5，S △ABC ＝25，角C 为锐角．且满足f ⎝ ⎛⎭⎪⎫C 2－π12＝76，求c 的值．解 (1)f (x )＝32sin ()ωx ＋φ＋12[1－cos(ωx ＋φ)] ＝sin ⎝ ⎛⎭⎪⎫ωx ＋φ－π6＋12. ∵两个相邻对称中心的距离为π2，则T ＝π， ∴2π|ω|＝π，∵ω>0，∴ω＝2. 又f (x )过点⎝ ⎛⎭⎪⎫π3，1， ∴sin ⎝ ⎛⎭⎪⎫2π3－π6＋φ＋12＝1，即sin ⎝ ⎛⎭⎪⎫π2＋φ＝12，∴cos φ＝12.又∵0<φ<π2，∴φ＝π3， ∴f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π6＋12. (2)f ⎝ ⎛⎭⎪⎫C 2－π12＝sin ⎝ ⎛⎭⎪⎫C －π6＋π6＋12＝sin C ＋12＝76，∴sin C ＝23，又∵0<C <π2，∴cos C ＝53.又a ＝5，S △ABC ＝12ab sin C ＝12×5×b ×23＝25，∴b ＝6，由余弦定理，得c 2＝a 2＋b 2－2ab cos C ，即c 2＝5＋36－25×6×53＝21， ∴c ＝21.623073 5A21 娡29239 7237 爷31834 7C5A 籚fP27984 6D50 浐37192 9148 酈 39340 99AC 馬_21649 5491 咑R"d。

2021年福建省高考数学二轮解答题专项复习：三角函数及解三角形(含答案解析)

（1）求sinA；
（2）若，且△ABC的面积为6，求△ABC的周长．
16．已知a，b，c分别为锐角△ABC三个内角A，B，C的对边，满足sin2A﹣sin2B﹣sin2C+sinBsinC＝0．
（1）求A；
（2）若b＝2，求△ABC面积的取值范围．
17．在△ABC中，内角A，B，C的对边分别是a，b，c，满足条件c＝2b ，C ．
（1）求B；
（2）若a＝2 ，b ，求△ABC的面积．
8．已知△ABC的内角A，B，C的对边分别为a，b，c．满足2c＝a+2bcosA．
（1）求B；
（2）若a+c＝5，b＝3，求△ABC的面积．
9．△ABC的内角A，B，C的对边分别为a，b，c且满足a＝2，acosB＝（2c﹣b）cosA．
（1）求角A的大小；
（1）求角A；
（2）若△ABC边AB上的高为，求AB的长．
18．在△ABC中，已知内角A，B，C所对的边分别为a，b，c，向量，向量，且，角B为锐角．
（1）求角B的大小；
（2）若b＝2，求△ABC面积的最大值．
19．△ABC的内角A，B，C的对边分别为a，b，c，已知a＝1，B ，△ABC的面积为．
（1）求角C的大小；
（2）若b a，△ABC的面积为 sinAsinB，求sinA及c的值．
33．在△ABC中，角A，B，C的对边分别为a，b，c，已知a＝2，b ，B＝2A．
（1）求sinB的值；
（2）若b＝2，△ABC的面积为，求△ABC的周长．
29．已知f（x） sinωx﹣2sin2 （ω＞0）的最小正周期为3π．
（1）求ω的值；
（2）当x∈[ ]时，求函数f（x）的最小值．

(2021年整理)高中数学必修4三角函数综合测试题及答案详解

（完整）高中数学必修4三角函数综合测试题及答案详解编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）高中数学必修4三角函数综合测试题及答案详解）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）高中数学必修4三角函数综合测试题及答案详解的全部内容。

必修4三角函数综合测试题及答案详解一、选择题1．下列说法中，正确的是( ）A ．第二象限的角是钝角B ．第三象限的角必大于第二象限的角C ．－831°是第二象限角D ．－95°20′，984°40′,264°40′是终边相同的角2．若点(a ，9)在函数y ＝3x 的图象上，则tan 错误!的值为（ )A ．0 B.错误! C ．1 D.错误!3．若|cos θ|＝cos θ，｜tan θ|＝－tan θ，则θ2的终边在（） A ．第一、三象限B ．第二、四象限C ．第一、三象限或x 轴上D ．第二、四象限或x 轴上4．如果函数f (x )＝sin （πx ＋θ）（0〈θ〈2π)的最小正周期是T ,且当x ＝2时取得最大值，那么（ )A ．T ＝2，θ＝π2B ．T ＝1，θ＝πC ．T ＝2,θ＝π D．T ＝1，θ＝错误!5．若sin 错误!＝－错误!，且π<x <2π，则x 等于（）A.错误!πB.错误!πC.错误!π D 。

错误!π 6．已知a 是实数，而函数f (x )＝1＋a sin ax 的图象不可能是（ )7．将函数y ＝sin x 的图象向左平移φ(0≤φ<2π）个单位长度后，得到y ＝sin 错误!的图象，则φ＝( )A 。

【精准解析】2021新高考数学二轮(山东)：主观题专练三角函数与解三角形(2)

13 5，
5
所以 sin∠ADB＝2 13. 13
所以 sin∠ADC＝2 13，cos∠ADC＝3 13，所以 tan∠ADC＝2，所以 AC＝2.
13
13
3
3
所以△ABC 的面积为1×2 5×2×2 5＝4.
2
353
若选条件②，
sin∠BAC＝sin(90°＋∠BAD)＝cos∠BAD＝2 5， 5
2．[2020·山东济南历城二中模拟]在△ABC 中，已知 a，b，c 分别是角 A，B，C 的对边， bcos C＋ccos B＝4，B＝π.
4 请在下列三个条件①(a＋b＋c)(sin A＋sin B－sin C)＝3asin B，②b＝4 2，③ 3csin B＝
bcos C 中任意选择一个，添加到题目的条件中，求△ABC 的面积．注：如果选择多个条件分别解答，按第一个解答计分．
－1 得 a2＝(11－a)2＋49－2(11－a)×7× 7 ， ∴a＝8.
(2)∵cos A＝－1，A∈(0，π)，∴sin A＝4 3.
7
7
由正弦定理 a ＝ c ，得 sin C＝csin A＝7×473＝ 3，
sin A sin C
a
8
2
由(1)知 b＝11－a＝3，
∴S△ABC＝1absin C＝1×8×3× 3＝6 3.
在△ABC 中，由正弦定理得(a＋b＋c)(a＋b－c)＝3ab，所以(a＋b)2－c2＝3ab，整理得 a2
＋b2－c2＝ab，
所以由余弦定理得 cos C＝1，又 C∈(0，π)，故 C＝π.
2
3
又 B＝π，所以 A＝π－π－π＝5π.
4
3 4 12

2021年高考数学二轮复习三角函数的图象与性质专题训练(含解析)

2021年高考数学二轮复习三角函数的图象与性质专题训练（含解析）一、选择题1．(xx·全国大纲卷)已知角α的终边经过点(－4,3)，则cos α＝( ) A.45 B.35 C ．－35D ．－45解析 cos α＝－4－42＋32＝－45.答案 D2．(xx·四川卷)为了得到函数y ＝sin(2x ＋1)的图象，只需把函数y ＝sin2x 的图象上所有的点( )A ．向左平行移动12个单位长度B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度解析 ∵y ＝sin(2x ＋1)＝sin2⎝ ⎛⎭⎪⎫x ＋12，∴只需把y ＝sin2x 图象上所有的点向左平移12个单位长度即得到y ＝sin(2x ＋1)的图象．答案 A3．(xx·北京东城一模)将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能取值为( )A.3π4B.π2C.π4D ．－π4解析 y ＝sin(2x ＋φ)错误!sin 错误!＝sin 错误!是偶函数，即错误!＋φ＝k π＋错误!(k ∈Z )⇒φ＝k π＋π4(k ∈Z )，当k ＝0时，φ＝π4，故选C.答案 C4．函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫A >0，ω>0，|φ|<π2的部分图象如图所示，若x 1，x 2∈⎝ ⎛⎭⎪⎫－π6，π3，且f (x 1)＝f (x 2)，则f (x 1＋x 2)＝( )A ．1 B.12 C.22D.32解析观察图象可知，A ＝1，T ＝π， ∴ω＝2，f (x )＝sin(2x ＋φ)．将⎝ ⎛⎭⎪⎫－π6，0代入上式得sin ⎝ ⎛⎭⎪⎫－π3＋φ＝0，由|φ|<π2，得φ＝π3，则f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π3. 函数图象的对称轴为x ＝－π6＋π32＝π12.又x 1，x 2∈⎝ ⎛⎭⎪⎫－π6，π3，且f (x 1)＝f (x 2)，∴x 1＋x 22＝π12，∴x 1＋x 2＝π6， ∴f (x 1＋x 2)＝sin ⎝⎛⎭⎪⎫2×π6＋π3＝32.故选D.答案 D5．函数f (x )＝sin(ωx ＋φ)(ω>0，|φ|<π2)的最小正周期是π，若其图象向右平移π6个单位后得到的函数为奇函数，则函数f (x )的图象( )A ．关于点⎝ ⎛⎭⎪⎫π12，0对称B ．关于直线x ＝π12对称C ．关于点⎝ ⎛⎭⎪⎫π6，0对称 D ．关于直线x ＝π6对称解析 ∵T ＝2πω＝π，∴ω＝2.∴f (x )＝sin(2x ＋φ)向右平移π6个单位，得y ＝sin ⎝⎛⎭⎪⎫2x －π3＋φ为奇函数， ∴－π3＋φ＝k π(k ∈Z )，∴φ＝π3＋k π(k ∈Z )，∴φ＝π3，∴f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π3. ∵sin ⎝ ⎛⎭⎪⎫2×π12＋π3＝1，∴直线x ＝π12为函数图象的对称轴．故选B.答案 B6．已知函数f (x )＝cos ⎝⎛⎭⎪⎫2x ＋π3－cos2x ，其中x ∈R ，给出下列四个结论：①函数f (x )是最小正周期为π的奇函数；②函数f (x )图象的一条对称轴是直线x ＝2π3；③函数f (x )图象的一个对称中心为⎝ ⎛⎭⎪⎫5π12，0；④函数f (x )的递增区间为k π＋π6，k π＋2π3，k ∈Z .则正确结论的个数是( ) A ．1 B ．2 C ．3D ．4解析由已知得，f (x )＝cos ⎝⎛⎭⎪⎫2x ＋π3－cos2x ＝cos2x cos π3－sin2x sin π3－cos2x ＝－sin ⎝ ⎛⎭⎪⎫2x ＋π6，不是奇函数，故①错；当x ＝2π3时，f ⎝ ⎛⎭⎪⎫2π3＝－sin ⎝ ⎛⎭⎪⎫4π3＋π6＝1，故②正确；当x＝5π12时，f ⎝ ⎛⎭⎪⎫5π12＝－sinπ＝0，故③正确；令2k π＋π2≤2x ＋π6≤2k π＋32π，k ∈Z ，得k π＋π6≤x ≤k π＋23π，k ∈Z ，故④正确．综上，正确的结论个数为3.答案 C 二、填空题7．若sin ⎝ ⎛⎭⎪⎫π3＋α＝13，则sin ⎝ ⎛⎭⎪⎫π6＋2α＝________. 解析 sin ⎝ ⎛⎭⎪⎫π6＋2α＝－cos ⎝ ⎛⎭⎪⎫π2＋π6＋2α＝－cos ⎝ ⎛⎭⎪⎫2π3＋2α＝2sin 2⎝ ⎛⎭⎪⎫π3＋α－1＝－79.答案－798．(xx·江苏卷)已知函数y ＝cos x 与y ＝sin(2x ＋φ)(0≤φ<π)，它们的图象有一个横坐标为π3的交点，则φ的值是________．解析利用函数y ＝cos x 与y ＝sin(2x ＋φ)(0≤φ<π)的图象交点横坐标，列方程求解．由题意，得sin ⎝⎛⎭⎪⎫2×π3＋φ＝cos π3，因为0≤φ<π，所以φ＝π6.答案π69．(xx·北京卷)设函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ是常数，A >0，ω>0)．若f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫2π3＝－f ⎝ ⎛⎭⎪⎫π6，则f (x )的最小正周期为________．解析由f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝－f ⎝ ⎛⎭⎪⎫π6知，f (x )有对称中心⎝ ⎛⎭⎪⎫π3，0，由f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫23π知f (x )有对称轴x ＝12⎝ ⎛⎭⎪⎫π2＋23π＝712π，记T 为最小正周期，则12T ≥π2－π6⇒T ≥23π，从而712π－π3＝T4，故T ＝π.答案 π 三、解答题10．(xx·重庆卷)已知函数f (x )＝3sin(ωx ＋φ)(ω>0，－π2≤φ<π2)的图象关于直线x ＝π3对称，且图象上相邻两个最高点的距离为π.(1)求ω和φ的值；(2)若f ⎝ ⎛⎭⎪⎫α2＝34⎝ ⎛⎭⎪⎫π6<α<2π3，求cos ⎝ ⎛⎭⎪⎫α＋3π2的值．解 (1)因f (x )的图象上相邻两个最高点的距离为π，所以f (x )的最小正周期T ＝π，从而ω＝2πT＝2.又因f (x )的图象关于直线x ＝π3对称，所以2·π3＋φ＝k π＋π2，k ＝0，±1，±2，….因－π2≤φ<π2得k ＝0，所以φ＝π2－2π3＝－π6.(2)由(1)得f ⎝ ⎛⎭⎪⎫α2＝3sin ⎝ ⎛⎭⎪⎫2·α2－π6＝34，所以sin ⎝ ⎛⎭⎪⎫α－π6＝14.由π6<α<2π3得0<α－π6<π2，所以cos ⎝⎛⎭⎪⎫α－π6＝1－sin 2⎝⎛⎭⎪⎫α－π6＝ 1－⎝ ⎛⎭⎪⎫142＝154.因此cos ⎝ ⎛⎭⎪⎫α＋3π2＝sin α＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π6＋π6 ＝sin ⎝⎛⎭⎪⎫α－π6cos π6＋cos ⎝⎛⎭⎪⎫α－π6sin π6 ＝14×32＋154×12＝3＋158. 11．(xx·山东菏泽一模)已知函数f (x )＝2sin ωx cos ωx ＋23sin 2ωx －3(ω>0)的最小正周期为π.(1)求函数f (x )的单调增区间； (2)将函数f (x )的图象向左平移π6个单位，再向上平移1个单位，得到函数y ＝g (x )的图象，若y ＝g (x )在[0，b ](b >0)上至少含有10个零点，求b 的最小值．解 (1)由题意得f (x )＝2sin ωx cos ωx ＋23sin 2ωx －3＝sin2ωx －3cos2ωx ＝2sin ⎝⎛⎭⎪⎫2ωx －π3，由最小正周期为π，得ω＝1，所以f (x )＝2sin ⎝⎛⎭⎪⎫2x －π3，由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，整理得k π－π12≤x ≤k π＋5π12，k ∈Z ，所以函数f (x )的单调增区间是⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12，k ∈Z . (2)将函数f (x )的图象向左平移π6个单位，再向上平移1个单位，得到y ＝2sin2x ＋1的图象，所以g (x )＝2sin2x ＋1. 令g (x )＝0，得x ＝k π＋7π12或x ＝k π＋11π12(k ∈Z )，所以在[0，π]上恰好有两个零点，若y ＝g (x )在[0，b ]上有10个零点，则b 不小于第10个零点的横坐标即可，即b 的最小值为4π＋11π12＝59π12.B 级——能力提高组1．设函数f (x )＝3cos(2x ＋φ)＋sin(2x ＋φ)⎝ ⎛⎭⎪⎫|φ|<π2，且其图象关于直线x ＝0对称，则( )A ．y ＝f (x )的最小正周期为π，且在⎝ ⎛⎭⎪⎫0，π2上为增函数B ．y ＝f (x )的最小正周期为π，且在⎝⎛⎭⎪⎫0，π2上为减函数 C ．y ＝f (x )的最小正周期为π2，且在⎝ ⎛⎭⎪⎫0，π4上为增函数 D ．y ＝f (x )的最小正周期为π2，且在⎝⎛⎭⎪⎫0，π4上为减函数解析 f (x )＝3cos(2x ＋φ)＋sin(2x ＋φ) ＝2sin ⎝⎛⎭⎪⎫2x ＋π3＋φ， ∵其图象关于x ＝0对称，∴f (x )是偶函数． ∴π3＋φ＝π2＋k π，k ∈Z . 又∵|φ|<π2，∴φ＝π6. ∴f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π3＋π6＝2cos2x .易知f (x )的最小正周期为π，在⎝⎛⎭⎪⎫0，π2上为减函数．答案 B2．(xx·全国大纲卷)若函数f (x )＝cos2x ＋a sin x 在区间⎝ ⎛⎭⎪⎫π6，π2是减函数，则实数a 的取值范围是________．解析 f (x )＝1－2sin 2x ＋a sin x ＝－2sin 2x ＋a sin x ＋1，sin x ∈⎝ ⎛⎭⎪⎫12，1，令t ＝sin x ∈⎝ ⎛⎭⎪⎫12，1，则y ＝－2t 2＋at ＋1在⎝ ⎛⎭⎪⎫12，1是减函数，∴对称轴t ＝a 4≤12，∴a ≤2.答案 (－∞，2]3．(xx·湖北卷)某实验室一天的温度(单位：℃)随时间t (单位：h)的变化近似满足函数关系：f (t )＝10－3cos π12t －sin π12t ，t ∈[0,24)．(1)求实验室这一天的最大温差；(2)若要求实验室温度不高于11 ℃，则在哪段时间实验室需要降温？解 (1)因为f (t )＝10－2⎝ ⎛⎭⎪⎫32cos π12t ＋12sin π12t ＝10－2sin ⎝ ⎛⎭⎪⎫π12t ＋π3，又0≤t <24，所以π3≤π12t ＋π3<7π3，－1≤sin ⎝ ⎛⎭⎪⎫π12t ＋π3≤1. 当t ＝2时，sin ⎝ ⎛⎭⎪⎫π12t ＋π3＝1；当t ＝14时，sin ⎝ ⎛⎭⎪⎫π12t ＋π3＝－1. 于是f (t )在[0,24)上取得最大值12，取得最小值8.故实验室这一天最高温度为12 ℃，最低温度为8 ℃，最大温差为4 ℃. (2)依题意，当f (t )>11时实验室需要降温．由(1)得f (t )＝10－2sin ⎝ ⎛⎭⎪⎫π12t ＋π3，故有10－2sin ⎝ ⎛⎭⎪⎫π12t ＋π3>11，即sin ⎝ ⎛⎭⎪⎫π12t ＋π3<－12.又0≤t <24，因此7π6<π12t ＋π3<11π6，即10<t <18. 在10时至18时实验室需要降温． 36014 8CAE 貮33058 8122 脢39755 9B4B 魋21980 55DC 嗜34759 87C7 蟇 30825 7869 硩f33504 82E0 苠 ?" y。

2021年辽宁省高考数学二轮解答题专项复习：三角函数及解三角形（含答案解析）

2021年辽宁省高考数学二轮解答题专项复习：三角函数及解
三角形（含答案解析）
预览说明:预览图片所展示的格式为文档的源格式展示,下载源文件没有水印,内容可编辑和复制
第 1 页共 57 页
2021年辽宁省高考数学二轮解答题专项复习：三角函数及解三
角形
1．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且sin 2C ﹣sin 2A ＝sin B sin C +cos 2B
﹣1．
（1）求A ；
（2）若△ABC 为锐角三角形，且a ＝1，求△ABC 周长的取值范围．
2．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且sin 2A +sin 2C ﹣sin A sin C ＝sin 2B ．
（1）求角B 的大小；
（2）若△ABC 为锐角三角形，其外接圆的半径为
5√33，求△ABC 的周长的取值范围．。

2021年高考数学二轮复习三角函数的图象与性质专题检测(含解析)

2021年高考数学二轮复习三角函数的图象与性质专题检测（含解析）1．已知函数y ＝A sin(ωx ＋φ)＋k (0<φ<π2)的最大值为4，最小值为0，最小正周期为π2，直线x ＝π3是其图象的一条对称轴，则函数解析式为________．答案 y ＝2sin(4x ＋π6)＋2解析由题意得⎩⎨⎧A ＋k ＝4，－A ＋k ＝0，解得⎩⎨⎧A ＝2，k ＝2.又函数y ＝A sin(ωx ＋φ)＋k 的最小正周期为π2，所以ω＝2ππ2＝4，所以y ＝2sin(4x ＋φ)＋2. 又直线x ＝π3是函数图象的一条对称轴，所以4 ×π3＋φ＝k π＋π2(k ∈Z )，所以φ＝k π－5π6(k ∈Z )，又∵0<φ<π2，故φ＝π6.故得y ＝2sin(4x ＋π6)＋2.2．已知函数f (x )＝sin 2ωx ＋3sin ωx ·cos ωx ，x ∈R ，又f (α)＝－12，f (β)＝12，若|α－β|的最小值为3π4，则正数ω的值为________．答案 13解析 f (x )＝1－cos 2ωx 2＋32sin 2ωx＝32sin 2ωx －12cos 2ωx ＋12＝sin(2ωx －π6)＋12，又由f (α)＝－12，f (β)＝12，且|α－β|的最小值为3π4可知T ＝3π，于是ω＝13.3.函数f (x )＝A sin(ωx ＋φ)(其中A >0，|φ|<π2)的图象如图所示，为了得到g (x )＝sin 3x的图象，则只要将f (x )的图象向________平移________个单位长度．(答案不唯一)答案右 π12解析由题意，得函数f (x )的周期T ＝4⎝ ⎛⎭⎪⎫5π12－π4＝2π3，ω＝3，所以sin ⎝ ⎛⎭⎪⎫3×5π12＋φ＝－1，又|φ|<π2，所以φ＝π4，所以f (x )＝sin ⎝ ⎛⎭⎪⎫3x ＋π4＝sin ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫x ＋π12，所以将函数f (x )的图象向右平移π12个单位长度可以得到函数g (x )＝sin 3x 的图象．4.已知函数f (x )＝A tan(ωx ＋φ)(ω>0，|φ|<π2)，y ＝f (x )的部分图象如图所示，则f (π24)＝________. 答案3解析由图象知，T ＝πω＝2(3π8－π8)＝π2，ω＝2.由2×3π8＋φ＝k π，k ∈Z ，得φ＝k π－3π4，k ∈Z .又∵|φ|＜π2，∴φ＝π4.由A tan(2×0＋π4)＝1，知A ＝1，∴f (x )＝tan(2x ＋π4)，∴f (π24)＝tan(2×π24＋π4)＝tan π3＝ 3.5．若函数f (x )＝sin ωx (ω>0)在区间[0，π3]上单调递增，在区间[π3，π2]上单调递减，则ω＝________.答案 32解析由题意知f (x )的一条对称轴为直线x ＝π3，和它相邻的一个对称中心为原点，则f (x )的周期T ＝4π3，从而ω＝32.6．将函数f (x )＝－4sin ⎝⎛⎭⎪⎫2x ＋π4的图象向右平移φ个单位，再将图象上每一点的横坐标缩短到原来的12倍，所得图象关于直线x ＝π4对称，则φ的最小正值为________．答案 38π解析依题意可得y ＝f (x )⇒y ＝－4sin[2(x －φ)＋π4]＝－4sin[2x －(2φ－π4)]⇒y ＝g (x )＝－4sin[4x －(2φ－π4)]，因为所得图象关于直线x ＝π4对称，所以g ⎝ ⎛⎭⎪⎫π4＝±4，得φ＝k 2π＋38π(k ∈Z )．故φ的最小正值为3π8.7．已知函数f (x )＝3sin(ωx －π6)(ω>0)和g (x )＝2cos(2x ＋φ)＋1的图象的对称轴完全相同．若x ∈[0，π2]，则f (x )的取值范围是________．答案 [－32，3]解析 ∵f (x )和g (x )的对称轴完全相同， ∴二者的周期相同，即ω＝2，f (x )＝3sin(2x －π6)．∵x ∈[0，π2]，∴2x －π6∈[－π6，5π6]，sin(2x －π6)∈[－12，1]，∴f (x )∈[－32，3]．8．(xx·北京)设函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ是常数，A >0，ω>0)．若f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫2π3＝－f ⎝ ⎛⎭⎪⎫π6，则f (x )的最小正周期为________．答案 π 解析 ∵f (x )在⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，∴T 2≥π2－π6， ∴T ≥2π3.∵f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫2π3， ∴f (x )的一条对称轴为x ＝π2＋2π32＝7π12.又∵f ⎝ ⎛⎭⎪⎫π2＝－f ⎝ ⎛⎭⎪⎫π6， ∴f (x )的一个对称中心的横坐标为π2＋π62＝π3.∴14T ＝7π12－π3＝π4，∴T ＝π. 9．函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π3(x ∈R )的图象为C ，以下结论正确的是________．(写出所有正确结论的编号)①图象C 关于直线x ＝11π12对称；②图象C 关于点⎝ ⎛⎭⎪⎫2π3，0对称；③函数f (x )在区间⎝ ⎛⎭⎪⎫－π12，5π12内是增函数； ④由y ＝sin 2x 的图象向右平移π3个单位长度可以得到图象C .答案 ①②③解析当x ＝11π12时，f ⎝ ⎛⎭⎪⎫11π12＝sin ⎝ ⎛⎭⎪⎫2×11π12－π3＝sin ⎝⎛⎭⎪⎫11π6－π3＝sin 3π2＝－1，为最小值，所以图象C 关于直线x ＝11π12对称，所以①正确；当x ＝2π3时，f ⎝ ⎛⎭⎪⎫2π3＝sin ⎝ ⎛⎭⎪⎫2×2π3－π3＝sin π＝0，图象C 关于点⎝ ⎛⎭⎪⎫2π3，0对称，所以②正确；当－π12≤x ≤5π12时，－π2≤2x －π3≤π2，此时函数单调递增，所以③正确；y ＝sin 2x 的图象向右平移π3个单位长度，得到y ＝sin 2⎝ ⎛⎭⎪⎫x －π3＝sin ⎝ ⎛⎭⎪⎫2x －2π3，所以④错误，所以正确的是①②③.10．已知函数f (x )＝sin ωx ·cos ωx ＋3cos 2ωx －32(ω>0)，直线x ＝x 1，x ＝x 2是y ＝f (x )图象的任意两条对称轴，且|x 1－x 2|的最小值为π4.(1)求f (x )的表达式；(2)将函数f (x )的图象向右平移π8个单位长度后，再将得到的图象上各点的横坐标伸长为原来的2倍，纵坐标不变，得到函数y ＝g (x )的图象，若关于x 的方程g (x )＋k ＝0在区间⎣⎢⎡⎦⎥⎤0，π2上有且只有一个实数解，求实数k 的取值范围．解 (1)f (x )＝12sin 2ωx ＋31＋cos 2ωx 2－32＝12sin 2ωx ＋32cos 2ωx ＝sin ⎝⎛⎭⎪⎫2ωx ＋π3，由题意知，最小正周期T ＝2×π4＝π2，T ＝2π2ω＝πω＝π2，所以ω＝2，所以f (x )＝sin ⎝⎛⎭⎪⎫4x ＋π3. (2)将f (x )的图象向右平移π8个单位长度后，得到y ＝sin ⎝⎛⎭⎪⎫4x －π6的图象，再将所得图象所有点的横坐标伸长到原来的2倍，纵坐标不变，得到y ＝sin ⎝⎛⎭⎪⎫2x －π6的图象．所以g (x )＝sin ⎝⎛⎭⎪⎫2x －π6. 令2x －π6＝t ，∵0≤x ≤π2，∴－π6≤t ≤5π6.g (x )＋k ＝0在区间⎣⎢⎡⎦⎥⎤0，π2上有且只有一个实数解，即函数g (x )＝sin t 与y ＝－k 在区间⎣⎢⎡⎦⎥⎤－π6，5π6上有且只有一个交点．如图，由正弦函数的图象可知－12≤－k <12或－k ＝1.所以－12<k ≤12或k ＝－1.11．(xx·天津)已知函数f (x )＝cos x ·sin(x ＋π3)－3cos 2x ＋34，x ∈R .(1)求f (x )的最小正周期；(2)求f (x )在闭区间[－π4，π4]上的最大值和最小值．解 (1)由已知，有f (x )＝cos x ·(12sin x ＋32cos x )－3cos 2x ＋34＝12sin x ·cos x －32cos 2x ＋34 ＝14sin 2x －34(1＋cos 2x )＋34 ＝14sin 2x －34cos 2x ＝12sin(2x －π3)．所以f (x )的最小正周期T ＝2π2＝π. (2)因为f (x )在区间[－π4，－π12]上是减函数，在区间[－π12，π4]上是增函数，f (－π4)＝－14，f (－π12)＝－12，f (π4)＝14，所以，函数f (x )在闭区间[－π4，π4]上的最大值为14，最小值为－12.12．已知函数f (x )＝A sin(ωx ＋π4)(A >0，ω>0)，g (x )＝tan x ，它们的最小正周期之积为2π2，f (x )的最大值为2g (17π4)．(1)求f (x )的单调递增区间；(2)设h (x )＝32f 2(x )＋23cos 2x .当x ∈[a ，π3)时，h (x )有最小值为3，求a 的值．解 (1)由题意，得2πω·π＝2π2，所以ω＝1.又A ＝2g (17π4)＝2tan 174π＝2tan π4＝2，所以f (x )＝2sin(x ＋π4)．令2k π－π2≤x ＋π4≤2k π＋π2(k ∈Z )，得2k π－3π4≤x ≤2k π＋π4(k ∈Z )．故f (x )的单调递增区间为[2k π－3π4，2k π＋π4](k ∈Z )．(2)因为h (x )＝32f 2(x )＋23cos 2x＝32×4×sin 2(x ＋π4)＋23cos 2x ＝3(sin x ＋cos x )2＋23cos 2x ＝3＋3sin 2x ＋3(cos 2x ＋1)＝3＋3＋23sin(2x ＋π6)，又h (x )有最小值为3，所以有3＋3＋23sin(2x ＋π6)＝3，即sin(2x ＋π6)＝－12.因为x ∈[a ，π3)，所以2x ＋π6∈[2a ＋π6，5π6)，所以2a ＋π6＝－π6，即a ＝－π6.20577 5061 偡29060 7184 熄27359 6ADF 櫟X40754 9F32 鼲_39861 9BB5 鮵+24680 6068 恨=,25127 6227 戧29507 7343 獃31378 7A92 窒。

2021年北京市高考数学二轮解答题专项复习：三角函数及解三角形(含答案解析)

（1）若，求B；
（2）若a＝2c，求△ABC的面积．
31．在锐角△ABC中，角A，B，C对应的边分别是a，b，c，且cos2A+sin（ A）+1＝0．
（1）求角A的大小；
（2）若△ABC的面积S＝3 ，b＝3．求sinC的值．
32．在△ABC中，角A、B、C所对的边分别为a、b、c，且﹣2sin2C+2 cosC+3＝0．
（1）求B；
（2）若a＝2 ，b ，求△ABC的面积．
8．已知△ABC的内角A，B，C的对边分别为a，b，c．满足2c＝a+2bcosA．
（1）求B；
（2）若a+c＝5，b＝3，求△ABC的面积．
9．△ABC的内角A，B，C的对边分别为a，b，c且满足a＝2，acosB＝（2c﹣b）cosA．
（1）求角A的大小；
（2）求△ABC周长的范围．
10．已知△ABC的内角A，B，C的对边分别为a，b，c，且满足acosB+bcosA＝2ccosC．
（1）求C；
（2）若b＝2，△ABC的面积为，求△ABC的周长．
11．在△ABC中，角A，B，C所对的边分别为a，b，c．已知4c＝b+4acosB．
（1）求sinA；
（Ⅰ）求角A的大小；
（Ⅱ）求b+2c的取值范围．
14．△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为．
（1）求sinAsinC；
（2）若cosAcosC ，b＝3，求a+c的值．
15．已知△ABC的内角A，B，C的对边分别为a，b，c，且13acosA﹣5ccosB＝5bcosC．
（2）若AB＝5，BC＝7，求BC边上的高．

2021届高考二轮复习数学专题训练：三角函数(2018-2020年全国卷高考题选)

2018-2020年高考全国卷数学之三角函数专题训练一．选择题（共25小题）1．（2018•全国）要得到y＝cos x，则要将y＝sin x（）A．向左平移π个单位B．向右平移π个单位C．向左平移个单位D．向右平移个单位2．（2018•全国）已知α为第二象限的角，且tanα＝﹣，则sinα+cosα＝（）A．﹣B．﹣C．﹣D．3．（2020•新课标Ⅰ）已知α∈（0，π），且3cos2α﹣8cosα＝5，则sinα＝（）A．B．C．D．4．（2020•新课标Ⅰ）设函数f（x）＝cos（ωx+）在[﹣π，π]的图象大致如图，则f（x）的最小正周期为（）A．B．C．D．5．（2020•新课标Ⅱ）若α为第四象限角，则（）A．cos2α＞0B．cos2α＜0C．sin2α＞0D．sin2α＜0 6．（2020•新课标Ⅲ）已知2tanθ﹣tan（θ+）＝7，则tanθ＝（）A．﹣2B．﹣1C．1D．27．（2020•新课标Ⅲ）在△ABC中，cos C＝，AC＝4，BC＝3，则cos B＝（）A．B．C．D．8．（2020•新课标Ⅲ）在△ABC中，cos C＝，AC＝4，BC＝3，则tan B＝（）A．B．2C．4D．8 9．（2020•新课标Ⅲ）已知sinθ+sin（θ+）＝1，则sin（θ+）＝（）A．B．C．D．10．（2019•新课标Ⅰ）△ABC的内角A，B，C的对边分别为a，b，c．已知a sin A﹣b sin B ＝4c sin C，cos A＝﹣，则＝（）A．6B．5C．4D．3 11．（2019•新课标Ⅰ）tan255°＝（）A．﹣2﹣B．﹣2+C．2﹣D．2+ 12．（2019•新课标Ⅱ）下列函数中，以为最小正周期且在区间（，）单调递增的是（）A．f（x）＝|cos2x|B．f（x）＝|sin2x|C．f（x）＝cos|x|D．f（x）＝sin|x| 13．（2019•新课标Ⅱ）已知α∈（0，），2sin2α＝cos2α+1，则sinα＝（）A．B．C．D．14．（2019•新课标Ⅱ）若x1＝，x2＝是函数f（x）＝sinωx（ω＞0）两个相邻的极值点，则ω＝（）A．2B．C．1D．15．（2019•新课标Ⅲ）设函数f（x）＝sin（ωx+）（ω＞0），已知f（x）在[0，2π]有且仅有5个零点．下述四个结论：①f（x）在（0，2π）有且仅有3个极大值点②f（x）在（0，2π）有且仅有2个极小值点③f（x）在（0，）单调递增④ω的取值范围是[，）其中所有正确结论的编号是（）A．①④B．②③C．①②③D．①③④16．（2019•全国）已知tan A＝2，则＝（）A．B．C．3D．5 17．（2018•新课标Ⅱ）若f（x）＝cos x﹣sin x在[0，a]是减函数，则a的最大值是（）A．B．C．D．π18．（2018•新课标Ⅲ）函数f（x）＝的最小正周期为（）A．B．C．πD．2π19．（2018•新课标Ⅱ）若f（x）＝cos x﹣sin x在[﹣a，a]是减函数，则a的最大值是（）A．B．C．D．π20．（2018•新课标Ⅱ）在△ABC中，cos＝，BC＝1，AC＝5，则AB＝（）A．4B．C．D．2 21．（2018•新课标Ⅲ）△ABC的内角A，B，C的对边分别为a，b，c．若△ABC的面积为，则C＝（）A．B．C．D．22．（2018•新课标Ⅲ）若sinα＝，则cos2α＝（）A．B．C．﹣D．﹣23．（2018•新课标Ⅰ）已知角α的顶点为坐标原点，始边与x轴的非负半轴重合，终边上有两点A（1，a），B（2，b），且cos2α＝，则|a﹣b|＝（）A．B．C．D．1 24．（2018•新课标Ⅰ）已知函数f（x）＝2cos2x﹣sin2x+2，则（）A．f（x）的最小正周期为π，最大值为3B．f（x）的最小正周期为π，最大值为4C．f（x）的最小正周期为2π，最大值为3D．f（x）的最小正周期为2π，最大值为425．（2017•全国）cos20°cos25°﹣sin20°sin25°＝（）A．B．C．0D．二．填空题（共7小题）26．（2020•新课标Ⅱ）若sin x＝﹣，则cos2x＝．27．（2019•新课标Ⅰ）函数f（x）＝sin（2x+）﹣3cos x的最小值为．28．（2019•新课标Ⅱ）△ABC的内角A，B，C的对边分别为a，b，c．若b＝6，a＝2c，B ＝，则△ABC的面积为．29．（2019•新课标Ⅱ）△ABC的内角A，B，C的对边分别为a，b，c．已知b sin A+a cos B＝0，则B＝．30．（2018•新课标Ⅱ）已知tan（α﹣）＝，则tanα＝．31．（2018•新课标Ⅱ）已知sinα+cosβ＝1，cosα+sinβ＝0，则sin（α+β）＝．32．（2018•新课标Ⅰ）△ABC的内角A，B，C的对边分别为a，b，c．已知b sin C+c sin B＝4a sin B sin C，b2+c2﹣a2＝8，则△ABC的面积为．三．解答题（共8小题）33．（2020•新课标Ⅰ）△ABC的内角A，B，C的对边分别为a，b，c．已知B＝150°．（1）若a＝c，b＝2，求△ABC的面积；（2）若sin A+sin C＝，求C．34．（2020•新课标Ⅱ）△ABC中，sin2A﹣sin2B﹣sin2C＝sin B sin C．（1）求A；（2）若BC＝3，求△ABC周长的最大值．35．（2020•新课标Ⅱ）△ABC的内角A，B，C的对边分别为a，b，c，已知cos2（+A）+cos A＝．（1）求A；（2）若b﹣c＝a，证明：△ABC是直角三角形．36．（2019•新课标Ⅰ）△ABC的内角A，B，C的对边分别为a，b，c．设（sin B﹣sin C）2＝sin2A﹣sin B sin C．（1）求A；（2）若a+b＝2c，求sin C．37．（2019•新课标Ⅲ）△ABC的内角A、B、C的对边分别为a，b，c．已知a sin＝b sin A．（1）求B；（2）若△ABC为锐角三角形，且c＝1，求△ABC面积的取值范围．38．（2019•全国）已知函数f（x）＝2sin2x﹣4cos2x+1．（1）求f（x）的最小正周期；（2）设g（x）＝f（），求g（x）在区间[0，]的最大值与最小值．39．（2018•新课标Ⅰ）在平面四边形ABCD中，∠ADC＝90°，∠A＝45°，AB＝2，BD＝5．（1）求cos∠ADB；（2）若DC＝2，求BC．40．（2018•全国）在△ABC中，角A、B、C对应边a、b、c，外接圆半径为1，已知2（sin2A ﹣sin2C）＝（a﹣b）sin B．（1）证明a2+b2﹣c2＝ab；（2）求角C和边c．2021年02月06日步步高的高中数学组卷参考答案与试题解析一．选择题（共25小题）1．【解答】解：要将y＝sin x的图象向左平移个单位，可得y＝sin（x+）＝cos x的图象，故选：C．2．【解答】解：tanα＝＝﹣，①，sin2α+cos2α＝1，②，又α为第二象限的角，∴sinα＞0，cosα＜0，联立①②，解得，，则sinα+cosα＝．故选：C．3．【解答】解：由3cos2α﹣8cosα＝5，得3（2cos2α﹣1）﹣8cosα﹣5＝0，即3cos2α﹣4cosα﹣4＝0，解得cosα＝2（舍去），或cos．∵α∈（0，π），∴α∈（，π），则sinα＝＝．故选：A．4．【解答】解：由图象可得最小正周期小于π﹣（﹣）＝，大于2×（）＝，排除A，D；由图象可得f（﹣）＝cos（﹣ω+）＝0，即为﹣ω+＝kπ+，k∈Z，（*）若选B，即有ω＝＝，由﹣×+＝kπ+，可得k不为整数，排除B；若选C，即有ω＝＝，由﹣×+＝kπ+，可得k＝﹣1，成立．故选：C．5．【解答】解：α为第四象限角，则﹣+2kπ＜α＜2kπ，k∈Z，则﹣π+4kπ＜2α＜4kπ，∴2α是第三或第四象限角或为y轴负半轴上的角，∴sin2α＜0，故选：D．6．【解答】解：由2tanθ﹣tan（θ+）＝7，得2tanθ﹣＝7，即2tanθ﹣2tan2θ﹣tanθ﹣1＝7﹣7tanθ，得2tan2θ﹣8tanθ+8＝0，即tan2θ﹣4tanθ+4＝0，即（tanθ﹣2）2＝0，则tanθ＝2，故选：D．7．【解答】解：在△ABC中，cos C＝，AC＝4，BC＝3，由余弦定理可得AB2＝AC2+BC2﹣2AC•BC•cos C＝42+32﹣2×4×3×＝9；故AB＝3；∴cos B＝＝＝，故选：A．8．【解答】解：∵cos C＝，AC＝4，BC＝3，∴tan C＝＝，∴AB＝＝＝3，可得A＝C，∴B＝π﹣2C，则tan B＝tan（π﹣2C）＝﹣tan2C＝＝＝4．故选：C．9．【解答】解：∵sinθ+sin（）＝1，∴sinθ+sinθ+cosθ＝1，即sinθ+cosθ＝1，得（cosθ+sinθ）＝1，即sin（）＝1，得sin（）＝故选：B．10．【解答】解：∵△ABC的内角A，B，C的对边分别为a，b，c，a sin A﹣b sin B＝4c sin C，cos A＝﹣，∴，解得3c2＝，∴＝6．故选：A．11．【解答】解：tan255°＝tan（180°+75°）＝tan75°＝tan（45°+30°）＝＝＝．故选：D．12．【解答】解：f（x）＝sin|x|不是周期函数，可排除D选项；f（x）＝cos|x|的周期为2π，可排除C选项；f（x）＝|sin2x|在处取得最大值，不可能在区间（，）单调递增，可排除B．故选：A．13．【解答】解：∵2sin2α＝cos2α+1，∴可得：4sinαcosα＝2cos2α，∵α∈（0，），sinα＞0，cosα＞0，∴cosα＝2sinα，∵sin2α+cos2α＝sin2α+（2sinα）2＝5sin2α＝1，∴解得：sinα＝．故选：B．14．【解答】解：∵x1＝，x2＝是函数f（x）＝sinωx（ω＞0）两个相邻的极值点，∴T＝2（）＝＝∴ω＝2，故选：A．15．【解答】解：当x∈[0，2π]时，ωx+∈[，2πω+]，∵f（x）在[0，2π]有且仅有5个零点，∴5π≤2πω+，∴，故④正确，因此由选项可知只需判断③是否正确即可得到答案，下面判断③是否正确，当x∈（0，）时，ωx+∈[，]，若f（x）在（0，）单调递增，则，即ω＜3，∵，故③正确．故选：D．16．【解答】解：tan A＝2，则＝＝＝．故选：B．17．【解答】解：f（x）＝cos x﹣sin x＝﹣（sin x﹣cos x）＝﹣sin（x﹣），由﹣+2kπ≤x﹣≤+2kπ，k∈Z，得﹣+2kπ≤x≤+2kπ，k∈Z，取k＝0，得f（x）的一个减区间为[﹣，]，由f（x）在[0，a]是减函数，得a≤．则a的最大值是．故选：C．18．【解答】解：函数f（x）＝＝＝sin2x的最小正周期为＝π，故选：C．19．【解答】解：f（x）＝cos x﹣sin x＝﹣（sin x﹣cos x）＝，由，k∈Z，得，k∈Z，取k＝0，得f（x）的一个减区间为[，]，由f（x）在[﹣a，a]是减函数，得，∴．则a的最大值是．故选：A．20．【解答】解：在△ABC中，cos＝，cos C＝2×＝﹣，BC＝1，AC＝5，则AB＝＝＝＝4．故选：A．21．【解答】解：∵△ABC的内角A，B，C的对边分别为a，b，c．△ABC的面积为，∴S△ABC＝＝，∴sin C＝＝cos C，∵0＜C＜π，∴C＝．故选：C．22．【解答】解：∵sinα＝，∴cos2α＝1﹣2sin2α＝1﹣2×＝．故选：B．23．【解答】解：∵角α的顶点为坐标原点，始边与x轴的非负半轴重合，终边上有两点A（1，a），B（2，b），且cos2α＝，∴cos2α＝2cos2α﹣1＝，解得cos2α＝，∴|cosα|＝，∴|sinα|＝＝，|tanα|＝||＝|a﹣b|＝＝＝．故选：B．24．【解答】解：函数f（x）＝2cos2x﹣sin2x+2＝2cos2x﹣sin2x+2sin2x+2cos2x＝4cos2x+sin2x＝3cos2x+1＝＝，故函数的最小正周期为π，函数的最大值为，故选：B．25．【解答】解：因为cos20°cos25°﹣sin20°sin25°＝cos（20°+25°）＝．故选：A．二．填空题（共7小题）26．【解答】解：∵sin x＝﹣，∴cos2x＝1﹣2sin2x＝1﹣2×（﹣）2＝．故答案为：．27．【解答】解：∵f（x）＝sin（2x+）﹣3cos x，＝﹣cos2x﹣3cos x＝﹣2cos2x﹣3cos x+1，令t＝cos x，则﹣1≤t≤1，令g（t）＝﹣2t2﹣3t+1的开口向下，对称轴t＝，在[﹣1，1]上先增后减，故当t＝1即cos x＝1时，函数有最小值﹣4．故答案为：﹣428．【解答】解：由余弦定理有b2＝a2+c2﹣2ac cos B，∵b＝6，a＝2c，B＝，∴36＝（2c）2+c2﹣4c2cos，∴c2＝12，∴S△ABC＝，故答案为：6．29．【解答】解：∵b sin A+a cos B＝0，∴由正弦定理可得：sin A sin B+sin A cos B＝0，∵A∈（0，π），sin A＞0，∴可得：sin B+cos B＝0，可得：tan B＝﹣1，∵B∈（0，π），∴B＝．故答案为：．30．【解答】解：∵tan（α﹣）＝，∴tan（α）＝，则tanα＝tan（α+）＝＝＝＝＝，故答案为：．31．【解答】解：sinα+cosβ＝1，两边平方可得：sin2α+2sinαcosβ+cos2β＝1，①，cosα+sinβ＝0，两边平方可得：cos2α+2cosαsinβ+sin2β＝0，②，由①+②得：2+2（sinαcosβ+cosαsinβ）＝1，即2+2sin（α+β）＝1，∴2sin（α+β）＝﹣1．∴sin（α+β）＝．故答案为：．32．【解答】解：△ABC的内角A，B，C的对边分别为a，b，c．b sin C+c sin B＝4a sin B sin C，利用正弦定理可得sin B sin C+sin C sin B＝4sin A sin B sin C，由于0＜B＜π，0＜C＜π，所以sin B sin C≠0，所以sin A＝，则A＝由于b2+c2﹣a2＝8，则：，①当A＝时，，解得bc＝，所以．②当A＝时，，解得bc＝﹣（不合题意），舍去．故：．故答案为：．三．解答题（共8小题）33．【解答】解：（1）△ABC中，B＝150°，a＝c，b＝2，cos B＝＝＝，∴c＝2（负值舍去），a＝2，∴＝．（2）sin A+sin C＝，即sin（180°﹣150°﹣C）+＝，化简得＝，sin（C+30°）＝，∵0°＜C＜30°，∴30°＜C+30°＜60°，∴C+30°＝45°，∴C＝15°．34．【解答】解：（1）设△ABC的内角A，B，C所对的边分别为a，b，c，因为sin2A﹣sin2B﹣sin2C＝sin B sin C，由正弦定理可得a2﹣b2﹣c2＝bc，即为b2+c2﹣a2＝﹣bc，由余弦定理可得cos A＝＝﹣＝﹣，由0＜A＜π，可得A＝；（2）由题意可得a＝3，又B+C＝，可设B＝﹣d，C＝+d，﹣＜d＜，由正弦定理可得＝＝＝2，可得b＝2sin（﹣d），c＝2sin（+d），则△ABC周长为a+b+c＝3+2[sin（﹣d）+sin（+d）]＝3+2（cos d﹣sin d+cos d+sin d），＝3+2cos d，当d＝0，即B＝C＝时，△ABC的周长取得最大值3+2．另解：a＝3，A＝，又a2＝b2+c2﹣2bc cos A，∴9＝b2+c2+bc＝（b+c）2﹣bc≥（b+c）2﹣（b+c）2，由b+c＞3，则b+c≤2（当且仅当b＝c时，“＝”成立），则△ABC周长的最大值为3+2．35．【解答】解：（1）∵cos2（+A）+cos A＝sin2A+cos A＝1﹣cos2A+cos A═，∴cos2A﹣cos A+＝0，解得cos A＝，∵A∈（0，π），∴A＝；（2）证明：∵b﹣c＝a，A＝，∴由正弦定理可得sin B﹣sin C＝sin A＝，∴sin B﹣sin（﹣B）＝sin B﹣cos B﹣sin B＝sin B﹣cos B＝sin（B﹣）＝，∵B，B﹣∈（﹣，），∴B﹣＝，可得B＝，可得△ABC是直角三角形，得证．36．【解答】解：（1）∵△ABC的内角A，B，C的对边分别为a，b，c．∵（sin B﹣sin C）2＝sin2A﹣sin B sin C．∴sin2B+sin2C﹣2sin B sin C＝sin2A﹣sin B sin C，∴由正弦定理得：b2+c2﹣a2＝bc，∴cos A＝＝＝，∵0＜A＜π，∴A＝．（2）∵a+b＝2c，A＝，∴由正弦定理得，∴解得sin（C﹣）＝，∴C﹣＝，C＝，∴sin C＝sin（）＝sin cos+cos sin＝+＝．37．【解答】解：（1）a sin＝b sin A，即为a sin＝a cos＝b sin A，可得sin A cos＝sin B sin A＝2sin cos sin A，∵sin A＞0，∴cos＝2sin cos，若cos＝0，可得B＝（2k+1）π，k∈Z不成立，∴sin＝，由0＜B＜π，可得B＝；（2）若△ABC为锐角三角形，且c＝1，由余弦定理可得b＝＝，由三角形ABC为锐角三角形，可得a2+a2﹣a+1＞1且1+a2﹣a+1＞a2，且1+a2＞a2﹣a+1，解得＜a＜2，可得△ABC面积S＝a•sin＝a∈（，）．38．【解答】解：f（x）＝2sin2x﹣4cos2x+1＝1﹣cos2x﹣2（1+cos2x）+1＝﹣3cos2x．（1）f（x）的最小正周期T＝；（2）g（x）＝f（）＝，∵x∈[0，]，∴﹣3cos x∈[﹣3，]．即g（x）在区间[0，]的最大值为﹣，最小值为﹣3．39．【解答】解：（1）∵∠ADC＝90°，∠A＝45°，AB＝2，BD＝5．∴由正弦定理得：＝，即＝，∴sin∠ADB＝＝，∵AB＜BD，∴∠ADB＜∠A，∴cos∠ADB＝＝．（2）∵∠ADC＝90°，∴cos∠BDC＝sin∠ADB＝，∵DC＝2，∴BC＝＝＝5．40．【解答】证明：（1）∵在△ABC中，角A、B、C对应边a、b、c，外接圆半径为1，∴由正弦定理得：＝2R＝2，∴sin A＝，sin B＝，sin C＝，∵2（sin2A﹣sin2C）＝（a﹣b）sin B，∴2（）＝（a﹣b）•，化简，得：a2+b2﹣c2＝ab，故a2+b2﹣c2＝ab．解：（2）∵a2+b2﹣c2＝ab，∴cos C＝＝＝，解得C＝，∴c＝2sin C＝2•＝．。

2021年高考新题型——数学三角函数与解三角形多选题专项练习含答案

2021年高考新题型——数学三角函数与解三角形多选题专项练习含答案一、三角函数与解三角形多选题1．在ABC 中，角,,A B C 所对的边分别为,,a b c ，下列命题正确的是（）A ．若::4:5:6a b c =，ABC 的最大内角是最小内角的2倍B ．若cos cos a B b A c -=，则ABC 一定为直角三角形 C ．若4,5,6a b c ===，则ABCD ．若()()()cos cos cos 1A B B C C A ---=，则ABC 一定是等边三角形【答案】ABD 【分析】对于A 选项，求得2A C =，由此确定选项正确.对于B 选项，求得2A π=，由此确定选项正确.对于C 选项，利用正弦定理求得ABC 外接圆半径，由此确定选项错误.对于D 选项，证得()()()cos cos cos 1A B B C C A -=-=-=，得到A B C ==，确定选项正确. 【详解】对于A 选项，A 角最小，C 角最大.由余弦定理得253616453cos 0256604A +-===>⨯⨯，16253651cos 0245408C +-===>⨯⨯，2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭，cos2cos A C =.0,022A C ππ<<<<，则02A π<<，所以2A C =，所以A 选项正确.对于B 选项，cos cos a B b A c -=，由正弦定理得sin cos sin cos sin A B B A C -=，()sin cos cos sin sin sin cos cos sin A B A B A B A B A B -=+=+，cos sin 0=A B ，由于0,0A B ππ<<<<，所以2A π=，故B 选项正确.对于C 选项，16253651cos 245408C +-===⨯⨯，0C π<<，sin C ==，设三角形ABC 外接圆半径为R，则2sin 2sin c cR R C C=⇒===，故C 选项错误.对于D 选项，0,0,A B A B ππππ<<-<-<-<-<，故()1cos 1A B -<-≤，同理可得()()1cos 1,1cos 1B C C A -<-≤-<-≤，要使()()()cos cos cos 1A B B C C A ---=，则需()()()cos cos cos 1A B B C C A -=-=-=，所以0,0,0A B B C C A -=-=-=，所以A B C ==，所以D 选项正确. 故选：ABD 【点睛】利用正弦定理可求得三角形外接圆的半径R ，要注意公式是2sin aR A=，而不是sin aR A =.2．中国南宋时期杰出数学家秦九韶在《数书九章》中提出了“三斜求积术”，即以小斜幂，并大斜幂，减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂，减上，余四约之，为实；一为从隅，开平方得积.把以上文字写成公式，即S =S 为三角形的面积，a 、b 、c 为三角形的三边）.现有ABC 满足sin :sin :sin 2:A B C =，且ABC 的面积ABC S =△，则下列结论正确的是（）A ．ABC 的周长为10+B ．ABC 的三个内角A 、C 、B 成等差数列C ．ABC 的外接圆半径为3D ．ABC 的中线CD 的长为【答案】AB 【分析】本题首先可根据sin :sin :sin 2:A B C =得出::2:3:a b c =ABCS =△以及S =A 正确，然后根据余弦定理求出1cos 2C =，则π3C =，2A B C +=，B 正确，再然后根据2sin c R C =即可判断出C 错误，最后根据余弦定理求出cos B =，再根据cos B =求出CD 长，D 错误. 【详解】A 项：设ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ，因为sin :sin :sin 2:A B C =，所以由正弦定理可得::2:a b c =设2a t =，3b t =，()0c t =>，因为ABCS =△，所以=解得2t =，则4a =，6b =，c =故ABC 的周长为10+A 正确；B 项：因为2221636281cos 22462a b c C ab +-+-===⨯⨯，所以π3C =，π2ππ233A B C +=-==，故ABC 的三个内角A 、C 、B 成等差数列，B 正确；C 项：因为π3C =，所以sin C =由正弦定理得2sin c R C ===R =C 错误；D 项：由余弦定理得222cos214a cb B ac +-===，在BCD △中4BC =，BD =由余弦定理得2cos14B ==，解得CD =，D 错误，故选：AB. 【点睛】本题考查解三角形相关问题的求解，考查的公式有2sin c R C =、222cos 2a c b B ac+-=，考查正弦定理边角互换的灵活应用，考查根据等差中项的性质证明数列是等差数列，考查计算能力，考查转化与化归思想，是难题.3．设函数()2sin sin 2cos2f x x x =++，给出下列四个结论：则正确结论的序号为（） A ．()20f >B ．()f x 在53,2ππ⎛⎫--⎪⎝⎭上单调递增 C ．()f x 的值域为[]12cos2,32cos2-++ D ．()f x 在[]0,2π上的所有零点之和为4π 【答案】ABD 【分析】由()23sin 22cos2f =+，结合3224ππ<<，可判定A 正确；作出函数2sin sin y x x =+的图象，可得函数()f x 的值域及单调性，可判定B 正确，C 不正确；结合函数的图象，可得()f x 在[]0,2π上的所有零点之和，可判定D 正确. 【详解】由题意，函数()2sin sin 2cos2f x x x =++，可得()22sin 2sin 22cos23sin 22cos2f =++=+ 因为3224ππ<<，所以sin 2cos20>->，所以()20f >，所以A 正确；由3sin ,222sin sin ,sin ,222x k x k y x x k Z x k x k πππππππ≤≤+⎧=+=∈⎨-+≤≤+⎩，作出函数2sin sin y x x =+的图象，如图所示，可得函数()f x 是以2π为周期的周期函数，由函数2sin sin y x x =+的图象可知，函数()f x 在3(,)2ππ上单调递增，又由()f x 是以2π为周期的周期函数，可得函数()f x 在5(3,)2ππ--上单调递增，所以B 是正确的；由由函数2sin sin y x x =+的图象可知，函数()f x 的值域为[2cos 2,32cos 2]+，所以C 不正确；又由2223ππ<<，所以1cos 202-<<，则02cos21<-<，令()0f x =，可得2sin sin 2cos2x x +=-，由图象可知，函数()f x 在[]0,2π上的所有零点之和为4π，所以D 正确. 故选：ABD.【点睛】本题主要考查了三角函数的图象与性质的综合应用，其中解答中熟记三角函数的图象与性质是解答的关键，着重考查转化思想，以及数形结合思想的应用，以及推理与运算能力，属于中档试题.4．函数()sin()f x x ωϕ=+的部分图像如图中实线所示，图中的M 、N 是圆C 与()f x 图像的两个交点，其中M 在y 轴上，C 是()f x 图像与x 轴的交点，则下列说法中正确的是（）A ．函数()y f x =的一个周期为56B ．函数()f x 的图像关于点4,03成中心对称C ．函数()f x 在11,26⎛⎫-- ⎪⎝⎭上单调递增 D ．圆C 的面积为3136π【答案】BD 【分析】根据图象，结合三角函数的对称性、周期性、值域以及圆的中心对称性，可得,,C M N 的坐标，进而可得()f x 的最小正周期、对称中心、单调减区间，及圆的半径，故可判断选项的正误. 【详解】由图知：1(,0)3C ，3(0,)2M ，23(,)32N ， ∴()f x 中111()2362T =--=，即1T =；对称中心为1,0,23k k Z ⎛⎫+∈ ⎪⎝⎭；单调减区间为17,,1212k k k Z ⎡⎤++∈⎢⎥⎣⎦；圆的半径221331()()326r =+=，则圆的面积为3136π；综上，知：AC 错误，而BD 正确. 故选：BD. 【点睛】本题考查了三角函数的性质，结合了圆的中心对称性质判断三角函数的周期、对称中心、单调区间及求圆的面积，属于难题.5．（多选题）如图，设ABC 的内角、、A B C 所对的边分别为a b c 、、，若a b c 、、成等比数列，、、A B C 成等差数列，D 是ABC 外一点，1,3DC DA ==，下列说法中，正确的是（）A ．3B π=B ．ABC 是等边三角形C ．若A B CD 、、、四点共圆，则13AC =D ．四边形ABCD 面积无最大值【答案】ABC 【分析】根据等差数列的性质和三角形内角和可得3B π=，根据等比中项和余弦定理可得a c =，即ABC 是等边三角形，若A B C D 、、、四点共圆，根据圆内接四边形的性质可得23D π=，再利用余弦定理可求13AC =211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+和2222cos AC AD CD AD CD D 可得3335353sin cos 3sin()22232S D D D π=-+=-+，从而求出最大面积. 【详解】由、、A B C 成等差数列可得，2A+C =B ，又A B C π++=，则3B π=，故A 正确；由a b c 、、成等比数列可得，2b ac =，根据余弦定理，2222cos b a c ac B =+-，两式相减整理得，2()0a c -=，即a c =，又3B π=，所以，ABC 是等边三角形，故B 正确；若A B C D 、、、四点共圆，则B D π+=，所以，23D π=， ADC 中，根据余弦定理，2222cos AC AD CD AD CD D ，解得13AC =C 正确；四边形ABCD 面积为：211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+233sin 2D AC = 又2222cos 106cos AC AD CD AD CD D D =+-⋅=-，所以，3335353sin cos 3sin()23S D D D π=-+=-+，因为(0,)D π∈，当四边形面积最大时，sin()13D π-=，此时max 533S =+，故D 错误. 故选：ABC 【点睛】本题考查解三角形和平面几何的一些性质，同时考查了等差等比数列的基本知识，综合性强，尤其是求面积的最大值需要一定的运算，属难题.6．已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，下列说法正确的是（）A ．函数()y f x =的周期为πB ．函数()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦单调递减 C ．函数()y f x =的图象关于直线512x π=-对称 D ．该图象向右平移6π个单位可得2sin 2y x =的图象【答案】ACD 【分析】先根据图像求出()y f x =的解析式，再分别验证A 、B 、C 、D 是否正确. 对于A ：利用周期公式求周期；对于B ：利用复合函数“同增异减”求单调区间；对于C ：计算512f π⎛-⎫⎪⎝⎭，看512x π=-是否经过顶点；对于D ：利用“左加右减”判断.【详解】由图像可知：A =2，周期24,2312T T ππππω⎛⎫=-=∴==⎪⎝⎭；由=2sin 2212122f ππϕπϕ⎧⎛⎫⎛⎫⨯+= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎨⎪<⎪⎩解得：3πϕ=故函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭对于A ：4312T πππ⎛⎫=-= ⎪⎝⎭，故A 正确；对于B ：当236x ππ-≤≤- 时203x ππ-≤+≤，所以()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦上不单调.故B 错误；对于C ：当512x π=-时255s 2121232in f πππ⎛⎫⎛⎫=-=- ⎪ ⎭⎝-⎪⎭+⎝⨯，即直线512x π=-是()y f x =的一条对称轴.故C 正确；对于D ：()y f x =向右平移6π个单位得到2sin 222sin 263y x x ππ⎛⎫=-⨯+= ⎪⎝⎭，故D 正确. 故选：ACD 【点睛】求三角函数解析式的方法： (1)求A 通常用最大值或最小值； (2)求ω通常用周期；()求φ通常利用函数上的点带入即可求解.7．已知函数22()(sin cos )2cos f x x x x =++，则（） A ．()f x 的最小正周期是π B ．()f x的图像可由函数()22g x x =+的图像向左平移8π个单位而得到 C ．4x π=是()f x 的一条对称轴D ．()f x 的一个对称中心是,08π⎛⎫- ⎪⎝⎭【答案】AB 【分析】首先化简函数()224f x x π⎛⎫=++ ⎪⎝⎭，再根据三角函数形式的公式，以及代入的方法判断选项. 【详解】()1sin 2cos 21224f x x x x π⎛⎫=+++=++ ⎪⎝⎭，A.函数的最小正周期22T ππ==，故A 正确；B.根据图象的平移变换规律，可知函数()22g x x =+的图像向左平移8π个单位而得到()222284f x x x ππ⎛⎫⎛⎫=++=++ ⎪ ⎪⎝⎭⎝⎭，故B 正确；C.当4x π=时，32444πππ⨯+=，不是函数的对称轴，故C 不正确； D.当8x π=-时，2084ππ⎛⎫⨯-+= ⎪⎝⎭，此时函数值是2，故函数的一个对称中心应是,28π⎛⎫- ⎪⎝⎭，故D 不正确. 故选：AB 【点睛】思路点睛：本题考查()sin y A ωx φ=+的解析式和性质的判断，可以整体代入验证的方法判断函数性质：（1）对于函数()sin y A ωx φ=+，其对称轴一定经过图象的最高点或最低点，对称中心的横坐标一定是函数的零点，因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时，可通过验证()0f x 的值进行判断；（2）判断某区间是否是函数的单调区间时，也可以求x ωϕ+的范围，验证此区间是否是函数sin y x =的增或减区间.8．设函数()()1sin 0222f x x x πωωω⎛⎫=++> ⎪⎝⎭，已知()f x 在[]0,π有且仅有3个零点，则（）A ．在()0,π上存在1x 、2x ，满足()()122f x f x -=B ．()f x 在()0,π有且仅有1个最小值点C ．()f x 在0,2π⎛⎫⎪⎝⎭上单调递增 D ．ω的取值范围是1723,66⎡⎫⎪⎢⎣⎭ 【答案】AD【分析】化简函数()f x 的解析式为()sin 6f x x πω⎛⎫=+ ⎪⎝⎭，令6t x πω=+，由[]0,x π∈可求得,66t ππωπ⎡⎤∈+⎢⎥⎣⎦，作出函数sin ,066y t t ππωπω⎛⎫=≤≤+> ⎪⎝⎭的图象，可判断AB 选项的正误；由图象得出346ππωππ≤+<可判断D 选项的正误；取3ω=，利用正弦型函数的单调性可判断C 选项的正误. 【详解】()3131sin sin sin cos sin 2226f x x x x x x ππωωωωω⎛⎫⎛⎫=++=+=+ ⎪ ⎪⎝⎭⎝⎭，当[]0,x π∈时，,666x πππωωπ⎡⎤+∈+⎢⎥⎣⎦，令6t x πω=+，则,66t ππωπ⎡⎤∈+⎢⎥⎣⎦，作出函数sin ,066y t t ππωπω⎛⎫=≤≤+> ⎪⎝⎭的图象如下图所示：对于A 选项，由图象可知，max 1y =，min 1y =-，所以，在()0,π上存在1x 、2x ，满足()()122f x f x -=，A 选项正确；对于B 选项，()f x 在()0,π上有1个或2个最小值点，B 选项错误；对于D 选项，由于函数()f x 在[]0,π有且仅有3个零点，则346ππωππ≤+<，解得172366ω≤<，D 选项正确；对于C 选项，由于172366ω≤<，取3ω=，当0,2x π⎛⎫∈ ⎪⎝⎭时，53663x πππ<+<，此时，函数()f x 在区间0,2π⎛⎫⎪⎝⎭上不单调，C 选项错误. 故选：AD. 【点睛】关键点点睛：本题考查利用正弦型函数在区间上的零点个数判断正弦型函数的基本性质，解本题的关键在于换元6t x πω=+，将问题转化为函数sin y t =在区间,66ππωπ⎡⎤+⎢⎥⎣⎦上的零点个数问题，数形结合来求解.9．在ABC 中，下列说法正确的是（）A ．若AB >，则sin sin A B >B ．若2C π>，则222sin sin sin C A B >+C ．若sin cos A B <，则ABC 为钝角三角形D ．存在ABC 满足cos cos 0A B +≤【答案】ABC【分析】根据大角对大边，以及正弦定理，判断选项A ；利用余弦定理和正弦定理边角互化，判断选项B ；结合诱导公式，以及三角函数的单调性判断CD.【详解】A.A B >，a b ∴>，根据正弦定理sin sin a b A B =，可知sin sin A B >，故A 正确； B.2C π>，222cos 02a b c C ab +-∴=<，即222a b c +<，由正弦定理边角互化可知222sin sin sin C A B >+，故B 正确；C.当02A π<<时，sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭，即22A B A B ππ->⇒+<，即2C π>，则ABC 为钝角三角形，若2A π>，sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭，即22A B A B ππ->⇒>+成立，A 是钝角，当2A π=是，sin cos A B >，所以综上可知：若sin cos A B <，则ABC 为钝角三角形，故C 正确；D.A B A B ππ+<⇒<-，0,0A B πππ<<<-<，()cos cos cos A B B π∴>-=-，即cos cos 0A B +>，故D 不正确.故选：ABC【点睛】关键点点睛：本题考查判断三角形的形状，关键知识点是正弦定理和余弦定理，判断三角形形状，以及诱导公式和三角函数的单调性.10．已知函数()()cos 22f x x πϕϕ⎛⎫=+< ⎪⎝⎭，()()124F x f x f x π⎛⎫=+ ⎪⎝⎭为奇函数，则下述四个结论中说法正确的是（）A ．tan ϕ=B ．()f x 在[],a a -上存在零点，则a 的最小值为6π C ．()F x 在3,44ππ⎛⎫ ⎪⎝⎭上单调递增 D ．()F x 的图象可由()f x 的图象向左平移2π个单位得到【答案】ABC【分析】首先得到()()1224F x f x f x π⎛⎫=++ ⎪⎝⎭的解析式，再根据函数的奇偶性求出参数ϕ，最后结合三角函数的性质一一验证即可.【详解】解：因为()cos(2)f x x ϕ=+，所以11()()+cos(2))cos 22423F x f x f x x x x ππϕϕϕ⎛⎫⎛⎫==++=++ ⎪ ⎪⎝⎭⎝⎭，因为()F x 为奇函数，则(0)0F =，即cos 03πϕ⎛⎫+= ⎪⎝⎭，所以32k ππϕπ+=+，k Z ∈，因为||2ϕπ<，所以6π=ϕ；对于A ，tan tan 6πϕ==，故A 正确；对于B ，令()cos 206f x x π⎛⎫=+= ⎪⎝⎭，得26k x ππ=+，k ∈Z ，若()f x 在[,]a a -上存在零点，则0a >且a 的最小值为6π，故B 正确；对于C ，()cos 2sin 263F x x x ππ⎛⎫=++=- ⎪⎝⎭，当3,44x ππ⎛⎫∈ ⎪⎝⎭时，2,232x ππ⎛⎫∈ ⎪⎝⎭，则()F x 在3,44ππ⎛⎫ ⎪⎝⎭上单调递增，故C 正确. 对于D ，因为()cos 26f x x π⎛⎫=+ ⎪⎝⎭， ()cos 266F x x ππ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦，根据“左加右减”，()F x 的图象可由()f x 的图象向左平移6π个单位得到，故D 错误.故选：ABC .【点睛】关键点点睛：本题解答的关键是先根据()()124F x f x f x π⎛⎫=++ ⎪⎝⎭为奇函数，确定参数ϕ的值，再结合三角函数的性质逐一判断即可.。

2021届高考数学二轮复习三角函数综合练(5)

2021届高考数学二轮复习三角函数综合练（5）1.扇形的中心角为120︒，半径为3，则此扇形的面积为( ) A ．π B ．4π5C ．3π D ．223π 2.若ππ2α<<，则点()cos ,sin Q αα位于( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3.若1tan 3α=，则2sin cos2αα-=( )A.710 B.58-C.710-D.710±4.已知α是第二象限角，且3π1cos 24α⎛⎫+= ⎪⎝⎭，则cos α=( )A ．15- B ．14- C ．14D ．155.设函数π()cos()6f x x ω=+在[]π,π-的图像大致如下图，则()f x 的最小正周期为( )A.10π9B.7π6C.4π3D.3π26.将函数sin 2y x =的图象向左平移π6个单位长度后得到曲线1C ，再将1C 上所有点的横坐标伸长到原来的2倍得到曲线2C ，则2C 的解析式为( ) A ．πsin 3y x ⎛⎫=+ ⎪⎝⎭B ．πsin 6y x ⎛⎫=+ ⎪⎝⎭C ．πsin 3y x ⎛⎫=- ⎪⎝⎭D ．πsin 43y x ⎛⎫=+ ⎪⎝⎭7.若0ω>，函数πcos 3y x ω⎛⎫=+⎪⎝⎭的图像向右平移π3个单位长度后与函数sin y x ω=的图像重合，则ω的最小值为( ) A.112B.52C.12D.328.若函数π()sin 3f x x ⎛⎫=+ ⎪⎝⎭在(,)a a -上是增函数，则实数a 的取值范围是( )A.π0,3⎛⎤ ⎥⎝⎦B.π0,6⎛⎤ ⎥⎝⎦C.ππ,63⎡⎤⎢⎥⎣⎦D.π5π,66⎡⎤⎢⎥⎣⎦9.已知函数22π()sin sin 3f x x x ⎛⎫=++ ⎪⎝⎭，则()f x 的最小值为( )A.12B.14C.3 D.2210.已知函数()2cos()(0,0π)f x x ωϕωϕ=+><≤的图象如图所示，则下列说法错误的是( )A.函数()f x 在17π11π,1212⎡⎤--⎢⎥⎣⎦上单调递减 B.函数()f x 在3ππ,2⎡⎤⎢⎥⎣⎦上单调递增C.函数()f x 的对称中心是ππ,0(Z)26k k ⎛⎫-∈ ⎪⎝⎭D.函数()f x 的对称轴是π5π(Z)212k x k =-∈ 11.已知1sin cos 5θθ-=，则sin cos θθ的值是__________.12.若π1sin 63α⎛⎫-= ⎪⎝⎭，则2πcos 23α⎛⎫+= ⎪⎝⎭______.13.函数π()sin(2)4f x x =+的最小正周期为_________；若函数()f x 在区间(0,)α上单调递增，则α的最大值为________.14.已知函数()sin cos f x a x b x =+（其中,a b 为非零实数），且22π4f a b ⎛⎫=+ ⎪⎝⎭题：①函数()f x 2|a ； ②3π4f x ⎛⎫+ ⎪⎝⎭为奇函数；③若()()1212,0x x f x f x ∃≠==，则12x x -必是3π2的整数倍； ④若2a ，且ππ()2||42g x f x ϕϕ⎛⎫⎛⎫=+-< ⎪⎪⎝⎭⎝⎭，将函数()g x 的图象向右平移π12个单位长度后的图象关于y 轴对称，则函数()g x 在π0,2⎡⎤⎢⎥⎣⎦上的最小值为3-其中正确命题的序号是____________.（将所有正确命题的序号都填上） 15.已知函数2π()sin()sin 32f x x x x =-.(1)求()f x 的最小正周期和最大值； (2)求()f x 在π2π,63⎡⎤⎢⎥⎣⎦上的单调区间.答案以及解析1.答案：A 解析：∵2π1203︒=弧度，∴此扇形的面积(221112π3π2223S lr r α===⨯⨯=，故答案为A.2.答案：B 解析：∵ππ2α<<，则cos 0α<，sin 0α>.∴点()cos ,sin Q αα位于第二象限.故选B. 3.答案：C解析：由题意得()2222sin cos2sin cos sin ααααα-=--2222222sin cos 2sin cos sin cos αααααα-=-=+22221212tan 173tan 110113αα⎛⎫⨯- ⎪-⎝⎭===-+⎛⎫+ ⎪⎝⎭，故选C. 4.答案：A解析：因为3π1cos 24α⎛⎫+= ⎪⎝⎭，由诱导公式可得，1sin 4α=，因为22sin cos 1αα+=，α是第二象限角，所以2115cos 1sin 116αα=---.故选：A 5.答案：C解析：通解由题图知，4π09f ⎛⎫-= ⎪⎝⎭，4ππππ()962k k ω∴-+=+∈Z ，解得39()4k k ω+=-∈Z .设()f x 的最小正周期为T ，易知2π2T T <<， 2π4π2π||||ωω∴<<，1||2ω∴<<，当且仅当 1k =-时，符合题意，此时32ω=，2π4π3T ω∴==.故选C. 秒解由题图知，4π09f ⎛⎫-= ⎪⎝⎭且(π)0f -<，(0)0f >，4πππ(0)962ωω∴-+=->，解得32ω=，()f x ∴的最小正周期2π4π3T ω==.故选C. 6.答案：A解析：将函数sin2y x =的图象向左平移π6，可得函数ππsin 2sin 263y x x ⎛⎫⎛⎫=+=+⎪ ⎪⎝⎭⎝⎭的图象；然后把所有图象上各点的横坐标伸长到原来的2倍，所得图象的解析式πsin 3y x ⎛⎫=+ ⎪⎝⎭，故选：A. 7.答案：B解析：(方法一)将函数πcos 3y x ω⎛⎫=+⎪⎝⎭的图像向右平移π3个单位长度后可得函数ππππcos cos 3333y x x ωωω⎡⎤⎛⎫⎛⎫=-+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图像.因为平移后的函数图像与函数sin y x ω=的图像重合，所以ππππ332k ω-=+.因为0ω>，所以当1k =-时， ω的最小值为52.故选B.(方法二)因为πππ5cos sin sin π3236y x x x ωωω⎛⎫⎛⎫⎛⎫=+=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以将函数5sin π6y x ω⎛⎫=+ ⎪⎝⎭的图像向右平移π3个单位长度后可得函数π55sin πsin ππ3636y x x ωωω⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图像.又因为平移后的函数图像与函数sin y x ω=的图像重合，所以5ππ2π36k ω-+=.因为0ω>，所以当0k =时，ω的最小值为52.故选B. 8.答案：B解析：易知π()sin 3f x x ⎛⎫=+ ⎪⎝⎭的递增区间为5ππ2π,2π()66k k k ⎡⎤-++∈⎢⎥⎣⎦Z .根据函数()f x 在(,)a a -上是增函数，可得0,5π,6π,6a a a ⎧⎪>⎪⎪-≥-⎨⎪⎪≤⎪⎩解得π06a <≤.故选B.9.答案：A 解析：函数222222π13533()sin sin sin sin sin cos 23244f x x x x x x x x x ⎛⎫⎛⎫=++=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭ 1πsin 2126x ⎛⎫=+ ⎪⎝⎭，当πsin 216⎛⎫⨯=- ⎪⎝⎭时，函数min 11()122f x =-=．故选A ． 10.答案：D解析：由图象可得，函数的周期5ππ2π63T ⎛⎫=⨯-= ⎪⎝⎭，所以2π2T ω==将点π(,0)3代入()2cos(2)f x x ϕ=+中，得ππ22π(Z)32k k ϕ⨯+=-∈，解得7π2π(Z)6k k ϕ=-∈，由0πϕ<≤，可得5π6ϕ=，所以5π()2cos 26f x x ⎛⎫=+ ⎪⎝⎭，令5π2π22ππ(Z)6k x k k ≤+≤+∈，得5ππππ()1212k x k k Z -≤≤+∈故函数()f x 在5πππ,π(Z)1212k k k ⎡⎤-+∈⎢⎥⎣⎦上单调递减，故函数()f x 在1711π,π1212⎡⎤--⎢⎥⎣⎦上单调递减，故A 正确；令5π2ππ22π(Z)6k x k k -≤+≤∈，得11π5πππ(Z)1212k x k k -≤≤-∈ 故函数()f x 在11π5ππ,π(Z)1212k k k ⎡⎤--∈⎢⎥⎣⎦上单调递增.故函数()f x 在13π19π,1212⎡⎤⎢⎥⎣⎦上单调递增.故B 错误；令5ππ2π(Z)62x k k +=+∈，得ππ(Z)26k x k =-∈ 故函数()f x 的对称中心是ππ,0(Z)26k k ⎛⎫-∈ ⎪⎝⎭故C 正确；令5π2π(Z)6x k k +=∈得π5π()212k x k Z =-∈，故函数()f x 的对称轴是π5π(Z)212k x k =-∈.故D 正确. 11.答案：1225解析：由1sin cos 5θθ-=，平方可得221sin cos 2sin cos 12sin cos 25θθθθθθ+-=-=.解得12sin cos 25θθ=.故答案为：1225. 12.答案：79-解析：已知π1sin 63α⎛⎫-= ⎪⎝⎭，且πππ632αα⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭，则ππ1cos sin 363αα⎛⎫⎛⎫+=-= ⎪ ⎪⎝⎭⎝⎭，故22ππ7cos 22cos 1339αα⎛⎫⎛⎫+=+-=- ⎪ ⎪⎝⎭⎝⎭.13.答案：ππ;8解析：π()sin 24f x x ⎛⎫=+ ⎪⎝⎭，故2ππ2T ==，当(0,)x α∈时，πππ2,2444x α⎛⎫+∈+ ⎪⎝⎭故ππ242α+≤，解得π8α≤，故答案为：ππ;814.答案：①②④ 解析：①π2)4f a b ⎛⎫+ ⎪⎝⎭，由22π4f a b ⎛⎫=+ ⎪⎝⎭222)a b a b ++，则22222()a b a b +=+，整理可得2()0a b -=，于是a b =.π()2sin 4f x a x ⎛⎫∴=+ ⎪⎝⎭，故①正确；②π3π()2sin ,2sin(π)2sin 44f x a x f x a x a x ⎛⎫⎛⎫=+∴+=+= ⎪ ⎪⎝⎭⎝⎭为奇函数，故②正确；③函数π()2sin 4f x a x ⎛⎫=+ ⎪⎝⎭的周期为2π，若()()1212,0x x f x f x ∃≠==，则12x x -必是π的整数倍，而不是3π2的整数倍，故③错误； ④2a =，则π()22sin(2)4g x f x x ϕϕ⎛⎫=+-=+ ⎪⎝⎭，于是ππ2π2sin(22cos 21263g x x x ϕϕ⎛⎫⎫⎛⎫-=-+=+- ⎪⎪ ⎪⎝⎭⎭⎝⎭，又平移后图象关于y 轴对称，π12g x ⎛⎫∴- ⎪⎝⎭为偶函数，于是2ππ()3k k ϕ-=∈Z ，即2ππ()3k k ϕ=+∈Z .又ππ||,,()23g x ϕϕ<∴=-∴π2sin 23x ⎛⎫=- ⎪⎝⎭，又min πππ2ππ0,,2,,()2sin 23333x x g x ⎡⎤⎡⎤⎛⎫∈∴-∈-∴=- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭3=-，故④正确.15.答案：(1)2π()sin()sin 32f x x x x =-3133π3cos sin cos2)sin 2sin(2)23x x x x x x =+=-=-，因此()f x 的最小正周期为π23-(2)当π2π,63x ⎡⎤∈⎢⎥⎣⎦时，π02π3x ≤-≤，从而当ππ0232x ≤-≤，即π5π612x ≤≤时，()f x 单调递增，当ππ2π23x ≤-≤，即5π2π123x ≤≤时，()f x 单调递减．综上可知，()f x 在π5π,612⎡⎤⎢⎥⎣⎦上单调递增；在5π2π,123⎡⎤⎢⎥⎣⎦上单调递减．。