RSA算法原理以及PKI系统简介
PKI原理
PKI原理1976年,Whitfield Diffie和Martin Hellman提出了公开密钥理论,奠定了PKI体系的基础。
PKI(Public Key Infrastructure 的缩写)即"公开密钥体系",是一个利用现代密码学的公钥密码技术、并在开放的Internet网络环境中提供数据加密以及数字签名服务的、统一的技术框架。
常用的公开密钥算法有RSA、DSA和Diffie Hellman等。
使用公开密钥算法(又叫非对称加密算法)的用户同时拥有公钥和私钥。
私钥不能通过公钥计算出来。
私钥由用户自己持有,公钥可以明文发送给任何人,公开密钥理论解决了对称加密系统的密钥交换问题。
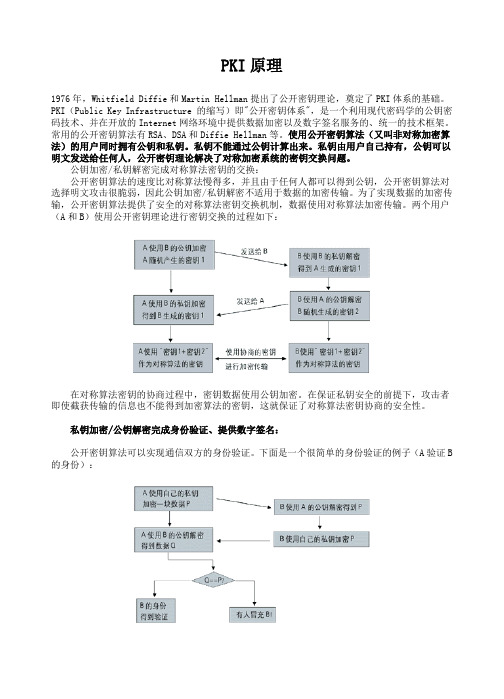
公钥加密/私钥解密完成对称算法密钥的交换:公开密钥算法的速度比对称算法慢得多,并且由于任何人都可以得到公钥,公开密钥算法对选择明文攻击很脆弱,因此公钥加密/私钥解密不适用于数据的加密传输。
为了实现数据的加密传输,公开密钥算法提供了安全的对称算法密钥交换机制,数据使用对称算法加密传输。
两个用户(A和B)使用公开密钥理论进行密钥交换的过程如下:在对称算法密钥的协商过程中,密钥数据使用公钥加密。
在保证私钥安全的前提下,攻击者即使截获传输的信息也不能得到加密算法的密钥,这就保证了对称算法密钥协商的安全性。
私钥加密/公钥解密完成身份验证、提供数字签名:公开密钥算法可以实现通信双方的身份验证。
下面是一个很简单的身份验证的例子(A验证B 的身份):同样的原理,公开密钥算法可以进行数据的签名和验证。
A需要对一块数据签名,A只需要使用自己的私钥加密该数据就可以完成签名。
A把数据和数据签名(私钥加密的结果)一起发送给B,B使用A的公钥解密签名,然后和数据进行比较,如果相同则该签名确实是A签署的,并且数据没有被篡改。
同样是因为公开密钥的算法较慢,数据签名一般不直接使用私钥加密数据,而是加密数据的散列值。
数据块的散列值可以通过消息摘要算法计算得到。
简述rsa加密算法原理

简述rsa加密算法原理RSA加密算法原理RSA加密算法是一种非对称加密算法,由三位数学家Rivest、Shamir 和Adleman于1977年提出。
它的安全性基于大数分解的困难性,可以用于数字签名、密钥交换等领域。
下面将从以下几个方面详细介绍RSA加密算法原理。
1. 公钥密码学公钥密码学是一种密码学技术,它采用两个不同但相关的密钥:一个公钥和一个私钥。
公钥可以自由地分发给任何人,而私钥则只能由其拥有者保管。
使用公钥加密的数据只能使用相应的私钥进行解密,反之亦然。
公钥密码学具有高度的安全性和灵活性,可以广泛应用于数据传输、数字签名等方面。
2. RSA算法生成密钥对RSA算法生成密钥对的过程如下:(1)选择两个大质数p和q,并计算它们的乘积n=pq。
(2)计算欧拉函数φ(n)=(p-1)(q-1)。
(3)选择一个整数e(1<e<φ(n)),使得e与φ(n)互质。
(4)计算d=d^-1(mod φ(n)),其中d满足de≡1(mod φ(n))。
(5)公钥为(n,e),私钥为(n,d)。
其中,p和q是足够大的质数,n是它们的乘积,φ(n)是n的欧拉函数,e是一个与φ(n)互质的整数,d是e在模φ(n)意义下的逆元。
3. RSA算法加密过程RSA算法加密过程如下:(1)将明文转换成整数m(0<=m<n)。
(2)计算密文c≡m^e(mod n),其中e为公钥中的指数。
(3)将密文c发送给接收者。
其中,m是明文,n和e是接收者的公钥,c是密文。
4. RSA算法解密过程RSA算法解密过程如下:(1)接收到密文c。
(2)计算明文m≡c^d(mod n),其中d为私钥中的指数。
其中,c是密文,n和d是接收者的私钥,m是明文。
5. RSA算法安全性分析RSA算法安全性基于大数分解的困难性。
即如果能够快速地分解出p 和q,则可以轻松地计算出d,并从而破解RSA加密。
但目前尚未发现快速分解大整数的有效方法。
PKI体系

PKI体系公钥基础设施PKI技术与应用发展公钥基础设施PKI技术与应用发展一、概述PKI是“Public Key Infrastructure”的缩写,意为“公钥基础设施”。
简单地说,PKI技术就是利用公钥理论和技术建立的提供信息安全服务的基础设施。
公钥体制是目前应用最广泛的一种加密体制,在这一体制中,加密密钥与解密密钥各不相同,发送信息的人利用接收者的公钥发送加密信息,接收者再利用自己专有的私钥进行解密。
这种方式既保证了信息的机密性,又能保证信息具有不可抵赖性。
目前,公钥体制广泛地用于CA认证、数字签名和密钥交换等领域。
PKI似乎可以解决绝大多数网络安全问题,并初步形成了一套完整的解决方案,它是基于公开密钥理论和技术建立起来的安全体系,是提供信息安全服务的具有普适性的安全基础设施。
该体系在统一的安全认证标准和规范基础上提供在线身份认证,是CA认证、数字证书、数字签名以及相关安全应用组件模块的集合。
作为一种技术体系,PKI 可以作为支持认证、完整性、机密性和不可否认性的技术基础,从技术上解决网上身份认证、信息完整性和抗抵赖等安全问题,为网络应用提供可靠的安全保障。
但PKI绝不仅仅涉及到技术层面的问题,还涉及到电子政务、电子商务以及国家信息化的整体发展战略等多层面问题。
PKI作为国家信息化的基础设施,是相关技术、应用、组织、规范和法律法规的总和,是一个宏观体系,其本身就体现了强大的国家实力。
PKI的核心是要解决信息网络空间中的信任问题,确定信息网络空间中各种经济、军事和管理行为主体(包括组织和个人)身份的惟一性、真实性和合法性,保护信息网络空间中各种主体的安全利益。
公钥基础设施(PKI)是信息安全基础设施的一个重要组成部分,是一种普遍适用的网络安全基础设施。
PKI是20世纪80年代由美国学者提出来了的概念,实际上,授权管理基础设施、可信时间戳服务系统、安全保密管理系统、统一的安全电子政务平台等的构筑都离不开它的支持。
RSA算法原理(简单易懂)

RSA算法原理(简单易懂)1. 什么是RSARSA算法是现今使⽤最⼴泛的公钥密码算法,也是号称地球上最安全的加密算法。
在了解RSA算法之前,先熟悉下⼏个术语根据密钥的使⽤⽅法,可以将密码分为对称密码和公钥密码对称密码:加密和解密使⽤同⼀种密钥的⽅式公钥密码:加密和解密使⽤不同的密码的⽅式,因此公钥密码通常也称为⾮对称密码。
2. RSA加密RSA的加密过程可以使⽤⼀个通式来表达密⽂=明⽂EmodN密⽂=明⽂EmodN也就是说RSA加密是对明⽂的E次⽅后除以N后求余数的过程。
就这么简单?对,就是这么简单。
从通式可知,只要知道E和N任何⼈都可以进⾏RSA加密了,所以说E、N是RSA加密的密钥,也就是说E和N的组合就是公钥,我们⽤(E,N)来表⽰公钥公钥=(E,N)公钥=(E,N)不过E和N不并不是随便什么数都可以的,它们都是经过严格的数学计算得出的,关于E和N拥有什么样的要求及其特性后⾯会讲到。
顺便啰嗦⼀句E是加密(Encryption)的⾸字母,N是数字(Number)的⾸字母3. RSA解密RSA的解密同样可以使⽤⼀个通式来表达明⽂=密⽂DmodN明⽂=密⽂DmodN也就是说对密⽂进⾏D次⽅后除以N的余数就是明⽂,这就是RSA解密过程。
知道D和N就能进⾏解密密⽂了,所以D和N的组合就是私钥私钥=(D,N)私钥=(D,N)从上述可以看出RSA的加密⽅式和解密⽅式是相同的,加密是求“E次⽅的mod N”;解密是求“D次⽅的mod N”此处D是解密(Decryption)的⾸字母;N是数字(Number)的⾸字母。
⼩结下公钥(E,N)私钥(D,N)密钥对(E,D,N)加密密⽂=明⽂EmodN密⽂=明⽂EmodN解密明⽂=密⽂DmodN明⽂=密⽂DmodN4. ⽣成密钥对既然公钥是(E,N),私钥是(D,N)所以密钥对即为(E,D,N)但密钥对是怎样⽣成的?步骤如下:1. 求N2. 求L(L为中间过程的中间数)3. 求E4. 求D4.1 求N准备两个质数p,q。
RSA加密算法及实现

RSA加密算法及实现RSA加密算法是一种非对称加密算法,广泛应用于网络通信中的数据加密和数字签名等方面。
RSA算法的核心思想是基于大数分解的难解性问题,通过数论中的数学原理实现加密过程。
下面将详细介绍RSA加密算法的原理和实现。
RSA算法的原理如下:1.密钥的生成:-随机选择两个不同的大质数p和q。
-计算n=p*q。
-计算欧拉函数φ(n)=(p-1)*(q-1)。
-选择一个整数e,使得1<e<φ(n),且e与φ(n)互质。
- 计算e关于φ(n)的模反元素d,使得d * e ≡ 1 (modφ(n))。
-公钥为(n,e),私钥为(n,d)。
2.加密算法:-将明文m转化为整数。
- 计算密文c = m^e mod n。
3.解密算法:- 计算明文m = c^d mod n。
1.密钥的生成:首先,使用一个大数库来生成大质数p和q,确保p和q均为质数。
然后,计算n=p*q,并计算φ(n)=(p-1)*(q-1)。
选择一个合适的e,可以是小于φ(n)的质数或者与φ(n)互质的数。
使用扩展欧几里德算法,计算e关于φ(n)的模反元素d。
最终得到公钥为(n,e),私钥为(n,d)。
2.加密算法:将明文m转化为整数。
然后,使用快速模幂算法计算密文c = m^e mod n。
3.解密算法:使用快速模幂算法,计算明文m = c^d mod n。
需要注意的是,RSA算法对加密和解密的数据长度有限制,一般建议将要加密的数据分块进行加密。
同时,为了增强安全性,一般会使用大的素数来生成密钥。
总结:RSA加密算法是一种非对称加密算法,通过数论中的数学原理实现加密过程。
它的核心思想是基于大数分解的难解性问题。
RSA算法的实现需要生成密钥对、加密和解密三个步骤。
密钥的生成需要随机选择两个大质数,并进行相应的计算。
加密算法通过快速模幂算法进行加密,解密算法也通过快速模幂算法进行解密。
RSA算法在实际应用中广泛用于保护数据的机密性和完整性,同时也是数字签名等功能实现的基础。
rsa算法的原理

rsa算法的原理RSA算法是一种公钥密码算法,它经常被用于信息安全领域中的加密和数字签名等方面,是目前最广泛使用的公钥加密算法之一。
本文将介绍RSA算法的原理,从密钥生成、加密和解密三个方面详细讲解。
一、密钥生成RSA算法是一种基于大素数因子分解的加密方法,其密钥包括公钥和私钥两部分。
公钥由两个参数n和e组成,其中n为两个大质数p和q 的乘积,e为整数且满足1<e<φ(n)且e与φ(n)互质。
私钥由两个参数n和d组成,其中n相同,d为整数,满足ed≡1(modφ(n)),φ(n)=(p-1)(q-1)是欧拉函数。
密钥生成的具体流程如下:1.选取两个不同的大质数p和q,并计算它们的积n=p*q。
2.计算φ(n)=(p-1)*(q-1)。
3.选取一个大于1且小于φ(n)的整数e,使得e与φ(n)互质。
4.使用扩展欧几里得算法计算出d。
具体地,我们需要求出方程ed=k*φ(n)+1的正整数解d。
5.将n和e组成公钥,n和d组成私钥。
二、加密RSA算法的加密过程如下:1.将明文M转化为整数m,确保0 <= m < n。
2.计算密文C = m^e mod n。
其中,C为密文。
三、解密RSA算法的解密过程如下:1.将密文C转化为整数c,确保0 <= c < n。
2.计算明文M = c^d mod n。
当然,在实际应用中还需要考虑信息安全领域常常面临的各种攻击手段,比如重放攻击、中间人攻击等等。
此外,RSA算法的安全性也与密钥长度有关。
通常情况下,我们需要保证密钥长度足够长,这样攻击者才会愈发显得无能为力。
综上所述,RSA算法是一种基于大素数不易分解原理的公钥密码算法。
密钥包括公钥和私钥两部分,其加密和解密过程都依赖于密钥的组成。
在使用时需要注意信息安全问题,并根据具体应用需求确定密钥长度。
rsa加密原理

rsa加密原理RSA加密算法(RSAencryptionalgorithm)是一种非对称加密算法,属于公钥加密算法中的代表性算法。
1979年,美国研究人员Ron Rivest、Adi Shamir和Leonard Adleman将它发表出来,他们凭着这个算法获得了2002年图灵奖。
RSA加密算法是基于数论研究而来,它不仅可以进行加密,还可以用来进行数字签名和密码学中的验证。
RSA加密算法的基本原理是公钥加密,即发送者使用接收者的公钥对数据进行加密,接收者使用该公钥的私钥对加密后的数据进行解密。
RSA加密算法的基本原理是:1、它视每一个公钥对(Public Key, PK)由两部分组成,称为e和n,其中n是一个大数,而e是小质数,它们都是唯一的并且同时公开的,但是n是一个很大的数,是不可能由人们推断出来的。
2、在RSA加密算法中,发送者使用接收者的公钥来加密信息,而接收者使用自己的私钥进行解密。
加密的前提是:发送者必须知道对方的公钥,而接收者必须记住自己的私钥,在RSA加密算法中,任何人都不可能通过仅有的一个公钥来计算出私钥。
3、在RSA加密算法中,数据是按照单个字节加密,然后被转换为一个二进制文件,信息将会被分割成一个个小段,每个小段都将会按照公钥加密,最终会组合在一起,来储存加密过的文件(Cipher text)。
而解密时,过程刚好相反:将加密后的文件分割成小段,分别按照私钥解密,最终将所有解密后的段组合在一起,恢复原始文本。
4、RSA加密算法的安全性取决于计算机的处理能力,它的安全性体现在:首先,只有拥有接收者的私钥的人才能够解密信息,即使把加密后的信息公开,也不会有安全隐患;其次,暴力破解RSA加密算法也是难以完成的,因为n这个大数是不能被推断出来的。
总之,RSA加密算法具有较高的安全性,可以有效地保护网络安全,是现代信息安全的重要组成部分。
当我们使用网银、购物网站等网络服务时,应该提高对RSA加密算法的安全性的认识,这样才能更好地保护自己的信息安全。
RSA公钥密码体制简介

32
例:
计算: 152013(mod 2539) 13 23 1 22 0 2 1 1101 B
(e3 , e2 , e1, e0 ) (1,1,0,1)
152013 mod2539
(((1520e3 )2 1520e2 )2 1520e1 )2 1520e0 (mod 2539) ((15202 1520)2 15200 )2 1520 (mod 2539)
14
RSA算法论证
假设截获密文C,从中求出明文M。他知道 M≡Cd mod n ,
因为n是公开的,要从C中求出明文M,必须先求 出d,而d是保密的。但他知道,
ed≡1 mod φ(n), e是公开的,要从中求出d,必须先求出φ(n),而 φ(n)是保密的。但他又知道,
φ(n)=(p-1)(q-1),
9
RSA算法论证
于是,M tφ(n) =bq+1,其中b为某整数。 两边同乘M, M tφ(n)+1 =bqM+M 。 因为M=ap,故 M tφ(n)+1 =bqap+M =abn+M 。 取模n得, M φ(n)+1 =M mod n 。
10
RSA算法论证
第二种情况:M=0 当M=0时,直接验证,可知命题成立。
加密过程:c=me mod n 解密过程:m=cd mod n
3
2、工作原理
定义:任给一个正整数m,如果用m去除任意两个整 数a、b所得的余数相同,称a、b对模m同余。记 为: a bmodm,若余数不同,则a、b对模m不同余。 记为: a b modm。
定理: a bmodm ,当且仅当m|(a-b)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究生综合应用报告课程名称《高级计算机网络》学院计算机学院年级计算机科学与技术专业班6班学生姓名唐洪奎学号20141402021开课时间2014 至2015 学年第 1 学期RSA原理学习与PKI简述摘要随着计算机网络的发展,计算机网络所能提供的服务也越来越丰富。
特别是一些和银行、电子商务、军事通信相关的网络服务,对应计算机网络上信息通信安全提出了严苛的要求;密码学也在这种情况下得以发展;RSA作为重要的公钥加密算法,其应用和算法思想应信息安全都有很重要的意义,本文再述了RSA的证明、原理,并简单介绍了PKI系统,并在结尾处进行一定程度的反思。
关键字:RSA算法费马小定理PKIAbstractWith the development of Internet, Internet provides more and more services to public. Some services referring to Bank Transient, E-Commercials needs a safer communication on the Internet. Cryptography was developed in this case. As an important public key encryption algorithm, RSA’s applications and algorithms thinking has a very important significance to Information Security. This paper describes the proof of RSA, principles, and briefly describes the PKI system, and a certain degree of rethinking about RSA and PKI at the end.Keywords: RSA algorithm Fermat's little theorem PKI一、RSA概述RSA公钥加密算法是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。
当时他们三人都在麻省理工学院工作。
RSA就是他们三人姓氏开头字母拼在一起组成的。
RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密码攻击,已被ISO推荐为公钥数据加密标准。
今天只有短的RSA钥匙才可能被强力方式解破。
到2008年为止,世界上还没有任何可靠的攻击RSA算法的方式。
只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被解破的。
但在分布式计算和量子计算机理论日趋成熟的今天,RSA加密安全性受到了挑战。
RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但是想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
本文简单探头了RSA的证明原理,以及用类似RSA这样的算法构建的PKI系统的运作方式。
二、RSA数学基础1.概述RSA的数学基础来自离散数学的分支—数论。
数论,也可以看成是高等代数中的一部分,通过用多项式的方式,定义素数或者是互素关系、整除、辗转相除法、最大公约数、最小公倍数等等,并且在此基础上讨论数论的定理证明。
一般的信息安全数学教材利用整数进行讨论。
RSA 算法基于“大数难分解”,理论基础是模数运算。
在证明,过程用到了素数、互素、同余、同余方程的概念,这些可以再一般的信息安全书籍中找到。
证明中比较重要的是费马小定理、RSA 定理,我们再述其证明过程。
2.费马小定理费马小定理:设任意整数a 与素数p 互素,则 ()11mod p a n -≡证明:由a 与素数p 互素,知p 不是a 的素因数,又因为p 也不是1,2,3,...,1p - 的素因数,所以a 乘以此数列各项所得新数列,2,3,...,(1)a a a p a - 各项都不能被整除从而,2,3,...,(1)a a a p a -中的每一项只能和数列1,2,3,...,1p -中的一项模同余又由于,2,3,...,(1)a a a p a -中的任意两项都不能模p 同余(事实上, 如果存在不同的两ra 与sa (不妨设0r s p <<<)模p 同余, 即()mod sa ra p ≡ , 因a 与p 互素,据同余式的消去律可得()mod s r p ≡ , 与假设r s <矛盾), 所以,2,3,...,(1)a a a p a -中恰有一项和1,2,3,...,1p -中的1 同余, ,2,3,...,(1)a a a p a -中恰有一项和1,2,3,...,1p -中的2 同余,,2,3,...,(1)a a a p a -中恰有一项和1,2,3,...,1p -中的1p - 同余,从而可以建立1p - 个同余式. 将这1p - 个同余式相乘得:(),2,3,...,(1)123...(1)mod a a a p a p p -≡- .因为,123...(1)p ⋅⋅⋅⋅- 与p 互素,有同余的消去律的()11mod p a n -≡.3.RAS 定理定理 设p 、q 是不同的素数,n pq = ,记()(1)(1)n p q ϕ=-- ,如果e 、d 是与()n ϕ 互素的两个正整数,并满足1(mod ())ed n ϕ≡ ,则对于每个整数x ,都有(mo d )ed x x n ≡. 分析 由同余定义的等价表述, 只要证n 是ed x x - 的因数,但n pq = , 且p 、q都是素数,所以,只要证p 、q 分别是ed x x -的因数, 即只要证对于每个, 都有:(mod )ed x x p ≡ 公式一(mod )ed x x q ≡ 公式二证明:公式一只要证0(mod )ed x x p -≡ . 如果p 是x 的因数,则上式显然成立;如果p 不是x 的因数,即p 与x 互素,由题设 1(mod ())ed n ϕ≡,知()n ϕ是1ed -的因素,故存在整数k 使得1()(1)(1)ed n k p q k ϕ-==-- ,从而1(1)(1)ed p q k =+-- ,1(1)(1)1(1)()ed p q k p q k x x x x +----==⋅ ,因 p 与x 互素,由费马小定律()11mod p a n -≡,可得(1)(1)(mod )ed q k x x x p -≡⋅≡ . 同理可证公式二也成立.因此有:(mod )ed x x p ≡ 三、 RSA 算法原理以下公钥体制实施的步骤, 会帮我们理解它的基本原理(1) 取两个大素数p 和q , 求出n pq = 和()(1)(1)n p q ϕ=-- 的值.(2) 选一个与()n ϕ互素的正整数e ,解同余方程1(mod ())ed n ϕ≡,得到解d ,则{,}e d 是可供一个用户使用的密钥对. 其中e 为公钥,d 为私钥.(3) 构造两个定义域为(0,1,2,...,1)n -的函数:()(mod )e E x x n =为加密函数,()(mod )d D x x n =为解密函数.(4) 根据RSA 定理,()(mod )e e d ed DEx Dx x x x n ===≡ 即在()D x 和()E x 的作用下,经加密和解密后,明文信息x 变换为密文y 后又恢复为明文x ,所以()E x 和()D x 是互逆的.(5) 把供某用户使用的私钥d 交该用户, 并将其公钥e 和n 公开,()n ϕ则由密钥制作者秘密保管.(6) 别的用户要与该用户秘密通信时,先将明文信息x 用该用户的公钥e 建立的加密函数()E x 加密, 得密文()(mod )e y E x x n =≡ , 该用户收到密文y 后, 用自己的私钥d 建立解密函数()D x 解密,得明文()(m o d )()d e d e d x D y y n x x x n=≡≡≡≡ .为什么这里构建的加密函数()(mod )e E x x n ≡是单向函数? 因为n 是素因数为p 与q 很大的整数, 所以即使知道n , 也极难求出p 和q , 从而也无法得到()n ϕ. 因此在能查到公钥e 的情况下, 也不能建立同余方程1(mod ())ed n ϕ≡,不能得到私钥d ,故()(mod )e E x x n ≡为单向函数 四、 RSA 公钥体制进行数字签名和身份认证RSA 公钥体制提出后, 人们立刻发现也能用它来解决数字签名和身份认证问题当甲与乙通信时, 把明文信息x 先用自己的解密函数对它签名:()D x y =甲. 如果信息内容无需保密, 甲就可将经他签名的信息y 发给乙. 乙收到信息就从公钥薄上查到甲的公钥得到加密函数作用于y :()(())E y E D x x ==甲甲甲, 得到明文信息x , 从而确认信息x 是来自甲. 如果信息内容需要保密, 甲在签名后又在公钥薄上查到乙的公钥得到加密函数, 用它对已经签名的信息y 加密:()E y z =乙, 然后把z 发给乙. 乙收到z 后, 先用自己的解密函数作用于z :()()D z D E y y ==乙乙乙, 再从公钥薄上查到甲的公钥得到加密函数作用于y ,==E y E D x x()(())甲甲甲, 得到并确认来自甲的明文信息x.五、PKI体系及运行原理简单概述1.基本概述PKI是“Public Key Infrastructure”的缩写,意为“公钥基础设施”。
简单地说,PKI技术就是利用公钥理论和技术建立的提供信息安全服务的基础设施。
公钥体制是目前应用最广泛的一种加密体制,在这一体制中,加密密钥与解密密钥各不相同,发送信息的人利用接收者的公钥发送加密信息,接收者再利用自己专有的私钥进行解密。
这种方式既保证了信息的机密性,又能保证信息具有不可抵赖性。
目前,公钥体制广泛地用于CA认证、数字签名和密钥交换等领域。
PKI似乎可以解决绝大多数网络安全问题,并初步形成了一套完整的解决方案,它是基于公开密钥理论和技术建立起来的安全体系,是提供信息安全服务的具有普适性的安全基础设施。
该体系在统一的安全认证标准和规范基础上提供在线身份认证,是CA认证、数字证书、数字签名以及相关安全应用组件模块的集合。
作为一种技术体系,PKI可以作为支持认证、完整性、机密性和不可否认性的技术基础,从技术上解决网上身份认证、信息完整性和抗抵赖等安全问题,为网络应用提供可靠的安全保障。
