中考基础训练几何填空
初中数学几何填空题练习
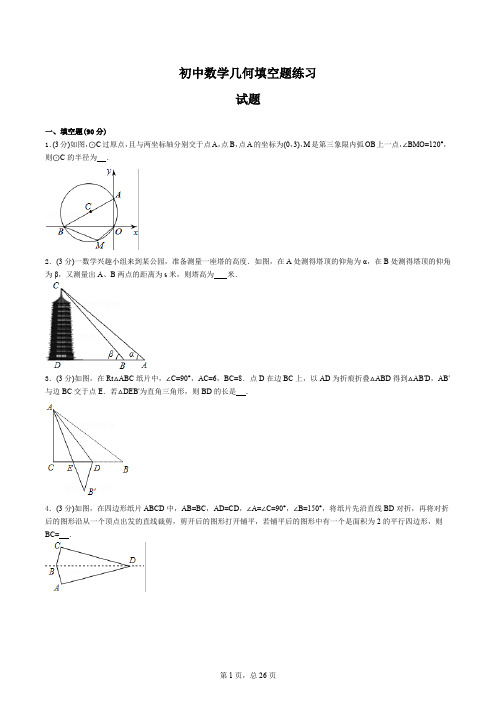
初中数学几何填空题练习试题一、填空题(90分)1.(3分)如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径为.2.(3分)一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为米.3.(3分)如图,在Rt△ABC纸片中,∠C=90°,AC=6,BC=8.点D在边BC上,以AD为折痕折叠△ABD得到△AB'D,AB'与边BC交于点E.若△DEB'为直角三角形,则BD的长是.4.(3分)如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°,将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为2的平行四边形,则BC=.5.(3分)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是.x上,6.(3分)如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-√33x上,依次进行下去…若点B的坐标再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-√33是(0,1),则点O12的纵坐标为.,M,N分别在边AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段7.(3分)如图,在菱形ABCD中,tan A=43EF经过顶点D,当EF⊥AD时,BN的值为.CN8.(3分)如图,已知△ABC中,AB=AC=√3cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C 运动,点P、Q分别从点C、B同时出发,速度均为1 cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=s 时,△PAQ为直角三角形.9.(3分)长为20,宽为a的矩形纸片(10<a<20),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的矩形为正方形,则操作停止.当n=3时,a的值为.10.(3分)如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF 的中点,连接GH,则GH的长为.S菱形ABCD,则PC+PD的最小值11.(3分)如图,在菱形ABCD中,AB=6,∠A=135°,点P是菱形内部一点,且满足S△PCD=16是.12.(3分)如图,点A(0,4),B(4,0),C(10,0),点P在直线AB上,且∠OPC=90°,则点P的坐标为.13.(3分)如图,在平行四边形ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是.14.(3分)已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为√2的等腰直角三角形DEF的费马点,则PD+PE+PF=.15.(3分)已知△ABC中,BC=6,AB、AC的垂直平分线分别交边BC于点M、N,若MN=2,则△AMN的周长是.16.(3分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AB=OB,点E、点F分别是OA、OD的中点,连接EF,∠CEF=45°,EM⊥BC于点M,EM交BD于点N,FN=√10,则线段BC的长为.17.(3分)如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是.(1)EF=√2OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=√2OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=3;(5)OG•BD=AE2+CF2.418.(3分)如图所示的网格是正方形网格,∠BAC∠DAE.(填“>”,“=”或“<”)19.(3分)如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是.20.(3分)如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=5,ON=12,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为.21.(3分)如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=.22.(3分)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为4,则线段CF的最小值是.23.(3分)如图,在平面直角坐标系中,点A,B分别在y轴和x轴上,∠ABO=60°,在坐标轴上找一点P,使得△PAB是等腰三角形,则符合条件的点P共有个.24.(3分)如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形AB4C4C3的面积为.25.(3分)如图,菱形ABCD的边长为3,∠BAD=60°,点E、F在对角线AC上(点E在点F的左侧),且EF=1,则DE+BF 最小值为.26.(3分)如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为.27.(3分)如图,CA⊥AB,垂足为A,AB=24,AC=12,射线BM⊥AB,垂足为B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过秒时,△DEB与△BCA 全等.28.(3分)如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③PB=2PH;④∠APH=∠BPC,其中正确的结论是.29.(3分)如图,在平面直角坐标系中,已知点A(0,1),B(0,1+m),C(0,1-m)(m>0),点P在以D(-4,-2)为圆心,√2为半径的圆上运动,且始终满足∠BPC=90°,则m的取值范围是.30.(3分)如图,正△ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,△ABO沿x轴正方向作无滑动的翻滚,经一次翻滚后得到△A1B1O,则翻滚3次后点B的对应点的坐标是,翻滚2017次后AB中点M经过的路径长为.初中数学几何填空题练习试卷答案一、填空题1. 【答案】3【解析】∵点A 的坐标为(0,3),∴OA=3,∵四边形ABMO 是圆内接四边形,∴∠BMO+∠A=180°,又∠BMO=120°,∴∠A=60°,则∠ABO=30°,∴AB=2OA=6,则⊙C 的半径为3.故答案为:3.2.【答案】tanα⋅tanβ⋅s tanβ−tanα 【解析】在Rt △BCD 中,∵tan ∠CBD=CD BD ,∴BD=CD tanβ,在Rt △ACD 中,∵tan ∠A=CD AD =CD BD+AB ,∴tanα=CDCD tanβ+s ,解得:CD=tanα⋅tanβ⋅stanβ−tanα.故答案为:tanα⋅tanβ⋅s tanβ−tanα.3. 【答案】2或5【解析】∵Rt △ABC 纸片中,∠C=90°,AC=6,BC=8,∴AB=10.∵以AD 为折痕△ABD 折叠得到△AB′D ,∴BD=DB′,AB′=AB=10.如图1所示:当∠B′DE=90°时,过点B′作B′F ⊥AF ,垂足为F ,设BD=DB′=x ,则AF=6+x ,FB′=8-x ,在Rt △AFB′中,由勾股定理得:AB′2=AF 2+FB′2,即(6+x)2+(8-x)2=102,解得:x1=2,x2=0(舍去),∴BD=2;如图2所示:当∠B′ED=90°时,C与点E重合,∵AB′=10,AC=6,∴B′E=4,设BD=DB′=x,则CD=8-x,在Rt△′BDE中,DB′2=DE2+B′E2,即x2=(8-x)2+42,解得:x=5,∴BD=5.综上所述,BD的长为2或5.故答案为:2或5.4.【答案】2或1【解析】第一种情况:如图1所示:作AE∥BC,延长AE交CD于点N,过点B作BT⊥EC于点T,当四边形ABCE为平行四边形,∵AB=BC,∴四边形ABCE是菱形;∵∠A=∠C=90°,∠B=150°,BC∥AN,∴∠ADC=30°,∠BAN=∠BCE=30°,则∠NAD=60°,∴∠AND=90°.∵四边形ABCE面积为2,∴设BT=x,则BC=EC=2x,故2x·x=2,解得:x=1或-1(负数舍去),故BC=2.第二种情况:如图2,当四边形BEDF是平行四边形,∵BE=BF,∴平行四边形BEDF是菱形;∵∠A=∠C=90°,∠B=150°,∴∠ADB=∠BDC=15°,∵BE=DE,∴∠AEB=30°.∴设AB=y,则BE=2y,∵四边形BEDF面积为2,∴AB×DE=2y2=2,解得:y=1,故BC=1.综上所述:BC=2或1.故答案为:2或1.5.【答案】3【解析】如图连接PC.在Rt△ABC中,∵∠A=30°,BC=2,∴AB=4,根据旋转的性质可知,A′B′=AB=4,∵A′P=PB′,即P为A'B'的中点,∴PC=1A′B′=2,2∵CM=BM=1,又∵PM≤PC+CM,即PM≤3,∴PM的最大值为3(此时P、C、M共线).故答案为:3.6.【答案】9+3√3x时,【解析】观察图象可知,O12在直线y=-√33OO12=6·OO2=6(1+√3+2)=18+6√3,∴O12的横坐标=-(18+6√3)·cos30°=-9-9√3,OO12=9+3√3.O12的纵坐标=12故答案为:9+3√3.7.【答案】27【解析】延长NF与DC交于点H,∵∠ADF=90°,∴∠A+∠FDH=90°,∵∠DFN+∠DFH=180°,∠A+∠B=180°,∠B=∠DFN,∴∠A=∠DFH,∴∠FDH+∠DFH=90°,∴NH ⊥DC ,设DM=4k ,DE=3k ,EM=5k ,∴AD=9k=DC ,DF=6k ,∵tan A=tan ∠DFH=43,则sin ∠DFH=45,∴DH=45DF=245k ,∴CH=9k -245k=215k ,∵cos C=cos A=CH NC =35,∴CN=53CH=7k ,∴BN=2k ,∴BN CN =27. 故答案为:27.8.【答案】1或2或(8√3-12)或(6√3-9)【解析】①当PA ⊥AB 时,△PAQ 是直角三角形.∵∠B=30°,AB=√3,∴PA=1,PB=2,∵BC=3,∴PC=1,∴t=1时,△PAQ 是直角三角形.②当PQ ⊥AB 时,△PAQ 是直角三角形.此时BQ=√32PB , ∴t=√32(3-t),解得t=6√3-9. ③当点Q 在AC 上时,PQ ⊥AC 时,△PAQ 是直角三角形,则CQ=√32PQ , ∴√32t=2√3−t ,解得t=8√3-12. ④当点Q 在AC 上时,PA ⊥AC 时,△PAQ 是直角三角形,此时PC=2,t=2,∴t=2时,△PAQ 是直角三角形.综上所述,t=1或2或(8√3-12)或(6√3-9)时,△PAQ 是直角三角形.故答案为:1或2或(8√3-12)或(6√3-9).9. 【答案】12或15【解析】由题意,可知当10<a<20时,第一次操作后剩下的矩形的长为a ,宽为20-a ,所以第二次操作时剪下正方形的边长为20-a ,第二次操作以后剩下的矩形的两边分别为20-a ,2a -20. 此时,分两种情况:①如果20-a >2a -20,即a<403,那么第三次操作时正方形的边长为2a -20,则2a -20=(20-a)-(2a -20),解得a=12;②如果20-a<2a -20,即a >403,那么第三次操作时正方形的边长为20-a ,则20-a=(2a -20)-(20-a),解得a=15.∴当n=3时,a 的值为12或15.故答案为:12或15.10.【答案】√342 【解析】∵四边形ABCD 为正方形,∴∠BAE=∠D=90°,AB=AD ,在△ABE 和△DAF 中,∵{AB =AD ∠BAE =∠D AE =DF,∴△ABE ≌△DAF(SAS),∴∠ABE=∠DAF ,∵∠ABE+∠BEA=90°,∴∠DAF+∠BEA=90°,∴∠AGE=∠BGF=90°,∵点H 为BF 的中点,∴GH=12BF , ∵BC=5,CF=CD -DF=5-2=3,∴BF=√BC 2+CF 2=√34,∴GH=12BF=√342. 故答案为:√342. 11.【答案】2√11【解析】如图在BC 上取一点E ,使得EC=13BC=2,作EF ∥AB ,作点C 关于EF 的对称点C′,CC′交EF 于G ,连接DC′交EF 于P ,连接PC ,此时此时S △PCD =16S 菱形ABCD ,PD+PC 的值最小.PC+PD 的最小值=PD+PC′=DC′,∵四边形ABCD 是菱形,∠A=135°,∴∠B=∠CEG=45°,∠BCD=135°∵∠CGE=90°,CE=2,∴CG=GE=GC′,∴∠GCE=45°,∠DCC′=90°,∴DC '=√62+(2√2)2=2√11. 故答案为:2√11.12. 【答案】(1,3)或(8,-4)【解析】∵A(0,4),B(4,0),∴直线AB 为y=-x+4,设点P 的坐标为(a ,-a+4),过点P 作PH ⊥OC 于点H ,∵∠OPC=90°,∴△PHO∽△CHP,∴PH2=OH·CH.∵(-a+4)2=a(10-a),∴a2-8a+16=10a-a2,∴2a2-18a+16=0,解得a1=1,a2=8.∴P1(1,3),P2(8,-4).故答案为:(1,3)或(8,-4).13.【答案】66°【解析】如图,取DE的中点Q,连接AQ,∵平行四边形ABCD,∴AD∥BC,∵AF⊥BC,∴FA⊥AD,∴DE=2AQ=2DQ,∵DE=2AB,∴AQ=AB,∴∠AQB=∠ABD,∵AQ=DQ,∴∠QAD=∠ADQ,∴∠ABD=∠AQB=∠QAD+∠ADQ=2∠ADQ,∵AF⊥BC,∠ABC=∠ADC=72°,∴∠BAF=90°-72°=18°,∵∠ABD+∠ADB+∠BAD=180°,∴3∠ADB=180°-90°-18°=72°,∴∠ADB=24°,∵∠FAD=90°,∴∠AED=180°-∠FAD-∠ADE=66°.故答案为:66°.14.【答案】√3+1 【解析】如图:等腰Rt △DEF 中,DE=DF=√2,过点D 作DM ⊥EF 于点M ,过E 、F 分别作∠MEP=∠MFP=30°,则EM=DM=1,故cos 30°=EM EP ,解得:PE=PF=2√3=2√33,则PM=√33, 故DP=1-√33, 则PD+PE+PF=2×2√33+1-√33=√3+1. 故答案为:√3+1.15. 【答案】6或10【解析】如图1,∵直线MP 为线段AB 的垂直平分线,∴MA=MB ;又直线NQ 为线段AC 的垂直平分线,∴NA=NC ;∴△AMN 的周长l=AM+MN+AN=BM+MN+NC=BC .又BC=6,则△AMN 的周长为6.如图2,△AMN 的周长l=AM+MN+AN=BM+MN+NC=BC+2MN ,又BC=6,则△AMN 的周长为10.故答案为:6或10.16.【答案】4√2【解析】设EF=x,∵点E、点F分别是OA、OD的中点,∴EF是△OAD的中位线,∴AD=2x,AD∥EF,∴∠CAD=∠CEF=45°,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2x,∴∠ACB=∠CAD=45°,∵EM⊥BC,∴∠EMC=90°,∴△EMC是等腰直角三角形,∴∠CEM=45°,连接BE,∵AB=OB,AE=OE∴BE⊥AO∴∠BEM=45°,∴BM=EM=MC=x,∴BM=FE,易得△ENF≌△MNB,∴EN=MN=1x,BN=FN=√10,2Rt△BNM中,由勾股定理得:BN2=BM2+MN2,x)2,∴(√10)2=x2+(12x=2√2或-2√2(舍),∴BC=2x=4√2.故答案为:4√2.17.【答案】(1),(2),(3),(5)【解析】(1)∵四边形ABCD是正方形,∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,∴∠BOF+∠COF=90°,∵∠EOF=90°,∴∠BOF+∠COE=90°,∴∠BOE=∠COF,在△BOE和△COF中,,∴△BOE≌△COF(ASA),∴OE=OF,BE=CF,∴EF=√2OE,故正确;(2)∵S 四边形OEBF =S △BOE +S △BOE =S △BOE +S △COF =S △BOC =14S 正方形ABCD , ∴S 四边形OEBF :S 正方形ABCD =1:4,故正确;(3)∴BE+BF=BF+CF=BC=√2OA ,故正确;(4)过点O 作OH ⊥BC ,∵BC=1,∴OH=12BC=12,设AE=x ,则BE=CF=1-x ,BF=x ,∴S △BEF +S △COF =12BE•BF+12CF•OH=12x(1-x)+12(1-x)×12=-12(x -14)2+, ∵a=-12<0,∴当x=14时,S △BEF +S △COF 最大;即在旋转过程中,当△BEF 与△COF 的面积之和最大时,AE=14,故错误; (5)∵∠EOG=∠BOE ,∠OEG=∠OBE=45°,∴△OEG ∽△OBE ,∴OE :OB=OG :OE ,∴OG•OB=OE 2,∵OB=12BD ,OE=EF ,∴OG•BD=EF 2,∵在△BEF 中,EF 2=BE 2+BF 2,∴EF 2=AE 2+CF 2,∴OG•BD=AE 2+CF 2,故正确.故答案为:(1),(2),(3),(5).18. 【答案】>【解析】连接NH ,BC ,过N 作NP ⊥AD 于P ,S △ANH =2×2-12×1×2×2−12×1×1=12AH·NP ,求得PN=3√5,Rt△ANP中,sin∠NAP=PNAN =3√5√5=35=0.6,Rt△ABC中,sin∠BAC=BCAB =22√2=√22>0.6,∵正弦值随着角度的增大而增大,∴∠BAC>∠DAE.故答案为:>.19.【答案】5√2+√102【解析】解法一:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE,∵DC∥AB,∴PQ⊥AB.∵四边形ABCD是正方形,∴∠ACD=45°,∴△PEC是等腰直角三角形,∴PE=PC.设PC=x,则PE=x,PD=4-x,EQ=4-x,∴PD=EQ,∵∠DPE=∠EQF=90°,∠PED=∠EFQ,∴△DPE≌△EQF(AAS),∴DE=EF.∵DE⊥EF,∴△DEF是等腰直角三角形,易证明△DEC≌△BEC,∴DE=BE,∴EF=BE.∵EQ⊥FB,∴FQ=BQ=12BF,∵AB=4,F是AB的中点,∴BF=2,∴FQ=BQ=PE=1,∴CE=√2,PD=4-1=3,Rt△DAF中,DF=√42+22=2√5,DE=EF=√10.如图2,∵DC ∥AB ,∴△DGC ∽△FGA ,∴CG AG =DC AF =DG FG =42=2,∴CG=2AG ,DG=2FG ,∴FG=13×2√5=2√53.∵AC=√42+42=4√2,∴CG=23×4√2=8√23,∴EG=8√23−√2=5√23.连接GM 、GN ,交EF 于H ,∵∠GFE=45°,∴△GHF 是等腰直角三角形,∴GH=FH=2√53√2=√103, ∴EH=EF -FH=√10−√103=2√103, 由折叠得:GM ⊥EF ,MH=GH=√103,∴∠EHM=∠DEF=90°,∴DE ∥HM ,∴△DEN ∽△MNH ,∴DE MH =ENNH ,∴√10√103=ENNH =3,∴EN=3NH ,∵EN+NH=EH=2√103,∴EN=√102,∴NH=EH -EN=2√103−√102=√106.Rt△GNH中,GN=√GH2+NH2=√(√103)2+(√106)2=5√26,由折叠得:MN=GN,EM=EG,∴△EMN的周长=EN+MN+EM=√102+5√26+5√23=5√2+√102.解法二:如图3,过G作GK⊥AD于K,作GR⊥AB于R,∵AC平分∠DAB,∴GK=GR,∴S△ADG S△AGF =12AD⋅KG12AF⋅GR=ADAF=42=2,∵S△ADG S△AGF =12DG⋅ℎ12GF⋅ℎ=2,∴DGGF=2,同理,S△DNFS△MNF=DFFM=DNMN=3,其它解法同解法一,可得:∴△EMN的周长=EN+MN+EM=√102+5√26+5√23=5√2+√102.解法三:如图4,过E作EP⊥AP,EQ⊥AD,∵AC是对角线,∴EP=EQ,易证△DQE和△FPE全等,∴DE=EF,DQ=FP,且AP=EP,设EP=x,则DQ=4-x=FP=x-2,解得x=3,所以PF=1,∴AE=√32+32=3√2,∵DC ∥AB ,∴△DGC ∽△FGA ,∴同解法一得:CG=23×4√2=8√23, ∴EG=8√23−√2=5√23, AG=13AC=4√23, 过G 作GH ⊥AB ,过M 作MK ⊥AB ,过M 作ML ⊥AD ,则易证△GHF ≌△FKM 全等,∴GH=FK=43,HF=MK=23,∵ML=AK=AF+FK=2+43=103,DL=AD -MK=4-23=103,即DL=LM ,∴∠LDM=45°∴DM 在正方形对角线DB 上,过N 作NI ⊥AB ,则NI=IB ,设NI=y ,∵NI ∥EP∴NI EP =FI FP∴y 3=2−y1,解得y=1.5,所以FI=2-y=0.5,∴I 为FP 的中点,∴N 是EF 的中点,∴EN=0.5EF=√102, ∵△BIN 是等腰直角三角形,且BI=NI=1.5,∴BN=32√2,BK=AB -AK=4-103=23,BM=23√2,MN=BN -BM=32√2−23√2=56√2,∴△EMN 的周长=EN+MN+EM=√102+5√26+5√23=5√2+√102. 故答案为:5√2+√102. 20. 【答案】13【解析】作M 关于OB 的对称点M′,作N 关于OA 的对称点N′,连接M′N′,与OB 交点P ,OA 交点Q ,即为MP+PQ+QN的最小值,根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,OM′=OM=5,ON′=ON=12, ∴△ONN′为等边三角形,△OMM′为等边三角形,∴∠N′OM′=90°,∴在Rt△M′ON′中,M′N′=√OM'2+ON'2=13.故答案为:13.21.【答案】22016【解析】∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°.∵∠MON=30°,∴∠1=180°-120°-30°=30°.又∵∠3=60°,∴∠5=180°-60°-30°=90°.∵∠MON=∠1=30°,∴OA1=A1B1=1,∴A2B1=1.∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°.∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴a2=2a1,a3=4a1=4,a4=8a1=8,a5=16a1,以此类推:a2017=22016.故答案为:22016.22.【答案】2√5-2【解析】在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,{AD=BCAM=BN,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2.在△DCE和△BCE中,{BC=CD∠DCE=∠BCECE=CE,∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3.∵∠ADF+∠3=∠ADC=90°,∴∠1+∠ADF=90°,∴∠AFD=180°-90°=90°.取AD的中点O,连接OF、OC,则OF=DO=12AD=2,在Rt△ODC中,OC=√DO2+DC2=√22+42=2√5.根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC-OF=2√5-2.故答案为:2√5-2.23.【答案】6【解析】①当AB=AP时,在y轴上有2点满足条件的点P,在x轴上有1点满足条件的点P;②当AB=BP时,在y轴上有1点满足条件的点P,在x轴上有2点满足条件的点P,其中有1点与AB=AP时的x轴正半轴的点P重合;③当AP=BP时,在x轴、y轴上各有一点满足条件的点P,其中有1点与AB=AP时的x轴正半轴的点P重合.综上所述:符合条件的点P共有6个.故答案为:6.24.【答案】5427【解析】∵四边形ABCD是矩形,∴AD⊥DC,∴AC=√AD2+CD2=√22+12=√5,∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,∴矩形AB1C1C的边长和矩形ABCD的边长的比为√5:2∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,∵矩形ABCD的面积=2×1=2,∴矩形AB1C1C的面积=52,依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4,∴矩形AB2C2C1的面积=5223,∴矩形AB3C3C2的面积=5325,按此规律第4个矩形的面积为5427.故答案为:5427.25.【答案】√10【解析】如图,作DM∥AC,使得DM=EF=1,连接BM交AC于F,∵DM=EF,DM∥EF,∴四边形DEFM是平行四边形,∴DE=FM,∴DE+BF=FM+FB=BM,根据两点之间线段最短可知,此时DE+FB最短,∵四边形ABCD是菱形,AB=3,∠BAD=60°,∴AD=AB,∴△ABD是等边三角形,∴BD=AB=3,在Rt△BDM中,BM=√12+32=√10,∴DE+BF的最小值为√10.故答案为:√10.26.【答案】4√3或4【解析】当△A′EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图1,∵△A′BC与△ABC关于BC所在直线对称,∴A'C=AC=4,∠ACB=∠A'CB,∵点D,E分别为AC,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE=∠A'EF,∴AC∥A'E,∴∠ACB=∠A'EC,∴∠A'CB=∠A'EC,∴A'C=A'E=4,∵在Rt△A'CB中,E是斜边BC的中点,∴BC=2A'E=8,由勾股定理得:AB2=BC2-AC2,∴AB=√82−42=4√3;②当∠A'FE=90°时,如图2,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A′BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC是等腰直角三角形,∴AB=AC=4.综上所述,AB的长为4√3或4.故答案为:4√3或4.27.【答案】0,4,12,16【解析】设点E经过t秒时,△DEB≌△BCA,此时AE=3t.分情况讨论:(1)当点E在点B的左侧时,BE=24-3t=12,∴t=4.(2)当点E在点B的右侧时,①BE=AC时,3t=24+12,∴t=12;②BE=AB时,3t=24+24,∴t=16.(3)当点E与A重合时,AE=0,t=0.综上所述,故答案为:0,4,12,16.28.【答案】①②③④【解析】如图作,PM⊥BC于M,PN⊥BA于N,∵∠PAH=∠PAN,PN⊥AD,PH⊥AC,∴PN=PH ,同理PM=PH ,∴PN=PM ,∴PB 平分∠ABC ,∴∠ABP=12∠ABC=30°,故①正确; ∵在Rt △PAH 和Rt △PAN 中,{PA =PA PN =PH , ∴△PAN ≌△PAH ,同理可证,△PCM ≌△PCH ,∴∠APN=∠APH ,∠CPM=∠CPH ,∵∠MPN=180°-∠ABC=120°,∴∠APC=12∠MPN=60°,故②正确;在Rt △PBN 中,∵∠PBN=30°, ∴PB=2PN=2PH ,故③正确;∵∠BPN=∠CPA=60°,∴∠CPB=∠APN=∠APH ,故④正确.故答案为:①②③④.29.【答案】5-√2≤m≤5+√2【解析】∵A(0,1),B(0,1+m),C(0,1-m)(m>0), ∴AB=AC=m ,∵∠BPC=90°,∴PA=AB=AC ,∵D(-4,-2),A(0,1),∴AD=√32+42=5,∵点P 在⊙D 上运动,∴PA 的最小值为5-√2,PA 的最大值为5+√2, ∴满足条件的m 的取值范围为:5-√2≤m≤5+√2. 故答案为:5-√2≤m≤5+√2.30.【答案】(5,√3) (1346√33+896)π【解析】如图作B 3E ⊥x 轴于E ,易知OE=5,B 3E=√3,∴B 3(5,√3);观察图象可知三次一个循环,一个循环点M 的运动路径为120⋅π⋅√3180+120π⋅1180+120π⋅1180=(2√3+43)π, ∵2017÷3=672…1,∴翻滚2017次后AB 中点M 经过的路径长为672·(2√3+43)π+2√33π=(1346√33+896)π.+896)π.故答案为:(5,√3);(1346√33。
初中数学几何选择填空难题及答案

《几何》选择填空姓名:一、【勾股定理】1、如图,直角梯形ABCD 中,AD ∥BC ,∠ADC =∠BAC =90°,AB =2,CD =3,E 是BC 的中点,则DE 的长为7 .【解】等量迁移。
直角三角形中线性质,勾股定理2、如图,Rt △ABC 中,∠ABC =90°,DE 垂直平分AC ,垂足为O ,AD ∥BC ,且AB =3,BC =4,则AD 的长为825.【解】AE=CE=AD 设AE= x , 222AE BE AB =+ ∴222)4(3x x =-+ ∴825=x 3、两张大小相同的纸片,每张都分成7个大小相同的矩形,如图放置,重合的顶点记作A ,顶点C 在另一张纸的分隔线上,若BC =28,则AB 的长是_______1414_____.4、如图,在正方形ABCD 中,对角线AC 与BD 相交于点O ,E 为BC 上一点,CE =5,F 为DE 的中点.若E DCBAAB C△CEF的周长为18,则OF的长为(D)A.3 B.4 C.D.【解】直角三角形的性质,勾股定理,三角形中位线定理。
∵CE=5,△CEF的周长为18,∴CF+EF=18﹣5=13.∵F为DE的中点,∴DF=EF.∵∠BCD=90°,∴CF=DE,∴EF=CF=DE=6.5,∴DE=2EF=13,∴CD=.∵四边形ABCD是正方形,∴BC=CD=12,O为BD的中点,∴OF是△BDE的中位线,∴OF=(BC﹣CE)=(12﹣5)=.5、如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,26CF,M为CF的中点,则AM的长为2【解】连接AC,∵四边形ABCD是正方形,∴∠BAC=45°.∵EF⊥AE,EF=AE,∴△AEF是等腰直角三角形,∴∠EAF=45°,∴∠CAF=90°.∵AB=BC=2,∴AC==2.∵AE=EF=AB+BE=2+1=3,∴AF==3,∴CF===.∵M为CF的中点,∴AM=CF=.6、如图,在矩形ABCD 中,AB =3,BC =4,点E 是AD 上一个动点,把△BAE 沿BE 向矩形内部折叠,当点A 的对应点A 1恰落在∠BCD 的平分线上时,CA 1的长为 122±【解】设FC =x , 则x FC F A ==1, x CA 21=,在直角BF A 1∆中:22121BF F A B A +=∴ 222)4(3x x +-= ∴ 222±=x ∴ 12221±==x CA二、【对折问题】1、如图,在R t △ABC 中,∠ACB =90°,∠A <∠B ,CM 是斜边AB 的中线,将△ACM 沿直线CM 折叠,点A 落在点D 处,如果CD 恰好与AB 垂直,则∠A = 30 °【解】直角三角形中线性质。
历年初三数学中考基础训练几何填空

几何填空1、填空:(1)sin45°= ,cos60°= (3)tan30°= ,cot45°=2、在ΔABC 中,∠C=90O ,sinA=53,那么cosB=3、在△ABC 中,∠C=900,BC=3, AB=5,则cos B =____________ 4、如果某人沿着4:3 i 的斜坡前进20m ,那么他所在的位置比原来的位置升高 m 。
5、如果一传送带和地面所成斜坡的坡度为1︰2,它把物体从地面送到离地面9米的地方,那么物体所经过的路程为_____米6、在坡度为i =1∶7的斜坡上前进10米,则高度升高了 米7、在相同时刻的物高与影长成比例,如果一古塔在地面上的影长为50米,同时高为1.5米的测竿的影长为2.5米,那么古塔的高为___米。
8、在山坡上种树,要求株距是3米,测得斜坡的倾斜角是30º 求相邻两树的坡面距离是______米9、⊙O 的半径为10,弦AB 长为6,则点O 到的AB 距离为______10、平面内到定点A 的距离为4的点的轨迹是 11、如图,水平放着的圆柱形的排水管,它的截面看作是圆,已知截面圆的直径为650mm ,水面的宽AB = 600mm ,则截面上有水的最大深度是______mm 。
12、如图,半圆的直径=8,正方形的顶点在半圆上一边在上,则这个正方形的面积等于( )A 、16B 、15.4C 、12.8D 、12AD13、如图,四边形ABCD 内接于⊙O ,∠BOD=160°,则 ∠ BAD 的度数是_________,∠BCD 的度数是_______;14、四边形ABCD 内接于⊙O ,∠BCD=120°,则∠BOD = 度。
15、如图,⊙O 中,∠AOB =88°,那么∠ACB =______.16、圆内接四边形ABCD 中,∠A ∶∠B ∶∠C=4∶3∶5,那么∠D=17、两圆的圆心距为6,它们的半径是一元二次方程x 2-7x+4=0的两个根,则两圆的位置关系是 ,此时两圆的外公切线长为 。
几何基础训练题

几何基础训练题一、选择题(每题3分,共30分)1. 一个三角形的内角和是多少度?A. 90度B. 180度C. 360度D. 720度答案:B。
解析:三角形内角和定理表明三角形的内角和为180度。
2. 以下哪种图形不是四边形?A. 正方形B. 三角形C. 长方形D. 平行四边形答案:B。
解析:三角形有三条边,不属于四边形,四边形是有四条边的封闭图形。
3. 直角三角形的一个锐角是30度,另一个锐角是多少度?A. 30度B. 45度C. 60度D. 90度答案:C。
解析:直角三角形两锐角和为90度,一个锐角是30度,另一个就是90 - 30 = 60度。
4. 圆的直径是半径的几倍?A. 1倍B. 2倍C. 3倍D. 4倍答案:B。
解析:根据圆的定义,直径等于半径的2倍。
5. 等腰三角形的两条边叫做?A. 长腰和短腰B. 上腰和下腰C. 腰D. 斜边答案:C。
解析:等腰三角形相等的两条边叫做腰。
6. 正方体有几个面?A. 4个B. 5个C. 6个D. 8个答案:C。
解析:正方体是一种特殊的六面体,有六个面。
7. 梯形的一组对边是什么关系?A. 平行B. 垂直C. 相等D. 既不平行也不垂直答案:A。
解析:梯形是只有一组对边平行的四边形。
8. 一个多边形的外角和是多少度?A. 180度B. 360度C. 540度D. 720度答案:B。
解析:多边形的外角和恒为360度。
9. 等边三角形的每个内角是多少度?A. 30度B. 45度C. 60度D. 90度答案:C。
解析:因为等边三角形三个角相等,三角形内角和180度,所以每个内角是180÷3 = 60度。
10. 长方形的面积公式是?A. 长+宽B. 长×宽C. (长+宽)×2D. 长÷宽答案:B。
解析:长方形面积等于长乘以宽。
二、填空题(每题3分,共30分)1. 三角形按角分类可分为锐角三角形、直角三角形和(钝角三角形)。
中考复习简单几何练习题及答案

中考复习简单几何练习题(试卷满分 120 分,考试时间90 分钟)董义刚134********一、选择题(每小题3分)1.已知∠AOB=30°,自∠AOB的顶点O引射线OC,若∠AOC : ∠AOB=4 : 3 ,则∠BOC等于( ).A.10°B.40° C.70° D.10°或70°2.用一副三角板可以作出大于0°而小于180°的角的个数()。
A. 5个 B.10个 C. 11个D.以上都不对3.如果两条平行线被第三条直线所截得的8个角中,有一个角的度数已知, 则()。
A.只能求出其余3个角的度数 B.能求出其余5个角的度数C.只能求出其余6个角的度数 D.能求出其余7个角的度数4.若两条平行线被第三条直线所截,则下列说法错误的是( )。
A.一对同位角的平分线互相平行B.一对内错角的平分线互相平行C.一对同旁内角的平分线互相垂直D.一对同旁内角的平分线互相平行5.下列说法,其中正确的是( )。
A.两条直线被第三条直线所截,内错角相等;B.不相交的两条直线就是平行线;C.点到直线的垂线段,叫做点到直线的距离;D.同位角相等,两直线平行。
6.下列关于对顶角的说法:(1)相等的角是对顶角(2)对顶角相等(3)不相等的角不是对顶角(4)不是对顶角不相等其中正确的有()。
A.1个 B.2个 C.3个 D.4个7.如果∠α与∠β是邻补角,且∠α> ∠β,那么∠β的余角是()。
A .12 (∠α±∠β) B . 错误!∠α C . 错误!(∠α-∠β) D.不能确定8.下列说法①平角是一条直线;②点到直线的距离指的是直线外一点到这条直线的垂线段; ③两个互补的角一定是邻补角;④同位角,内错角一定相等,同旁内角一定互补 ,其中正确的个数有( )A 、0个B 、1个C 、2个D 、3个9.在ABC △中,AB=AC ,AB 的垂直平分线与AC 所在的直线相交所得的锐角为50°,则∠B 等于_____________度.A .14B .13C .612D .5611.在同一平面内,下列说法:①过两点有且只有一条直线;②两条不相同的直线有且只有一个公共点;③经过直线外一点有且只有一条直线与已知直线垂直;④经过直线外一点有且只有一条直线与已知直线平行,其中正确的个数为( )A .1个B .2个C .3个D .4个12。
2024年数学九年级上册几何基础练习题(含答案)

2024年数学九年级上册几何基础练习题(含答案)试题部分一、选择题(每题2分,共20分)1. 在直角三角形ABC中,∠C是直角,AC=3cm,BC=4cm,求AB的长度。
A. 5cmB. 6cmC. 7cmD. 8cm2. 在等腰三角形ABC中,AB=AC,∠BAC=60°,求∠ABC的度数。
A. 60°B. 120°C. 30°D. 45°3. 在平行四边形ABCD中,AB=CD,AD=BC,∠A=90°,求∠C的度数。
A. 90°B. 45°C. 135°D. 180°4. 在梯形ABCD中,AB//CD,AD=BC,∠ABC=60°,求∠ADC的度数。
A. 60°B. 120°C. 90°D. 45°5. 在正方形ABCD中,对角线AC和BD相交于点O,求∠AOD的度数。
A. 45°B. 90°C. 135°D. 180°6. 在圆O中,半径OA=5cm,弦AB=8cm,求∠AOB的度数。
A. 30°B. 60°C. 90°D. 120°7. 在三角形ABC中,∠BAC=90°,BC=10cm,AC=6cm,求AB的长度。
A. 8cmB. 12cmC. 16cmD. 20cm8. 在等边三角形ABC中,AB=AC=BC,求∠ABC的度数。
A. 60°B. 120°C. 30°D. 45°9. 在矩形ABCD中,AB=CD,AD=BC,∠ABC=90°,求∠ADC的度数。
A. 90°B. 45°C. 135°D. 180°10. 在菱形ABCD中,AB=BC=CD=DA,∠ABC=60°,求∠ADC的度数。
中考数学几何选择填空

中考数学几何选择填空压轴题优选一.选择题1.如图,点 O 为正方形 ABCD 的中心, BE 均分∠DBC 交 DC 于点 E,延伸 BC 到点 F,使 FC=EC,连结 DF 交 BE 的延伸线于点H,连结 OH 交 DC 于点 G,连结 HC.则以下四个结论中正确结论的个数为()①OH= BF;②∠CHF=45°;③ GH= BC;④ DH 2=HE?HB .A. 1个B. 2 个C. 3 个D. 4 个解:作 EJ⊥ BD 于 J,连结 EF① ∵BE 均分∠ DBC∴EC=EJ,∴△ DJE≌△ ECF∴DE=FE∴∠HEF=45°°° ∴∠HFE=° ∴∠EHF=180°﹣°﹣°=90°∵DH=HF , OH是△ DBF 的中位线∴OH∥BF∴ OH= BF② ∵四边形 ABCD 是正方形, BE 是∠DBC 的均分线,∴BC=CD,∠BCD=∠ DCF,∠°,∵CE=CF,∴ Rt△BCE≌Rt△ DCF,∴∠EBC= ∠°,∴∠BFH=90°﹣∠CDF=90°﹣°°,∵OH 是△DBF 的中位线, CD⊥ AF,∴ OH 是 CD 的垂直均分线,∴DH=CH ,∴∠CDF=∠°,∴∠HCF=90°﹣∠DCH=90°﹣°°,∴∠CHF=180°﹣∠ HCF﹣∠BFH=180°﹣°﹣°=45°,故②正确;③ ∵OH 是△ BFD 的中位线,∴DG=CG= BC, GH= CF,∵CE=CF,∴ GH= CF= CE∵CE<CG= BC,∴GH< BC,故此结论不建立;④ ∵∠DBE=45°, BE 是∠DBF 的均分线,∴∠DBH=22.5 °,由② 知∠HBC= ∠°,∴∠DBH= ∠CDF,∵∠BHD= ∠BHD ,∴△DHE ∽△BHD ,∴ = ∴ DH=HE ?HB,故④建立;所以①②④正确.应选 C.2.如图,梯形 ABCD 中,AD ∥BC,,∠ABC=45°,AE⊥ BC于点E,BF⊥ AC于点F,交AE 于点 G,AD=BE ,连结 DG、CG.以下结论:① △BEG≌△ AEC;②∠GAC= ∠GCA ;③ DG=DC;④ G 为 AE 中点时,△AGC 的面积有最大值.此中正确的结论有()A. 1 个B. 2 个C. 3 个D. 4 个解:依据 BE=AE ,∠GBE=∠CAE,∠BEG=∠ CEA 可判断① △ BEG≌△AEC ;用反证法证明② ∠ GAC≠∠GCA ,假定∠ GAC=∠ GCA,则有△ AGC 为等腰三角形, F 为 AC 的中点,又 BF⊥AC ,可证得 AB=BC ,与题设不符;由① 知△BEG≌△ AEC 所以 GE=CE 连结 ED、四边形 ABED 为平行四边形,∵∠ABC=45 °,AE ⊥BC 于点 E,∴∠ GED=∠ CED=45°,∴△GED≌△ CED,∴DG=DC;④设 AG 为 X ,则易求出 GE=EC=2﹣ X所以, S△AGC=S AEC﹣ S GEC=﹣+x= ﹣(x2﹣ 2x)=﹣( x2﹣2x+1﹣1)=﹣(x﹣1)2+ ,当X 取 1 时,面积最大,所以 AG 等于 1,所以 G 是 AE 中点,故G 为 AE 中点时, GF 最长,故此时△AGC 的面积有最大值.故正确的个数有 3 个.应选 C.3.如图,正方形 ABCD 中,在 AD 的延伸线上取点 E,F,使 DE=AD ,DF=BD ,连结 BF 分别交 CD,CE 于 H,G 以下结论:① EC=2DG;② ∠GDH=∠ GHD ;③ S△CDG=S?DHGE;④图中有 8 个等腰三角形.此中正确的选项是()A. ①③B. ②④C. ①④D. ②③解:∵ DF=BD ,∴∠DFB=∠DBF ,∵AD ∥BC,DE=BC ,∴∠ DEC=∠DBC=45°,∴∠DEC=2∠ EFB,∴∠°,∠CGB=∠°,∴CG=BC=DE ,∵DE=DC,∴∠DEG=∠DCE ,∵∠GHC=∠CDF+∠ DFB=90°°°,∠DGE=180°﹣(∠BGD+∠ EGF) =180°﹣(∠ BGD+∠BGC),=180°﹣( 180°﹣∠ DCG)÷2=180°﹣( 180°﹣45°)÷°,∴∠GHC=∠DGE,∴△CHG≌△EGD,∴∠EDG=∠ CGB=∠CBF,∴∠GDH= ∠GHD ,∴ S△CDG =S?DHGE.应选 D.4.如,矩形 ABCD 的面 5,它的两条角交于点 O1,以 AB ,AO 1两作平行四形 ABC 1O1,平行四形 ABC 1O1的角交 BD 于点 02,同以 AB ,AO 2两作平行四形ABC 2O2.⋯,依此推,平行四形ABC 2009O2009的面()A.B. C. D.解:∵矩形 ABCD 的角相互均分,面5,∴平行四形 ABC 1O1的面,∵平行四形 ABC 1O1的角相互均分,∴平行四形 ABC 2O2的面× =,⋯,依此推,平行四形ABC 2009 2009的面.故B .O5.(2013?牡丹江)如,在△ABC 中∠A=60°,BM ⊥AC 于点 M ,CN⊥AB 于点 N,P BC的中点,接PM,PN,以下:①PM=PN;②;③ △PMN等三角形;④当∠ ABC=45° , BN=PC.此中正确的个数是()A. 1 个B. 2 个C. 3 个D. 4 个解:① ∵BM ⊥AC 于点 M ,CN⊥ AB 于点 N,P BC 的中点,∴PM= BC, PN= BC,∴PM=PN,正确;②在△ABM 与△ACN 中,∵∠A= ∠A ,∠AMB= ∠ANC=90 °,∴△ABM ∽△ACN ,∴,正确;③ ∵∠A=60°,BM ⊥AC 于点 M ,CN⊥AB 于点 N,∴∠ABM= ∠ACN=30 °,在△ABC 中,∠BCN+ ∠CBM ═180° 60° 30°×2=60°,∵点 P 是 BC 的中点, BM ⊥AC ,CN⊥AB ,∴ PM=PN=PB=PC,∴∠BPN=2∠ BCN,∠CPM=2∠ CBM ,∴∠BPN+∠CPM=2( ∠BCN+∠ CBM ) =2×60°=120°,∴∠MPN=60°,∴△ PMN 是等边三角形,正确; ④ 当∠ABC=45 °时, ∵CN ⊥AB 于点 N ,∴∠BNC=90°,∠BCN=45 °, ∴BN=CN , ∵P 为 BC 边的中点, ∴ PN ⊥ BC ,△BPN 为等腰直角三角形∴BN= PB= PC ,正确.应选 D .6.(2012?黑河)Rt △ ABC 中,AB=AC ,点 D 为 BC 中点.∠MDN=90 °,∠MDN 绕点 D 旋转,DM 、DN 分别与边 AB 、 AC 交于 E 、F 两点.以下结论:① ( BE+CF ) = BC ; ② △ △ABC ;③ S 四边形 AEDF =AD ?EF ;S AEF ≤ S④ AD ≥EF ;⑤ AD 与 EF 可能相互均分,此中正确结论的个数是()A. 1 个B. 2 个C. 3 个D. 4 个解: ∵ Rt △ABC 中, AB=AC ,点 D 为 BC 中点, ∴∠ C=∠ BAD=45 °,AD=BD=CD , ∵∠MDN=90 °,∴∠ADE+ ∠ ADF= ∠ADF+ ∠CDF=90°,∴∠ADE= ∠CDF .在 △ AED 与△CFD 中, ∵,∴△AED ≌△ CFD ( ASA ),∴AE=CF ,在 Rt △ABD 中, BE+CF=BE+AE=AB== BD= BC .故 ① 正确;设 AB=AC=a ,AE=CF=x ,则 AF=a ﹣x .∵S △AEF = AE?AF= x ( a ﹣x )=﹣ ( x ﹣ a )2 + a 2, ∴当 x= a 时, S △ AEF 有最大值 a 2,又∵ S △ ABC = × a 2= a 2, ∴S △ AEF ≤ S △ABC .故 ② 正确;EF 2=AE 2+AF 2=x 2+(a ﹣x )2=2(x ﹣ a )2+ a 2,∴ 当 x= a 时, EF 2 获得最小值 a 2,∴EF ≥ a (等号当且仅当 x= a 时建立),而 AD=a , ∴EF ≥AD .故 ④ 错误;由① 的证明知 △AED ≌△ CFD ,∴S 四边形 AEDF =S △ AED +S △ADF =S △ CFD +S △ADF =S △ADC = AD 2,∵EF≥AD ,∴ AD ?EF≥AD 2,∴AD ?EF>S 四边形AEDF故③ 错误;当E、 F 分别为 AB 、AC 的中点时,四边形 AEDF 为正方形,此时 AD 与 EF 相互均分.故⑤ 正确.综上所述,正确的有:①②⑤,共3个.应选C.7.如图,在正方形纸片ABCD 中,对角线 AC 、BD 交于点 O,折叠正方形纸片ABCD ,使 AD 落在BD 上,点 A 恰巧与 BD 上的点 F 重合,睁开后折痕 DE 分别交 AB 、AC 于点 E、G,连结 GF.以下结论① ∠ADG=22.5 °;② tan∠ AED=2 ;③ S△AGD =S△OGD;④ 四边形 AEFG 是菱形;⑤ BE=2OG.此中正确的结论有()A. ①④⑤B.①②④C.③④⑤D.②③④解:∵四边形 ABCD 是正方形,∴∠GAD= ∠ADO=45 °,由折叠的性质可得:∠ADG=∠ °,故① 正确.∵t an∠AED= ,由折叠的性质可得: AE=EF,∠ EFD=∠EAD=90 °,∴AE=EF<BE,∴ AE<AB ,∴tan∠AED=>2,故② 错误.∵∠AOB=90 °,∴AG=FG >OG,△AGD 与△OGD 同高,∴S△AGD>S△OGD,故③错误.∵∠EFD=∠AOF=90°,∴ EF∥ AC,∴∠FEG=∠AGE ,∵∠AGE= ∠FGE,∴∠ FEG=∠FGE,∴EF=GF,∵AE=EF,∴ AE=GF,故④正确.∵AE=EF=GF ,AG=GF ,∴AE=EF=GF=AG ,∴四边形 AEFG 是菱形,∴∠OGF=∠ OAB=45°,∴EF=GF= OG,∴BE= EF=×OG=2OG.故⑤正确.∴此中正确结论的序号是:①④⑤.应选:A.8.如图,正方形 ABCD 中, O 为 BD 中点,以 BC 为边向正方形内作等边△ BCE,连结并延伸 AE 交CD 于 F,连结 BD 分别交 CE、 AF 于 G、H,以下结论:①∠CEH=45°;② GF∥DE;③ 2OH+DH=BD ;④ BG= DG;⑤.此中正确的结论是()A. ①②③B.①②④C.①②⑤D.②④⑤解:① 由∠ ABC=90°,△BEC 为等边三角形,△ABE 为等腰三角形,∠AEB+ ∠ BEC+∠CEH=180°,可求得∠CEH=45°,此结论正确;②由△EGD≌△DFE,EF=GD,再由△ HDE 为等腰三角形,∠DEH=30°,得出△ HGF 为等腰三角形,∠HFG=30°,可求得 GF∥ DE,此结论正确;③由图可知 2(OH+HD )=2OD=BD ,所以 2OH+DH=BD 此结论不正确;④如图,过点 G 作 GM⊥ CD 垂足为 M , GN⊥ BC 垂足为 N,设 GM=x ,则 GN=x,进一步利用勾股定理求得GD= x ,BG=x,得出 BG=GD,此结论不正确;⑤由图可知△BCE 和△ BCG 同底不等高,它们的面积比即是两个三角形的高之比,由④ 可知△ BCE 的高为( x+x)和△BCG 的高为x,所以 S△BCE:S△BCG=(x+x): x=,此结论正确;故正确的结论有①②⑤.应选 C.9.如图,在正方形ABCD 中, AB=4 ,E 为 CD 上一动点, AE 交 BD 于 F,过 F 作 FH⊥ AE 于 H,过H 作 GH⊥ BD 于 G,以下有四个结论:① AF=FH ,②∠HAE=45 °,③ BD=2FG,④ △ CEH 的周长为定值,此中正确的结论有()A. ①②③B. ①②④C. ①③④D. ①②③④解:(1)连结FC,延伸 HF 交 AD 于点 L,∵BD 为正方形 ABCD 的对角线,∴∠ADB= ∠ CDF=45°.∵AD=CD ,DF=DF,∴△ADF ≌△CDF.∴ FC=AF,∠ECF=∠DAF .∵∠ALH+ ∠LAF=90 °,∴∠ LHC+∠ DAF=90°.∵∠ECF=∠DAF ,∴∠FHC=∠ FCH,∴FH=FC.∴FH=AF .(2)∵FH ⊥AE ,FH=AF ,∴∠HAE=45 °. (3)连结 AC 交 BD 于点 O ,可知: BD=2OA ,∵∠AFO+ ∠GFH=∠ GHF+∠GFH ,∴∠ AFO=∠ GHF . ∵AF=HF ,∠ AOF=∠ FGH=90°,∴△ AOF ≌△ FGH . ∴OA=GF . ∵BD=2OA , ∴BD=2FG . (4)延伸 AD 至点 M ,使 AD=DM ,过点 C 作 CI ∥ HL ,则: LI=HC ,依据 △ MEC ≌△CIM ,可得: CE=IM ,同理,可得: AL=HE , ∴HE+HC+EC=AL+LI+IM=AM=8 .∴△ CEH 的周长为 8,为定值.故( 1)(2)( 3)(4)结论都正确.应选 D .10.正方形点 G 在线段ABCD 、正方形 DK 上,正方形BEFG 和正方形 BEFG 的边长为RKPF 的地点如下图,4,则 △DEK 的面积为()A. 10B. 12C. 14D. 16 解:如图,连 DB ,GE ,FK ,则 DB ∥GE ∥FK ,在梯形 GDBE 中, S △DGE =S △GEB (同底等高的两三角形面积相等) ,同理 S △GKE △ GFE .=S△ GEF 正方形 GBEF =4×4=16应选 D . ∴S 暗影=S △DGE △GKE △GEB+S =S +S=S二.填空 1.如 , 察 中菱形的个数: 1 中有 1 个菱形, 2 中有 5 个菱形, 3 中有 14 个菱形,4 中有 30 个菱形 ⋯, 第 6 个 中菱形的个数是 个.解: 察 形, 律: 1 中有 1 个菱形, 2 中有 1+22=5 个菱形,3 中有 5+32=14 个菱形, 4 中有 14+42=30 个菱形,第 5 个 中菱形的个数是 30+52,第 6个 中菱形的个数是 2 个.故答案 .=5555+6 =91912.如 ,在 △ABC 中, ∠A= α.∠ABC 与 ∠ACD 的均分 交于点 A ,得 ∠A ;11∠A 1BC 与∠A 1CD 的均分 订交于点 A 2,得 ∠A 2; ⋯;∠A 2011BC 与∠A 2011CD 的均分 订交于点 A 2012,得 ∠ A 2012, ∠A 2012=.解: ∵∠ABC 与∠ ACD 的均分 交于点A 1,∴∠A 1BC= ∠ABC ,∠ A 1CD= ∠ACD ,依据三角形的外角性 , ∠ A+∠ ABC= ∠ACD ,∠ A 1+∠A 1BC=∠A 1CD ,∴∠A 1+∠A 1BC=∠A 1+ ∠ABC= (∠A+ ∠ABC ),整理得, ∠A 1= ∠ A= ,同理可得, ∠ A 2 ∠ 1 × = , ⋯,= A =∠A 2012=.故答案 :.3.如 ,已知 Rt △ABC 中, AC=3,BC=4, 直角 点 C 作 A 1C 1⊥ BC ,垂足 C 1, C 1 作 C 1A 2⊥ AB ,垂足 A 2,再CA 1⊥AB ,垂足 A 1,再 A 1 作 A 2 作 A 2C 2⊥ BC ,垂足 C 2, ⋯,向来做下去,获得了一 段CA 1, 1 1, 1 2,⋯,1,=.A C C A CA =解:在 Rt△ ABC 中, AC=3, BC=4,∴ AB=,又因 CA 1⊥ AB ,∴ AB ?CA 1= AC?BC,即 CA 1===.∵C4A 5⊥AB ,∴△BA 5C4∽△BCA ,∴,∴==.所以填和.4.如,点 A 1,A 2, A 3,A 4,⋯,A n在射 OA 上,点 B1,B2,B3,⋯, B n﹣1在射 OB 上,且A B ∥ A B ∥ A B ∥⋯∥A B ,A B∥A B∥A B∥⋯∥A B ,△A A B ,△ A A B,⋯,△ A1 12 23 3n﹣ 1 n﹣ 1 2 1 3 24 3n n ﹣ 11 2 12 3 2n A n n﹣1 暗影三角形,若△ 2 12,△32 3 的面分、,△12 1 的面;﹣1B A B B A B B 1 4A A B面小于 2011 的暗影三角形共有6个.解:由意得,△A 2B1B2∽△A 3B2B3,∴== ,== ,又∵A 1B1∥A 2B2∥A 3B3,∴=== ,== ,∴OA 1=A 1A2,B1B2= B2B3而可得出律: A 1A 2= A2A 3= A 3A 4⋯;B1B2= B2B3= B3 B4⋯又△A 2B1B2,△A 3B2B3的面分 1、4,∴ S△A1B1A2 = ,S△A2B2A3 =2,而可推出 S△A3B3A4 =8,S△A4B4A5 =32,S△A5B5A6 =128,S△A6B6A7 =512,S△A7B7A8 =2048,故可得小于 2011 的暗影三角形的有:△A 1B1A 2,△ A 2B2A 3,△ A3B3A 4,△A 4B4A 5,△A 5B5A 6,△ A 6B6A 7,共 6 个.故答案是:;6.5.如图,已知点 A 1( a, 1)在直线 l:上,以点A1为圆心,以为半径画弧,交x 轴于点B1、B2,过点 B2作 A 1B1的平行线交直线 l 于点 A 2,在 x 轴上取一点 B3,使得 A 2B3=A2B2,再过点B3作 A 2B2的平行线交直线 l 于点 A 3,在 x 轴上取一点 B4,使得 A 3 B4=A 3B3,按此规律持续作下去,则① a=;② △A 4 4 5的面积是.B B解:如下图:①将点 A1(a,1)代入直线 1 中,可得,所以 a= .② △A B B 的面积为: S== ;112由于△ OA1B1∽△OA 2B2,所以2A 1B1=A 2B2,又由于两线段平行,可知△A 1B1B2∽△A 2B2B3,所以△ A 2 2 3 的面积为1;以此类推,△ 4 4B 5 的面积等于64S=.B B S =4S A B6.如图,在梯形ABCD 中,AD ∥BC,EA ⊥AD ,M 是AE 上一点,F、G 分别是AB 、CM 的中点,且∠BAE= ∠MCE ,∠MBE=45 °,则给出以下五个结论:① AB=CM ;② A E⊥ BC;③∠BMC=90 °;④ EF=EG;⑤△BMC 是等腰直角三角形.上述结论中一直正确的序号有.解:∵梯形 ABCD 中, AD ∥BC, EA⊥ AD ,∴AE ⊥BC,即②正确.∵∠MBE=45 °,∴BE=ME .在△ ABE 与△CME 中,∵∠BAE= ∠MCE ,∠ AEB= ∠CEM=90 °,BE=ME ,∴△ABE ≌△CME ,∴AB=CM ,即①正确.∵∠MCE= ∠BAE=90 °﹣∠ABE <90°﹣∠MBE=45 °,∴∠ MCE+∠ MBC < 90°,∴∠BMC > 90°,即③⑤错误.∵∠AEB= ∠CEM=90°, F、 G 分别是 AB 、CM 的中点,∴EF= AB , EG= CM .又∵AB=CM ,∴ EF=EG,即④正确.故正确的选项是①②④.7.如, 1 的菱形 ABCD 中,∠DAB=60 度.接角 AC ,以 AC 作第二个菱形ACC1D1,使∠D1AC=60°;接 AC 1,再以 AC1作第三个菱形 AC 1C2D2,使∠D2AC 1=60°;⋯,按此律所作的第n 个菱形的.解:接 DB,∵四形 ABCD 是菱形,∴AD=AB . AC⊥ DB ,∵∠DAB=60 °,∴△ ADB 是等三角形,∴DB=AD=1 ,∴ BM=,∴AM== ,∴AC=,同理可得 AC 1=AC=()2, AC2=1=()3,AC =3按此律所作的第n 个菱形的()n﹣ 1故答案()n﹣ 1.EFGH,若8.如,将矩形 ABCD 的四个角向内折起,恰巧拼成一个既无隙又无重叠的四形EH=3,EF=4,那么段 AD 与 AB 的比等于.解:∵∠1=∠ 2,∠3=∠ 4,∴∠2+∠3=90°,∴∠HEF=90°,同理四形 EFGH 的其余内角都是90°,∴四形 EFGH 是矩形.∴EH=FG(矩形的相等);又∵∠ 1+∠4=90°,∠4+∠5=90°,∴∠1=∠ 5(等量代),同理∠ 5=∠7=∠8,∴∠ 1=∠8,∴ R t △ AHE ≌ Rt △CFG ,∴AH=CF=FN ,又∵HD=HN ,∴ AD=HF ,在 Rt △HEF 中, EH=3,EF=4,依据勾股定理得 HF=,∴ HF=5,又∵HE?EF=HF?EM , ∴EM=,又∵AE=EM=EB (折叠后 A 、B 都落在 M 点上), ∴AB=2EM=,∴AD :AB=5 : =.故答案为: .9.如图, E 、 F 分别是平行四边形 ABCD 的边 AB 、 CD 上的点, AF 与 DE 订交于点 P ,BF 与 △APD 2, S △BQC 2,则暗影部分的面积为 cm 2. CE 订交于点 Q ,若 S =15cm =25cm解:如图,连结 EF∵△ADF 与 △DEF 同底等高, ∴ S △ADF =S △DEF即 S △ ADF ﹣S △DPF =S △DEF ﹣ S △ DPF ,即 S △APD =S △EPF =15cm 2,同理可得 S △BQC =S △ EFQ =25cm 2,∴暗影部分的面积为 S △EPF +S △ EFQ =15+25=40cm 2.故答案为 40.。
最新成都中考B卷填空题 几何专练7套学生知识讲解

成都中考B 填几何专练(一)1. 如图,等边△ABC 中,点D 、E 、F 分别在边BC 、CA 、AB 上,且BD=2DC ,CE=2EA ,AF=2FB ,AD 与BE 相交于点P ,BE 与CF 相交于点Q ,CF 与AD 相交于点R ,则AP :PR :RD= .若△ABC 的面积为1,则△PQR 的面积为 .2. 如图所示,已知∠AOB =30°,P 是∠AOB 内一点,且点P 到OA 、OB 的距离分别为1、2,以P 点为圆心的圆分别与OA 、OB 相交于点M 、N ,且MN 恰为圆的直径,则该圆的半径为____________.3.在直角坐标系中,O 为坐标原点,A 是双曲线y = kx (k >0)在第一象限图象上的一点,且直线OA 是第一象限的角平分线,直线OA 交双曲线于另一点C .将OA 向上平移 32个单位后与双曲线在第一象限的图象交于点M ,交y 轴于点N ,若MN OA=12,则k =__________.4.如图,扇形AOB 中,OA =1,∠AOB =90°,半圆O 1的圆心O 1在OA 上,并与AB ︵内切于点A ,半圆O 2的圆心O 2在OB 上,并与AB ︵内切于点B ,半圆O 1与半圆O 2相切.设两半圆的面积之和为S ,则S 的取值范围是______________________.5.如图,平行四边形ABCD中,AM⊥BC于M,AN⊥CD于N,已知AB=10,BM=6,MC=3,则MN 的长为____________.6.如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径作⊙M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F.若AE=5,CE=3,BF=___________,DF=___________.7.如图,正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且EG与FH的夹角为45°.若正方形ABCD的边长为1,FH的长为52,则EG的长为____________.8.已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,顶点为C,当△ABC为等腰直角三角形时,b2-4ac的值为__________;当△ABC为等边三角形时,b2-4ac的值为__________.9.如图,△ABC中,AB=7,BC=12,CA=11,内切圆O分别与AB、BC、CA相切于点D、E、F,则AD:BE:CF=_______________.成都中考B填几何专练(二)1.如图,△ABC内接于⊙O,BC=a,AC=b,∠A-∠B=90°,则⊙O的半径为_______________.2.如图,Rt△ABC中,∠ACB=90°,AC=2BC,CD⊥AB于点D,过AC的中点E作AC的垂线,交AB于点F,交CD的延长线于点G,M为CD中点,连接AM交EF于点N,则ENFG=____________.3.如图,半径为r1的⊙O1内切于半径为r2的⊙O2,切点为P,⊙O2的弦AB过⊙O1的圆心O1,与⊙O1交于C、D,且AC:CD:DB=3:4:2,则r1r2=___________.4.(1)如图1,在边长为1的正方形ABCD内,两个动圆⊙O1与⊙O2互相外切,且⊙O1与边AB、AD相切,⊙O2与边BC、CD相切,设⊙O1与⊙O2面积之和为S,则S的取值范围是_________________;(2)如图2,在矩形ABCD中,AB=32,BC=1,两个动圆⊙O1与⊙O2互相外切,且⊙O1与边AB、AD相切,⊙O2与边BC、CD相切,设⊙O1与⊙O2面积之和为S,则S的取值范围是_________________.5.如图,等腰梯形ABCD中,AD∥BC,∠B=60°,AB=CD=AD=2,M是BC的中点.将△DMC绕点M旋转,得△D′MC′,D′M与AB交于点E,C′M与AD交于点F,连接EF,则△AEF的周长的最小值为_____________.6.如图,已知矩形ABCD的面积为2011cm2,梯形AFGE的顶点F在BC上,D是腰EG的中点,则梯形AFGE的面积为____________cm2.7.如图,在边长为1的正方形ABCD中,分别以A、B、C、D为圆心,1为半径画四分之一圆,交点为E、F、G、H,则中间阴影部分的周长为_____________,面积为_____________.8.如图,在边长为1的正方形ABCD中,E、F分别是BC、CD边上的动点,满足∠EAF=45°,则△CEF 内切圆半径的最大值为_____________.9.如图,在边长为1的正方形ABCD中,点M、N分别在CB、DC的延长线上,且∠MAN=45°.过D作DP⊥AN交AM于点P,连接PC,若C为DN的中点,则PC的长为_____________.成都中考B填几何专练(三)1.如图,正方形ABCD的边长为2,M是AB的中点,点P是射线DC上的动点.若以C为圆心,CP为半径的圆与线段DM只有一个公共点,则PD的取值范围是__________________________________.2.如图,点A、B分别在x轴正半轴和y轴负半轴上,OA=OB=2,点E是y轴正半轴上一动点,连接EA,过O作OP⊥EA于P,连接PB,过P作PF⊥PB交x轴正半轴于F,连接EF.当OE=1时,S△EAF =S1;OE=2时,S△EAF =S2;…;OE=n时,S△EAF =S n ,则S1+S2+S3+…+S n =___________.3.如图,直线y=x-3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x 轴的另一交点为A,顶点为D,且对称轴是直线x=1.若平行于x轴的直线y=k与△BCD的外接圆有公共点,则k的取值范围是_____________________.4.如图,在Rt△ABC中,∠ACB=90°,半径为4的⊙A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.已知tan∠BPD=12,CE=2,则△ABC的周长为.5.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,H是△AEF的垂心.若AC=20,EF=16,则AH=__________.6.如图,AD平分∠BAC,交△ABC的外接圆于点D,DE∥BC,交AC的延长线于点E.若AB=4,AD =5,CE=1,则DE=__________.7.将一副三角板如图放置,∠BAC=∠BDC=90°,∠ABC=45°,∠DBC=30°,BC=42,则△ADC的面积为_____________.8.已知△ABC中,AB=6,AC=BC=5,将△ABC折叠,使点A落在BC边上的点D处,折痕为EF(点E、F分别在边AB、AC上).(1)当ED⊥BC时,BE的长为___________;(2)当以B、E、D为顶点的三角形与△DEF相似时,BE的长为___________.成都中考B填几何专练(四)1.如图,将正方形沿图中虚线(其中a<b)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则ab的值为_____________.2.如图是一块矩形钢板ABCD,AB=4,BC=3.工人师傅想用它裁出两块全等的、面积最大的△APB和△CP′D钢板,且∠APB=∠CP′D=60°,则△APB的面积为______________,请在图中画出符合要求的点P和P′.(2小题变练)已知矩形ABCD中,AB=43,BC=m,P是矩形ABCD边上的一动点,且使得∠APB=60°,如果这样的点P有4个,则m的取值范围是______________.3.已知△ABC中,∠ABC=30°,AB=3,BC=4,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD的长为____________.(3题变练)已知△ABC中,∠ABC=45°,AB=72,BC=17,以AC为斜边在△ABC外作等腰直角三角形ACD,连接BD,则BD的长为____________.4.已知正方形ABCD的面积是144,E、M分别是边AB、AD上的点,分别以BE、DM为边在正方形ABCD 内作正方形BEFG和正方形DMNP.若两个小正方形重叠部分的面积是1,A、F、P三点共线,则tan∠DAP =__________.5.如图,矩形纸片ABCD中,AB=4,折叠纸片,使顶点A落在CD边上的点A′处,EF为折痕(点E、F分别在边BC、AD上),连接AE、A′E.若△ECA′的外接圆恰好与AE相切于点E,且与AD边也相切,则AD=__________.6.已知△ABC中,∠ABC=45°,AB=522,BC=12,将线段AC绕点A逆时针旋转90°,得线段AD,连接BD,则BD的长为____________.7.如图,等腰直角三角形OAB 和BCD 的底边OB 、BD 都在x 轴上,直角顶点A 、C 都在反比例函数y = kx图象上,若D (-8,0),则k =__________.成都中考B 填几何专练(五)1.如图,直线y =-x +b 与双曲线y = 1x (x >0)交于A 、B 两点,与x 轴、y 轴分别交于E 、F 两点,AC ⊥x轴于C ,BD ⊥y 轴于D ,当b =__________时,△ACE 、△BDF 与△AOB 面积的和等于△EOF 面积的34.2.如图,△ABC 中,∠ACB =90°,AC =6- 2,BC =6+ 2,半圆O 过A 、B 、C 三点,M 是AB ︵的中点,ME ⊥AC 于E ,MF ⊥BC 于F ,则图中阴影部分的面积为_______________.3.直线y=-2x-4与x轴交于点A,与y轴交于点B,将线段AB绕着平面内的某个点旋转180°后,得到点C、D,恰好落在反比例函数y=kx的图象上,且D、C两点横坐标之比为3:1,则k=_________.4.如图,AB、AP、PB分别是半圆O、O1、O2的直径,点P在直径AB上,PQ⊥AB交半圆O于点Q,圆O3的与半圆O、O2及PQ都相切,若圆O3的半径为3,阴影部分的面积为39π,则AB=___________.5.如图,正方形ABCD的边长为2,E是AB边上一点,将△ADE绕点D逆时针旋转至△CDF,连接EF 交CD于点G.若ED=EG,则AE=___________.6.已知Rt△ABC中,∠ACB=90°,BC=2AC,CD⊥AB于D,E是BC边上一点,且BE=2CE,连接AE,与CD相交于点G,EF⊥AE,与AB边相交于点F.将∠FEG绕点E顺时针旋转,旋转后EF边所在的直线与AB边相交于点F′,EG边所在的直线与AC边相交于点H,与CD相交于点G′.若AH=35,且FF′CG′=27,则线段G′H的长为____________.7.如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)、B(3,0),D为抛物线的顶点,∠DAB=45°.过A作AC⊥AD交抛物线于点C,动直线l过点A,与线段CD交于点P,设点C、D到直线l的距离分别为d1、d2,则d1+d2的最大值为__________.8.如图,在梯形ABCD中,AD∥BC,∠B+∠C=120°,AD=3,BC=7,则梯形ABCD面积的最大值为__________.成都中考B填几何专练(六)1.如图,Rt△ABC和Rt△BCD有公共斜边BC,M是BC的中点,E、F分别是边AB、BD上的动点.若∠ABC=30°,∠BCD=45°,BC=4,△ECF的周长的最小值为_____________.2.如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=8x(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,那么图中阴影部分的面积之和为____________.3.在反比例函数y=10x(x>0)的图象上,有一系列点A1、A2、A3、…、A n、A n+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、A n、A n+1作x轴与y 轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,S n,则S1 +S2 +S3 +…+S n=____________(用含n的代数式表示).4.如图,点A(x1,y1)、B(x2,y2)都在双曲线y=kx(x>0)上,且x2-x1=4,y1-y2=2;分别过点A、B向x轴、y轴作垂线段,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析式为_______________.5.如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是_________.6.已知线段AB的长为202,点D在线段AB上,△ACD是边长为10的等边三角形,过点D作与CD 垂直的射线DP,过DP上一动点E(不与D重合)作矩形CDEF,记矩形CDEF的对角线交点为O,连接OB,则线段OB长的最小值为_____________.7.如图,△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,∠BAE=135°,AC=22,AD=1,F为BE中点,则CF的长为_______________.将△ADE绕点A旋转一周,则点F运动路径的长为_______________.土木工程专业英语词汇表(和所使用的环境有关系,仅供参考)to build, to construct 建设,建筑,修建architecture 建筑学building 修筑,建筑物house 房子skyscraper 摩天大楼block of flats 公寓楼(美作:apartment block)monument 纪念碑palace 宫殿temple 庙宇basilica 皇宫,教堂cathedral 大教堂church 教堂tower 塔,塔楼ten-storey office block 十层办公大楼column 柱colonnade 柱列arch 拱town planning 市政(美作:city planning)building permission 营建许可证,建筑开工许可证greenbelt 绿地elevation 建筑物的三面图plan 设计图scale 比例尺to prefabricate 预制excavation 挖土,掘土foundations 基to lay the foundations 打地基course of bricks 砌好的砖列scaffold 脚手架scaffolding 脚手架质量合格证书certification of fitness 原材料raw material底板bottom plate垫层cushion侧壁sidewall中心线center line条形基础strip footing附件accessories型钢profile steel。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考基础训练几何填空
1、填空:(1)sin45°= ,cos60°= (3)tan30°= ,cot45°=
2、在ΔABC 中,∠C=90O ,sinA=53
,那么cosB=
3、在△ABC 中,∠C=900
,BC=3, AB=5,则cos B =____________ 4、假如某人沿着4:3 i 的斜坡前进20m ,那么他所在的位置比原先的位置升高 m 。
5、假如一传送带和地面所成斜坡的坡度为1︰2,它把物体从地面送到离地面9米的地点,那么物体所通过的路程为_____米
6、在坡度为i =1∶7的斜坡上前进10米,则高度升高了 米
7、在相同时刻的物高与影长成比例,假如一古塔在地面上的影长为50米,同时高为1.5米的测竿的影长为2.5米,那么古塔的高为___米。
8、在山坡上种树,要求株距是3米,测得斜坡的倾斜角是30º 求相邻两树的坡面距离是______米
9、⊙O 的半径为10,弦AB 长为6,则点O 到的AB 距离为______
10、平面内到定点A 的距离为4的点的轨迹是 11、如图,水平放着的圆柱形的排水管,它的截面看作是圆,
已知截面圆的直径为650mm ,水面的宽AB = 600mm ,
则截面上有水的最大深度是______mm 。
12、如图,半圆的直径=8,正方形的顶点在半圆上一边在上,
则那个正方形的面积等于( )
A 、16
B 、15.4
C 、12.8
D 、12
A
D
13、如图,四边形ABCD 内接于⊙O ,∠BOD=160°,
则 ∠ BAD 的度数是_________,∠BCD 的度数是_______;
14、四边形ABCD 内接于⊙O ,∠BCD=120°,则∠BOD = 度。
15、如图,⊙O 中,∠AOB =88°,那么∠ACB =______.
16、圆内接四边形ABCD 中,∠A ∶∠B ∶∠C=4∶3∶5,那么∠D=
17、两圆的圆心距为6,它们的半径是一元二次方程x 2
-7x+4=0的两个根,则两圆的位置关系是 ,现在两圆的外公切线长为 。
18、两圆相交,已知公共弦长为16,两圆半径分别为10、17, 求两圆圆心距为 。
A B
O A B
C D O
图1
O
D C
A
B
D O B A
C E 19、△ABC 中,AB =3cm ,BC =4cm ,AC =5cm ,分别以A 、B 、C 为圆心画三个圆两两外切,则⊙A 、⊙B 、⊙C 的半径比是________.
20、两个以 O 为圆心的同心圆, AB 切大圆于 B , AC 切小圆于 C 交大圆于 D 、E , AB=12 , DE=10 , cot ∠BAO=
3
4
, 求两圆的半径为________.
21、P 是⊙O 外一点,PA 、PB 分别和⊙O 切于A 、B ,C 是弧AB 上任意一点,过C 作⊙O 的切线分别交PA 、PB 于D 、E ,若△PDE 的周长为12,则PA 长为______________;
22、如图,四边形ABCD 为⊙O 的内接四边形,E 为AB 延长线上一点。
∠CBE=40°,则∠AOC=____________
23、如图,AB 、AC 是 O 的两条切线,切点分别为B 、C ,D 是优弧BC 上的一点,已知∠BAC=80︒,那么∠BDC= 度。
B
A
C
D
O
24、如图Rt △ABC ,∠ACB = 90O
O 在BC 上,☉O 切AB 于D, 若OC :OB = 1 :3,AD = 2,
BE 的长为______
A
B C D
E
P
O
25、已知:如图CD 是⊙O 的直径,AE 切⊙O 于点B ,
DC 的延长线交AB 于点A ,020=∠A ,则=∠DBE ______
26、如图,BC 是 O 的直径,P 是CB 延长线上一点,PA 切 O 于点A ,假如PA=3,PB=1,那么∠APC= 度。
P
27、如图,O 是梯形ABCD 的边AB 上一点,⊙O 分别与AD 、DC 、CB 相切,若 AB ∥CD ,AD =4,BC =5,则AB = .
28、如图:⊙O 的割线PAB 交⊙O 于A 、B ,PO 交⊙O 于C , 若PA=8,AB=6,PO=16,则⊙O 的半径为________ 29、已知⊙O 的直径AB 与弦AC 的夹角为30º,过C 的切线PC
与AB 延长线交于P ,PC =5,则⊙O 的半径为( ) (A )
335 (B )6
3
5 (C )10 (D )5
30、已知:如图,.PA 切⊙O 于点A ,PBC 为割线,AC 为直径, PB =3,BC =9,则PA = ,∠PAB = .
31、 △ABC 的内切圆⊙I 分别切BC 、CA 、AB 于D 、E 、F 。
若 ∠A=70°,则 ∠BIC= °,∠EDF= 度.
E
B
B
A
32、圆内两弦相交,一弦长为6cm,且被交点平分,另一弦被交点分为1∶3,则另一弦长
为_________________
33、正六边形的半径为3 ,它的面积为 _________
34、半径为4的圆内接正六边形的面积是
35、半径为R的圆内接正三角形的边长是,边心距为,面积
是。
36、半径为2的圆的内接正三角形的边长为,边心距为。
37、在半径为9cm的圆中,60º的圆心角所对的弧长为 .
38、已知弧的长度为10π,半径为9,则这条弧所对的圆心角为。
39、若扇形的圆心角为60°,半径为6cm,则那个扇形的面积为___ cm2.
40、圆心角为120°,半径为4cm的扇形的弧长等于_______________
41、已知扇形面积是60 cm ,扇形所在圆的半径是12 cm ,则扇形的圆心角的度数是
_______
42、已知圆柱的底面积为9π,侧面积为216π,则圆柱的母线长为。
43、已知圆柱的母线长是5cm,底面半径是2cm,则那个圆柱的侧面积是 .
44、圆柱的高为10cm,底面半径为6cm,则该圆柱的侧面积为______cm2,
表面积为___cm2.
45、圆柱的侧面积为10л,母线长为4,则圆柱的底面半径为。
46、长方形的长为5,宽为2,以一边所在的直线为轴旋转一周,则所得圆柱的侧面积为__________________
47、、已知矩形ABCD的一边AB=10cm,另一边AD=3cm,假如以直线AB为轴旋转一周,那么
所得的圆柱的侧面积是 cm2(不取近似值)
48、已知Rt△ABC的直角边AC=6cm、BC=4cm, 以AC所在的直线为轴旋转一周所得到的
图形是__, 其表面积是__.
49、已知一个圆锥的高为8厘米,底面积为36π平方厘米,
那么此圆锥的侧面展开图的面积为㎝2
50、A为半径为2的⊙O外一点,且OA∥弦BC,OA=4, 且AB切⊙O于点B,连结AC,则图中的阴影部分的面积是
_______。
