广东省湛江第一中学2020-2021学年高二年级第一学期数学11月28日周六测试题(十)
广东省湛江市第一中学高二数学上学期第二次月考试题文
湛江一中2015—2016学年度第一学期第二次考试高二级 文科数学试卷考试时间：120分钟 满分：150分一、选择题（共12题，每道题5分，共60分）1．设集合{}{}=⋂≤≤=<-+=N M ,3x 1x N ,0)2x )(3x (x M 则( )A ．[)2,1B ．[]2,1 C. (]3,2 D ．[]3,2 2．====∆AC ,23BC ,45B ,60A ABC 则中，若在 ( )A ．34B ．32 C.3 D.233. 数列，，，95,7453,321 …的一个通项公式n a ＝( ) A.1n 2n + B.1n 2n- C.3n 2n - D.3n 2n +4.设R x ∈，则命题:1q x >-是命题:0p x >的（ ）.A ． 充分不必要条件B ． 必要不充分条件C ． 充要条件D ． 既不充分又不必要条件 5．命题“存在0m x 2x ,Z x 2≤++∈使”的否定是( )A ．存在0m x 2x ,Z x 2>++∈使B ．不存在0m x 2x ,Z x 2>++∈使C ．对于任意0m x 2x ,Z x 2≤++∈都有D ．对于任意0m x 2x ,Z x 2>++∈都有6．已知等差数列{}n a 的公差为)0d (d ≠,且32a a a a 131063=+++,若8a m =, 则=m ( )A.8B.4C.6D.127．在23S ABC 2AB ,60A ABC ABC =∆==∆∆的面积，且中， ，则边BC 的边长为( )A. 3 B ．3 C.7 D ．78. 已知公比为2的等比数列{}n a 中，3a a a 642=++，则=++975a a a ( )A ．12B ．18C ．24D ．6 9. 已知命题p:01x x ,R x :q ;45x cos ,R x 2>+-∈∀=∈∃命题, 则下列结论正确的是( )(A)命题p ∧q 是真命题 (B)命题q p ⌝∧是真命题 (C)命题q p ∧⌝是真命题 (D)命题q p ⌝∨⌝是假命题 10．不等式02x 7x 32<+-的解集为( )A ．⎭⎬⎫⎩⎨⎧<<2x 31xB ．⎭⎬⎫⎩⎨⎧><2x 31x x 或C ．⎭⎬⎫⎩⎨⎧-<<-31x 21x D ．{}2x x >11．已知数列{}n a 满足4,0a 311==++a a n n ，则{}n a 的前10项和等于( )A. ）（10-3-16-B.）（10-3-191C ．）（10-3-13 D ．）（10-313+12．设21F F ，分别为双曲线)0b ,0a (1by a x 2222>>=-的左、右焦点，双曲线上存在一点P使得ab 49PF PF ,b 3PF PF 2121=⨯=+，则该双曲线的离心率为( ) A.43 B.53 C.94 D ．3二、填空题（共4题，每道题5分，共20分）13. 已知y ,x 都是正数，如果15xy =，则y x +的最小值是________；14. 在ABC ∆中，若222b a c +>，则ABC ∆必是______(填锐角，钝角，直角)三角形．15．设变量y ,x 满足约束条件：⎪⎩⎪⎨⎧-≥≤+≥,2x ,2y 2x ,x y 则y 3x z -=的最小值为____________.16．给定下列命题：①“若0k x 2x ,0k 2=-+>则方程有实数根”的逆否命题； ②“若B sin A sin ,B A ==则”的逆命题； ③“若b ab ,0b1a 1<<<则2”的逆否命题； ④“若0xy =，则y ,x 中至少有一个为零”的否命题． ⑤“若0b a ,baa b <<>则”的逆命题。
广东省湛江一中2022-2022学年高二数学上学期期末考试 理 【会员独享】
湛江一中2022——2022学年度第一学期期末考试高二级〔理科〕数学科试卷考试时间：120分钟 总分值：150分一．选择题：本大题共8小题，每题5分，共40分.在每题给出的四个选项中，只有一项为哪一项符合题目要求的.1.点A )4,1,3(--，那么点A 关于x 轴对称的点的坐标为〔 〕 A. )4,1,3(-- B.)4,1,3(--- C. )4,1,3(-- D. )4,1,3(2．椭圆2213649x y +=上的一点P 到椭圆的一个焦点的距离为3，那么P 点到另一个焦点的距离〔 〕A . 3B . 4 C. 9 D . 113．假设直线l 的方向向量为a ，平面α的法向量为n ，能使l ∥α的是 ( ) A ．a ＝(1,0,0)，n ＝(－2,0,0) B ．a ＝(1,3,5)，n ＝(1,0,1) C ．a ＝(0,2,1)，n ＝(－1,0，－1) D ．a ＝(1，－1,3)，n ＝(0,3,1)4.曲线221259x y +=与曲线221259x y k k+=--(9)k <的〔 〕 A. 长轴长相等 B. 焦距相等 C. 离心率相等 D. 短轴长相等5.给出以下命题：①对空间任意两个向量,a b 〔b ≠0〕，那么a ∥b 的充要条件是存在实数λ,使得b a λ=; ②假设0a b •=，那么00a b ==或; ③假设,,OA OB OC 不能构成空间的一个基底，那么O,A,B,C 四点共面; ④对于非零向量c b a ,,，那么)()(c b a c b a •=•一定成立. 正确命题的个数为〔 〕A ．1 B.2 C. 3 D. 46．正方体1111ABCD A B C D -中，,E F 分别是11,BB CC 的中点，那么异面直线AE 与BF 所成角的余弦为〔 〕 A ．25 B ．15- C ．15 D ．25- 7．过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ，2F 为右焦点，假设1260F PF ∠=，那么椭圆的离心率为〔 〕A．2 B．3 C ．12 D ．138．假设点O 和点(2,0)F -分别是双曲线2221(a>0)ax y -=的中心和左焦点,点P 为双曲线右支上的任意一点,那么OP FP ⋅的取值范围为 ( )A．)+∞ B．[3)++∞ C ．7[-,)4+∞ D ．7[,)4+∞ 二、填空题：本大题共6小题，每题5分，共30分．9.(,4,3),(3,2,)a x b z ==假设a ∥b ，那么x z ⋅=10.假设抛物线22y px =的焦点与双曲线22163x y -=的右焦点重合，那么p 的值为 ． 11.双曲线221y x a-=的一条渐近线与直线230x y -+=垂直，那么a =_________ 12．抛物线C 的顶点在坐标原点，焦点为F(1，0)，直线l 与抛物线C 相交于A ，B 两点。
广东省湛江市第一中学高二上学期第一次大考试题数学(理)Word版含答案
湛江一中2018-2019学年度第一学期“第一次大考”高二级理科数学试卷考试时间：120分钟 满分：150 命题人：何佩锦；审题人：许振广；做题人：陈振宇一. 选择题（本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.）1．数列1,3,6,10，…的一个通项公式是( ) A ．a n ＝n 2－n ＋1 B ．a n ＝n (n －1)2C ．a n ＝n 2＋1D ．a n ＝n (n ＋1)22.已知下列四个条件：①b ＞0＞a ，②0＞a ＞b ，③a ＞0＞b ，④a ＞b ＞0，能推出1a ＜1b 成立的有( )A.1个B.2个C.3个D.4个3.把1,3,6,10,15,21，…这些数叫做三角形数，这是因为用这些数目的点可以排成一个正三角形(如图).则第7个三角形数是( )A.27B.28C.29D.304.在△ABC 中，A ∶B ＝1∶2，sin C ＝1，则a ∶b ∶c 等于( ) A ．1∶3∶2 B ．3∶2∶1 C ．1∶2∶3D ．2∶3∶15. 若x ，y 满足⎩⎪⎨⎪⎧2x －y≤0，x ＋y≤3，x ≥0，则2x ＋y 的最大值为( )A.0B.3C.4D.56．在△ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边，若a ＝2bcos C ，则此三角形一定是( )A ．等腰直角三角形B ．等腰三角形C ．直角三角形D ．等腰或直角三角形{}{}157.3717.1941.4119.,3432,,,.7483759D C B A b b a b b a n n T S n T S n b a n n n n n n ）的值为（则都有若对任意自然数项和分别为的前设等差数列+++--=8. 已知函数),(1)(22R b R a b b ax x x f ∈∈+-++-=，对任意实数x 都有)-1()1(x f x f =+成立，若当[]1,1-∈x 时，0)(>x f 恒成立，则b 的取值范围是( )A.(－1，0)B.(2，＋∞)C.(－∞，－1)∪(2，＋∞)D.不能确定9.已知数列{}n a 是等比数列，数列{}n b 是等差数列，若161116117a a a b b b π⋅⋅=-++=,则3948tan 1b b a a +-⋅的值是（ ）A. B.22 C . 22- D.310．若2α＋β＝π，则y ＝cos β－6sin α的最大值和最小值分别是( ) A ．5，－112 B ．7，－112C ．7,5D ．7，－511．不等式x 2＋2x <a b ＋16ba 对任意a ，b ∈(0，＋∞)恒成立，则实数x 的取值范围是( )A ．(－4，2)B ．(－2，0)C ．(－∞，－2)∪(0，＋∞)D ．(－∞，－4)∪(2，＋∞)12.记方程①：2110x a x ++=，方程②：2220x a x ++=，方程③：2340x a x ++=，其中1a ，2a ，3a 是正实数．当1a ，2a ，3a 成等比数列时，下列选项中，能推出方程③无实根的是（ ）A ．方程①无实根，且②有实根B ．方程①无实根，且②无实根C ．方程①有实根，且②有实根D ．方程①有实根，且②无实根二．填空题（本大题共4小题,每小题5分,共20分.）13．在等差数列{}n a 中，91110a a +=，则数列{}n a 的前19项之和是___________． 14．给出平面区域如图阴影部分所示，若使目标函数z ＝ax ＋y (a >0)取得最大值的最优解有无穷多个，则a 的值为________．15．CD CB AD AC AD AB ，AB D ABC 3,,3,===∆且的一个三等分点为中在，则B cos =16．已知a >b ，不等式ax 2＋2x ＋b ≥0对一切实数x 恒成立．又存在x 0∈R ，使ax 20＋2x 0＋b＝0成立，则a 2＋b 2a －b 的最小值为三．解答题：解答应写出文字说明,证明过程或演算步骤（共70分）17. （本题10分）如图所示，在四边形ABCD 中， D ∠=2B ∠，且1AD =，3CD =，cos 3B =． （Ⅰ）求△ACD 的面积；（Ⅱ）若BC =AB 的长．18.（本题12分）已知数列{a n }的前n 项和是S n ，且S n ＋12a n ＝1(n ∈N *).(1)求数列{a n }的通项公式；(2)设b n ＝log 13(1－S n ＋1)(n ∈N *)，令T n ＝1b 1b 2＋1b 2b 3＋…＋1b n b n ＋1，求T n .19．（本题12分）如图，四棱锥S ABCD -中，M 是SB 的中点,//AB CD ，BC CD ⊥，SCDMABCD且2AB BC ==，1CD SD ==，又SD ⊥面SAB . (1) 证明:CD SD ⊥; (2) 证明://CM 面SAD ; (3) 求四棱锥S ABCD -的体积.20．（本题12分）已知2()cos cos 222x x xf x =+. （Ⅰ）若()1f α=，求cos(2)3πα+的值；（Ⅱ）在锐角ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，且满足A c C a b cos cos )2(=-，求)(B f 的取值范围．21. （本题12分） 解关于x 的不等式ax 2－(2a ＋1)x ＋2＜0(a ∈R ).22. （本题12分）数列{}n a 的通项n a 是关于x 的不等式2x x nx -<的解集中正整数的个（1）求数列{}n a 的通项公式；（2）若2nn na b =，求数列{}n b 的前n 项和n S ； （3）求证：对2n ≥且*n N ∈恒有7()112f n ≤<．湛江一中2018-2019学年度第一学期“第一次大考”高二级理科数学普通卷（A ）答案一. 选择题（本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.）二．填空题(本大题共4小题,每小题5分,共20分.)13．95 14． 35 15．1867 16．三．解答题:解答应写出文字说明,证明过程或演算步骤（共70分）17.解：（Ⅰ）311cos 22cos cos 2-=-==B B D ……………………………………………….…………2分因为()0,D π∠∈，所以sin D =，……………………………………………………………………………3分 所以△ACD 的面积1sin 2S AD CD D =⋅⋅⋅=…………………………………………………..………5分 （Ⅱ）在△ACD 中，12cos 2222=⋅⋅-+=D DC AD DC AD AC ， 所以AC =．…………………………………………………………………………………….....………………7分在△ABC 中，12cos 2222=⋅⋅-+=B BC AB BC AB AC …………………………………….………9分把已知条件代入并化简得：042=-AB AB 因为0AB ≠，所以4AB = …………………10分18. 解 (1)当n ＝1时，a 1＝S 1，由S 1＋12a 1＝1，得a 1＝23，…………………………………1分当n ≥2时，S n ＝1－12a n ，S n －1＝1－12a n －1，…………………………………………………………………2分则S n －S n －1＝12(a n －1－a n )，即a n ＝12(a n －1－a n )，所以a n ＝13a n －1(n ≥2). ……………4分故数列{a n }是以23为首项，13为公比的等比数列.故a n ＝23·⎝ ⎛⎭⎪⎫13n －1＝2·⎝ ⎛⎭⎪⎫13n (n ∈N *).………………………………………………………………………………………5分. (2)因为1－S n ＝12a n ＝⎝ ⎛⎭⎪⎫13n.………………………………………………………………………………………………………6分所以b n ＝log 13(1－S n ＋1)＝log 13⎝ ⎛⎭⎪⎫13n ＋1＝n ＋1，……………………………………………………………7分因为1b n b n ＋1＝1（n ＋1）（n ＋2）＝1n ＋1－1n ＋2，………………………………………………………9分 所以T n ＝1b 1b 2＋1b 2b 3＋…＋1b n b n ＋1＝⎝ ⎛⎭⎪⎫12－13＋⎝ ⎛⎭⎪⎫13－14＋…＋⎝ ⎛⎭⎪⎫1n ＋1－1n ＋2＝12－1n ＋2＝n 2（2n ＋2）.……………………12分 19. （1）证明：由SD ⊥面SAB .，AB SAB ⊂面 所以S ⊥………………………………………………………………………………………………………………………1分 又//AB CD …………………………………………………………………………………………………………………………2分 所以C ⊥………………………………………………………………………………………………………………………3分（2）取SA 中点N ，连结,ND NM ………………………………………………………………………..…………4分则//NM AB ，且12MN AB DC ==，//AB CD 所以N 是平行四边形…………………………………………………………………………………..…..…………5分//ND MC ，……………………………………………………………………………………………………………..…………6分 且,ND SAD MC SAD ⊂⊄面面 所以//CM 面SAD ;………………………………………………………………………………………………..…………7分 （3）::3:2S ABCD S ABD ABCD ABD V V S S --∆∆==………………………………………………………..…………8分过D 作DH AB⊥，交于H，由题得BD AD ==..…………9分在,Rt DSA Rt DSB∆∆中，12S A S B ==-=……………………………….…………..…………10分 所以133S ABD D SAB ABS V V DS S --∆==⋅⋅=……………………..………………………………………….……11分所以3323S AV -=⋅-……………………..……………………………………………….……………….……12分(注：其他解法按步骤相应给分) 20．（本小题满分12分）解：（Ⅰ）=)(x f 2s s 222x x xco co ⋅+21cos 21sin 23++=x x ， ………………………………………………2分 21)6sin(++=πx ．………………………………………………………3分由()1f α= ，得1sin()162πα++=，∴1sin()62πα+=．……………………4分 ∴21)6(sin 21)6(2cos )32cos(2=+-=+=+πππx x x ． ………………………5分（Ⅱ）由A c C a b cos cos )2(=-及正弦定理得：A C C AB cos sin cos )sin sin 2(⋅=⋅-．………………………………………………6分 ∴A C C A C B cos sin cos sin cos sin 2⋅=-，B C A C B sin )sin(cos sin 2=+=．……………………………………………8分∵0sin ≠B ，且ABC ∆是锐角三角形，∴21cos =C ，3π=C ． ∴32π=+B A ，A B -=32π． ………………………………………………10分∵20π<<A ， ∴26ππ<<B ． ∴3263πππ<+<B ． ∴1)6sin(23≤+<πB ．………………………………………………………11分 ∵21)6sin()(++=πB B f ，∴)(B f 的取值范围是]23,213(+． ………………………………………12分21. 解关于x 的不等式ax2－(2a ＋1)x ＋2＜0(a ∈R).解：原不等式可化为(ax －1)(x －2)＜0. ……………………………………………………………….……..1分(1) 当a ＞0时，原不等式可以化为a(x －2)⎝⎛⎭⎫x －1a ＜0，等价于(x －2)·⎝⎛⎭⎫x －1a ＜0.(2) 当0＜a ＜12时，2＜1a ，则原不等式的解集是⎩⎨⎧⎭⎬⎫x|2＜x ＜1a ；……………………………………...3分当a ＝12时，原不等式的解集是∅；………………………………………………………………….……….……..5分当a ＞12时，1a ＜2，则原不等式的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪1a ＜x ＜2.………………………………………….……..7分 (2)当a ＝0时，原不等式为－(x －2)＜0，解得x ＞2，即原不等式的解集是{x|x ＞2}.…………………………………………………………………..…………….……..9分 (3)当a ＜0时，原不等式可以化为a(x －2)⎝⎛⎭⎫x －1a ＜0，根据不等式的性质，这个不等式等价于(x －2)·⎝⎛⎭⎫x －1a ＞0，由于1a ＜2，故原不等式的解集是⎩⎨⎧⎭⎬⎫x|x ＜1a 或x ＞2.…………………………………………..….……..11分综上所述，当a ＜0时，不等式的解集为⎩⎨⎧⎭⎬⎫x|x ＜1a 或x ＞2；当a ＝0时，不等式的解集为{x|x ＞2}；当0＜a ＜12时，不等式的解集为⎩⎨⎧⎭⎬⎫x|2＜x ＜1a ； 当a ＝12时，不等式的解集为∅；当a ＞12时，不等式的解集为⎩⎨⎧⎭⎬⎫x|1a ＜x ＜2.……..12分22. 解：（1）2x x nx -<等价于(1)0x x n --<，解得(0,1)x n ∈+ 其中有正整数n 个，于是n a n = …………………………………………..….……...….……..….…….2分（2）1()22nn n n b n ==⋅ 21211112()()222n n n S b b b n =+++=⨯+⨯++⨯……23111111()2()()2222n n S n +=⨯+⨯++⨯… ………………………………..….……...….……..….….3分 两式相减得231111111111()()()()1()()22222222n n n n n S n n ++=++++-⨯=--⨯…….4分 故11112()()=2(2)()222n n n n S n n -=--⨯-+ …………………………..….……...….……..….….6分（3 1111n nn<+++= ………………………………..….……...….……..…...….……..….……...….……...8分 由111111()1212n n n f n a a a n n n n n=+++=+++++++++…… 知11111(+1)++2322122f n n n n n n =+++++++… 于是111111(1)()021********f n f n n n n n n n +-=+->+-=++++++.….……...10分故(1)()f n f n +>()f n ∴当2n ≥且*n N ∈时为增函数7()(2)12f n f ∴≥=综上可知7()112f n ≤< ……………………………..….……...….……..…...….……..….……...….……..12分。
广东省湛江第一中学高二数学上学期第一次大考试题 理
湛江一中2016-2017学年度第一学期“第一次大考”高二级数学理科试卷考试时间：120分钟 满分：150分第Ⅰ卷（选择题 满分60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.)1. ,a b 是任意实数，a b >，且0a ≠，则下列结论正确的是（ ） A. 33a b --< B.1b a< C. 1lg()lga b a b ->- D. 22a b > 2. 在各项均为正数的等比数列{}n a 中，若389a a =，则31310log log a a +=（ ） A. 1 B. 4 C. 2 D. 3log 53. 下列函数中，最小值为4的是( ) A.4()f x x x =+B.4()cos cos f x x x=+ C.()343x xf x -=+⨯ D.()lg 4log 10x f x x =+4．ABC ∆中，1b =，6B π∠=，则ABC ∆的形状一定为（ ）A ．等腰直角三角形B ．直角三角形C ．等边三角形D ．等腰三角形或直角三角形5．已知数列{a n }满足a n ＋1＝⎩⎪⎨⎪⎧2a n⎝⎛⎭⎪⎫0≤a n<12，2a n－1 ⎝ ⎛⎭⎪⎫12≤a n<1.若a 1＝67，则a 2014的值为( )A ．57B ． 67C ．37D ．176．某船开始看见灯塔在南偏东30o 方向，后来船沿南偏东60o的方向航行45km 后，看见灯塔在正西方向，则这时船与灯塔的距离是（ ）A B.30km C ．15km D.7.数列{}n a 满足1a ，21a a -，32a a -，，1n n a a --是首项为1，公比为2的等比数列，那么na 等于( )A ．41n- B ．121n -- C ．21n + D ．21n-8.设n s 是等差数列{}n a 的前n 项和，若5359a a =，则95ss 等于( ) A ．1 B ．－1 C ．2 D ．129．已知n S 是等差数列{}n a 的前n 项和，且675S S S >>，给出下列四个命题：①0d <；②110S >；③ 使0n S >的最大n 值为12；④数列{}n S 中的最大项为11s ，其中正确命题的个数是（ ）A ．4B ．3C ．2D ．1 10.已知ABC ∆是锐角三角形，若B A 2=，则ba的取值范围是( ) A. )3,2( B. )2,2( C. )3,1( D. )2,1(11. 若实数y x ,满足⎪⎩⎪⎨⎧≥+-≤--≥-+01032033my x y x y x ，且y x +的最大值等于9，则实数m 等于( )A ．2-B ．1C ．1-D ．212.己知等差数列{}n a 的公差0d ≠，且1313,,a a a 成等比数列，若11a =，n S 为数列{}n a 的前n 项和，则21445n n S a ++的最小值为（ ）A ．4 B ．272 C ．1219D ．675 第Ⅱ卷 （非选择题 满分90分）二、填空题(本大题共4小题，每小题5分，共20分)13.已知实数,x y 满足1000x y x y x +-≤⎧⎪-≤⎨⎪≥⎩，则2x y -的最大值为 .14．ABC ∆中，角,,A B C 所对的边分别为,,a b c ，已知60,2,A b =︒=ABC S ∆=，则a = .15．已知数列1,111,,,,,12123123n++++++则其前n 项的和等于 .16．给出下列命题：① ,A B 是ABC ∆的内角，且A B >，则sin sin A B >; ② {}n a 是等比数列，则{}1n n a a ++也为等比数列；③ 在数列{}n a 中,如果n 前项和22n S n n =++，则此数列是一个公差为2的等差数列；④ O 是ABC ∆所在平面上一定点，动点P 满足：sin sin AB AC OP OA C B λ⎛⎫=++ ⎪ ⎪⎝⎭，()0,λ∈+∞，则直线AP 一定通过ABC ∆的内心；则上述命题中正确的有 （填上所有正确命题的序号）三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤) 17（本小题满分10分)已知等差数列{}n a 的前n 项和为n S ，且990S =，15240S =． （I ）求{}n a 的通项公式n a ；(II)若数列{}n b 满足：3n n b a =，求{}n b 的前n 项和n T ．18（本小题满分12分）已知函数23()cos()cos()2f x x x x ππ=+--. （I ）求()f x 的最小正周期和最大值； (II) 求()f x 在2[,]63ππ上的单调递增区间．19（本小题满分12分） 已知不等式的解集为或（I ）求a ,b 的值；(II)解不等式2()0ax am b x bm -++<.20.(本小题满分12分)假设我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年，每厘米厚的隔热层建造成本是6万元，天宫一号每年的能源消耗费用H （万元）与隔热层厚度x (厘米)满足关系式：)100(53)(≤≤+=x x kx H （当0=x 时表示无隔热层），若无隔热层，则每年能源消耗费用为8万元.设)(x f 为隔热层建造费用与20年的能源消耗费用之和. （I ）求k 的值和)(x f 的表达式；(II)当隔热层修建多少厘米厚时，总费用)(x f 最小，并求出最小值.21（本小题满分12分）在ABC ∆中,内角,,A B C 对应的边长分别为,,a b c ,已知(,)m c a b =+, (,n a b a =-//m n（I ）求角A ；(II)若a =求b c +的取值范围．22（本小题满分12分）已知数列{}n a 的前n 项和是n S ,12-=n n a S ()*n N ∈. （I ）求数列{}n a 的通项公式；(II)若数列{}n b 满足n n a n b ⋅=2，求数列{}n b 的前n 项和n T ；(III)若数列{}n c 满足()n n nn a c λ1123--+=（λ为非零常数），确定λ的取值范围,使*n N∈时，都有n n c c >+1.湛江一中2016-2017学年度第一学期“第一次大考”高二级数学理科试卷答案 第Ⅰ卷（选择题 满分60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.)第Ⅱ卷 （非选择题 满分90分）二、填空题(本大题共4小题，每小题5分，共20分) 13.1214. 15. 21n n + 16. ①④三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤) 17. （本小题满分10分)解：（I ）设等差数列{}n a 的首项为1a ，公差为d ，由已知可得1193690,15105240a d a d +=+=， ——————— 1分解得12a d ==————————3分2n a n = ————————5分(II) 323n nn b a ==⋅ —— ——————7分 由13n nb b +=，{b n }是首项为6，公比为2的等比数列 ———————8分 则13(13)23313n n n T +-==-- ————————10分18（本小题满分12分）解：1cos 2()-cos )(sin )2x f x x x +=⋅-+（1sin 2cos 2sin(2)223x x x π=-=- ——————4分 （I ）()f x 的最小正周期为π，最大值为1； —————— 8分(II) 当()f x 递增时，222 ()232k x k k Z πππππ-≤-≤+∈，即51212k x k ππππ-≤≤+()k Z ∈, ——————10分 所以，()f x 在5[,]612ππ上递增即()f x 在2[,]63ππ上的单调递增区间是5[,]612ππ —— ———12分 19（本小题满分12分） 解：（I ）因为不等式的解集为或所以，是方程的两个解 —————1分所以， ———————3分解得———————5分(II) 由（I ）知原不等式为，即， —————— 6分当时，不等式解集为 ————————8分当时，不等式解集为; ———————10分当时，不等式解集为; ———————12分20.(本小题满分12分)解：（I ）当0=x 时，8=H ，即85=k，解得40=k ————2分故5340)(+=x x H ——————3分5380065340206)(++=+⨯+=∴x x x x x f )100(≤≤x ————6分 (II) 由（I ）知35535≤+≤x ————7分7010160021053800)53(25340206)(=-≥-+++=+⨯+=∴x x x x x f —————10分当且仅当53800106+=+x x ，即5=x 时)(x f 取得最小值 ————11分即隔热层修建5厘米厚时，总费用达到最小值，最小值为70万元. —12分 21（本小题满分12分） （I ）∵//m n 221cos 2c a B b a b ⎛⎫-=- ⎪⎝⎭, —————1分 由余弦定理得2222222a c b bc a b +--=-,222a b c bc =+- ——————3分 ∵2222cos a b c bc A =+-,∴1cos 2A =————————4分∵()0,πA ∈,∴π3A =————————5分(II)由余弦定理得2sin sin sin a b cA B C===,∴2sin b B =,2sin c C =—————6分∴()2sin 2sin 2sin 2sin b c B C B A B +=+=++ ———————7分2sin 2sin cos 2cos sin B A B A B =++12sin 2cos 2sin 22B B B =+⨯+⨯ π3sin 6B B B ⎛⎫=+=+ ⎪⎝⎭； ————————9分∵2π0,3B ⎛⎫∈ ⎪⎝⎭,∴ππ5π,666B ⎛⎫+∈ ⎪⎝⎭, π1sin ,162B ⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦． ————————11分所以b c +∈————————12分22（本小题满分12分）解：（I ）当n =1时，11121a s a ==-，11a ∴= ————— 1分当1n >时，21n n s a =-，1121n n s a --∴=-112n n n n s s a a --∴-=-122n n n a a a -∴=-12n n a a -∴={}n a 是首项为1，公比为2的等比数列1*2,n n a n N -∴=∈ —————3分(II) 22nn n b n a n =⋅=⋅212222n n T n =⋅+⋅+⋅ ① 23121222(1)22n n n T n n +=⋅+⋅+-⋅+⋅ ②①-②得23122222n n n T n +-=+++-⋅1(1)22n n +=-⋅-1(1)22n n T n +∴=-⋅+ ———————7分(III) ∵11-2)1(23--⋅+=n n n n C λn n n 2)1(31λ--+=∴n n C C >+1即 >-+++112)1(3n n n λn n n 2)1(31λ--+即02)1(2)1(33111>---+--++n n n n n n λλ即0)22()1(321>+-+⋅+n n nnλ即023)1(32>⋅-+⋅nnnλ∴>-λn)1(nn 2332⋅⋅- 即>-λn)1(1)23(--n ——————8分 当n 为偶数时≤--1)23(n 23-∴23->λ ————— 10分当n 为奇数时≤--1)23(n 1- ∴1->-λ即 1<λ 又∵0λ≠∴ 123<<-λ且0λ≠ ——————12分。
广东省湛江市2020-2021学年高二上学期数学期末试卷及答案
广东2020-2021学年第一学期高二期末考试数学（考试时间：120分钟满分：150分）一、选择题（共12小题，每小题5分，共60分）1．命题“∀x∀[0，+∞），x2+2x≥0”的否定是（）A．∀x∀（﹣∞，0），x2+2x≥0B．∀x∀（﹣∞，0），x2+2x＜0C．∀x0∀[0，+∞），x02+2x0≥0D．∀x0∀[0，+∞），x02+2x0＜02．双曲线＝1的焦距是（）A．10B．20C．2D．43．在数列{a n}中，a1＝0，a n＝3a n﹣1+2（n≥2），则a3＝（）A．2B．6C．8D．144．在∀ABC中，角A，B，C所对的边分别为a，b，c，，，，则b＝（）A．B．C．D．5．已知点P（﹣2，4）在抛物线y2＝2px（p＞0）的准线上，则该抛物线的焦点坐标是（）A．（0，2）B．（0，4）C．（2，0）D．（4，0）6．已知双曲线＝1的焦点与椭圆＝1的焦点相同，则m＝（）A．1B．3C．4D．57．“﹣1＜m＜3”是“方程+＝1表示椭圆”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件8．已知双曲线的左、右焦点分别为F1，F2，点P是该双曲线上的一点，且|PF1|＝10，则|PF2|＝（）A．2或18B．2C．18D．49．在∀ABC中，角A，B，C所对的边分别为a，b，c，a sin2B＝b cos A cos B，则∀ABC的形状是（）A．锐角三角形B．直角三角形C．钝角三角形D．不确定10．直线l：y＝kx+2与椭圆C：＝1有公共点，则k的取值范围是（）A．[﹣，]B．（﹣∞，﹣]∀[，+∞）C．[﹣，]D．（﹣∞，﹣]∀[，+∞）11．已知等差数列{a n}的前n项和S n有最小值，且，则使得S n＞0成立的n 的最小值是（）A．11B．12C．21D．2212．双曲线的左、右焦点分别为F1，F2，渐近线分别为l1，l2，过点F1且与l1垂直的直线l交l1于点P，交l2于点Q，若，则双曲线的离心率为（）A．B．C．2D．3二．填空题（共4小题，每小题5分，共20分）13．椭圆4x2+6y2＝24的短轴长是．14．已知a＞b＞0，且a+b＝2，则的最小值是．15．从某建筑物的正南方向的A处测得该建筑物的顶部C的仰角是45°，从该建筑物的北偏东30°的B处测得该建筑物的顶部C的仰角是30°，A，B之间的距离是35米，则该建筑物的高为米．16．已知抛物线C：y2＝4x，点Q在x轴上，直线l：（m﹣2）x﹣y﹣2m+4＝0与抛物线C 交于M，N两点，若直线QM与直线QN的斜率互为相反数，则点Q的坐标是．三．解答题（共6小题，17题10分，18-22每小题12分，共70分）17．已知p：函数f（x）＝|ax﹣m|（a≠0）在区间[1，+∞）上单调递增，q：关于x的不等式x2+mx+m≤0的解集非空．（1）当a＝3时，若p为真命题，求m的取值范围；（2）当a＞0时，若p为假命题是q为真命题的充分不必要条件，求a的取值范围．18．∀ABC的内角A，B，C的对边分别为a，b，c，已知b＝2a，．（1）求C；（2）若，求∀ABC的面积．19．已知抛物线C：x2＝8y的焦点为F，直线l与抛物线C交于M，N两点．（1）若直线l的方程为y＝x+3，求|MF|+|NF|的值；（2）若直线l的斜率为2，l与y轴的交点为P，且＝2，求|MN|．20．已知数列{a n}的前n项和Sn＝2﹣a n，数列{b n}满足b1＝1，b3+b7＝18．且b n+1+b n﹣1＝2b n （n≥2）．（I）数列{a n}和{b n}的通项公式．（II）若b n＝a n•c n，求数列{c n}的前n项和T n．21．如图，在四棱锥P﹣ABCD中，AB∀AD，AD∀BC，P A＝PB＝PD，PE＝2EC，O为BD 的中点．（1）证明：OP∀平面ABCD．（2）若AB＝2，BC＝2AD＝4，P A＝4，求二面角C﹣BD﹣E的余弦值．22．已知椭圆E：＝1（a＞b＞0）的焦距为2，点A在椭圆E上，且|OA|的最小值是（O为坐标原点）．（1）求椭圆E的标准方程；（2）已知动直线l与圆O：x2+y2＝t2（t＞0）相切，且与椭圆E交于P，Q两点．是否存在实数t，使得OP∀OQ？若存在，求出t的值；若不存在，请说明理由．广东2020-2021学年第一学期高二期末考试数学一．选择题（共12小题，每小题5分，共60分）1．命题“∀x∈[0，+∞），x2+2x≥0”的否定是（）A．∀x∈（﹣∞，0），x2+2x≥0B．∀x∈（﹣∞，0），x2+2x＜0C．∃x0∈[0，+∞），x02+2x0≥0D．∃x0∈[0，+∞），x02+2x0＜0【解答】解：命题为全称命题，则命题“∀x∈[0，+∞），x2+2x≥0”的否定：∃x0∈[0，+∞），x02+2x0＜0，故选：D．2．双曲线＝1的焦距是（）A．10B．20C．2D．4【解答】解：双曲线﹣＝1中a＝8，b＝6，∴c＝＝10，∴2c＝20．故选：B．3．在数列{a n}中，a1＝0，a n＝3a n﹣1+2（n≥2），则a3＝（）A．2B．6C．8D．14【解答】解：因为a1＝0，a n＝3a n﹣1+2，所以a2＝3a1+2＝2，则a3＝3a2+2＝8．故选：C．4．在△ABC中，角A，B，C所对的边分别为a，b，c，，，，则b＝（）A．B．C．D．【解答】解：利用正弦定理：因为，所以．故选：A．5．已知点P（﹣2，4）在抛物线y2＝2px（p＞0）的准线上，则该抛物线的焦点坐标是（）A．（0，2）B．（0，4）C．（2，0）D．（4，0）【解答】解：因为点P（﹣2，4）在抛物线y2＝2px的准线上，所以，所以p＝4，则该抛物线的焦点坐标是（2，0）．故选：C．6．已知双曲线＝1的焦点与椭圆＝1的焦点相同，则m＝（）A．1B．3C．4D．5【解答】解：因为椭圆＝1的焦点坐标（，0），双曲线＝1的焦点坐标（，0）所以＝，解得m＝1．故选：A．7．“﹣1＜m＜3”是“方程+＝1表示椭圆”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【解答】解：若方程表示椭圆，则，解得﹣1＜m＜3或3＜m＜7，故“﹣1＜m＜3”是“方程表示椭圆”的充分不必要条件．故选：A．8．已知双曲线的左、右焦点分别为F1，F2，点P是该双曲线上的一点，且|PF1|＝10，则|PF2|＝（）A．2或18B．2C．18D．4【解答】解：因为|PF1|＝10＜a+c＝12，所以点P在该双曲线左支上，则|PF2|＝2a+|PF1|＝2×4+10＝18．故选：C．9．在△ABC中，角A，B，C所对的边分别为a，b，c，a sin2B＝b cos A cos B，则△ABC的形状是（）A．锐角三角形B．直角三角形C．钝角三角形D．不确定【解答】解：因为a sin2B＝b cos A cos B，所以sin A sin2B＝sin B cos A cos B，所以sin B（sin A sin B﹣cos A cos B）＝0，即﹣sin B cos（A+B）＝0．因为0＜A＜π，0＜B＜π，所以，故△ABC是直角三角形．故选：B．10．直线l：y＝kx+2与椭圆C：＝1有公共点，则k的取值范围是（）A．[﹣，]B．（﹣∞，﹣]∪[，+∞）C．[﹣，]D．（﹣∞，﹣]∪[，+∞）【解答】解：∵直线l：y＝kx+2与椭圆C：＝1有公共点，∴联立方程，消去y得：（1+2k2）x2+8kx+6＝0，∴△＝64k2﹣24（1+2k2）≥0，解得：或，故选：B．11．已知等差数列{a n}的前n项和S n有最小值，且，则使得S n＞0成立的n 的最小值是（）A．11B．12C．21D．22【解答】解：由题意可得等差数列{a n}的公差d＞0．因为，所以a12＞0，a11＜0，所以a11+a12＞0，则，S21＝21a11＜0．故使得S n＞0成立的n的最小值是22．故选：D．12．双曲线的左、右焦点分别为F1，F2，渐近线分别为l1，l2，过点F1且与l1垂直的直线l交l1于点P，交l2于点Q，若，则双曲线的离心率为（）A．B．C．2D．3【解答】解：记O为坐标原点．由题意可得F1（﹣c，0），不妨设l1：，l2：，则直线l：．联立，解得，则，故|PF1|＝b，|OP|＝a．因为，所以|PQ|＝2|PF1|，所以|PQ|＝2b，，则．因为，所以，所以，整理得c4﹣4a2c2+3a4＝0，则e4﹣4e2+3＝0，解得．故选：B．二．填空题（共4小题，每小题5分，共20分）13．椭圆4x2+6y2＝24的短轴长是4．【解答】解：由题意椭圆4x2+6y2＝24，即：，可得b＝2，则短轴长是2b＝4．故答案为：4．14．已知a＞b＞0，且a+b＝2，则的最小值是．【解答】解：因为a+b＝2，所以，因为a＞b＞0，所以（当且仅当，时，等号成立），所以，故答案为：．15．从某建筑物的正南方向的A处测得该建筑物的顶部C的仰角是45°，从该建筑物的北偏东30°的B处测得该建筑物的顶部C的仰角是30°，A，B之间的距离是35米，则该建筑物的高为米．【解答】解：设该建筑物的高|OC|＝h（O为该建筑物的底部），由题意可得|OA|＝h，，|AB|＝35，∠AOB＝150°，则|AB|2＝|OA|2+|OB|2﹣2|OA||OB|cos∠AOB，即，解得．故答案为：．16．已知抛物线C：y2＝4x，点Q在x轴上，直线l：（m﹣2）x﹣y﹣2m+4＝0与抛物线C 交于M，N两点，若直线QM与直线QN的斜率互为相反数，则点Q的坐标是（﹣2，0）．【解答】解：如图所示，直线QM、QN交Y轴分别于A、B点，不妨设m＝3，则直线方程为y+2＝x，联立抛物线y2＝4x，得：y2﹣4y﹣8＝0，∴y1+y2＝4，y1y2＝﹣8，设Q（n，0），M（x1，y1），N（x2，y2）∵直线QM与直线QN的斜率互为相反数，∴，∴y1（x2﹣n）+y2（x1﹣n）＝0，∵x＝y+2∴y1（y2+2）+y2（y1+2）﹣n（y1+y2）＝02y1y2+2（y1+y2）﹣n（y1+y2）＝0﹣16+8﹣4n＝0∴n＝﹣2．故答案为：（﹣2，0）．三．解答题（共6小题，17题10分，18-22每小题12分，共70分）17．已知p：函数f（x）＝|ax﹣m|（a≠0）在区间[1，+∞）上单调递增，q：关于x的不等式x2+mx+m≤0的解集非空．（1）当a＝3时，若p为真命题，求m的取值范围；（2）当a＞0时，若p为假命题是q为真命题的充分不必要条件，求a的取值范围．【解答】解：（1）当a＝3时，f（x）＝|3x﹣m|．因为p为真命题，所以，即m≤3，故m的取值范围是（﹣∞，3]．（2）因为p为假命题，所以，因为a＞0，所以m＞a．记满足p为假命题的m的取值集合为A＝（a，+∞）．因为q为真命题，所以m2﹣4m≥0，解得m≤0或m≥4．记满足q为真命题的m的取值集合为B＝（﹣∞，0]∪[4，+∞）．因为p为假命题是q为真命题的充分不必要条件，所以集合A是集合B的真子集，则a ≥4．故a的取值范围是[4，+∞）．18．△ABC的内角A，B，C的对边分别为a，b，c，已知b＝2a，．（1）求C；（2）若，求△ABC的面积．【解答】解：（1）因为b＝2a，所以c2＝a2+b2﹣2ab cos C＝5a2﹣4a2cos C．所以，可得sin C+cos C＝1，整理得．又因为C∈（0，π），所以．（2）由（1）可知，c2＝5a2﹣4a2cos C＝7a2，又因为，所以a＝2，b＝2a＝4．所以．19．已知抛物线C：x2＝8y的焦点为F，直线l与抛物线C交于M，N两点．（1）若直线l的方程为y＝x+3，求|MF|+|NF|的值；（2）若直线l的斜率为2，l与y轴的交点为P，且＝2，求|MN|．【解答】解：（1）设直线l与抛物线C交点M（x1，y1），N（x2，y2），联立方程组，消去x，整理得y2﹣14y+9＝0，所以y1+y2＝14，所以|MF|+|NF|＝y1+2+y2+2＝18，所以|MF|+|NF|的值18；（2）设直线P（0，t），直线l的方程为y＝2x+t，M（x1，y1），N（x2，y2），联立方程组，消去y，整理得x2﹣16x﹣8t＝0，由△＝162+4×8t＞0，则t＞﹣8，所以x1+x2＝16，x1x2＝﹣8t，①因为＝2，（0﹣x1，t﹣y1）＝2（0﹣x2，t﹣y2），所以x1＝2x2，②由①②解得t＝﹣，满足t＞﹣8，所以|MN|＝•＝．20．已知数列{a n}的前n项和Sn＝2﹣a n，数列{b n}满足b1＝1，b3+b7＝18．且b n+1+b n﹣1＝2b n（n≥2）．（I）数列{a n}和{b n}的通项公式．（II）若b n＝a n•c n，求数列{c n}的前n项和T n．【解答】解由题意可得S n＝2﹣a n，①当n≥2时，S n﹣1＝2﹣a n﹣1，②①﹣②得，a n＝S n﹣S n﹣1＝a n﹣1﹣a n，即又a1＝S1＝2﹣a1，可得a1＝1，易知a n﹣1≠0，故数列{a n}是以1为首项，为公比的等比数列，所以由b n+1+b n﹣1＝2b n可知数列{b n}为等差数列，设其公差为d，则，所以d＝＝2，故b n＝b1+（n﹣1）d＝2n﹣1（II）由（I）结合题意可得，＝（2n﹣1）•2n﹣1．则+…+（2n﹣1）×2n﹣1③两边同乘以2得，+…+（2n﹣1）×2n④③﹣④得，﹣T n＝1+2（21+22+23+…+2n﹣1）﹣（2n﹣1）2n整理得，﹣T n＝1+＝﹣（2n﹣3）•2n﹣3故21．如图，在四棱锥P﹣ABCD中，AB⊥AD，AD∥BC，P A＝PB＝PD，PE＝2EC，O为BD 的中点．（1）证明：OP⊥平面ABCD．（2）若AB＝2，BC＝2AD＝4，P A＝4，求二面角C﹣BD﹣E的余弦值．【解答】解：（1）证明：取AD的中点F，连接PF，OF．因为P A＝PD，F为AD的中点，所以AD⊥PF．因为O为BD的中点，F为AD的中点，所以OF∥AB．因为AB⊥AD，所以OF⊥AD，因为OF∩PF＝F，OF⊂平面POF，PF⊂平面POF，所以AD⊥平面POF．又OP⊂平面POF，所以AD⊥OP．因为PB＝PD，O为BD的中点，所以PO⊥BD．因为AD∩BD＝D，AD⊂平面ABCD，BD⊂平面ABCD，所以OP⊥平面ABCD．（2）解：以O为坐标原点，平行AD的直线为x轴，FO所在直线为y轴，OP所在直线为z轴，建立如图所示的空间直角坐标系O﹣xyz．则O（0，0，0），B（﹣，1，0），D（，﹣1，0），C（3，1，0），P（0，0，2）．因为PE＝2EC，所以E（2，，），故＝（2，﹣2，0），＝（，，），＝（0，0，2）．设平面BDE的法向量＝（x，y，z），则，取x＝1，则＝（1，，﹣4）．记二面角C﹣BD﹣E的大小为θ，由图可知θ为锐角，则cosθ＝|cos＜＞|＝＝＝．∴二面角C﹣BD﹣E的余弦值为．22．已知椭圆E：＝1（a＞b＞0）的焦距为2，点A在椭圆E上，且|OA|的最小值是（O为坐标原点）．（1）求椭圆E的标准方程；（2）已知动直线l与圆O：x2+y2＝t2（t＞0）相切，且与椭圆E交于P，Q两点．是否存在实数t，使得OP⊥OQ？若存在，求出t的值；若不存在，请说明理由．【解答】解：（1）因为|OA|的最小值是，所以b＝，因为椭圆E的焦距为2，所以2c＝2，即c＝，所以a2＝b2+c2＝4，故椭圆E的标准方程是；（2）①当直线l的斜率不存在时，因为直线l与圆O相切，所以直线l的方程为x＝±t，则直线l与椭圆E的交点为（t，）或（﹣t，），因为OP⊥OQ，所以，所以，即t＝，②当直线l的斜率存在时，可设直线l的方程为y＝kx+m，P（x1，y1），Q（x2，y2），联立，整理得：（2k2+1）x2+4kmx+2m2﹣4＝0，则，，因为P（x1，y1），Q（x2，y2），在直线l上，所以y1y2＝（kx1+m）（kx2+m）＝，将则，代入上式，得：，因为OP⊥OQ，所以，即3m2＝4（k2+1），因为动直线l与圆O相切，所以，所以，即t＝，综上，存在t＝，使得OP⊥OQ．。
广东省湛江市第一中学高二上学期期末考试数学(文)试卷
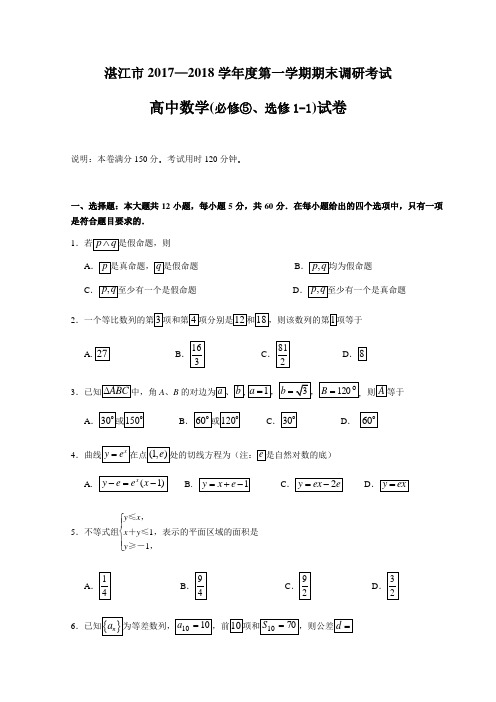
湛江市2017—2018学年度第一学期期末调研考试高中数学(必修⑤、选修1-1)试卷说明：本卷满分150分．考试用时120分钟．一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1A BC D2A B C D3A 、BA B C D ．4A .B .C D5．不等式组⎩⎪⎨⎪⎧y ≤x ，x ＋y ≤1，y ≥－1，表示的平面区域的面积是A B C D6A B C.D.7ABCD8.A.B.C.D.9A.B.C.D.10A B C D11A B C D12．A B C D二、填空题：本大题共4小题，每小题5分，满分20分．13__________．1415__________.16________.三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17.（本小题满分10分）18.（本小题满分12分）.19.（本小题满分12分）（Ⅰ）求椭圆的方程；20.（本小题满分12分）某农场计划种植甲、乙两个品种的水果，甲、问该农场如何分配甲、乙两种水果的种植面积，可使农场的总收益最大？最大收益是多少万元？21.（本小题满分12分）在.22.（本小题满分12分）F，抛物线上的点A到y轴的距离等于（Ⅰ）求p的值；（Ⅱ）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，求N的横坐标的取值范围．湛江市2017—2018学年度第一学期期末调研考试高中数学（必修⑤、选修1-1）参考答案与评分标准一、选择题：本大题共12小题，每小题5分，共60分．二、填空题：本大题共4小题，每小题5分，共20分．1314．1；15；16．三、解答题：解答应写出文字说明、证明过程或演算步骤．17. 解：2分………………………………………………………5分∴. ……………………………………………………5分6分∴7分10分18．解：1分．…………………………………3分5分nb++①…………………………………6分得②……………………7分①-8分9分……………………………………………………………………………11分12分19. 解：（Ⅰ）由题得：2分解得,…………………………………………………………………………………………………4分椭圆的方程为…………………………………………………………………………………………5分 （Ⅱ），直线的方程是6分由（*）…………………………………………………………………………7分 设，（*）8分………………10分的面积是 (12)分20. 解：设甲、乙两种水果的种植面积分别为x ，y 亩，农场的总收益为z 万元，则 ………1分…………4分……………5分可行域如图所示，……………………………7分由此可知当目标函数对应的直线经过点M9分10分11分 答：分别种植甲乙两种水果75亩和225亩，可使农场的总收益最大，最大收益为67.5万元． ………………………………………………………………………………12分21.………………………………………2分…………………………4分………………………………………6分（Ⅱ）由（I ）知7分8分.10分，………………………………………………………………12分22.解：（Ⅰ）由题意可得抛物线上点A到焦点F的距离等于点A 离.……………………2分由抛物线的定义得，即p=2. …………………………………………………………………………………4分（Ⅱ）由（Ⅰ）得抛物线的方程为，可设……………………………5分由题知AF不垂直于yx6分故，所以…………………………………………………………………………………7分又直线AB FN从而的直线FN:，直线BN9分 由解得N 的横坐标是，其中10分综上，点N 的横坐标的取值范围是…………………………………………………………12分注:如上各题若有其它解法，请评卷老师酌情给分.。
广东省湛江市第一中学2024届高三上学期开学考试数学试题及参考答案
湛江第一中学2024届高三级开学考试数学全卷满分150分，考试时间120分钟.注意事项：1.答题前，先将自己的姓名､准考证号填写在试卷和答题卡上，并将条形码粘贴在答题卡上的指定位置.2.请按题号顺序在答题卡上各题目的答题区域内作答，写在试卷､草稿纸和答题卡上的非答题区域均无效.3.选择题用2B 铅笔在答题卡上把所选答案的标号涂黑；非选择题用黑色签字笔在答题卡上作答；字体工整，笔迹清楚.4.考试结束后，请将试卷和答题卡一并上交.5.本卷主要考查内容：高考范围.一､单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}12e 1,20x M x N x x x −=>=−<∣∣，则M N ∪=（ ） A.()0,1 B.()0,∞+ C.()1,2 D.()2,∞+2.已知复数()()12i 12i z +−=−+，则z =（ ）3.在ABC 中，D 为BC 中点，M 为AD 中点，BM mAB nAC =+ ，则m n +=（ ） A.12 B.1 C.12− D.-1 4.已知函数()2313xx f x −+=，则()f x 的增区间为（ ） A.3,2∞ + B.3,2∞ −+ C.3,2∞ −− D.3,2∞ −5.设公差不为零的等差数列{}n a 的前n 项和为451,2n S a a =，则94S S =（ ） A.15 B.1 C.-1 D.-96.已知抛物线2:2(0)C x py p =>的焦点为F ，准线为l ，点()()00,10P x x >在抛物线C 上，过P 作l 的垂线，垂足为Q ，若PO PQ =（O 为坐标原点），则0x =（ ）A. B.3 C.7.已知θ为钝角，2cos2sin2cos θθθ−=，则tan3θ的值为（ ） A.43− B.-2 C.83− D.211− 8.已知函数()2sin (0)3f x x πωω=+> 且满足236f x f x ππ −=−，则ω的最小值为（ ） A.12 B.23C.1D.2 二､多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.一组数据：0,1,5,6,7,11,12，则（ ）A.这组数据的平均数为6B.这组数据的方差为16C.这组数据的极差为11D.这组数据的第70百分位数为710.已知函数()2ln f x x x x x =−−，则（ ） A.()f x 有两个零点 B.()f x 有两个极值点C.()0f x 恒成立D.()0f x ′ 恒成立11.已知圆22:(3)(1)1C x y −+−=与圆222:()(2)(,0)M x m y m r m r −+−=∈>R 相交于,A B 两点，则（ ）A.圆C 的圆心坐标为()3,1B.当2r =时，11m <<+C.当MA CA ⊥且3r =时，2m =D.当2AB =时，r12.《九章算术》里说：“斜解立方，得两堑堵，斜解堑堵，其一为阳马，一为鳖臑”.如图，底面是直角三角形的直三棱柱称为“堑堵”，沿截面PAC 将一个“堑堵”截成两部分，其三棱锥称为“鳖臑”.在鳖臑P ABC −中，,PA AB AB ⊥16π，当此鳖臑的体积V 最大时，下列结论正确的是（ ）A.PA BC ==B.此鳖臑的体积VC.直线PC 与平面PAB 所成角的余弦值为34D.三棱锥P ABC − 三､填空题：本题共4小题，每小题5分，共20分.13.二项式52x的展开式中含5x 的系数为__________. 14.小张､小陈､小胡独立的做一道数学题，小张做出这道题的概率为23，小陈做出这道题的概率为45，小胡做出这道题的概率为56，每个人是否做出这道题相互没有影响，则这道题被做出来的概率为__________. 15.已知函数()()12ln e x f x a x x =−− 在()1,∞+上单调递增，则实数a 的取值范围为__________.16.双曲线2222:1(0,0)x y C a b a b−=>>的左，右焦点分别为12,F F ，右支上有一点M ，满足121290,F MF F MF ∠= 的内切圆与y 轴相切，则双曲线C 的离心率为__________.四､解答题：本题共6小题，共70分.解答应写出必要的文字说明､证明过程及演算步骤. 17.（本小题满分10分）在ABC 中，内角,,A B C 所对的边分别为,,a b c ，已知cos A =.（1）若2b c ，求a 的值；（2）若22a bc=，求角,B C 的大小. 18.（本小题满分12分）已知数列{}n a 满足1111,13n n a a a n+==+. （1）求数列{}n a 的通项公式；（2）求数列{}n a 的前n 项和n S .19.（本小题满分12分）如图，直三棱柱111ABC A B C −中，平面1A BC ⊥平面11ABB A .（1）证明：AB BC ⊥；（2）若12,AA AC BC E ==为1BB 上一点，且13BE EB =，求二面角1E A C B −−的余弦值. 20.（本小题满分12 分）2023年的高考已经结束，考试前一周，某高中进行了一场关于高三学生课余学习时间的调查问卷，现从高三12个班级每个班随机抽取10名同学进行问卷，统计数据如下表：课余学习时间超过两小时 课余学习时间不超过两小时 200名以前40 10x + 200名以后 310x −40 （1）求x 的值；（2）依据上表，根据小概率值0.001α=的独立性检验，分析学生成绩与课余学习超过两个小时是否有关系；（3）学校在成绩200名以前的学生中，采用分层抽样，按课余学习时间是否超过两小时抽取6人，再从这6人中随机抽取3人，记这3人中课余学习时间超过两小时的学生人数为X ，求X 的分布列和数学期望.附：参考公式：()()()()22()n ad bc a b cd a c b d χ−=++++，其中n a b c d =+++. a 0.10 0.05 0.010 0.005 0.001a x 2.706 3.841 6.635 7.879 10.82821.（本小题满分12分）已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ，上顶点为,2B BF =，离心率为12. （1）求椭圆E 的标准方程；（2）若直线():20l y x m m =−≠与椭圆E 相交于,A C 两点，且点()0,N m ，当ACN 的面积最大时，求直线l 的方程.22.（本小题满分12分）已知函数()1e ln x f x x −=−.（1）求函数()f x 的最小值；（2）求证：()()1e e 1ln e 02x xf x x x +−−+>. 湛江第一中学2024届高三级开学考试•数学参考答案､提示及评分细则1.B 由1e 1x −>得10e e x −>，函数e x y =在R 上单调递增，则10x −>，即{1}M x x =>∣，又由220x x −<得02x <<，即{02}N xx =<<∣，所以{0}M N x x ∪=>∣.故选B.2.A ()()()()2i 12i 2i 5i 1111i 12i 12i 12i 5z −+−−+=+=+=+=+++−，则z =.故选A. 3.C ()111131311,,,222444442BM BA BD AB AC AB AB AC m n m n =+=−+−=−+∴=−=∴+=− .故选C. 4.A 令231,3u u x x y =−+=，又3u y =在R 上单调递增，231u x x =−+的增区间为3,2∞ +，所以()f x 的增区间为3,2∞ +.故选A. 5.D ()454445141411,,,2.32,22a a a a d a d a d a a d d a a d =∴=+==∴=−=−+=− .()()()199541414929499444a a S a d S a a a a d +×××∴====−+×+×−×.故选D.6.A 因为PO PQ PF ==，所以122p =×，即2204,8,81p x y x ===×，又000,x x >∴ 7.D 由2cos2sin2cos θθθ−=得22sin cos sin θθθ−=，化简得2cos sin ,tan 2θθθ−==−， 则22tan 4tan2tan 2tan2,tan31tan 31tan2tan 11θθθθθθθθ+====−−−.故选D. 8.B 由236f x f x ππ −=−可知：()f x 关于4x π=对称，故2,4,04323k k k πππωπω⋅+=+=+=时，ω取最小值为23.故选B. 9.AD A ：()101567111267×++++++=，故A 正确； B ：()22222221124651015677×++++++=，故B 错误； C :12012−=，故C 错误；D :770% 4.9×=，故70百分位数是第5个数7.故D 正确.故选AD.10.BC ():01ln 0,1ln A f x x x x x =⇔−−− ，当且仅当1x =时取等号，故A 错误，C 正确；B ：()()12122ln ,2x f x x x f x x x ′′−−−′=−，在10,2 上，()()0,f x f x <′′′为减函数，在1,2∞ +上，()0f x ′′>，()f x ′为增函数，又()2110,0,10e 2f f f ><= ′′ ′ ，有2个零点，B 正确，D 错误.故选BC.11.ABD 由圆C 的方程可知圆C 的圆心坐标为()3,1，即A 正确；当2r =时，圆22:()(2)4M x m y m −+−=，此时易知21MC >−，所以有3MC =<，解得11m −<<B 正确； 因为MA CA ⊥，且3r =，所以222||3110CM =+=，即22(3)(21)10m m −+−=，解得0m =或2m =，即C 错误；因为圆C 的直径为2，所以当2AB =时，AB 为圆C 的直径，所以222222||1(3)(21)1510115(1)6r MC m m m m m =+=−+−+=−+=−+，当且仅当1m =时，min r =，即D 正确.故选ABD.12.BC 由题可知，PC 的中点即为P ABC −的外接球的球心，设外接球的半径为R ，则2416R ππ=，得2R =，因为222224PA AB BC PC R ++==，所以2214PA BC +=，鳖臑P ABC −的体积()()2211232P ABC V AB BC PA BC PA BC PA −=×⋅⋅⋅+，当且仅当BC PA ==()max P ABC V −=，故A 项错误，B 项正确； 因为三棱柱为直三棱柱，故BC ⊥平面PAB ，所以直线PC 与平面PAB 所成的角即为3,sin 4BP BPC BPC PC ∠∠==；故C 项正确； 设鳖臑P ABC −的内切球半径为r，由等体积法1111132222P ABC V AB BC AB PA AC PA PB BC r − =×⋅+⋅+⋅+⋅⋅(13r ，所以r =，故D 项错误.故选BC. 13.10 展开式通项公式为()()551252155C C (1)rr r r r r r T x x −−−+ =⋅=⋅−⋅ ，令()5152r −=，得3r =， ∴展开式中含5x 的系数为325C (1)10⋅−=. 14.8990 记“这道题被做出来”为事件()11189,1135690A P A P A =−=−××=. 15.[)2,∞+ ()()2212ln e 2ln e 0x x f x a a x x ax x x x =−+−−=−− ′ ，即22ln 0ax x x −− ，对()1,x ∞∈+恒成立，当2a 时，()()22222222222ln 22ln ,2x x ax x x x g x g x x x x x x−+−−−−==+−=>′ 0，故()()10g x g >=符合题意，当2a <时，()()120,1,g a m ∞=−<∃∈+，在()1,m 上，()0g x <不合题意，故2a .1+ 内切圆Q 分别与1212,,F M F M F F 切于点,,S T N ，则四边形QSMT 为正方形，故1212122,2F M F M F F a F M F M a +−=−=，2222212,(2)(2)22, 1.F M c a c a c c c a ac e =+∴++=⇒=++17.解：（1）根据余弦定理，222cos 22b c a A b c bc +−==，解得1a =；（2）因为2222cos 22b c a a A bc bc+−===−，，则2()02b c bc −=， 即2()0b c −=，所以b c =，因此三角形为等腰三角形，又知道6A π=，所以512B C π==18.解：（1）由1113n n a a n +=+，得131n n a a n n+=×+， 又11,1n a a n =∴是以1为首项，3为公比的等比数列， 113,3n n n n a a n n−−∴==×； （2）01113233n n S n −=×+×++× ，① ①3×得12313233n n S n =×+×++× ，② ①-②得121133121333333132n n n nn n n S n n n −−−−=++++−×=−×=−×−，()21314n n n S −×+∴=. 19.证明：（1）过A 作1AD A B ⊥于D ，平面1A BC ⊥平面11ABB A ，且平面1A BC ∩平面111ABB A A B =，AD ∴⊥平面1A BC ，故AD BC ⊥，在直三棱柱111ABC A B C −中，1AA ⊥平面ABC ，故1BC AA ⊥，由1AD AA A ∩=可知，BC ⊥平面11AA B B ，故BC AB ⊥；（2）以B 为坐标原点，1,,BC BA BB 为,,x y z 轴建立空间直角坐标系， 不妨设2BC = ，则()()()()()112,0,0,0,,0,0,4,0,4,0,0,3C A B A E ，则()()()112,4,0,4,2,0,3CA BA CE −=− ， 设平面1A EC 的法向量为()111,,m x y z =， 则10,0,m CA m CE ⋅= ⋅=即11111240,230,x z x z −++= −+=令1z =111x y ==−，即(1,m =−，设平面1A BC 的法向量为()222,,n x y z =， 则110,0,n CA n BA ⋅= ⋅=即2222220,20,x z z −++= +=令2z =220,2x y ==−，即(0,n =− ，则cos ,m n m n m n ⋅==⋅ ， 二面角1E A C B −−. 20.解：（1）由题意可得高三12个班级共抽取120名，所以401031040120x x +++−+=，解得10x =；（2）利用列联表可得22120(40402020)4013.33310.828606060603χ××−×==≈>×××， 根据小概率值0.001α=的独立性检验，我们认为学生课余学习时间超过两小时跟学生成绩有关，此推断犯错误概率不大于0.001；（3）这6人中课余学习时间超过两小时的人数为40644020×=+，课余学习时间不超过两小时的人数为2， X 的取值为1,2,3，有()124236C C 11C 5P X ===； ()214236C C 32;C 5P X === ()3436C 13C 5P X ===. 故X 的分布列为：()1311232555E X =×+×+×=.21.解：（1）由题意可知22212,e ,1,32c BF a c b a c a ======−=，所以椭圆E 的方程为22143x y +=； （2）由直线l 的方程为2y x m =−，则点()0,N m 到直线l的距离为d = 联立方程组221,432,x y y x m += =−整理可得2271616120x mx m −+−=， 由判别式()22Δ2564716120m m =−×−>，解得m ∈∪ ，设()()1122,,,A x y C x y ，则21212161612,77m m x x x x −+=⋅=， 可得AC ====所以1122ACN S AC d =⋅=227442m m −+==m =∪时，等号成立），所以所求直线的方程为y x=+y x =22.（1）解：()1e ln x f x x −=− ，()11e x f x x−=−′∴， 设()()11211e ,e 0x x x x x x µµ−−=−+′=>， ()x µ∴在()0,∞+上为单调递增函数， ()()10,10f µ′=∴=，当()0,1x ∈时，()0f x ′<，当()1,x ∞∈+时，()0,1f x x >∴=′时，()f x 取得最小值，()min ()11f x f ==； （2）证明：()()1e e 1ln e 02x xf x x x +−−+>，只需证()()11e e ln e 1ln e 02x x x x x x −−+−−+>， 即()11e ln 02x x x −−+>，令()()11e ln 2x g x x x =−−+，则()1e (0)x g x x x x =−>′， 当0x >时，令()()1e x h x g x x x′==−，则()()()211e 0,x h x x h x x =++>′在()0,∞+上单调递增， 即()1e x g x x x=−′在()0,∞+上为增函数， 又因为222333223227e e 0,(1)e 1033238g g ′′ =−=−<=−> ， 所以存在02,13x ∈，使得()00g x ′=， 由()00200000e 11e 0x x x g x x x x ′−=−==， 得020e 1x x =，即0201e x x =，即002ln x x −=， 所以当()00,x x ∈时，()()1e 0,x g x x g x x=−<′单调递减， 当()0,x x ∞∈+时，()()1e 0,x g x x g x x=−>′单调递增， 所以()()03200000min 000220012211()1e ln 2222x x x x x x g x g x x x x x −++−−−+++， 令()3222213x x x x x ϕ =++−<<， 则()22153223033x x x x ϕ =++=++>′， 所以()x ϕ在2,13上单调递增，所以()0220327x ϕϕ >=> ，所以()()()002002x g x g x x ϕ=> ，所以()11e ln 02x x x −−+>， 即()()1e e 1ln e 0.2x xf x x x +−−+>。
广东省湛江一中2020-2021学年高二数学上学期期末考试 理 新人教A版
广东省湛江一中2020-2021学年高二上学期期末考试含答案（数学理）考试时间：120分钟 满分：150分一．选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.命题“若3a b +≠，则12a b ≠≠或”的逆否命题为（ ）A. 若3a b +=，则12a b ==且B. 若12a b ==或，则3a b +=C. 若12a b ≠≠或，则3a b +≠D. 若12a b ==且，则3a b +=2.抛物线y =42x 的焦点坐标是（ ）A. （1,0）B. (0,1)C. (0,161) D. ()0,161 3.已知)5,2,3(-=a ，)1,,1(-=x b ，2=•b a ，则x 的值为（ ）A. 3B. 4C. 5D. 64.“13-<<-m ”是方程11222=+++m y m x 表示双曲线的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件5. 以下四个命题中正确的是 ( )A ．若1123OP OA OB =+,则P 、A 、B 三点共线; B ．若{,,}a b c 为空间的一个基底，则{,,}a b b c c a +++构成空间的另一个基底;C ．|()|||||||a b c a b c •=⋅⋅;D ．ABC ∆为直角三角形的充要条件是0AB AC ⋅=．6. 在棱长为1的正方体1111D C B A ABCD -中，M 和N 分别为11B A 和1BB 的中点，那么直线AM 与CN 所成角的余弦值是（ ） A ．1010 B ． 52- C ．53 D ．527.设双曲线)0,0(12222>>=-b a by a x 的一条渐近线与抛物线12+=x y 有公共点，则双曲线的离心率e 的取值范围是（ ）A. [)+∞,5B. [)+∞,5C. ⎪⎪⎭⎫⎢⎣⎡+∞,25D. ⎪⎭⎫⎢⎣⎡+∞,45 8.若椭圆或双曲线上存在点P ，使得点P 到两个焦点的距离之比为2:1，则称此椭圆或双曲线为“倍分曲线”，则下列曲线中是“倍分曲线”的是（ ）A. 1151622=+y xB. 1242522=+y x C. 11522=-y x D. 122=-y x 二、填空题：本大题共6小题，每小题5分，共30分．9.抛物线x y 82=上与焦点的距离等于6的点的坐标是 .10.已知向量),215,,3(),5,3,2(λ=-=b a 且a ∥b ，则λ= . 11.点)1,4(P 平分双曲线4422=-y x 的一条弦，则这条弦所在的直线方程是12.过椭圆22154x y +=的右焦点作一条斜率为2的直线与椭圆交于A 、B 两点，O 为坐标原点，则△OAB 的面积为______________13.已知=a (3cos ,3sin ,1)αα，(2cos ,2sin ,1)b ββ=，则b a -的取值范围是 . 14.给出下列命题：①椭圆12322=+y x 的离心率35=e ，长轴长为32；②抛物线22y x =的准线方程为;81-=x ③双曲线1254922-=-x y 的渐近线方程为x y 75±=；④方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率. 其中所有正确命题的序号是 .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤。
广东省湛江第一中学高二数学上学期第一次大考试题 理
湛江一中2016-2017学年度第一学期“第一次大考”高二级数学理科试卷考试时间：120分钟 满分：150分第Ⅰ卷（选择题 满分60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.)1. ,a b 是任意实数，a b >，且0a ≠，则下列结论正确的是（ ） A. 33a b --< B.1b a< C. 1lg()lga b a b ->- D. 22a b > 2. 在各项均为正数的等比数列{}n a 中，若389a a =，则31310log log a a +=（ ） A. 1 B. 4 C. 2 D. 3log 53. 下列函数中，最小值为4的是( ) A.4()f x x x =+B.4()cos cos f x x x=+ C.()343x xf x -=+⨯ D.()lg 4log 10x f x x =+4．ABC ∆中，1b =，6B π∠=，则ABC ∆的形状一定为（ ）A ．等腰直角三角形B ．直角三角形C ．等边三角形D ．等腰三角形或直角三角形5．已知数列{a n }满足a n ＋1＝⎩⎪⎨⎪⎧2a n⎝⎛⎭⎪⎫0≤a n<12，2a n－1 ⎝ ⎛⎭⎪⎫12≤a n<1.若a 1＝67，则a 2014的值为( )A ．57B ． 67C ．37D ．176．某船开始看见灯塔在南偏东30o 方向，后来船沿南偏东60o的方向航行45km 后，看见灯塔在正西方向，则这时船与灯塔的距离是（ ）A B.30km C ．15km D.7.数列{}n a 满足1a ，21a a -，32a a -，L ，1n n a a --是首项为1，公比为2的等比数列，那么n a 等于( )A ．41n- B ．121n -- C ．21n + D ．21n-8.设n s 是等差数列{}n a 的前n 项和，若5359a a =，则95ss 等于( ) A ．1 B ．－1 C ．2 D ．129．已知n S 是等差数列{}n a 的前n 项和，且675S S S >>，给出下列四个命题：①0d <；②110S >；③ 使0n S >的最大n 值为12；④数列{}n S 中的最大项为11s ，其中正确命题的个数是（ ）A ．4B ．3C ．2D ．1 10.已知ABC ∆是锐角三角形，若B A 2=，则ba的取值范围是( ) A. )3,2( B. )2,2( C. )3,1( D. )2,1(11. 若实数y x ,满足⎪⎩⎪⎨⎧≥+-≤--≥-+01032033my x y x y x ，且y x +的最大值等于9，则实数m 等于( )A ．2-B ．1C ．1-D ．212.己知等差数列{}n a 的公差0d ≠，且1313,,a a a 成等比数列，若11a =，n S 为数列{}n a 的前n 项和，则21445n n S a ++的最小值为（ ）A ． 4194-B ．272 C ．1219D ．675 第Ⅱ卷 （非选择题 满分90分）二、填空题(本大题共4小题，每小题5分，共20分)13.已知实数,x y 满足1000x y x y x +-≤⎧⎪-≤⎨⎪≥⎩，则2x y -的最大值为 .14．ABC ∆中，角,,A B C 所对的边分别为,,a b c ，已知60,2,A b =︒=23ABC S ∆=，则a = .15．已知数列1,111,,,,,12123123n ++++++L L L 则其前n 项的和等于 . 16．给出下列命题：① ,A B 是ABC ∆的内角，且A B >，则sin sin A B >; ② {}n a 是等比数列，则{}1n n a a ++也为等比数列；③ 在数列{}n a 中,如果n 前项和22n S n n =++，则此数列是一个公差为2的等差数列；④ O 是ABC ∆所在平面上一定点，动点P 满足：sin sin AB AC OP OA C B λ⎛⎫=++ ⎪ ⎪⎝⎭u u u r u u u ru u u r u u u r ，()0,λ∈+∞，则直线AP 一定通过ABC ∆的内心；则上述命题中正确的有 （填上所有正确命题的序号）三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤) 17（本小题满分10分)已知等差数列{}n a 的前n 项和为n S ，且990S =，15240S =． （I ）求{}n a 的通项公式n a ；(II)若数列{}n b 满足：3n n b a =，求{}n b 的前n 项和n T ．18（本小题满分12分）已知函数233()cos()cos()3cos 22f x x x x ππ=+--+. （I ）求()f x 的最小正周期和最大值； (II) 求()f x 在2[,]63ππ上的单调递增区间．19（本小题满分12分） 已知不等式的解集为或（I ）求a ,b 的值；(II)解不等式2()0ax am b x bm -++<.20.(本小题满分12分)假设我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年，每厘米厚的隔热层建造成本是6万元，天宫一号每年的能源消耗费用H （万元）与隔热层厚度x (厘米)满足关系式：)100(53)(≤≤+=x x kx H （当0=x 时表示无隔热层），若无隔热层，则每年能源消耗费用为8万元.设)(x f 为隔热层建造费用与20年的能源消耗费用之和. （I ）求k 的值和)(x f 的表达式；(II)当隔热层修建多少厘米厚时，总费用)(x f 最小，并求出最小值.21（本小题满分12分）在ABC ∆中,内角,,A B C 对应的边长分别为,,a b c ,已知(,)m c a b =+u r , 1(,cos )2n a b a B b =--r ,//m n u r r（I ）求角A ；(II)若3a =求b c +的取值范围．22（本小题满分12分）已知数列{}n a 的前n 项和是n S ,12-=n n a S ()*n N ∈. （I ）求数列{}n a 的通项公式；(II)若数列{}n b 满足n n a n b ⋅=2，求数列{}n b 的前n 项和n T ；(III)若数列{}n c 满足()n n nn a c λ1123--+=（λ为非零常数），确定λ的取值范围,使*n N∈时，都有n n c c >+1.湛江一中2016-2017学年度第一学期“第一次大考”高二级数学理科试卷答案 第Ⅰ卷（选择题 满分60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.)第Ⅱ卷 （非选择题 满分90分）二、填空题(本大题共4小题，每小题5分，共20分) 13.1214. 315. 21n n + 16. ①④三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤) 17. （本小题满分10分)解：（I ）设等差数列{}n a 的首项为1a ，公差为d ，由已知可得1193690,15105240a d a d +=+=， ——————— 1分解得12a d ==————————3分2n a n = ————————5分(II) 323n nn b a ==⋅ —— ——————7分 由13n nb b +=，{b n }是首项为6，公比为2的等比数列 ———————8分 则13(13)23313n n n T +-==-- ————————10分18（本小题满分12分）解：1cos 23()-cos )(sin )32x f x x x +=⋅-+（ 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ACCDBADABABC13sin 2cos 2sin(2)223x x x π=-=- ——————4分 （I ）()f x 的最小正周期为π，最大值为1； —————— 8分(II) 当()f x 递增时，222 ()232k x k k Z πππππ-≤-≤+∈，即51212k x k ππππ-≤≤+()k Z ∈, ——————10分 所以，()f x 在5[,]612ππ上递增即()f x 在2[,]63ππ上的单调递增区间是5[,]612ππ —— ———12分 19（本小题满分12分） 解：（I ）因为不等式的解集为或所以，是方程的两个解 —————1分所以， ———————3分解得———————5分(II) 由（I ）知原不等式为，即， —————— 6分当时，不等式解集为 ————————8分当时，不等式解集为; ———————10分当时，不等式解集为; ———————12分20.(本小题满分12分)解：（I ）当0=x 时，8=H ，即85=k，解得40=k ————2分故5340)(+=x x H ——————3分5380065340206)(++=+⨯+=∴x x x x x f )100(≤≤x ————6分 (II) 由（I ）知35535≤+≤x ————7分7010160021053800)53(25340206)(=-≥-+++=+⨯+=∴x x x x x f —————10分当且仅当53800106+=+x x ，即5=x 时)(x f 取得最小值 ————11分即隔热层修建5厘米厚时，总费用达到最小值，最小值为70万元. —12分 21（本小题满分12分） （I ）∵//m n u r r221cos 2c a B b a b ⎛⎫-=- ⎪⎝⎭, —————1分 由余弦定理得2222222a c b bc a b +--=-,222a b c bc =+- ——————3分 ∵2222cos a b c bc A =+-,∴1cos 2A =————————4分∵()0,πA ∈,∴π3A =————————5分(II)由余弦定理得2sin sin sin a b cA B C===,∴2sin b B =,2sin c C =—————6分∴()2sin 2sin 2sin 2sin b c B C B A B +=+=++ ———————7分2sin 2sin cos 2cos sin B A B A B =++312sin 2cos 2sin 22B B B =+⨯+⨯ π3sin 3cos 23sin 6B B B ⎛⎫=+=+ ⎪⎝⎭； ————————9分∵2π0,3B ⎛⎫∈ ⎪⎝⎭,∴ππ5π,666B ⎛⎫+∈ ⎪⎝⎭, π1sin ,162B ⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦． ————————11分所以(3,23b c ⎤+∈⎦ ————————12分22（本小题满分12分）解：（I ）当n =1时，11121a s a ==-，11a ∴= ————— 1分当1n >时，21n n s a =-，1121n n s a --∴=-112n n n n s s a a --∴-=-122n n n a a a -∴=-12n n a a -∴={}n a 是首项为1，公比为2的等比数列1*2,n n a n N -∴=∈ —————3分(II) 22nn n b n a n =⋅=⋅212222n n T n =⋅+⋅+⋅L ① 23121222(1)22n n n T n n +=⋅+⋅+-⋅+⋅L ②①-②得23122222n n n T n +-=+++-⋅L 1(1)22n n +=-⋅-1(1)22n n T n +∴=-⋅+ ———————7分(III) ∵11-2)1(23--⋅+=n n n n C λn n n 2)1(31λ--+=∴n n C C >+1即 >-+++112)1(3n n n λn n n 2)1(31λ--+即02)1(2)1(33111>---+--++n n n n n n λλ即0)22()1(321>+-+⋅+n n nnλ即023)1(32>⋅-+⋅nnnλ∴>-λn)1(nn 2332⋅⋅- 即>-λn)1(1)23(--n ——————8分 当n 为偶数时≤--1)23(n 23-∴23->λ ————— 10分当n 为奇数时≤--1)23(n 1- ∴1->-λ即 1<λ 又∵0λ≠∴ 123<<-λ且0λ≠ ——————12分。
湛江市高中上学期高二数学11月月考试卷汇总(共11套)
湛江市高中上学期高二数学11月月考试卷汇总（共11套）上学期高二数学11月月考试题01时间120分钟 分数150分第Ⅰ卷一、选择题:(本大题共12小题，每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知全集{1,2,3,4,5},{1,2,3},{3,4},()U U A B C A B ===⋃=则（ ）A ．{3}B ．{5}C ．{1，2，4，5}D ．{1，2，3，4}2.“m .n 〉0”是“方程表示焦点在x 轴上的双曲线”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 3.已知命题p ：0x ∃∈R ，021x =．则p ⌝是（ ）A.0x ∀∈R ，021x ≠B.0x ∀∉R ，021x ≠C.0x ∃∈R ，021x ≠D.0x ∃∉R ，021x ≠4.若m 是2和8的等比中项，则圆锥曲线221y x m+=的离心率为（ ） 3535355.已知函数x x x g x x x f cos sin )(,cos sin )(-=+=，下列四个命题：①将)(x f 的图像向右平移2π个单位可得到)(x g 的图像；②)()(x g x f y =是偶函数； ③]4,4[)()(ππ-均在区间与x g x f 上单调递增；④)()(x g x f y =的最小正周期为π2.其中真命题的个数是（ ）A.1B.2C.3D.46.若n S 是等差数列{}n a 的前n 项和，且8320S S -=，则11S 的值为 ( ) A.44B.22C.2203D.887.已知点12,F F 是椭圆2222x y 的两个焦点，点P 是该椭圆上的一个动点，那么12PF PF 的最小值是（ ）A.0B.1C.2D.228.已知直线m 、n 、l 不重合，平面、β不重合，下列命题正确的是( ) A.若ββ⊂⊂n m ,，α//m ，α//n ，则βα// B.若ββ⊂⊂n m ,，n l m l ⊥⊥,，则β⊥l C.若βαβα⊂⊂⊥n m ,,，则n m ⊥； D. 若n m m //,α⊥，则α⊥n9．从221x y m n-=（其中,{1,2,3}m n ∈-）所表示的椭圆或双曲线方程中任取一个，则此方程是焦点在x 轴上的双曲线方程的概率为（ ） A ．12 B ．47C ．23 D ．3410.若不论k 为何值，直线(2)y k x b =-+与曲线221x y -=总有公共点，则b 的取值范围是A.(3,3)-B.3,3⎡⎤-⎣⎦C.(2,2)-D.[]2,2-11．设F 为抛物线)0(22>=p px y 的焦点，A 、B 、C 为该抛物线上三点，当FA →＋FB →＋FC →＝，且|FA →|＋|FB →|＋|FC →|＝3时，此抛物线的方程为( )A ．x y 22= B ．x y 42= C ．x y 62= D ．x y 82=12.已知椭圆C ：22221(0)x y a b a b+=>>的左、右焦点为12,F F ，过2F 的直线与圆222b y x =+相切于点A ，并与椭圆C 交与不同的两点P ，Q ，如图，若A 为线段PQ 的靠近P 的三等分点，则椭圆的离心率为 A ．23B ．33C ．53D ．73第Ⅱ卷（非选择题 共90分）二、填空题：(本大题共4小题，每小题5分，共20分．将答案填写在答题纸上) 13.过点A(1,2)且与原点距离最大的直线方程是 14.直线3430x y -+=与圆221x y +=相交所截的弦长为_________ 15.若P 为抛物线210yx =上的动点,则点P 到直线50x y ++=的距离的最小值为 .16.已知椭圆C ：)0(12222>>=+b a by a x 的离心率为23，双曲线x ²-y ²＝1的渐近线与椭圆有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C 的方程为三、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）17．（本小题满分10分）已知命题222:8200,:210(0)p x x q x x m m -->-+->>，若p 是q 的充分不必要条件，求实数m 的取值范围.18．（本小题满分12分）已知函数f(x)＝2sinxcosx ＋cos2x. (Ⅰ)求()4f π的值；(Ⅱ)设3(0,),4πα∈1()25f α=，求cos2α的值.19.（本小题满分12分）等比数列{}n a 的各项均为正数，且212326231,9.a a a a a +==(Ⅰ)求数列{}n a 的通项公式. (Ⅱ)设 nn a nb =，求数列{n b }的前n 项和Sn .20.（本题满分12分）甲打靶射击，有4发子弹，其中有一发是空弹（“空弹”即只有弹体没有弹头的子弹）. （1）如果甲只射击1次，求在这一枪出现空弹的概率； （2）如果甲共射击3次，求在这三枪中出现空弹的概率；（3）如果在靶上画一个边长为10的等边PQR ∆，甲射手用实弹瞄准了三角形PQR 区域随机射击，且弹孔都落在三角形PQR 内。
2020-2021学年广东省湛江一中高二上学期第一次大考数学理试卷Word版含答案
2020-2021学年广东省湛江一中高二上学期第一次大考数学理试卷考试时间：120分钟 满分：150分第Ⅰ卷（选择题 满分60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.)1. ,a b 是任意实数，a b >，且0a ≠，则下列结论正确的是（ ） A. 33a b --< B.1b a < C. 1lg()lga b a b->- D. 22a b > 2. 在各项均为正数的等比数列{}n a 中，若389a a =，则31310log log a a +=（ ） A. 1 B. 4 C. 2 D. 3log 53. 下列函数中，最小值为4的是( ) A.4()f x x x =+B.4()cos cos f x x x=+ C.()343x xf x -=+⨯ D.()lg 4log 10x f x x =+4．ABC ∆中，1b =，6B π∠=，则ABC ∆的形状一定为（ ）A ．等腰直角三角形B ．直角三角形C ．等边三角形D ．等腰三角形或直角三角形5．已知数列{a n }满足a n ＋1＝⎩⎪⎨⎪⎧2a n ⎝ ⎛⎭⎪⎫0≤a n <12，2a n－1 ⎝ ⎛⎭⎪⎫12≤a n<1.若a 1＝67，则a 2014的值为( )A ．57B ．67C ．37D ．176．某船开始看见灯塔在南偏东30方向，后来船沿南偏东60的方向航行45km 后，看见灯塔在正西方向，）A B.30km C ．15km D.7.数列n a 满足1a ，21a a -，32a a -，，1n n a a --是首项为1，公比为2的等比数列，那么n a 等于( )A ．41n-B ．121n -- C ．21n+D ．21n-8.设n s 是等差数列{}n a 的前n 项和，若5359a a =，则95ss 等于( ) A ．1 B ．－1C ．2 D ．129．已知n S 是等差数列{}n a 的前n 项和，且675S S S >>，给出下列四个命题：①0d <；②110S >；③ 使0n S >的最大n 值为12；④数列{}n S 中的最大项为11s ，其中正确命题的个数是（）A ．4B ．3C ．2D ．1 10.已知ABC ∆是锐角三角形，若B A 2=，则ba的取值范围是( ) A.)3,2( B.)2,2( C.)3,1( D.)2,1(11. 若实数y x ,满足⎪⎩⎪⎨⎧≥+-≤--≥-+01032033my x y x y x ，且y x +的最大值等于9，则实数m 等于( )A ．2-B ．1C ．1-D ．212.己知等差数列{}n a 的公差0d ≠，且1313,,a a a 成等比数列，若11a =，n S 为数列{}n a 的前n 项和，则21445n n S a ++的最小值为（ ）A ．4 B ．272 C ．1219D ．675 第Ⅱ卷 （非选择题 满分90分）二、填空题(本大题共4小题，每小题5分，共20分)13.已知实数,x y 满足1000x y x y x +-≤⎧⎪-≤⎨⎪≥⎩，则2x y -的最大值为.[14．ABC ∆中，角,,A B C 所对的边分别为,,a b c ，已知60,2,A b =︒=ABC S ∆=a =. 15．已知数列1,111,,,,,12123123n++++++则其前n 项的和等于.16．给出下列命题：① ,A B 是ABC ∆的内角，且A B >，则sin sin A B >; ② {}n a 是等比数列，则{}1n n a a ++也为等比数列；③ 在数列{}n a 中,如果n 前项和22n S n n =++，则此数列是一个公差为2的等差数列；④ O 是ABC ∆所在平面上一定点，动点P 满足：sin sin AB AC OP OA C B λ⎛⎫=++ ⎪ ⎪⎝⎭，()0,λ∈+∞，则直线AP 一定通过ABC ∆的内心；则上述命题中正确的有（填上所有正确命题的序号）三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤) 17（本小题满分10分)已知等差数列{}n a 的前n 项和为n S ，且990S =，15240S =． （I ）求{}n a 的通项公式n a ；(II)若数列{}n b 满足：3n n b a =，求{}n b 的前n 项和n T ．18（本小题满分12分）已知函数233()cos()cos()3cos 2f x x x x ππ=+--+. （I ）求()f x 的最小正周期和最大值； (II) 求()f x 在2[,]63ππ上的单调递增区间．19（本小题满分12分） 已知不等式的解集为或（I ）求a ,b 的值；(II)解不等式2()0ax am b x bm -++<.20.(本小题满分12分)假设我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年，每厘米厚的隔热层建造成本是6万元，天宫一号每年的能源消耗费用H （万元）与隔热层厚度x (厘米)满足关系式：)100(53)(≤≤+=x x kx H （当0=x 时表示无隔热层），若无隔热层，则每年能源消耗费用为8万元.设)(x f 为隔热层建造费用与20年的能源消耗费用之和. （I ）求k 的值和)(x f 的表达式；(II)当隔热层修建多少厘米厚时，总费用)(x f 最小，并求出最小值.21（本小题满分12分）在ABC ∆中,内角,,A B C 对应的边长分别为,,a b c ,已知(,)m c a b =+1(,cos )2n a b a B b =--//m n（I ）求角A ；(II)若3a =求b c +的取值范围．22（本小题满分12分）已知数列{}n a 的前n 项和是n S ,12-=n n a S ()*n N ∈. （I ）求数列{}n a 的通项公式；(II)若数列{}n b 满足n n a n b ⋅=2，求数列{}n b 的前n 项和n T ；(III)若数列{}n c 满足()n n nn a c λ1123--+=（λ为非零常数），确定λ的取值范围,使*n N ∈时，都有n n c c >+1.2020-2021学年广东省湛江一中高二上学期第一次大考数学理试卷参考答案第Ⅰ卷（选择题 满分60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.)第Ⅱ卷 （非选择题 满分90分）二、填空题(本大题共4小题，每小题5分，共20分) 13.1214. 21n n +16. ①④三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤) 17. （本小题满分10分)解：（I ）设等差数列{}n a 的首项为1a ，公差为d ，由已知可得1193690,15105240a d a d +=+=， ——————— 1分 解得12a d ==————————3分2n a n = ————————5分(II) 323n nn b a ==⋅ —— ——————7分 由13n nb b +=，{b n }是首项为6，公比为2的等比数列 ———————8分 则13(13)23313n n n T +-==-- ————————10分18（本小题满分12分）解：1cos 23()-cos )(sin )32x f x x x +=⋅--⋅+（ 13sin 2cos 2sin(2)223x x x π=-=- —————— 4分 （I ）()f x 的最小正周期为π，最大值为1； —————— 8分 (II) 当()f x 递增时，222 ()232k x k k Z πππππ-≤-≤+∈，即51212k x k ππππ-≤≤+()k Z ∈, —————— 10分 所以，()f x 在5[,]612ππ上递增 即()f x 在2[,]63ππ上的单调递增区间是5[,]612ππ————— 12分 19（本小题满分12分） 解：（I ）因为不等式的解集为或所以，是方程的两个解————— 1分所以， ——————— 3分解得——————— 5分(II) 由（I ）知原不等式为，即，—————— 6分当时，不等式解集为 ———————— 8分当时，不等式解集为; ——————— 10分当时，不等式解集为; ——————— 12分20.(本小题满分12分)解：（I ）当0=x 时，8=H ，即85=k，解得40=k ————2分故5340)(+=x x H ——————3分5380065340206)(++=+⨯+=∴x x x x x f )100(≤≤x ————6分 (II) 由（I ）知35535≤+≤x ————7分7010160021053800)53(25340206)(=-≥-+++=+⨯+=∴x x x x x f —————10分当且仅当53800106+=+x x ，即5=x 时)(x f 取得最小值 ————11分即隔热层修建5厘米厚时，总费用达到最小值，最小值为70万元. —12分 21（本小题满分12分） （I ）∵//m n 221cos 2c a B b a b ⎛⎫-=- ⎪⎝⎭, —————1分 由余弦定理得2222222a c b bc a b +--=-,222a b c bc =+- ——————3分 ∵2222cos a b c bc A =+-,∴1cos 2A =————————4分 ∵()0,πA ∈,∴π3A =————————5分 (II)由余弦定理得2sin sin sin a b cA B C===,∴2sin b B =,2sin c C =—————6分∴()2sin 2sin 2sin 2sin b c B C B A B +=+=++ ———————7分2sin 2sin cos 2cos sin B A B A B =++12sin 22sin 2B B B =++⨯ π3sin 6B B B ⎛⎫==+ ⎪⎝⎭； ————————9分∵2π0,3B ⎛⎫∈ ⎪⎝⎭,∴ππ5π,666B ⎛⎫+∈ ⎪⎝⎭, π1sin ,162B ⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦． ————————11分所以b c +∈————————12分22（本小题满分12分）解：（I ）当n =1时，11121a s a ==-，11a ∴=————— 1分 当1n >时，21n n s a =-，1121n n s a --∴=-112n n n n s s a a --∴-=-122n n n a a a -∴=-12n n a a -∴={}n a 是首项为1，公比为2的等比数列1*2,n n a n N -∴=∈————— 3分(II) 22nn n b n a n =⋅=⋅212222n n T n =⋅+⋅+⋅①23121222(1)22n n n T n n +=⋅+⋅+-⋅+⋅②①-②得23122222n n n T n +-=+++-⋅1(1)22n n +=-⋅-1(1)22n n T n +∴=-⋅+——————— 7分(III)∵11-2)1(23--⋅+=n n n n C λn n n2)1(31λ--+=∴n n C C >+1即 >-+++112)1(3n n n λn n n 2)1(31λ--+即02)1(2)1(33111>---+--++n n n n n n λλ即0)22()1(321>+-+⋅+n n nnλ即023)1(32>⋅-+⋅nnnλ∴>-λn)1(nn 2332⋅⋅- 即>-λn)1(1)23(--n —————— 8分 当n 为偶数时≤--1)23(n 23- ∴23->λ ————— 10分当n 为奇数时≤--1)23(n 1- ∴1->-λ即 1<λ 又∵0λ≠∴ 123<<-λ且0λ≠ —————— 12分。
广东省湛江市2020-2021学年高二上学期期末调研考试数学试卷 PDF版含答案
2020-2021学年广东省湛江市高二（上）期末数学试卷一、选择题（共8小题）.1．设集合A＝{x|（x﹣7）（x+12）＜0}，B＝{x|x+6＞0}，则A∩B＝（）A．{x|﹣6＜x＜12}B．{x|﹣6＜x＜7}C．{x|x＞﹣12}D．{x|6＜x＜7} 2．“四边形ABCD是菱形”是“四边形ABCD的对角线互相垂直”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．双曲线x2﹣4y2＝﹣8的渐近线方程为（）A．y＝±2x B．C．D．4．“一尺之棰，日取其半，万世不竭”这句话出自《庄子•天下篇》，其意思为“一根一尺长的木棰，每天截取其一半，永远都取不完”．设第一天这根木棰被截取一半剩下a1尺，第二天被截取剩下的一半剩下a2尺，…，第五天被截取剩下的一半剩下a5尺，则＝（）A．18B．20C．22D．245．已知抛物线C的焦点到准线的距离大于2，则C的方程可能为（）A．y2＝4x B．y2＝﹣3x C．x2＝6y D．y＝﹣8x26．如图，在正方体ABCD﹣A1B1C1D1中，E为BB1的中点，若O为底面A1B1C1D1的中心，则异面直线C1E与AO所成角的余弦值为（）A．B．C．D．7．P为椭圆上一动点，F1，F2分别为左、右焦点，延长F1P至点Q，使得|PQ|＝|PF2|，则动点Q的轨迹方程为（）A．（x+2）2+y2＝34B．（x+2）2+y2＝68C．（x﹣2）2+y2＝34D．（x﹣2）2+y2＝688．如图，某人在一条水平公路旁的山顶P处测得小车在A处的俯角为30°，该小车在公路上由东向西匀速行驶7.5分钟后，到达B处，此时测得俯角为45°．已知小车的速度是20km/h，且，则此山的高PO＝（）A．1km B．C．D．二、选择题（共4小题）.9．设命题p：∀n∈N，6n+7为质数，则（）A．￢p为假命题B．￢p：∃n∈N，6n+7不是质数C．￢p为真命题D．￢p：∀n∈N，6n+7不是质数10．设S n是等差数列{a n}的前n项和，且a1＝2，a3＝8，则（）A．a5＝12B．公差d＝3C．S2n＝n（6n+1）D．数列{}的前n项和为11．已知a＞b＞0，且a+3b＝1，则（）A．ab的最大值为B．ab的最小值为C．的最小值为16D．a2+15b2的最小值为12．已知椭圆的左、右顶点分别为A，B，点P为Ω上一点，且P不在坐标轴上，直线AP与直线y＝﹣3交于点C，直线BP与直线y＝﹣3交于点D．设直线AP 的斜率为k，则满足|CD|＝36的k的值可能为（）A．1B．C．D．三、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上．13．设向量，，，则实数m＝．14．若双曲线的虚轴长为，则该双曲线的离心率为．15．在△ABC中，若，，AC＝2，则AB＝．16．已知点P（m，n）是抛物线x2＝﹣8y上一动点，则的最小值为．四、解答题．本大题共6小题，共70分，解答应写出文字说期、证时过程或演算步骤．17．△ABC的内角A，B，C所对的边分别为a，b，c．已知，sin C＝2sin B．（1）求cos A；（2）若△ABC的周长为，求△ABC的面积．18．如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，AC＝AA1＝2BC，E，F分别为侧棱BB1，CC1中点．（1）证明：BF∥平面A1C1E．（2）求B1C与平面A1C1E所成角的正弦值．19．已知数列{a n}的首项为4．（1）若数列是等差数列，且公差为2，求{a n}的通项公式．（2）在①a3﹣a2＝48且a2＞0，②a3＝64且a4＞0，③a2021＝16a2a2017这三个条件中任选一个，补充在下面的问题中并解答．问题，若{a n}是等比数列，______，求数列{（3n﹣1）a n}的前n项和S n．20．如图，平面ABCDE⊥平面CEFG，四边形CEFG为正方形，点B在正方形ACDE的外部，且AB＝BC＝，AC＝4．（1）证明：AD⊥CF．（2）求平面BFG与平面ABCDE所成锐二面角的余弦值．21．已知抛物线C：y2＝2px（p＞0）与双曲线有相同的焦点F．（1）求C的方程，并求其准线l的方程；（2）如图，过F且斜率存在的直线与C交于不同的两点A（x1，y1），B（x2，y2），直线OA与准线l交于点N．过点A作l的垂线，垂足为M．证明：y1y2为定值，且四边形AMNB为梯形．22．已知椭圆的离心率为，且焦距为8．（1）求C的方程；（2）设直线l的倾斜角为，且与C交于A，B两点，点O为坐标原点，求△AOB面积的最大值．参考答案一、选择题（共8小题）.1．设集合A＝{x|（x﹣7）（x+12）＜0}，B＝{x|x+6＞0}，则A∩B＝（）A．{x|﹣6＜x＜12}B．{x|﹣6＜x＜7}C．{x|x＞﹣12}D．{x|6＜x＜7}解：∵A＝{x|﹣12＜x＜7}，B＝{x|x＞﹣6}，∴A∩B＝{x|﹣6＜x＜7}．故选：B．2．“四边形ABCD是菱形”是“四边形ABCD的对角线互相垂直”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解：当四边形ABCD是菱形时，根据菱形的性质可知，对角线互相垂直，当四边形ABCD的对角线互相垂直时，四边形不一定是菱形，比如可以是梯形，故“四边形ABCD是菱形”是“四边形ABCD的对角线互相垂直”的充分不必要条件．故选：A．3．双曲线x2﹣4y2＝﹣8的渐近线方程为（）A．y＝±2x B．C．D．解：根据题意，双曲线的方程为：x2﹣4y2＝﹣8，变形可得，则其焦点在y轴上，且a＝，b＝2，则其渐近线方程为：y＝±2x，故选：A．4．“一尺之棰，日取其半，万世不竭”这句话出自《庄子•天下篇》，其意思为“一根一尺长的木棰，每天截取其一半，永远都取不完”．设第一天这根木棰被截取一半剩下a1尺，第二天被截取剩下的一半剩下a2尺，…，第五天被截取剩下的一半剩下a5尺，则＝（）A．18B．20C．22D．24解：设这根木棰的长度为1尺，第一天这根木棰被截取一半为，剩下a1＝1﹣＝尺，第二天被截取剩下的一半为×，剩下a2＝﹣×＝尺，第三天被截取剩下的一半×，剩下a3＝﹣×＝尺，第四天被截取剩下的一半×，剩下a4＝﹣×＝尺，第五天被截取剩下的一半×，剩下a5＝﹣×＝尺，则＝＝24，故选：D．5．已知抛物线C的焦点到准线的距离大于2，则C的方程可能为（）A．y2＝4x B．y2＝﹣3x C．x2＝6y D．y＝﹣8x2解：抛物线C的焦点到准线的距离大于2，可得p＞2，y2＝4x中p＝2，所以A不正确；y2＝﹣3x中p＝，所以B不正确；x2＝6y中p＝3，所以C正确；y＝﹣8x2，即x2＝y，所以p＝，所以D不正确；故选：C．6．如图，在正方体ABCD﹣A1B1C1D1中，E为BB1的中点，若O为底面A1B1C1D1的中心，则异面直线C1E与AO所成角的余弦值为（）A．B．C．D．解：如图所示，建立空间直角坐标系.不妨设AB＝2，则A（2，0，0），O（1，1，2），E（2，2，1），C1（0，2，2），∴＝（﹣1，1，2），＝（﹣2，0，1），∴cos＜，＞＝＝＝．∴异面直线C1E与AO所成角的余弦值为．故选：D．7．P为椭圆上一动点，F1，F2分别为左、右焦点，延长F1P至点Q，使得|PQ|＝|PF2|，则动点Q的轨迹方程为（）A．（x+2）2+y2＝34B．（x+2）2+y2＝68C．（x﹣2）2+y2＝34D．（x﹣2）2+y2＝68解：由已知椭圆的方程可得：a2＝17，b2＝13，则a＝，由椭圆的定义可得|PF，又因为|PQ|＝|PF2|，所以|PF，所以|QF，所以点Q的轨迹是以F1（﹣2，0）为圆心，2为半径的圆，所以点Q的轨迹方程为：（x+2）2+y2＝68，故选：B．8．如图，某人在一条水平公路旁的山顶P处测得小车在A处的俯角为30°，该小车在公路上由东向西匀速行驶7.5分钟后，到达B处，此时测得俯角为45°．已知小车的速度是20km/h，且，则此山的高PO＝（）A．1km B．C．D．解：设OP＝x，由题意可得：Rt△OBP中，∠PBO＝45°，∴OB＝OP＝x．在Rt△OAP中，∠PAO＝30°，∴OA＝x•tan60°＝x．又AB＝×20＝2.5，在△OAB中，由余弦定理可得：＝，解得x＝1．故选：A．二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分．9．设命题p：∀n∈N，6n+7为质数，则（）A．￢p为假命题B．￢p：∃n∈N，6n+7不是质数C．￢p为真命题D．￢p：∀n∈N，6n+7不是质数解：命题p：∀n∈N，6n+7为质数，当n＝3时，6×3+7＝25不是质数，故命题p为假命题，￢p：∃n∈N，6n+7不是质数，所以￢p为真命题．故选：BC．10．设S n是等差数列{a n}的前n项和，且a1＝2，a3＝8，则（）A．a5＝12B．公差d＝3C．S2n＝n（6n+1）D．数列{}的前n项和为解：由题意，设等差数列{a n}的公差为d，则d＝＝＝3，故选项B正确，a5＝2+3×（5﹣1）＝14，故选项A不正确，∵S2n＝2n×2+×3＝n（6n+1），选项C正确，∵a n＝2+3×（n﹣1）＝3n﹣1，∴＝＝（﹣），∴数列{}的前n项和为++…+＝×（﹣）+×（﹣）+…+×（﹣）＝×（﹣+﹣+…+﹣）＝×（﹣）＝，选项D正确．故选：BCD．11．已知a＞b＞0，且a+3b＝1，则（）A．ab的最大值为B．ab的最小值为C．的最小值为16D．a2+15b2的最小值为解：对于A，B：∵a＞b＞0，且a+3b＝1，∴1＝a+3b≥2，故≤，0＜ab＜，故A正确，B错误；对于C：∵a＞b＞0，且a+3b＝1，∴+＝（+）（a+3b）＝10+3（+）≥10+3•2＝16，当且仅当a＝b＝时“＝”成立，故C正确；对于D：a2+15b2＝a2+15＝a2﹣a+＝+≥，当且仅当a＝时“＝”成立，故D正确；故选：ACD．12．已知椭圆的左、右顶点分别为A，B，点P为Ω上一点，且P不在坐标轴上，直线AP与直线y＝﹣3交于点C，直线BP与直线y＝﹣3交于点D．设直线AP 的斜率为k，则满足|CD|＝36的k的值可能为（）A．1B．C．D．解：由椭圆的方程可得A（﹣3，0），B（3，0），设P（x0，y0），则k＝，因为k PA＝k，所以k，又直线PA的方程为y＝k（x+3），则令y＝﹣3，得x，直线PB的方程为y＝﹣，令y＝﹣3，得x D＝27k+3，所以|CD|＝|27k+|＝36，整理可得：9k2+14k+1＝0或9k2﹣10k+1＝0，解得k＝或1或，故选：AD．三、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上．13．设向量，，，则实数m＝﹣6．解：∵向量，，，∴•＝m+2+4＝0，解得m＝﹣6，故答案为：﹣6．14．若双曲线的虚轴长为，则该双曲线的离心率为2．解：双曲线的虚轴长为，可得b＝3，a＝，所以c＝＝2，所以双曲线的离心率为：e＝＝2，故答案为：2．15．在△ABC中，若，，AC＝2，则AB＝．解：因为＝，可得cos C＝，又sin2C+cos2C＝1，所以，因为，AC＝2，由正弦定理得，可得．故答案为：．16．已知点P（m，n）是抛物线x2＝﹣8y上一动点，则的最小值为3．解：抛物线的准线为y＝2，焦点F坐标为（0，﹣2），所以＝+，表示点P（m，n）与点F（0，﹣2）的距离与点P（m，n）与点A（2，﹣1）的距离之和，所以的最小值为线段AB长度，又|AB|min为点A到准线y＝2的距离，即|AB|min＝3，故答案为：3．四、解答题．本大题共6小题，共70分，解答应写出文字说期、证时过程或演算步骤．17．△ABC的内角A，B，C所对的边分别为a，b，c．已知，sin C＝2sin B．（1）求cos A；（2）若△ABC的周长为，求△ABC的面积．解：（1）因为，所以．（2）因为sin C＝2sin B，所以c＝2b．由余弦定理得，则．因为△ABC的周长为，所以，解得b＝2．所以△ABC的面积为．18．如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，AC＝AA1＝2BC，E，F分别为侧棱BB1，CC1中点．（1）证明：BF∥平面A1C1E．（2）求B1C与平面A1C1E所成角的正弦值．解：（1）证明：∵在直三棱柱ABC﹣A1B1C1中，E，F分别为侧棱BB1，CC1中点．∴BE C1F，∴四边形BEC1F是平行四边形，∴BF∥EC1，∵BF⊄平面A1C1E，EC1⊂平面A1C1E，∴BF∥平面A1C1E．（2）∵在直三棱柱ABC﹣A1B1C1中，AC⊥BC，AC＝AA1＝2BC，E，F分别为侧棱BB1，CC1中点．∴以C为原点，CA为x轴，CB为y轴，CC1为z轴，建立空间直角坐标系，设AC＝AA1＝2BC＝2，则B1（0，1，2），C（0，0，0），A1（2，0，2），C1（0，0，2），E（0，1，1），＝（0，﹣1，﹣2），＝（2，0，0），＝（0，1，﹣1），设平面A 1C 1E 的法向量＝（x ，y ，z ），则，取y ＝1，得＝（0，1，1），设B 1C 与平面A 1C 1E 所成角为θ，则sin θ＝＝＝．∴B 1C 与平面A 1C 1E 所成角的正弦值为．19．已知数列{a n }的首项为4．（1）若数列是等差数列，且公差为2，求{a n }的通项公式．（2）在①a 3﹣a 2＝48且a 2＞0，②a 3＝64且a 4＞0，③a 2021＝16a 2a 2017这三个条件中任选一个，补充在下面的问题中并解答．问题，若{a n }是等比数列，______，求数列{（3n ﹣1）a n }的前n 项和S n ．解：（1）数列是等差数列，且公差为2，首项为4，所以，整理得．（2）选①：a 3﹣a 2＝48且a 2＞0，{a n }是等比数列，设公比为q ，由于首项为4，则由a 3﹣a 2＝48，得q ＝4，所以，选②：由于首项为4，且a 3＝64，{a n }是等比数列，所以q＝±4，且a4＞0，所以，选③：由于数列，{a n}的首项为4，且满足a2021＝16a2a2017，解得q＝4，所以，设，则①，所以4②，①﹣②得﹣3，所以．20．如图，平面ABCDE⊥平面CEFG，四边形CEFG为正方形，点B在正方形ACDE的外部，且AB＝BC＝，AC＝4．（1）证明：AD⊥CF．（2）求平面BFG与平面ABCDE所成锐二面角的余弦值．解：（1）证明：∵四边形ACDE为正方形，∴AD⊥CE，∵平面ABCDE⊥平面CEFG，平面ABCDE∩平面CEFG＝CE，∴AD⊥平面FECG．又CF⊂平面FECG，∴AD⊥CF；（2）∵四边形CEFG为正方形，∴CG⊥CE，∵平面ABCDE⊥平面CEFG，平面ABCDE∩平面CEFG＝CE，∴CG⊥平面ABCDE．故EA，ED，EF两两垂直，所以以E为原点建立空间直角坐标系，∵AB＝BC＝，AC＝4，∴B到AC的距离为1．∴B（5，2，0），F（0，0，4），G（4，4，4），则，，设面BFG的法向量为，由，可得＝（4，﹣4，3）又平面ABCDE的法向量为，cos＝＝∴平面BFG与平面ABCDE所成锐二面角的余弦值为．21．已知抛物线C：y2＝2px（p＞0）与双曲线有相同的焦点F．（1）求C的方程，并求其准线l的方程；（2）如图，过F且斜率存在的直线与C交于不同的两点A（x1，y1），B（x2，y2），直线OA与准线l交于点N．过点A作l的垂线，垂足为M．证明：y1y2为定值，且四边形AMNB为梯形．解：（1）因为双曲线的右焦点为（2，0），所以F（2，0），则，即p＝4，故C的方程为y2＝8x，其准线l的方程为x＝﹣2．（2）证明：由题意可知，直线AB过点F且斜率存在，设其方程为y＝k（x﹣2）（k≠0），联立，整理得ky2﹣8y﹣16k＝0，所以△＝64+64k2＞0恒成立，所以，故y1⋅y2为定值．因为点N在准线l上，设点N为（﹣2，m），则由k OA＝k ON，可得．又，所以．因此BN∥x轴∥AM，易知，x1≠x2，|AM|≠|BN，故四边形AMNB为梯形．22．已知椭圆的离心率为，且焦距为8．（1）求C的方程；（2）设直线l的倾斜角为，且与C交于A，B两点，点O为坐标原点，求△AOB面积的最大值．解：（1）依题意可知，解得a＝2，b＝2，c＝4故C的方程为．（2）依题意可设直线l的方程为，联立，整理得，则△＝300m2﹣64（5m2﹣20）＞0，解得﹣8＜m＜8．设A（x1，y1），B（x2，y2），则，，，原点到直线l的距离，则△AOB的面积，当且仅当m2＝32，即时，△AOB的面积有最大值，且最大值为2．。
广东省湛江第一中学2020-2021学年高二上学期第二次大考数学(理)试题
【全国百强校】广东省湛江第一中学2020-2021学年高二上学期第二次大考数学（理）试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列说法正确的是( )A ．2x R,x 0∀∈>”的否定是200x R,x 0∃∈<B ．命题“设a,b R ∈，若a b 4+≠，则a 2≠或b 2≠是一个假命题C ．“m ＝1”是“函数()2m 2f x m x+=为幂函数”的充分不必要条件D ．向量()()a 3,4,b 0,1==，则a 在b 方向上的投影为5 2．数列3579,,,24816--，…的一个通项公式为（ ） A ．()n nn n21a 12+=-⋅B ．()nn n 2n 1a 12+=-⋅C ．()n n 1n n 21a 12++=-⋅ D ．()n 1n n2n 1a 12++=-⋅ 3．双曲线2212x y -=-的渐近线方程为（ ）A ．2y x =±B ．y =C ．12y x =±D ．2y x =±4．等差数列{}n a 的前n 项和为n S ，若3114a a +=，则13S =（ ） A ．13B ．26C ．39D ．525．已知线段PQ 的中点为(0,4)M ，若点P 在直线20x y +-=上运动，则点Q 的轨迹方程是 A ．.60x y +-= B ．60x y ++= C ．20x y --= D ．20x y -+=6．下列结论正确的是（ ）A ．当x ＞0且x ≠1时，lgx +1lgx≥2 B ．当x ＞1≥2 C ．当x ≥2时，x +1x有最小值2 D ．当0＜x≤2时，x ﹣1x 有最大值327．条件p ：－2<x <4，条件q ：(x ＋2)(x ＋a )<0；若q 是p 的必要而不充分条件，则a 的取值范围是( ) A ．(4，＋∞)B ．(－∞，－4)C ．(－∞，－4]D ．[4，＋∞)8．ABC ∆中，,A B ∠∠的对边分别为,a b ，5,4a b ==，且60A ∠=，那么满足条件的ABC ∆( ) A ．有一个解 B ．有两个解 C ．无解D ．不能确定9．若两个正实数,x y 满足211x y+=，则2x y +的最小值为（ ） A ．8B ．6C ．4D ．210．等比数列{}n a 满足13a =，且1234,2,a a a 成等差数列，则数列{}n a 的公比为( ) A ．1B ．-1C ．-2D ．211．已知变量,x y 满足约束条件290230x y y x y ＞--≤⎧⎪≤⎨⎪+-⎩，若使z ax y =+取得最小值的最优解有无穷多个，则实数a 的取值集合是（ ） A ．{}2,0-B ．{}1,2-C ．{}0,1D ．{}2,0,1-12．已知12,F F 分别是椭圆的左，右焦点，现以2F 为圆心作一个圆恰好经过椭圆中心并且交椭圆于点,M N ，若过1F 的直线1MF 是圆2F 的切线，则椭圆的离心率为（ ） A1 B．2C．2D．2二、填空题13．如图所示，为测一建筑物CD 的高度，在地面上选取,A B 两点，从,A B 两点分别测得建筑物顶端的仰角为30,45，且,A B 两点间的距离为20m ，则该建筑物的高度为________m .14．已知函数4(1)1y x x x =+>-，则函数的最小值是___． 15．已知命题2:,1p x R x m ∀∈+>；命题:()(3)x q f x m =-是增函数.若“p q ∧”为假命题且“p q ∨”为真命题，则实数m 的取值范围为_______.16．已知数列{}n a 满足n n 1a 2a 1-=+（*n N ∈，n 2≥），且1a 1=，n n b a 1=+．则数列{}n nb 的前n 项和n T 为_____________．三、解答题17．在锐角ABC ∆2sin c A =. （1）求角C 的值；（2）若c =ABC S ∆=+a b 的值. 18．已知正项数列{}n a 满足：2423n n n S a a =+-，其中n S 为{}n a 的前n 项和. （1）求数列{}n a 通项公式. （2）设211n n b a =-，求数列{}n b 前n 项和n T .19．如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，AB AD ⊥，AC CD ⊥，60ABC ∠=︒，PA AB BC ==，E 是PC 的中点．（1）求证：CD AE ⊥； （2）求证：PD ⊥面ABE ； （3）求二面角E-AB-C 的正切值．20．已知圆C:()()22122x y -+-=,P 点的坐标为(2,-1),过点P 作圆C 的切线,切点为A,B ．（1）求直线PA ,PB 的方程;（2）求过P 点的圆的切线长即PA ,PB 的长.21．在平面直角坐标系xOy 中，抛物线1C ：24x y =，直线l 与抛物线1C 交于A ，B 两点.（1）若直线OA ，OB 的斜率之积为14-，证明：直线l 过定点；（2）若线段AB 的中点M 在曲线2C ：214(4y x x =--<<上，求AB 的最大值.22．在平面直角坐标系xOy 中，已知椭圆2222:1(0)x y C a b a b +=>>且椭圆C 的短轴恰好是圆224x y +=的一条直径. (1)求椭圆C 的方程(2)设12,A A 分别是椭圆C 的左，右顶点，点P 是椭圆C 上不同于12,A A 的任意点，是否存在直线x m =，使直线1A P 交直线x m =于点Q ，且满足221PA QA k k ⋅=-，若存在，求实数m 的值；若不存在，请说明理由.参考答案1．C 【分析】对于A 选项，用全称命题的否定是特称命题来判断.对于B 选项，用它的逆否命题来判断.对于C 选项，利用幂函数的定义来判断.对于D 选项，利用a b b⋅来验证选项.【详解】对于A 选项，全称命题的否定是特称命题，要注意否定结论，故A 选项错误.对于B 选项，原命题的逆否命题是“若2a =且2b =，则4a b +=”为真命题，故原命题为真命题，故B 选项错误.对于C 选项，()f x 是幂函数，需满足21,1m m ==±，故C 选项正确.对于D 选项，441a b b⋅==故错误.综上所述，选C. 【点睛】本小题考查全称命题与特称命题，考查原命题和逆否命题真假性，考查充要条件以及向量投影等知识，属于中档题. 2．D 【分析】根据分子、分母还有正负号的变化，得到正确的选项. 【详解】根据分子、分母还有正负号的变化，可知，()12112n n nn a ++=-⋅.故选D. 【点睛】本小题主要考查根据给定数列的前几项，猜想数列的通项公式.通过分子、分母还有正负号的变化，来得到正确的选项.属于基础题. 3．D 【解析】双曲线2212x y -=-的渐近线方程为2202x y -=，化简得到：2y x =±。
2020-2021学年广东省湛江市遂溪县第一中学高二数学理上学期期末试题含解析
2020-2021学年广东省湛江市遂溪县第一中学高二数学理上学期期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。
在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知函数，则的最小值为（）A． B． C． D．参考答案：B略2. 若且，则实数m=（）A. 1或-3B. 1或3C. -3D. 1参考答案：A【分析】令代入，结合题中条件，即可求出结果.【详解】令，由可得，所以或，解得或.故选A【点睛】本题主要考查由二项展开式的系数和求参数，熟记二项式定理即可，属于常考题型.3. 已知对任意的a∈[﹣1，1]，函数f（x）=x2+（a﹣4）x+4﹣2a的值总大于0，则x的取值范围是（）A．x＜1或x＞3 B．1＜x＜3 C．1＜x＜2 D．x＜2或x＞3参考答案：A【考点】二次函数的性质．【分析】把二次函数的恒成立问题转化为y=a（x﹣2）+x2﹣4x+4＞0在a∈[﹣1，1]上恒成立，再利用一次函数函数值恒大于0所满足的条件即可求出x的取值范围．【解答】解：原题可转化为关于a的一次函数y=a（x﹣2）+x2﹣4x+4＞0在a∈[﹣1，1]上恒成立，只需??x＜1或x＞3．故选：A．【点评】本题的做题方法的好处在于避免了讨论二次函数的对称轴和变量间的大小关系，而一次函数在闭区间上的最值一定在端点处取得，所以就把解题过程简单化了．4. 某厂共有64名员工，准备选择4人参加技术评估，现将这64名员工编号，准备运用系统抽样的方法抽取，已知8号，24号，56号在样本中，那么样本中还有一个员工的编号是（）A、35B、40C、45D、50参考答案：B5. 设命题，，则为（）A. ，B. ，C. ，D. ，参考答案：B本题主要考查命题及其关系，全称量词与存在量词.因为全称量词的否定是存在量词，的否定是.所以：，故本题正确答案为B.6. 已知x＞﹣1，则函数y=x+的最小值为（）A．﹣1 B．0 C．1 D．2参考答案：C【考点】基本不等式在最值问题中的应用．【分析】y=x+=x+1+﹣1，利用基本不等式求最值．【解答】解：y=x+=x+1+﹣1≥2﹣1=2﹣1=1（当且仅当x+1=，即x=0时，等号成立）．故选：C．7. 对于三次函数，给出定义：设是函数的导数，是的导数，若方程有实数解，则称点为函数的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数，则（）A. 2016B. 2015C. 4030D. 1008参考答案：B【分析】由题意对已知函数求两次导数可得图象关于点（，1）对称，即f（x）+f（1﹣x）＝2，即可得到结论．【详解】解：函数g（x），函数的导数g′（x）＝x2﹣x+3，g″（x）＝2x﹣1，由g″（）＝0得2﹣1＝0解得，而g（）＝1，故函数g（x）关于点（，1）对称，∴g（x）+g（1﹣x）＝2，故设g（）+g（）+…+g（）＝m，则g（）+g（）+…+g（）＝m，两式相加得2×2015＝2m，则m＝2015．故选：B．【点睛】本题主要考查导数的基本运算，利用条件求出函数的对称中心是解决本题的关键．求和的过程中使用了倒序相加法．8. 设则等于（）参考答案：A略9. 设命题p：，，则为（）A．，B．，C．，D．，参考答案：B10. 点（-1，2）关于直线的对称点的坐标是（）A．(3,2) B．(-3,-2) C．(-3,2) D．(3,-2)参考答案：D略二、填空题:本大题共7小题,每小题4分,共28分11. 椭圆上一点P与椭圆的两个焦点F1、F2的连线互相垂直，则△PF1F2的面积为．参考答案：9【考点】椭圆的简单性质．【分析】椭圆，可得a=5，b=3，c=．设|PF1|=m，|PF2|=n，则m+n=2a=10，m2+n2=（2c）2，联立解出即可得出．【解答】解：∵椭圆，∴a=5，b=3，c==4．设|PF1|=m，|PF2|=n，则m+n=2a=10，m2+n2=（2c）2=64，∴mn=18．∴△PF1F2的面积=mn=9．故答案为：9．12. 计算：，，，……，．以上运用的是什么形式的推理？ __ __ ．参考答案：归纳推理13. 若数列的通项公式，记，试通过计算的值，推测出；参考答案：14. 从5名学生中选出4名分别参加数学，物理，化学，生物四科竞赛，其中甲不能参加生物竞赛，则不同的参赛方案种数为_________.参考答案：96【分析】根据题意，分2种情况讨论选出参加竞赛的4人，①选出的4人没有甲；②选出的4人有甲；分别求出每一种情况下分选法数目，由分类计数原理计算可得答案【详解】根据题意，从5名学生中选出4人分别参加竞赛，分2种情况讨论：①选出的4人没有甲，即选出其他4人即可，有种情况；②选出的4人有甲，由于甲不能参加生物竞赛，则甲有3种选法，在剩余4人中任选3人，参加剩下的三科竞赛，有，则此时共有种选法；综上，总共有种不同的参赛方案；答案选D【点睛】本题考查分类计数原理，属于基础题15. 若△ABC的内角满足sinA+sinB=2sinC，则cosC的最小值是．参考答案：【考点】余弦定理；正弦定理．【分析】根据正弦定理和余弦定理，利用基本不等式即可得到结论．【解答】解：由正弦定理得a+b=2c，得c=（a+b），由余弦定理得cosC====≥=，当且仅当时，取等号，故≤cosC＜1，故cosC的最小值是．故答案为：．16. 若，则实数m的值为．参考答案：﹣【考点】定积分．【专题】计算题；函数思想；定义法；导数的概念及应用．【分析】根据定积分的计算法则计算即可．【解答】解：（x2+mx）dx=（+mx2）|=+m=0，∴m=﹣，故答案为：﹣【点评】本题考查了定积分的计算，关键是求出原函数，属于基础题．17. 复数z满足(i为虚数单位)，则z=________参考答案：【分析】由题意求出，根据复数的除法即可求得的值.【详解】由题意，所以.所以本题答案为.【点睛】本题主要考查复数的运算及复数的求模问题，属基础题.三、解答题：本大题共5小题，共72分。
广东省湛江1中2020-学年高2数学上学期期末考试 理 新人教A版
广东省湛江一中2021 -2021学年高二上学期期末考试 (数学理 )考试时间：120分钟 总分值：150分一．选择题：本大题共8小题 ,每题5分 ,共40分.在每题给出的四个选项中 ,只有一项为哪一项符合题目要求的.1.命题 "假设3a b +≠ ,那么12a b ≠≠或〞的逆否命题为 ( )A. 假设3a b += ,那么12a b ==且B. 假设12a b ==或 ,那么3a b +=C. 假设12a b ≠≠或 ,那么3a b +≠D. 假设12a b ==且 ,那么3a b +=y =42x 的焦点坐标是 ( )A. (1,0 )B. (0,1)C. (0,161) D. ()0,1613.)5,2,3(-=a ,)1,,1(-=x b ,2=•b a ,那么x 的值为 ( ) A. 3 B. 4 C. 5 D. 64. "13-<<-m 〞是方程11222=+++m y m x 表示双曲线的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 5. 以下四个命题中正确的选项是 ( )A ．假设1123OP OA OB =+,那么P 、A 、B 三点共线; B ．假设{,,}a b c 为空间的一个基底 ,那么{,,}a b b c c a +++构成空间的另一个基底;C ．|()|||||||a b c a b c •=⋅⋅;D ．ABC ∆为直角三角形的充要条件是0AB AC ⋅=． 6. 在棱长为1的正方体1111D C B A ABCD -中 ,M 和N 分别为11B A 和1BB 的中点 ,那么直线AM 与CN 所成角的余弦值是( ) A ．1010B ． 52-C ．53 D ．52)0,0(12222>>=-b a by a x 的一条渐近线与抛物线12+=x y 有公共点 ,那么双曲线的离心率e 的取值范围是 ( )A. [)+∞,5 B. [)+∞,5 C. ⎪⎪⎭⎫⎢⎣⎡+∞,25 D. ⎪⎭⎫⎢⎣⎡+∞,45P ,使得点P 到两个焦点的距离之比为2:1 ,那么称此椭圆或双曲线为 "倍分曲线〞 ,那么以下曲线中是 "倍分曲线〞的是 ( )A.1151622=+y x B. 1242522=+y xC. 11522=-y x D. 122=-y x 二、填空题：本大题共6小题 ,每题5分 ,共30分．x y 82=上与焦点的距离等于6的点的坐标是 .),215,,3(),5,3,2(λ=-=b a 且a ∥b ,那么λ = . )1,4(P 平分双曲线4422=-y x 的一条弦 ,那么这条弦所在的直线方程是22154x y +=的右焦点作一条斜率为2的直线与椭圆交于A 、B 两点 ,O 为坐标原点 ,那么△OAB 的面积为______________13.=a (3cos ,3sin ,1)αα ,(2cos ,2sin ,1)b ββ= ,那么b a -的取值范围是 .14.给出以下命题：①椭圆12322=+y x 的离心率35=e ,长轴长为32；②抛物线22y x =的准线方程为;81-=x ③双曲线1254922-=-x y 的渐近线方程为x y 75±=；④方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率.其中所有正确命题的序号是 .三、解答题：本大题共6小题 ,总分值80分．解答须写出文字说明、证明过程和演算步骤 . 15. (本小题总分值12分 )在平行六面体1111D C B A ABCD -中 ,N 是1AD 的中点 ,MB AM 2=. (1)化简：12121AA AD BN --; (2) 设a AB = ,b AD = ,c AA =1 ,假设c z b y a x MN ++=,求z y x ++.16. (本小题总分值12分 )如图 ,设圆C ：1)1(22=+-y x ,过原点O 作圆的任意弦OM ,求所作弦OM 的中点P 的轨迹方程.17． (本小题总分值14分 )如图 ,正方体1111D C B A ABCD -的棱长为a ,E 为1DD 的中点.(1 )求证：1BD //平面EAC ； (2 )求点1D 到平面EAC 的距离．18．(本小题总分值14分 )设椭圆方程125222=+by x (05>>b ) ,F 为椭圆右焦点 ,P 为椭圆在短轴上的一个顶点 ,POF ∆的面积为6, (O 为坐标原点 )； (1 )求椭圆方程；(2 )在椭圆上是否存在一点Q ,使QF 的中垂线过点O ?假设存在 ,求出Q 点坐标；假设不存在 ,说明理由.19. (此题总分值14分 )如图 ,PA ⊥平面ABCD ,四边形ABCD 是矩形 ,1PA AB == ,PD 与平面ABCD 所成角是30 ,点F 是PB 的中点 ,点E 在矩形ABCD 的边BC 上移动． (1 )证明：无论点E 在边BC 的何处 ,都有PE AF ⊥； (2 )当CE 等于何值时 ,二面角P DE A --的大小为45．20． (此题总分值14分 )椭圆12822=+y x 经过点)1,2(M ,O 为坐标原点 ,平行于OM 的直线l 在y 轴上的截距为m )0(≠m .(1 )当3=m 时 ,判断直线l 与椭圆的位置关系 (写出结论 ,不需证明 )； (2 )当3=m 时 ,P 为椭圆上的动点 ,求点P 到直线 l 距离的最||小值；(3 )如图 ,当l 交椭圆于A 、B 两个不同点时 ,求证：直线MA 、MB 与x 轴始终围成一个等腰三角形.湛江一中2021 - -2021学年度第|一学期期末考试 高二级|| (理科 )数学科试卷 (参考 )答案一．选择题：本大题共8小题 ,每题5分 ,共40分.在每题给出的四个选项中 ,只有一项为哪一项符合题目要求的.1 2 3 4 5 6 7 8 DCCBBDAD二、填空题 本大题共6小题 ,每题5分 ,共30分 . ) 9． )24,4(或)24,4(- 10. 29- 11. 03=--y x 12.3513. []5,1 14. ②④ 三、解答题：本大题共6小题 ,总分值80分．解答须写出文字说明、证明过程和演算步骤 ,16. (本小题总分值12分 )解：设),(y x P , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -2分∵点P 是弦OM 的中点 ,∴)2,2(y x M - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -4分 ∵点M 在圆C ：1)1(22=+-y x 上 ,∴1)2()12(22=+-y x , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -8分 即41)21(22=+-y x , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - -10分 由圆的范围知 ,10≤<x .故点M 的轨迹方程为41)21(22=+-y x (10≤<x ). - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -12分 (此题其它解法可酌情给分 )17．(本小题总分值14分 )解法一： (1 )证明：连接BD 交AC 于F ,连EF . - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -2分 因为F 为正方形ABCD 对角线的交点 ,(2 )解：设1D 到平面EAC 的距离为d . 在EAC ∆中 ,AC EF ⊥ ,且a AC 2=,a EF 23=, 所以24621a AC EF S EAC =•=∆ , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - -9分 于是d a dS V EAC EAC D 2126311==∆-. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - -10分 因为31212121313111a a a a S AD V C ED C ED A =⨯⨯⨯=•=∆-. - - - - - - - - - - - - - - - - - - - - - - - - - -12分 又C ED A EAC D V V 11--= ,即32121126a d a = , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - -13分 解得a d 66=, 故点1D 到平面EAC 的距离为a 66. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -14分即⎪⎩⎪⎨⎧=-=-0202z aay z a ax ,令2=z ,那么1==y x∴)2,1,1(=n - - - - - - - - - - - - - - - - - - - - - - - - - - - - -4分∵0)2,1,1(),,(1=•--=•a a a n BD ,∴n BD ⊥1 , - - - - - - - - - - - - - - - - - - - - - - - -6分又∵1BD ⊄平面EAC ,所以1BD //平面EAC . - - - - - - - - - - - - - - - - - - - - - - - - - - - -7分(2 ))2,0,0(1a ED = , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - -9分)2,1,1(=n 是平面EAC 的一个法向量.∴点1D 到平面EAC 的距离a nED n d 661=•=. - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - -14分 18. (本小题总分值14分 ) 解： (1 )设)0,(c F∵P 为椭圆在短轴上的一个顶点 ,且POF ∆的面积为6, ∴621=bc . - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 1分又∵2522=+c b - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -2分 ∴⎩⎨⎧==43c b 或⎩⎨⎧==34c b - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -4分∴椭圆方程为192522=+y x 或1162522=+y x - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -6分 (2 )假设存在点Q ,使QF 的中垂线过点O .假设椭圆方程为1162522=+y x ,那么)0,3(F ,由题意 ,3==OF OQ ∴Q 点的轨迹是以O 为圆心 ,以3为半径的圆.设),(y x Q ,那么其轨迹方程为922=+y x - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -8分显然与椭圆1162522=+y x 无交点. 即假设不成立 ,点Q 不存在. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -9分假设椭圆方程为192522=+y x , 那么)0,4(F ,4==OF OQ∴Q 点的轨迹是以O 为圆心 ,以4为半径的圆.那么其轨迹方程为1622=+y x - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -1 1分那么⎪⎩⎪⎨⎧=+=+1925162222y x y x ,∴475±=x ,49±=y - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - 13分故满足题意的Q 点坐标分别为)49,475(,)49,475(- ,)49,475(-- ,)49,475(- - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 14分(2 )过A 作AG DE ⊥于G ,连PG ,又∵PA DE ⊥ , 那么⊥DE 平面PAG ,那么PGA ∠是二面角P DE A --的平面角 ,∴45=∠PGA - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 9分∵PD 与平面ABCD 所成角是30 ,∴30=∠PDA , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 10分∴3AD = ,1PA AB ==. ∴1AG = ,2DG = , - - - - - - - - - - - - - - - - - - - - - - - - - - 11分 设BE x = ,那么GE x = ,3CE x =- , 在Rt DCE ∆中 ,()()222231xx +=-+ ,得32BE x ==-.故2CE = . - - - - - - - - - - -- - - - - - - 14分法二: (1 )建立如下列图空间直角坐标系 ,那么()0,0,1P , ∵PD 与平面ABCD 所成角是30 ,∴30=∠PDA , ∴3AD = , ()0,1,0B ,110,,22F ⎛⎫⎪⎝⎭,()3,0,0D . - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - 3分 设BE x = ,那么(),1,0E x0)21,21,0()1,1,(=⋅-=⋅x AF PE AF PE ∴⊥. - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - -6分而平面ADE 的法向量为)1,0,0(=AP , - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 9分∵二面角P DE A --的大小是45, 所以45cos =||||22AP m AP m =PAFB EDCxy z2211133x =⎛⎫+-+ ⎪⎝⎭ , - - - - - - - - - - - - - - - - - - - 11分 得32BE x == 或 23+==x BE (舍 ). ∴32BE =故2CE = . - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 14分20. 解： (1 )当3=m 时 ,直线l 与椭圆相离. ……2分(2 )可知直线l 的斜率为21 设直线a 与直线l 平行 ,且直线a 与椭圆相切 ,设直线a 的方程为b x y +=21 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 3分 联立⎪⎪⎩⎪⎪⎨⎧=++=1282122y x b x y ,得042222=-++b bx x - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 4分0)42(4)2(22=--=∆∴b b ,解得2±=b - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 5分∴直线a 的方程为221±=x y . 所求点P 到直线l 的最||小距离等于直线l 到直线221+=x y 的距离 552)21(12322=+-=d . - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 7分而)2)(2()2)(1()2)(1(2121211221221121----+--=--+--=+x x x y x y x y x y k k - - - - - - -- - - - 10分)2)(2()2)(121()2)(121(211221----++--+=x x x m x x m x)2)(2()1(4))(2(212121----+-+=x x m x x m x x- - - - - - - - - - - 12分)2)(2()1(4)2)(2(42212------+-=x x m m m m 0)2)(2(4442422122=--+-+--=x x m m m m ∴1k +02=k直线MA 、MB 与x 轴始终围成一个等腰三角形 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -14分。
广东省湛江1中2020-学年高2数学上学期期末考试 文 新人教A版
广东省湛江一中2021 -2021学年高二上学期期末考试 (数学文 )考试时间：120分钟 总分值：150分一、选择题：本大题共10小题 ,每题5分 ,总分值50分 .在每题给出的四个选项中 ,只有一项为哪一项符合题目要求的．1．抛物线2x y -=的焦点坐标为 ( )A ． (0 ,41-) B. (0 ,41 ) C ． (41-,0 ) D ． (41,0 )2．设()ln f x x x = ,假设0'()2f x = ,那么0x =( )A. 2e B. e C. ln 22D. ln 23．曲线13-=x y 在1=x 处的切线方程为 ( ) A. 1=x B. 1=y C. 33-=x y D. 22-=x y4．命题甲：(,),()0'∀∈-∞+∞<x f x ,命题乙：函数)(x f 在(,)-∞+∞上是减函数 ,那么甲是乙的 ( )A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分也非必要条件 5．函数()(3)xf x x e =-的单调递增区间是 ( ) A ．(),2-∞ B ． (0 ,3 ) C ． (1 ,4 ) D ．()2,+∞6．椭圆的焦点为)0,2(),0,1()0,1(P 点和-在椭圆上,那么椭圆的方程为 ( )134.22=+y x A 14.22=+y x B 134.22=+x y C 14.22=+x y D7．函数3()2f x x ax =+-在区间[1,)+∞内是增函数 ,那么实数a 的取值范围是 ( )． A ．[3,)+∞ B ．[3,)-+∞ C ．(3,)-+∞ D ．(,3)-∞-8．椭圆22135x y a a +=--上的一个焦点坐标为 (1,0 ) ,那么a 点值为( )A ．5B ．92C ． 4D ．729. 直线2-=kx y 与抛物线x y 82=交于不同两点B A ,,假设线段AB 中点的纵坐标为2,那么k 等于 ( ).1.-A .12.-或B .2.C.21.D10. 函数()ln f x ax x =- ,假设()1f x >在区间(1,)+∞内恒成立 ,那么实数a 的取值范围是 ( )． ),1[.);,1(.];1,(.).1,(.+∞+∞-∞-∞D C B A二、填空题：本大题共4小题 , 每题5分 ,总分值20分．11．函数4431)(3+-=x x x f 在]3,0[∈x 上的最||小值是 .12．与双曲线4422=-y x 有共同的渐近线 ,且过点(2,)5的双曲线的标准方程为＿＿ 13. 函数()()0≠++=x b x ax x f ,其中R b a ∈,.在点()()2,2f P 处的切线方程为13+=x y ,那么函数a = ,b = .14．双曲线22221(0,0)x y a b a b -=>>与抛物线28y x =有一个公共的焦点F ,且两曲线的一个交点为P ,假设5PF = ,那么双曲线的离心率为 .三、解答题：本大题共6小题 ,总分值80分 .解答须写出文字说明、证明过程和演算步骤 .15． (本小题总分值12分 ):p 关于x 的方程210x mx ++=有两个不等的负根；:q 关于x 的方程244(2)10x m x +-+=无实根 .假设""p q ∨为真 ,""p q ∧为假 ,求m 的取值范围16. (本小题总分值12分 )椭圆C:)0(12222>>=+b a b y a x ,它的离心率为33.直线2:+=x y l 与以原点为圆心,以C 的短半轴为半径的圆O 相切. 求椭圆C 的方程.17． (本小题总分值14分 )设函数32()2338f x x ax bx c =+++在1x =及2x =时取得极值． (Ⅰ )求a 、b 的值；(Ⅱ )假设对于任意的[03]x ∈， ,都有2()f x c <成立 ,求c 的取值范围 .18. (本小题总分值14分 )在平面直角坐标系中 ,N 为圆C ：22(1)16x y ++=上的一动点 ,点D (1,0 ) ,点M 是DN 的中点 ,点P 在线段CN 上 ,且0MP DN ⋅=. (Ⅰ )求动点P 表示的曲线E 的方程；(Ⅱ )假设曲线E 与x 轴的交点为,A B ,当动点P 与A ,B 不重合时 ,设直线PA 与PB 的斜率分别为12,k k ,证明：12k k 为定值；19 (此题总分值14分 )动圆过定点P(1,0)且与定直线1:-=x l 相切,点C 在l 上. (Ⅰ )求动圆圆心M 的轨迹方程;(Ⅱ )设过点P 且斜率为3-1:-=x l 上是否存在点C ,使得ABC ∆是以ACB ∠为直角的直角三角形 ?如果存在 ,求出点C 的坐标;假设不能,请说明理由.湛江一中2021 - -2021学年度第|一学期期末考试高二级|| (文科 )数学科试卷 (参考 )答案选择题： (本大题共10个小题 ,每题5分 ,共50分 )题号 1 2 3 4 5 6 7 8 910答案 A B C A D A B B CD二、填空题 (本大题共4个小题 ,每题5分,共20分 )三、解答题 (本大题共6小题 ,共80分 .解容许写出文字说明 ,证明过程或演算步骤 )16.解：(1)直线:2l y x=+ ,即20x y-+=与以原点O为圆心 ,b为半径的圆相切2200221(1)b++∴=+-.4分又椭圆的离心率为3,3ca∴=又2222b a c=-=8分解得3a=10分故椭圆C的方程为22132x y+=.12分11.43-12.221416y x-=13. -8 , 9 14. 217 解： (1 )2()663f x x ax b '=++, 1分依题意 ,得⎩⎨⎧==0)2('0)1('f f ,即6630241230a b a b ++=⎧⎨++=⎩，．⎩⎨⎧=-=⇒43b a4分 经检验 ,3a =- ,4b =符合题意．5分(2 )由 (1 )可知 ,32()29128f x x x x c =-++ , 2()618126(1)(2)f x x x x x '=-+=--．7分所以 ,当[]03x ∈，时 ,()f x 的最||大值为(3)98f c =+．11分 因为对于任意的[]03x ∈， ,有2()f x c <恒成立 ,所以 298c c +<,13分 因此c 的取值范围为(1)(9)-∞-+∞，，．14分(Ⅱ )证明：易知A ( -2,0 ) ,B (2,0 ). 设000(,)(0)P x y y ≠ ,那么2200143x y += ,即2200314x y ⎛⎫=- ⎪⎝⎭ , 那么0102y k x =+ ,0202y k x =- , - - - - - - - - -x0 (0,1) 1 (1,2) 2 (2,3) 3 '()f x +-+()f x递增极大值5+8c递减极小值 递增9 +8c- - - - - - - - - - - - -10分即20220012222000331(4)4344444x x y k k x x x ⎛⎫- ⎪--⎝⎭⋅====---- , ∴12k k为定值19-． - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - -14分19.解：①据 ,动圆圆心M 到P 点的距离与M 到直线1x =-的距离相等||||MP MN = .由抛物线的定义 ,可知2p = .∴动圆圆心M 的轨迹方程为抛物线：24y x = .…….5分求得332-=m ,所以 ,直线1:-=x l 上存在点)332,1(--C ,使得ABC ∆是以ACB ∠为直角的直角三角形 . ………14分 法二:设D 为AB 中点,过D 作DC 垂直于l 于C. ∵P 为抛物线焦点 ∴BPBB AP AA ==11,,又∵D 为AB 中点,CD AA //1,∴CD 为梯形B B AA 11的中位线. ∴()AB BB AA CD 212111=+=,∴∠ 90=ACB设),1(m C -,332232332-=-=m .所以 ,直线1:-=x l 上存在点)332,1(--C ,使得ABC ∆是以ACB ∠为直角的直角三角形 . ………..14分20．解： (Ⅰ )因为()2f x ax b '=+ ,由图可知 ,()21f x x '=+ , - - - - - -- - - - - - - - - - - - -2分∴221a b =⎧⎨=⎩ ,得11a b =⎧⎨=⎩ ,故所求函数解析式为c x x x f ++=2)(． - - - - - - - - - - - - - -4分(Ⅱ )2()()1f x x x c cg x x x x x ++===++ ,那么2222(()1c x c x x g x x x x --'=-==． - - - - - -6分1< ,即01c <<时 ,()0g x '> ,∴()g x 在[1,2]上是增函数 ,故max 1()(2)32g x g c ==+． - - - - - - - - -- - - - - - - -8分 ②假设12≤≤ ,即14c ≤≤ ,当1x ≤<时 ,()0g x '<；当2x ≤≤时 ,()0g x '>；∵(1)2g c =+ ,1(2)32g c =+ ,∴当12c ≤≤时 ,(1)(2)g g ≤ ,max 1()(2)32g x g c ==+；当24c <≤时 ,(1)(2)g g > ,max ()(1)2g x g c ==+． - - - - - - - - -- - - - - -10分2> ,即4c >时 ,()0g x '< ,∴()g x 在[1,2]上是减函数 ,故max ()(1)2g x g c ==+． - - - - - - - - -- - - - - -12分综上所述 ,当02c <≤时 ,max 1()32g x c =+；当2c >时 ,max ()2g x c =+． - - --14分法二： 当0x ≤< ,()0g x '<；当x ≥ ,()0g x '>； - - - - -- - - -8分∴当1=x 或2=x 时 ,)(x g 取得最||大值 ,其中2)1(+=c g ,32)2(+=c g ,当20≤<c 时 ,32)2()(max +==cg x g ；当2≥c 时 ,2)1()(max +==c g x g ．- - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - -14分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
湛江一中2022届高二级第一学期数学周六测试题（十）班别： 姓名： ， 考试时间：2020/11/28一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．若点P 到直线x ＝－1的距离比到点(2，0)的距离小1，则点P 的轨迹是( ) A ．圆 B ．椭圆 C ．双曲线 D ．抛物线 2.已知向量a=(cos x,sin x),b=(sin x,cos x),f(x)=a ·b,要得到函数y=sin(2x+)的图象,只需将f(x)的图象( ) A 、向左平移个单位B 、向右平移个单位C 、向左平移个单位D 、向右平移个单位3、直线l 过点(2，0)且与双曲线x 2－y 2＝2仅有一个公共点，则这样的直线有( ) A ．1条 B ．2条 C ．3条D ．4条4．已知双曲线与椭圆x 216＋y 264＝1有共同的焦点，且双曲线的一条渐近线方程为x ＋y ＝0，则双曲线的方程为( )A ．x 2－y 2＝50B ．x 2－y 2＝24C ．x 2－y 2＝－50D ．x 2－y 2＝－245. 设p:f(x)=2x 2+mx+1在(0,+∞)内单调递增,q:m ≥-5,则⌝p 是⌝q 的( ) A 、充分不必要条件 B 、必要不充分条件C 、充分必要条件D 、既不充分也不必要条件6．已知直线y ＝k (x ＋2)(k >0)与抛物线C ：y 2＝8x 相交于A 、B 两点，F 为C 的焦点．若|F A |＝2|FB |，则k 等于( )A ．13B ．23C ．23D ．2237．已知椭圆C 1：x 2a 2＋y 2b 2＝1(a >b >0)与双曲线C 2：x 2－y 24＝1有公共的焦点，C 2的一条渐近线与以C 1的长轴为直径的圆相交于A ，B 两点．若C 1恰好将线段AB 三等分，则( ) A ．a 2＝132 B ．a 2＝13 C ．b 2＝12 D ．b 2＝28、已知双曲线x 24－y 2b 2＝1(b >0)，以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A ，B ，C ，D 四点，四边形ABCD 的面积为2b ，则双曲线的方程为( )A.x24－3y24＝1 B.x24－4y23＝1 C.x24－y24＝1 D.x24－y212＝1二、多选题：本题共4小题，每小题5分，每小题全部选对得5分，部分选对得3分，有选错得0分．9.若直线mx+ny=4和☉O:x2+y2=4没有交点,则过点P(m,n)的直线与椭圆+=1的交点个数错误的为( )A、2个B、至多一个C、1个D、0个10．对于曲线C：x24－k＋y2k－1＝1，给出下面四个命题，其中正确命题有（）A、曲线C不可能表示椭圆；B、当1<k<4时，曲线C表示椭圆；C、若曲线C表示双曲线，则k<1或k>4；D、若曲线C表示焦点在x轴上的椭圆，则1<k<5 2.11.若椭圆或双曲线上存在点P,使得点P到两个焦点的距离之比为2∶1,则称此椭圆或双曲线存在“Ω点”,下列曲线中不存在“Ω点”的是( )A、+=1B、+=1C、x2-=1D、x2-y2=112.设椭圆C:+=1(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足·=0,|FB|≤|FA|≤2|FB|,则椭圆C的离心率e的取值不可能是( )A、B、C、D、二、填空题：本题共4小题，每小题5分．13．若椭圆x2a2＋y2b2＝1过抛物线y2＝8x的焦点，且与双曲线x2－y2＝1有相同的焦点，则该椭圆的方程为________．14.抛物线y=x2上的一动点到直线l:x-y-1=0距离的最小值是.15.扎花灯是中国一门传统手艺,逢年过节时常常在大街小巷看到各式各样的美丽花灯.现有一个花灯,它外围轮廓是由两个形状完全相同的抛物线绕着它们自身的对称轴旋转而来(如图),花灯的下顶点为A,上顶点为B,AB=8米,在它的内部放有一个半径为1米的球形灯泡,球心C在轴AB上,且AC=2米.若球形灯泡的球心C到四周轮廓上的点的最近距离是在下顶点A处取到.建立适当的坐标系可得抛物线方程为y=ax2(a>0),则实数a的取值范围是.16．已知y＝f(x)是定义在R上的奇函数，在(0，＋∞)上是增函数，且f(2)＝0，则满足f(x－1)＜0的x的取值范围是________．三、解答题：本大题共6小题，解答应写出文字说明、证明过程或演算步骤．17．（本小题10分）已知数列{a n}是等比数列，a2＝4，a3＋2是a2和a4的等差中项．(1)求数列{a n}的通项公式；(2)设b n＝2log2a n－1，求数列{a n b n}的前n项和T n.18．（本小题12分）在△ABC中，a，b，c分别为内角A，B，C的对边，且2a sin A＝(2b＋c)sin B＋(2c＋b)sin C.(1)求A的大小；(2)若sin B＋sin C＝1，试判断△ABC的形状．19．（本小题12分）全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI)，数据统计如下表：空气质量指数[0,50](50,100](100,150](150,200](200,250](μg/m3)空气质量等级优良轻度污染中度污染重度污染天数2040m 10 5(1)(2)由频率分布直方图，求该组数据的平均数与中位数；(3)在空气质量指数分别为(50,100]和(150,200]的监测数据中，用分层抽样的方法抽取5天，从中任意选取2天，求事件A“两天空气质量等级都为良”发生的概率．20.(本小题满分12分)已知四棱锥P ABCD 如图所示,AB ∥CD,BC ⊥CD,AB=BC=2,CD=PD=1,△PAB 为等边三角形. (1)证明:PD ⊥平面PAB;(2)求二面角P CB A 的余弦值.21．(本小题满分12分)设椭圆E 的方程为x 2a 2＋y 2b2＝1(a >b >0)，点O 为坐标原点，点A 的坐标为(a,0)，点B 的坐标为(0，b )，点M 在线段AB 上，满足|BM |＝2|MA |，直线OM 的斜率为510. (1)求E 的离心率e ；(2)设点C 的坐标为(0，－b )，N 为线段AC 的中点，证明：MN ⊥AB ．22、(本小题满分12分)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的右焦点为F (1,0)，右顶点为A ，且|AF |＝1.(1)求椭圆C 的标准方程；(2)若动直线l ：y ＝kx ＋m 与椭圆C 有且只有一个交点P ，且与直线x ＝4交于点Q ，问：是否存在一个定点M (t,0)，使得 MP →·MQ →＝0.若存在，求出点M 的坐标；若不存在，说明理由．湛江一中2022届高二级第一学期数学周六测试题（十）参考答案班别： 姓名： ， 考试时间：2020/11/28一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1、解析：选D.点P 到直线x ＝－1的距离比到点(2，0)的距离小1，即点P 到直线x ＝－2的距离与到点(2，0)的距离相等，根据抛物线的定义可知，点P 的轨迹是抛物线．2、解析: 选C.f(x)=a ·b=sin xcos x+sin xcos x=sin 2x.而y=sin(2x+)=sin 2(x+),于是只需将f(x)的图象向左平移个单位.3、解析：选C.点(2，0)为双曲线的右顶点，过该点有两条与双曲线的渐近线平行的直线，这两条直线与双曲线仅有一个公共点，另外，过该点且与x 轴垂直的直线也与双曲线只有一个公共点．所以共有3条．4、解析：选D.因为双曲线与椭圆x 216＋y 264＝1有共同的焦点，所以双曲线的焦点在y 轴上，且焦点坐标为(0，－43)，(0，43)．又双曲线的一条渐近线方程为x ＋y ＝0，所以可设双曲线方程为y 2－x 2＝λ(λ>0)，则2λ＝48，λ＝24，故所求双曲线的方程为y 2－x 2＝24，即x 2－y 2＝－24.5、解析: 选B.f (x)=2x 2+mx+1在(0,+∞)内单调递增,则需满足对称轴x=- ≤0,即m ≥0,故⌝p:m<0.又⌝q:m<-5,由m<-5⇒m<0,故⌝p 是⌝q 的必要不充分条件.6、解析：选D.设A (x 1，y 1)，B (x 2，y 2)，易知x 1>0，x 2>0，y 1>0，y 2>0.由⎩⎨⎧y ＝k (x ＋2)，y 2＝8x 得k 2x 2＋(4k 2－8)x ＋4k 2＝0，所以x 1x 2＝4，①根据抛物线的定义得， |F A |＝x 1＋p2＝x 1＋2，|FB |＝x 2＋2.因为|F A |＝2|FB |，所以x 1＝2x 2＋2，② 由①②得x 2＝1(x 2＝－2舍去)，所以B (1，22)，代入y ＝k (x ＋2)得k ＝223.7、解析：选C.由题意，知a 2＝b 2＋5，因此椭圆方程为(a 2－5)x 2＋a 2y 2＋5a 2－a 4＝0，双曲线的一条渐近线方程为y ＝2x ，联立方程消去y ，得(5a 2－5)x 2＋5a 2－a 4＝0，所以直线截椭圆的弦长d ＝5×2a 4－5a 25a 2－5＝23a ，解得a 2＝112，b 2＝12.8、解析：选D。
由双曲线x24－y2b2＝1(b>0)知其渐近线方程为y＝±b2x，又圆的方程为x2＋y2＝4，①不妨设渐近线与圆在第一象限的交点为B，将y＝b2x代入方程①式，可得点B⎝⎛⎭⎪⎫44＋b2，2b4＋b2.由双曲线和圆的对称性得四边形ABCD为矩形，其相邻两边长为84＋b2，4b4＋b2，故8×4b4＋b2＝2b，得b2＝12.故双曲线的方程为x24－y212＝1.二、多选题：本题共4小题，每小题5分，每小题全部选对得5分，部分选对得3分，有选错得0分．9、解析: 选B、C、D.若直线与圆没有交点,则d=>2,解得m2+n2<4,即<1,∴+<1,∴点(m,n)在椭圆内部,故直线与椭圆有2个交点.10、解析：选C、D。
A错误，当k＝2时，方程表示椭圆；B错误，因为k＝52时，方程表示圆；验证可得C、D正确．11、解析:选A BC。
不妨设曲线的焦点为F1,F2,假设|PF1|=2|PF2|.若是椭圆,则|P F1|+|P F2|=2|P F2|+|P F2|=3|P F2|=2a,即|P F1|=,|P F2|=;若是双曲线,则|PF1|-|PF2|=2|PF2|-|PF2|=|PF2|=2a,即|PF1|=4a,|PF2|=2a.结合选项验证,对于选项A,B,C,上述条件下的数量关系都不能保证构成三角形PF1F2,只有选项D,由于a=1,c=,所以|P F1|=4,|P F2|=2,|F1F2|=2能构成三角形.即存在“Ω点”的曲线是x2-y2=1..12、解析: 选ABCD。