Cpk与PPM转换原理
CPK与PPK介绍
根据3σ原理，在分布范围μ ±3 σ内，包含了 99.73%的数据，接近于1，因此以±3 σ，即
6 σ为标准来衡量过程是否具有足够的精确度
和良好的经济特性的。过程能力记为B，则
B= 6 σ
估计Sigma
过 程 Sigma
R ˆ d2
S ˆ c4
计算Sigmam
S
0.505 0.5014 0.5018 0.5018 0.004 18 0.499 0.500 0.502 0.500 0.501 0.003 19 0.501 0.500 0.502 0.500 0.500 0.004 20 0.505 0.505 0.500 0.501 0.502 0.004 21 0.501 0.502 0.499 0.499 0.500 0.500 0.003
案例分析
我们再来看前面的作控制图的案例：
案例分析
过程有一个异常点，是由于偶然因素造成， 调查表明是该检验员当时委托他人代为测量，
而这代理人不适于操作精密测量设备，可能
读数不准确，也有可能伪造了数据。
剔除这个异常点，过程是受控的。
剔除异常点数据表
SubNo 1 2 3 4 5 X bar Range SubNo 1 0.498 0.501 0.504 0.503 0.502 2 0.504 0.502 0.505 0.500 0.503 3 0.500 0.499 0.501 0.502 0.504 4 0.499 0.503 0.502 0.503 0.502 5 0.505 0.506 0.506 0.502 0.506 6 0.503 0.501 0.502 0.501 0.500 7 0.503 0.501 0.504 0.501 0.500 8 0.502 0.499 0.502 0.503 0.503 9 0.502 0.502 0.504 0.502 0.500 10 0.504 0.502 0.501 0.503 0.503 11 0.503 0.498 0.501 0.501 0.502 12 0.500 0.501 0.499 0.498 0.501 13 0.504 0.503 0.503 0.499 0.496 0.501 0.008
课外学习-Cp、Cpk、Pp、Ppk、Ppm公式
Pp Ppu Ppl Ppk
0
Pp （USL - LSL）/（6σoverall） Ppu （USL - x）/（3σoverall）
Ppl （x - LSL）/（3σoverall）
Ppk min（Ppu，Ppl）
DMAI指数
T m时Cpm （USL - LSL）/[6
2 （x i T） /（n 1 ） ] i 1
Cpm
T m时Cpm min （ { T - LSL, USL - T）/[3 （x
i 1 n i 2 T） /（n 1 ） ]}
© Haier Equipment Product Group
Cp 传统 过程 能力 指数
Cpu Cpl
Cp （USL - LSL）/（6σwithin）
Cpu （USL - x）/（ 3σwithin）
Cpu （x - LSL）/（3σ within）
Cpk
Cpk min（Cpu，Cpl） Cpk （1 - k）Cp k M - μ /(T /2)
过程能力及过程绩效度量方法公式
区分 指标 计算公式 特点
潜在过程能力指数 （不考虑过程偏移和μ ）
只有规格上限时 只有规格下限时 实际过程能力指数 （不考虑过程偏移和μ ） 其中M=(USL+LSL)/2 T=USL-LSL Xbar是样本的均值 是过程固有散步 期望过程能力指数 （反映过程期望损失） （强调向目标靠近的重 要性） 其中： T=期望的目标值 m=(USL+LSL)/2 潜在过程绩效指数 只有规格上限时 只有规格下限时 实际过程绩效指数
cpk&ppm
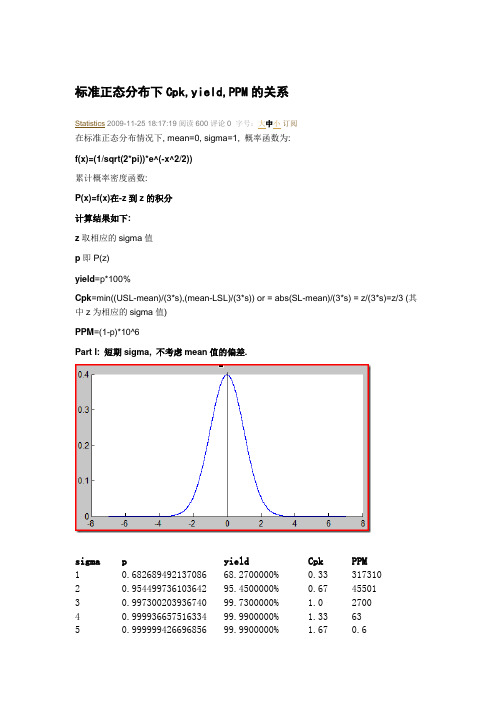
标准正态分布下Cpk,yield,PPM的关系Statistics 2009-11-25 18:17:19 阅读600 评论0字号：大中小订阅在标准正态分布情况下, mean=0, sigma=1, 概率函数为:f(x)=(1/sqrt(2*pi))*e^(-x^2/2))累计概率密度函数:P(x)=f(x)在-z到z的积分计算结果如下:z取相应的sigma值p即P(z)yield=p*100%Cpk=min((USL-mean)/(3*s),(mean-LSL)/(3*s)) or = abs(SL-mean)/(3*s) = z/(3*s)=z/3 (其中z为相应的sigma值)PPM=(1-p)*10^6Part I: 短期sigma, 不考虑mean值的偏差.sigma p yield Cpk PPM1 0.682689492137086 68.2700000% 0.33 3173102 0.954499736103642 95.4500000% 0.67 455013 0.997300203936740 99.7300000% 1.0 27004 0.999936657516334 99.9900000% 1.33 635 0.999999426696856 99.9900000% 1.67 0.66 0.999999998026825 99.9999998% 2.0 0.002PartII 长期sigma, 考虑到1.5倍sigma的均值偏差(即mean=1.5或-1.5)考虑到对称性, 以f(x)=(1/sqrt(2*pi))*e^(-(x-1.5)^2/2))来计算p值p=f(x)在-6到+6的积分, 计算结果如下表(由于Cpk只是针对于短期的sigma, 在此不计算Cpk值, 只计算对应的yield和ppm)sigma p yield Cpk PPM1 0.302327873400211 30.2300000% -- 6976722 0.691229832194978 69.1200000% -- 3087703 0.933189401058017 93.3100000% -- 668114 0.993790315684661 99.3700000% -- 62105 0.999767370880804 99.9700000% -- 2336 0.999996602326843 99.9900000% -- 3.4PartIII CL/LSL/USL与mean, z的关系***以下共两个表格, 分短期sigma和长期sigmaPart I : 短期sigma情况下, 即不考虑均值的偏差, mean=0, sigma=1时, Cpk,yield,ppm 的关系如下:附表一: short term sigma, sigma=1~6z p(即phai(z)-phai(-z))Yield Cpk PPM 10.68268949213708668.269%0.333317310 1.10.72866787810723572.867%0.367271332 1.20.76986065955658476.986%0.400230139 1.30.80639903082877980.640%0.433193600 1.40.83848668153245883.849%0.467161513 1.50.86638559746228486.639%0.500133614 1.60.89040141660088489.040%0.533109598 1.70.91086907448291491.087%0.56789130 1.80.92813936177414892.814%0.60071860 1.90.94256688036799694.257%0.63357433 20.95449973610364195.450%0.66745500 2.10.96427115887436796.427%0.70035728 2.20.97219310497300397.219%0.73327806 2.30.97855177995664897.855%0.76721448 2.40.98360492815080898.360%0.80016395 2.50.98758066934844898.758%0.83312419 2.60.99067762395256399.068%0.8679322 2.70.99306605239391999.307%0.9006933 2.80.99488973933914499.489%0.9335110 2.90.99626837339923399.627%0.9673731 30.99730020393674099.730% 1.0002699 3.10.99806479357356499.806% 1.0331935 3.20.99862572412416899.863% 1.0671374 3.30.99903315171523299.903% 1.1009663.40.99932614146864799.933% 1.133673 3.50.99953474184193299.953% 1.167465 3.60.99968178281968499.968% 1.200318 3.70.99978440053304499.978% 1.233215 3.80.99985530391215199.986% 1.267144 3.90.99990380731197199.990% 1.30096.1 40.99993665751632699.994% 1.33363.34.10.99995868498616099.996% 1.36741.3 4.20.99997330850197899.997% 1.40026.6 4.30.99998292018904799.998% 1.43317 4.40.99998917491218499.999% 1.46710.8 4.50.99999320465373399.999% 1.500 6.79 4.60.999995775090593100.000% 1.533 4.22 4.70.999997398384935100.000% 1.567 2.6 4.80.999998413343529100.000% 1.600 1.58 4.90.999999041633524100.000% 1.6330.958 50.999999426696856100.000% 1.6670.5735.10.999999660346519100.000% 1.7000.339 5.20.999999800711474100.000% 1.7330.199 5.30.999999884197319100.000% 1.7670.115 5.40.999999933359103100.000% 1.8000.066 5.50.999999962020875100.000% 1.8330.037 5.60.999999978564819100.000% 1.8670.021 5.70.999999988019257100.000% 1.9000.011 5.80.999999993368508100.000% 1.9330.00665.90.999999996364984100.000% 1.9670.003660.999999998026825100.000% 2.0000.0019Part II: 长期sigma情况下, 即考虑均值的偏差, mean=1.5*sigma=1.5, sigma=1时, Cpk,yield,ppm的关系如下:附表二: long term sigma, z=1~6z p(即phai(z)-phai(-z))Yield Cpk PPM10.30232787340021130.233%6976721.10.33991707036595733.992%6600821.20.37862160400800737.862%6213781.30.41818516023046941.819%5818141.40.45830634942258745.831%5416931.50.49865010196837049.865%5013491.60.53886023406381153.886%4611391.70.57857257150118757.857%4214271.80.61742799804656861.743%3825721.90.65508481234464865.508%34491520.69122983219497969.123%3087702.10.72558777365976972.559%2744122.20.75792854804344975.793%2420712.30.78807225337267978.807%2119272.40.81589177830922681.589%1841082.50.84131307482670684.131%1586862.60.86431328154669886.431%1356862.70.88491698402928188.492%1150832.80.90319097550891390.319%968092.90.91923792822232191.924%80762 30.93318940105800893.319%66810 3.10.94519859584573994.520%54801 3.20.95543323643392495.543%44566 3.30.96406888755883996.407%35931 3.40.97128296100076097.128%28717 3.50.97724958140024997.725%22750 3.60.98213540961044398.214%17864 3.70.98609645284223898.610%13903 3.80.98927583207698498.928%10724 3.90.99180243075495599.180%8198 40.99379031568466299.379%6210 4.10.99533880125869199.534%4661 4.20.99653302020658899.653%3467 4.30.99744486635382699.744%2555 4.40.99813418488210999.813%1866 4.50.99865010098178299.865%1350 4.60.99903239625643999.903%968 4.70.99931286177976899.931%687 4.80.99951657570879399.952%483 4.90.99966307065663499.966%337 50.99976737088080699.977%233 5.10.99984089138928399.984%159 5.20.99989220025610199.989%108 5.30.99992765195084599.993%725.40.99995190365338299.995%485.50.99996832875688399.997%325.60.99997934249245699.998%215.70.99998665425068899.999%135.80.99999146009438099.999%8.55.90.99999458745602499.999% 5.460.999996602326834100.000% 3.4CL对应于mean, USL对应于z, LSL对应于-z; 一般而言, 由于LSL和USL为固定值, 要提高Cpk, 只能通过改进工艺, 减小制程波动, 以减小sigma, 使sigma<(USL-LSL)/2/3/Cpk_expectedCpk_expected为期望的Cpk值, 一般取1.67或2.0ps: 1. 以上表格中相应sigma的P(x)值为MATLAB计算的结果, 也可以通过正态分布表查表计算(正态分布表精度不是很高,另外一般只有z=0.01~3.99的正态分布值)或excel计算2. 更详细的数据见本空间的其他blog, 如需更多的数据, 可以发邮件给我.。
cpk计算公式与解释
客户来审核了，检查以我们提供的PPAP，发现我们计算的CPK值小于PPK值，我跟他回复说CPK要求大于1.33，而PPK要求大于1.67，所以这样看应该是要求PPK大于CPK,但是他不认可，说是看到同一组数据计算出来的，说应该是CPK值大于PPK值。
查了相关资料也说是PPK大于CPK.到底该是怎么样啊!何谓工程能力？所谓工程能力是指在某种产品的生产中，是否能够均一地生产优质产品，这是产品质量管理的一个重要部分。
生产工程生产均一产品的能力叫做工程能力。
利用±3σ来作为表示这种能力的数值。
利用±3σ作为工程能力值的原因如果某种产品的质量特征是正态分布的话，以平均数为中心，在±3σ范围内包含有99.73%的产品，因此，将工程能力值设定为±3σ就几乎包括了所有产品。
工程能力指数存在一定的管理规格时，工程能力值与管理规格的比值叫做工程能力指数。
作为工程能力指数，我们学习了Cp和Cpk。
Cp和CpkCp表现了短期内最佳的Process状态，因此称为“短期工程能力指数”。
Cpk另一个工程能力指数Cpk则考虑到随着时间的流逝，每次抽取测定的data的样本时，中间值都有些差异，在这种情况下计算工程能力，叫做“长期工程能力指数”。
工程能力指数的计算－－存在两边规格的时候这是在假定给定data的平均数与基准Spec的中间值相同的情况下计算的。
工程能力指数的计算－－只有一边规格的时候6σ水平的工程能力指数产品的质量规格在±6之间，最糟糕的情况下，不合格产品率的上限、下限也各自不超过3.4ppm。
6σ水平的工程能力指数的目标值是Cp=2.0，Cpk=1.5。
最佳答案CPK：Complex Process Capability index 的缩写，是现代企业用于表示制成能力的指标。
CPK值越大表示品质越佳。
CPK=min（（X-LSL/3s），（USL-X/3s））Cpk——过程能力指数CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s]Cpk应用讲议1. Cpk的中文定义为：制程能力指数，是某个工程或制程水准的量化反应，也是工程评估的一类指标。
CPK与PPK计算入门
CPK与PPK计算入门一、CPK1、定义CPK，过程能力指数（Process capability index），是指过程在一定时间内，处于控制状态（稳定状态）下，固有的满足产品质量标准要求（规格范围等）的能力。
CPK表示过程的潜在固有能力，主要用于周期性的过程评价，大批量生产后的生产能力的评价。
2、计算公式CPK=Min（CPU,CPL）CPU=（USL-X bar）/3σCPL=（X bar-LSL）/3σσ=R bar/d2式中，USL为规格上限；LSL为规格下限；R bar为各个子组极差的平均值；d2为修正值，可查表（附后）。
（1）当公差双侧对称时，CPK=CP*(1-|Ca|)CP=（USL-LSL）/（6σ）Ca=（X bar-U）/（（USL-LSL）/2）式中，U为规格中心值。
（2）当公差双侧不对称时，则分别计算CPU和CPL，取最小值。
（3）当公差为单侧时，有上限公差则只计算CPU，有下限公差则只计算CPL。
3、数值选取Cpk计算之前，一定要检查过程是否稳定，要求受控。
一般要求至少有100个数据，25个均值。
也就是说，采值是进行分组，涉及到子组，子组容量，采值频次等，它针对的是一个长期的过程。
4、指数意义CPK，是进入大批量生产后，为保证批量生产下的产品的品质状况不至于下降，且为保证与小批生产具有同样的控制能力，所进行的生产能力的评价。
·Cpk≥2.0 特优，可考虑成本的降低；·2.0 > Cpk ≥ 1.67 优，应当保持之；·1.67 > Cpk ≥ 1.33 良，能力良好，状态稳定，但应尽力提升；·1.33 > Cpk ≥ 1.0 一般，状态一般，制程因素稍有变异即有产生不良的危险，应利用各种资源及方法将其提升；·1.0 > Cpk ≥ 0.67 差，制程不良较多，必须提升其能力；·0.67 > Cpk 不可接受，其能力太差，应考虑重新整改设计制程。
关于Cp、Cpk、Ppk
关于Cp、Cpk、Cpm、Cpmk、Pp、Ppk什么是过程能力？过程能力是指加工方面满足加工质量的能力。
此种能力表现在过程稳定的程度，σ越小，过程能力越稳定，|M-μ|的值越小，表示过程能力的偏差越小，99.73％的质量特性散布区间在[μ-3σ,μ+3σ]。
过程能力指数Cp、CpkCp是表征过程固有的波动状态，即技术水平。
它是在过程的平均值μ与目标值M重合的情形，过程处于统计控制状态时（非分析状态），过程能力指数Cp可用下式表示：Cp=(USL-LSL)/6σ=T/6σCp与不良品率的关系Cp P1.0 0.27%1.33 0.007%1.5 6.8PPm2.0 2.0PPb实际过程中，平均值与目标志重合的情形非常少，因此引入了偏移度的概念，即过程平均值与目标值的偏离过程K=2|M-μ|/TCp-Cpk=|M-μ|/3σCpk与不良品率的关系Cpk P(%)1.0 0.13~0.271.1 0.05~0.101.2 0.02~0.031.3 48.1~96.2PPM1.4 13.4~26.7PPM过程能力指数Cpm、Cpmk过程能力指数是根据田口玄一关于质量损失函数而设计出来的。
将目标值与均值的偏差也考虑进来，因为有实际的改进意义Cpm=(USL-LSL)/6SQRT((σp)2+(|M-μ|)2)Cpm<Cp，这是因为考虑了过程平均值与目标值发生偏差的结果过程能力指数Cpmk是考虑过程能力与平均值偏离目标值的综合结果，因此又叫综合过程能力指数Cpmk=Cpk/SQRT(1+((|M-μ|)/σ)2)过程绩效指数Pp、Ppk过程Pp=(USL-LSL)/6σ总Ppk=min((USL-u)/3σ总,(u-LSL)/3σ总)Cpk——过程能力指数CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s]Cpk应用讲义1. Cpk的中文定义为：制程能力指数，是某个工程或制程水准的量化反应，也是工程评估的一类指标。
CPK VS PPM
CPk=1.33和CPk=1.67对应的不良率是多少分布中心无偏移时，即样本均值与分布中心重合时, 分布中心无偏移为理想状态.Cpk PPM Cpk PPM Cpk PPM0.51 126016.73 1.01 2445.54 1.51 5.900.52 118759.88 1.02 2213.37 1.52 5.120.53 111834.81 1.03 2001.56 1.53 4.430.54 105232.28 1.04 1808.51 1.54 3.840.55 98942.94 1.05 1632.70 1.55 3.320.56 92957.32 1.06 1472.75 1.56 2.870.57 87265.87 1.07 1327.35 1.57 2.480.58 81859.02 1.08 1195.30 1.58 2.140.59 76727.14 1.09 1075.47 1.59 1.840.60 71860.64 1.10 966.85 1.60 1.590.61 67249.94 1.11 868.46 1.61 1.370.62 62885.53 1.12 779.42 1.62 1.170.63 58757.96 1.13 698.93 1.63 1.010.64 54857.90 1.14 626.21 1.64 0.86540.65 51176.12 1.15 560.59 1.65 0.74210.66 47703.53 1.16 501.41 1.66 0.63580.67 44431.19 1.17 448.11 1.67 0.54430.68 41350.33 1.18 400.13 1.68 0.46550.69 38452.34 1.19 356.98 1.69 0.39780.70 35728.84 1.20 318.22 1.70 0.33970.71 33171.61 1.21 283.42 1.71 0.28970.72 30772.67 1.22 252.22 1.72 0.24690.73 28524.24 1.23 224.25 1.73 0.21030.74 26418.77 1.24 199.22 1.74 0.17890.75 24448.95 1.25 176.83 1.75 0.15210.76 22607.69 1.26 156.83 1.76 0.12920.77 20888.15 1.27 138.97 1.77 0.10960.78 19283.74 1.28 123.03 1.78 0.09290.79 17788.09 1.29 108.84 1.79 0.07870.80 16395.07 1.30 96.19 1.80 0.06660.81 15098.82 1.31 84.95 1.81 0.05640.82 13893.70 1.32 74.95 1.82 0.04760.83 12774.31 1.33 66.07 1.83 0.04020.84 11735.48 1.34 58.20 1.84 0.03390.85 10772.29 1.35 51.22 1.85 0.02860.86 9880.03 1.36 45.04 1.86 0.02410.87 9054.22 1.37 39.57 1.87 0.02020.88 8290.60 1.38 34.73 1.88 0.01700.89 7585.12 1.39 30.46 1.89 0.01430.90 6933.95 1.40 26.69 1.90 0.01200.91 6333.43 1.41 23.37 1.91 0.01000.92 5780.14 1.42 20.44 1.92 0.00840.93 5270.80 1.43 17.87 1.93 0.00700.94 4802.36 1.44 15.60 1.94 0.00590.95 4371.92 1.45 13.61 1.95 0.00490.96 3976.75 1.46 11.87 1.96 0.00410.97 3614.29 1.47 10.34 1.97 0.00340.98 3282.12 1.48 9.00 1.98 0.00290.99 2978.00 1.49 7.82 1.99 0.00241.00 2699.80 1.50 6.802.00 0.0020CPK=1.00为 3σCPK=1.33为 4σ CPK=1.67为5σ CPK=2.0为6σ分布中心无偏移时，即样本均值与分布中心重合时，4西格玛水平对应的不合格率为6210ppm；6西格玛水平对应的不合格率为十亿分之二，即0.0024ppm。
【秒懂】PPK与CPK定义，差异分析及计算
【秒懂】PPK与CPK定义，差异分析及计算定义：PP （Performance Index of Process）不考虑过程有⽆偏移，容差范围除以过程性能。
Cpk （Preliminary process Capability）考虑过程有偏差时，样本数据的过程性能。
*ppk 通常⽤来与cp及Cpk对⽐，度量和确认内改进的优先次序。
适⽤环境ppk：过程性能指数，表⽰的是过程在⼀段时间内的表现1:输出满⾜规格要求+预测图形+长期不稳定过程（不要求过程稳定）2:⼩批⽣产（试产）的过程性能评价，要求Ppk>1.67；3·⽤于实时过程性能研究和初始过程能⼒评估.Cpk：过程能⼒指数，表⽰过程本⾝的能⼒，⼀种理想的状态下的指数。
1:过程稳定+⾜够历史数据/初始数据（More than 100个体数据&25⼦组2:⼤批量⽣产后的⽣产能⼒的评价，要求Cpk>1.333:主要⽤于周期性的过程评价.注解：1、有时CPK需要借助PPK的控制界限来作控制2、PPK表⽰所有数据之间的变差；CPK剔除组内变差（组内均值），仅考虑⼦组变差。
3、PPK和CPK的区别就好像是⼀个⼈的⼯作表现和⼯作能⼒之间的差别⼀样。
4、Cpk计算之前，⼀定要检查过程是否稳定。
⼀般要求有100个数据，25个均值。
取样⽅式：⼦样定间隔时间选取（如：每隔1⼩时连续取4个样本，计算均值。
通过xbar-R图来检查过程是否稳定。
如果稳定，计算得到的是Cpk。
5、PPK不要求检查过程是否稳定。
取样⽅式：⽆需1⼩时间隔，连续取100个数据。
因PPK未检查过程是否稳定（风险），要求⽬标PPK>1.67.因PPK中可能有特殊原因变差不能称之为过程能⼒指数，⽽是过程性能指数。
6、过程不稳定，则需查明特殊原因并消除后重新进⾏评估（过程繁琐）。
对于初期数据匮乏案例，在客户同意后可采⽤PPK。
7、当过程稳定+CPK满⾜要求时，利⽤控制图来监视过程。
CPK、Sigma和PPM的换算关系
过程能力指数（Cp和Cpk）表示的是过程在稳定（即没有特殊原因干扰产出品的特性或者说是在可控（under control）的）状态下能使其产出品达到可接受标准的程度的指标。
按照常识，Cpk越高越好，产品的不良率也越低。
SQE在PPAP审核时，要求供应商提交的过程能力报告，关键特性的Cpk大于1.33，此时供应商内部的百万分之不良率PPM为63。
拓展到Cpk=1.0，Cpk=1.67的PPM如下：在不考虑偏移的情况下：Cpk=1.33 对应4σ 水平其PPM=63.3；Cpk=1.67 对应5σ 水平其PPM=0.570；Cpk=2.0 对应6σ 水平其PPM=0.0020；那么，这个值是怎么来的，其他Cpk对应的PPM数值是多少？过程能力指数Cp或Cpk在产品或制程特性分布为正态且在稳定状态下时，通过正态分布的概率计算，可以换算为该产品或制程特性的良率或不良率，同时也可以几个Sigma来对照。
CPK是过程能力，西格玛水平是管理水平，PPM是管理结果。
下文将以产品或制程特性中心没偏移目标值和中心偏移目标值1.5σ说明。
我们从正态分布讲起。
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。
其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。
当μ = 0，σ = 1时的正态分布是标准正态分布。
若随机变量X，服从一个位置参数为μ、尺度参数为σ的概率分布，其概率密度函数为：当μ=0，σ=1时，正态分布就成为标准正态分布。
我们对其积分，也就是求面积，所得值为1。
（每个质量人追求的100.00%合格）接下来，我们谈一下什么是西格玛水平。
西格玛水平Sigma Level：过程能力的一种衡量指标，将过程分布的平均值、标准偏差与质量特性的目标值、规格线结合起来。
西格玛水平越高，过程满足质量要求的能力就越强，反之，西格玛水平越低，过程满足质量要求的能力就越低。
我们可以简单的理解为规格线与目标值间的距离最少能容纳k个标准偏差σ，当k = 3时，我们称之为3西格玛水平，上下规格极限之差为6σ。
CPK—PPM换算模板
CPK—PPM换算模板CPK（也称为Process Capability Index，过程能力指数）和PPM（也称为Parts Per Million，百万分之一）是在质量管理中常用的两种指标，用于评估一个工艺或过程的稳定性和可控性。
CPK通过比较过程的变异性和其规格限的差异来衡量工艺的能力，而PPM则用于度量产品或过程不合格件的概率。
下面是一个基本的CPK和PPM换算模板。
首先，我们需要了解一些基本的概念和背景知识。
1. 规格限（Specification Limits）：规格限是指产品或过程必须满足的上限和下限。
它们通常由设计要求、客户需求或行业标准确定。
2. 过程能力指数（Process Capability Index，CPK）：CPK衡量了一个工艺或过程以多大程度上可以产生合格的产品或结果。
它更关注过程的稳定性和可控性。
3. 百万分之一（Parts Per Million，PPM）：PPM用于度量产品或过程每一百万个单位中不合格件的数量。
它是一个相对较小的概率，用于描述工艺的可靠性。
接下来，我们将介绍如何使用CPK和PPM之间的换算关系。
1.CPK到PPM的换算：CPK和PPM之间的计算可以通过正态分布的统计方法来完成。
具体的计算公式如下：其中，Φ是标准正态分布表中CPK对应的累积概率。
2.PPM到CPK的换算：如果我们已知PPM，可以使用下面的公式来计算对应的CPK值：现在，我们将利用这些概念和公式来演示一个CPK和PPM的换算实例。
假设我们所考虑的过程的规格限为25至30个单位，已知该过程无法做到完全满足要求，并估计在这个过程下有50个不合格件（PPM=50）。
我们将使用上述公式来计算过程能力指数CPK。
首先，我们需要计算Φ的值。
根据标准正态分布表，当CPK为0时，Φ的值为0.5000。
因此，Φ(0)=0.5000。
然后，我们可以将PPM值代入公式进行计算：换算结果表明，即使过程的规格限比实际值宽松得多，该过程的能力仍然较差。
Cp_Cpk_PPM_西格玛关系
注：潜在过程能力Cp：是指该工序能够达到的能力，它是假定加工产品的尺寸均值与公差中心重合，没有任何偏离的情况下计算得出。
主要评 价该工序的散差符合规范的能力
实际过程能力Cpk：一般情况下，产品加工尺寸均值与公差中心都有偏离，实际过程能力Cpk即是在考虑这个偏离时计算得到。
它不但评价工序散差，而且也评价了工序均值与公差中心的偏离程度。
偏离度k衡量了产品加工尺寸均值与公差中心的偏离度，在上表中设定偏移量为1.5σ
PPM：上表中的PPM计算值都是考虑了尺寸均值与公差中心偏移了1.5σ距离。
如果无偏移，则PPM会少很多；如果实际偏移大于1.5σ，PPM还会高；在实际的工序能力计算中，是按照实际偏移量计算得到的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
CPK与PPM之间到底什么关系？首先给大家看一张总结的表（下图）：
￠(X)是标准正态分布函数--- Array
没学过积分这个概率是算不出来的，但伟大的科学家给我们已制定好了一个正态分布表（截
图一部分）：
例如：加工一批螺丝，外径要求为10±0.2mm 。
测量了100pcs 产品，算出平均值为10.1mm 、标准差σ=0.05mm ，假设数量符合正态分布，求其CPK 及不良率。
解：
CPK =MIN{(平均值-LSL)/3σ,（USL-平均值）/3σ} =0.67
PPM=P=￠[(LSL-u)/σ)]+[1-(USL-u)/σ] =￠（-6）+[1-￠(2)] =1-￠（6）+1-￠（2）=2-￠（6）-￠（2）
查正态分布表得：PPM=（P=0.977250）*1000000=22750PPM 。
由此我们由此我们可以看出可以看出可以看出：：当CPK=0.67时，PPM=22750.是存在转换是存在转换联系的联系的联系的！！
下面再解释下中心线偏移对不良率的影响（公式麻烦就直接用手做了个图）：
从此图我们可以看到，中心偏移对Cpk 是有影响的，但到底是偏大还是偏小，这个还很难讲，需要根据实际情况来看。
还有人提到，过程偏移不一定是 1.5σ，这个也确实是对的，因为
1.5σ偏移好像是根据晶圆磨损长期监控得出的一个结果，由此可以知道，这个结果是不能推广到所有的过程，每个过程实际偏移多少，也是需要实际分析的。