高中数学必修4公式大全(可编辑修改word版)
高中数学必修四公式
高中数学必修四公式以下是高中数学必修四中常用的一些公式：1. 二次函数的顶点坐标公式：当二次函数的标准式为 y = ax^2 + bx + c 时，顶点的横坐标为 x = -b/(2a)，纵坐标为 y = -Δ/(4a)，其中Δ =b^2 - 4ac 为二次函数的判别式。
2. 二次函数的根与系数之间的关系：若二次函数的标准式为 y = ax^2 + bx + c，其中a ≠ 0，则方程 ax^2 + bx + c = 0 的根公式为x1 = (-b + √Δ)/(2a)，x2 = (-b - √Δ)/(2a)3. 等差数列的通项公式：若等差数列的第一项为 a1，公差为 d，则第 n 项 an = a1 + (n - 1)d。
4. 等差数列的前 n 项和公式：若等差数列的前 n 项和为 Sn，则 Sn = n/2 * (a1 + an) = n/2 * (2a1 + (n-1)d)。
5. 等比数列的通项公式：若等比数列的第一项为 a1，公比为 q，则第 n 项 an = a1 * q^(n-1)。
6. 等比数列的前 n 项和公式：若等比数列的前 n 项和为 Sn，则 Sn = a1 * (1 -q^n)/(1 - q)，其中q ≠ 1。
7. 三角函数的基本关系式：sin^2θ + cos^2θ = 11 + tan^2θ = sec^2θ1 + cot^2θ = csc^2θ8. 三角函数的和差化简公式：sin(α ± β) = sinαcosβ ± cosαsinβcos(α ± β) = cosαcosβ ∓ sinαsinβtan(α ± β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)以上是一些常用的高中数学必修四的公式，希望对你有帮助！。
(完整word版)高中数学人教版必修四常见公式及知识点系统总结(全)
必修四常考公式及高频考点第一部分 三角函数与三角恒等变换考点一 角的表示方法 1.终边相同角的表示方法：所有与角α终边相同的角，连同角α在内可以构成一个集合：{β|β= k ·360 °+α,k ∈Z } 2.象限角的表示方法： 第一象限角的集合为{α| k ·360 °<α<k ·360 °+90 °,k ∈Z }第二象限角的集合为{α| k ·360 °+90 °<α<k ·360 °+180 °,k ∈Z } 第三象限角的集合为{α| k ·360 °+180 °<α<k ·360 °+270 °,k ∈Z } 第四象限角的集合为{α| k ·360 °+270 °<α<k ·360 °+360 °,k ∈Z }3.终边在某条射线、某条直线或两条垂直的直线上(如轴线角)的表示方法：（1）若所求角β的终边在某条射线上，其集合表示形式为{β|β= k ·360 °+α,k ∈Z },其中α为射线与x 轴非负半轴形成的夹角（2）若所求角β的终边在某条直线上，其集合表示形式为{β|β= k ·180 °+α,k ∈Z },其中α为直线与x 轴非负半轴形成的任一夹角（3）若所求角β的终边在两条垂直的直线上，其集合表示形式为{β|β= k ·90 °+α,k ∈Z },其中α为直线与x 轴非负半轴形成的任一夹角 例：终边在y 轴非正半轴上的角的集合为{α|α= k ·360 °+270 °,k ∈Z }终边在第二、第四象限角平分线上的集合为{α|α= k ·180 °+135 °,k ∈Z } 终边在四个象限角平分线上的角的集合为{α|α= k ·90 °+45 °,k ∈Z } 易错提醒：区别锐角、小于90度的角、第一象限角、0～90、小于180度的角 考点二 弧度制有关概念与公式 1.弧度制与角度制互化π=︒180，1801π=︒，1弧度︒≈︒=3.57180π2.扇形的弧长和面积公式（分别用角度制、弧度制表示方法）弧长公式：R Rn l απ==180, 其中α为弧所对圆心角的弧度数 扇形面积公式：lR R n S 213602==π=12 R 2|α|, 其中α为弧所对圆心角的弧度数 易错提醒：利用S=12R 2|α|求解扇形面积公式时，α为弧所对圆心角的弧度数，不可用角度数规律总结：“扇形周长、面积、半径、圆心角”4个量，“知二求二”，注意公式选取技巧考点三 任意角的三角函数 1.任意角的三角函数定义设α是一个任意角，它的终边与单位圆交于点()y x P ,，那么sin y r α=，cos x r α=，tan y x α=（||r OP ==；化简为xyx y ===αααtan ,cos ,sin . 2.三角函数值符号规律总结：利用三角函数定义或“一全正、二正弦、三正切、四余弦”口诀记忆象限角或轴线角的三角函数值符号. 3.特殊角三角函数值SIN15º=SIN(60º-45º)=SIN60ºCOS45º-SIN45ºCOS60º=(√6-√2)/4 COS15º=COS(60º-45º)=COS60ºCOS45º+SIN60ºSIN45º=(√6+√2)/4除此之外，还需记住150、750的正弦、余弦、正切值 4.三角函数线经典结论： (1)若(0,)2x π∈，则sin tan x x x <<(2)若(0,)2x π∈，则1sin cos x x <+≤(3)|sin ||cos |1x x +≥考点四 三角函数图像与性质,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭考点五 正弦型（y=Asin(ωx ＋φ)）、余弦型函数（y=Acos(ωx ＋φ)）、正切性函数（y=Atan(ωx ＋φ)）图像与性质 1.解析式求法A 、B 通过图像易求，重点讲解φ、ω求解思路： ①φ求解思路：代入图像的确定点的坐标.如带入最高点),(11y x 或最低点坐标),(22y x ，则)(221Z k k x ∈+=+ππϕω或)(2232Z k k x ∈+=+ππϕω，求ϕ值． 易错提醒：y=Asin(ωx ＋φ)，当ω>0，且x=0时的相位（ωx+φ=φ）称为初相.如果不满足ω>0，先利用诱导公式进行变形，使之满足上述条件，再进行计算.如y=-3sin(-2x+600)的初相是-600②ω求解思路：利用三角函数对称性与周期性的关系，解ω.相邻的对称中心之间的距离是周期的一半；相邻的对称轴之间的距离是周期的一半；相邻的对称中心与对称轴之间的距离是周期的四分之一. 2.“一图、两域、四性” “一图”：学好三角函数，图像是关键。
高中数学必修4常用公式
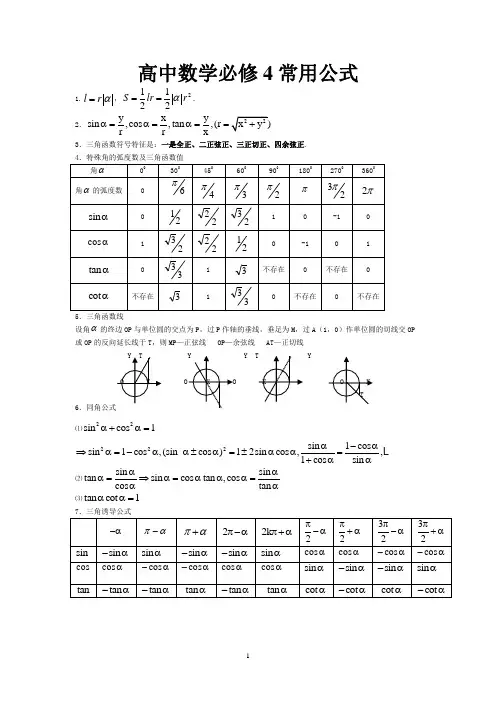
高中数学必修4常用公式1.l r α=，21122S lr r α==．2．y x ysin ,cos ,tan ,(r r r xα=α=α==3．三角函数符号特征是：一是全正、二正弦正、三正切正、四余弦正.4．特殊角的弧度数及三角函数值5．三角函数线设角α的终边OP 与单位圆的交点为P ，过P 作轴的垂线，垂足为M ，过A （1，0）作单位圆的切线交OP 或OP 的反向延长线于T ，则MP —正弦线 OP —余弦线 AT —正切线6⑪22sin cos 1α+α=222sin 1cos sin 1cos ,(sin cos )12sin cos ,,1cos sin α-α⇒α=-αα±α=±αα=+αα⑫sin sin tan sin cos tan ,cos cos tan ααα=⇒α=ααα=αα⑬tan cot 1αα= 7．三角诱导公式8．正弦函数、余弦函数、正切函数的图象与性质{x |x k ,k Z}π≠+π∈9．函数()sin (0,0)=A +>>y x A ωϕω的图象可以由y sin x =经过哪些图象变换而得到？ 法一: 由y sin x =图象上有点向左（右）平移ϕ个单位长度，得到函数()sin y x ϕ=+的图象；再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长（或缩短）到期的1ω倍（纵坐标不变），得到函数()sin y x ωϕ=+的图象；再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长（缩短）到原来的A 倍（横坐标不变），得到函数()sin y x ωϕ=A +的图象．法二：将函数()sin y x ϕ=+的图象上所有点的横坐标伸长（缩短）到原来的1ω倍（纵坐标不变），得到函数sin y x ω=的图象；再将函数sin y x ω=的图象上所有点向左（右）平移ϕω个单位长度，得到函数()sin y x ωϕ=+的图象；再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长（缩短）到原来的A 倍（横坐标不变），得到函数()sin y x ωϕ=A +的图象． 10．函数()()sin 0,0y x ωϕω=A +A >>的性质： ①振幅：A ；②周期：2πωT =；③频率：12f ωπ==T；④相位：x ωϕ+；⑤初相：ϕ．函数()sin y x ωϕ=A ++B ，当1x x =时，取得最小值为min y ；当2x x =时，取得最大值为m ax y ，则()m ax m in 12y y A =-，()m ax m in 12y y B =+，()21122x x x x T =-<．11．sin()sin cos cos sin ,cos()cos cos sin sin ,tan tan tan()tan tan tan()(1tan tan )1tan tan α±β=αβ±αβα±β=αβαβα±βα±β=⇒αβ=α±βαβαβsin 22sin cos α=αα222222221cos 22sin ,1cos 22cos ,cos 2cos sin 12sin 2cos 11cos 21cos 2sin ,cos 22⎧-α=α+α=α⎪α=α-α=-α=α-⇒⎨-α+αα=α=⎪⎩22tan tan 21tan αα=-αsin 2tan12tan22ααα+=cos 2tan12tan122ααα+-=tan 2tan12tan 22ααα-=12.三角函数变换主要是：角、函数名、次数、系数(常值)的变换，其核心是“角的变换”!角的变换主要有：已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换.如()()ααββαββ=+-=-+， 2()()ααβαβ=++-，2()()αβαβα=+--22αβαβ++=⋅，()()222αββααβ+=---等.常值变换主要指“1”的变换：22221sin cos sec tan tan cot tan sin cos 042x x x x x x ππ=+=-=⋅==== 等.三角式变换主要有：三角函数名互化(切割化弦)、三角函数次数的降升(降次、升次)、运算结构的转化(和式与积式的互化). 解题时本着“三看”的基本原则来进行:“看角、看函数、看特征”,基本的技巧有:巧变角,公式变形使用,化切割为弦,用倍角公式将高次降次.注意：和(差)角的函数结构与符号特征；余弦倍角公式的三种形式选用；降次(升次)公式中的符号特征.“正余弦‘三兄妹—sin cos sin cos x x x x ±、’的内存联系”(常和三角换元法联系在一起sin cos t x x =±[sin cos x x ∈= .辅助角公式中辅助角的确定：()sin cos a x b x x θ+=+(其中θ角所在的象限由b a , 的符号确定，θ角的值由tan b aθ=确定)在求最值、化简时起着重要作用.尤其是两者系数绝对值之比为1或的情形.sin cos A x B x C +=有实数解222A B C ⇔+≥. 13．⑪正弦定理R Cc Bb Aa 2sin sin sin ===（R 2是ABC ∆外接圆直径）注：①C B A c b a sin :sin :sin ::=；②C R c B R b A R a sin 2,sin 2,sin 2===；③CB A c b a Cc Bb Aa sin sin sin sin sin sin ++++===。
高中数学必修四全部公式资料
乘法与因式分解a^2-b^2=(a+b)(a-b)a^3+b^3=(a+b)(a^2-ab+b^2) •a^3-b^3=(a-b(a^2+ab+b^2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解-b+√(b^2-4ac)/2a -b-√(b^2-4ac)/2a根与系数的关系X1+X2=-b/a X1*X2=c/a 注：韦达定理判别式b^2-4ac=0 注：方程有两个相等的实根b^2-4ac>0 注：方程有两个不等的实根b^2-4ac<0 注：方程没有实根，有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍角公式tan2A=2tanA/[1-(tanA)^2]cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA)) 和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B) )2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n2 -2+4+6+8+10+12+14+…+(2n)=n(n+1) 51^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2+…+n^2=n(n+1)(2n+1)/61^3+2^3+3^3+4^3+5^3+6^3+…n^3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注：其中R 表示三角形的外接圆半径余弦定理b^2=a^2+c^2-2accosB 注：角B是边a和边c的夹角圆的标准方程(x-a)^2+(y-b)^2=^r2 注：（a,b）是圆心坐标圆的一般方程x^2+y^2+Dx+Ey+F=0 注：D^2+E^2-4F>0抛物线标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h必修四：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝c otαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为：对于k·π/2±α(k∈Z)的个三角函数值，①当k是偶数时，得到α的同名函数值，即函数名不改变；②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan.（奇变偶不变）然后在前面加上把α看成锐角时原函数值的符号。
人教版高中数学必修四常用公式大全
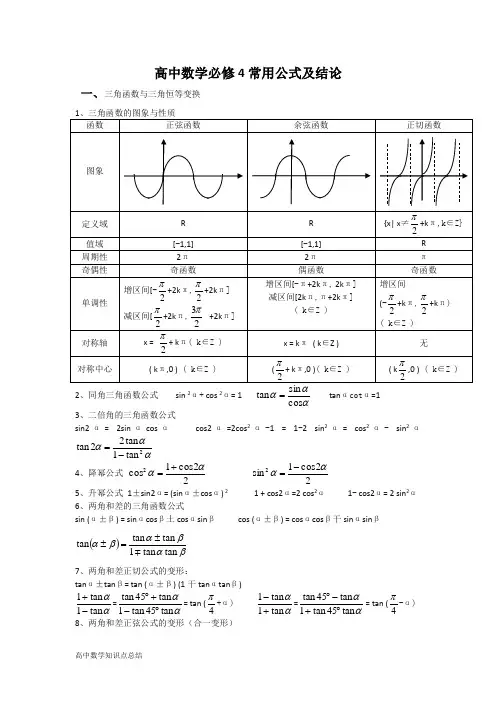
高中数学必修4常用公式及结论一、三角函数与三角恒等变换2、同角三角函数公式 sin 2α+ cos 2α= 1 ααcos tan = tan αcot α=13、二倍角的三角函数公式sin2α= 2sin αcos α cos2α=2cos 2α-1 = 1-2 sin 2α= cos 2α- sin 2αααα2tan 1tan 22tan -=4、降幂公式 22cos 1cos 2αα+=22cos 1sin 2αα-= 5、升幂公式 1±sin2α= (sin α±cos α) 2 1 + cos2α=2 cos 2α 1- cos2α= 2 sin 2α6、两角和差的三角函数公式sin (α±β) = sin αcos β土cos αsin β cos (α±β) = cos αcos β干sin αsin β()βαβαβαtan tan 1tan tan tan ±=±7、两角和差正切公式的变形：tan α±tan β= tan (α±β) (1干tan αtan β)ααtan 1tan 1-+=ααtan 45tan 1tan 45tan ︒-+︒= tan (4π+α) ααtan 1tan 1+-=ααtan 45tan 1tan 45tan ︒+-︒= tan (4π-α)8、两角和差正弦公式的变形（合一变形）()ϕααα++=+sin cos sin 22b a b a （其中ab =ϕtan ） 9、半角公式：212ααcos sin-±= 212ααcos cos +±= αααααααsin cos cos sin cos cos tan-=+=+-±=1111210、三角函数的诱导公式 “奇变偶不变，符号看象限。
”sin (π－α) = sin α， cos (π－α) = －cos α， tan (π－α) = －tan α； sin (π+α) = －sin α cos (π+α) = －cos α tan (π+α) = tan α sin (2π－α) = －sin α cos (2π－α) = cos α tan (2π－α) = －tan αsin (－α) = －sin α cos (－α) = cos α tan (－α) = －tan αsin (2π－α) = cos α cos (2π－α) = sin α tan (2π－α) = cot α sin (2π+α) = cos α cos (2π+α) = －sin α tan (2π+α) = －cot α11.三角函数的周期公式函数sin()y x ωϕ=+，x ∈R 及函数cos()y x ωϕ=+，x ∈R(A,ω,ϕ为常数，且A ≠0，ω＞0)的周期2T πω=；函数tan()y x ωϕ=+，,2x k k Z ππ≠+∈(A,ω,ϕ为常数，且A≠0，ω＞0)的周期T πω=.二、平面向量 （一）、向量的有关概念 1、向量的模计算公式：（1）向量法：|a=；（2）坐标法：设a =（x ，y ），则|a | =22y x +2、单位向量的计算公式：（1）与向量a =（x ，y ）同向的单位向量是⎪⎪⎭⎫⎝⎛++2222y x y ,y x x ； （2）与向量a =（x ，y ）反向的单位向量是⎪⎪⎭⎫ ⎝⎛+-+-2222y x y,y x x； 3、平行向量规定：零向量与任一向量平行。
高中数学必修四公式大全
必修四—第一章 三角函数1. ❖终边落在x 轴上的角的集合： .❖ 终边落在y 轴上的角的集合： .❖ 终边落在坐标轴上的角的集合： .2弧长公式： =l，=S .3.同角三角函数的基本关系：①平方关系： ②乘积关系:◆ 诱导公式（一）()()=+=+=+)2tan(2cos 2sin παπαπαk k k◆ 诱导公式（二） ()()()=+=+=+απαπαπtan cos sin◆ 诱导公式（三） ()()()=-=-=-αααtan cos sin◆ 诱导公式（四） ()()()=-=-=-απαπαπtan cos sin◆ 诱导公式（五）=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-απαπ2cos 2sin◆ 诱导公式（六）=⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛+απαπ2cos 2sin4.三角函数（x x x tan ,cos ,sin ）的性质5.函数)sin(ϕ+=wx A y 的图像振幅变化：x y sin = x A y sin = 左右伸缩变化 x A y ωsin =左右平移变化)sin(ϕω+=x A y 上下平移变化 k x A y ++=)sin(ϕω第二章：平面向量1.平面向量共线定理： 一般地，对于两个向量 ()如果有,,0,b a a ≠()是共线向量与是共线向量；反之如果与则使得一个实数a b a b a a b ,0,,≠=λλ .,a b λλ=使得那么又且只有一个实数2.向量的一个定理的类似推广①向量共线定理： )0(≠=a a b λ②平面向量基本定理： 2211e e a λλ+=（其中21,e e 为平面内不共线的两向量）3.线段的定比分点点P 分有向线段21P P 所成的比的定义式21PP P P λ=,这时=x ，=y . 4.一般地，设向量()(),0,,,2211≠==a y x b y x a 且 ①那么如果b a // . ②如果b a ⊥，那么 .5.一般地，对于两个非零向量b a , 有 θb a =⋅，其中θ为两向量的夹角。
高中数学必修4公式汇总
高中数学必修4公式汇总
学习数学要学会对知识点进行归纳整理，高中数学必修4公式有哪些呢？下面是店铺为大家整理的高中必修4数学公式，希望对大家有所帮助!
高中数学必修4公式汇总
一)两角和差公式 (写的都要记)
sin(A+B)=sinAcosB+cosAsinB
sin(A-B)=sinAcosB-sinBcosA ?
cos(A+B)=cosAcosB-sinAsinB
cos(A-B)=cosAcosB+sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB)
tan(A-B)=(tanA-tanB)/(1+tanAtanB)
二)用以上公式可推出下列二倍角公式
tan2A=2tanA/[1-(tanA)^2]
cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2
(上面这个余弦的很重要)
sin2A=2sinA*cosA
三)半角的只需记住这个：
tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA)
四)用二倍角中的余弦可推出降幂公式
(sinA)^2=(1-cos2A)/2
(cosA)^2=(1+cos2A)/2
五)用以上降幂公式可推出以下常用的化简公式
1-cosA=sin^(A/2)*2
1-sinA=cos^(A/2)*2。
高一数学必修4所有公式归纳
高一数学必修4所有公式归纳同角三角函数间的基本关系式：·平方关系：sin^(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系：sinα=tanα·cosα cosα=cotα·sinαtanα=sinα·secα cotα=cosα·cscαsecα=tanα·cscα cscα=secα·cotα·倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1三角函数恒等变形公式·两角和与高的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·辅助角公式：asinα+bcosα=(a^2+b^2)^(1/2)sin(α+t)，其中sint=b/(a^2+b^2)^(1/2)cost=a/(a^2+b^2)^(1/2)·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式：sin3α=3sinα-4sin^3(α)cos3α=4cos^3(α)-3cosα·半角公式：sin(α/2)=差值√((1-cosα)/2)cos(α/2)=正负√((1+cosα)/2)tan(α/2)=差值√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2cos^2(α)=(1+cos(2α))/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他：sinα+sin(α+2π/n)+sin(α+2π·2/n)+sin(α+2π·3/n)+……+sin[α+2π·(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π·2/n)+cos(α+2π·3/n)+……+cos[α+2π·(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanatanbtan(a+b)+tana+tanb-tan(a+b)=0高中数学自学方法总结大辞典1培养良好的学习兴趣两千多年前孔子说道过：“知之者不如不好之者，不好之者不如乐之者。
数学必修4公式汇总
，定义域是
，值域是
，
单调增区间是
，单调减区间是
。
三角函数周期的计算公式：
2π y＝ Asin( ω x＋φ ) 或 y＝ Acos( ωx＋ φ )( A， ω ，φ 是常数，且 A≠0， ω ≠0) ， T＝| ω | ；
正切函数的性质：
1．定义域： x x∈ R且 x≠π2 ＋ kπ， k∈ Z .
资料收集于网络，如有侵权 请联系网站删除
数学必修
1、 扇形的弧长 l ＝
2、 扇形的面积 S＝
=
3、 一些特殊角的度数与弧度数的对应表
4 公式汇总
度
0° 30° 45° 60° 90° 120° 135° 150° 180°
弧度
0
π
π
π
π
2
3
5
6
4
3
2
3π
4π
6π
π
4、任意角的三角函数的定义
角 α 终边上一点 P的坐标为 ( x， y) ，则 r ＝
， cos( － α ) ＝
，tan( － α ) ＝
.
11、诱导公式公式（四）
sin( π － α) ＝
， cos( π － α) ＝
， tan( π － α ) ＝ .
12、诱导公式公式（五）
sin
π 2
－
α
＝
， Hale Waihona Puke osπ 2－α
＝
.
π sin 2 ＋ α ＝
π
， cos 2 ＋ α ＝
.
13、诱导公式公式（六）
上述三角恒等式告诉我们已知 个式子的值均可求出．
sin θ ＋ cosθ ， sin θ－ cos θ， sin θ cosθ 中的任何一个，则另两
高中数学必修四公式
- 正弦定理：a/sinA = b/sinB = c/sinC
- 余弦定理：c^2 = a^2 + b^2 - 2abcosC
- 余切定理：cotC = (a^2 + b^2 - c^2)/(4∆)
- 正弦和余弦的平方和恒为1：sin^2x + cos^2x = 1
4. 平方差公式：
- (a + b)(a - b) = a^2 - b^2
5. 同底数幂的乘法法则：
- a^m * a^n = a^(m + n)
6. 幂函数的指数法则：
- (a^m)^n = a^(mn)
7. 对数函数的乘法法则：
- log_a (mn) = log_a m + log_a n
8. 对数函数的除法法则：
- log_a (m/n) = log_a m - log_a n
9. 对数函数的幂法则：
- log_a (m^n) = n*log_a m
这些公式是高中数学必修四的重要内容，可以帮助求解各种数学题目。
高中数学必修四公式
高中数学必修四的公式包括:
1. 二次函数的标准形式：f(x) = ax^2 + bx + c
- 顶点坐标：(-b/2a, f(-b/2a))
- 对称轴方程：x = -b/2a
- 判别式：Δ = b^2 - 4ac
2. 二次函数的一般形式：y = ax^2 + bx + c
- 顶点坐标：(-b/2a, c - b^2/4a)
高中数学必修四公式
高中数学必修四公式一、函数公式1. 一次函数的公式一次函数的一般公式为：y = kx + b其中，k为斜率，表示函数的变化速率；b为截距，表示函数与y轴交点的纵坐标值。
2. 二次函数的公式二次函数的一般公式为：y = ax^2 + bx + c其中，a、b、c为常数，a不等于0。
a决定了抛物线开口的方向，b影响了抛物线在x轴上的位置，c决定了抛物线与y轴的交点纵坐标。
3. 指数函数的公式指数函数的一般公式为：y = a^x其中，a为底数，x为指数。
指数函数的特点是随着指数增大，函数值也随之增大（当a大于1时），或者随着指数增大，函数值趋近于0（当0 < a < 1时）。
4. 对数函数的公式对数函数的一般公式为：y = log<sub>a</sub>(x)其中，a为底数，x为函数值。
对数函数表示的是一个数在某个底数下的指数，也可以看作是某个数的幂次方等于x。
二、三角函数公式1. 正弦函数的公式正弦函数的一般公式为：y = Asin(Bx + C) + D其中，A为振幅，表示正弦函数的最大值与最小值之间的差；B为周期，表示正弦函数的一个周期内的长度；C为相位，表示正弦函数的水平方向的偏移；D为垂直偏移，表示正弦函数的纵向平移。
2. 余弦函数的公式余弦函数的一般公式为：y = Acos(Bx + C) + D其中，A为振幅，表示余弦函数的最大值与最小值之间的差；B为周期，表示余弦函数的一个周期内的长度；C为相位，表示余弦函数的水平方向的偏移；D为垂直偏移，表示余弦函数的纵向平移。
3. 正切函数的公式正切函数的一般公式为：y = Atan(Bx + C) + D其中，A为振幅，表示正切函数的最大值与最小值之间的差；B为周期，表示正切函数的一个周期内的长度；C为相位，表示正切函数的水平方向的偏移；D为垂直偏移，表示正切函数的纵向平移。
三、立体几何公式1. 三角形面积的公式三角形的面积可以通过以下公式计算：S = 0.5 * 底边长度 * 高其中，S为三角形的面积，底边长度为三角形底边的长度，高为从底边到顶点的垂直距离。
高中数学必修四的全部公式整理
高中数学必修四的全部公式整理
常用公式：
一、抛物线公式
1.抛物线的准确方程：y=ax2+bx+c (a ≠ 0)
2.其中a为凹凸性系数，且当a>0时，抛物线是凹性曲线；当a<0时，抛物线是凸性曲线。
3.顶点坐标：(x0，y0)=（－b/2a，c-b2/4a）
4.顶点方程：y=－b2/4a+c
5.焦点坐标(-c/a,0)
6.过焦点作平行于y轴的直线的斜率：-b/2a
7.过焦点作垂直于x轴的直线的斜率：-1/b
二、椭圆公式
1.椭圆的准确方程：(x-x0)2/a2+(y-y0)2/b2=1 (a>b)
2.中心：(x0,y0)
3.长轴：2a
4.短轴：2b
5.长短轴方向：与坐标轴平行
6.焦点坐标：(±c,0)，其中c=√a2-b2。
三、双曲线公式
1.双曲线的准确方程：y2/a2-x2/b2=1 (a>b)
2.中心：(0,0)
3.长轴：2a
4.短轴：2b
5.长短轴方向：与坐标轴正交
6.焦点坐标：(±c,0)，其中c=√a2+b2。
四、圆的公式
1.圆的准确方程：(x-x0)2+(y-y0)2=r2
2.圆心：(x0,y0)
3.半径：r
4.圆面积：S=πr2
5.圆周长：C=2πr。
高中数学必修四公式总结
高中数学必修四公式总结高中数学必修四公式总结在高中数学学习过程中，必修四是其中一门非常重要且内容较为深入的课程。
在必修四中，有许多重要的公式需要掌握，这些公式能够帮助我们解决各种数学问题。
下面将对高中数学必修四中的一些核心公式进行总结，希望对同学们的学习有所帮助。
一、平面几何1. 直线的方程：(1) 点斜式：y-y₁ = k(x-x₁)(2) 两点式：(y-y₁) / (y₂-y₁) = (x-x₁) / (x₂-x₁)(3) 一般式：Ax + By + C = 0(4) 截距式：x/a + y/b = 12. 圆的方程：(1) 标准方程：(x-a)² + (y-b)² = r²(2) 一般方程：x² + y² + Dx + Ey + F = 03. 直线与圆的关系：(1) 切线方程：y-y₁ = k(x-x₁) ± √(1+k²)(r²-x₁²)(2) 弦长公式：√[(x₂-x₁)²+(y₂-y₁)²](3) 弦的中点：[ (x₁+x₂)/2 , (y₁+y₂)/2 ](4) 弦的斜率：(y₂-y₁) / (x₂-x₁)二、解析几何1. 坐标系及坐标点的距离、中点、斜率公式：(1) 两点间距离：√[(x₂-x₁)²+(y₂-y₁)²](2) 中点坐标：[ (x₁+x₂)/2 , (y₁+y₂)/2 ](3) 斜率：k = (y₂-y₁) / (x₂-x₁)2. 二次函数：(1) 顶点坐标：[ -b/2a , f( -b/2a ) ](2) 对称轴方程：x = -b/2a(3) 解析式：y = ax² + bx + c3. 平面向量：(1) 向量坐标法：A[ a₁, a₂ ] , B[ b₁, b₂ ] , AB = [ b₁-a₁, b₂-a₂ ](2) 向量模长公式：|AB| = √[(b₁-a₁)²+(b₂-a₂)²](3) 向量共线判定：若AB = kCD，则k = 0 或 AB // CD(4) 两向量夹角余弦公式：cosθ = (a·b) / (|a|·|b|)(5) 向量投影：P = |a|·cosθ三、数列与数学归纳法1. 等差数列：(1) 通项公式：aₙ = a₁ + (n-1)·d(2) 等差和公式：Sₙ = n [ (a₁+aₙ) / 2 ]2. 等比数列：(1) 通项公式：aₙ = a₁ · q^(n-1)(2) 等比和公式：Sₙ = a₁(qⁿ-1) / (q-1) (q ≠ 1)3. 递推数列：(1) 递推公式：aₙ = f(aₙ₋₁)(2) 递推和公式：Sₙ = a₁ + a₂ + ... + aₙ四、三角函数1. 任意角的正弦、余弦、正切定义：(1) 正弦：sinθ = y / r(2) 余弦：cosθ = x / r(3) 正切：tanθ = y / x2. 任意角的诱导公式：(1) sin(π/2 + θ) = cosθ(2) cos(π/2 + θ) = -sinθ(3) tan(π/2 + θ) = -cotθ3. 三角函数的基本公式：(1) sin²θ + cos²θ = 1(2) 1 + tan²θ = sec²θ(3) 1 + cot²θ = csc²θ以上是高中数学必修四中的一些重要公式的总结。
数学必修4公式汇总
数学必修4公式汇总1、 扇形的弧长l ＝2、 扇形的面积S ＝ =3、 一些特殊角的度数与弧度数的对应表4角α终边上一点P 的坐标为(x ，y )，则r ＝ ，sin α＝ ，cos α＝ ， tan α＝ 。
5、三角函数值的符号记忆口诀：正弦 ，余弦 ，正切 。
6、诱导公式(一) sin(2k π＋α)＝ (k ∈Z )，cos(2k π＋α)＝ (k ∈Z )，tan(2k π＋α)＝ (k ∈Z )。
7、同角三角函数的基本关系式平方关系：sin 2α＋cos 2α＝ ，商数关系：tan α＝ .（弦化切或切化弦公式） 8、sin θ＋cos θ，sin θ－cos θ及sin θcos θ之间的关系是怎样的？（知一求二公式）①(sin θ＋cos θ)2＝1＋2sin θcos θ； ②(sin θ－cos θ)2＝1－2sin θcos θ； ③(sin θ＋cos θ)2＋(sin θ－cos θ)2＝2；④(sin θ－cos θ)2＝(sin θ＋cos θ)2－4sin θcos θ.上述三角恒等式告诉我们已知sin θ＋cos θ，sin θ－cos θ，sin θcos θ中的任何一个，则另两个式子的值均可求出． 9、诱导公式公式（二）sin(π＋α)＝ ，cos(π＋α)＝ ，tan(π＋α)＝ . 10、诱导公式公式（三）sin(－α)＝ ，cos(－α)＝ ，tan(－α)＝ . 11、诱导公式公式（四）sin(π－α)＝ ，cos(π－α)＝ ，tan(π－α)＝ . 12、诱导公式公式（五）sin ⎝ ⎛⎭⎪⎫π2－α＝ ，cos ⎝ ⎛⎭⎪⎫π2－α＝ . sin ⎝ ⎛⎭⎪⎫π2＋α＝ ，cos ⎝ ⎛⎭⎪⎫π2＋α＝ . 13、诱导公式公式（六）sin ⎝ ⎛⎭⎪⎫32π＋α＝ ，cos ⎝ ⎛⎭⎪⎫32π＋α＝ . sin ⎝ ⎛⎭⎪⎫32π－α＝ ，cos ⎝ ⎛⎭⎪⎫32π－α＝ .14、五点法作图中的五个关键点分别是什么？正弦曲线五个关键点为(0,0)，⎝ ⎛⎭⎪⎫π2，1，(π，0)，⎝ ⎛⎭⎪⎫32π，－1，(2π，0)． 余弦曲线五个关键点为(0,1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫32π，0，(2π，1)． 正弦函数y ＝sin x (x ∈R )是奇函数，图象关于原点对称，周期是 ，定义域是 ，值域是 ，单调增区间是 ，单调减区间是 。
高一数学必修四公式总结
高一数学必修四公式归纳公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinα cos（2kπ＋α）＝cosα tan（2kπ＋α）＝tanα cot（2kπ＋α）＝cotα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinα cos（π＋α）＝－cosα tan（π＋α）＝tanα cot（π＋α）＝cotα 公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinα cos（－α）＝cosα tan（－α）＝－tanα cot（－α）＝－cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinα cos（π－α）＝－cosα tan（π－α）＝－tanα cot（π－α）＝－cotα 公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinα cos（2π－α）＝cosα tan（2π－α）＝－tanα cot（2π－α）＝－cotα 公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosα cos（π/2＋α）＝－sinα tan（π/2＋α）＝－cotα cot（π/2＋α）＝－tanα sin（π/2－α）＝cosα cos（π/2－α）＝sinα tan（π/2－α）＝cotα cot（π/2－α）＝tanα sin（3π/2＋α）＝－cosα cos（3π/2＋α）＝sinα tan（3π/2＋α）＝－cotα cot（3π/2＋α）＝－tanα sin（3π/2－α）＝－cosα cos（3π/2－α）＝－sinα tan（3π/2－α）＝cotα cot（3π/2－α）＝tanα (以上k∈Z)诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为：∈Z)的个三角函数值，对于k·π/2±α(k①当k是偶数时，得到α的同名函数值，即函数名不改变；②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan.（奇变偶不变）然后在前面加上把α看成锐角时原函数值的符号。
高中数学必修四公式大全
高中数学必修四公式大全1. 数列公式1.1 等差数列公式•通项公式：a n=a1+(n−1)d•前n项和公式：$S_n = \\frac{n(a_1 + a_n)}{2}$1.2 等比数列公式•通项公式：$a_n = a_1 \\cdot q^{(n-1)}$•前n项和公式（当q eq1）：$S_n = \\frac{a_1(q^n - 1)}{q - 1}$ 2. 平面几何公式2.1 长方形公式•面积公式：$A = l \\cdot w$•周长公式：P=2(l+w)•对角线长度公式：$d = \\sqrt{l^2 + w^2}$2.2 正方形公式•面积公式：A=s2•周长公式：P=4s•对角线长度公式：$d = s\\sqrt{2}$2.3 圆公式•面积公式：$A = \\pi r^2$•周长公式：$C = 2\\pi r$•弧长公式：$L = 2\\pi r \\cdot \\frac{\\theta}{360^\\circ}$•扇形面积公式：$A = \\frac{1}{2}r^2\\theta$•弓形面积公式：$A = \\frac{1}{2}(R^2\\theta - r^2\\theta)$3. 三角函数公式3.1 基本公式•正弦函数公式：$\\sin\\theta = \\frac{\\text{对边}}{\\text{斜边}}$ •余弦函数公式：$\\cos\\theta = \\frac{\\text{邻边}}{\\text{斜边}}$ •正切函数公式：$\\tan\\theta = \\frac{\\text{对边}}{\\text{邻边}}$3.2 和差公式•正弦函数和差公式：$\\sin(A\\pm B) = \\sin A \\cos B \\pm \\cos A \\sin B$•余弦函数和差公式：$\\cos(A\\pm B) = \\cos A \\cos B \\mp \\sinA \\sin B$•正切函数和差公式：$\\tan(A\\pm B) = \\frac{\\tan A \\pm \\tan B}{1 \\mp \\tan A \\tan B}$3.3 二倍角公式•正弦函数二倍角公式：$\\sin(2\\theta) = 2\\sin\\theta \\cos\\theta$•余弦函数二倍角公式：$\\cos(2\\theta) = \\cos^2\\theta - \\sin^2\\theta$•正切函数二倍角公式：$\\tan(2\\theta) = \\frac{2\\tan\\theta}{1 - \\tan^2\\theta}$4. 指数与对数公式4.1 指数公式•指数乘法公式：$a^m \\cdot a^n = a^{m + n}$•指数除法公式：$\\frac{a^m}{a^n} = a^{m - n}$•指数幂公式：(a m)n=a mn•零指数公式：a0=1•负指数公式：$a^{-m} = \\frac{1}{a^m}$4.2 对数公式•对数乘法公式：$\\log_ab + \\log_ac = \\log_a(bc)$•对数除法公式：$\\log_ab - \\log_ac =\\log_a\\left(\\frac{b}{c}\\right)$•对数幂公式：$\\log_ab^m = m\\log_ab$•换底公式：$\\log_ab = \\frac{\\log_cb}{\\log_ca}$以上是高中数学必修四公式大全，掌握并熟练运用这些公式，能够更好地解决各种数学问题。
必修四数学公式知识点大全
必修四数学公式知识点大全智慧书屋-USQ369IS必修四数学公式知识点大全多数的数学创造是直觉的结果，对事实多少有点儿直接的知觉或快速的理解，而与任何冗长的或形式的推理过程无关。
接下来小编在这里给大家分享一些关于必修四数学公式知识点，供大家学习和参考，希望对大家有所帮助。
必修四数学公式知识点高一数学必修4重点公式汇总一)两角和差公式(写的都要记)sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosA ?cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)二)用以上公式可推出下列二倍角公式tan2A=2tanA/[1-(tanA) ]cos2a=(cosa) -(sina) =2(cosa) -1=1-2(sina) (上面这个余弦的很重要)sin2A=2sinA_osA=a(n-2)+2r=...=a[n-(n-1)]+(n-1)r=a(1)+(n-1)r=a+(n-1)r.可用归纳法证明。
n=1时，a(1)=a+(1-1)r=a。
成立。
假设n=k时，等差数列的通项公式成立。
a(k)=a+(k-1)r则，n=k+1时，a(k+1)=a(k)+r=a+(k-1)r+r=a+[(k+1)-1]r.通项公式也成立。
因此，由归纳法知，等差数列的通项公式是正确的。
求和公式：S(n)=a(1)+其是高阶段的数学学习数学,必须遵循“分层原则”和“循序渐进”的原则。
与教学内容的第一周甚至是从基础开始,一周后的头几天,在教学难以提升。
以及提升的困难进步一步一步,最好不要去追求所谓的“困难”除了(感兴趣),不利于解决问题方法掌握连续性。
同时,根据时间和课程安排的长度适当的审查,只有这样才能记住和使用在长期学习数学知识,不要忘记前面的学习。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
必修 4 常用公式手册
公式一： 设 α 为任意角，终边相同的角的同一三角函数的值相等： sin （2kπ
＋α）＝sinα
cos （2kπ＋α）＝cosα tan （2kπ＋α）＝tanα 公式二： 设 α 为任意角，π+α 的三角函数值与 α 的三角函数值之间的关系： sin （π＋α）＝－sinα cos （π＋α）＝－cosα tan （π＋α）＝tanα 公式三： 任意角 α 与 -α 的三角函数值之间的关系：
sin （－α）＝－sinα cos （－α）＝cosα tan （－α）＝－tanα 公式四： 利用公式二和公式三可以得到 π-α 与 α 的三角函数值之间的关系： sin （π－α）＝sinα cos （π－α）＝－cosα tan （π－α）＝－tanα 公式五： 利用公式一和公式三可以得到 2π-α 与 α 的三角函数值之间的关系： sin （2π－α）＝－sinα
cos （2π－α）＝cosα tan （2π－α）＝－tanα 3
公式六： ±α 及 ±α 与 α 的三角函数值之间的关系：
2 2
3 3 sin(
+α)＝cosα sin( -α)＝cosα sin( ＋α)＝－cosα sin( －α)＝－cosα 2 2 2
2 3 3 cos( +α)＝－sinα cos( -α)＝sinα cos( ＋α)＝sinα cos( －α)＝－sinα
2 2 2 2 1.同角三角函数的基本关系式 sin
商的关系：
＝tan cos 平方关系： sin 2＋cos 2＝1
⒉两角和与差的三角函数公式 1 cos 2 = 1 + tan 2
si （n ＋）＝sin cos ＋cos sin
si （n －）＝sin cos －cos sin
co （s ＋）＝cos cos －sin sin co （s －）＝cos cos ＋sin sin
ta （n ＋）＝ tan ＋tan
tan (－)= tan －tan
1－tan ·tan
⒊二倍角的正弦、余弦和正切公式
1 + tan tan sin 2＝2sin cos cos 2＝cos 2－sin 2＝2cos 2－1＝1－2sin 2
tan 2＝ 2tan
1－tan 2
⒋半角的正弦、余弦和正切公式
2 1 - c os 2 1 + cos 2 1 - cos sin ( ) = 2 2 cos ( ) = 2 2 tan ( ) = 2 1 + cos。