坐标点换算经纬度
三维坐标转经纬度程序

三维坐标转经纬度程序在地理空间分析和导航等领域,经纬度是一种常见的地理坐标系统,用于确定地球上任意位置的准确位置。
然而,在一些应用中,我们可能需要将三维坐标转换为经纬度,以便更好地理解和使用这些数据。
本文将介绍一个简单而有效的三维坐标转经纬度的程序。
我们需要明确三维坐标和经纬度的定义。
三维坐标是一个由X、Y 和Z三个分量组成的点在三维空间中的位置表示,通常用(x, y, z)表示。
而经纬度是由纬度和经度两个分量组成的地理位置表示,通常用(纬度, 经度)表示。
接下来,我们将介绍一个基于球面三角学的算法,用于将三维坐标转换为经纬度。
这个算法基于以下几个步骤进行:1. 首先,我们需要确定球体的半径。
根据实际情况,我们可以选择使用地球的平均半径,约为6371公里。
2. 然后,我们需要计算出点的矢量长度。
通过计算点到原点的欧几里得距离,即√(x^2 + y^2 + z^2),可以得到点的矢量长度。
3. 接下来,我们可以通过计算点在球面上的投影点的经度和纬度来确定经纬度。
投影点的经度可以通过使用反正切函数atan2(y, x)计算得到,注意要将弧度转换为角度。
投影点的纬度可以通过使用反正弦函数asin(z / 矢量长度)计算得到,同样要将弧度转换为角度。
4. 最后,我们可以得到点的经纬度表示,即(纬度, 经度)。
下面是一个简单的Python代码示例,用于实现三维坐标转经纬度的功能:```pythonimport mathdef convert_3d_to_latlon(x, y, z):radius = 6371vector_length = math.sqrt(x**2 + y**2 + z**2)longitude = math.degrees(math.atan2(y, x))latitude = math.degrees(math.asin(z / vector_length))return (latitude, longitude)```以上代码定义了一个名为`convert_3d_to_latlon`的函数,该函数接受三个参数x、y和z,表示三维坐标的三个分量。
经纬度换算公式

经纬度换算公式
经纬度换算公式又称经纬度转换公式,是从一个地名到另一个地
名的经纬度之间的转换计算方法。
它是由两个相关的算术公式构成的。
这些公式可以用来将地球上任何一个地名的经纬度坐标,转换为另一
个地名的经纬度坐标。
经纬度换算公式通常只有两部分,分别是换算经度公式和换算纬
度公式。
换算经度公式类似于“x = a * x”的形式,其中“x”表示
要转换的经度坐标,“a”代表转换系数,以千米单位表示。
换算纬度
公式则类似“y = b * y”的形式,其中“y”表示要转换的纬度坐标,“b”代表转换系数,以千米单位表示。
经纬度换算公式是一种根据地点间距离来确定经纬度坐标之间的
转换关系,而不是根据地名来确定。
经纬度换算公式也可以用来计算
相对位置,例如在全球定位系统(GPS)中。
经纬度换算公式的最大优
势在于它消除了地名的影响,可以更为精确地使用经纬度坐标作为查
找位置的标准。
因此,经纬度换算公式是从一个地名到另一个地名的经纬度之间
的转换算法,其优势在于它消除了地名的影响,可以更准确地进行定位。
另外,经纬度换算公式还可以用来计算全球定位系统中相对位置。
大地坐标和经纬度之间的换算

大地坐标和经纬度之间的换算地质工作中常要对进行大地坐标转经纬度和经纬度换大地坐标,我写一下一般的过程,希望对大家有点帮助.大地座标f经纬度(地理坐标)1,输入大地坐标数据,格式为丫空格X,输入到文本就行如下,原始的大地坐标由一8位的丫和一个7位的X组成,这组坐标数据中的丫的前两位为31,是分带号,一般使用的分带有三分带,六分带,这里的坐标是三分带的,记下丫前的这两位数,在原始数据中去除掉,现在数据变为,丫,6位,X,7位保存这个TXT的文本文件2,打开MAPGIS启动坐标投影变形程序接下来选择投影转换>>>湘户文件投影转换千♦千{百旺E嗝裁当前投影就数型晝当前地團参数匚设置转换信琴数瞄行投影箜换口作区克接投影转换漏幕采点投影攻件间捋见投厳站数回:件间拷贝TI匚宜瞒抑方式投影丽财比丈件投影转换3錐数据宦成閔形E輸入里点投影購鞍G高程曲梯球佯投影醸制投影经纬网工经鋒财明诃数露喩椭瑚面上側民礎事橢球面上梯形面蘇求国域实地面祝眸标系转换扁辑坐桩转换奏數点打开文件,打开刚才的大地坐标的文本文件,设置输入数据的格式,点击用户投影参数,并完成设置这里我们的大地座标为3度带的第31带,注意填好,坐标单位为米好了以为设置输出的格式,我们要求输出的是经纬度,点结果转换参数,完成以下设置我们输出的经纬度的单位应该是DDDMMMS S S注意点写到文件,保存就大功告成了,注意保存的文件要写上.TXT的后缀F面是计算出的结果文件文件CE〕編辑® 格式@ 査肴⑷ 帮助CH)000Stp=l23U23ii. .357yp= 403950 -255 5A5OOa.H0O^=4^03^00.QOS xp=1234607. ,Z02yp= 4 03颂.893X s5d50M.OOB y^USOZSOO・ 000 xp=123U608, .692 yp= 40^156 .555x = y=U507500.SOB xp=123U837. .762 卵二il0^l157 -535號二円彌弓Elik 090 lfp=123U836. .192卵二40394^ 5释5加.000 y=^Q35;og, oog xp=123512fi. .462 卵=40394645x =5725呱咖P=UU96^O0.BOS Kp=1235123. ・£&T yp=«l035S9,739w =^60000.000BOB Mp=123U231. .9^6 卵m403603-9H1XP为经度,1234234。
坐标转换经纬度方法

坐标转换经纬度方法
在不同的地图和GIS系统中,使用的坐标系可能会有所不同,如平面
坐标系、投影坐标系等。
为了能够在不同坐标系间进行位置的准确转换,
我们需要一些数学和地理学知识。
下面我将介绍几种常用的坐标转换经纬
度的方法。
1.WGS84转换方法:
WGS84坐标系是一种全球标准的地理坐标系,被广泛应用于地图制图
和导航系统中。
如果我们的原坐标系不是WGS84,需要将其转换为WGS84
坐标系,再进行经纬度的计算和转换。
2.地球椭球体模型方法:
地球不是完美的球体,而是稍微椭圆形状的。
因此,在进行坐标转换时,我们需要考虑地球的椭球体模型,以提高计算的准确性。
3.投影方法:
在地图制图和GIS系统中,常常需要将地球表面的三维坐标转换为二
维平面坐标。
这时,我们需要采用投影方法,将经纬度坐标投射到平面坐
标系中。
4.基准面转换方法:
在一些特殊的地理环境中,可能存在多个坐标基准面,如北京54坐
标系、西安80坐标系等。
当我们需要进行不同基准面之间的坐标转换时,需要特定的转换参数和数学模型。
5.GIS软件和工具方法:
在实际的坐标转换过程中,我们可以使用一些专业的GIS软件和在线工具来进行坐标的转换计算。
这些工具通常提供了多种常用的坐标系之间的转换方法,并能够以图形化的方式呈现转换结果。
总结起来,坐标转换经纬度的方法包括WGS84转换方法、地球椭球体模型方法、投影方法、基准面转换方法和GIS软件和工具方法。
根据不同的需求和环境,可以选择合适的方法来进行坐标转换,以获取准确的经纬度坐标。
大地坐标和经纬度之间的换算
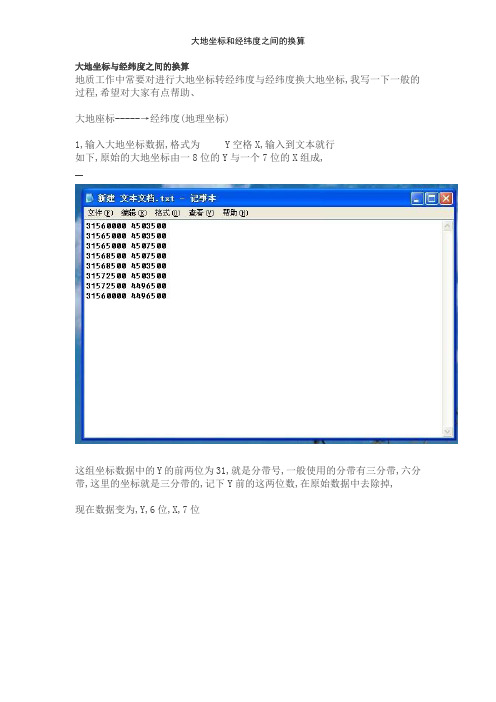
大地坐标与经纬度之间的换算地质工作中常要对进行大地坐标转经纬度与经纬度换大地坐标,我写一下一般的过程,希望对大家有点帮助、大地座标-----→经纬度(地理坐标)1,输入大地坐标数据,格式为 Y空格X,输入到文本就行如下,原始的大地坐标由一8位的Y与一个7位的X组成,这组坐标数据中的Y的前两位为31,就是分带号,一般使用的分带有三分带,六分带,这里的坐标就是三分带的,记下Y前的这两位数,在原始数据中去除掉,现在数据变为,Y,6位,X,7位保存这个TXT的文本文件。
2,打开MAPGIS,启动坐标投影变形程序接下来选择投影转换>>>>用户文件投影转换点打开文件,打开刚才的大地坐标的文本文件,设置输入数据的格式,点击用户投影参数,并完成设置。
这里我们的大地座标为3度带的第31带,注意填好,坐标单位为米好了以为设置输出的格式,我们要求输出的就是经纬度,点结果转换参数,完成以下设置我们输出的经纬度的单位应该就是DDDMMMSS。
SS注意点写到文件,保存就大功告成了,注意保存的文件要写上、TXT的后缀下面就是计算出的结果文件XP为经度,1234234。
357就就是123度42分34。
357秒,YP为纬度,403950。
225就就是40度39分50。
255秒(纬度没有最多90,所以没有三位数)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~经纬度——→大地座标输入文件格式如下,这里面的数据前面的为经度,格式为DDDMMSS,后面的为纬度,格式为DDMMSS接下来的转换过程与大地坐标转换一样,只要将刚才的用户转换参数与结果转换参数交换即可,要注意分带号的确定,如果您不知道分带号,就应该先计算分带号,算法就是经度/3得到的整数为三度带的分带号经度/6得到的整数为六度带的分带号其中的XP为地图上的Y坐标,记得在前面加上带号,其中的YP为地图上的X坐标。
xy转换成经纬度计算方法

xy转换成经纬度计算方法
将坐标从平面直角坐标系(xy平面)转换成经纬度的方法通常需要以下步骤:
1. 确定地球的参考椭球体:地球的形状并非完美的球体,而是略微扁平的椭球。
选择合适的椭球体作为地球的参考椭球体,常用的有WGS84和国际1924椭球体。
2. 确定原点和投影方式:需要确定一个原点,将原点映射到地理坐标系上的某一点,常用的原点有地理坐标系的原点(例如0度经度和赤道),或者是特定的投影中心点。
此外,还需要确定投影方式,常见的有等距投影和等角投影等。
3. 计算椭球体的参数:根据所选椭球体的参数,如长半轴a、短半轴b、偏心率e等,计算椭球体的各种辅助参数,如偏心率平方e'、扁率f等。
4. 转换坐标:根据所选的投影方式,将xy平面上的坐标通过一定的公式转换成地理坐标系中的经纬度。
具体转换公式会因不同的投影方式而有所差异,常见的转换公式有墨卡托投影、UTM投影等。
需要注意的是,这些计算方法通常需要使用专业的地理信息系统(GIS)软件或相关编程语言的库函数来实现。
大地坐标和经纬度之间地换算

大地坐标和经纬度之间的换算地质工作中常要对进行大地坐标转经纬度和经纬度换大地坐标,我写一下一般的过程,希望对大家有点帮助.大地座标-----→经纬度(地理坐标)1,输入大地坐标数据,格式为 Y空格X,输入到文本就行如下,原始的大地坐标由一8位的Y和一个7位的X组成,这组坐标数据中的Y的前两位为31,是分带号,一般使用的分带有三分带,六分带,这里的坐标是三分带的,记下Y前的这两位数,在原始数据中去除掉,现在数据变为,Y,6位,X,7位保存这个TXT的文本文件。
2,打开MAPGIS,启动坐标投影变形程序接下来选择投影转换>>>>用户文件投影转换点打开文件,打开刚才的大地坐标的文本文件,设置输入数据的格式,点击用户投影参数,并完成设置。
这里我们的大地座标为3度带的第31带,注意填好,坐标单位为米好了以为设置输出的格式,我们要求输出的是经纬度,点结果转换参数,完成以下设置我们输出的经纬度的单位应该是DDDMMMSS。
SS注意点写到文件,保存就大功告成了,注意保存的文件要写上.TXT的后缀下面是计算出的结果文件XP为经度,1234234。
357就是123度42分34。
357秒,YP为纬度,403950。
225就是40度39分50。
255秒(纬度没有最多90,所以没有三位数)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~经纬度——→大地座标输入文件格式如下,这里面的数据前面的为经度,格式为DDDMMSS,后面的为纬度,格式为DDMMSS接下来的转换过程和大地坐标转换一样,只要将刚才的用户转换参数和结果转换参数交换即可,要注意分带号的确定,如果你不知道分带号,就应该先计算分带号,算法是经度/3得到的整数为三度带的分带号经度/6得到的整数为六度带的分带号其中的XP为地图上的Y坐标,记得在前面加上带号,其中的YP为地图上的X坐标标准文档。
坐标点换算经纬度公式

坐标点换算经纬度公式好的,以下是为您生成的文章:在我们探索地球这个神奇的大球体时,坐标点换算经纬度公式就像是一把神奇的钥匙,能帮我们打开了解地球位置的大门。
想象一下,你正在进行一场刺激的环球旅行。
每到一个新的地方,你都想准确地知道自己在地球上的位置,这时候坐标点换算经纬度公式就派上用场啦!咱们先来说说什么是坐标点。
简单来说,坐标点就是在一个特定的坐标系中用来确定一个位置的一组数字。
就好像你在一个巨大的棋盘上,每个格子都有自己的编号,坐标点就是告诉你站在哪一格。
而经纬度呢,就像是地球的“身份证号码”。
经度表示东西方向的位置,纬度表示南北方向的位置。
有了经纬度,我们就能精确地知道地球上任何一个地方的位置。
那坐标点怎么换算成经纬度呢?这就得用到一些数学公式啦。
比如说,我们常见的是把平面直角坐标系中的坐标点(x,y)转换成经纬度(λ,φ)。
公式看起来可能有点复杂,但是别怕,我给您举个例子就明白啦。
假设我们有一个坐标点(100,200),要把它转换成经纬度。
首先,我们得知道一些基础的参数,比如地球的半径啥的。
然后,通过一系列的计算,就能得出对应的经纬度啦。
我记得有一次,我和几个朋友一起去野外探险。
我们带着地图和指南针,想要找到一个传说中的神秘洞穴。
可是走着走着,我们发现迷路了。
这时候,我突然想到了坐标点和经纬度的知识。
我拿出手机,查看了我们当前的坐标点,然后运用我所知道的换算公式,努力算出了大概的经纬度。
虽然过程中有点小紧张,也担心算错,但最后还真让我们找到了正确的方向,顺利找到了那个神秘洞穴。
那次的经历让我深深感受到,这些知识在关键时刻真能派上大用场!在实际应用中,坐标点换算经纬度的公式可不仅仅是用于探险哦。
比如在航海中,船长需要准确知道船只的位置,就得靠这个公式;在地理信息系统中,工作人员分析数据、绘制地图也离不开它;甚至在卫星导航中,也是通过坐标点和经纬度的转换来为我们指引方向。
总之,坐标点换算经纬度公式虽然有点复杂,但只要我们认真去学,多练习,就能掌握这把神奇的钥匙,更好地探索我们生活的这个美丽星球!希望通过我的讲解,能让您对坐标点换算经纬度公式有更清晰的认识和理解。
