2006年黑龙江省数学中考试题及答案非课改
2006年中考数学试题汇编及解析探索型问题
2006年中考数学试题汇编及解析探索型问题探索型问题这类问题往往涉及面很广,主要是探索题设结论是否存在,或是否成立,或是让学生自己先猜想结论,再进行研究从而得出正确的结论等等,这些题通常有一定的难度,几乎在全国各地的中考数学试卷中都能见到。
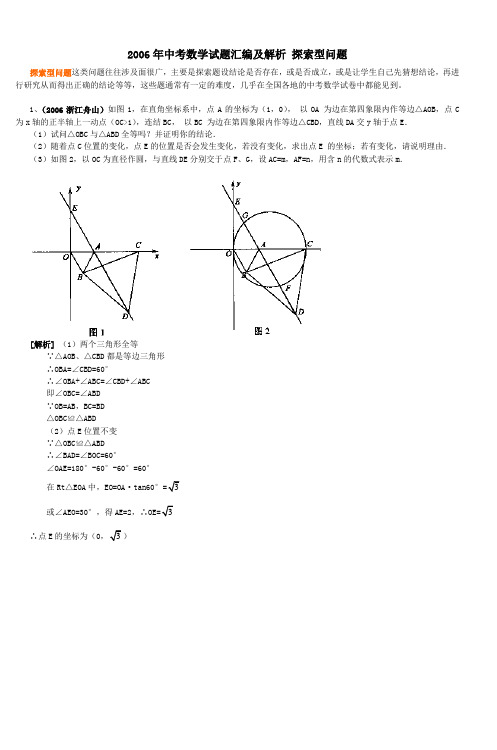
1、(2006浙江舟山)如图1,在直角坐标系中,点A的坐标为(1,0),•以OA•为边在第四象限内作等边△AOB,点C 为x轴的正半轴上一动点(OC>1),连结BC,•以BC•为边在第四象限内作等边△CBD,直线DA交y轴于点E.(1)试问△OBC与△ABD全等吗?并证明你的结论.(2)随着点C位置的变化,点E的位置是否会发生变化,若没有变化,求出点E•的坐标;若有变化,请说明理由.(3)如图2,以OC为直径作圆,与直线DE分别交于点F、G,设AC=m,AF=n,用含n的代数式表示m.[解析](1)两个三角形全等∵△AOB、△CBD都是等边三角形∴OBA=∠CBD=60°∴∠OBA+∠ABC=∠CBD+∠ABC即∠OBC=∠ABD∵OB=AB,BC=BD△OBC≌△ABD(2)点E位置不变∵△OBC≌△ABD∴∠BAD=∠BOC=60°∠OAE=180°-60°-60°=60°在Rt△EOA中,EO=OA²tan60°或∠AEO=30°,得AE=2,∴∴点E的坐标为(0(3)∵AC=m ,AF=n ,由相交弦定理知1²m=n ²AG ,即AG=m n又∵OC 是直径,∴OE 是圆的切线,OE 2=EG ²EF在Rt △EOA 中,2=(2-m n)(2+n ) 即2n 2+n-2m-mn=0解得m=222n nn ++.2、(2006浙江金华)如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式;(2)若S 梯形OBCD =3,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的三角形与△OBA 相似.若存在,请求出所有符合条件 的点P 的坐标;若不存在,请说明理由. [解析] (1)直线AB 解析式为:y=33-x+3. (2)方法一:设点C坐标为(x ,33-x+3),那么OD =x ,CD =33-x+3. ∴OBCD S 梯形=()2CD CD OB ⨯+=3632+-x . 由题意:3632+-x =334,解得4,221==x x (舍去) ∴ C(2,33) 方法二:∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形=334,∴63=∆ACD S .由OA=3OB ,得∠BAO =30°,AD=3CD .∴ ACD S ∆=21CD ³AD =223CD =63.可得CD =33. ∴ AD=1,OD =2.∴C (2,33). (3)当∠OBP =Rt ∠时,如图①若△BOP ∽△OBA ,则∠BOP =∠BAO=30°,BP=3OB=3,∴1P (3,33). ②若△BPO ∽△OBA ,则∠BPO =∠BAO=30°,OP=33OB=1. ∴2P (1,3).当∠OPB =Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图),此时△PBO ∽△OBA ,∠BOP =∠BAO =30° 过点P 作PM ⊥OA 于点M . 方法一: 在Rt △PBO 中,BP =21OB =23,OP =3BP =23. ∵ 在Rt △P MO 中,∠OPM =30°, ∴ OM =21OP =43;PM =3OM =433.∴3P (43,433). 方法二:设P(x ,33-x+3),得OM =x ,PM =33-x+3 由∠BOP =∠BAO,得∠POM =∠ABO .∵tan ∠POM==OMPM =x x 333+-,tan ∠ABOC=OBOA =3.∴33-x+3=3x ,解得x =43.此时,3P (43,433).④若△POB ∽△OBA(如图),则∠OBP=∠BAO =30°,∠POM =30°. ∴ PM =33OM =43. ∴ 4P (43,43)(由对称性也可得到点4P 的坐标). 当∠OPB =Rt ∠时,点P 在x轴上,不符合要求.综合得,符合条件的点有四个,分别是:1P (3,33),2P (1,3),3P (43,433),4P (43,43).3、(2006湖南常德)如图,在直角坐标系中,以点A 为圆心,以x 轴相交于点B C ,,与y 轴相交于点D E ,.(1)若抛物线213y x bx c =++经过C D ,两点,求抛物线的解析式,并判断点B 是否在该抛物线上. (2)在(1)中的抛物线的对称轴上求一点P ,使得PBD △的周长最小.(3)设Q 为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M ,使得四边形BCQM 是平行四边形.若存在,求出点M 的坐标;若不存在,说明理由.[解析] (1)OA =∵AB AC ==(B ∴,C又在Rt AOD △中,AD =OA =3OD ==∴D ∴的坐标为(03)-,又D C ,两点在抛物线上,23103c c =-⎧⎪⎨++=⎪⎩ ∴解得3b c ⎧=⎪⎨⎪=-⎩ ∴抛物线的解析式为:21333y x x =--当x =0y = ∴点(B 在抛物线上(2)2133y x x =-∵21(43x =- ∴抛物线2133y x x =-的对称轴方程为x = 在抛物线的对称轴上存在点P ,使PBD △的周长最小.BD ∵的长为定值 ∴要使PBD △周长最小只需PB PD +最小. 连结DC ,则DC 与对称轴的交点即为使PBD △周长最小的点. 设直线DC 的解析式为y mx n =+.由30n n =-⎧⎪⎨+=⎪⎩得3m n ⎧=⎪⎨⎪=-⎩∴直线DC的解析式为3y x =-由3y x x ⎧=-⎪⎨⎪=⎩得2x y ⎧=⎪⎨=-⎪⎩ 故点P的坐标为2)-(3)存在,设)Q t为抛物线对称轴x =M 在抛物线上要使四边形BCQM 为平行四边形,则BC QM ∥且BC QM =,点M 在对称轴的左侧.于是,过点Q 作直线L BC ∥与抛物线交于点()m M x t , 由BC QM =得QM =从而m x =-,12t =故在抛物线上存在点(M ,使得四边形BCQM 为平行四边形.4、(2006湖南常德)把两块全等的直角三角形ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D 与三角板ABC的斜边中点O 重合,其中90ABC DEF ∠=∠= ,45C F ∠=∠=,4AB DE ==,把三角板ABC 固定不动,让三角板DEF 绕点O 旋转,设射线DE 与射线AB 相交于点P ,射线DF 与线段BC 相交于点Q .(1)如图9,当射线DF 经过点B ,即点Q 与点B 重合时,易证APD CDQ △∽△.此时,APCQ =· . (2)将三角板DEF 由图1所示的位置绕点O 沿逆时针方向旋转,设旋转角为α.其中090α<< ,问AP CQ ·的值是否改变?说明你的理由.(3)在(2)的条件下,设CQ x =,两块三角板重叠面积为y ,求y 与x 的函数关系式.[解析] (1)8(2)APCQ ·的值不会改变. 理由如下:在APD △与CDQ △中,45A C ∠=∠=18045(45)9A P D a a ∠=--+=-90CDQ a ∠=-BEE 图1 图3图3E即APD CDQ ∠=∠APD CDQ ∴△∽△AP CDAD CQ=∴22182A P C QA D C D A D A C⎛⎫==== ⎪⎝⎭∴ (3)情形1:当045a <<时,24CQ <<,即24x <<,此时两三角板重叠部分为四边形DPBQ ,过D 作DG AP⊥于G ,DN BC ⊥于N ,2D GD N ==∴ 由(2)知:8AP CQ = 得8AP x=于是111222y AB AC CQ DN AP DG =--88(24)x x x=--<<情形2:当4590a <≤时,02CQ <≤时,即02x <≤,此时两三角板重叠部分为DMQ △, 由于8AP x =,84PB x=-,易证:PBM DNM △∽△, B M P B M N D N =∴即22BM PB BM =-解得28424PB x BM PB x-==+- 84444xMQ BM CQ x x-=--=---∴于是1844(02)24xy MQ DN x x x-==--<- ≤ 综上所述,当24x <<时,88y x x=--当02x <≤时,8444xy x x-=---2484y x x x =⎛⎫-+ ⎪-⎝⎭或法二:连结BD ,并过D 作DN BC ⊥于点N ,在DBQ △与MCD △中,45DBQ MCD ∠=∠=45DQB QCB QDC QDC MDQ QDC MDC ∠=∠+∠=+∠=∠+∠=∠DBQ MCD ∴△∽△ M CD B C D B Q=∴4x =- 84MC x =-∴ 284844x x MQ MC CD x x x-+=-=-=--∴BG2148(02)24x x y DN MQ x x-+==<- ∴≤法三:过D 作DN BC ⊥于点N ,在Rt DNQ △中,222D Q D N NQ =+ 24(2)x =+- 248x x =-+于是在BDQ △与DMQ △中45DBQ MDQ ∠=∠= DMQ DBM BDM ∠=∠+∠ 45BDM =+∠ BDQ =∠BDQ DMQ ∴△∽△BQ DQDQ MQ =∴即4x DQDQ MQ-= 224844DQ x x MQ x x-+==--∴2148(02)24x x y DN MQ x x-+==<- ∴≤5、(2006湖北宜昌)如图,点O 是坐标原点,点A (n ,0)是x 轴上一动点(n <0)以AO 为一边作矩形AOBC ,点C 在第二象限,且OB =2OA .矩形AOBC 绕点A 逆时针旋转90o得矩形AGDE .过点A 的直线y =kx +m 交y 轴于点F ,FB =FA .抛物线y=ax 2+bx+c 过点E 、F 、G 且和直线AF 交于点H ,过点H 作HM ⊥x 轴,垂足为点M .(1)求k 的值;(2)点A 位置改变时,△AMH 的面积和矩形AOBC 的面积的比值是否改变?说明你的理由.[解析] (1)根据题意得到:E (3n ,0), G (n ,-n )当x =0时,y =kx +m =m ,∴点F 坐标为(0,m )∵Rt △AOF 中,AF 2=m 2+n 2, ∵FB =AF ,∴m 2+n 2=(-2n -m)2, 化简得:m =-0.75n , 对于y =kx +m ,当x =n 时,y =0, ∴0=kn -0.75n , ∴k =0.75(2)∵抛物线y=ax 2+bx+c 过点E 、F 、G ,∴ ⎪⎩⎪⎨⎧=-++=-++=c c nb a n n c nb a n 75.039022解得:a =n 41,b =-21,c =-0.75n∴抛物线为y=n 41x 2-21x -0.75n解方程组:⎪⎩⎪⎨⎧-=--=nx y n x x n y 75.075.075.021412 得:x 1=5n ,y 1=3n ;x 2=0,y 2=-0.75n∴H 坐标是:(5n ,3n ),HM =-3n ,AM =n -5n =-4n ,∴△AMH 的面积=0.5³HM ³AM =6n 2;而矩形AOBC 的面积=2n 2,∴△AMH 的面积∶矩形AOBC 的面积=3:1,不随着点A 的位置的改变而改变. 6、(2006山东日照)如图(1),在以AB 为直径的半圆O 内有一点P ,AP 、BP 的延长线分别交半圆O 于点C 、D .求证:AP ²AC+BP ²BD=AB 2.证明:连结AD 、BC ,过P 作PM ⊥AB ,则∠ADB =∠AMP =90o,∴点D 、M 在以AP 为直径的圆上;同理:M 、C 在以BP 为直径的圆上. 由割线定理得: AP ²AC=AM ²AB ,BP ²BD=BM ²BA ,所以,AP ²AC+BP ²BD=AM ²AB+BM ²AB=AB ²(AM+BM )=AB 2.当点P 在半圆周上时,也有AP ²AC+BP ²BD=AP 2+BP 2=AB 2成立,那么:(1)如图(2)当点P 在半圆周外时,结论AP ²AC+BP ²BD=AB 2是否成立?为什么? (2)如图(3)当点P 在切线BE 外侧时,你能得到什么结论?将你得到的结论写出来.[解析] (1)成立.证明:如图(2),∵∠PCM=∠PDM=900, ∴点C 、D 在以PM 为直径的圆上, ∴AC ²AP=AM ²MD ,BD ²BP=BM ²BC , ∴AC ²AP+BD ²BP=AM ²MD+BM ²BC ,由已知,AM ²MD+BM ²BC=AB 2,∴AP ²AC+BP ²BD=AB 2. (2)如图(3),过P 作PM ⊥AB ,交AB 的延长线于M ,连结AD 、BC , 则C 、M 在以PB 为直径的圆上,∴AP ²AC=AB ²AM ,① D 、M 在以PA 为直径的圆上,∴BP ²BD=AB ²BM ,② 由图象可知:AB=AM-BM ,③由①②③可得:AP ²AC-BP ²BD=AB ²(AM-BM )=AB 2. 7、(2006江西南昌)问题背景;课外学习小组在一次学习研讨中,得到了如下两个命题:①如图1,在正三角形ABC 中,M ,N 分别是AC 、AB 上的点,BM 与CN 相交于点O ,若∠BON =60°.则BM =CN :②如图2,在正方形ABCD 中,M 、N 分别是CD 、AD 上的点.BM 与CN 相交于点O ,若∠BON =90°.则BM =CN. 然后运用类似的思想提出了如下命题:③如图3,在正五边形ABCDE 中,M 、N 分别是CD ,DE 上的点,BM 与CN 相交于点O ,若∠BON =108°,则BM =CN .任务要求(1)请你从①.②,③三个命题中选择一个进行证明; (2) 请你继续完成下面的探索;①如图4,在正n (n ≧3)边形ABCDEF ⋅⋅⋅中,M ,N 分别是CD 、DE 上的点,BM 与CN 相交于点O ,试问当∠BON 等于多少度时,结论BM =CN 成立(不要求证明)②如图5,在正五边形ABCDE 中,M 、N 分别是DE ,AE 上的点,BM 与CN 相交于点O ,∠BON =108°时,试问结论BM =CN 是否还成立,若成立,请给予证明.若不成立,请说明理由 (I)我选[解析] (1) 如选命题①证明:在图1中,∵∠BON =60°∴∠1+∠2=60° ∵∠3+∠2=60°,∴∠1=∠3又∵BC =CA ,∠BCM =∠CAN =60°∴ΔBCM ≌ΔCAN ∴BM =CN(2)如选命题②证明:在图2中,∵∵∠BON =90°∴∠1+∠2=90° ∵∠3+∠2=90°,∴∠1=∠3又∵BC =CD ,∠BCM =∠CDN =90°∴ΔBCM ≌ΔCDN ∴BM =CN (3)如选命题③证明;在图3中,∵∠BON =108°∴∠1+∠2=108° ∵∠2+∠3=108°∴∠1=∠3 又∵BC =CD ,∠BCM =∠CDN =108° ∴ΔBCM ≌ΔCDN ∴BM =CN(2)①答:当∠BON=0(n-2)180n时结论BM =CN 成立.②答当∠BON =108°时。
中考数学试题沈阳市2006年中考数学试题(非课改实验区).doc

2006年中考数学试题*考试时间120分钟,试题满分150分一、选择题(每小题3分,共24分)1.下列各式中,与2是同类二次根式的是()A.3B.4C.12D.122.若点()23P-,与点()Q a b,关于x轴对称,则a,b的值分别是()A.2-,3B.2,3C.2-,3-D.2,3-3.已知Rt ABC△中,90C=∠,9BC=,15AB=,则sin A的值是()A.34B.35C.45D.434.如图1,已知点A,B,C,D,E是O的五等分点,则BAD∠的度数是()A.36B.48C.72D.965.抛物线()2361y x=-+-的对称轴是直线()A.6x=-B.1x=-C.1x=D.6x=6.已知两个圆的半径分别是5和3,圆心距是2,则这两个圆的位置关系是()A.内切B.相交C.外切D.外离7.已知圆锥的侧面积是212πcm,底面半径是3cm,则这个圆锥的母线长是()A.3cmB.4cmC.5cmD.8cm8.图2是某班40名学生一分钟跳绳测试成绩的频率分布直方图,从左起第一、二、三、四个小长方形的高的比是1:4:3:2,那么一分钟跳绳次数在100次以上的学生有()A.6人B.8个C.16人20图1频率组距次数图2二、填空题(每小题3分,共24分)9.一元二次方程()30x x +=的根是____________.10.已知点I 是ABC △的内心,130BIC =∠,则BAC ∠的度数是____________.11.函数y =x 的取值范围是____________.12.在ABC △中,2AB AC ==,BD 是AC 边上的高,且BD =ACB ∠的度数是____________.13.用换元法解分式方程224232x x x x-=--,若设22x x y -=,则原方程可化为关于y 的整式方程是____________. 14.在O 中,90的圆心角所对的弧长是2πcm ,则O 的半径是____________cm .15.若甲、乙两名同学五次数学模拟考试成绩的平均分都是135分,且甲同学成绩的方差2 1.05s =甲,乙同学成绩的方差20.41s =乙,则甲、乙两名同学成绩相对稳定的是___________.(填“甲”或“乙”)16.有一个边长是5cm 的正六边形,若要剪一张圆形纸片完全盖住这个正六边形,则这个圆形纸片的最小半径是____________cm . 三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分)1718.解方程组:221870x y y x -=⎧⎨-+=⎩19.已知关于x 的一元二次方程2410x x m ++-=.(1)请你为m 选取一个合适的整数,使得到的方程有两个不相等的实数根; (2)设αβ,是(1)中你所得到的方程的两个实数根,求22αβαβ++的值.20.如图3,已知直线2y x =-与双曲线()0ky x x=>交于点()3Am ,. (1)求m ,k 的值;(2)连结OA ,在x 轴的正半轴上是否存在点Q ,使AOQ △是等腰三角形?若存在,请直接写出所有符合条件的点Q 的坐标;若不存在,请说明理由.四、(每小题10分,共20分)21.如图4,已知O 的直径8cm AB =,直线DM 与O 相切于点E ,连结BE ,过点B 作BC DM ⊥于点C ,BC 交O 于点F ,6cm BC =. 求:(1)线段BE 的长; (2)图中阴影部分的面积.22.随着我国经济的发展,对技术工人的需求量不断增加.某技工学校2005年秋季招收了600名新生,学校为了了解这600名新生中考成绩(成绩为整数)的情况,从中随机抽取部分学生的中考成绩进行分析,绘制了下面尚未完成的频率分布表:分组 频数累计 频数 频率 350.5~360.5 正 40.08 360.5~370.5 正正 6370.5~380.5 正正0.20 380.5~390.5 正正正 150.30 390.5~400.5 正正正 11400.5~410.5 正 40.08 合计1.00图3图4(1)补全上面的频率分布表;(2)你从表格信息中能否确定抽取的部分学生的中考成绩的众数落在哪一个小组内? 答:__________(填“能”或“不能”)(3)从表格信息可知抽取的部分学生的中考成绩的中位数在_________小组内; (4)在2005年秋季招收的新生中,中考成绩在390.5~410.5的新生约有多少人? 五、(12分)23.如图5,某市郊外景区内一条笔直的公路a 经过三个景点A B C ,,.景区管委会又开发了风景优美的景点D .经测量景点D 位于景点A 的北偏东30方向8千米处,位于景点B 的正北方向,还位于景点C 的北偏西75方向上.已知5AB =千米.(1)景区管委会准备由景点D 向公路a 修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1千米) (2)求景点C 与景点D 之间的距离.(结果精确到1千米)(参考数据:3 1.73=,5 2.24=,sin 53cos370.80==,sin 37cos530.60==, tan 53 1.33=,tan 370.75=,sin 38cos520.62==,sin 52cos380.79==, tan 380.78tan 52 1.28==,,sin750.97cos750.26tan 75 3.73===,,.)六、(12分)24.某小型企业获得授权生产甲、乙两种奥运吉祥物,生产每种吉祥物所需材料及所获利润如下表:A 种材料(2m )B 种材料(2m )所获利润(元)每个甲种吉祥物 0.3 0.5 10 每个乙种吉祥物0.60.2 20该企业现有A 种材料2900m ,B 种材料2850m ,用这两种材料生产甲、乙两种吉祥物共东 北 A B C D a2000个.设生产甲种吉祥物x 个,生产这两种吉祥物所获总利润为y 元.(1)求出y (元)与x (个)之间的函数关系式,并求出自变量x 的取值范围;(2)该企业如何安排甲、乙两种吉祥物的生产数量,才能获得最大利润?最大利润是多少? 七、(12分) 25.如图6,在O 中,BC BD =,点M 是CD 上任意一点,弦CD 与弦BM 交于点F ,连结MC ,MD ,BD .(1)请你在图6中过点B 作O 的切线AE ,并证明AE CD ∥;(不写作法,作图允许使用三角板)(2)求证:MC MD MF MB =;(3)如图7,若点M 是BC 上任意一点(不与点B ,点C 重合),弦BM ,DC 的延长线交于点F ,连结MC ,MD ,BD ,则结论MC MD MF MB =是否仍然成立?如果成立,请写出证明过程;如果不成立,请说明理由. 八、(14分) 26.如图8,在平面直角坐标系中,直线31y x =-+分别与x 轴,y 轴交于点A ,点B . (1)以AB 为一边在第一象限内作等边ABC △及ABC △的外接圆M (用尺规作图,不要求写作法,但要保留作图痕迹);(2)若M 与x 轴的另一个交点为点D ,求A ,B ,C ,D 四点的坐标;(3)求经过A ,B ,D 三点的抛物线的解析式,并判断在抛物线上是否存在点P ,使ADP △的面积等于ADC △的面积?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.图6 图7图8。
2006年中考全真模拟试卷参考答案-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-

2006年中考全真模拟试卷参考答案-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载---------------------------------------2006年中考全真模拟试卷(一)参考答案一、选择题题号123456789101112答案BACABDDDBCCB二、填空题13、2.4×101114、略(所举事件应在抛两枚骰子的情境下,且不应出现“不可能”等判断性词语)15、2016、∠ACE的度数和线段BD的长17、9018、17元三、解答下列各题19、原式====当x=时原式=20、∠如图见右图∠四边形OCED为菱形证明:∠DE∠OC,CE∠OD∠四边形OCED为平行四边形∠四边形ABCD为矩形∠AC=BD,OA=OC=1/2AC,OB=OD=1/2BD∠OC=OD(2分)∠四边形OCED为平行四边形且OC=OD∠四边形OCED为菱形21、∠68%,74%,78%,69%,70.5%,70.1%∠当n很大时,频率将会接近70%∠获得可乐的概率为30%,圆心角约为360º×30%=108º∠模拟实验方案:在一不透明口袋内放置红球3个、蓝球7个,搅均后从中随机摸出一个球,摸出红球获得可乐,摸出蓝球获得铅笔. (本方案仅供参考,其他方案酌情加分)22、∠直线BE垂直平分线段AC;C为BD中点(或C为半圆圆心),点A放在角的一边上,角的另一边与半圆相切,BE经过角的顶点.∠∠BE垂直平分AC∠EA=EC∠EA=EC且EB∠AC∠∠AEB=∠BEC∠EF为半圆切线∠CF∠EF∠CB∠EB,CF∠EF且CB=CF∠∠BEC=∠CEF∠∠AEB=∠BEC=∠CEF23、∠设抛物线解析式为y=a(x-14)2+32/3∠经过点M(30,0)∠a=-1/24∠y=-1/24(x-14)2+32/3当x=0时y=5/2∠y=2.5>2.44∠球不会进球门∠当x=2时,y=14/3∠y=14/3>2.75∠守门员不能在空中截住这次吊射.24、图形不唯一,符合要求即可.25、∠5n+21-8(n-1)>05n+21-8(n-1)<5解得8<n<29/3∠n为整数∠n=9∠物资总吨数=5×9+21=66吨∠设载重量5吨的汽车辆数为x, 载重量8吨的汽车辆数为y, 则5x+8y=66,200x+300y=2600解得x=10y=2∠载重量5吨的汽车10辆, 载重量8吨的汽车2辆.∠设汽车总辆数为y,载重量5吨的汽车辆数为x(x≥0)则y=x+(66-5x)/8=(3x+66)/8由函数解析式知当x最小且使3x+66为8的倍数时y最小∠当x最小=2时y最小=926、(1) (2) D(3) 符合条件的点M存在, 或2006年中考全真模拟试卷(二)参考答案一、选择题题号123456789101112答案BCCABACCCDBA二、填空题13、x≥314、a=12或-12, b为一个完全平方数15、略(形式为y=,k<0)16、∠A=∠D或∠ABC=∠DCB或AC=DB17、内切18、20三、解答下列各题19、因为原式=0与x的取值无关.所以x=2004错抄成x=2040不影响结果.20、四边形AEBC为平行四边形, 证明略.21、(1)由中位数可知,8 5分排在第2 5位以后,从位次讲不能说8 5分是上游;但也不能单纯以位次来判定学习的好差,小刚得8 5分,说明他对这阶段的学习内容掌握较好,从掌握学习内容讲也可以说属于上游.(2)初三(1)班成绩的中位数为8 7分,说明高于8 7分的人数占一半以上,而均分为7 9分,标准差又很大,说明低分也多,两极分化严重,建议加强对学习困难者的帮助.初三(2)班成绩的中位数和均分都为7 9分,标准差又小,说明学生之间差别较小,学习很差的学生少,但学习优异的学生也少,建议采取措施提高优生率.22、(1)A(1,0),B(0,2)易证∠ADC∠∠BOA得AD=OB=2(2)易得抛物线对称轴为直线x=2∠设抛物线解析式为y=a(x-2)2 +k∠过点A(1,0)、B(0,2)∠a+k=0 ,4a+k=2∠a=,k=-,解析式为y=(x-2)2-23、(1) 树状图如下:列表如下:有6种可能结果:(A,D),(A,E),(B,D),(B,E),(C,D),(C,E).(2) 因为选中A型号电脑有2种方案,即(A,D)(A,E),所以A型号电脑被选中的概率是(3) 由(2)可知,当选用方案(A,D)时,设购买A型号、D型号电脑分别为x,y台,根据题意,得解得经检验不符合题意,舍去;当选用方案(A,E)时,设购买A型号、E型号电脑分别为x,y台,根据题意,得解得所以希望中学购买了7台A型号电脑.24、∠同学乙的方案较为合理,因为相似的等腰三角形底角和顶角大小不变, 保证了相似三角形的“正度”相等;而同学甲的方案不能保证相似三角形的“正度”相等.∠同学甲的方案可修改为:用式子来表示“正度”,的值越小,表示等腰三角形越接近正三角形(仅供参考, 方案合理即可);∠用式子、、、来表示“正度”,“正度”的值越小,表示等腰三角形越接近正三角形(仅供参考,方案合理即可).25、(1)设存水量y与放水时间x的解析式为y=kx+b把(2,17)、(12,8)代入y=kx+b得解得k=-,b=y=-x+(2≤x≤)(2)由图可得每个同学接水量是0.25升,则前22个同学需接水0.25×22=5.5升存水量y=18-5.5=12.5升∠12.5=-x+∠x=7∠前22个同学接水共需7分钟.(3)当x=10时存水量y=-×10+= ,用去水18-=8.2升8.2÷0.25=32.8∠课间10分钟最多有32人及时接完水.或设课间10分钟最多有z人及时接完水,由题意可得0.25z≤8.2z≤32.826、(1),(2)不变,(3)(),(3)存在,30°、90°、133.2°或346.8°2006年中考全真模拟试卷(三)参考答案题号123456789101112答案ABBBCCDBDBCB二、填空题:13. x(xy +2)(xy -2)14. 1/515. 3a16.17. 三18.(2,5)或(4,4)19、去分母,得20. 说明:本题共有四个命题,其中命题二、命题三是真命题,命题一、命题四是假命题.命题一:在∠ABC和∠DEF中,B、E、C、F在同一直线上,AB=DE,AC = DF,∠ABC=∠DEF。
2006年各省中考试题汇编(31套)(348页)

2007年常熟市初三教学质量调研测试英语试卷本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
共6大题,满分113分(不含口试12分)。
考试用时100分钟。
第一卷(三大题,共68分)一、听力选择(满分24分)(请先用两分钟时间熟悉听力试题,然后再动笔答题。
做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
)A)回答问题(共6小题;每小题1分,满分6分)听下面6个问题。
每个问题后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
每个问题读两遍。
1. A. Eight. B. Seven. C. Nine.2. A. Ten o’clock. B. Ten yuan a kilo. C. I like it very much.3. A. Of course. Here you are. B. No hurry. C. Good idea.4. A. That’s great. B. Yes, I don’t. C. Of course not.5. A. That’s OK. B. It doesn’t matter. C. I’m sorry to hear that.6. A. He’s fine. B. He is 34. C. He’s a teacher.B)对话理解(共8小题;每小题1分,满分8分)听下面8段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
每段对话读两遍。
7. Where was Kate just now?A. In the library.B. To the library.C. In the park.8. What can we learn about Bill?A. He’s fine.B. He needs to have more rest.C. He has to stay with a doctor.9. What time will the next bus leave for Nanjing?A. At 8:20.B. At 8:40.C. At 8:50.10. What’s the weather like in Lushan?A. It often rains, and it’s hot.B. It never rains, and it’s pleasant.C. It sometimes rains, but it’s pleasant and comfortable.11. When did the man begin his teaching here?A. Since three years ago.B. About three years ago.C. Last year.12. Why does the man tell the woman to design some posters?A. To raise much more money for the woman.B. To make the charity show interesting.C. To attract more people to come to the charity show.13. How many students haven’t got the books?A. Five.B. Thirty-five.C. Forty.14. What would the man like to drink?A. He would like to drink neither coffee nor water.B. He would like to drink water.C. He would like to drink either coffee or tea.C)短文理解(共5小题;每小题2分,满分10分)听下面的短文。
06年长春中考数学试题

2006年长春市初中毕业生学业考试数 学 试 题(含答案)一、选择题(每小题3分,共24分) 1.计算2(1)-的值是( ) A.1B.1-C.2D.2-2.化简()m n m n --+的结果是( )A.0 B.2m C.2n - D.22m n - 3.在数轴上表示不等式260x -≥的解集,正确的是( )4.如图,BD 为O e 的直径,30A =o∠,则CBD ∠A.30oB.45oC.60o5.从某班学生中随机选取一名学生是女生的概率为35,则该班女生与男生的人数比是( )A.32 B.35C.23 D.256.由6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是( )A.正视图的面积最大 B.左视图的面积最大 C.俯视图的面积最大 D.三个视图的面积一样大 7.如图,双曲线8y x=的一个分支为( ) A.① B.② C.③ D.④8.如图,将圆桶中的水倒入一个直径为40cm ,高为55cm 的圆口容器中,圆桶放置的角度与水平线的夹角为45o.若使容器中的水面与圆桶相接触,则容器中水的深度至少应为( ) A.10cm B.20cm C.30cm D.35cm二、填空题(每小题3分,共18分)A. B. C. (第4题)(第6题) (第8题)9_______=.10.函数2y x bx c =+-的图象经过点(12),,则b c -的值为 .11.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm ):2,2-,1-,1,0,则这组数据的极差为 cm .12.图中_______x =.13.两圆有多种位置关系,图中不存在的位置关系是 .14.如图,将AOB △绕点O 逆时针旋转90o,得到A OB ''△.若点A 的坐标为()a b ,,则点A '的坐标为 .三、解答题(每小题5分,共20分)15.将直尺与三角尺按如图所示的方式叠放在一起.在图中标记的角中,写出所有与1∠互余的角.16.计算:42xx x x ⎛⎫-⎪-⎝⎭g.17.下面的两个网格中,每个小正方形的边长均为1cm .请你分别在每个网格中画出一个顶点在格点上,且周长为12cm 的形状和大小不同的凸多边形.(第12题) 30o 45o30o105o1 2 x(第13题)(第14题)18.小刚想给小东打电话,但忘了电话号码中的一位数字,只记得号码是2849456□(□表示忘记的数字).(1)若小刚从0至9的自然数中随机选取一个数放在□位置,则他拨对小东电话号码的概率是 .(2分)(2)若□位置的数字是不等式组2110142x x x ->⎧⎪⎨+⎪⎩,≤的整数解,求□可能表示的数字.(3分)四、解答题(每小题6分,共12分)19.某服装厂准备加工300套演出服.在加工60套后,采用了新技术,使每天的工作效率是原来的2倍,结果共用9天完成任务.求该厂原来每天加工多少套演出服.20.如图,矩形ABCD 是供一辆机动车停放的车位示意图.请你参考图中数据,计算车位所占街道的宽度EF .(参考数据:sin 400.64cos 400.77tan 400.84ooo≈,≈,≈,结果精确到0.1m .)五、解答题(每小题6分,共12分) 21.如图,P 为抛物线2331424y x x =-+上对称轴右侧的一点,且点P 在x 轴上方,过点P 作PA 垂直x 轴于点A ,PB 垂直y 轴于点B ,得到矩形PAOB .若1AP =,求矩形PAOB 的面积.22.某班组织一次数学测试,全班学生成绩的分布情况如下图:(1)全班学生数学成绩的众数是 分,全班学生数学成绩为众数的有 人.(2分) (2)全班学生数学成绩的中位数是 分.(2分)(3)分别计算两个小组超过全班数学成绩中位数的人数占全班人数的百分比.(2分)六、解答题(每小题7分,共14分) 23.如图,P 为正比例函数32y x =图象上的一个动点,P e 的半径为3,设点P 的坐标为()x y ,.(1)求P e 与直线2x =相切时点P 的坐标.(4分)(2)请直接写出P e 与直线2x =相交、相离时x 的取值范围.(3分)24.如图,在ABCD Y中,E 为BC 边上一点,且AB AE =. (1)求证:ABC EAD △≌△.(4分) (2)若AE 平分DAB ∠,25EAC =o∠,求AED ∠的度数.(3分)某班数学成绩统计图学生数0 24 68 10 12 80 85 90 95100 分数 第一组 第二组 2x =32y x =xO Py AC七、解答题(每小题10分,共20分)25.小张骑车往返于甲、乙两地,距甲地的路程y (千米)与时间x (小时)的函数图象如图所示.(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时.(3分) (2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止..,途中小李与小张共相遇3次.请在图中..画出小李距甲地的路程y (千米)与时间x (小时)的函数的大致图象.(3分)(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程y (千米)与时间x (小时)的函数关系式为1210y x =+.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.(4分)26.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒.(1)求正方形ABCD 的边长.(2分)(2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度.(2分)(3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标.(4分) (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =o∠的点P 有 个.(2分)y(抛物线()20y ax bx c a=++≠的顶点坐标是2424b ac ba a⎛⎫-- ⎪⎝⎭,.)2006年长春市初中毕业生学业考试数学试卷参考答案及评分标准一、选择题(每小题3分,共24分)1.A2.C3.B4.C5.A6.C7.D8.D二、填空题(每小题3分,共18分)910.111.412.213.相交14.()b a-,三、解答题(每小题5分,共20分)15.234∠,∠,∠.(写对一个得2分,写对两个得4分,写对三个得5分,多写扣1分)16.42xxx x⎛⎫-⎪-⎝⎭g242x xx x-=-g(2分)()()222x x xx x+-=-g2x=+.(5分)17.提供以下方案供参考:图①图②(画对一个得3分,画对两个得5分) 18.(1)110. (2分)(2)由2110142x x x ->⎧⎪⎨+⎪⎩,≤,得5.58x <≤. x Q 是整数,∴所求的数字为6或7或8.(5分)四、解答题(每小题6分,共12分)19.设服装厂原来每天加工x 套演出服. 根据题意,得603006092x x-+=. (3分)解得20x =.经检验,20x =是原方程的根.答:服装厂原来每天加工20套演出服.(6分)20.在Rt CDF △中, 5.440CD DCF ==o,∠,sin 40 5.40.64 3.46DF CD ∴=⨯o g ≈≈.(2分)在Rt ADE △中, 2.240AD ADE DCF ===o,∠∠,cos 40 2.20.77 1.69DE AD ∴=⨯o g ≈≈. (4分) 5.15 5.2(m)EF DF DE ∴=+≈≈.(6分)即车位所占街道的宽度为5.2m .五、解答题(每小题6分,共12分)21.PA x ⊥Q 轴,1AP =,∴点P 的纵坐标为1. 当1y =时,23311424x x -+=,即2210x x --=.解得1211x x ==(4分)Q 抛物线的对称轴为1x =,点P 在对称轴的右侧,1x ∴=∴矩形PAOB的面积为(1个平方单位.(6分)22.(1)95,20. (2分) (2)92.5. (4分)(3)121324265050==Q%,%, ∴第一、二小组超过全班数学成绩的中位数的人数占全班人数的百分比分别为2426%,%.(6分)六、解答题(每小题7分,共14分)23.(1)过P 作直线2x =的垂线,垂足为A .当点P 在直线2x =右侧时,23AP x =-=,得5x =,1552P ⎛⎫∴ ⎪⎝⎭,.(2分)当点P 在直线2x =左侧时,23PA x =-=,得1x =-,312P ⎛⎫∴-- ⎪⎝⎭,. (4分)∴当P e 与直线2x =相切时,点P 的坐标为1552⎛⎫ ⎪⎝⎭,或312⎛⎫-- ⎪⎝⎭,.(2)当15x -<<时,P e 与直线2x =相交.当1x <-或5x >时,P e 与直线2x =相离. (7分)24.(1)Q 四边形ABCD 为平行四边形, AD BC AD BC ∴=∥,. DAE AEB ∴=∠∠. AB AE AEB B =∴=Q ,∠∠. B DAE ∴=∠∠. ABC EAD ∴△≌△.(4分)(2)DAE BAE DAE AEB ==Q ∠∠,∠∠, BAE AEB B ∴==∠∠∠. ABE ∴△为等边三角形.60BAE ∴=o ∠.2585EAC BAC =∴=o o Q ∠,∠.ABC EAD Q △≌△,85AED BAC ∴==o ∠∠.(7分)七、解答题(每小题10分,共20分)25.(1)1,30.(2)所画图象如图所示.要求图象能正确反映起点与终点.(6分)(3)由函数1210y x =+的图象可知,小王与小张在途中共相遇2次,并在出发后 2小时到4小时之间第一次相遇. 当24x ≤≤时,2020y x =-.y由20201210y x y x =-⎧⎨=+⎩,,得154x =.所以第一次相遇的时间为154小时. (10分)26.(1)作BF y ⊥轴于F .()()01084A B Q ,,,,86FB FA ∴==,. 10AB ∴=.(2分)(2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=Q ,.P Q ∴,两点的运动速度均为每秒1个单位.(4分)(3)方法一:作PG y ⊥轴于G ,则PG BF ∥.GA AP FA AB ∴=,即610GA t=.35GA t ∴=.3105OG t ∴=-.4OQ t =+Q ,()113410225S OQ OG t t ⎛⎫∴=⨯⨯=+- ⎪⎝⎭.(6分)即231920105S t t =-++. 19195323210b a -=-=⎛⎫⨯- ⎪⎝⎭Q ,且190103≤≤, ∴当193t =时,S 有最大值. 此时4763311051555GP t OG t ===-=,, ∴点P 的坐标为7631155⎛⎫⎪⎝⎭,.(8分)方法二:当5t =时,1637922OG OQ S OG OQ ====g ,,.设所求函数关系式为220S at bt =++.Q 抛物线过点()63102852⎛⎫⎪⎝⎭,,,,1001020286325520.2a b a b ++=⎧⎪∴⎨++=⎪⎩,31019.5a b ⎧=-⎪⎪∴⎨⎪=⎪⎩,231920105S t t ∴=-++. (6分)19195323210b a -=-=⎛⎫⨯- ⎪⎝⎭Q ,且190103≤≤, ∴当193t =时,S 有最大值. 此时7631155GP OG ==,,∴点P 的坐标为7631155⎛⎫⎪⎝⎭,.(8分) (4)2. (10分)阿。
中考数学--2006中考数学试题课标卷

)
A.①②④ B.②③④ C.①③④ D.①②③ 6.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有 4 个红
1 球且摸到红球的概率为 , 个 D.3 个 7.小刚学习了有理数运算法则后,编了一个计算程序.当他输入任意一个有理数时,显示屏 上出现的结果总等于所输入的有理数的平方与1的和.当他第一次输入 −2 ,然后又将所得的 结果再次输入后,显示屏上出现的结果应是( )
1 中,自变量 x 的取值范围是 x−2
11.右图中阴影部分是一个正方体的表面展开平面图形的一部分,请你 在方格纸中补全这个正方体的表面展开平面图. (只填一种情形即可) 12 .如图, A,B,C 是⊙ O 上三点,∠ ACB=30 °,则∠ BAO 的度数 . 是
x − 2 > −1 13.不等式组 的解集为 3 x + 1 < 8
3.一鞋店试销一种新款女鞋,一周内各种型号的鞋卖出的情况如下表所示: 型号 数量(双) ) 22 3 22.5 5 23 10 23.5 15 24 8 24.5 4 25 2
对这个鞋店的经理来说,他最关注的是数据的( ) A.平均数 B.众数 C.中位数 D.极差 4.一个三角形的两边长为 3 和 6,第三边的边长是方程 ( x − 2)( x − 4) = 0 的根,则这个三角形 的周长是( ) A.11 B.11 或 13 C.13 D.11 和 13 5.李明设计了下面四种正多边形的瓷砖图案,用同一种瓷砖可以平面密铺的是(
.
14.已知二次函数 y = ax 2 + bx + c(a ≠ 0) ,其中 a b c
第 2 页 共 9 页
ERROR: limitcheck OFFENDING COMMAND: string STACK: 66038 33018 32512 33019
2006年中考数学试题分类汇编-中考数学试题、初中数学中考试卷、模拟题-初中数学试卷

2006年中考数学试题分类汇编-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载2006年中考数学试题分类汇编--数与式一、选择题:1. (邵阳市) 的相反数为()2. (仙桃市) 的绝对值是()A. B. C.D.3.(宜昌市)如果a与2互为倒数,则下列结论正确的为().(A)a=(B)a=-2(C)a=-(D)a=24.(福州市)-2的相反效是()A.2B.-2C.D.-5.(杭州市)已知与互为倒数,则满足条件的实数的个数是()A.0B.1C.2D.36.(北京市)-5的相反数是()A、5B、-5C、D、7.(贵阳市)的绝对值等于()(A)(B)(C)(D)8、(济宁市)的相反数是()A. B.5 C. D.9.(海南省)计算2-3的结果是()A.5B.-5C.1D.-110. (济宁市)能被下列数整除的是()A. 3B.5 C.7 D.911.(杭州市)()A.-2B.0C.1D.212.(长春市)计算的值是()(A)1.(B).(C)2.(D).13.(绍兴卷)冬季的一天,室内温度是8℃,室外温度是-2℃,则室内外温度相差()A、4℃B、6℃C、10℃D、16℃14. (荆门市)点A在数轴上表示+2,从点A沿数轴向左平移3个单位到点B,则点B所表示的实数是()(A)3(B)-1(C)5(D)-1或3.15. (仙桃市)吸烟有害健康.5月31日是世界无烟日,今年世界无烟日来临之际,中国国家卫生部公布了我国吸烟的人数约为3.5亿,占世界吸烟人数的.用科学记数法表示全世界吸烟人数约为()A.B.C.D.16.(宜昌市)宜昌市2005年财政总收入达到105.5亿元.用科学记数法(保留三位有效数字)表示105.5亿元约为()元.(A)1.055×1010(B)1. 06 ×1010(C)1. 05×1011(D)1. 06×101117.(海南省)今年1至4月份,我省旅游业一直保持良好的发展势头,旅游收入累计达元,用科学记数法表示是()A. 5163×106元B. 5.163×108元C. 5.163×109元D. 5.163×1010元18.(福州市)用科学记数法表示180 000的结果是()A.18×104B.1.8×105C.0.18×105D. 1.8×10619.(武汉市)同位素的半衰期(half-life)表示衰变一半样品所需的时间。
2006年黑龙江哈尔滨市初中升学考试数学试卷

2006年黑龙江哈尔滨市初中升学考试数学试卷第I 卷 选择题(共30分)一、选择题(每小题3分,共计30分) 1.下列各式正确的是( ) A .523)(x x =B .22))((b a a b b a -=-+C .23522=-y x y xD .65x x x =⋅2.若x 的相反数是3,| y |=5,则x +y 的值为( ) A .-8B .2C .8或-2D .-8或23.若点P (a ,b )在第四象限,则点Q (-a ,b -1)在( ) A .第一象限B .第二象限C .第三象限D .第四象限4.下列各命题正确的是( ) A .812,是同类二次根式 B .梯形同一底上的两个角相等C .过一点有且只有一条直线与已知直线平行D .两条直线被第三条直线所截,同位角相等5.已知一个等腰三角形的底边长为5,这个等腰三角形的腰长为x ,则x 的取值范围是( ) A .250<<x B .25≥xC .25>xD .100<<x6.下列图形中,既是轴对称图形,又是中心对称图形的是( ) A .等边三角形B .矩形C .正五边形D .等腰梯形7.下列命题中,正确命题的个数是( ) ①垂直于弦的直径平分这条弦 ②平行四边形对角互补③有理数与数轴上的点是一一对应的 ④相交两圆的公共弦垂直平分两圆的连心线 A .0个B .1个C .2个D .3个8.已知圆O 1与圆O 2半径的长是方程01272=+-x x 的两根,且2121=O O ,则圆O 1与圆O 2的位置关系是( )A .相交B .内切C .内含D .外切9.如图,PB 为圆O 的切线,B 为切点,连结PO 交圆O 于点A ,PA=2,PO=5,则PB 的长为( ) A .4B .10C .62D .3410.在平面直角坐标系内,直线343+=x y 与两坐标轴交于A 、B 两点,点O 为坐标原点,若在该坐标平面内有以点P (不与点A 、B 、O 重合)为顶点的直角三角形与Rt △ABO 全等,且这个以点P 为顶点的直角三角形与Rt △ABO 有一条公共边,则所有符合条件的P 点个数为( ) A .9个B .7个C .5个D .3个第II 卷 非选择题(共90分)二、填空题(每小题3分,共计30分)11.据新华网消息,去年我国城镇固定资产投资为75096亿元,用科学记数法表示约为______________________。
