几何第25讲_沙漏模型(学生版)A4
几何第25讲_沙漏模型(学生版)A4

相似三角形模型,就是形状相同,大小不同的三角形.沙漏模型是特殊的相似三角形. 1.AD AE DE AFAB AC BC AG===(对应线段之比等于相似比) 2.22::ADEABCS SAF AG =(面积比等于相似比的平方)重难点:寻找平行线,进而找到沙漏模型,利用沙漏模型解决线段比例关系或图形的面积比例关系.题模一:简单沙漏模型例1.1.1如图,DC 平行AB ,AC 和DB 交于点O ,AB :DC =3:2,则DO :OB =__________.例1.1.2如图所示,AC 与BD 平行,AB 与CD 垂直,交点为O .已知2AO =,4OB =,3OC =,则△OBD 的面积是△AOC 面积的__________倍.例1.1.3如图,AD 平行BC ,AC 与BD 交于点O ,AD 长12厘米,BC 长20厘米,BO 比OD 长4厘米,那么BD 长__________厘米.几何第25讲_沙漏模型F GACBDE沙漏模型 A BCDOA DOB C题模二:梯形沙漏例1.2.1如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米,而三角形ABO的面积为12平方厘米.则梯形ABCD的面积为多少平方厘米?例1.2.2梯形ABCD的面积是100,上底和下底的比是2:3,那么三角形ABO的面积是多少?A BOD C例1.2.3如下图,梯形ABCD的AB平行于CD,对角线AC、BD交于O,已知△AOB与△BOC的面积分别为25平方厘米与35平方厘米,那么梯形ABCD的面积是____________平方厘米.题模三:构造沙漏例1.3.1如图所示,已知长方形ABCD中,△FDC的面积为4,△FDE的面积为2,则阴影四边形AEFB的面积为多少?例1.3.2如图,已知平行四边形ABCD 的面积为72,E 点是BC 上靠近B 点的三等分点,则图中阴影部分的面积为____________.例1.3.3如图,长方形ABCD 被CE 、DF 分成四块.已知其中3块面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为__________平方厘米.例 1.3.4如图所示,图中的两个正方形的边长分别是6和4,那么阴影部分的面积是__________.例1.3.5如图所示,正方形ABCD 的边长是6,E 点是BC 的三等分点.△AOD 的面积为_________.FA BDC E42ABCODEABC DEFO258?A HG FE D CB例1.3.6如图,平行四边形ABCD 的面积是12,13DE AD =,AC 与BE 的交点为F ,那么图中阴影部分面积是__________.例 1.3.7已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是___________平方厘米.例1.3.8如图,正六边形面积为6,那么阴影部分面积为多少?例1.3.9如图,四边形ABCD 和EFGH 都是平行四边形,四边形ABCD 的面积是16,:3:1BG GC =,则四边形EFGH 的面积=________.例1.3.10如图,正方形ABCD 和正方形CGEF ,AG 交CF 于点H ,且CF =3CH ,△CHG 的面积是6,求正方形ABCD 的面积.OEAB C DH G FEDCBAAOEDC B随练1.1如图,DC 平行AB ,AC 和DB 交于点O ,AB :DC =2:1,则DO :OB =____________.随练1.2如图所示,AB 与CD 平行.已知:3:4AB CD =,6AO =,那么OC =__________.随练1.3如图,梯形ABCD 中,:2:5AB CD =.已知△COD 的面积是5,那么梯形的面积是多少?随练1.4如图,22S =,34S =,则梯形的面积为________.随练1.5如图所示,正方形ABCD 的面积是1,M 是AB 边的中点,则图中阴影部分的面积为__________.S 4S 3S 2S 1ABCDOA ODC BAODC B随练1.6如图所示,梯形ABCD 的面积是50,下底长是上底长的1.5倍,阴影三角形的面积是_________.随练1.7如图所示,图中的两个正方形的边长分别是10和6,那么阴影部分的面积是多少?作业1如图,AB 与CD 垂直,交点为O .已知4AO =,3CO =,5AC =,15BD =.求△BOD 的面积.作业2如图,AD 平行BC ,AC 与BD 交于点O ,AD 长9厘米,BC 长15厘米,BO 比OD 长4厘米,那么BD 长__________厘米.A HG FED C BAODCB ADB CO作业3如图,DC 平行AB ,AC 和DB 交于点O ,DO 长4厘米,OB 长10厘米,AO 长15厘米,那么OC 长__________厘米.作业4如图,梯形ABCD 中,DC 平行AB ,且AB :DC =2:1,请问图中4块小三角形的面积比,即S 1:S 2:S 3:S 4是__________.作业5梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,则三角形AOD 与三角形BOC 的面积之比为________.作业6如图,在梯形ABCD 中,三角形BCO 的面积是18平方厘米,三角形OCD 的面积是12平方厘米,那么梯形ABCD 的面积是__________平方厘米.作业7图中的两个正方形的边长分别为6分米和8分米,则阴影部分的面积为作业8下图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是___________平方厘米.OAB CD A BCDOABCDO S 1 S 2S 3S 4ADB CO作业9如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH 的面积是23,求四边形EGFH 的面积.作业10如图所示,图中的两个正方形的边长分别是8和4,那么阴影部分的面积是__________.HFE CDG BA。
数学沙漏模型定理

数学沙漏模型定理今天咱们来聊一个特别有趣的数学知识,叫沙漏模型定理。
你们见过沙漏吗?就是那种中间细细的,上下两头大大的东西,沙子从上面慢慢漏到下面。
咱们数学里的沙漏模型啊,就和这个沙漏长得有点像呢。
想象一下,有两个三角形,它们的形状就像沙漏的上下两个部分。
比如说,我们有一个大三角形ABC,还有一个小三角形ADE,这两个三角形的顶点A是重合的,而且DE这条边和BC这条边是平行的哦。
这就像沙漏的上下部分,中间是平行的关系。
那这个沙漏模型定理有什么神奇的地方呢?咱们来看个例子吧。
假如大三角形ABC的底边BC长是10厘米,小三角形ADE的底边DE长是4厘米。
这时候啊,我们会发现这两个三角形的高也是有一定关系的。
就好像你把大三角形和小三角形比一比,它们高的比例就和底边的比例是一样的。
那怎么用这个来解决问题呢?比如说我们想知道小三角形ADE的面积和大三角形ABC的面积的关系。
我们知道三角形的面积是底乘以高再除以2。
那因为这两个三角形的底和高的比例是一样的,所以它们面积的比例就和边长比例的平方是一样的。
底边的比例就是4比10,化简一下就是2比5。
那面积的比例呢,就是2的平方比5的平方,也就是4比25啦。
再给你们讲个故事吧。
有一个小画家,他要画一幅画,画面里有两座三角形的小房子。
一座大一点的房子ABC,一座小一点的房子ADE,这两座房子的屋顶是平行的,就像咱们的沙漏模型里的三角形一样。
小画家想知道小房子的面积是大房子面积的多少。
他就量了一下,大房子的底边是12米,小房子的底边是6米。
他按照咱们说的沙漏模型定理,算出底边比例是1比2,那面积比例就是1的平方比2的平方,也就是1比4。
小画家可高兴了,他很快就根据大房子的面积算出了小房子的面积。
沙漏模型定理是不是很有趣呀?我们在遇到这种形状像沙漏的两个三角形的时候,就可以用这个定理来解决很多关于边长和面积的问题呢。
只要记住它们边的比例和面积比例的关系,就像记住一个小秘密一样,在做数学题的时候就能很快得出答案啦。
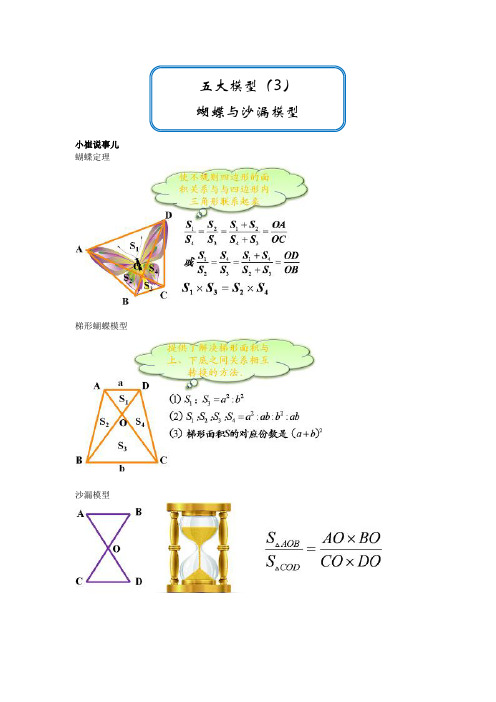
五大模型(3)蝴蝶与沙漏模型
小崔说事儿
蝴蝶定理
梯形蝴蝶模型
沙漏模型
五大模型(3)
蝴蝶与沙漏模型
奥数练练看
【例1】★★
如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?
【例2】★★★(06年南京智力数学冬令营)
如下图,梯形ABCD的AB平行于CD,对角线AC,BD交于O,已知△AOB与△BOC的面积分别为25平方厘米与35平方厘米,那么梯形ABCD的面积是多少平方厘米。
【例3】★★★(2007年“迎春杯”高年级初赛)
如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为_____平方厘米。
【例4】★★★
如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为________.
【例5】★★★(08年三帆中学考题)
右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是多少平方厘米。
【例6】★★★★
如右图,正方形ABCD的面积是a,正三角形△BPC的面积是b,求阴影△BPD的面积。
【例7】★★★★★
如下图,在梯形ABCD中,与CD平行,且CD=2AB,点E、F分别是AD和BC的中点,已知阴影四边形EMFN的面积是54平方厘米,则梯形ABCD的面积是多少平方厘米。
崔氏三十六计
崔氏三十六计之崔氏三步法
必杀技:分片,数份,算数
本周阴题。
沙漏模型的公式及定理推导

沙漏模型的公式及定理推导沙漏模型,或称为沙漏问题,是数学上的一个经典问题,它涉及到时间的问题以及两个容器之间物质的运动。
本文将从基本公式开始,逐步推导出沙漏模型的定理。
首先,我们定义一个沙漏模型,它由两个等高、相连的圆锥形容器构成。
这两个圆锥形容器的上底和下底的圆面积分别为A1和A2,两底的半径分别为r1和r2,容器的高度为h。
现在,我们考虑在这两个容器之间运动的物质。
假设容器中有一固定量的物质,我们用V表示它的体积。
由于沙漏两底的扁平性,在任意时刻,容器中的物质会形成一个沙漏形状,即物质在两个容器之间形成的界面是一个水平的面积为A的圆环。
这个圆环的半径我们用r表示。
那么,根据圆锥容器的几何关系,我们可以得到以下公式:V=A1*h1+A2*h2其中h1和h2分别表示物质在两个容器中的高度。
根据沙漏的形状,我们可以通过几何关系得到r和h之间的关系:h=h1+h2r1/h1=r/h=r2/h2将r1/h1和r2/h2两个式子分别代入第一个式子得:V=A1*h1+A2*(h-h1)V=A1*h1+A2*(h-r1*h1/r2)进一步化简得到:V=(A2*r1/r2-A2)*h1+A2*h为了推导出沙漏模型的定理,我们需要引入一个前提,即V和A是已知量。
通过观察发现,在V和A不变的情况下,h1和h2之间存在一个最大最小关系。
也就是说,当我们改变h1时,h2会相应地发生变化,而他们的乘积h1*h2是一个常数。
这个常数我们用K来表示。
由此,我们可以得到以下公式:K=h1*h2接下来,我们来证明K的常数性质。
将h2的值代入到K的公式中得:K=h1*(h-h1)对K求导:dK / dh1 = 1 * (h - 2h1)要使得K为常数,即dK / dh1 = 0,我们得到h1的取值:h1=h/2这说明当沙漏呈现对称形状时,容器中的物质分布是处于均衡状态的。
因此,根据以上推导,我们得出沙漏模型的定理:在一个呈沙漏形状的容器中,当物质量V和沙漏截面面积A都是已知量时,物质在容器中的分布会处于一个均衡状态。
沙漏模型原理及公式

沙漏模型原理及公式好的,以下是为您生成的文章:咱先来说说啥是沙漏模型。
打个比方,就像你在沙滩上玩,用沙子堆出两个形状相似的小城堡,一个大一个小。
这两个城堡之间的关系,就有点像沙漏模型。
在数学里,沙漏模型其实是个很有趣的东西。
它说的是,如果有两个三角形,它们的对应边互相平行,那就形成了沙漏模型。
比如说,一个大三角形 ABC 和一个小三角形 A'B'C',AB 平行于 A'B',AC 平行于 A'C',BC 平行于 B'C',这就是典型的沙漏模型啦。
那沙漏模型有啥特点呢?咱来仔细瞧瞧。
比如说,这两个相似三角形对应的边的比例是相等的。
啥意思呢?就是 AB 比 A'B' 等于 AC 比A'C' 等于 BC 比 B'C'。
这就好比大城堡的边长和小城堡的边长,按照一定的比例缩放。
还有哦,沙漏模型里对应角也是相等的。
就像大城堡的角和小城堡的角,角度都是一样的。
再来说说沙漏模型的公式。
假设大三角形的边长分别是 a、b、c,小三角形的对应边长是 a'、b'、c',那它们的比例关系可以表示为 a : a'= b : b' = c : c' 。
给您举个例子吧,有一次我在课堂上讲这个沙漏模型,有个同学就一脸懵地问我:“老师,这有啥用啊?”我就笑了笑,拿起教室里的两个三角板,一个大的一个小的,跟他说:“你看,这两个三角板是不是有点像沙漏模型里的两个三角形?咱们来量量它们的边,算算比例,看看是不是符合咱们讲的公式。
”结果这一操作,那同学一下子就明白了,还兴奋地跟其他同学说:“嘿,这还挺有意思的!”在做题的时候,沙漏模型的公式用处可大了。
比如说,给你一个沙漏模型,知道了其中几条边的长度,让你求其他边的长度,这时候就可以用上咱们的公式啦。
再比如说,有时候会遇到那种图形比较复杂的题目,里面藏着沙漏模型,你就得有一双“火眼金睛”,把它找出来,然后运用公式去解题。
小学奥数几何模型 之 沙漏模型 例题+作业 带答案

小学几何模型之沙漏模型课前引入:相似三角形例题1如图:在平行四边形ABCD中,AB=16厘米,AD=10厘米,BE=4厘米,求FC的长。
BC=AD=10厘米CD=AB=16厘米CF:BF=CD:BE=4:1FC的长:10÷(4+1)×4=8(厘米)练习1如图:在平行四边形ABCD中,CD=14厘米,BE=2厘米,AE和DE的长度相同,求DF 的长。
AB=CD=14厘米DE=AE=14+2=16(厘米)DF:FE=CD:BE=7:1DF的长:16÷(7+1)×7=14(厘米)例题2如图:在正方形ABCD中,CE=2DE。
已知正方形ABCD的面积是96平方厘米,求阴影部分的面积。
△ABD的面积为96÷2=48(cm2)假设S△DEF为1份,那么S△ABF为9份,S△ADF为3份阴影部分面积:48÷(9+3)×1=4(cm2)练习2如图:在长方形ABCD中,点E是边DC的三等分点。
已知三角形DQE的面积是1平方厘米,求长方形ABCD的面积。
DE:AB=1:3△ABQ的面积为9cm2△ADQ的面积为3cm2△ABD的面积为9+3=12 (cm2)长方形ABCD的面积为12×2=24 (cm2)例题3如图:在三角形ABC中,DE、FG、BC互相平行,并且AD=DF=FB,求三角形ADE、四边形DEGF和四边形FGCB之间的面积比。
AD:AF:AB=1:2:3S△ADE:S△AFG:S△ABC=1:4:9假设△ADE的面积为1份,那么△AFG的面积为4份,△ABC的面积为9份四边形DEGF的面积为4-1=3(份)四边形FGCB的面积为9-4=5(份)S△ADE:S四边形DEGF:S四边形FGCB=1:3:5练习3如图:在三角形ABC中,DE、FG、BC互相平行。
已知AD=3厘米,DF=2厘米,FB=1厘米,求三角形ADE、三角形AFG和三角形ABC之间的面积比。
平面几何五大基本模型第25课
平面几何五大基本模型第25课【最新版】目录一、引言二、五大基本模型的概念和意义1.蝴蝶定理2.沙漏模型3.筝型模型4.其他两种模型三、模型的结论和论证过程1.蝴蝶定理的结论和论证过程2.沙漏模型的结论和论证过程3.筝型模型的结论和论证过程四、其他两种模型的结论和论证过程五、总结正文一、引言平面几何是数学中的一个重要分支,它研究的是平面内的点、线、面及其相关性质。
在小学阶段,平面几何的学习主要涉及一些基本的模型和定理。
本文将介绍小学奥数平面几何五大基本模型:蝴蝶定理、沙漏模型、筝型模型以及其他两种模型。
二、五大基本模型的概念和意义1.蝴蝶定理:蝴蝶定理是指在平面几何中,如果一个三角形的两边分别等于另外两个三角形的两边之和,那么这两个三角形面积之比等于这两个三角形的边长之比的平方。
2.沙漏模型:沙漏模型是指在平面几何中,两个相同的三角形通过一个共顶点三角形连接,所形成的四边形面积等于两个三角形面积之和。
3.筝型模型:筝型模型是指在平面几何中,一个矩形被分成两个三角形和一个梯形,这三个图形的面积之和等于原矩形的面积。
4.其他两种模型:除了以上三种模型外,还有两种基本模型,分别是:A 型和 X 型。
A 型模型是指两个相同的三角形通过一个共顶点三角形连接,所形成的四边形面积等于两个三角形面积之和;X 型模型是指在平面几何中,一个矩形被分成两个三角形和一个平行四边形,这三个图形的面积之和等于原矩形的面积。
三、模型的结论和论证过程1.蝴蝶定理的结论和论证过程:蝴蝶定理的结论是两个三角形面积之比等于这两个三角形的边长之比的平方。
论证过程主要是通过相似三角形的性质和面积公式推导出来的。
2.沙漏模型的结论和论证过程:沙漏模型的结论是两个相同的三角形通过一个共顶点三角形连接,所形成的四边形面积等于两个三角形面积之和。
论证过程主要是通过等腰三角形的性质和面积公式推导出来的。
3.筝型模型的结论和论证过程:筝型模型的结论是一个矩形被分成两个三角形和一个梯形,这三个图形的面积之和等于原矩形的面积。
小学奥数几何模型专项课件-金字塔、沙漏模型
专题解析 例题讲授 总结归纳 巩固提升
专题解析
专题解析
类似模型 类似模型作为诸多几何模型中最为重要的一种,也是随后学习过程中应用最广泛的一个基础模型, 其主要研究的是三角形对应线段的长度比,及三角形面积比与对应线段比之间的关系.
基本要求 类似模型的基本情势较多,其中“金字塔模型”和“沙漏模型”是目前接触最多的两种情势,也 是我们现阶段学习的重点.
巩固提升
作业4:如图,正方形ABCD的边长是6,边上各点均为三等分点,求图中阴影部分的面积.
巩固提升
作业5:如图,正方形ABCD的边长是2,边上各点均为中点,求图中阴影部分的面积.
巩固提升
作业6:如图,正方形ABCD的边长是6,边上各点均为三等分点,求图中阴影部分的面积.
例题讲授
例2:如图,正方形ABCD和正方形CEFG的边长分别是8和12,求图中阴影部分的面积.
例题讲授
练一练2:3个同样大小的正方形如图放置,已知正方形边长是6,求图中阴影部分的面积.
例题讲授
例3:如图,正方形ABCD的边长是10,E、F分别是BC、CD的中点,求图中阴影部分的面积.
例题讲授
AB BD DA CA AD CD
例题讲授
例题讲授
例1:如图,三角形ABC的面积是18,D、E分别是AB的三等分点,F、G分别是AC的三等分点, 求图中阴影部分的面积.
例题讲授
练一练1:如图,三角形ABC的面积是1,D、E分别是AB的三等分点,F、G分别是AC的三等分点, 求,正方形ABCD的边长是3,边上各点均为三等分点,求图中阴影部分的面积.
例题讲授
例7:如图,正方形ABCD的边长是1,边上各点均为中点,求图中阴影部分的面积.
沙漏模型的证明过程
沙漏模型的证明过程沙漏模型是指一个上下对称的图形,由两个三角形和一个矩形组成。
其中,两个三角形分别位于矩形的上下两部分,它们的顶点相接并且底边与矩形的底边平行。
沙漏模型的性质是其三角形的面积之和等于矩形的面积。
接下来,我们将从几何方面逐步证明这个性质。
首先,设沙漏模型的上三角形的底边长度为a,高度为h;下三角形的底边长度为b,高度为h;矩形的宽度为c,高度为h。
根据三角形的面积公式,我们可以计算出上三角形的面积为S1=(1/2)*a*h,下三角形的面积为S2=(1/2)*b*h,矩形的面积为S3=c*h。
我们需要证明的是:S1+S2=S3为了开始证明,我们先计算出沙漏模型的总面积S。
沙漏模型由三个部分组成,即上三角形、下三角形和矩形。
因此,总面积等于这三个部分的面积之和,即S=S1+S2+S3接下来,我们将计算出三个部分的面积。
1.上三角形的面积:由于上三角形的底边长度为a,高度为h,根据三角形的面积公式,可得其面积为S1=(1/2)*a*h。
2.下三角形的面积:由于下三角形的底边长度为b,高度为h,同样根据三角形的面积公式,可得其面积为S2=(1/2)*b*h。
3.矩形的面积:由于矩形的宽度为c,高度为h,根据矩形的面积公式,可得其面积为S3=c*h。
将上述三个面积代入总面积公式,可得总面积S=S1+S2+S3=(1/2)*a*h+(1/2)*b*h+c*h。
将h提取出来,可得总面积为S=(1/2)*(a+b)*h+c*h。
由于沙漏模型是上下对称的,我们可以知道上下三角形的高度h是相等的。
所以,我们可以将总面积S重写为S=(1/2)*(a+b+2c)*h。
同时,由于矩形的高度h是固定不变的,所以可以将h视为一个常数。
现在我们可以将S1+S2=S3的等式改写为(1/2)*a*h+(1/2)*b*h=c*h。
进一步化简,得到a+b=2c。
将这个等式代入总面积的公式,可得 S = (1/2)*(a + b + 2c)*h = (1/2)*(2c + 2c)*h = 2ch。
七下几何沙漏模型讲解教案
七下几何沙漏模型讲解教案一、教学目标1. 了解沙漏模型的基本概念和特点;2. 掌握沙漏模型的相关性质和定理;3. 能够运用沙漏模型解决几何问题。
二、教学重点和难点1. 沙漏模型的基本概念和特点;2. 沙漏模型的相关性质和定理;3. 运用沙漏模型解决几何问题。
三、教学过程1. 导入教师出示一个沙漏模型,让学生观察并描述其形状和特点,引出沙漏模型的概念。
2. 概念讲解介绍沙漏模型的定义:沙漏模型是由两个相似的圆锥体组成,上下底面相连而成的几何体。
讲解沙漏模型的特点:两个圆锥体的底面积相等,高相等,上下底面重合。
3. 相关性质和定理(1)沙漏模型的体积设沙漏模型的上下底面半径分别为r1和r2,高为h,则沙漏模型的体积V=1/3πh(r1^2+r1r2+r2^2)。
(2)沙漏模型的表面积沙漏模型的表面积S=π(r1+r2)√(r1-r2)^2+h^2+πr1^2+πr2^2。
4. 解题方法(1)利用沙漏模型解决几何问题的基本思路是建立两个相似三角形的关系,然后运用相似三角形的性质进行计算。
(2)通过实例演练,让学生掌握运用沙漏模型解决几何问题的方法和技巧。
5. 练习让学生进行一些练习题,巩固所学知识。
6. 拓展介绍沙漏模型在实际生活中的应用,如建筑中的锥形塔、灯塔等。
7. 总结总结沙漏模型的相关性质和定理,强化学生对沙漏模型的理解和掌握。
四、教学反思本节课主要围绕沙漏模型展开教学,通过引入沙漏模型的概念和特点,让学生了解沙漏模型的基本性质和定理,并通过实例演练,让学生掌握运用沙漏模型解决几何问题的方法和技巧。
在教学过程中,要注重启发式教学,激发学生的兴趣,培养学生的逻辑思维能力和解决问题的能力。
同时,要注重拓展,让学生了解沙漏模型在实际生活中的应用,增强学生对数学知识的实际运用能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形模型,就是形状相同,大小不同的三角形.沙漏模型是特殊的相似三角形. 1
.
AD AE DE AF
AB AC BC AG
==
=
(对应线段之比等于相似比)
2.2
2::ADE
ABC
S S
AF AG =(面积比等于相似比的平方)
重难点:寻找平行线,进而找到沙漏模型,利用沙漏模型解决线段比例关系或图形的面积比例关系.
几何第25讲_沙漏模型
F G
A
C
B
D
E
沙漏模型
题模一:简单沙漏模型
例1.1.1如图,DC 平行AB ,AC 和DB 交于点O ,AB :DC =3:2,则DO :OB =__________.
例1.1.2如图所示,AC 与BD 平行,AB 与CD 垂直,交点为O .已知2AO =,4OB =,3OC =,则△OBD 的面积是△AOC 面积的__________倍.
例1.1.3如图,AD 平行BC ,AC 与BD 交于点O ,AD 长12厘米,BC 长20厘米,BO 比OD 长4厘米,那么BD 长__________厘米.
题模二:梯形沙漏
例1.2.1如图,梯形ABCD 的上底AD 长为3厘米,下底BC 长为9厘米,而三角形ABO 的面积为12平方厘米.则梯形ABCD 的面积为多少平方厘米?
例1.2.2梯形ABCD 的面积是100,上底和下底的比是2:3,那么三角形ABO 的面积是多少?
A B
C
D
O
A
D
B C
O
例1.2.3如下图,梯形ABCD 的AB 平行于CD ,对角线AC 、BD 交于O ,已知△AOB 与△BOC 的面积分别为25平方厘米与35平方厘米,那么梯形ABCD 的面积是____________平方厘米.
题模三:构造沙漏
例1.3.1如图所示,已知长方形ABCD 中,△FDC 的面积为4,△FDE 的面积为2,则阴影四边形AEFB 的面积为多少?
例1.3.2如图,已知平行四边形ABCD 的面积为72,E 点是BC 上靠近B 点的三等分点,则图中阴影部分的面积为____________.
例1.3.3如图,长方形ABCD 被CE 、DF 分成四块.已知其中3块面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为__________平方厘米.
O
A
B
D
C F
A B
D
C E
4
2
A
B
C
O
D
E
例 1.3.4如图所示,图中的两个正方形的边长分别是6和4,那么阴影部分的面积是__________.
例 1.3.5
如图所示,正方形ABCD 的边长是6,E 点是BC 的三等分点.△AOD 的面积为_________.
例1.3.6如图,平行四边形ABCD 的面积是12,1
3
DE AD =,AC 与BE 的交点为F ,那么图中阴影部分面积是__________.
例1.3.7已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是___________平方厘米.
O
E
A
B C D
A
B
C D
E
F
O
2
5
8
?
A H
G F
E D C
B A
O
E
D
C B
例1.3.8如图,正六边形面积为6,那么阴影部分面积为多少?
例 1.3.9如图,四边形ABCD 和EFGH 都是平行四边形,四边形ABCD 的面积是16,:3:1BG GC =,则四边形EFGH 的面积=________.
例1.3.10如图,正方形ABCD 和正方形CGEF ,AG 交CF 于点H ,且CF =3CH ,△CHG 的面积是6,求正方形ABCD 的面积.
随练1.1如图,DC 平行AB ,AC 和DB 交于点O ,AB :DC =2:1,则DO :OB =____________.
随练1.2如图所示,AB 与CD 平行.已知:3:4AB CD =,6AO =,那么OC =__________.
H G F
E
D
C
B
A
A
B
C
D
O
随练1.3如图,梯形ABCD中,:2:5
AB CD=.已知△COD的面积是5,那么梯形的面积是多少?
随练1.4如图,
22
S=
,
3
4
S=,则梯形的面积为________.
随练1.5如图所示,正方形ABCD的面积是1,M是AB边的中点,则图中阴影部分的面积为__________.
随练1.6如图所示,梯形ABCD的面积是50,下底长是上底长的1.5倍,阴影三角形的面积是_________.
随练1.7如图所示,图中的两个正方形的边长分别是10和6,那么阴影部分的面积是多少?
S4
S3
S2
S1
A
O
D C
B
A
O
D C
B
作业1如图,AB 与CD 垂直,交点为O .已知4AO =,3CO =,5AC =,15BD =.求△BOD 的面积.
作业2如图,AD 平行BC ,AC 与BD 交于点
O ,AD 长9厘米,BC 长15厘米,BO 比OD 长4厘米,那么BD 长__________厘米.
作业3如图,DC 平行AB ,AC 和DB 交于点O ,DO 长4厘米,OB 长10厘米,AO 长15厘米,那么OC 长__________厘米.
A H
G F
E
D C B
A
O
D
C
B A
D
B C
O
A B
C
D
O
作业4如图,梯形ABCD 中,DC 平行AB ,且AB :DC =2:1,请问图中4块小三角形的面积比,即S 1:S 2:S 3:S 4是__________.
作业5梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的
2
3
,则三角形AOD 与三角形BOC 的面积之比为________.
作业6如图,在梯形ABCD 中,三角形BCO 的面积是18平方厘米,三角形OCD 的面积是12平方厘米,那么梯形ABCD 的面积是__________平方厘米.
作业7图中的两个正方形的边长分别为6分米和8分米,则阴影部分的面积为____________.
作业8下图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是___________平方厘米.
O A
B
C
D A
B
C
D
O S 1 S 2
S 3
S 4
A
D
B C
O
作业9如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH 的面积是23,求四边形EGFH 的面积.
作业10如图所示,图中的两个正方形的边长分别是8和4,那么阴影部分的面积是__________.
H
F
E C
D
G B
A。
