大学物理课件:第五章学物理第五章总结
大学物理 第5章刚体定轴转动

赵 承 均
转动平面 某质点所在的圆周平面,称为转动平面。
参考线
转心 矢径
转动平面内任一过转轴的直线,如选 x 轴。
某质点所在的轨迹圆的圆心,称为转心。 某质点对其转心的位矢,称为该质点的矢径。
第一篇
力学
重 大 数 理 学 院
显然:转动刚体内所有点有相同的角量,故用角量描述刚体 的转动更方便,只需确定转动平面内任一点的角量即可。 1.角坐标— 描写刚体转动位臵的物理量。 角坐标 转动平面内刚体上任一点 P 到转轴 O 点的连线与 参考线间的夹角 。
赵 承 均
第二类问题:已知J和力矩M:求出运动情况和 b及 F 。
第三类问题:已知运动情况和力矩M,求刚体转动惯量 J 。
第一篇
力学
重 大 数 理 学 院
第一类问题:已知运动情况和 J ,确定运动学和动力学的联 系 例 :长为 l,质量为 m 的细杆,初始时的角速 度为 ωo ,由于细杆与 桌面的摩擦,经过时间 t 后杆静止,求摩擦力 矩 Mf 。
Fi cos i Fi cos i mi ain mi ri 2 法向:
e i
第一篇
力学
重 大 数 理 学 院
由于法向力的作用线穿过转轴,其力矩为零。可在切向 方程两边乘以 ri ,得到:
Fi e ri sin i Fi i r i sin i mi ri 2
4.角加速度— 描写角速度变化快慢和方向的物理量。 ⑴ 平均角加速度 t
即:刚体的角速度变化与发生变化所用的时间之比。
赵 承 均
⑵ 角加速度 ①用平均角加速度代替变化的角加速度; ②令 t 0 取极限;
d d lim 2 t 0 t dt dt
大学物理教程课件第五章

M
dE dE dV Cp = +p 可得: 代入上式 可得: dT dT dT
µ
CV (T2 − T1 )
dV C p = CV + p dT 利用1摩尔理想气体的状态方程 利用 摩尔理想气体的状态方程 PV=RT,将两边求微分并考 , 虑到此时的P为常量 为常量, 代入上式得: 虑到此时的 为常量,可得 PdV=RdT 或 R=PdV/dT代入上式得: 代入上式得
T1 T2
对于质量为M的工作物质 温度从 升到T 对于质量为 的工作物质,温度从 1升到 2时向外界吸收 的工作物质 温度从T 的热量为: 的热量为: M Q = νC p (T2 − T1 ) = C p (T2 − T1 )
µ
第五章 热力学
对于一般的准静态过程中系统所吸收的热量, 对于一般的准静态过程中系统所吸收的热量,可以通过对 T2 两边求得: 式dQ = νCdT 两边求得: Q = ∫ dQ = ∫ νCdT = νC (T2 − T1 )
在热传递过程中所传递的能量就称为热量。 在热传递过程中所传递的能量就称为热量。 功与热量的异同
1)过程量:与过程有关; )过程量:与过程有关;
T1 < T2
T1 Q T2
2)等效性:改变系统热运动状态作用相同; )等效性:改变系统热运动状态作用相同; 1卡 = 4.18 J , 1 J = 0.24 卡 卡 3)功与热量的物理本质不同 . )
热力学
相辅相成
气体动理论
第五章 热力学
第一节 热力学第一定律及其对理想气体的应用
一、热力学系统 热力学所研究的对象称为热力学系统,简称系统。 热力学所研究的对象称为热力学系统,简称系统。 按系统与外界的相互作用可将系统分为三类: 、 按系统与外界的相互作用可将系统分为三类:1、开放 系;2、封闭系;3、孤立系。 、封闭系; 、孤立系。 热力学平衡态:如果孤立系达到一个各种宏观性质不再随时间 热力学平衡态: 改变的状态,则这种状态就称为热力学平衡态。 改变的状态,则这种状态就称为热力学平衡态。 二.热力学过程 热力学系统的状态随时间的变化叫做热力学过程。 热力学系统的状态随时间的变化叫做热力学过程。 1、如按过程的平衡性质分,热力学过程可分为准静态过程和 、如按过程的平衡性质分, 非准静态过程。 非准静态过程。
大学物理第五章汇总

2.球壳内的场强;
3. 球壳外的场强;
解:(1)由静电感应知识知 球壳内表面带电量为-q, 球壳内表面带电量为q
(2)由分析知空间电场具有球对称性,选半径为r的同心球 面为高斯面,由高斯定理
ÒS
rr EgdS
q内
0
r E
5-6 长 l =15cm的直导线AB上均匀地
分布着线密度为 l = 5×10-9 C/m:的电荷
(如图) 。求:
(1)在导线的延长线上与导线一端 B 相 距 d = 5cm处P 点的场强;
(2)在导线的垂直平分线上与导线中点 相距 d =5cm处Q点的场强。
.Q
A
d l
B .P d
题号 结束
已知:l =15cm, l = 5×10-9 C/m,
0
a.rR时,高斯面内电荷 q
d
V
4 3
r
3
R
E r 3 0
b.rR时,高斯面内电荷
q 4 R3
3
E
R3 3 0
1 r2
高斯定理的应用
均匀带电球体的电场分布
r
rR
E
3 0 R3 1 3 0 r 2
rR
R
E Er 关系曲线
R
3 0
r 2
O
R
r
例. 点电荷q ,处在导体球壳的中心,壳的
q内
4 0 r 2
eˆr
r R1时
r E
q
4r0 r 2
e)r
R1 r R2 时 E 0
r R2时
r E
q
4 0 r 2
大学物理 第五章.

时,
刚体定轴转动的 角动量守恒定律
35
§5.4 刚体的角动量定理及守恒定律
例5.6:如图,质量为M,半径为R的转台,可绕通过中心竖直轴
转动,阻力忽略不计,质量为m的人站在台的边缘,人和台原来都 静止,如果人沿转台的边缘绕行了一周,问相对地面转台转过了多 少角度?
解:把人和转台看做一个系统
系统的角动量守恒 规定:逆时针转动为正方向,以 地面为参考系。 设人的角速度为ω,转台的角速度为Ω。
或
A = ∫ Mdθ = Mθ
42
例5.9:一质量为m,长为 l的匀质杆,两端用绳悬挂杆处于水平 状态,现突然将杆右端的悬线剪断,求(1)此瞬间另一根绳受到 的张力 ;(2)剪断绳子之后任一时刻杆的角速度 ω与转过角度 θ之 间的关系。 解: (1)首先考虑杆绕O点的的转动 根据转动定律: T O
匀变速运动
6
§5.1 刚体及其定轴转动描述
例5.1:一汽车发动机的转速在5s内由200r(转)/min均匀地增加 到3000r(转)/min。(1)求在这段时间内的初角速度、末角速 度和角加速度;(2)求这段时间内转过的角度;(3)发动机轴 上装有一半径为R=0.15m的飞轮,求轮边缘上一点在这第5s末的 切向加速度、法向加速度和总加速度。
24
§5.3 刚体转动的功和能
回顾: 质点 质量 牛顿运动定律
M = Jβ
刚体 转动惯量 转动定律
力做功
力矩做功
25
§5.3 刚体转动的功和能
一、力矩的功
轴
dθ dr α r
α
F 在转动平面内
ω
元功: dA = F • dr = F dr cos α = F ( rdθ ) cos α F ( r cos α )dθ = Mdθ
大学物理课件 第五章-1
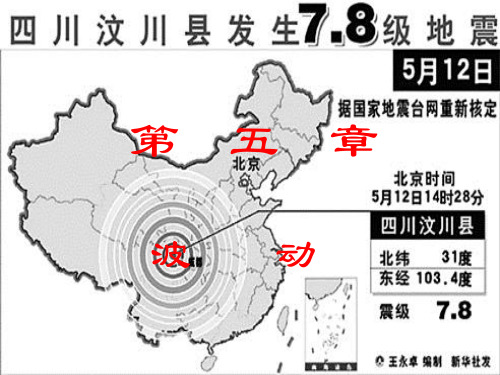
三. 波的特征量
1.波速u
概念:振动状态传播的速度 由媒质的性质决定与波源情况无关。
弹性媒质中u
波速
பைடு நூலகம்模量 密度
波速仅仅取 决于媒质的 弹性和惯性
模密
量 度
横波 纵波
固体:u G
柔绳:u
T
T : 绳张力 : 线密度
固体:u Y
液气:u B
12
2. 周期T: 一个完整的波通过波线上的某点所需的时间。
(x-
xo)] x0 }
结论:确定波动方程的二个条件 1. 已知u
2. 波线上一点的振动方程
18
三、波动方程物理意义(正向传播波为例)
y
A
cos[
(t
x u
)
0
]
1. 在空间某位置 x = x1,有
2. 它在表某示时y 刻x A=tco=xs1t1处ω,的t有振xu1动 函o数 ,A其cos中ωtooux1ω为ux1初 相。
2 T
14
§5-3平面简谐波
一、平面简谐波概念 所有质点作谐振且波面为平面的波
二、平面简谐波的波动方程:y=f(x,t)
描述媒质中各质点位移y随各点平衡位置x和时间t变化 的函数关系
平面简谐波,在无吸收的、
均匀无限大介质中传播。
源
以坐标原点O点为参考点
y
则O点处质点的振动方程为 A
u
y0 Acos(t 0 )
因媒质各部分间的弹性联系,会使振动传播开去,
这就形成了波动 — 机械波
4
“上游”的质元依次带动“下游”的质元振动。 质元的振动状态将在较晚时刻于“下游”出现。
波动是振动状态的传播,不是媒质的传播。
大学物理第5章

第二节 刚体的定轴转动定律
如图5-9所示,假设一个刚体绕固定轴Oz轴转动,将此 刚体分成许多质元,每个质元都在各自的转动平面上做圆周 运动,它们各自的转动平面不尽相同,各自做圆周运动的圆 心也不相同.但是,这些圆心都在z轴上.在刚体中取一质元i, 其质量为Δmi,离转轴的距离为ri,设该质元受到的合外力为 Fi,来自刚体内其他质元对它的合内力为fi,并假设合外力Fi 和合内力fi都位于质元i所在的转动平面内(都与转轴垂直). 设质元的加速度为ai,则有
第一节 刚体运动的描述
二、 刚体的定轴转动
定轴转动是刚体转动中最简单的运动形式. 刚体做定轴转动时,刚体上各点都绕同一转轴做圆周运动,而转轴 本身在空间的位置不动,轴上各点始终静止不动.例如,门的开或关、机 器上飞轮的转动等都是定轴转动.如图5-3所示,刚体上P点处任意一个 质元都将在通过该点且与转轴垂直的平面内做圆周运动,该平面称为转 动平面,圆心O点是转轴与转动平面的交点.显然,这种转动平面可以有 无数个,对于刚体的转动而言,它们是等价的,在研究刚体转动时可任 选一个.因此可以看出,刚体的定轴转动实质上就是刚体上各个质元在垂 直于转轴的转动平面内的圆周运动.
第一节 刚体运动的描述
图5- 4 刚体的角量描述
第二节 刚体的定轴转动定律
一、 力对转轴的力矩
对于刚体的定轴转动而言,若 作用在刚体上p点的力F在转动平面 内,力的作用点p相对于转轴的位 矢为r,力臂为d,则力F对转轴的 力矩为
M=r×F 其中,力矩的大小M=Frsin θ 如图5-5所示.
图5- 5 力在转动平面内
第二节 刚体的定轴转动定律
【例5-5】
如图5- 15所示,一个可绕固定轴O自由转动的均质细棒, 质量为m,长度为l,初始时刻处于水平位置.求其自由释放至θ 角时的角加速度和角速度.
大学物理第五章 气体动理论总结

三种速率比较:
vp
2kT m0
2RT M mol
f (v)
v 8kT 8RT
m0
M mol
v
v 2
3kT
3RT
m0
M mol
O
v p
v
v2
温度一定,同种气体
vp温度。
1
T2 T1
M mol 一定
2
T2 T1
v p2 v p1
v o
f (v)
5. 速率分布函数
f (v) dN
Ndv
dv
v
速率分布函数
f (v) 速率分布函数物理意义---
在速率v 的附近,单位速率间隔内的 分子数占总分子数的百分比 .
f (v)dv dN N
归一化条件
代表速率v 附近dv (或v~v+dv)区间的分子数概率
0
f
(v)dv
dN N
1
---曲线下面积
f (v)
2. 氢气分子的最概然速 率是多少?
0
1000
2
vm / s
v pHe
2RT 4 103
1000 m / s
2RT v pH2 2 103
2 1000
m/s
麦克斯韦速率分布律
例* 已知f()为麦克斯韦速率分布函数,p为分子 的最可几速率,则
p f ()d 表示 速率小于 p的分子数占总分子数的百分比
0
或分子速率小于 p的概率。
f ()d 表示 速率大于 p的分子数占总分子数的百分比
p
或分子速率大于 p的概率。
0
1 2
m0
2
f
(
)d
大学物理一复习 第五章 静电场和习题小结

q 4 π
0
dr r
2
r
q
1 q ( ) 4 r r 4 r q
0 0
r
E
V
q 4 π 0r
q 0, V 0 q 0, V 0
三、电势叠加原理
点电荷系
Va
q1
q2
a
E dl
V1 V 2 V n
第 五 章 静电场
Nothing in life is to be feared. It is only to be understood. ----(Marie Curie)
本章参考作业:P190
5-1,5-2、5-9①、5-14、5-21、 5-23、5-26、5-27、5-30。
学 习 要 点
的大小处处相等,且有
cos 1
cos 0
(目的是把“ E ”从积分号里拿出来)
计算高斯面内的电荷,由高斯定理求 E。
高斯定理运用举例: ---计算有对称性分布的场强
掌握所有 例题
1、球对称——球体、球面、球壳等。 2、轴对称——无限长直线、圆柱体、圆柱面。 3、面对称——无限大均匀带电平面。
E
0
R
r
三、面对称——无限大均匀带电平面。
例6、求无限大均匀带电平面的场 分布。已知面电荷密度为
o
p
dE
dE
解:对称性分析: 垂直平面 E
选取闭合的柱形高斯面
左底 侧
右底
侧 0
左底
E S
S'
E S
右底
2 ES
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理课件:第五章学物理第五章总结热力学基础一、基本要求1.掌握功、热量、内能的概念,理解准静态过程。
2.掌握热力学第一定律,能分析、计算理想气体等值过程和绝热过程中功、热量、内能的改变量。
3.掌握循环过程和卡诺循环等简单循环效率的计算。
4.了解可逆过程和不可逆过程。
5.理解热力学第二定律及其统计意义,了解熵的玻耳兹曼表达式及其微观意义。
二、基本内容1. 准静态过程过程进行中的每一时刻,系统的状态都无限接近于平衡态。
准静态过程可以用状态图上的曲线表示。
2. 体积功功是过程量。
3. 热量系统和外界之间或两个物体之间由于温度不同而交换的热运动能量。
热量也是过程量。
4. 理想气体的内能式中为气体物质的量,为摩尔气体常量。
内能是状态量,与热力学过程无关。
5. 热容定体摩尔热容定压摩尔热容迈耶公式比热容比6.热力学第一定律(微分形式)7.理想气体热力学过程主要公式(1)等体过程体积不变的过程,其特征是体积=常量。
过程方程:常量系统对外做功:系统吸收的热量:系统内能的增量:(2)等压过程压强不变的过程,其特征是压强=常量。
过程方程:常量系统对外做功:系统吸收的热量:系统内能的增量:(3)等温过程温度不变的过程,其特征是温度常量。
过程方程:常量系统内能的增量:系统对外做功:系统吸收的热量:(4)绝热过程不与外界交换热量的过程,,其特点是。
过程方程:常量系统吸收的热量:系统内能的增量:系统对外做功:或8. 循环过程系统由某一平衡态出发,经过一系列变化过程又回到原来平衡态的整个过程叫做循环过程(简称循环)。
其特点,准静态循环在图上用一条闭合曲线表示。
正循环:系统从高温热源吸热,对外做功,向低温热源放热。
效率为逆循环:也称制冷循环,系统从低温热源吸热,接受外界做功向高温热源放热。
制冷系数9. 卡诺循环系统只和两个恒温热源进行热交换的准静态循环过程。
正循环的效率制冷系数10. 可逆和不可逆过程一个系统,由某一状态出发,经过某一过程到达另一状态,如果存在另一过程,它能使系统和外界完全复原,则原来的过程称为可逆过程;反之,如果用任何方法都不能使系统和外界完全复原,则称为不可逆过程。
各种自然宏观过程都是不可逆的,且各种不可逆性之间是相互沟通的。
11. 热力学第二定律克劳修斯表述:热量不能自动地由低温物体传向高温物体。
开尔文表述:其唯一效果是热全部转变为功的循环过程是不可能的。
微观意义:自然过程总是沿着使分子运动更加无序的方向进行。
12. 热力学概率和同一宏观状态对应的微观状态数。
自然过程沿着向增大的方向进行。
平衡态相应于一定宏观条件下最大的状态。
13.玻耳兹曼熵公式的定义:熵增加原理:对孤立系的各种自然过程总有这是一条统计规律。
14.克劳修斯熵公式熵增加原理:(孤立系,等号用于可逆过程)。
三、习题选解5-1 非弹性小球互相碰撞时会发热,完全弹性小球相碰撞时则不会发热。
我们已经假设理想气体分子的碰撞是完全弹性的,问理想气体是否具有热运动能?解:小球作非弹性碰撞时,小球运动的动能转化为小球内部大量分子无规则运动的能量,或者说产生了热,作弹性碰撞时,小球宏观运动的动能并不转化为分子无规则运动的能量,不产生热。
对大量气体分子作杂乱运动的热运动形式而言,分子间碰撞是频繁的,经典统计中引用了两个分子间作弹性碰撞的假设,仍然认为分子的运动是杂乱的,这并没有否定气体分子具有热运动。
分子间作完全弹性碰撞假设的涵义是分子无规则运动的能量与原子内部的能量不发生转换。
5-2 一质量为,温度为的冰块,以的速度沿水平表面滑动。
由于冰块与水平表面摩擦的结果,使冰块滑了一段路程后停了下来。
已知冰的熔解热为,假设没有其它热交换,问冰融化了多少?解:以表示冰的熔解热,并设冰块滑行停止后融化的质量为,冰块吸收的热量为。
摩擦力对冰块做负功,根据机械能守恒定律,摩擦力的功应为冰块动能变化量。
由于没有其他能量交换方式,由热力学定律有5-3 如图所示,一系统由态沿到达态时,吸收了的热量,同时对外做的功。
(1)如果沿进行,则系统做功,问这时系统吸收了多少热量? (2)当系统由态沿着曲线返回态时,如果是外界对系统做功,问这时系统是吸热还是放热?热量传递是多少?解:(1)系统从进行过程中,吸收热量,系统对外做功,。
题5-3图故态与态能量之差为系统经过程之后,系统做功。
系统吸收热量为(2)系统沿曲线由态返回态时,系统对外做功,这时系统内能减少。
,负号表示系统放热。
5-4 如图所示,一定量的理想气体由状态经到达(为一直线),求此过程中:(1)气体对外做的功;(2)气体内能的增量;(3)气体吸收的热量。
解:(1)气体对外界做功题5-4图(2)由理想气体状态方程有由于,状态和的温度相同,这一过程中内能增量为零。
(3)由热力学第一定律由,有5-5 根据热力学第一定律,一个系统内能的增加等于外界对它做的功加上传递给它的热量。
问在活塞和内壁间有摩擦力的情况下,对于封闭于此活塞内的理想气体,应用热力学第一定律时,要注意什么问题?答:当活塞和内壁间有摩擦力时,外界所做的功一部分要抵消摩擦力做的功,剩下的另一部分才对内能的增加有贡献。
在处理有摩擦力存在的问题时,要注意外界做的功对内能增加有贡献的应当是外界做的功减去摩擦力做的功。
5-6 如图所示,使一定质量的理想气体的状态按图中的曲线沿着箭头所示的方向发生变化。
图线的段是以轴和轴为渐进轴的双曲线。
(1)已知气体在状态时的温度,求气体在、、状态时的温度;(2)从到气体对外做的功共是多少?(3)将上述过程在图上画出,并标明过程进行的方向。
解:(1)由理想气体方程题5-6 图有(2)从过程是等压过程,因而气体对外界做功为由的过程是双曲线,,其中,过程中,气体对外界做功从又是等压过程,其中,故过程中,气体对外界做功为所以,从到气体对外界所做的总功(3)在图上对应到的过程如图所示。
题5-6图5-7 (1)气体比热的数值可以有无穷多个,为什么?在什么情况下,气体的比热是零?什么情况下气体比热是无穷大?什么情况下是正值?什么情况下是负值?(2)气缸中储有的单原子理想气体,在压缩过程中,外力做功,气体温度升高,试计算气体内能的增量和所吸收的热量。
在此过程中,气体摩尔热容是多少?答:(1)比热的定义,对于一定量的气体从状态1变化到状态2,温度变化有确定的值,但是从状态1过渡到状态2的变化过程可以有无穷多个,每个过程吸热都不同,是与过程有关的量。
所以对应有无穷多个数值。
对绝热过程所以。
对等温过程所以。
若体系的温度增加,并且是吸热过程,或体系的温度降低,并且是放热过程,这种情况。
若体系的温度增加,并且放出热量,或体系的温度降低,并且吸收热量,以上情况。
(2)已知,,。
对于单原子气体定容摩尔热容量气体摩尔热容5-8 摩尔数相同的三种气体,,均可看作理想气体。
它们从相同的初态出发,都经过等体吸热过程,若吸收的热量相同,试问:(1)温度的升高是否相等?(2)压强的升高是否相等?解:(1)等容过程所以,以及分别是单原子分子气体,,双原子分子气体,;多原子分子气体,。
它们的摩尔数相同,吸热相同,它们的温度升高依次是最多,次之,最少。
(2)等容过程=常数,,以及的压强增加以的最多,次之,最少。
5-9 的氢气,在压强为,温度为时,其体积为,今使其经以下两种过程到达同一状态:(1)先保持体积不变,加热使其温度升高到,然后令其作等温膨胀,体积变为原体积的两倍;(2)先使其等温膨胀到原体积的两倍,然后保持其体积不变,加热到。
试分别计算上述两种过程中气体吸收的热量、气体对外所作的功和气体内能的增量,并做出图。
题5-9图解:(1)氢气的定容摩尔热容量为.在等容过程中气体不做功,内能增量在等温过程中内能不变,氢气体积从增加到,氢气对外做功在过程中气体吸收的热量对外所做的功内能的增量(2)在等温过程中内能不变,气体对外做功的在等容吸热过程中气体不做功,内能增量为在过程中气体吸收的热量对外所做的功内能的增量5-10 的单原子理想气体从加热至,(1)体积没有变化;(2)压强保持不变,问在这两个过程中各吸收了多少热量?增加了多少内能?气体对外做了多少功?解:单个单原子分子的平均动能为,温度为时,一摩尔单原子理想气体的内能为当温度从升至时,内能变化(1)当体积不变时,系统对外界做功,气体吸收热量(2)当压强不变时,气体对外界做功气体吸收热量5-11 当气体从体积膨胀到体积时,压强和体积之间的关系为式中、和均为常量,试计算该气体所做的功。
解:由得当气体从体积膨胀到体积时,该气体所作的功为5-12 设氮气作极缓慢的减压膨胀,其压强与体积的关系为;初始时,气体的体积;终止时,气体的体积,求氮气在上述过程中做的功、吸收的热量和内能的增量。
解:此氮气为理想气体,则由理想气体状态方程代入,可求得初始时系统温度同理终止时系统温度在此过程中,气体对外做功气体内能的增量为系统吸收的热量为5-13 证明多方过程中理想气体的摩尔热容量为说明多方指数和时各是什么过程及各过程中的摩尔热容量值。
解:气体多方过程的状态方程可表示为用代表多方过程中摩尔热容量,由定义可知,当系统温度变化时,系统从外界吸收热量为为气体的摩尔数。
同样,当温度变化时,理想气体的内能改为其为摩尔定容热容量。
由热力学第一定律有① 再由理想气体状态方程微分有② 再将多方过程状态方程两边取对数,再微分,可得③ 将①、②、③式中消去,和,从而有再由有其中,由(1)当时,常数,这是等压过程。
这时(2)当时,常数,是等温过程。
这时等温过程中,温度保持不变,这时气体吸收热量全部转化为气体对外界做的功,而内能保持不变。
(3)当时,常数。
这时这是绝热过程。
5-14 气缸内有单原子理想气体,若绝热压缩使其容积减半,问气体分子的平均速率变为原平均速率的几倍?若为双原子理想气体又为几倍?解:气体分子平均速率为对于一定量气体气体绝热压缩时,体积从变为温度从变到,由绝热方程所以对于单原子分子对双原子分子5-15 如图所示,一定量的理想气体,当它的体积为,压强为,有确定的内能。
(1)设它经准静态绝热压缩由到,此时正比于,求此过程中外界所做的功。
(2)气体从状态到状态,也可以通过其他不同的过程,,直线到达,分别计算这些过程外界对气体做题5-15图功和向气体传递的热量。
解:(1)设,则与绝热方程常量,比较得(单原子分子气体)。
气体经绝热压缩从,外界对气体做的功为因为从是绝热压缩的过程,,因而内能增加(2)过程是等压过程,气体对外界做功从是等容过程,气体对外界做功所以过程气体对外界做功外界对气体做功气体吸收热量过程是等容过程,气体对外界做功是等压过程,气体对外界做功所以过程气体对外界做功外界对气体做功气体吸收热量负号表示气体放出热量(3)过程是直线,气体对外界做功外界对气体做功气体吸收热量同样负号表示这一过程中气体向外界释放热量。
