2013浙江省高考考试科目及选拔模式
2013年3月浙江省技术高考试卷

机密★考试结束前2013年3月普通高等学校招生浙江省统一考试技术 试题本试题卷分两部分,即:第一部分通用技术,第二部分信息技术。
全卷共16页,第一部分 1至6页,第二部分7至16页。
满分140分,考试时间90分钟。
答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上. 并按规定用笔将所有试题的答案涂、写在答题纸上。
第一部分 通用技术(共90分)注意事项:1.选择题:每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改 动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
2.非选择题:用黑色字迹的签字笔或钢笔将答案写在答题纸上。
作图时,可先使用2B 铅 笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
不能答在试题卷上。
一、选择題(本大题15小题,每小题3分,共45分。
在每小题给出的四个选项中,只有一个是 符合题目要求的)1.近期全国多地出现雾霾天气,尤其是长三角、珠三角等地区污染特为严重。
对造成这一结果的原因,下列分析不正确...的是 ( ) A.粗放式经济增长和自然生态被破坏 B.企业的高耗能高排放C.机动车保有量快速增长、油品质量不高D.技术发展过快2.如图所示是一款钥匙寻找器。
把钥匙和寻找器串在一起,找钥匙的时候,只需吹响口哨,寻找器就会发出响声。
从人机关系角度分析,以下有关寻找器设计的说法不正确的是 ( ) A.实现了人机关系的信息交互 B.实现了人机关系的安全目标 C.实现了人机关系的高效目标 D.考虑了普通人群和特殊人群的需求3.设计学生用的台灯时要考虑的因素很多,归结起来分别属于“物”、“人”、“环境”三个方面。
以下设计分析中从“物”的角度分析的是( ) A.学生看书的时间较长,光线要柔和 B.根据学生的特点,外形要新颖美观 C.尽可能采用标准件,简化制作 D.应适合在书桌、床头等场合使用第1题图第2题图4.如图所示是按照相同评价标准对电动车使用铅酸电池作出的评价坐标图,根据坐标图,下列说法不正确的是()A.铅酸电池比锂电池质量小B.铅酸电池比锂电池价格低C.锂电池比铅酸电池环保D.该坐标图是对最终产品的评价5.如图所示是某汽车在鹅卵石路面上进行性能试验,这种事试验方式属于()A.优选试验B.虚拟试验C.强化试验D.移植试验6.如图所示的尺寸标注错误的是()A.14的标注B.32的标注C.R5的标注D.R6的标注7钳工操作中一些工具需要配合使用,以下搭配中不合理的是()A.划针与钢直尺B.样冲与扳手C.丝锥与扳手D.锉刀与台虎钳第5题图第6题图8.如图所示的篮球架,仅考虑自重的情况下,下列受力分析中正确的是 ( )A.立柱受压,横梁受弯曲,拉杆受拉B.立柱受扭转,横梁受弯曲,拉杆受拉C.立柱受压,横梁受弯曲,拉杆受压D.立柱受压,横梁受拉,拉杆受压9.在如图所示的秋千椅中,主要是为了保持结构形状稳定的杆件是( ) A .1、2 B .1、4 C .3、4 D .2、310.如图所示为小推车转向轮的轮叉,现用3mm 厚的钢板制作,合理的工艺流程是 ( ) A.划线→锯割→锉削→钻孔→弯折 B.划线→弯折→钻孔→锉削→锯割 C.划线→锉削→锯割→钻孔→弯折 D.锯割→划线→钻孔→锉削→弯折11.某洗衣机洗涤时的控制流程为:正转30秒,停2秒,然后反转30秒,停2秒;如此循环若干次后开始排水,排空后脱水30秒,然后进入清洗流程。
2013年浙江省高考数学试卷(理科)

2013年浙江省高考数学试卷(理科)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知i是虚数单位,则(﹣1+i)(2﹣i)=()A.﹣3+i B.﹣1+3i C.﹣3+3i D.﹣1+i2.(5分)设集合S={x|x>﹣2},T={x|x2+3x﹣4≤0},则(∁R S)∪T=()A.(﹣2,1]B.(﹣∞,﹣4]C.(﹣∞,1]D.[1,+∞)3.(5分)已知x,y为正实数,则()A.2lgx+lgy=2lgx+2lgy B.2lg(x+y)=2lgx•2lgyC.2lgx•lgy=2lgx+2lgy D.2lg(xy)=2lgx•2lgy4.(5分)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ=”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.(5分)某程序框图如图所示,若该程序运行后输出的值是,则()A.a=4 B.a=5 C.a=6 D.a=76.(5分)已知,则tan2α=()A.B.C.D.7.(5分)设△ABC,P0是边AB上一定点,满足,且对于边AB上任一点P,恒有则()A.∠ABC=90°B.∠BAC=90°C.AB=AC D.AC=BC8.(5分)已知e为自然对数的底数,设函数f(x)=(e x﹣1)(x﹣1)k(k=1,2),则()A.当k=1时,f(x)在x=1处取得极小值B.当k=1时,f(x)在x=1处取得极大值C.当k=2时,f(x)在x=1处取得极小值D.当k=2时,f(x)在x=1处取得极大值9.(5分)如图F1、F2是椭圆C1:+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是()A.B.C.D.10.(5分)在空间中,过点A作平面π的垂线,垂足为B,记B=fπ(A).设α,β是两个不同的平面,对空间任意一点P,Q1=fβ[fα(P)],Q2=fα[fβ(P)],恒有PQ1=PQ2,则()A.平面α与平面β垂直B.平面α与平面β所成的(锐)二面角为45°C.平面α与平面β平行D.平面α与平面β所成的(锐)二面角为60°二、填空题:本大题共7小题,每小题4分,共28分.11.(4分)设二项式的展开式中常数项为A,则A=.12.(4分)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于cm3.13.(4分)设z=kx+y,其中实数x,y满足,若z的最大值为12,则实数k=.14.(4分)将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有种(用数字作答)15.(4分)设F为抛物线C:y2=4x的焦点,过点P(﹣1,0)的直线l交抛物线C于两点A,B,点Q为线段AB的中点,若|FQ|=2,则直线l的斜率等于.16.(4分)△ABC中,∠C=90°,M是BC的中点,若,则sin∠BAC=.17.(4分)设、为单位向量,非零向量=x+y,x、y∈R.若、的夹角为30°,则的最大值等于.三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.18.(14分)在公差为d的等差数列{a n}中,已知a1=10,且a1,2a2+2,5a3成等比数列.(Ⅰ)求d,a n;(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|a n|.19.(14分)设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.求ξ分布列;(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若,求a:b:c.20.(15分)如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2.M 是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.(1)证明:PQ∥平面BCD;(2)若二面角C﹣BM﹣D的大小为60°,求∠BDC的大小.21.(15分)如图,点P(0,﹣1)是椭圆C1:+=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.(1)求椭圆C1的方程;(2)求△ABD面积的最大值时直线l1的方程.22.(14分)已知a∈R,函数f(x)=x3﹣3x2+3ax﹣3a+3.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)当x∈[0,2]时,求|f(x)|的最大值.2013年浙江省高考数学试卷(理科)参考答案与试题解析一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知i是虚数单位,则(﹣1+i)(2﹣i)=()A.﹣3+i B.﹣1+3i C.﹣3+3i D.﹣1+i【分析】直接利用两个复数代数形式的乘法法则,以及虚数单位i的幂运算性质,运算求得结果.【解答】解:(﹣1+i)(2﹣i)=﹣2+i+2i+1=﹣1+3i,故选:B.【点评】本题主要考查两个复数代数形式的乘法,虚数单位i的幂运算性质,属于基础题.2.(5分)设集合S={x|x>﹣2},T={x|x2+3x﹣4≤0},则(∁R S)∪T=()A.(﹣2,1]B.(﹣∞,﹣4]C.(﹣∞,1]D.[1,+∞)【分析】先根据一元二次不等式求出集合T,然后求得∁R S,再利用并集的定义求出结果.【解答】解:∵集合S={x|x>﹣2},∴∁R S={x|x≤﹣2},T={x|x2+3x﹣4≤0}={x|﹣4≤x≤1},故(∁R S)∪T={x|x≤1}故选:C.【点评】此题属于以一元二次不等式的解法为平台,考查了补集及并集的运算,是高考中常考的题型.在求补集时注意全集的范围.3.(5分)已知x,y为正实数,则()A.2lgx+lgy=2lgx+2lgy B.2lg(x+y)=2lgx•2lgyC.2lgx•lgy=2lgx+2lgy D.2lg(xy)=2lgx•2lgy【分析】直接利用指数与对数的运算性质,判断选项即可.【解答】解:因为a s+t=a s•a t,lg(xy)=lgx+lgy(x,y为正实数),所以2lg(xy)=2lgx+lgy=2lgx•2lgy,满足上述两个公式,故选:D.【点评】本题考查指数与对数的运算性质,基本知识的考查.4.(5分)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ=”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【分析】φ=⇒f(x)=Acos(ωx+)⇒f(x)=﹣Asin(ωx)(A>0,ω>0,x ∈R)是奇函数.f(x)为奇函数⇒f(0)=0⇒φ=kπ+,k∈Z.所以“f(x)是奇函数”是“φ=”必要不充分条件.【解答】解:若φ=,则f(x)=Acos(ωx+)⇒f(x)=﹣Asin(ωx)(A>0,ω>0,x∈R)是奇函数;若f(x)是奇函数,⇒f(0)=0,∴f(0)=Acos(ω×0+φ)=Acosφ=0.∴φ=kπ+,k∈Z,不一定有φ=“f(x)是奇函数”是“φ=”必要不充分条件.故选:B.【点评】本题考查充分条件、必要条件和充要条件的判断,解题时要认真审题,仔细解答,注意三角函数性质的灵活运用.5.(5分)某程序框图如图所示,若该程序运行后输出的值是,则()A.a=4 B.a=5 C.a=6 D.a=7【分析】根据已知流程图可得程序的功能是计算S=1++…+的值,利用裂项相消法易得答案.【解答】解:由已知可得该程序的功能是计算并输出S=1++…+=1+1﹣=2﹣.若该程序运行后输出的值是,则2﹣=.∴a=4,故选:A.【点评】本题考查的知识点是程序框图,其中分析出程序的功能是解答的关键.6.(5分)已知,则tan2α=()A.B.C.D.【分析】由题意结合sin2α+cos2α=1可解得sinα,和cosα,进而可得tanα,再代入二倍角的正切公式可得答案.【解答】解:∵,又sin2α+cos2α=1,联立解得,或故tanα==,或tanα=3,代入可得tan2α===﹣,或tan2α===故选:C.【点评】本题考查二倍角的正切公式,涉及同角三角函数的基本关系,属中档题.7.(5分)设△ABC,P0是边AB上一定点,满足,且对于边AB上任一点P,恒有则()A.∠ABC=90°B.∠BAC=90°C.AB=AC D.AC=BC【分析】设||=4,则||=1,过点C作AB的垂线,垂足为H,在AB上任取一点P,设HP0=a,则由数量积的几何意义可得||2﹣(a+1)||+a≥0恒成立,只需△=(a+1)2﹣4a=(a﹣1)2≤0即可,由此能求出△ABC是等腰三角形,AC=BC.【解答】解:设||=4,则||=1,过点C作AB的垂线,垂足为H,在AB上任取一点P,设HP0=a,则由数量积的几何意义可得,=||•||=||2﹣(a+1)||,•=﹣a,于是•≥••恒成立,整理得||2﹣(a+1)||+a≥0恒成立,只需△=(a+1)2﹣4a=(a﹣1)2≤0即可,于是a=1,因此我们得到HB=2,即H是AB的中点,故△ABC是等腰三角形,所以AC=BC.故选:D.【点评】本题主要考查了平面向量的运算,向量的模及向量的数量积的概念,向量运算的几何意义的应用,还考查了利用向量解决简单的几何问题的能力8.(5分)已知e为自然对数的底数,设函数f(x)=(e x﹣1)(x﹣1)k(k=1,2),则()A.当k=1时,f(x)在x=1处取得极小值B.当k=1时,f(x)在x=1处取得极大值C.当k=2时,f(x)在x=1处取得极小值D.当k=2时,f(x)在x=1处取得极大值【分析】通过对函数f(x)求导,根据选项知函数在x=1处有极值,验证f'(1)=0,再验证f(x)在x=1处取得极小值还是极大值即可得结论.【解答】解:当k=1时,函数f(x)=(e x﹣1)(x﹣1).求导函数可得f'(x)=e x(x﹣1)+(e x﹣1)=(xe x﹣1),f'(1)=e﹣1≠0,f'(2)=2e2﹣1≠0,则f(x)在在x=1处与在x=2处均取不到极值,当k=2时,函数f(x)=(e x﹣1)(x﹣1)2.求导函数可得f'(x)=e x(x﹣1)2+2(e x﹣1)(x﹣1)=(x﹣1)(xe x+e x﹣2),∴当x=1,f'(x)=0,且当x>1时,f'(x)>0,当x0<x<1时(x0为极大值点),f'(x)<0,故函数f(x)在(1,+∞)上是增函数;在(x0,1)上是减函数,从而函数f(x)在x=1取得极小值.对照选项.故选:C.【点评】本题考查了函数的极值问题,考查学生的计算能力,正确理解极值是关键.9.(5分)如图F1、F2是椭圆C1:+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是()A.B.C.D.【分析】不妨设|AF1|=x,|AF2|=y,依题意,解此方程组可求得x,y 的值,利用双曲线的定义及性质即可求得C2的离心率.【解答】解:设|AF1|=x,|AF2|=y,∵点A为椭圆C1:+y2=1上的点,∴2a=4,b=1,c=;∴|AF1|+|AF2|=2a=4,即x+y=4;①又四边形AF1BF2为矩形,∴+=,即x2+y2=(2c)2==12,②由①②得:,解得x=2﹣,y=2+,设双曲线C2的实轴长为2m,焦距为2n,则2m=|AF2|﹣|AF1|=y﹣x=2,2n=2c=2,∴双曲线C2的离心率e===.故选:D.【点评】本题考查椭圆与双曲线的简单性质,求得|AF1|与|AF2|是关键,考查分析与运算能力,属于中档题.10.(5分)在空间中,过点A作平面π的垂线,垂足为B,记B=fπ(A).设α,β是两个不同的平面,对空间任意一点P,Q1=fβ[fα(P)],Q2=fα[fβ(P)],恒有PQ1=PQ2,则()A.平面α与平面β垂直B.平面α与平面β所成的(锐)二面角为45°C.平面α与平面β平行D.平面α与平面β所成的(锐)二面角为60°【分析】设P1是点P在α内的射影,点P2是点P在β内的射影.根据题意点P1在β内的射影与P2在α内的射影重合于一点,由此可得四边形PP1Q1P2为矩形,且∠P1Q1P2是二面角α﹣l﹣β的平面角,根据面面垂直的定义可得平面α与平面β垂直,得到本题答案.【解答】解:设P1=fα(P),则根据题意,得点P1是过点P作平面α垂线的垂足∵Q1=fβ[fα(P)]=fβ(P1),∴点Q1是过点P1作平面β垂线的垂足同理,若P2=fβ(P),得点P2是过点P作平面β垂线的垂足因此Q2=fα[fβ(P)]表示点Q2是过点P2作平面α垂线的垂足∵对任意的点P,恒有PQ1=PQ2,∴点Q1与Q2重合于同一点由此可得,四边形PP1Q1P2为矩形,且∠P1Q1P2是二面角α﹣l﹣β的平面角∵∠P1Q1P2是直角,∴平面α与平面β垂直故选:A.【点评】本题给出新定义,要求我们判定平面α与平面β所成角大小,着重考查了线面垂直性质、二面角的平面角和面面垂直的定义等知识,属于中档题.二、填空题:本大题共7小题,每小题4分,共28分.11.(4分)设二项式的展开式中常数项为A,则A=﹣10.【分析】先求出二项式展开式的通项公式,再令x的系数等于0,求得r的值,即可求得展开式中的常数项的值.=••(﹣1)【解答】解:二项式的展开式的通项公式为T r+1r•=(﹣1)r••.令=0,解得r=3,故展开式的常数项为﹣=﹣10,故答案为﹣10.【点评】本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.12.(4分)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于24cm3.【分析】先根据三视图判断几何体的形状,再利用体积公式计算即可.【解答】解:几何体为三棱柱去掉一个三棱锥后的几何体,底面是直角三角形,直角边分别为3,4,侧面的高为5,被截取的棱锥的高为3.如图:V=V棱柱﹣V棱锥==24(cm3)故答案为:24.【点评】本题考查几何体的三视图及几何体的体积计算.V椎体=Sh,V柱体=Sh.考查空间想象能力.13.(4分)设z=kx+y,其中实数x,y满足,若z的最大值为12,则实数k=2.【分析】先画出可行域,得到角点坐标.再对k进行分类讨论,通过平移直线z=kx+y 得到最大值点A,即可得到答案.【解答】解:可行域如图:由得:A(4,4),同样地,得B(0,2),z=kx+y,即y=﹣kx+z,分k>0,k<0两种情况.当k>0时,目标函数z=kx+y在A点取最大值,即直线z=kx+y在y轴上的截距z最大,即12=4k+4,得k=2;当k<0时,①当k>﹣时,目标函数z=kx+y在A点(4,4)时取最大值,即直线z=kx+y 在y轴上的截距z最大,此时,12=4k+4,故k=2.②当k时,目标函数z=kx+y在B点(0,2)时取最大值,即直线z=kx+y在y轴上的截距z最大,此时,12=0×k+2,故k不存在.综上,k=2.故答案为:2.【点评】本题主要考查简单线性规划.解决此类问题的关键是正确画出不等式组表示的可行域,将目标函数赋予几何意义.14.(4分)将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有480种(用数字作答)【分析】按C的位置分类,在左1,左2,左3,或者在右1,右2,右3,因为左右是对称的,所以只看左的情况最后乘以2即可.【解答】解:按C的位置分类,在左1,左2,左3,或者在右1,右2,右3,因为左右是对称的,所以只看左的情况最后乘以2即可.当C在左边第1个位置时,有A,当C在左边第2个位置时,A和B有C右边的4个位置可以选,有A A,当C在左边第3个位置时,有A A+A A,共为240种,乘以2,得480.则不同的排法共有480种.故答案为:480.【点评】本题考查排列、组合的应用,关键在于明确事件之间的关系,同时要掌握分类讨论的处理方法.15.(4分)设F为抛物线C:y2=4x的焦点,过点P(﹣1,0)的直线l交抛物线C于两点A,B,点Q为线段AB的中点,若|FQ|=2,则直线l的斜率等于不存在.【分析】由题意设直线l的方程为my=x+1,联立得到y2﹣4my+4=0,△=16m2﹣16=16(m2﹣1)>0.设A(x1,y1),B(x2,y2),Q(x0,y0).利用根与系数的关系可得y1+y2=4m,利用中点坐标公式可得=2m,x0=my0﹣1=2m2﹣1.Q(2m2﹣1,2m),由抛物线C:y2=4x得焦点F(1,0).再利用两点间的距离公式即可得出m及k,再代入△判断是否成立即可.【解答】解:由题意设直线l的方程为my=x+1,联立得到y2﹣4my+4=0,△=16m2﹣16=16(m2﹣1)>0.设A(x1,y1),B(x2,y2),Q(x0,y0).∴y1+y2=4m,∴=2m,∴x0=my0﹣1=2m2﹣1.∴Q(2m2﹣1,2m),由抛物线C:y2=4x得焦点F(1,0).∵|QF|=2,∴,化为m2=1,解得m=±1,不满足△>0.故满足条件的直线l不存在.故答案为不存在.【点评】本题综合考查了直线与抛物线的位置关系与△的关系、根与系数的关系、中点坐标关系、两点间的距离公式等基础知识,考查了推理能力和计算能力.16.(4分)△ABC中,∠C=90°,M是BC的中点,若,则sin∠BAC=.【分析】作出图象,设出未知量,在△ABM中,由正弦定理可得sin∠AMB=,进而可得cosβ=,在RT△ACM中,还可得cosβ=,建立等式后可得a=b,再由勾股定理可得c=,而sin∠BAC═=,代入化简可得答案.【解答】解:如图设AC=b,AB=c,CM=MB=,∠MAC=β,在△ABM中,由正弦定理可得=,代入数据可得=,解得sin∠AMB=,故cosβ=cos(﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB=,而在RT△ACM中,cosβ==,故可得=,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,解之可得a=b,再由勾股定理可得a2+b2=c2,联立可得c=,故在RT△ABC中,sin∠BAC====,另解:设∠BAM为α,∠MAC为β,正弦定理得BM:sinα=AM:sin∠BBM:sinβ=AM又有sinβ=cos∠AMC=cos(α+∠B),联立消去BM,AM得sin∠Bcos(α+∠B)=sinα,拆开,将1化成sin2∠B+cos2∠B,构造二次齐次式,同除cos2∠B,可得tanα=,若,则cos∠BAM=,tan∠BAM=,解得tan∠B=,cosB=易得sin∠BAC=.另解:作MD⊥AB交于D,设MD=1,AM=3,AD=2,DB=x,BM=CM=,用△DMB和△CAB相似解得x=,则cosB=,易得sin∠BAC=.故答案为:【点评】本题考查正弦定理的应用,涉及三角函数的诱导公式以及勾股定理的应用,属难题.17.(4分)设、为单位向量,非零向量=x+y,x、y∈R.若、的夹角为30°,则的最大值等于2.【分析】由题意求得=,||==,从而可得===,再利用二次函数的性质求得的最大值.【解答】解:∵、为单位向量,和的夹角等于30°,∴=1×1×cos30°=.∵非零向量=x+y,∴||===,∴====,故当=﹣时,取得最大值为2,故答案为2.【点评】本题主要考查两个向量的数量积的运算,求向量的模,利用二次函数的性质求函数的最大值,属于中档题.三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.18.(14分)在公差为d的等差数列{a n}中,已知a1=10,且a1,2a2+2,5a3成等比数列.(Ⅰ)求d,a n;(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|a n|.【分析】(Ⅰ)直接由已知条件a1=10,且a1,2a2+2,5a3成等比数列列式求出公差,则通项公式a n可求;(Ⅱ)利用(Ⅰ)中的结论,得到等差数列{a n}的前11项大于等于0,后面的项小于0,所以分类讨论求d<0时|a1|+|a2|+|a3|+…+|a n|的和.【解答】解:(Ⅰ)由题意得,即,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.当d=﹣1时,a n=a1+(n﹣1)d=10﹣(n﹣1)=﹣n+11.当d=4时,a n=a1+(n﹣1)d=10+4(n﹣1)=4n+6.所以a n=﹣n+11或a n=4n+6;(Ⅱ)设数列{a n}的前n项和为S n,因为d<0,由(Ⅰ)得d=﹣1,a n=﹣n+11.则当n≤11时,.当n≥12时,|a1|+|a2|+|a3|+…+|a n|=﹣S n+2S11=.综上所述,|a1|+|a2|+|a3|+…+|a n|=.【点评】本题考查了等差数列、等比数列的基本概念,考查了等差数列的通项公式,求和公式,考查了分类讨论的数学思想方法和学生的运算能力,是中档题.19.(14分)设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.求ξ分布列;(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若,求a:b:c.【分析】(1)ξ的可能取值有:2,3,4,5,6,求出相应的概率可得所求ξ的分布列;(2)先列出η的分布列,再利用η的数学期望和方差公式,即可得到结论.【解答】解:(1)由题意得ξ=2,3,4,5,6,P(ξ=2)==;P(ξ=3)==;P(ξ=4)==;P(ξ=5)==;P(ξ=6)==.故所求ξ的分布列为ξ23456P(2)由题意知η的分布列为η123PEη==Dη=(1﹣)2+(2﹣)2+(3﹣)2=.得,解得a=3c,b=2c,故a:b:c=3:2:1.【点评】本题主要考查随机事件的概率和随机变量的分布列、数学期望等概念,同时考查抽象概括、运算能力,属于中档题.20.(15分)如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2.M 是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.(1)证明:PQ∥平面BCD;(2)若二面角C﹣BM﹣D的大小为60°,求∠BDC的大小.【分析】(1)取BD的中点O,在线段CD上取点F,使得DF=3CF,连接OP、OF、FQ.根据平行线分线段成比例定理结合三角形的中位线定理证出四边形OPQF是平行四边形,从而PQ∥OF,再由线面平行判定定理,证出PQ∥平面BCD;(2)过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH.根据线面垂直的判定与性质证出BM⊥CH,因此∠CHG是二面角C﹣BM﹣D的平面角,可得∠CHG=60°.设∠BDC=θ,用解直角三角形的方法算出HG和CG关于θ的表达式,最后在Rt△CHG中,根据正切的定义得出tan∠CHG==,从而得到tanθ=,由此可得∠BDC.【解答】(1)取BD的中点O,在线段CD上取点F,使得DF=3CF,连接OP、OF、FQ∵△ACD中,AQ=3QC且DF=3CF,∴QF∥AD且QF=AD∵△BDM中,O、P分别为BD、BM的中点∴OP∥DM,且OP=DM,结合M为AD中点得:OP∥AD且OP=AD∴OP∥QF且OP=QF,可得四边形OPQF是平行四边形∴PQ∥OF∵PQ⊄平面BCD且OF⊂平面BCD,∴PQ∥平面BCD;(2)过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH∵AD⊥平面BCD,CG⊂平面BCD,∴AD⊥CG又∵CG⊥BD,AD、BD是平面ABD内的相交直线∴CG⊥平面ABD,结合BM⊂平面ABD,得CG⊥BM∵GH⊥BM,CG、GH是平面CGH内的相交直线∴BM⊥平面CGH,可得BM⊥CH因此,∠CHG是二面角C﹣BM﹣D的平面角,可得∠CHG=60°设∠BDC=θ,可得Rt△BCD中,CD=BDcosθ=2cosθ,CG=CDsinθ=sinθcosθ,BG=BCsinθ=2sin2θRt△BMD中,HG==;Rt△CHG中,tan∠CHG==∴tanθ=,可得θ=60°,即∠BDC=60°【点评】本题在底面为直角三角形且过锐角顶点的侧棱与底面垂直的三棱锥中求证线面平行,并且在已知二面角大小的情况下求线线角.着重考查了线面平行、线面垂直的判定与性质,解直角三角形和平面与平面所成角求法等知识,属于中档题.21.(15分)如图,点P(0,﹣1)是椭圆C1:+=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.(1)求椭圆C1的方程;(2)求△ABD面积的最大值时直线l1的方程.【分析】(1)由题意可得b=1,2a=4,即可得到椭圆的方程;(2)设A(x1,y1),B(x2,y2),D(x0,y0).由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx﹣1.利用点到直线的距离公式和弦长公式即可得出圆心O到直线l1的距离和弦长|AB|,又l2⊥l1,可得直线l2的方程为x+kx+k=0,与椭圆的方程联立即可得到点D的横坐标,即可得出|PD|,即可得到三角形ABD 的面积,利用基本不等式的性质即可得出其最大值,即得到k的值.【解答】解:(1)由题意可得b=1,2a=4,即a=2.∴椭圆C1的方程为;(2)设A(x1,y1),B(x2,y2),D(x0,y0).由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx﹣1.又圆的圆心O(0,0)到直线l1的距离d=.∴|AB|==.又l2⊥l1,故直线l2的方程为x+ky+k=0,联立,消去y得到(4+k2)x2+8kx=0,解得,∴|PD|=.==,∴三角形ABD的面积S△令4+k2=t>4,则k2=t﹣4,f(t)===,=,当且仅,即,当时取等号,∴S△故所求直线l1的方程为.【点评】本题主要考查了椭圆的几何性质、直线与圆及椭圆的位置关系等基础知识,同时考查了推理能力和计算能力及分析问题和解决问题的能力.22.(14分)已知a∈R,函数f(x)=x3﹣3x2+3ax﹣3a+3.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)当x∈[0,2]时,求|f(x)|的最大值.【分析】(1)求出原函数的导函数,求出函数取x=1时的导数值及f(1),由直线方程的点斜式写出切线方程;(2)求出原函数的导函数,分a≤0,0<a<1,a≥1三种情况求|f(x)|的最大值.特别当0<a<1时,仍需要利用导数求函数在区间(0,2)上的极值,然后在根据a的范围分析区间端点值与极值绝对值的大小.【解答】解:(1)因为f(x)=x3﹣3x2+3ax﹣3a+3,所以f′(x)=3x2﹣6x+3a,故f′(1)=3a﹣3,又f(1)=1,所以所求的切线方程为y=(3a﹣3)x﹣3a+4;(2)由于f′(x)=3(x﹣1)2+3(a﹣1),0≤x≤2.故当a≤0时,有f′(x)≤0,此时f(x)在[0,2]上单调递减,故|f(x)|max=max{|f(0)|,|f(2)|}=3﹣3a.当a≥1时,有f′(x)≥0,此时f(x)在[0,2]上单调递增,故|f(x)|max=max{|f(0)|,|f(2)|}=3a﹣1.当0<a<1时,由3(x﹣1)2+3(a﹣1)=0,得,.所以,当x∈(0,x1)时,f′(x)>0,函数f(x)单调递增;当x∈(x1,x2)时,f′(x)<0,函数f(x)单调递减;当x∈(x2,2)时,f′(x)>0,函数f(x)单调递增.所以函数f(x)的极大值,极小值.故f(x1)+f(x2)=2>0,.从而f(x1)>|f(x2)|.所以|f(x)|max=max{f(0),|f(2)|,f(x1)}.当0<a<时,f(0)>|f(2)|.又=故.当时,|f(2)|=f(2),且f(2)≥f(0).又=.所以当时,f(x1)>|f(2)|.故.当时,f(x1)≤|f(2)|.故f(x)max=|f(2)|=3a﹣1.综上所述|f(x)|max=.【点评】本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数求闭区间上的最值,考查了分类讨论的数学思想方法,正确的分类是解答(2)的关键,此题属于难题.。
在浙招生普通高校专业 选考科目要求

在浙招生普通高校专业选考科目要求
浙江省普通高校招生选考科目要求,是指在高考报名时需选择的文理
科目及其对应的考试科目。
根据浙江省教育考试院最新公布的要求,浙江
省普通高校招生选考科目共分为以下几个方面:
一、文科专业
文科专业包括文史类、法学类、经济管理类、教育类、新闻传播类等。
在选考科目要求上,文科类专业要求参加文化统考,即语文、数学、外语
三门科目,其中数学为选考科目,要求须选择数学(文)考试。
此外,在
报考文科类专业时,还需选择一门文化专业课,可以选择历史、地理、政
治等相关科目,其中历史为必选。
二、理科专业
理科专业包括工科类、理科类、农林类等。
在选考科目要求上,理科
类专业参加文化统考,即语文、数学、外语三门科目,其中数学为必考科目,选择数学(理)考试。
此外,在报考理科类专业时,还需选择一门文
化专业课,可以选择物理、化学、生物等相关科目。
三、艺术类专业
艺术类专业包括音乐、美术等相关专业。
在选考科目要求上,艺术类
专业需要参加文化统考,即语文、数学、外语三门科目。
此外,还要参加
专业技能考试,根据所选专业的不同,技能考试内容也有所不同。
总体来说,浙江省普通高校招生选考科目要求是十分清晰明确的。
在
报考之前,考生必须仔细阅读官方要求,选择正确的科目,不仅能提高报
考成功率,还能为未来的大学学习打下更加坚实的基础。
浙江卷2013年高考试题及答案

2013年高考试题(浙江卷)一、语言文字运用(共24分,其中选择题每小题3分)1.下列词语中加点的字,注音全都正确的一项是()A. 漩(xuán)涡按捺(nài)饯别(jiàn)稍纵即(jí)逝B. 桑梓(zǐ)鬈(quán)发昭(zhāo)示图穷匕(bǐ)见C. 混(hùn)淆盘桓(huán)喷(pèn)香力能扛(káng)鼎D. 潜(qián)伏佝偻(lóu)拙(zhuó)劣戛(jiá)然而止2.下列各句中,没有错别字的一项是() A.辩论双方唇枪舌箭,针锋相对,相持不下,后来正方二辩出其不意地抛出三个论据,令反方措手不及,只好甘拜下风。
B.这位专家关于城镇化建设要防止落入“五大陷井”的说法得到了与会人员的认同,不少人对他的真知灼见竖起了大拇指。
C.在“中国情结”绘画大奖赛中,作品《瑞雪兆丰年》创造性地融入了民族文化元素,让人产生强烈的共鸣,最终拔得头筹。
D.初次登陆电子邮箱、微博或使用银行卡、会员卡时都须输入密码,而不同的密码容易混淆,这给人们平添了许多烦恼。
3.下列各句中,加点的词语运用正确的一项是() A.倒金字塔型的“421”家庭结构使得居家养老陷入困境,社会养老服务体系又不够完善,以至中国养老问题日趋严重。
B.有人多次为芦山灾民慷慨解囊,倾尽全部积蓄,也有人声明自己将细大不捐,以抗议某些慈善机构运作缺乏透明度。
C.面对河水严重污染的现状,大学生自愿组成暑期社会实践小分队,满怀热诚地进行生态环境调查,积极宣传环保理念。
D.随着出版业的市场化和多元化,类型多样、题材丰富的作品大量涌现,其中也有一些作品粗制滥造,令人不忍卒读。
4.下列各句中,没有语病的一项是()A.这部由第六代导演执导的青春片带有鲜明的时代印记,表现了主人公拒绝平庸、坚守梦想的成长故事,具有极强的感染力,深深地打动了观众。
2013年全国高考英语试题及答案-浙江卷

英语试题(选择题部分)第一部分:英语知识运用(共两节,满分30分)第一节:单项填空(共20题,每小题0.5分,满分10分)从A、B、C和D四个选项中,选出可以填入空白处的最佳选项,并在答题纸将该选项标号涂黑。
1.——Hey, can I ask you a favor?====_______A.Here you areB.just as I thoughtC.how is it going?D.what can I do for you?2.Mary worked here as a ____-secretary and ended up getting a full-time job with the company.A.pessimisticB.temporaryC.previousD.cautious3.I______myself more-----it was a perfect day.A.should n’t have enjoyedB.need n’t hav e enjoyedC.would n’t have enjoyedD.could n’t have enjoyed4.As the world’s population continues to grow, the ___of food becomes more and more of a concern.A.worthB.supplyC.packageD.list5.The children,____had played the whole day long, were worn out.A.all of whatB.all of whichC.all of themD.all of whom6.If we leave right away,____we’ll arrive on time.A.hopefullyB.curiouslyC.occasionallyD.gradually7.______how others react to the book you have just read creates an added pleasure.A.HearingB.HearC.Having heardD.To be hearing8.Eye doctors recommend that a child’s first eye exam____at the age of six months old.A.wasB.beC.wereD.is9.When the group discussion is nearing its end, make sure to ____it with important points.A.concludeB.leadC.avoidD.hold10.During the last three decades, the number of people participating in physical fitness programs___sharply.A.was increasingB.has increasedC.had increasedD.will be increasing11.Half of _____surveyed in 16 countries say they go first to their closest friend to share their deepest wishes and darkest fears.A.these B,.some C.ones D. those12.A good listener takes part in the conversation,____ideas and raising questions to keep the talk flowing.A.realizingB.copyingC.offeringD.misunderstanding13.The museum will open in the spring with an exhibition and a viewing platform____visitors can watch the big glasshouses being built.A.whatB.whereC.whenD.why14.It will be a big help if you go to the store and get what we need for dinner._____,I’ll set the table.A.As a resultB.On the wholeC.In the meanwhileD.As a matter of fact15.People develop______preference for a particular style of learning at______early age and these preferences affect learning.A.a; anB.a;不填C.不填;theD.the ;an16.The only way to succeed at the highest level is to have total belief_____you are better than anyone else on the sports field.A.how B,that C.which D.whether17.Bears_____fat stores throughout the summer and fall to have energy enough to last them through their winter sleep.A.pack upB.build upC.bring upD.take up18.If what your friend comes up with surprise you ,don’t reject it immediately._____,imagine that it i s true.A/Thus B.Besides C.Rather D.Otherwise19.There are some health problems that, when ____in time, can become bagger ones later on.A.not treated B,not being treated C.not to be treated D.not having been treated20.-----Excuse me, but could I trouble you for some change?------_______.Will pennies do?A.I knowB.Never mindC.I am sureD.Let me see第二节完型填空(共20小题,每小题1分,满分20分)阅读下面短文,掌握其大意,然后从21到40各题所给的4个选项A,B,C和D中选出最佳选项,并在答题纸上将该选项标号涂黑。
2013年高考理科数学浙江卷试题及答案解析
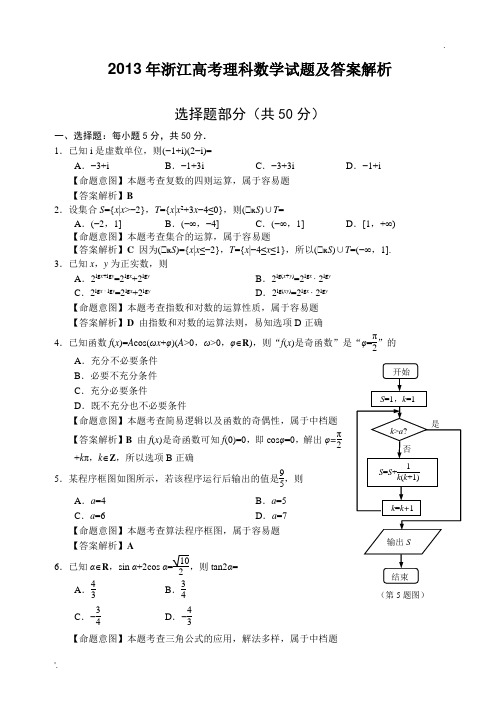
2013年浙江高考理科数学试题及答案解析选择题部分(共50分)一、选择题:每小题5分,共50分. 1.已知i 是虚数单位,则(−1+i)(2−i)=A .−3+iB .−1+3iC .−3+3iD .−1+i【命题意图】本题考查复数的四则运算,属于容易题【答案解析】B2.设集合S ={x |x >−2},T ={x |x 2+3x −4≤0},则( R S )∪T =A .(−2,1]B .(−∞,−4]C .(−∞,1]D .[1,+∞) 【命题意图】本题考查集合的运算,属于容易题【答案解析】C 因为( R S )={x |x ≤−2},T ={x |−4≤x ≤1},所以( R S )∪T =(−∞,1]. 3.已知x ,y 为正实数,则A .2lg x +lg y =2lg x +2lg yB .2lg(x +y )=2lg x ∙ 2lg yC .2lg x ∙ lg y =2lg x +2lg yD .2lg(xy )=2lg x ∙ 2lg y【命题意图】本题考查指数和对数的运算性质,属于容易题 【答案解析】D 由指数和对数的运算法则,易知选项D 正确4.已知函数f (x )=A cos(ωx +φ)(A >0,ω>0,φ∈R ),则“f (x )是奇函数”是“φ=π2”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【命题意图】本题考查简易逻辑以及函数的奇偶性,属于中档题【答案解析】B 由f (x )是奇函数可知f (0)=0,即cos φ=0,解出φ=π2+k π,k ∈Z ,所以选项B 正确5.某程序框图如图所示,若该程序运行后输出的值是95,则A .a =4B .a =5C .a =6D .a =7【命题意图】本题考查算法程序框图,属于容易题【答案解析】A 6.已知α∈R ,sin α+2cos α=102,则tan2α= A .43B .34C .−34D .−43【命题意图】本题考查三角公式的应用,解法多样,属于中档题(第5题图)【答案解析】C 由(sin α+2cos α)2=⎝⎛⎭⎫1022可得sin 2α+4cos 2α+4sin αcos α sin 2α+cos 2α=104,进一步整理可得3tan 2α−8tan α−3=0,解得tan α=3或tan α=−13,于是tan2α=2tan α1−tan 2α=−34.7.设△ABC ,P 0是边AB 上一定点,满足P 0B =14AB ,且对于AB 上任一点P ,恒有→PB ∙→PC ≥→P 0B∙→P 0C ,则A .∠ABC =90︒B .∠BAC =90︒ C .AB =ACD .AC =BC 【命题意图】本题考查向量数量积的几何意义,不等式恒成立的有关知识,属于中档题【答案解析】D 由题意,设|→AB |=4,则|→P 0B |=1,过点C 作AB 的垂线,垂足为H ,在AB 上任取一点P ,设HP 0=a ,则由数量积的几何意义可得,→PB ∙→PC =|→PH ||→PB |=(|→PB |−(a +1))|→PB |,→P 0B ∙→P 0C =−|→P 0H ||→P 0B |=−a ,于是→PB ∙→PC ≥→P 0B ∙→P 0C恒成立,相当于(|→PB |−(a +1))|→PB |≥−a 恒成立,整理得|→PB|2−(a +1)|→PB |+a ≥0恒成立,只需∆=(a +1)2−4a =(a −1)2≤0即可,于是a =1,因此我们得到HB =2,即H 是AB 的中点,故△ABC 是等腰三角形,所以AC =BC 8.已知e 为自然对数的底数,设函数f (x )=(e x −1)(x −1)k (k =1,2),则 A .当k =1时,f (x )在x =1处取到极小值 B .当k =1时,f (x )在x =1处取到极大值C .当k =2时,f (x )在x =1处取到极小值D .当k =2时,f (x )在x =1处取到极大值 【命题意图】本题考查极值的概念,属于中档题【答案解析】C 当k =1时,方程f (x )=0有两个解,x 1=0,x 2=1,由标根法可得f (x )的大致图象,于是选项A ,B 错误;当k =2时,方程f (x )=0有三个解,x 1=0,x 2=x 3=1,其中1是二重根,由标根法可得f (x )的大致图象,易知选项C 正确。
2013浙江高考英语试题及答案

2013年普通高等学校招生全国统一考试(浙江卷)英语第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A, B, C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题,每段对话仅读一遍。
1. When can the man see the headmaster?A. At 9:30.B. At 11:45.C. At 12:40.2. Why does the man want to keep the window shut?A. He is ill.B. He wants to open it himself.C. The air inside is fresh enough.3. What is Mike?A. A teacher.B. A student.C. A writer.4. What has made working at home possible?A. Progress on communication industryB. Communication industry.C. Living far from companies.5. Where is the woman?A. In a soap factory.B. In her house.C. At an in formation desk.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话,每段对话后有几个小题,从题中所给的A, B, C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话前,你将有时间阅读各个小题,每小题5秒钟;各小题给出5秒钟的作答时间。
每段对话读两遍。
听第6段材料,回答第6、7题6. Where does the conversation most probably take place?A. At home.B. On a bus.C. In the bank.7. Why do the two speakers want to buy a car?A. They have a lot of money.B. The man lives too far away from his office.C. The woman's office is too far away from her home.听第7段材料,回答第8至9题8. Why won't Mr. Stone come to the clinic tomorrow?A. He can't spare the time.B. The clinic will be closed.C. Dr. Milton won't come to work.9. When is the clinic open in a week?A. From Monday to Friday.B. On weekdays except Thursday.C. During the whole week.10. What time has finally been fixed for Mr. Stone to come?A. 5:30 p. m., Wednesday.B. 6:15 p. m., Wednesday.C. 6:15 p. m., Thursday.听第8段材料,回答第11至13题11. What's the relationship between the two speakers?A. Neighbors.B. Doctor and patient.C. Friends.12. When did the woman cough most seriously?A. In the morning.B. In the afternoon.C. At night.13. What did the man do for the woman?A. He examined the woman carefully.B. He gave her some medicine and some advice as well.C. He just told her not to worry too much.听第9段材料,回答第14至16题14. What's the possible relationship between the two speakers?A. Friends.B. Husband and wife.C. Strangers.15. Where does the conversation most probably take place?A. At the woman’s home.B. In a restaurant.C. At the man's home.16. What does the woman ask the man to do?A. Have some soup.B. Have more rice.C. Bring his wife next time.听第10段材料,回答第17至20题17. What did Nicholas do at eighteen months?A. He began to learn French.B. He read the newspaper.C. He took telephone messages.18. Why was Nicholas bored and unhappy at the two schools?A. He had too much homework.B. He almost couldn't learn anything special.C. His teachers often corrected his spelling.19. Who offered to help Nicholas finally?A. His classmates.B. His parents.C. A college.20. What is Nicholas' life like now?A. Busy without any social life.B. Full but boring.C. Busy at college and free at home.第二部分英语知识运用(共两节,满分45分)第一节单项填空(共15小题;每小题1分,满分15分)从A, B, C, D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
2013年 浙江省 高考物理 试卷及解析

2013年浙江省高考物理试卷一、解答题1.(3分)关于生活中遇到的各种波,下列说法正确的是()A.电磁波可以传递信息,声波不能传递信息B.手机在通话时涉及的波既有电磁波又有声波C.太阳光中的可见光和医院“B超”中的超声波传递速度相同D.遥控器发出的红外线波长和医院CT中的X射线波长相同2.(3分)磁卡的词条中有用于存储信息的磁极方向不同的磁化区,刷卡器中有检测线圈,当以速度v0刷卡时,在线圈中产生感应电动势。
其E﹣t关系如图所)示。
如果只将刷卡速度改为,线圈中的E﹣t关系可能是(D .3.(3分)与通常观察到的月全食不同,小虎同学在2012年12月10日晚观看1月全食时,看到整个月亮是暗红的.小虎画了月全食的示意图,并提出了如下猜想,其中最为合理的是()A.地球上有人用红色激光照射月球B.太阳照射到地球的红光反射到月球C.太阳光中的红光经地球大气层折射到月球D.太阳光中的红光在月球表面形成干涉条纹4.(3分)如图所示,水平板上有质量m=1.0kg的物块,受到随时间t变化的水平拉力F作用,用力传感器测出相应时刻物块所受摩擦力F f的大小。
取重力加速度g=10m/s2.下列判断正确的是()A.5s内拉力对物块做功为零B.4s末物块所受合力大小为4.0NC.物块与木板之间的动摩擦因数为0.4D.6s~9s内物块的加速度的大小为2.0m/s22二、选择题(本题共3小题.在每小题给出的四个选项中,至少有一个选项是符合题目要求的.全部选对的得6分,选对但不全的得3分,有选错的得0分.)5.(6分)如图所示,三颗质量均为m的地球同步卫星等间隔分布在半径为r 的圆轨道上,设地球质量为M,半径为R.下列说法正确的是()A .地球对一颗卫星的引力大小为B .一颗卫星对地球的引力小于C .两颗卫星之间的引力大小为D .三颗卫星对地球引力的合力大小为6.(6分)如图所示,总质量为460kg的热气球,从地面刚开始竖直上升时的加速度为0.5m/s2,当热气球上升到180m时,以5m/s的速度向上匀速运动.若离开地面后热气球所受浮力保持不变,上升过程中热气球总质量不变,重力加速度g=10m/s2.关于热气球,下列说法正确的是()3A.所受浮力大小为4830NB.加速上升过程中所受空气阻力保持不变C.从地面开始上升10s后的速度大小为5m/sD.以5m/s匀速上升时所受空气阻力大小为230N7.(6分)在半导体离子注入工艺中,初速度可忽略的离子P+和P3+,经电压为U 的电场加速后,垂直进入磁感应强度大小为B、方向垂直纸面向里,有一定的宽度的匀强磁场区域,如图所示.已知离子P+在磁场中转过θ=30°后从磁场右边界射出.在电场和磁场中运动时,离子P+和P3+()A.在电场中的加速度之比为1:1B .在磁场中运动的半径之比为:1C.在磁场中转过的角度之比为1:2D.离开电场区域时的动能之比为1:3三、解答题(共5小题,满分62分)8.(10分)如图所示,装置甲中挂有小桶的细线绕过定滑轮,固定在小车上;装置乙中橡皮筋的一端固定在导轨的左端,另一端系在小车上.一同学用装置甲和乙分别进行实验,经正确操作获得两条纸带①和②,纸带上的a、b、c …均为4打点计时器打出的点.(1)任选一条纸带读出b、c 两点间的距离为;(2)任选一条纸带求出c、e两点间的平均速度大小为,纸带①和②上c、e两点间的平均速度①②(填“大于”、”等于”或“小于”);(3)图中(填选项)A.两条纸带均为用装置甲实验所得B.两条纸带均为用装置乙实验所得C.纸带①为用装置甲实验所得,纸带②为用装置乙实验所得D.纸带①为用装置乙实验所得,纸带②为用装置甲实验所得.9.(10分)采用如图所示的电路“测定电池的电动势和内阻”.(1)除了选用照片中的部分器材外,(填选项)5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考生文化成绩总分按报考(含兼报)的不同考试类别分别合成。文理科一类为“3+综合+自选模块”的总分,满分为810分;二类为“3+综合”的总分,满分为750分;三类为“3+技术”的总分,满分为550分。
自选模块设语文、数学、英语、政治、历史、地理、物理、化学、生物9门学科的18个选修模块(每门课2个选修模块)共18题(每个模块1道试题),由考生任意选答6题。
技术科目(包括信息技术和通用技术)从2013年9月起与普通高中学业水平考试中的信息技术、通用技术考试二考合一,考试成绩既用于高校招生录取,又用于评定学业水平等第。2013年9月和2014年1月,两科采用合科考试和分科考试两种形式,高三及往届学生继续采用合科考试,其他学生参加分科考试。
二类考试科目为:语文、数学(文/理)、外语、综合(文/理);
三类考试科目为:语文、数学(文/理)、外语、技术(信息技术/通用技术)。
艺术、体育类考试科目分本、专科两类。本科考试科目为:语文、数学(文/理)、外语、综合(文/理)、艺术专业/体育术科。专科考试科目为:语文、数学(文/理)、外语、艺术专业/体育术科。
技术ቤተ መጻሕፍቲ ባይዱ目包括信息技术和通用技术从2013年9月起与普通高中学业水平考试中的信息技术通用技术考试二考合一考试成绩既用于高校招生录取又用于评定学业水平等第
2013浙江省高考考试科目及选拔模式
今年高考实行在全科会考基础上的分类测试、分批选拔、综合评价、全面考核、择优录取的选拔模式。
一类考试科目为:语文、数学(文/理)、外语、综合(文/理)、自选模块;
