许昌高级中学九年级数学下册第三单元《锐角三角函数》测试卷(答案解析)
(常考题)人教版初中数学九年级数学下册第三单元《锐角三角函数》检测题(有答案解析)(1)
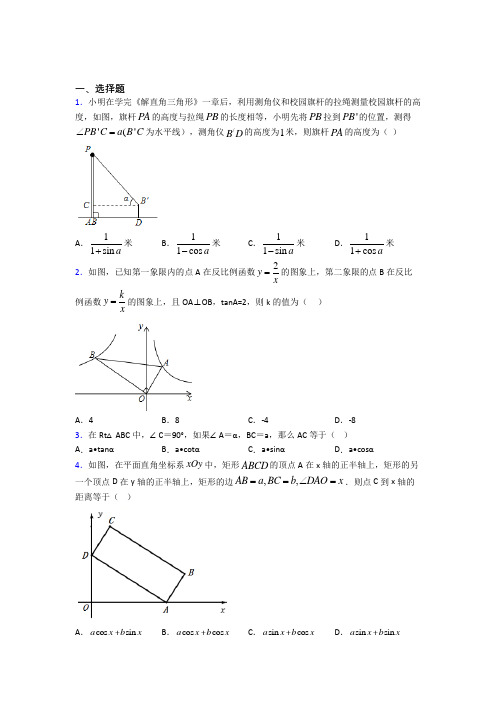
一、选择题1.小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆PA 的高度与拉绳PB 的长度相等,小明先将PB 拉到'PB 的位置,测得(''PB C a B C ∠=为水平线),测角仪/B D 的高度为1米,则旗杆PA 的高度为( )A .11sin a+米B .11cos a-米C .11sin a-米D .11cos a+米2.如图,已知第一象限内的点A 在反比例函数2y x=的图象上,第二象限的点B 在反比例函数ky x=的图象上,且OA ⊥OB ,tanA=2,则k 的值为( )A .4B .8C .-4D .-8 3.在Rt △ABC 中,∠C =90°,如果∠A =α,BC =a ,那么AC 等于( )A .a•tanαB .a•cotαC .a•sinαD .a•cosα4.如图,在平面直角坐标系xOy 中,矩形ABCD 的顶点A 在x 轴的正半轴上,矩形的另一个顶点D 在y 轴的正半轴上,矩形的边,,AB a BC b DAO x ==∠=.则点C 到x 轴的距离等于( )A .cos sin a x b xB .cos cos a x b xC .sin cos a x b xD .sin sin a x b x5.如图,在平面直角坐标系中,等边三角形OAB 的边长为4,点A 在第二象限内,将OAB 沿射线AO 平移,平移后点A '的横坐标为43,则点B ′的坐标为( )A .(63,2)-B .(63,23)-C .()6,2-D .(63,2)-6.如图,Rt △ABC 中,AB =4,BC =2,正方形ADEF 的边长为2,F 、A 、B 在同一直线上,正方形ADEF 向右平移到点F 与B 重合,点F 的平移距离为x ,平移过程中两图重叠部分的面积为y ,则y 与x 的关系的函数图象表示正确的是( )A .B .C .D .7.若菱形的周长为16,高为2,则菱形两个邻角的比为( ) A .6:1B .5:1C .4:1D .3:18.点E 在射线OA 上,点F 在射线OB 上,AO ⊥BO ,EM 平分∠AEF ,FM 平分∠BFE ,则tan ∠EMF 的值为( ) A .12B .33C .1D .39.如图,平行四边形ABCD 中,AB ⊥AC ,AB =3,BC =7,对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分别交B C ,AD 于点E ,F ,下列说法:①在旋转过程中,AF =CE . ②OB =AC ,③在旋转过程中,四边形ABEF 的面积为21,④当直线AC 绕点O 顺时针旋转30°时,连接BF ,DE 则四边形BEDF 是菱形,其中正确的是( )A .①②④B .① ②C .①②③④D .② ③ ④10.如图,在矩形ABCD 中,33AB =AD =9,点P 是AD 边上的一个动点,连接BP ,将矩形ABCD 沿BP 折叠,得到△A 1PB ,连接A 1C ,取A 1C 的三等分点Q (CQ <A 1Q ),当点P 从点A 出发,沿边AD 运动到点D 时停止运动,点Q 的运动路径长为( )A .πB .23πC .43π D .23π 11.如图,分别以直角三角形三边为边向外作等边三角形,面积分别为1S 、2S 、3S ;如图2,分别以直角三角形的三边为直径向外半圆,面积分别为4S 、5S 、6S .其中116S =,245S =,511S =,614S =,则34S S +=( )A .86B .64C .54D .4812.在平面直角坐标系中,正方形1111D C B A 、1122D E E B 、2222A B C D 、2343D E E B 、3333A B C D …按如图所示的方式放置,其中点1B 在y 轴上,点1C 、1E 、2C 、3E 、4E 、3C …在x 轴上,已知正方形1111D C B A 的边长为1,1160B C O ∠=︒,112233B C B C B C …则正方形2019201920192019A B C D 的边长是( )A .201812⎛⎫⎪⎝⎭B .201912⎛⎫⎪⎝⎭C .20193⎝⎭D .20183⎝⎭二、填空题13.如图,ABC 内接于O ,AB AC =,直径AD 交BC 于点E ,若1DE =,2cos 3BAC ∠=,则弦BC 的长为______.14.如图,已知在Rt ABC 中,C 90,AC BC 2∠=︒==,点D 在边BC 上,将ABC 沿直线AD 翻折,使点C 落在点C '处,联结AC ',直线AC '与边CB 的廷长线相交于点F ,如果DAB BAF ∠∠=,那么BF =_________.15.已知抛物线2y ax bx c =++过点()0,3A ,且抛物线上任意不同两点()11,M x y ,()22,N x y ,都满足:当120x x <<时,()()12120x x y y -->;当120x x <<时,()()12120x x y y --<.以原点O 为圆心,OA 为半径的圆与抛物线的另两个交点为B ,C ,且B 在C 的左侧,ABC ∆有一个内角为60︒,则抛物线的解析式为______. 16.如图,已知直线l :33y x =,过点()0,1A 作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点1A ;过点1A 作y 轴的垂线交直线l 于点1B ,过点1B 作直线l 的垂线交y 轴于点2A ;…;按此作法继续下去,则点2020A 的坐标为__________.17.如图,已知直线l :y =33x ,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;…;按此作法继续下去,则点A 4的坐标为_____.18.如图,在直角三角形ABC 中,∠C=90°,AC=12cm ,BC=5cm ,AB=13cm ,则点C 到AB 边的距离是______cm .19.如图,在ABC ∆中,3AB AC cm ==,120A ∠=︒,AB 的垂直平分线分别交,AB BC 于,D E ,则EC 的长为_________.20.如图,已知2AB a =,P 为线段AB 上的一个动点,分别以AP ,PB 为边在AB 的同侧作菱形APCD 和菱形PBFE .点P ,C ,E 在一条直线上,60DAP ∠=︒,M 、N 分别是对角线AC 、BE 的中点.当点P 在线段AB 上移动时,点M 、N 之间的距离最短为_______.三、解答题21.已知ABC 为等边三角形,6,AB P =是AB 上的一个动点,(与A B 、不重合),过点P 作AB 的垂线与BC 相交于点D ,以点D 为正方形的一个顶点,在ABC 内作正方形DEFG ,其中D E 、在BC 上,F 在AC 上,(1)设BP 的长为x ,正方形DEFG 的边长为y ,写出y 关于x 的函数解析式及定义域;(2)当2BP =时,求CF 的长;(3)GDP △是否可能成为直角三角形?若能,求出BP 的长;若不能,请说明理由.22.如图,已知⊙O 的直径 AB 与弦 CD 互相垂直,垂足为点 E.⊙O 的切线 BF 与弦 AC 的延长线相交于点 F,且AC=8,tan∠BDC=34.(1)求⊙O 的半径长;(2)求线段 CF 长.23.如图,在△ABC中,BD、CE是△ABC的高,连接DE.(1)求证:ABD∽ACE;(2)若∠BAC=60°,BC=2DE的长.24.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD 的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=5,求tan∠ABD的值.参考答案 25.理解写作如下图1,在探究锐角A ∠的对边与直角三角形斜边之比的数学实验中包含两个环节,一是通过在A ∠的边AB 上取不同的点B ', B '',分别作高B C '',B C ''''利用三角形相似,可以说明B C B C A ABB ''''''=''',即A ∠的对边与斜边的比值固定,与点B '的位置无关. 二是说明A ∠的度数发生变化时,A ∠的对边与斜边的比值也会发生变化.请根据下图2简要说明做法并证明第二个环节的结论,并在图3中再构造一种思路证明此结论.26.如图,小王在长江边某瞭望台D 处,测得江面上的渔船A 的俯角为40°,若DE =3米,CE =2米,CE 平行于江面AB ,DE ⊥CE ,迎水坡BC 的坡度i =1:0.75,坡长BC =10米,求此时AB 的长.(小数点后面保留一位,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)【参考答案】***试卷处理标记,请不要删除一、选择题 1.C解析:C 【分析】设PA=PB=PB′=x,在RT△PCB′中,根据sinαPCPB=',列出方程即可解决问题.【详解】解:设PA=PB=PB′=x,在RT△PCB′中,sinαPCPB='∴1sinαxx-=∴x1xsinα-=,∴(1-sinα)x=1,∴x=11sinα-.故选C.【点睛】本题考查解直角三角形、三角函数等知识,解题的关键是设未知数列方程,属于中考常考题型.2.D解析:D【分析】过点A、B分别作AC⊥x轴、BD⊥x轴,垂足分别为点C、D,如图,易证△AOC∽△OBD,则根据相似三角形的性质可得214AOCBODS OAS OB⎛⎫==⎪⎝⎭△△,再根据反比例函数系数k的几何意义即可求出k的值.【详解】解:过点A、B分别作AC⊥x轴、BD⊥x轴,垂足分别为点C、D,如图,则∠ACO=∠BDO=90°,∠OAC+∠AOC=90°,∵OA⊥OB,tan∠BAO=2,∴∠AOC+∠BOD=90°,OA:OB=1:2,∴∠OAC=∠BOD,∴△AOC∽△OBD,∴221124 AOCBODS OAS OB⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭△△,∵1212AOCS⨯==,12BODS k=△,∴11142k=,∴8k=,∵k<0,∴k=﹣8.故选:D.【点睛】本题考查了反比例函数系数k的几何意义、相似三角形的判定和性质以及三角函数的定义等知识,熟练掌握所学知识、明确解答的方法是解题的关键.3.B解析:B【分析】画出图形,根据锐角三角函数的定义求出即可.【详解】如图,∠C=90°,∠A=α,BC=a,∵cotαACBC=,∴AC=BC•cotα=a•cotα,故选:B.【点睛】本题考查了锐角三角函数的定义的应用,在直角三角形中,锐角的正弦是角的对边与斜边的比;余弦是角的邻边与斜边的比;正切是对边与邻边的比;余切是邻边与对边的比;熟练掌握三角函数的定义是解题关键.4.A解析:A【分析】作CE⊥y轴于E.解直角三角形求出OD,DE即可解决问题.【详解】作CE⊥y轴于E.在Rt △OAD 中,∵∠AOD=90°,AD=BC=b ,∠OAD=x , ∴OD=sin OAD sin AD b x ∠=, ∵四边形ABCD 是矩形, ∴∠ADC=90°, ∴∠CDE+∠ADO=90°, 又∵∠OAD+∠ADO=90°,∴∠CDE=∠OAD=x , ∴在Rt △CDE 中,∵CD=AB=a ,∠CDE=x , ∴DE= cos CDE cos CD a x ∠=,∴点C 到x 轴的距离=EO=DE+OD=cos sin a x b x , 故选:A . 【点睛】本题考查了解直角三角形的应用,矩形的性质,正确作出辅助线是解题的关键.5.D解析:D 【详解】如解图,过点A 作AC x ⊥轴,过点A '作A D x '⊥轴,∵AOB 是等边三角形,∴4AO BO ==,60AOB ∠=︒,∴30AOC ∠=︒,∴·cos 23CO OA AOC ==,2AC =,∴(23,2)A -,∵30AOD AOC ∠'=∠=︒,43OD =,∴·t 3434an A D OD A OD ⨯=∠'==',∴(43,4)A '-,∴点A '是将点A 向右平移63个单位,向下平移6个单位得到的,∴点B '也是将点B 向右平移63个单位,向下平移6个单位得到的,∵()0,4B ,∴B '的坐标为(63,2)-.6.B【分析】分三种情况分析:当0<x≤2时,平移过程中两图重叠部分为Rt △AA'M ;当2<x≤4时,平移过程中两图重叠部分为梯形F'A'MN ;当4<x≤6时,平移过程中两图重叠部分为梯形F'BCN .分别写出每一部分的函数解析式,结合排除法,问题可解.【详解】设AD 交AC 于N ,A D ''交AC 于M ,当0<x ≤2时,平移过程中两图重叠部分为Rt △AA 'M ,∵Rt △ABC 中,AB =4,BC =2,正方形ADEF 的边长为2,AA x '=,∴tan ∠CAB =A M BC AA AB ='', ∴A 'M =12x , 其面积y=12AA A M ''=12x •12x =14x 2, 故此时y 为x 的二次函数,排除选项D ; 当2<x ≤4时,平移过程中两图重叠部分为梯形F 'A 'MN ,AA x '=,2AF x '=-,同理:A 'M =12x ,()122F M x ='-, 其面积y=12AA A M ''-12AF F M ''=12x •12x ﹣12(x ﹣2)•12(x ﹣2)=x ﹣1, 故此时y 为x 的一次函数,故排除选项C .当4<x ≤6时,平移过程中两图重叠部分为梯形F 'BCN ,AF '=x ﹣2,F 'N =12(x ﹣2),F 'B =4﹣(x ﹣2)=6﹣x ,BC =2, 其面积y =12 [12(x ﹣2)+2]×(6﹣x )=﹣14x 2+x +3, 故此时y 为x 的二次函数,其开口方向向下,故排除A ;综上,只有B 符合题意.【点睛】本题考查了动点问题的函数图象以及三角函数的知识,数形结合并运用排除法,是解答本题的关键.7.B解析:B【分析】由锐角函数可求∠B 的度数,可求∠DAB 的度数,即可求解.【详解】如图,∵四边形ABCD 是菱形,菱形的周长为16,∴AB=BC=CD=DA=4,∵AE=2,AE ⊥BC ,∴sin ∠B=12BE AB = ∴∠B=30° ∵四边形ABCD 是菱形,∴AD ∥BC ,∴∠DAB+∠B=180°,∴∠DAB=150°,∴菱形两邻角的度数比为150°:30°=5:1,故选:B .【点睛】本题考查了菱形的性质,锐角三角函数,能求出∠B 的度数是解决问题的关键. 8.C解析:C【分析】根据三角形外角的性质求得∠AEF+∠BFE=270°,由角平分线定义可求得∠MEF+∠MFE=135°,根据三角形内角和定理可求出∠EMF=45°,从而可得出结论.【详解】如图,∵AO ⊥BO∴∠AOB=90°∴∠OEF+∠OFE=90°∵∠AEF 和∠BFE 是△EOF 的外角∴∠AEF=90°+∠OFE ,∠BFE=90°+∠OEF∴∠AEF+∠BFE=90°+90°+∠OFE+∠OEF=270°∵EM 平分∠AEF ,FM 平分∠BFE ,∴∠MEF+∠MFE=12(∠AEF+∠BFE) =135°, ∵∠MEF+∠MFE+∠M=180° ∴∠M=180°-(∠MEF+∠MFE)=180°-135°=45°∴tan ∠EMF=tan45°=1故选:C .【点睛】此题主要考查了三角形内角和定理、三角形外角的性质及三角函数,求出∠MEF+∠MFE=135°是解答此题的关键.9.A解析:A【分析】①通过证明AOF COE ≅△△即可判断;②分别利用勾股定理求出OB,AC 的长度即可得出答案;③先利用ABC 的面积求出AG 的长度,然后利用梯形的面积公式求解即可; ④易证四边形BEDF 是平行四边形,然后通过角度得出90DOF ∠=︒,然后证明DOF DOE ≅,则有DF DE =,则可证明结论.【详解】∵四边形ABCD 是平行四边形,,//,AO CO AD BC AD BC ∴== ,AFO CEO ∴∠=∠ .在AOF 和COE 中,AFO CEO AOF COE AO CO ∠=∠⎧⎪∠=∠⎨⎪=⎩()AOF COE AAS ∴≅,AF CE OF OE ∴==,故①正确;∵AB ⊥AC ,90BAC ∴∠=︒ .∵AB =3,BC=7,222AC BC AB ∴=-= ,112AO AC ∴== , 222OB AO AB ∴=+=,OB AC ∴=,故②正确;过点A 作AG BC ⊥交BC 于点G ,1122ABC S AB AC BC AG =⋅=⋅ , 322177AB AC AG BC ⋅∴===, 11221()73227ABEF S AF BE AG ∴=+⋅==四边形,故③错误; 连接DE,BF ,,AF CE AD BC ==,DF BE ∴= .∵//DF BE ,∴四边形BEDF 是平行四边形.3sin AB AOB OB ∠== , 60AOB ∴∠=︒ .30AOF ∠=︒,180603090DOF ∴∠=︒-︒-︒=︒,90DOE ∴∠=︒.在DOF △和DOE △中,FO OE DOF DOE DO DO =⎧⎪∠=∠⎨⎪=⎩()DOF DOE SAS ∴≅,DF DE ∴=,∴四边形BEDF 是菱形,故④正确;所以正确的有:①②④,故选:A .【点睛】本题主要考查平行四边形的性质,全等三角形的判定及性质,勾股定理和锐角三角函数,掌握平行四边形的性质,全等三角形的判定及性质,勾股定理和锐角三角函数是解题的关键.10.D解析:D【分析】连接AC ,BD ,相交于点O ,过点Q 作1//QE A B ,交BC 于点E ,即点E 为BC 的三等分点,根据平行线分线段成比例得出113QE A B =为定值,可得出点Q 的运动轨迹是以点E 为圆心,QE 为半径的圆弧,通过对点A 1运动轨迹的分析求出圆心角,最后根据弧长公式进行求解.【详解】连接AC ,BD ,相交于点O ,过点Q 作1//QE A B ,交BC 于点E ,即点E 为BC 的三等分点,∵在矩形ABCD 中,33AB =,AD =9,∴3tan 3AB ADB AD ∠==,即30ADB ︒∠=, ∴60ABD ︒∠=,∵将矩形ABCD 沿BP 折叠,得到△A 1PB ,∴133A B AB ==, ∴1133QE A B ==, 当点P 运动到点A 时,点A 1与点A 重合,当点P 运动到点D 时,点A 1与A 2重合,此时2120ABA ︒∠=,∴点Q 的运动轨迹是以点E 为圆心,QE 为半径,圆心角为120︒的圆弧,∴点Q 的运动路径长120323ππ⨯==, 故选D .【点睛】本题考查矩形与轴对称图形的性质,平行线分线段成比例,由三角函数值求锐角,弧长公式,构造平行线得出QE 的长为定值是解题的关键.11.C解析:C【分析】分别用AC ,AB 和BC 表示出123,,S S S ,然后根据222BC AB AC =-即可得出123,,S S S 的关系.同理,得出456,,S S S 的关系,从而可得答案.【详解】解:如图,1S 对应ACD ∆的面积,过D 作DH AC ⊥于H ,ACD ∆为等边三角形, 160,,,2DAC AH CH AC AD AC ∴∠=︒=== sin 60,DH AD ∴︒=33,22DH AD AC ∴== 2113,24S AC DH AC ∴=•=同理:222333,,S BC S AB == ∵222BC AB AC =-, ∴213,S S S -=如图2,同理可得:456S S S =+,∴3421564516111454.S S S S S S +=-++=-++=故选:C .【点睛】本题考查了勾股定理、等边三角形的性质.锐角三角函数等知识点,其中勾股定理:如果直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么222+=a b c .12.D解析:D【分析】利用正方形的性质结合锐角三角函数关系得出正方形的边长,进而得出变化规律即可得出答案.【详解】解:∵∠B 1C 1O=60°,B 1C 1//B 2C 2//B 3C 3,∴∠D 1C 1E 1=∠C 2B 2E 2=∠C 3B 3E 4=30°,∴D 1E 1=C 1D 1sin30°= 12, 则B 2C 2= 2230B E cos = 123= 13(), 同理可得:B 3C 3= 13= 23()3, 故正方形A n B n C n D n 的边长是:13()n -. 则正方形2019201920192019A B C D 的边长是:20183(). 故选D .【点睛】 此题主要考查了正方形的性质以及锐角三角函数关系,得出正方形的边长变化规律是解题关键.二、填空题13.【分析】连接OBOC 由题意易得AE ⊥BC 则有BE=EC ∠BOD=∠BAC 设OB=3rOE=2r 然后根据勾股定理可求解【详解】解:连接OBOC 如图所示:∵内接于AD 过圆心O ∴AE ⊥BC ∴BE=EC ∴∠解析:25【分析】连接OB 、OC ,由题意易得AE ⊥BC ,则有BE=EC ,∠BOD=∠BAC ,设OB=3r ,OE=2r ,然后根据勾股定理可求解.【详解】解:连接OB 、OC ,如图所示:∵ABC 内接于O ,AB AC =,AD 过圆心O ,∴AE ⊥BC ,∴BE=EC ,BD DC =,∴∠BAD=∠CAD ,∵∠BOD=2∠BAD ,∴∠BAC=∠BOD , ∵2cos 3BAC ∠=, ∴2cos 3BOD ∠=, ∵DE=1,∴设OB=3r ,OE=2r ,则有: 321r r =+,解得:1r =,∴3,2OB OE ==,∴在Rt △BEO 中,BE =, ∴BC =故答案为【点睛】本题主要考查垂径定理、三角形内接圆的性质及圆周角定理,熟练掌握垂径定理、三角形内接圆的性质及圆周角定理是解题的关键.14.【分析】首先根据题意画出图形再根据折叠的性质和可求出各角的度数再利用解直角三角形的知识分别求出CDDFBD 的长度最后根据线段之间的和差关系即可求出结果【详解】解:如图所示:∵△ADC 是由△ACD 翻折解析:2【分析】首先根据题意画出图形,再根据折叠的性质和DAB BAF ∠∠=,可求出各角的度数,再利用解直角三角形的知识分别求出CD ,DF ,BD 的长度,最后根据线段之间的和差关系即可求出结果.【详解】解:如图所示:∵△ADC’是由△ACD 翻折得到,∴DAC 'DAC ∠∠=, ∵DAB BAF ∠∠=, ∴DAC 2DAB ∠∠=. ∵AC 45B ∠=︒, ∴DAB BAF=15∠∠=︒.∴30CAD ∠=︒.在Rt △ACD 中,AC=2 ∴23tan 30CD AC =⋅︒= ,43cos30AC AD ==︒ . ∵'ADC F DAC ∠=∠+∠∴'30F DAC ∠=∠=︒ . ∴433DF AD ==. 23432232BF CD DF BC∴=+-=-= 故答案为32.【点睛】本题考查了翻折的性质和解 直角三角形的知识,根据题意画出图形是解题的关键. 15.【分析】由A 的坐标确定出c 的值根据已知不等式判断出y1-y2<0可得出抛物线的增减性确定出抛物线对称轴为y 轴且开口向下求出b 的值如图1所示可得三角形ABC 为等边三角形确定出B 的坐标代入抛物线解析式即 解析:2233=-+y x 【分析】由A 的坐标确定出c 的值,根据已知不等式判断出y 1-y 2<0,可得出抛物线的增减性,确定出抛物线对称轴为y 轴,且开口向下,求出b 的值,如图1所示,可得三角形ABC 为等边三角形,确定出B 的坐标,代入抛物线解析式即可.【详解】解:∵抛物线过点A (0,3),∴c=3,当x 1<x 2<0时,x 1-x 2<0,由(x 1-x 2)(y 1-y 2)>0,得到y 1-y 2<0,∴当x <0时,y 随x 的增大而增大,同理当x >0时,y 随x 的增大而减小,∴抛物线的对称轴为y 轴,且开口向下,即b=0,∵以O 为圆心,OA 为半径的圆与抛物线交于另两点B ,C ,如图所示,∴△ABC 为等腰三角形,∵△ABC 中有一个角为60°,∴△ABC 为等边三角形,且OC=OA=3,设线段BC 与y 轴的交点为点D ,则有BD=CD ,且∠OBD=30°,333cos30,sin 3022︒︒∴=⋅==⋅=BD OB OD OB ∵B 在C 的左侧, ∴B 的坐标为3332⎛⎫- ⎪ ⎪⎝⎭∵B 点在抛物线上,且c=3,b=0,327432∴+=-a 解得:23a =- 则抛物线解析式为2233=-+y x故答案为: 2233=-+y x . 【点睛】 此题属于二次函数综合题,涉及的知识有:待定系数法求二次函数解析式,二次函数的图象与性质,锐角三角函数定义,熟练掌握各自的性质是解本题的关键.16.【分析】先求出点B 的坐标为(1)得到OA=1OB=求出∠AOB=60°再求出∠得到求出(04);同理得到(0);由此得到规律求出答案【详解】将y=1代入中得x=∴B (1)∴OA=1OB=∴tan ∠A解析:()20200,4【分析】先求出点B 1),得到OA=1,∠AOB=60°,再求出∠130OA B =得到13AA =,求出1A (0,4);同理得到11A B =121112A A B ==,2A (0,24);由此得到规律求出答案.【详解】将y=1代入3y x =中得 ∴B,1),∴OA=1,∴tan ∠AOB=AB OA=, ∴∠AOB=60°,∵∠A 1BO=90°, ∴∠130OA B =,∴13AA =,∴14OA =,∴1A (0,4);同理:11A B =121112A AB =, ∴2OA =1624=,∴2A (0,24); ,∴点2020A 的坐标为()20200,4,故答案为:()20200,4. 【点睛】此题考查图形类规律的探究,一次函数的实际应用,锐角三角函数,根据图形的规律求出点的坐标得到点坐标的表示规律是解题的关键.17.(0256)【分析】利用锐角三角函数分别计算得到的坐标利用规律直接得到答案【详解】解:∵l :y =x ∴l 与x 轴的夹角为30°∵AB ∥x 轴∴∠ABO =30°∵OA =1∴AB =∵A1B ⊥l ∴∠ABA1=6解析:(0,256)【分析】利用锐角三角函数分别计算得到12,A A 的坐标,利用规律直接得到答案.【详解】解:∵l :y ∴l 与x 轴的夹角为30°∵AB ∥x 轴∴∠ABO =30°∵OA =1∴AB∵A 1B ⊥l∴∠ABA 1=60°∴AA 1=3∴A 1(0,4)同理可得A 2(0,16)…∴A 4纵坐标为44=256∴A 4(0,256)故答案为:(0,256).【点睛】本题考查的是一次函数综合题,先根据所给一次函数判断出一次函数与x 轴夹角是解决本题的突破点;根据含30°的直角三角形的特点依次得到123,,A A A …的点的坐标是解决本题的关键.18.【分析】根据△ABC 的面积相等选择AC 和BC 为底高算出的△ABC 的面积和选择AB 为底C 到AB 边的距离为高算出的面积一样列出等式求解【详解】解:在Rt △ABC 中设点C 到AB 边的距离为由△ABC 的面积相 解析:6013【分析】根据△ABC 的面积相等,选择AC 和BC 为底、高算出的△ABC 的面积和选择AB 为底,C 到AB 边的距离为高算出的面积一样列出等式求解.【详解】解:在Rt △ABC 中,设点C 到AB 边的距离为d ,由△ABC 的面积相等可列出如下等式:11=22⨯⨯AC BC AB d ,代入数据: 即:11125=1322⨯⨯⨯⨯d 解得:6013=d 故点C 到AB 边的距离是6013cm. 故答案为:6013. 【点睛】 本题结合直角三角形考查了三角形的面积公式,点到直线的距离垂线段最短等知识点,掌握好直角三角形的等面积法是解题的关键.19.【分析】根据等腰三角形的性质可求出两底角的度数连接AE 可得出AE=BE 推出解直角三角形即可得出答案【详解】解:∵∴连接AE ∵ED 垂直平分AB ∴AE=BE ∵∴∴故答案为:【点睛】本题考查的知识点是等腰解析:【分析】根据等腰三角形的性质可求出两底角的度数,连接AE ,可得出AE=BE ,30EAD =∠°,推出90EAC ∠=︒,解直角三角形即可得出答案.【详解】解:∵3AB AC cm ==,120A ∠=︒, ∴1(180120)302B C ,连接AE ,∵ED 垂直平分AB ,∴AE=BE ,30EAD =∠°,∵120A ∠=︒,∴90EAC ∠=︒,∴cos30AC CE ===︒故答案为:【点睛】本题考查的知识点是等腰三角形的性质、解直角三角形、垂直平分线的性质,综合性较强,但难度不大.20.【分析】连接PMPN 根据菱形的性质求出∠CAP=30°∠MPC=∠CPA=60°∠EPN=∠BPN=∠EPB=30°从而求出∠MPN=90°设AP=x 则PB=2a -x 然后利用锐角三角函数求出PM 和P 解析:32a 【分析】连接PM 、PN ,根据菱形的性质求出∠CAP=12∠=DAP 30°,∠MPC=12∠CPA=60°,∠EPN=∠BPN=12∠EPB=30°,从而求出∠MPN=90°,设AP=x ,则PB=2a -x ,然后利用锐角三角函数求出PM 和PN ,然后利用勾股定理求出MN 2与x 的函数关系式,化为顶点式即可求出MN 2的最小值,从而求出结论.【详解】 解:连接PM 、PN∵四边形APCD 和四边形PBFE 为菱形,60DAP ∠=︒∴∠CPA=180°-∠DAP=120°,∠EPB=∠DAP=60°,PM ⊥AC ,PN ⊥EB ,AC 平分∠DAP ,PM 平分∠APC ,PN 平分∠EPB∴∠CAP=12∠=DAP 30°,∠MPC=12∠CPA=60°,∠EPN=∠BPN=12∠EPB=30° ∴∠MPN=∠MPC +∠EPN=90°设AP=x ,则PB=2a -x ∴PM=AP·sin ∠CAP=12x ,PN=PB·cos ∠32a -x ) 在Rt △MON 中MN 2= PM 2+PN 2=214x +34(2a -x )2=(x -32a )2+34a 2 当x=32a 时,MN 2取最小值,最小为34a 2∴MN. 【点睛】 此题考查的是菱形的性质、锐角三角函数、勾股定理和二次函数的应用,掌握菱形的性质、锐角三角函数、勾股定理和利用二次函数求最值是解决此题的关键.三、解答题21.(1)))3903y x x =+-<≤;(2)32;(3) 【分析】(1)设BP 的长为 x ,正方形 DEFG 的边长为 y ,则由题意可得BD=2x ,DE=y ,3EC y =,然后根据BC=6可以得到y 关于 x 的函数解析式; (2)若BP=2,即x=2,由(1)可得正方形 DEFG 的边长EF 的长度,解直角三角形CEF 可得CF 的长度;(3)设△GDP 是直角三角形,则PG ⊥GD ,然后可得关于x 的方程,解方程可得x 的值,即BP 的长度.【详解】解:(1)设BP 的长为 x ,正方形 DEFG 的边长为 y ,由∠B=60°,PD 垂直AB ,则BD=2x ,DE=y ,EC=tan 303EF y ⨯︒=,∴有263x y y ++=,整理得: ))3903y x x =+-<≤;(2)若BP=2,即x=2,可得3y =,∴(3sin 6032CF EF =⨯︒==; (3)若△GDP 是直角三角形,则PG ⊥GD ,∴∠DPG=30°,即PD=2GD ,)(22329y x ==+-,解之得: x =,此即BP 的长度. 【点睛】本题考查解直角三角形与一次函数的综合应用,根据直角三角形边和角的关系求解是解题关键.22.(1)5;(2)92 【分析】(1)过O 作OH 垂直于AC ,利用垂径定理得到H 为AC 中点,求出AH 的长为4,根据同弧所对的圆周角相等得到tanA =tan ∠BDC ,求出OH 的长,利用勾股定理即可求出圆的半径OA 的长; (2)由AB 垂直于CD 得到E 为CD 的中点,得到EC =ED ,在直角三角形AEC 中,由AC 的长以及tanA 的值求出CE 与AE 的长,由FB 为圆的切线得到AB 垂直于BF ,得到CE 与FB 平行,由平行得比例列出关系式求出AF 的长,根据AF−AC 即可求出CF 的长.【详解】(1)作OH AC ⊥于H ,则142AH AC ==,在Rt AOH ∆中,344AH tanA tan BDC ==∠=,, 3OH ∴=,∴半径225OA AH OH =+=;(2)AB CD ⊥,E ∴为CD 的中点,即CE DE =, 在Rt AEC ∆中,384AC tanA ==,,设3CE k =,则4AE k =, 根据勾股定理得:222AC CE AE =+,即2291664k k +=,解得85k =则2432,55CE DE AE ===, BF 为圆O 的切线,FB AB ∴⊥,又AE CD ⊥,//CD FB ∴,AC AE AF AB ∴=,即328510AF =,解得:252AF =, 则92CF AF AC =-=. 【点睛】此题考查了切线的性质,垂径定理,锐角三角函数定义,勾股定理,以及平行线的性质,熟练掌握切线的性质是解本题的关键.23.(1)见解析;(2)【分析】(1)找出公共角即可求出相似(2)根据~ABD ACE ∆∆得出一个比例式AE AD AC AB=,再根据两边对应成比例且夹角相等得出~ADE ABC ∆∆,再结合60的余弦值即可求出答案.【详解】解:(1)证明:,BD CE 是ABC ∆的高90ADB AEC ∴∠=∠=A A ∠=∠~ABD ACE ∴∆∆(2)~ABD ACE ∆∆ AB AD AC AE ∴= AEAD AC AB∴= A A ∠=∠~ADE ABC ∴∆∆DE AD BC AB∴= 60BAC ∠=1cos 2AD BAC AB ∴∠== 又6BC ==DE ∴=【点睛】本题主要考察了相似三角形,三角函数等知识点,能找出根据第一个相似三角形的比例式来证第二个相似三角形是解题关键.24.(1)90°;(2)证明见解析;(3)2.【分析】(1)根据圆周角定理即可得∠CDE的度数;(2)连接DO,根据直角三角形的性质和等腰三角形的性质易证∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,即可判定DF是⊙O的切线;(3)根据已知条件易证△CDE∽△ADC,利用相似三角形的性质结合勾股定理表示出AD,DC的长,再利用圆周角定理得出tan∠ABD的值即可.【详解】解:(1)解:∵对角线AC为⊙O的直径,∴∠ADC=90°,∴∠EDC=90°;(2)证明:连接DO,∵∠EDC=90°,F是EC的中点,∴DF=FC,∴∠FDC=∠FCD,∵OD=OC,∴∠OCD=∠ODC,∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线;(3)解:如图所示:可得∠ABD=∠ACD,∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,∴∠DCA=∠E,又∵∠ADC=∠CDE=90°,∴△CDE∽△ADC,∴DC DEAD DC=,∴DC2=AD•DE∵,∴设DE=x,则,则AC2﹣AD2=AD•DE,期()2﹣AD2=AD•x,整理得:AD2+AD•x﹣20x2=0,解得:AD=4x或﹣4.5x(负数舍去),则2x=,故tan∠ABD=tan∠ACD=422AD xDC x==.25.答案见解析.【分析】环节一,我们用相似论证了当A ∠不变时,A ∠的对边与斜边的比值固定不变;环节二,再次为我们论证了当A ∠改变时,A ∠的对边与斜边的比值也随之变化,不再固定不变;进而从斜边相等,或直角边相等,两个方面论证即可.【详解】解:环节二证明过程如下:(1)如下图所示:过点A 在BAC ∠内部做射线AB ',截取AB AB '=,过点 B '作BC AC ''⊥,此时构造出了B AC ''∠,显然 BAC B AC ''∠≠∠此时sin BC BAC AB ∠=;sin B C B AC AB ''''∠=', 因为AB AB '=,而BC B C ''≠,所以 sin sin BAC B AC ''∠≠∠ 所以当A ∠的度数发生变化时,A ∠的对边与斜边的比值也会发生改变.(2)图3中构造另外一种思路证明:由上题我们自然想到控制变量法.环节二我们使斜边相等,现在我们使直角边BC 与B C ''与相等,如图所示:此时sin BC BAC AB ∠=;sin B C B AC AB ''''∠=';因为 BC B C ''=,而AB AB '≠,所以 sin sin BAC B AC ''∠≠∠.【点睛】本题考查了对边与斜边的比,即正弦值,会随着角度的变化而变化,熟悉相关性质是解题的关键.26.5.1米【分析】延长DE 交AB 延长线于点P 、作CQ AP ⊥于点Q ,根据矩形的判定和性质可得CE PQ 2==、CQ PE =,由坡度1:0.75i =,可设CQ 4x =、BQ 3x =,根据勾股定理可列出关于x 的方程、解方程即可求得x 的值,即由线段的和差可知11DP =,最后解Rt ADP 、线段的和差可求得答案.【详解】解:如图,延长DE 交AB 延长线于点P ,作CQ AP ⊥于点Q ,如图:∵//CE AP ,DE CE ⊥∴DP AP ⊥∴四边形CEPQ 为矩形∴CE PQ 2==,CQ PE = ∵140.753CQ i BQ === ∴设CQ 4x =、BQ 3x =∴在Rt BCQ 中, 222BQ CQ BC +=∴()()2224310x x += ∴12x =或22x =-(舍去)∴48CQ PE x ===,36BQ x ==∴DP DE PE 11=+=∵测得江面上的渔船A 的俯角为40︒∴40A ∠=︒∴在Rt ADP 中,1113.1tan 0.84DP AP A =≈≈∠ ∴13.162 5.1AB AP BQ PQ =--=--= ∴此时AB 的长为5.1米.故答案是:5.1米【点睛】本题考查了俯角、坡度、锐角三角函数、矩形的判定和性质、勾股定理、一元二次方程、线段的和差等,解题的关键在于通过添加辅助线构造出直角三角形.。
(常考题)人教版初中数学九年级数学下册第三单元《锐角三角函数》检测卷(有答案解析)(4)

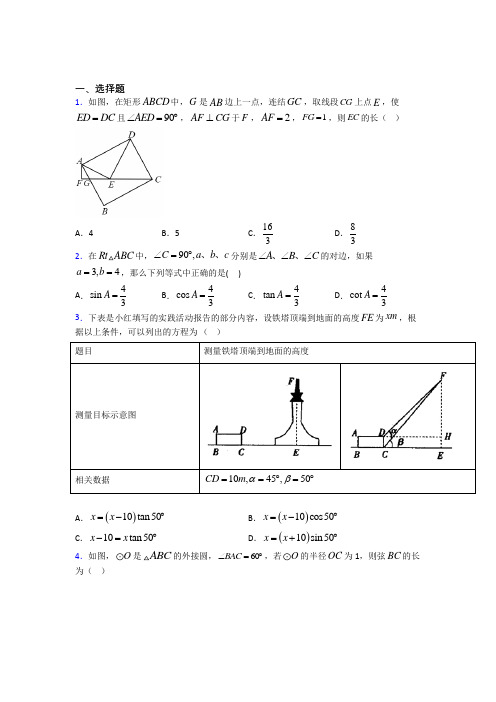
一、选择题1.如图,在矩形ABCD 中,G 是AB 边上一点,连结GC ,取线段CG 上点E ,使ED DC =且90AED ∠=︒,AF CG ⊥于F ,2AF =,1FG =,则EC 的长( )A .4B .5C .163D .83 2.在ABC 中,若21cos |1tan |02A B ⎛⎫-+-= ⎪⎝⎭,则C ∠的度数是( ) A .45︒ B .60︒ C .75︒ D .105︒3.下表是小红填写的实践活动报告的部分内容,设铁塔顶端到地面的高度FE 为xm ,根据以上条件,可以列出的方程为 ( )题目 测量铁塔顶端到地面的高度测量目标示意图 相关数据 10,45,50CD m αβ==︒=︒A .()10tan50x x =-︒B .()10cos50x x =-︒C .10tan50x x -=︒D .()10sin50x x =+︒4.下列计算中错误的是( ) A .sin60sin30sin30︒-︒=︒ B .22sin 45 cos 451︒+︒=C .sin 60tan 60sin 30︒︒=︒D .cos30tan 60cos60︒︒=︒5.如图,在正方形ABCD 中,边长为2的等边三角形AEF 的顶点E . F 分别在BC 和CD 上,下列结论:①CE=CF ;②∠AEB=75︒;③BE+DF=EF ;④正方形对角线3中正确的序号是( )A .①②④B .①②C .②③④D .①③④ 6.如图,在A 处测得点P 在北偏东60︒方向上,在B 处测得点P 在北偏东30︒方向上,若2AB =米,则点P 到直线AB 距离PC 为( ).A .3米B .3米C .2米D .1米7.如图,在矩形ABCD 中,AB =6,BC =62,点E 是边BC 上一动点,B 关于AE 的对称点为B ′,过B ′作B ′F ⊥DC 于F ,连接DB ′,若△DB ′F 为等腰直角三角形,则BE 的长是( )A .6B .3C .32D .62﹣6 8.如图,在ABC ∆中,90ACB ∠=︒,D 是BC 的中点,DE BC ⊥,//CE AD ,若2AC =,30ADC ∠=︒,①四边形ACED 是平行四边形;②BCE ∆是等腰三角形;③四边形ACEB 的周长是10213+;则以上结论正确的是( )A .①②③B .①②C .①③D .②③9.如图,在平面直角坐标系中,等边三角形OAB 的边长为4,点A 在第二象限内,将OAB 沿射线AO 平移,平移后点A '的横坐标为3B ′的坐标为( )A .(63,2)-B .(63,23)-C .()6,2-D .(63,2)-10.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt △ACB 中,∠C =90°,∠ABC =30°,延长CB 使BD =AB ,连接AD ,得∠D =15°,所以tan15°()()12323232323AC CD -====-++-.类比这种方法,计算tan22.5°的值为( )A .21+B .2﹣1C .2D .1211.如图,在△ABC 中,∠ABC =90°,D 为BC 的中点,点E 在AB 上,AD ,CE 交于点F ,AE =EF =4,FC =9,则cos ∠ACB 的值为( )A .35B .59C .512D .4512.在半径为1的O 中,弦AB 、AC 的长度分别是3,2,则BAC ∠为( )度. A .75 B .15或30 C .75或15 D .15或45二、填空题13.如图,正方形ABCD 绕点B 逆时针旋转30°后得到正方形BEFG ,EF 与AD 相交于点H ,延长DA 交GF 于点K .若正方形ABCD 边长为3,则AH=__.14.计算:tan60°﹣cos30°=________;如果∠A 是锐角,且sinA=12,那么∠A=________゜.15.已知抛物线2y ax bx c =++过点()0,3A ,且抛物线上任意不同两点()11,M x y ,()22,N x y ,都满足:当120x x <<时,()()12120x x y y -->;当120x x <<时,()()12120x x y y --<.以原点O 为圆心,OA 为半径的圆与抛物线的另两个交点为B ,C ,且B 在C 的左侧,ABC ∆有一个内角为60︒,则抛物线的解析式为______. 16.在直角三角形ABC 中,∠ACB=90°,D 、E 是边AB 上两点,且CE 所在直线垂直平分线段AD ,CD 平分∠BCE ,BC=23,则AB=_____.17.如图,正方形ABCD 的边长为22,过点A 作AE ⊥AC,AE=1,连接BE ,则tanE= .18.如图,在ABC 中,已知90,4,8C AC BC ∠=︒==,将ABC 绕着点C 逆时针旋转到''A B C 处,此时线段''A B 与BC 的交点D 为BC 的中点,那么'B D 的长度为_________.19.如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(6,0),∠BDO=15°,将△BDE 旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为__________.20.锐角α和锐角β互余,记f=sinα+sinβ,则f的取值范围为_____.参考答案三、解答题21.如图,有一个半径为3cm球形的零件不能直接放在地面上,于是我们找了两个三角形α=,的垫块把这个零件架起来,两个三角形与球的接触点分别是点P和Q,已知70β=,一侧接触点离地面距离PM是4cm40(≈≈≈≈≈≈sin700.94,cos700.34,tan70 2.75;sin400.64,cos400.77,tan400.84)(1)求圆心O距离地面的高度;∠与α、β的关系;(2)直接写出QOP(3)另一侧接触点离地面距离QN又是什么?22.小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知36a=︒,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin,360.80︒≈360.60tan≈)cos≈,360.7523.计算(1)cos 451-sin60︒︒ (2)(12)-2-(π-3.14)0-│tan60°-2│ 24.计算:()20120201232cos302π-⎛⎫----+︒ ⎪⎝⎭. 25.解答下列各题:(1)计算:()1012sin 6032202032-⎛⎫︒+--+- ⎪⎝⎭. (2)解方程:21133x x x-=--. 26.如图,在正方形ABCD 中,点E 是BC 边上的一动点,点F 是CD 上一点,,,CE DF AF DE =且相交于点G .(1)求证:ADF DCE ∆≅∆;(2)若BG BC =,求tan DAG ∠的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】如图,过D 作DP CE ⊥于,P 证明:,EP CP EDP CDP =∠=∠,,DEC DCE ∠=∠再证明,AEF BCG EDP ∠=∠=∠ 结合矩形的性质证明:,AFG EFA ∽利用相似三角形的性质可得4EF =,再求解,AG AE ,设,BG x = 可得2,DE x AD x =+= 利用勾股定理求解,x 再由,BCG EDP ∠=∠可得:1,2EP DP =设,EP m = 则2,DP m = 由勾股定理求解m , 从而可得答案.【详解】解:如图,过D 作DP CE ⊥于,P,DE DC =,EP CP EDP CDP ∴=∠=∠, ,DEC DCE ∠=∠90,AED DCB ∠=︒=∠90,AEF DEC DCE BCG DEC EDP ∴∠+∠=︒=∠+∠=∠+∠,AEF BCG EDP ∴∠=∠=∠,,90AGF CGB AF CG B ∠=∠⊥∠=︒,,FAG BCG ∴∠=∠,FAG AEF ∴∠=∠90AFG EFA ∠=∠=︒,,AFG EFA ∴∽,AF FG EF FA∴= 21AF FG ==,,21,2EF ∴= 4EF ∴=,AE ∴== AG == 设BG x =,则,AB CD x DE ==+=AEF BCG ∠=∠,1tan tan ,2AF AEF BCG EF ∴∠=∠== 1,2BG BC ∴= 2,BC x AD ∴== ()((2222,x x ∴=+235250,x x ∴--=55x ∴=5x = 55855DE ∴== ,EDP BCG ∠=∠1,2EP DP ∴= 设,EP m = 则2,DP m =()22285+2,m m ∴=⎝⎭ 83m ∴=(负根舍去) 162.3EC EP ∴==故选:.C【点睛】 本题考查的是矩形的性质,勾股定理的应用,等腰三角形的性质,三角形相似的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键.2.C解析:C【分析】 根据偶次方和绝对值的非负性可得1cos 02A -=,1tan 0B -=,利用特殊角的三角函数值可得A ∠和B 的度数,利用三角形内角和定理即可求解.【详解】 解:21cos |1tan |02A B ⎛⎫-+-= ⎪⎝⎭, 21cos 0,|1tan |02A B ⎛⎫∴-=-= ⎪⎝⎭,1cos 02A ∴-=,1tan 0B -=,则1cos 2A =,tan 1B =, 解得:60A ∠=︒,45B ∠=︒,则180604575C ∠=︒-︒-︒=︒.故选:C .【点睛】本题考查偶次方和绝对值的非负性、特殊角的三角函数值、三角形内角和定理,熟悉特殊角的三角函数值是解题的关键.3.A解析:A【分析】过D 作DH ⊥EF 于H ,则四边形DCEH 是矩形,根据矩形的性质得到HE =CD =10,CE =DH ,求得FH =x−10,得到CE =x−10,根据三角函数的定义列方程即可得到结论.【详解】过D 作DH ⊥EF 于H ,则四边形DCEH 是矩形,∴HE =CD =10,CE =DH ,∴FH =x−10,∵∠FDH =α=45°,∴DH =FH =x−10,∴CE =x−10,∵tanβ=tan50°=EF CE =-10x x , ∴x =(x−10)tan 50°,故选:A .【点睛】 本题考查了解直角三角形的应用,由实际问题抽象出边角关系的等式,正确的识别图形是解题的关键.4.A解析:A【分析】根据特殊角的三角函数值、二次根式的运算即可得.【详解】A 、11sin 60sin 303022︒-︒==︒=,此项错误;B 、222211sin 45 cos 4512222⎛⎫⎛︒+︒=+=+= ⎪ ⎪ ⎝⎭⎝⎭,此项正确;C、sin 602tan 601sin 302︒︒===︒sin 60tan 60sin 30︒︒=︒,此项正确; D、cos302tan 601cos 602︒︒===︒cos30tan 60cos60︒︒=︒,此项正确; 故选:A .【点睛】本题考查了特殊角的三角函数值、二次根式的运算,熟记特殊角的三角函数值是解题关键.5.A解析:A【分析】根据三角形的全等的判定和性质可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,根据三线合一的性质,可判定AC ⊥EF ,然后分别求得AG 与CG 的长,继而求得答案.【详解】∵四边形ABCD 是正方形,∴AB=AD= BC=DC ,∵△AEF 是等边三角形,∴AE=AF ,在Rt △ABE 和Rt △ADF 中,AB AD AE AF =⎧⎨=⎩, ∴Rt △ABE ≌Rt △ADF (HL ),∴BE=DF ,AE=AF ,∵BC=DC ,∴BC-BE=CD-DF ,∴CE=CF ,故①正确;∵CE=CF ,∴△ECF 是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,∴∠AEB=180°-60°-45°=75°,故②正确;如图,连接AC ,交EF 于G 点,∵AE=AF ,CE=CF ,∴AC ⊥EF ,且AC 平分EF ,∵∠CAF≠∠DAF ,∴DF≠FG ,∴BE+DF≠EF ,故③错误;∵△AEF 是边长为2的等边三角形,∠ACB=∠ACD=45°,AC ⊥EF ,∴EG=FG=1,∴AG=AE•sin60°3232=⨯=CG=112EF =, ∴31;故④正确.综上,①②④正确故选:A .【点睛】本题考查了正方形的性质,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,线段垂直平分线的判定和性质以及解直角三角形.注意准确作出辅助线是解此题的关键.6.B解析:B【分析】设点P 到直线AB 距离PC 为x 米,根据正切的定义用x 表示出AC 、BC ,根据题意列出方程,解方程即可.【详解】解:设点P 到直线AB 距离PC 为x 米,在Rt APC △中,3tan PC AC x PAC ==∠, 在Rt BPC △中,3tan 3PC BC x PBC ==∠, 332x x -=, 解得,3x =),故选:B .【点睛】本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.7.D解析:D【分析】根据 B 关于 AE 的对称点为 B′,可得2AB AD '=,1AB D ∴等腰直角三角形,可得D B E '、、三点共线,可求出BE 的长.【详解】解:6,AB AB AB AD AD ==='∴=', 又△DB′F 为等腰直角三角形,045FDB ∴∠=,又在矩形 ABCD ,090ADF ∠=,045ADB ∴='∠,又2AB AD '= AB D ∴'等腰直角三角形, 090AB D ∴='∠,090AB E ∠=',D BE ∴'、、三点共线,在等腰直角△RCE ,CE=CD=6,∴BE=BC-CE=6,故选D..【点睛】本题考查三角形的性质及解直角三角形,找出D B E '、、三点共线是解题关键. 8.A解析:A【分析】证明AC ∥DE ,再由条件CE ∥AD 可证明四边形ACED 是平行四边形;根据线段的垂直平分线证明AE=EB 可得△BCE 是等腰三角形;首先利用三角函数计算出AD=4,CD=出AB 长可得四边形ACEB 的周长是10+【详解】①∵∠ACB=90°,DE ⊥BC ,∴∠ACD=∠CDE=90°,∴AC ∥DE ,∵CE ∥AD ,∴四边形ACED 是平行四边形,故①正确;②∵D 是BC 的中点,DE ⊥BC ,∴EC=EB ,∴△BCE 是等腰三角形,故②正确;③∵AC=2,∠ADC=30°,∴AD=4,CD=cos30AD ⋅︒=23, ∵四边形ACED 是平行四边形, ∴CE=AD=4, ∵CE=EB ,∴EB=4,DB=23,∴BC=43,∴AB=()2222243213AC BC +=+=,∴四边形ACEB 的周长是10213+,故③正确;综上,①②③均正确,故选:A .【点睛】本题主要考查了平行四边形的判定和性质、等腰三角形的判定和性质、特殊角三角函数、勾股定理、线段的垂直平分线的性质等知识,解题的关键是熟练掌握平行四边形的判定方法.等腰三角形的判定方法.9.D解析:D【详解】如解图,过点A 作AC x ⊥轴,过点A '作A D x '⊥轴,∵AOB 是等边三角形,∴4AO BO ==,60AOB ∠=︒,∴30AOC ∠=︒,∴·cos 23CO OA AOC ==,2AC =,∴(23,2)A -,∵30AOD AOC ∠'=∠=︒,43OD =,∴·t 3434an A D OD A OD ⨯=∠'==',∴(43,4)A '-,∴点A '是将点A 向右平移63个单位,向下平移6个单位得到的,∴点B '也是将点B 向右平移63个单位,向下平移6个单位得到的,∵()0,4B ,∴B '的坐标为(63,2)-.10.B解析:B【分析】作Rt △ABC ,使∠C =90°,∠ABC =45°,延长CB 到D ,使BD =AB ,连接AD ,根据构造的直角三角形,设AC =x ,再用x 表示出CD ,即可求出tan22.5°的值.【详解】解:作Rt △ABC ,使∠C =90°,∠ABC =90°,∠ABC =45°,延长CB 到D ,使BD =AB ,连接AD ,设AC =x ,则:BC =x ,AB =2x ,CD =()1+2x , ()22.5==211+2AC C tan ta D x n D =∠=-︒故选:B.【点睛】本题考查解直角三角形,解题的关键是根据阅读构造含45°的直角三角形,再作辅助线得到22.5°的直角三角形.11.D解析:D【分析】如图,延长AD 到M ,使得DM=DF ,连接BM .利用全等三角形的性质证明BM=CF=9,AB=BM ,利用勾股定理求出BC ,AC 即可解决问题.【详解】解:如图,延长AD 到M ,使得DM=DF ,连接BM .∵BD=DC ,∠BDM=∠CDF ,DM=DF ,∴△BDM ≌△CDF (SAS ),∴CF=BM=9,∠M=∠CFD ,∵CE ∥BM ,∴∠AFE=∠M ,∵EA=EF ,∴∠EAF=∠EFA ,∴∠BAM=∠M ,∴AB=BM=9,∵AE=4,∴BE=5,∵∠EBC=90°,∴BC=2222135EC BE -=-=12,∴AC=2222912AB BC +=+=15,∴cos ∠ACB=124155BC AC == , 故选:D .【点睛】此题考查解直角三角形,全等三角形的判定和性质,等腰三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题. 12.C解析:C【分析】根据题意画出草图,因为C 点位置待定,所以分情况讨论求解.【详解】利用垂径定理可知:AD=32AE =, .sin ∠3∴∠AOD=60°; sin ∠AOE=22,∴∠AOE=45°; ∴∠BAC=75°.当两弦共弧的时候就是15°.故选:C .【点睛】此题考查垂径定理,特殊三角函数的值,解题关键在于画出图形.二、填空题13.1【分析】连接BH 证明Rt △ABH ≌△Rt △EBH (HL )得出∠ABH=30°在Rt △ABH 中解直角三角形即可【详解】解:连接BH 如图所示:∵四边形ABCD 和四边形BEFG 是正方形∴∠BAH=∠AB解析:1【分析】连接BH ,证明Rt △ABH ≌△Rt △EBH (HL ),得出∠ABH =30°,在Rt △ABH 中解直角三角形即可.【详解】解:连接BH ,如图所示:∵四边形ABCD 和四边形BEFG 是正方形,∴∠BAH=∠ABC=∠BEH=∠F=90°,由旋转的性质得:AB=EB ,∠CBE=30°,∴∠ABE=60°,在Rt △ABH 和Rt △EBH 中,∵BH=BH ,AB=EB ,∴Rt △ABH ≌△Rt △EBH (HL ),∴∠ABH=∠EBH=12∠ABE=30°, ∴AH=AB•tan ∠33, 故答案为:1.【点睛】本题考查了旋转的性质、正方形的性质、全等三角形的判定与性质、解直角三角形.能正确作出辅助线得出Rt △ABH ≌△Rt △EBH ,从而求得∠ABH =30°是解题关键.14.30【分析】由特殊角三角函数值进行计算即可求出答案【详解】解:;∵∠A 是锐角∴;故答案为:;30【点睛】本题考查了特殊角的三角函数值解题的关键是掌握特殊角的三角函数值进行解题 解析:3330 【分析】由特殊角三角函数值进行计算,即可求出答案.【详解】 解:323tan 60tan 303︒-︒==; ∵1sin 2A =,∠A 是锐角, ∴30A ∠=︒; 23;30. 【点睛】本题考查了特殊角的三角函数值,解题的关键是掌握特殊角的三角函数值进行解题. 15.【分析】由A 的坐标确定出c 的值根据已知不等式判断出y1-y2<0可得出抛物线的增减性确定出抛物线对称轴为y 轴且开口向下求出b 的值如图1所示可得三角形ABC 为等边三角形确定出B 的坐标代入抛物线解析式即 解析:2233=-+y x 【分析】由A 的坐标确定出c 的值,根据已知不等式判断出y 1-y 2<0,可得出抛物线的增减性,确定出抛物线对称轴为y 轴,且开口向下,求出b 的值,如图1所示,可得三角形ABC 为等边三角形,确定出B 的坐标,代入抛物线解析式即可.【详解】解:∵抛物线过点A (0,3),∴c=3,当x 1<x 2<0时,x 1-x 2<0,由(x 1-x 2)(y 1-y 2)>0,得到y 1-y 2<0,∴当x <0时,y 随x 的增大而增大,同理当x >0时,y 随x 的增大而减小,∴抛物线的对称轴为y 轴,且开口向下,即b=0,∵以O 为圆心,OA 为半径的圆与抛物线交于另两点B ,C ,如图所示,∴△ABC 为等腰三角形,∵△ABC 中有一个角为60°,∴△ABC 为等边三角形,且OC=OA=3,设线段BC 与y 轴的交点为点D ,则有BD=CD ,且∠OBD=30°,333cos30,sin 3022︒︒∴=⋅==⋅=BD OB OD OB ∵B 在C 的左侧, ∴B 的坐标为3332⎛⎫- ⎪ ⎪⎝⎭∵B 点在抛物线上,且c=3,b=0,327432∴+=-a解得:23a =- 则抛物线解析式为2233=-+y x 故答案为: 2233=-+y x . 【点睛】 此题属于二次函数综合题,涉及的知识有:待定系数法求二次函数解析式,二次函数的图象与性质,锐角三角函数定义,熟练掌握各自的性质是解本题的关键.16.4【解析】分析:由CE 所在直线垂直平分线段AD 可得出CE 平分∠ACD 进而可得出∠ACE=∠DCE 由CD 平分∠BCE 利用角平分线的性质可得出∠DCE=∠DCB 结合∠ACB=90°可求出∠ACE ∠A 的度解析:4【解析】分析:由CE 所在直线垂直平分线段AD 可得出CE 平分∠ACD ,进而可得出∠ACE=∠DCE ,由CD 平分∠BCE 利用角平分线的性质可得出∠DCE=∠DCB ,结合∠ACB=90°可求出∠ACE 、∠A 的度数,再利用余弦的定义结合特殊角的三角函数值,即可求出AB 的长度. 详解:∵CE 所在直线垂直平分线段AD ,∴CE 平分∠ACD ,∴∠ACE=∠DCE .∵CD 平分∠BCE ,∴∠DCE=∠DCB .∵∠ACB=90°,∴∠ACE=13∠ACB=30°, ∴∠A=60°, ∴AB=60BC sin =︒=4.故答案为4.点睛:本题考查了线段垂直平分线的性质、角平分线的性质以及特殊角的三角函数值,通过角的计算找出∠A=60°是解题的关键.17.【详解】如图延长CA 使AF=AE 连接BF 过B 点作BG ⊥AC 垂足为G ∵四边形ABCD 是正方形∴∠CAB=45°∴∠BAF=135°∵AE ⊥AC ∴∠BAE=135°∴∠BAF=∠BAE ∵在△BAF 和△B 解析:23【详解】如图,延长CA 使AF=AE ,连接BF ,过B 点作BG ⊥AC ,垂足为G ,∵四边形ABCD 是正方形,∴∠CAB=45°.∴∠BAF=135°.∵AE ⊥AC ,∴∠BAE=135°.∴∠BAF=∠BAE .∵在△BAF 和△BAE 中,BA BA{BAF BAE AE AF∠∠===,∴△BAF ≌△BAE (SAS ).∴∠E=∠F .∵四边形ABCD 是正方形,BG ⊥AC ,∴G 是AC 的中点.∴BG=AG=2.在Rt △BGF 中,BG 2tanF FG 3==,即tanE=23. 考点:正方形的性质,全等三角形的判定和性质,锐角三角函数的定义,18.【分析】根据题意先考虑多种情况①与D 重合=AB ;②与D 不重合过点C 作CE 于点E 利用的余弦值求出由等腰三角形三线合一得求出再用减去得到【详解】①如图与D 重合②如图与D 不重合过点C 作CE 于点E ∵旋转∴在 解析:1255,【分析】根据题意,先考虑多种情况,①A '与D 重合,B D '=AB ;②A '与D 不重合,过点C 作CE ⊥A B ''于点E ,利用CA B ''∠的余弦值求出A E ',由等腰三角形三线合一得2A D A E ''=,求出A D ',再用A B ''减去A D '得到B D '.【详解】①如图,A '与D 重合,45B D AB '==.②如图,A '与D 不重合,过点C 作CE ⊥A B ''于点E , ∵旋转,∴4AC A C '==,8BC B C '==,在Rt A B C ''△中,由勾股定理,22224845A B A C B C ''''=+=+=, 5cos 545A C CA B A B '''∠===', 在Rt A EC '中,5cos 4A E A E CA E A C '''∠===', ∴45A E '=∵D 是BC 中点∴4CD CA '== 在等腰三角形ACD '中,由“三线合一”得852A D A E ''==, ∴851254555B D A B A D ''''=-=-=.故答案是:555. 【点睛】本题考查图形的旋转,等腰三角形三线合一,锐角三角函数,关键在于要画出对应的图象进行分类讨论,把情况考虑全面.19.【分析】根据旋转的性质AB与BD的垂直平分线的交点即为旋转中心P连接PD过P作PF⊥x轴于F再根据点C在BD上确定出∠PDB=45°并求出PD的长然后求出∠PDO=60°根据直角三角形两锐角互余求出解析:(62,6)-【分析】根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x 轴于F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,然后解直角三角形求出点P的坐标.【详解】如图,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F,∵点C在BD上,∴点P到AB、BD的距离相等,都是12BD,即1422⨯=,∴∠PDB=45°,22PD=,∵∠BDO=15°,∴∠PDO=45°+15°=60°,∴∠DPF=30°,∴DF=12PD=12222⨯=,3cos302262PF PD︒=⋅=⨯=,∵点D的坐标是(6,0),∴OF=OD﹣DF=62-,∴旋转中心的坐标为(62,6)-,故答案为:(62,6)-.【点睛】本题考查坐标与图形变化-旋转,解直角三角形,熟练掌握旋转的性质确定出旋转中心的位置是解题的关键.20.1<f≤【分析】根据锐角三角函数的定义即可求出答案【详解】∵α+β=90°∴sinβ=sin(90°−α)=cosα∴f=sinα+cosα=sin(α+45°)∵α是锐角∴<sin(α+45°)≤解析:1<f≤2【分析】根据锐角三角函数的定义即可求出答案.【详解】∵α+β=90°,∴sinβ=sin(90°−α)=cosα,∴f=sinα+cosα=2sin(α+45°)∵α是锐角,∴2<sin(α+45°)≤1,∴1<f≤2,故答案为:1<f≤2.【点睛】本题考查锐角三角函数,解题的关键是正确理解锐角三角函数的定义,本题属于中等题型.三、解答题∠=+;(3)2.7121.(1)5.02;(2)QOPαβ【分析】(1)过O作OA⊥PM,与MP的延长线交于点A,根据互余角的性质求得∠OPA=70°,再解直角三角形得AP,进而求AM;(2)根据切线的性质求出∠OPC和∠OQB的度数,再通过邻补角的性质求得∠PCB和∠QBC,最后根据五边形的内角和求得∠POQ;(3)过O作OD⊥NQ,与NQ的延长线交于点D,仿(1)题方法求得DQ,再由圆心O距离地面的高度减去DQ便可得QN.【详解】(1)过O作OA⊥PM,与MP的延长线交于点A,连接OP,如图1,则OP =3cm ,∠OAP =90°,∵CP 是⊙O 的切线,∴∠OPC =90°,∴∠PCM +∠MPC =90°,∠APO +∠MPC =90°,∴∠APO =∠PCM =70°,∴PA =OP •cos70°≈3×0.34=1.02(cm ),∴圆心O 距离地面的高度:AM =AP +PM =1.02+4=5.02(cm );(2)∵BQ 与CP 都是⊙O 的切线,∴∠OPC =∠OQB =90°,∵∠PCM=α,∠QBN=β,∴∠PCB=180α︒-,∠QBC=180β︒-,∴∠POQ =540°﹣90°﹣90°﹣(180α︒-)﹣(180β︒-)=αβ+,∴∠POQ =7040110αβ+=︒+︒=︒;(3)过O 作OD ⊥NQ ,与NQ 的延长线交于点D ,如图3,按(1)的方法得,∠OQD =∠NBQ =40°,∴DQ =OQ •cos40°≈3×0.77=2.31(cm ),由(1)知,圆心O 距离地面的高度5.02cm ,DN=5.02cm∴QN =DN -DQ =5.02﹣2.31=2.71(cm ).【点睛】本题考查了解直角三角形的应用,圆的切线性质,多边形内角和定理,正确构造直角三角形是解题的关键所在.22.200mm【分析】求ABCD 的周长就是求AB 和AD 的长,可分别过B 、D 作垂线垂直于l ,通过构造直角三角形根据α=36°和ABCD 的四个顶点恰好在横格线且每个横格宽12mm 等条件来求出AB 、AD 的长.【详解】作BE ⊥m 于点E ,DF ⊥m 于点F ,∵α+∠DAF=180°-∠BAD=180°-90°=90°,∠ADF+∠DAF=90°,∴∠ADF=α=36°,根据题意,得 BE=24mm ,DF=48mm ,在Rt △ABE 中,BE sin AB α=, ∴2440sin 360.60BE AB ===︒( mm), 在Rt △ADF 中,DF cos ADF AD ∠=, ∴4860cos360.80DF AD ===︒( mm), ∴矩形ABCD 的周长=2(40+60)=200( mm).【点睛】本题考查了矩形的性质,解直角三角形的应用,通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中解决.23.(1)26+2)3【分析】(1)代入特殊角的三角函数值计算即可;(2)根据负整数指数幂、零次幂、特殊角三角函数值化简然后计算即可.【详解】(1)cos 451-sin60︒===︒(2)(12)-2-(π-3.14)0-│tan60°-2│=4-1-(【点睛】本题考查实数的混合运算,需要熟记特殊角度的三角函数值是解题的关键.24.6【分析】先计算负指数,零次幂,化去绝对值,与特殊三角函数再化简二次根式,合并同类项即可.【详解】()201202032cos302π-⎛⎫--+︒ ⎪⎝⎭【点睛】本题考查实数混合运算问题,关键掌握负指数,会用负指数计算,掌握零次幂的性质,能进行化简,掌握绝对值的意义,会利用绝对值意义去绝对值符号,记住特殊三角函数,能转化为,会化简二次根式为最简二次根式,会判断同类项,能合并同类项使问题得以解决.25.(1)1;(2)4x =-【分析】(1)原式利用特殊角的三角函数、绝对值的代数意义、负指数幂法则以及0指数幂的运算法则分别化简,即可得到结果;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,检验后即可得到分式方程的解的结果.【详解】解:(1)原式=2221++=1; (221133x x x-=-- 去分母得:()231x x --=-,去括号得:231x x -+=-,解得:4x =-,经检验4x =-是分式方程的解.【点睛】此题考查了实数的运算和解分式方程,实数运算的关键是掌握各运算类型的法则,解分式方程时把分式方程转化为整式方程求解,且一定注意要验根.26.(1)见解析;(2)12【分析】(1)根据正方形的性质得到AD=DC ,90ADF DCE ∠=∠=︒,可以证明()ADF DCE SAS ≅;(2)过点B 作BM AG ⊥于点M ,先根据(1)证明90AGD ∠=︒,再证明()ABM DAG AAS ≅,可以求出1tan 2ABM ∠=,根据ABM DAG ∠=∠,则可以得到DAG ∠的正切值.【详解】解:(1)∵ABCD 是正方形,∴AD=DC ,90ADF DCE ∠=∠=︒在ADF 和DCE 中,AD DC ADF DCE DF CE =⎧⎪∠=∠⎨⎪=⎩,∴()ADF DCE SAS ≅;(2)如图,过点B 作BM AG ⊥于点M ,∵ABCD 是正方形,∴AB=BC ,∵BC=BG ,∴AB=BG ,∵BM AG ⊥, ∴12AM AG =, ∵ADF DCE ≅,∴DAF CDE ∠=∠, ∵90ADG CDE ADC ∠+∠=∠=︒,∴90ADG DAF ∠+∠=︒,∴90AGD ∠=︒,∵BM AG ⊥,∴90BMA ∠=︒,∴90BAM ABM ∠+∠=︒,∵90BAM DAG ∠+∠=︒,∴ABM DAG ∠=∠,在ABM 和DAG △中,ABM DAG AMB DGA AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()ABM DAG AAS ≅,∴BM AG =, ∴112tan 2AG AM ABM BM AG ∠===, ∵ABM DAG ∠=∠,∴1tan 2DAG ∠=.【点睛】本题考查全等三角形的性质和判定,等腰三角形的性质,正方形的性质,锐角三角函数的求解,解题的关键是掌握这些性质定理并结合题目条件进行证明求解.。
(常考题)人教版初中数学九年级数学下册第三单元《锐角三角函数》测试卷(有答案解析)(5)
一、选择题1.如图,在矩形ABCD 中,G 是AB 边上一点,连结GC ,取线段CG 上点E ,使ED DC =且90AED ∠=︒,AF CG ⊥于F ,2AF =,1FG =,则EC 的长( )A .4B .5C .163D .832.在Rt ABC 中,90,C a b c ∠=︒、、分别是A B C ∠∠∠、、的对边,如果3,4a b ==,那么下列等式中正确的是( )A .4sin 3A =B .4cos 3A =C .4tan 3A =D .4cot 3A =3.下表是小红填写的实践活动报告的部分内容,设铁塔顶端到地面的高度FE 为xm ,根据以上条件,可以列出的方程为 ( ) 题目测量铁塔顶端到地面的高度测量目标示意图相关数据10,45,50CD m αβ==︒=︒A .()10tan50x x =-︒B .()10cos50x x =-︒C .10tan50x x -=︒D .()10sin50x x =+︒4.如图,O 是ABC 的外接圆,60BAC ∠=︒,若O 的半径OC 为1,则弦BC 的长为( )A .12B .32C .1D .35.在Rt △ABC 中,∠C =90°,如果∠A =α,BC =a ,那么AC 等于( ) A .a•tanαB .a•cotαC .a•sinαD .a•cosα6.如图,在平面直角坐标系中,Rt OAB 的斜边OA 在第一象限,并与x 轴的正半轴夹角为30度,C 为OA 的中点,BC=1,则A 点的坐标为( )A .()3,3B .()3,1C .()2,1D .()2,37.如图,在Rt ABC ∆中,90ACB ∠=︒,22AC BC ==,CD AB ⊥于点D .点P 从点A 出发,沿A D C →→的路径运动,运动到点C 停止,过点P 作PE AC ⊥于点E ,作PF BC ⊥于点F .设点P 运动的路程为x ,四边形CEPF 的面积为y ,则能反映y 与x 之间函数关系的图象是( )A.B.C.D.8.如图,为一幅重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为()A.322B.332C.32D.333229.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE 的长为5m,则树AB的高度是()m.A.10 B.15 C.3D.3510.如图,△ABC 中,∠C =90°,BC =2AC ,则cos A =( )A .12B .52C .255D .5511.在半径为1的O 中,弦AB 、AC 的长度分别是3,2,则BAC ∠为( )度.A .75B .15或30C .75或15D .15或4512.如图所示,矩形ABCD 的边长AB =2,BC =23,△ADE 为正三角形.若半径为R 的圆能够覆盖五边形ABCDE (即五边形ABCDE 的每个顶点都在圆内或圆上),则R 的最小值是( )A .23B .4C .2.8D .2.5二、填空题13.如图,河宽CD 为1003米,在C 处测得对岸A 点在C 点南偏西30°方向、对岸B 点在C 点南偏东45°方向,则A 、B 两点间的距离是_____米.(结果保留根号)14.先将一矩形ABCD 置于直角坐标系中,使点A 与坐标系的原点重合,边AB ,AD 分别落在x 轴、y 轴上(如图1),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图2),若4AB =,3BC =,则图1和图2中点B 点的坐标为_________,点C 的坐标_________.15.如图,ABC 内接于O ,AB AC =,直径AD 交BC 于点E ,若1DE =,2cos 3BAC ∠=,则弦BC 的长为______.16.如图,在矩形ABCD 中,6BC =,4cos 5CAB ∠=, P 为对角线AC 上一动点,过线段BP 上的点M 作EF BP ⊥,交AB 边于点E ,交BC 边于点 F ,点N 为线段EF 的中点,若四边形BEPF 的面积为18,则线段BN 的最大值为 ________ .17.3cosA <sin70°,则锐角A 的取值范围是_________ 18.如图,在直角坐标系xOy 中,已知点A (0,1),点P 在线段OA 上,以AP 为半径的⊙P 周长为1.点M 从A 开始沿⊙P 按逆时针方向转动,射线AM 交x 轴于点N (n ,0).设点M 转过的路程为m (01m <<),,随着点M 的转动,当m 从13变化到23时,点N 相应移动的路径长为___.19.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,AB,AC的夹角为θ(θ=30°).要在楼梯上铺一条地毯,已知BC=2m,楼梯宽1cm,则地毯的面积至少需要_____________平方米.20.如图,矩形ABCD中,AD=1,CD=3,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为__.三、解答题21.如图,在等腰△ABC中,AB=BC,∠A=30°,O为线段AC上一点,以O为圆心,线段OC的长为半径画圆恰好经过点B,与AC的另一个交点为D.(1)求证:AB是圆O的切线;(2)若⊙O的半径为1,求图中阴影部分的面积.22.“筒车”是一种以水流作动力,取水灌田的工具.据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造.明朝科学家徐光启在《农政全书》中用图画描绘“筒车”的工作原理.如图,“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆,已知圆心O在水面上方,且当圆被水面截得的弦AB为6米时,水面下盛水筒的最大深度为1米(即水面下方部分圆上一点距离水面的最大距离).(1)求该圆的半径;(2)若水面上涨导致圆被水面截得的弦 AB 从原来的6米变为8米时,则水面上涨的高度为多少米? 23.计算;(1)4sin 302cos 453tan 302sin 60--+︒︒︒︒ (2)()213tan 308cos 451tan 60cos60-++-︒︒︒︒24.如图,在平面直角坐标系中,矩形ABCO 的边6,12AB BC ==,直线32y x m =-+与y 轴交于点P ,与边BC 交于点E ,与边OA 交于点D .(1)已知矩形ABCO 为中心对称图形,对称中心(点F )为对角线AC OB ,的交点,若直线32y x m =-+恰好经过点F ,求点F 的坐标和m 的值﹒ (2)在(1)的条件下,过点P 的一条直线绕点P 顺时针旋转时,与直线BC 和x 轴分别交于点,N M 、试问是否存在ON 平分CNM ∠的情况.若存在,求线段AM 的长,若不存在,说明理由﹒(3)将矩形ABCO 落在(1)条件下的直线32y x m =-+折叠,若点О落在边CB 上,求出该点坐标,若不在边CB 上,请你说明将(1)中的直线32y x m =-+沿y 轴进行怎样的平移,使矩形ABCO 沿平移后的直线折叠,点O 恰好落在边CB 上.25.如图,在ABC 中,60ABC ∠=,23AB =,8BC =,以AC 为腰,点A 为顶点作等腰ACD △,且120DAC ∠=,则BD =______.26.如图,ABC 内接于O ,AB 是O 的直径,C 是AD 中点,弦CE AB ⊥于点H ,连结AD ,分别交CE 、BC 于点P 、Q ,连结BD .(1)求证:P 是线段AQ 的中点; (2)若O 的半径为5,D 是BC 的中点,求弦CE 的长.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】如图,过D 作DP CE ⊥于,P 证明:,EP CP EDP CDP =∠=∠,,DEC DCE ∠=∠再证明,AEF BCG EDP ∠=∠=∠ 结合矩形的性质证明:,AFG EFA ∽利用相似三角形的性质可得4EF =,再求解,AG AE , 设,BG x = 可得2,DE x AD x =+= 利用勾股定理求解,x 再由,BCG EDP ∠=∠可得:1,2EP DP =设,EP m = 则2,DP m = 由勾股定理求解m , 从而可得答案.【详解】解:如图,过D 作DP CE ⊥于,P,DE DC =,EP CP EDP CDP ∴=∠=∠, ,DEC DCE ∠=∠ 90,AED DCB ∠=︒=∠90,AEF DEC DCE BCG DEC EDP ∴∠+∠=︒=∠+∠=∠+∠ ,AEF BCG EDP ∴∠=∠=∠,,90AGF CGB AF CG B ∠=∠⊥∠=︒, ,FAG BCG ∴∠=∠ ,FAG AEF ∴∠=∠90AFG EFA ∠=∠=︒,,AFG EFA ∴∽ ,AF FGEF FA∴= 21AF FG ==,,21,2EF ∴= 4EF ∴=,AE ∴== AG == 设BG x =,则,AB CD x DE ==+= AEF BCG ∠=∠,1tan tan ,2AF AEF BCG EF ∴∠=∠== 1,2BG BC ∴= 2,BC x AD ∴== ()((2222,x x ∴=+235250,x x ∴--=55x ∴=5x = 55855DE ∴== ,EDP BCG ∠=∠ 1,2EP DP ∴= 设,EP m = 则2,DP m =()22285+2,m m ∴=⎝⎭83m ∴=(负根舍去)162.3EC EP ∴==故选:.C 【点睛】本题考查的是矩形的性质,勾股定理的应用,等腰三角形的性质,三角形相似的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键.2.D解析:D 【分析】分别算出∠A 的各个三角函数值即可得到正确选项. 【详解】解:由题意可得:2222345c a b =++=,∴3434sin ,cos ,tan ,,5543a b a b A A A cotA c c b a ======== ∴正确答案应该是D , 故选D . 【点睛】本题考查锐角三角函数的定义,正确理解锐角三角函数的定义是解题关键.3.A解析:A【分析】过D作DH⊥EF于H,则四边形DCEH是矩形,根据矩形的性质得到HE=CD=10,CE=DH,求得FH=x−10,得到CE=x−10,根据三角函数的定义列方程即可得到结论.【详解】过D作DH⊥EF于H,则四边形DCEH是矩形,∴HE=CD=10,CE=DH,∴FH=x−10,∵∠FDH=α=45°,∴DH=FH=x−10,∴CE=x−10,∵tanβ=tan50°=EFCE =-10xx,∴x=(x−10)tan 50°,故选:A.【点睛】本题考查了解直角三角形的应用,由实际问题抽象出边角关系的等式,正确的识别图形是解题的关键.4.D解析:D【分析】先作OD⊥BC于D,由于∠BAC=60°,根据圆周角定理可求∠BOC=120°,又OD⊥BC,根据垂径定理可知∠BOD=60°,BD=12BC,在Rt△BOD中,利用特殊三角函数值易求BD,进而可求BC.【详解】解:如右图所示,作OD⊥BC于D,∵∠BAC=60°,∴∠BOC=120°,又∵OD⊥BC,∴∠BOD=60°,BD=12BC,∴BD=sin60°×OB∴BC=2BD=故答案是【点睛】本题考查了圆周角定理、垂径定理、特殊三角函数计算,解题的关键是作辅助线OD⊥BC,并求出BD.5.B解析:B【分析】画出图形,根据锐角三角函数的定义求出即可.【详解】如图,∠C=90°,∠A=α,BC=a,∵cotαAC=,BC∴AC=BC•cotα=a•cotα,故选:B.【点睛】本题考查了锐角三角函数的定义的应用,在直角三角形中,锐角的正弦是角的对边与斜边的比;余弦是角的邻边与斜边的比;正切是对边与邻边的比;余切是邻边与对边的比;熟练掌握三角函数的定义是解题关键.6.B解析:B【分析】根据题画出图形,再根据直角三角形斜边上的中线等于斜边的一半可得AB的值,再根据勾股定理可得OB的值,进而可得点A的坐标.【详解】⊥轴于D点,解:如图,过A点作AD x∆的斜边OA在第一象限,并与x轴的正半轴夹角为30.Rt OAB30AOD ∴∠=︒, 12AD OA ∴=, C 为OA 的中点,1AD AC OC BC ∴====, 2OA ∴=,3OD ∴=,则点A 的坐标为:(3,1).故选:B .【点睛】本题考查了解直角三角形、坐标与图形性质、直角三角形斜边上的中线,解决本题的关键是综合运用以上知识.7.A解析:A 【分析】分两段来分析:①点P 从点A 出发运动到点D 时,写出此段的函数解析式,则可排除C 和D ;②P 点过了D 点向C 点运动,作出图形,写出此阶段的函数解析式,根据图象的开口方向可得答案.【详解】解:∵90ACB ∠=︒,22AC BC ==,∴45A ∠=︒,4AB =,又∵CD AB ⊥,∴2AD BD CD ===,45ACD BCD ∠=∠=︒,∵PE AC ⊥,PF BC ⊥,∴四边形CEPF 是矩形,I .当P 在线段AD 上时,即02x <≤时,如解图1∴2sin 2AE PE AP A x ===, ∴222CE x =, ∴四边形CEPF 的面积为2221222222y x x x x ⎛⎫==-+ ⎪ ⎪⎝⎭,此阶段函数图象是抛物线,开口方向向下,故选项CD 错误;II .当P 在线段CD 上时,即24x <≤时,如解图2:依题意得:4CP x =-,∵45ACD BCD ∠=∠=︒,PE AC ⊥,∴sin CE PE CP ECP ==⨯∠,∴())24sin 4542CE PE x x ==-︒=-, ∴四边形CEPF 的面积为()222144822x x x y ⎤-=-+⎥⎣⎦=,此阶段函数图象是抛物线,开口方向向上,故选项B 错误;故选:A .【点睛】本题考查了动点问题的函数图象,分段写出函数的解析式并数形结合进行分析是解题的关键.8.A解析:A【分析】分别过O 作OH ⊥BC ,过G 作GI ⊥OH ,由O 是中点,根据平行线等分线段定理,可得H为BC 的中点,则可得BH=32,再由三个角都是直角的四边形是矩形,可得GI=BH=32,在等腰直角三角形OGI 中,即可求解.【详解】解:过O 作OH ⊥BC 于H ,过G 作GI ⊥OH 于I ∵∠ABC=90°,∴AB ⊥BC ,∴OH ∥AB ,又O 为中点,∴H 为BC 的中点,∴BH=12BC=32∵GI ⊥OH ,∴四边形BHIG 为矩形,∴GI ∥BH ,GI=BH=32, 又∠F=45°,∴∠OGI=45°,∴在Rt △OGI 中,32cos 2GI OG OGI ==∠.故选:A【点睛】本题考查了解直角三角形及平行线等分线段定理,构造合适的辅助线是解题关键. 9.B解析:B【分析】先根据CD =10m ,DE =5m 得出∠DCE =30°,故可得出∠DCB =90°,再由∠BDF =30°可知∠DBE =60°,由DF ∥AE 可得出∠BGF =∠BCA =60°,故∠GBF =30°,所以∠DBC =30°,再由锐角三角函数的定义即可得出结论.【详解】解:在Rt △CDE 中,∵CD =10m ,DE =5m ,∴sin ∠DCE =51102DE CD ==, ∴∠DCE =30°.∵∠ACB =60°,DF ∥AE ,∴∠BGF =60°∴∠ABC =30°,∠DCB =90°.∵∠BDF =30°,∴∠DBF =60°,∴∠DBC =30°,∴BC =103tan303CD ==︒(m ), ∴AB =BC •sin60°=1033⨯=15(m ). 故选:B .【点睛】 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.10.D解析:D【分析】此题根据已知可设AC =x ,则BC =2x ,根据三角函数的定义即可得到结论.【详解】解:∵BC =2AC ,∴设AC =a ,则BC =2a ,∵∠C =90°,∴AB =225AC BC a +=, ∴cosA =555AC AB a==, 故选:D .【点睛】此题考查的知识点是锐角三角函数的定义,勾股定理,关键是熟练掌握锐角三角函数的定义.11.C解析:C【分析】根据题意画出草图,因为C 点位置待定,所以分情况讨论求解.【详解】利用垂径定理可知:AD=32AE =, .sin ∠AOD=2,∴∠AOD=60°;sin ∠AOE=2,∴∠AOE=45°; ∴∠BAC=75°.当两弦共弧的时候就是15°.故选:C .【点睛】此题考查垂径定理,特殊三角函数的值,解题关键在于画出图形.12.C解析:C【分析】连接AC 、BE 、CE ,取BC 的中点F ,连接EF ,根据勾股定理可得AC ,根据直角三角形的边角关系可得∠ACB =30°,∠CAD =30°,再根据正三角形的性质可得:∠EAD =∠EDA =60°,AE =AD =DE =△EAC 是直角三角形,由勾股定理可得EC 的长.判断△EAB ≌△EDC ,根据全等三角形的性质可得EB =EC ,继而根据题意可判断能够覆盖五边形ABCDE 的最小圆的圆心在线段EF 上,且此圆只要覆盖住△EBC 必能覆盖五边形ABCDE ,从而此圆的圆心到△BCE 的三个顶点距离相等.根据等腰三角形的判定和性质可得F 是BC 中点,BF =CF EF ⊥BC ,由勾股定理可得EF 的长,继而列出关于R 的一元二次方程,解方程即可解答.【详解】如图所示,连接AC 、BE 、CE ,取BC 的中点F ,连接EF ,∵四边形ABCD 是矩形,∴∠ABC=∠DAB =∠BCD =∠ADC =90°,AD ∥BC ,AD =BC =AB =CD =2∵BC=AB =2由勾股定理可得:AC 4∴sin ∠ACB =24AB AC ==12,sin ∠CAD =24CD AC ==12∴∠ACB =30°,∠CAD =30°∵△ADE 是正三角形 ∴∠EAD =∠EDA =60°,AE =AD =DE =∴∠EAC =∠EAD +∠CAD =90°,∴△EAC 是直角三角形,由勾股定理可得:EC∵∠EAB =∠EAD +∠BAD =150°∠EDC =∠EDA +∠ADC =150°∴∠EAB =∠EDC∵EA =ED ,AB =DC∴△EAB ≌△EDC ∴EB =EC =27即△EBC 是等腰三角形∵五边形ABCDE 是轴对称图形,其对称轴是直线EF ,∴能够覆盖五边形ABCDE 的最小圆的圆心在线段EF 上,且此圆只要覆盖住△EBC 必能覆盖五边形ABCDE .从而此圆的圆心到△BCE 的三个顶点距离相等.设此圆圆心为O ,则OE =OB =OC =R ,∵F 是BC 中点∴BF =CF =3,EF ⊥BC在Rt △BEF 中,由勾股定理可得:EF =22EB BF -=()()22273-=5 ∴OF =EF -OE =5-R在Rt △OBF 中,222BF OF OB 即()()22235R R +-= 解得:R =2.8∴能够覆盖五边形ABCDE 的最小圆的半径为2.8.故选C .【点睛】本题考查勾股定理的应用、全等三角形的判定及其性质、等腰三角形的判定及其性质、直角三角形的边角关系.解题的关键是理解圆内接五边形的特点,并且灵活运用所学知识.二、填空题13.100+100【分析】根据正切的定义求出AD 根据等腰直角三角形的性质求出BD进而得到AB的长【详解】在Rt△ACD中tan∠ACD=则AD=CD×tan∠ACD=100×=100(米)在Rt△CDB解析:【分析】根据正切的定义求出AD,根据等腰直角三角形的性质求出BD,进而得到AB的长.【详解】在Rt△ACD中,tan∠ACD=AD CD,则AD=CD×tan∠ACD=100(米),在Rt△CDB中,∠BCD=45°,∴BD=CD=∴AB=AD+BD=(故答案为:(【点睛】本题考查的是解直角三角形的应用−方向角问题,掌握方向角的概念、熟记锐角三角函数的定义是解题的关键.14.【分析】根据旋转的性质求解【详解】解:∵AB=4在x轴正半轴上∴图1中B坐标为(40)在图2中过B作BE⊥x轴于点E那么OE=4×cos30°=2BE=2在图2中B点的坐标为(22);易知图1中点C解析:()2⎝⎭【分析】根据旋转的性质求解.【详解】解:∵AB=4,在x轴正半轴上,∴图1中B坐标为(4,0),在图2中过B作BE⊥x轴于点E,那么OE=4×cos30°BE=2,在图2中B点的坐标为(2);易知图1中点C 的坐标为(4,3),在图2中,设CD 与y 轴交于点M ,作CN ⊥y 轴于点N ,那么∠DOM=30°,OD=3, ∴DM=3•tan30°=3,OM=3÷cos30°=23, 那么CM=4-3,易知∠NCM=30°,∴MN=CM•sin30°=43-,CN=CM•cos30°=433-, 则ON=OM+MN=334+, ∴图2中C 点的坐标为(433-,334+). 【点睛】此题主要考查了旋转性质的应用,旋转前后对应角的度数不变,对应线段的长度不变,注意构造直角三角形求解.15.【分析】连接OBOC 由题意易得AE ⊥BC 则有BE=EC ∠BOD=∠BAC 设OB=3rOE=2r 然后根据勾股定理可求解【详解】解:连接OBOC 如图所示:∵内接于AD 过圆心O ∴AE ⊥BC ∴BE=EC ∴∠解析:25【分析】连接OB 、OC ,由题意易得AE ⊥BC ,则有BE=EC ,∠BOD=∠BAC ,设OB=3r ,OE=2r ,然后根据勾股定理可求解.【详解】解:连接OB 、OC ,如图所示:∵ABC 内接于O ,AB AC =,AD 过圆心O ,∴AE ⊥BC ,∴BE=EC ,BD DC =,∴∠BAD=∠CAD ,∵∠BOD=2∠BAD ,∴∠BAC=∠BOD , ∵2cos 3BAC ∠=, ∴2cos 3BOD ∠=, ∵DE=1,∴设OB=3r ,OE=2r ,则有: 321r r =+,解得:1r =,∴3,2OB OE ==,∴在Rt △BEO 中,BE =, ∴BC =故答案为【点睛】本题主要考查垂径定理、三角形内接圆的性质及圆周角定理,熟练掌握垂径定理、三角形内接圆的性质及圆周角定理是解题的关键.16.【分析】在△ABC 中求出AC 与AB 的长点P 在AC 上则6≤BP≤8由点N 为线段EF 的中点∠ABC=90º则EF=2BN 根据四边形BEPF 的面积为18利用对角线乘积的一半求面积得BN 与PB 成反比例PB 最 解析:154【分析】在△ABC 中,6BC =,4cos 5CAB ∠=求出AC 与AB 的长,点P 在AC 上 则6≤BP≤8,由点N 为线段EF 的中点,∠ABC=90º,则EF=2BN ,根据四边形BEPF 的面积为18,EF BP ⊥利用对角线乘积的一半求面积得,PB BN=18,BN 与PB 成反比例, PB 最小时,BN 最大,当PB ⊥AC 时,PB 最小,求出最小值即可.【详解】在△ABC 中,6BC =,4cos 5CAB ∠=, ∵22sin cos 1CAB CAB ∠+∠=,∴3sin 5CAB ∠=,由正弦函数定义BC sin=ACCAB∠,∴AC=BC6==103sin5CAB∠,由勾股定理得AB=2222AC1068BC-=-=,点P在AC上则6≤BP≤8,∵点N为线段EF的中点,由∠ABC=90º,∴EF=2BN,∵四边形BEPF的面积为18,EF BP⊥,∴S四边形EBFP=11PB EF=PB2BN=PB BN=1822⨯,∴PB BN=18,∴18BN=PB,当PB最小时,BN最大,当PB⊥AC时,PB最小,即S△ABC=11AB BC=AC BP 22BP最小=AB BC8624== AC105⨯BN最大=1815= 2445故答案为:154.【点睛】本题考查锐角三角函数解直角三角形与点到直线距离最短问题,掌握锐角三角函数及其之间的关系,会用锐角三角函数解直角三角形,掌握垂线段最短,会利用面积或勾股定理求BP的最小值,解题时要理解BP最小,BN最大是解题关键.17.20°<∠A<30°【详解】∵<cosA<sin70°sin70°=cos20°∴cos30°<cosA<cos20°∴20°<∠A<30°解析:20°<∠A<30°.【详解】∵3<cosA<sin70°,sin70°=cos20°,∴cos30°<cosA<cos20°,∴20°<∠A<30°.18.【分析】当m从变化到时点N相应移动的路经是一条线段只需考虑始点和终点位置即可解决问题当m=时连接PM如图1点M从点A绕着点P逆时针旋转了一周的从而可得到旋转角为120°则∠APM=120°根据PA=解析:23 3【分析】当m从13变化到23时,点N相应移动的路经是一条线段,只需考虑始点和终点位置即可解决问题.当m=13时,连接PM,如图1,点M从点A绕着点P逆时针旋转了一周的13,从而可得到旋转角为120°,则∠APM=120°,根据PA=PM可得∠PAM=30°,在Rt△AON中运用三角函数可求出ON的长;当m=23时,连接PM,如图2,点M从点A绕着点P逆时针旋转了一周的23,从而可得到旋转角为240°,则∠APM=120°,同理可求出ON的长,问题得以解决.【详解】解:①当m=13时,连接PM,如图1,∠APM=13×360°=120°.∵PA=PM,∴∠PAM=∠PMA=30°.在Rt△AON中,NO=AO•tan∠OAN=1×33=33.②当m=23时,连接PM,如图2,∠APM=360°-23×360°=120°,同理可得:3综合①、②可得:点N相应移动的路径长为33+33=33.23【点睛】本题主要考查了旋转角、等腰三角形的性质、三角函数等知识,若动点的运动路径是一条线段,常常可通过考虑临界位置(动点的始点和终点)来解决.19.()【分析】由三角函数的定义得到AC得出AC+BC的长度由矩形的面积即可得出结果【详解】在Rt△ABC中(米)∴AC+BC=米∴地毯的面积至少需要1×()=()(米2);故答案为:()【点睛】本题考解析:(2+23【分析】由三角函数的定义得到AC,得出AC+BC的长度,由矩形的面积即可得出结果.【详解】在Rt△ABC中,2333BCACtanθ===∴AC+BC=(2+23)米,∴地毯的面积至少需要1×(2+23=(2+232);故答案为:(2+23).【点睛】本题考查了勾股定理、矩形面积的计算;由三角函数求出BC是解决问题的关键.20.﹣【分析】由勾股定理得到AC=2由三角函数的定义得到∠CAB=30°根据旋转的性质得到∠CAE=∠BAF=90°求得∠BAG=60°然后根据图形的面积即可求得【详解】在矩形ABCD中∵AD=1CD=解析:2π﹣2【分析】由勾股定理得到AC=2,由三角函数的定义得到∠CAB=30°,根据旋转的性质得到∠CAE=∠BAF=90°,求得∠BAG=60°,然后根据图形的面积即可求得.【详解】在矩形ABCD 中,∵AD=1,,∵AC=2,tan ∠CAB=BC AD AB CD == ∴∠CAB=30°,∵线段AC 、AB 分别绕点A 顺时针旋转90°至AE 、AF ,∴∠CAE=∠BAF=90°,∴∠BAG=60°,∵,∴阴影部分面积=S △ABC +S 扇形ABG -S △ACG 21601122360222ππ⋅⨯=+-=-.故答案为:2π﹣2. 【点睛】考查了扇形的面积计算,解题关键是灵活运用矩形、旋转的性质和熟记扇形的面积计算公式. 三、解答题21.(1)见解析;(26π- 【分析】(1)连接OB ,根据等边对等角可求得∠OBA=90°,根据切线的判定即可求出答案. (2)分别求出△ABO 与扇形OBD 的面积后即可求出阴影部分面积.【详解】解:(1)连接OB ,∵AB =BC ,∴∠C =∠A =30°,∠CBA =120°,∵OC =OB ,∴∠OBC =∠C =30°,∴∠OBA =∠CAB ﹣∠OBC =90°,∵OB 是⊙O 的半径,∴AB 是圆O 的切线;(2)∵∠A =30°,OB =1,∴AB =tan 30OB =3=3, ∴S △ABO =12×1×3=3, ∵∠AOB =2∠C=60°,∴S 扇形OBD =601360π︒︒⨯=6π, ∴S 阴影=S △ABO ﹣S 扇形OBD =326π-.【点睛】本题考查切线的判定、等腰三角形的性质、圆周角定理、锐角的三角函数、三角形的面积公式、扇形的面积公式,熟练掌握相关知识的运用是解答的关键.22.(1)该圆的半径为5m .;(2)2米.【分析】(1)连接OC ,延长CO 交AB 于点D ,利用垂径定理求出AD ,再利用勾股定理求出圆的半径.(2)过点O 作OE ⊥AB',利用垂径定理求出A'E 的长,再利用勾股定理求出OE 的长,然后求出水面上涨的高度.【详解】(1)解:连接OC ,延长CO 交AB 于点D ,∴CD ⊥AB∴116322AD AB ==⨯= , 设圆的半径为r ,OD=r-1在Rt △AOD 中 OD 2+AD 2=AO 2即(r-1)2+9=r 2. 解之:r=5.∴该圆的半径为5m .(2)解:过点O 作OE ⊥AB'∴A'E=1''2A B =4,∴2222''543OEA O A E , ∴水面上涨的高度为5-3=2米. 【点睛】 此题考查了解直角三角形的应用,垂径定理,以及圆周角定理,熟练掌握各自的性质是解本题的关键.23.(132)231【分析】(1)原式利用特殊角的三角函数值计算即可得到结果; (2)原式利用特殊角的三角函数值计算即可得到结果.【详解】解:(1)原式123342322232=⨯-+⨯ 2113=--+ 3=(2)原式()23123221312=-+-32231=+ 231=.【点睛】此题考查了实数的运算,熟练掌握特殊角的三角函数值及实数运算法则是解本题的关键. 24.(1)F (6,3),m=12;(2)存在,1243+或1243-;(3)不在,需将直线3122y x =-+沿y 轴向下平移94个单位长度. 【分析】(1)由题意得矩形的中心F 坐标为(6,3),代入32y x m =-+,得m=12; (2)分,M N 在y 轴左、右两侧两种情况,证明MON ∆是等边三角形即可得到结论; (3)假设沿直线3122y x =-+将矩形ABCO 折叠,点O 落在边AB 上O′处.连接PO′,OO′.则有PO′=OP ,由(1)得AB 垂直平分OP ,所以PO′=OO′,则△OPO′为等边三角形.则∠OPE=30°,则(2)知∠OPE >30°所以沿直线3122y x =-+将矩形ABCO 折叠,点O 不可能落在边AB 上.设沿直线32y x a =-+将矩形ABCO 折叠,点O 恰好落在边AB 上O′处.连接P′O′,OO′.则有P′O′=OP′=a ,则由题意得:AP′=a -6,∠OPE=∠AO′O ,Rt △OPE 中,OE OA OP AO '=,即8612AO =所以AO′=9,在Rt △AP′O′中,由勾股定理得:(a-6)2+92=a 2解得:394a =,所以将直线3122y x =-+沿y 轴向下平移94单位得直线,将矩形ABCO 沿直线折叠,点O 恰好落在边AB 上. 【详解】()1四边形ABCO 是矩形,6,12,AB BC ==()()()12,012,6,,0,6A B C ∴,F 是,AC OB 的交点,FO ∴是OB 的中点,()6,3P ,将()6,3F 代入32y m =-+, 得:363,2m -⨯+= 解得12,m = ∴点F 的坐标为()6,3,m 的值为12.(2)存在,①当,M N 在y 轴左侧时,如图1,直线3122y x =-+与y 轴交于点P , (),0,1212,P OP ∴=,PC OC MG ∴==过M 点作MG BC ⊥交BC 的延长线于点,G,,MNG PNC PCN MGN PC GM ∠=∠∠=∠=,()MGN PCN AAS ∴∆≅∆,,PN MN ∴=点N 是PM 的中点,1,2ON PM MN ∴== ON 平分,//,CNM BC AM ∠,MNO CNO NOM ∴∠=∠=∠MON ∴∆是等边三角形,60,NMO ∴∠=︒4333MO ∴=== 4312AM MO OA ∴=+=+.②当,M N 在y 轴右侧时,如图2,同理可得3,OM =1243,AM AO OM ∴=-=-综上所述,线段AM 的长为123+1243-()3不在,理由如下:假设沿直线y=-32x+12将矩形ABCO折叠,点O落在边AB上O′处.连接PO′,OO′,则有PO′=OP,由(1)得AB垂直平分OP,所以PO′=OO′,则△OPO′为等边三角形.则∠OPE=30°,则(2)知∠OPE>30°,所以沿直线y=-32x+12将矩形ABCO折叠,点O不可能落在边AB上.设沿直线y=-32x+a将矩形ABCO折叠,点O恰好落在边AB上O′处.连接P′O′,OO′.则有P′O′=OP′=a,则由题意得:AP′=a-6,∠OPE=∠AO′O,在Rt△OPE中,tanOEOPEOP∠=,在Rt△OAO′中,tanOAAO OAO'∠=',所以OE OAOP AO'=,即8612AO=',所以AO′=9,在Rt△AP′O′中,由勾股定理得:(a-6)2+92=a2解得:a=394,所以将直线y=-32x+12沿y轴向下平移94单位得直线y=-32x+394,将矩形ABCO沿直线y=-32x+394折叠,点O恰好落在边AB上.【点睛】主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象上点的意义和相似三角形的性质来表示相应的线段之间的关系,再结合具体图形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.25.10.【分析】以A 为旋转中心,把△BAC 逆时针旋转120°,得到△EAD ,连接BE ,作AP ⊥BE 于P ,根据等腰三角形的性质、余弦的概念求出BE ,根据旋转变换的性质得到∠DEB =90°,根据勾股定理计算即可.【详解】解:以A 为旋转中心,把△BAC 逆时针旋转120°,得到△EAD ,连接BE ,作AP ⊥BE 于P , 则∠BAE =120°,AB =AE ,DE =BC ,∴∠ABE =∠AEB =30°,∴BP =AB•cos ∠ABP =3,∠DEA =∠ABC =60°,∴∠DEB =30°+60°=90°,BE =2BP =6,在Rt △BED 中,BD 22ED BE +=10,故答案为:10.【点睛】本题考查了勾股定理、旋转性质以及等腰三角形的性质等知识的综合运用,综合熟练掌握相关知识并利用旋转构造直角三角形和等腰三角形模型是解题的关键.26.(1)见解析;(2)53CE= 【分析】(1)先证明CAD ACE ∠=∠可得PA=PC ,然再证明PC=PQ ,即可得到P 是AQ 的中点; (2)首先证明:△CAQC0△CB4,依据相似三角形的对应边的比相等求得AC 、BC 的长度,然后根据直角三角形的面积公式即可求得CH 的长,则可以求得CE 的长.【详解】(1)证明:∵CE AB ⊥,AB 是直径∴AC AE =又∵AC CD =∴AE CD =∴CAD ACE ∠=∠∴AP CP =∵AB 是O 的直径∴90ACB ∠=︒,∴90ACE BCP CAD CQA ∠+∠=∠+∠=°∴BCP CQA ∠=∠∴CP PQ =∴AP PQ =即P 是线段AQ 的中点;(2)∵C 是AD 中点, D 是BC 的中点∴==AC CD DB ,AB 是直径∴90ACB ∠=︒,30ABC ∠=︒,∠CAB=60°又∵5210AB =⨯=∴5AC =,∴BC ==又∵CE AB ⊥,∠CAB=60°∴CH=AC·sin60°∴22CE CH === 【点睛】本题主要考查了圆周角定理、弧的中点的性质以及三角形的面积公式,灵活应用相关相关性质是解答本题的关键.。
(易错题)初中数学九年级数学下册第三单元《锐角三角函数》检测(有答案解析)
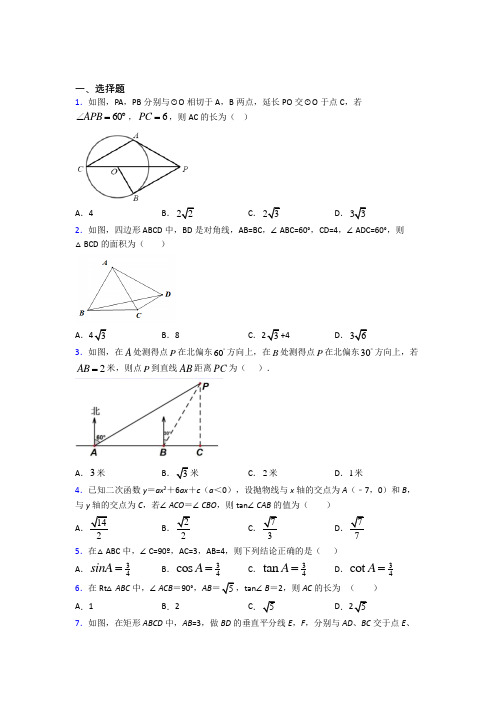
一、选择题1.如图,PA ,PB 分别与⊙O 相切于A ,B 两点,延长PO 交⊙O 于点C ,若60APB ∠=︒,6PC =,则AC 的长为( )A .4B .22C .23D .332.如图,四边形 ABCD 中,BD 是对角线,AB=BC ,∠ABC=60°,CD=4,∠ADC=60°,则△BCD 的面积为( )A .43B .8C .23+4D .363.如图,在A 处测得点P 在北偏东60︒方向上,在B 处测得点P 在北偏东30︒方向上,若2AB =米,则点P 到直线AB 距离PC 为( ).A .3米B 3米C .2米D .1米4.已知二次函数y =ax 2+6ax +c (a <0),设抛物线与x 轴的交点为A (﹣7,0)和B ,与y 轴的交点为C ,若∠ACO =∠CBO ,则tan ∠CAB 的值为( )A .142B .22C 7D 7 5.在△ABC 中,∠C=90º,AC=3,AB=4,则下列结论正确的是( )A .34sinA =B .34cos A =C .34tan A =D .34cot A = 6.在Rt △ABC 中,∠ACB =90°,AB 5tan ∠B =2,则AC 的长为 ( ) A .1 B .2 C 5D .57.如图,在矩形ABCD 中,AB =3,做BD 的垂直平分线E ,F ,分别与AD 、BC 交于点E 、F ,连接BE ,DF ,若EF =AE +FC ,则边BC 的长为( )A .23B .33C .63D .9328.如图,点A 为∠α边上的任意一点,作AC ⊥BC 于点C ,CD ⊥AB 于点D ,下列用线段比表示cosα的值,错误的是( )A .BD BCB .BC AB C .AD AC D .CD AC9.如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使得其面积变为原矩形面积的一半,则平行四边形ABCD 的内角BCD ∠的大小为( )A .100°B .120°C .135°D .150°10.如图,小明想要测量学校操场上旗杆AB 的高度,他作了如下操作:(1)在点C 处放置测角仪,测得旗杆顶的仰角ACE α∠=;(2)量得测角仪的高度CD a =;(3)量得测角仪到旗杆的水平距离DB b =.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )A .tan a b α+B .sin a b α+C .tan b a α+D .sin b a α+ 11.西南大学附中初2020级小李同学想利用学过的知识测量棵树的高度,假设树是竖直生长的,用图中线段AB 表示,小李站在C 点测得∠BCA =45°,小李从C 点走4米到达了斜坡DE 的底端D 点,并测得∠CDE =150°,从D 点上斜坡走了8米到达E 点,测得∠AED =60°,B ,C ,D 在同一水平线上,A 、B 、C 、D 、E 在同一平面内,则大树AB 的高度约为( )米.(结果精确到0.1米,参考数据:2≈1.41,3≈1.73)A .24.3B .24.4C .20.3D .20.412.如图,平行四边形ABCD 中,AB ⊥AC ,AB =3,BC =7,对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分别交B C ,AD 于点E ,F ,下列说法:①在旋转过程中,AF =CE . ②OB =AC ,③在旋转过程中,四边形ABEF 的面积为212,④当直线AC 绕点O 顺时针旋转30°时,连接BF ,DE 则四边形BEDF 是菱形,其中正确的是( )A .①②④B .① ②C .①②③④D .② ③ ④二、填空题13.点A 、B 、C 都在半径为6的O 上,且120AOC ∠=︒,点M 是弦AB 的中点,则CM 的长度的最大值为______.14.如图,矩形ABCD 的对角线AC 与BD 交于点O ,过点O 作BD 的垂线分别交,AD BC 于,E F 两点.若23,120AC AEO =∠=︒,则FC 的长度为_________,AOES 等于_____.15.某人顺着山坡沿一条直线型的坡道滑雪,当他滑过130米长的路程时,他所在位置的竖直高度下降了50米,则该坡道的坡比是_________.16.如图, 圆O 的直径AB 垂直于弦CD ,垂足是E ,22.5A ∠=︒,4OC =,CD 的长为__________.17.如图,在2×2的网格中,以顶点O 为圆心,以2个单位长度为半径作圆弧,交图中格线于点A ,则tan ∠ABO 的值为_____.18.如图,已知Rt △AC 1C 中,∠AC 1C =90°,∠A =30°,CC 1=1,作C 1C 2⊥AC 于点C 2,C 2C 3⊥AC 1于点C 3,C 3C 4⊥AC 于点C 4……C n ﹣1C n ⊥…于点C n ,分别记线段CC 1,C 1C 2,C 2C 3…C n ﹣1C n 的长为a 1,a 2,a 3…a n ,计算并观察其中的规律得a n =________________.19.乐乐同学的身高为166cm ,测得他站立在阳光下的影长为83cm ,紧接着他把手臂竖直举起,测得影长为103cm ,那么乐乐竖直举起的手臂超出头顶的长度约为___________cm .20.如图,在矩形ABCD 中,连接AC ,以点B 为圆心,BA 为半径画弧,交BC 于点E ,已知3BE =,33BC =,则图中阴影部分的面积为_______.(结果保留π)三、解答题21.“筒车”是一种以水流作动力,取水灌田的工具.据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造. 明朝科学家徐光启在《农政全书》中用图画描绘“筒车”的工作原理. 如图,“筒车”盛水筒的运行轨迹是以轴心 O 为圆心的圆,已知圆心 O 在水面上方,且当圆被水面截得的弦 AB 为6米时,水面下盛水筒的最大深度为1米(即水面下方部分圆上一点距离水面的最大距离).(1)求该圆的半径;(2)若水面上涨导致圆被水面截得的弦AB从原来的6米变为8米时,则水面上涨的高度为多少米?22.小明的爸爸准备驾车外出.启动汽车时,车载报警系统显示正前方有障碍物,此时在眼睛点A处测得汽车前端F的俯角为α,且tanα=13,若直线AF与地面l1相交于点B,点A到地面l1的垂线段AC的长度为1.6米,假设眼睛A处的水平线l2与地面l1平行.(1)求BC的长度;(2)假如障碍物上的点M正好位于线段BC的中点位置(障碍物的横截面为长方形,且线段MN为此长方形前端的边),MN⊥l1,若小强的爸爸将汽车沿直线l1后退0.6米,通过汽车的前端F1点恰好看见障碍物的顶部N点(点D为点A的对应点,点F1为点F的对应点),求障碍物的高度.23.如图,AB是圆O的一条弦,OD⊥AB,垂足为C,交圆O于点D,点E在圆O上.(1)若∠AOD=50°,求∠DEB的度数;(2)若OC=3,∠A=30°,求AB的长.24.如图,已知⊙O 的直径 AB 与弦 CD 互相垂直,垂足为点 E.⊙O 的切线 BF 与弦 AC 的延长线相交于点 F,且AC=8,tan∠BDC=34.(1)求⊙O 的半径长;(2)求线段 CF 长.25.定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.例如:如图1,点P 在△ABC 的内部,∠PBC=∠A ,∠PCB=∠ABC ,则△BCP ∽△ABC ,故点P 为△ABC 的自相似点.请你运用所学知识,结合上述材料,解决下列问题:在平面直角坐标系中,点M 是曲线C :33(0)y x =>上的任意一点,点N 是x 轴正半轴上的任意一点.(1) 如图2,点P 是OM 上一点,∠ONP=∠M, 试说明点P 是△MON 的自相似点; 当点M 的坐标是(3,3),点N 的坐标是(3,0)时,求点P 的坐标;(2) 如图3,当点M 的坐标是(3,3),点N 的坐标是(2,0)时,求△MON 的自相似点的坐标;(3) 是否存在点M 和点N,使△MON 无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.26.解直角三角形:在Rt ABC ∆中,90,,C A B C ∠=︒∠∠∠,的对边分别为,,a b c ,已知5,60a B =∠=.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】如图,设CP 交⊙O 于点D ,连接OA 、AD .由切线的性质易证△AOP 是含30度角的直角三角形,所以该三角形的性质求得半径=2;然后在等边△AOD 中得到AD=OA=2;最后通过解直角△ACD 来求AC 的长度.【详解】解:如图,设CP 交⊙O 于点D ,连接OA 、AD .设⊙O 的半径为r .∵PA 、PB 是⊙O 的切线,∠APB=60°,∴OA ⊥AP ,∠APO=12∠APB=30°. ∴OP=2OA ,∠AOP=60°,∴PC=2OA+OC=3r=6,则r=2,易证△AOD 是等边三角形,则AD=OA=2,又∵CD 是直径,∴∠CAD=90°,∴∠ACD=30°,∴AC=tan 30?AD =23 故选:C .【点睛】 本题考查了切线的性质,圆周角定理.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.2.A解析:A【分析】先证明△ABC 是等边三角形,以C 为圆心,CD 为半径作圆,交AD 边与点M ,可得△CDM是等边三角形,进而得到∆BCM ≅∆ACD ,可得到60BMC ∠=︒,得到BM ∥CD ,过点M 作MH CD ⊥,根据△BCD 的面积等于△CDM 的面积求解即可;【详解】∵BD 是对角线,AB=BC ,∠ABC=60°,∴△ABC 是等边三角形,以C 为圆心,CD 为半径作圆,交AD 边与点M ,延长BC ,交C 于点N ,如图所示,∵∠ADC=60°,CM=CD ,∴△CDM 是等边三角形,∴60MCD ∠=︒,∴∠ACB+∠ACM=∠MCD+∠ACM ,即:∠BCM=∠ACD ,∴∆BCM ≅∆ACD ,∴∠BMC=∠ADC=60°,∴∠BMC=∠MCD ,∴BM ∥CD ,根据平行线间的距离相等得到△BCD 的面积等于△CDM 的面积,过点M 作MH CD ⊥,∵CD=4,∴2==CH HD , ∴tan 602MH MH DH ︒==, ∴MH =,∴△△142BDC CDM S S ==⨯⨯= 故答案选A .【点睛】本题主要考查了四边形综合,结合等边三角形性质,构造等边△CDM 是解题的关键. 3.B解析:B【分析】设点P 到直线AB 距离PC 为x 米,根据正切的定义用x 表示出AC 、BC ,根据题意列出方程,解方程即可.【详解】解:设点P 到直线AB 距离PC 为x 米,在Rt APC △中,tan PC AC PAC ==∠,在Rt BPC △中,tan PC BC x PBC ==∠,23x -=,解得,x =),故选:B .【点睛】本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.4.D解析:D【分析】根据根和系数的关系,求出点B (1,0),利用tan ∠ACO =tan ∠CBO ,求出OC =7±,进而求解.【详解】解:如图所示,∵A (﹣7,0),则OA =7,设点B 的横坐标为b ,根据根和系数的关系,则﹣7+b =﹣6a a =﹣6, 解得b =1,∴ 点B (1,0),则OB =1,∵∠ACO =∠CBO ,∴tan ∠ACO =tan ∠CBO , ∴AO OC OC OB =,即71OC OC =,解得OC =7 tan ∠CAB =OC OA 7, 故选:D .【点睛】本题考查的是抛物线与x 轴的交点、三角函数公式,利用根和系数的关系求出点B 的坐标,是解题的关键.5.B解析:B【分析】按照锐角三角函数的定义求各函数值即可.【详解】解:如图,由勾股定理可得2222437AB AC -=-=选项A,74BCsinAAB==,故错误;选项B,3cos4ACAAB==,故正确;选项C,7tan3BCAAC,故错误;选项D,37cot77ACABC===,故错误;故应选:B【点睛】本题考查了锐角三角函数定义,解答关键是按照相关锐角三角函数定义解题.6.B解析:B【分析】根据正切的定义得到BC=12AC,根据勾股定理列式计算即可.【详解】在Rt△ABC中,∠ACB=90°,tan∠B=2,∴ACBC=2,∴BC=12AC,由勾股定理得,AB2=AC2+BC252=AC2+(12AC)2,解得,AC=2,故选B.【点睛】本题考查的是锐角三角函数的定义、勾股定理,掌握锐角A的对边a与邻边b的比叫做∠A的正切是解题的关键.7.B解析:B【分析】根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°,AB=BO=3,因为四边形BEDF 是菱形,所以可求出BE ,AE ,进而可求出BC 的长.【详解】解:∵四边形ABCD 是矩形,//,DE BF ∴,,DEO BFO EDO FBO ∴∠=∠∠=∠ EF 垂直平分BD ,OB OD ∴=,BOF DOE ∴∆∆≌,,OE OF ∴=∴ 四边形BEDF 是菱形,∵四边形ABCD 是矩形,四边形BEDF 是菱形,∴∠A=90°,AD=BC ,DE=BF ,OE=OF ,EF ⊥BD ,∠EBO=FBO ,∴AE=FC .又EF=AE+FC ,∴EF=2AE=2CF ,又EF=2OE=2OF ,AE=OE ,∴△ABE ≌OBE , ∴∠ABE=∠OBE ,∴∠ABE=∠EBD=∠DBC=30°,∴BE= cos30BO ︒= ∴BF=BE=∴∴BC=BF+CF=故选B .【点睛】本题考查了矩形的性质、菱形的性质以及在直角三角形中30°角所对的直角边时斜边的一半,解题的关键是求出∠ABE=∠EBD=∠DBC=30°. 8.C解析:C【分析】利用垂直的定义以及互余的定义得出∠α=∠ACD ,进而利用锐角三角函数关系得出答案.【详解】解:∵AC ⊥BC ,CD ⊥AB ,∴∠α+∠BCD =∠ACD +∠BCD ,∴∠α=∠ACD ,∴cosα=cos ∠ACD =BD BC =BC AB =DC AC,只有选项C 错误,符合题意.故选:C .【点睛】此题主要考查了锐角三角函数的定义,得出∠α=∠ACD 是解题关键.9.D解析:D【分析】作AE ⊥BC 于E ,根据平行四边形的面积=矩形面积的一半,得出AE=12AB ,再由三角函数即可求出∠ABC 的度数,即可得到答案. 【详解】解:作AE ⊥BC 于E ,如图所示:则∠AEB=90°,根据题意得:平行四边形的面积=BC•AE=12BC•AB , ∴AE=12AB , ∴sinB=12AE AB , ∴∠ABC=30°,∴∠BCD=150°.故选:D .【点睛】本题考查了平行四边形的性质、矩形的性质、面积的计算以及三角函数;熟练掌握平行四边形和矩形的性质,并能进行推理计算是解决问题的关键.10.A解析:A【分析】延长CE 交AB 于F ,得四边形CDBF 为矩形,故CF=DB=b ,FB=CD=a ,在直角三角形ACF 中,利用CF 的长和已知的角的度数,利用正切函数可求得AF 的长,从而可求出旗杆AB 的长.【详解】延长CE 交AB 于F ,如图,根据题意得,四边形CDBF 为矩形,∴CF=DB=b ,FB=CD=a ,在Rt △ACF 中,∠ACF=α,CF=b ,tan ∠ACF=AF CF∴AF=tan tan CF ACF b α∠=,AB=AF+BF=tan a b α+,故选:A .【点睛】主要考查了利用了直角三角形的边角关系来解题,通过构造直角三角形,将实际问题转化为数学问题是解答此类题目的关键所在.11.B解析:B【分析】过E 作EG ⊥AB 于G ,EF ⊥BD 于F ,则BG=EF ,EG=BF ,求得∠EDF=30°,根据直角三角形的性质得到EF=12DE=4,33即可得到结论.【详解】过E 作EG ⊥AB 于G ,EF ⊥BD 于F ,则BG =EF ,EG =BF ,∵∠CDE =150°,∴∠EDF =30°,∵DE =8,∴EF =12DE =4,DF =3 ∴CF =CD +DF =3,∵∠ABC =90°,∠ACB =45°,∴AB =BC ,∴GE =BF =AB 3,AG =AB ﹣4,∵∠AED =60°,∠GED =∠EDF =30°,∴∠AEG =30°,∴tan30°=3443AG GE AB ==++ , 解得:AB =14+63≈24.4,故选:B .【点睛】此题考查解直角三角形的应用-坡度坡角问题,根据题意作出辅助线是解题的关键. 12.A解析:A【分析】①通过证明AOF COE ≅△△即可判断;②分别利用勾股定理求出OB,AC 的长度即可得出答案;③先利用ABC 的面积求出AG 的长度,然后利用梯形的面积公式求解即可; ④易证四边形BEDF 是平行四边形,然后通过角度得出90DOF ∠=︒,然后证明DOF DOE ≅,则有DF DE =,则可证明结论.【详解】∵四边形ABCD 是平行四边形,,//,AO CO AD BC AD BC ∴== ,AFO CEO ∴∠=∠ .在AOF 和COE 中,AFO CEO AOF COE AO CO ∠=∠⎧⎪∠=∠⎨⎪=⎩()AOF COE AAS ∴≅,AF CE OF OE ∴==,故①正确;∵AB ⊥AC ,90BAC ∴∠=︒ .∵AB 3BC 7222AC BC AB ∴=-= ,112AO AC ∴== , 222OB AO AB ∴=+=,OB AC ∴=,故②正确;过点A 作AG BC ⊥交BC 于点G ,1122ABC S AB AC BC AG =⋅=⋅ , 3222177AB AC AG BC ⋅⨯∴=== , 11221()73227ABEF S AF BE AG ∴=+⋅=⨯⨯=四边形 ,故③错误; 连接DE,BF ,,AF CE AD BC ==,DF BE ∴= .∵//DF BE ,∴四边形BEDF 是平行四边形.3sin AB AOB OB ∠== , 60AOB ∴∠=︒ .30AOF ∠=︒,180603090DOF ∴∠=︒-︒-︒=︒,90DOE ∴∠=︒.在DOF △和DOE △中,FO OE DOF DOE DO DO =⎧⎪∠=∠⎨⎪=⎩()DOF DOE SAS ∴≅,DF DE ∴=,∴四边形BEDF 是菱形,故④正确;所以正确的有:①②④,故选:A .【点睛】本题主要考查平行四边形的性质,全等三角形的判定及性质,勾股定理和锐角三角函数,掌握平行四边形的性质,全等三角形的判定及性质,勾股定理和锐角三角函数是解题的关键.二、填空题13.【分析】如图取AO 的中点J 连接JMJC 过点J 作JH ⊥OC 交CO 的延长线于H 求出MJCJ 根据CM≤MJ+CJ 即可解决问题【详解】解:如图取的中点连接过点作交的延长线于的最大值为故答案为:【点睛】本题考 解析:337+【分析】如图,取AO 的中点J ,连接JM ,JC ,过点J 作JH ⊥OC ,交CO 的延长线于H .求出MJ ,CJ ,根据CM≤MJ+CJ 即可解决问题.【详解】解:如图,取AO 的中点J ,连接JM ,JC ,过点J 作JH OC ⊥,交CO 的延长线于H .120AOC ∠=︒,60JOH ∴∠=︒,JH OH ⊥,90JHO ∴∠=︒,132AJ JO OA ===,3cos602OH OJ ∴=︒=,sin 60JH OJ =︒=, 315622CH OH OC ∴=+=+=,CJ ∴===, AM MB =,AJ JO =,132MJ OB ∴==, CM MJ JC +,337CM ∴+,CM ∴的最大值为3+故答案为:3+【点睛】本题考查轨迹,三角形中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.14.1【分析】先根据矩形的性质推理得到OF=CF 再根据Rt △BOF 求得OF 的长即可得到CF 的长再由三角形面积公式可得结论【详解】解:∵EF ⊥BD ∠AEO=120°∴∠DEO=60°∠EDO=30°∵四边解析:14 【分析】先根据矩形的性质,推理得到OF=CF ,再根据Rt △BOF 求得OF 的长,即可得到CF 的长,再由三角形面积公式可得结论.【详解】解:∵EF ⊥BD ,∠AEO=120°,∴∠DEO=60°,∠EDO=30°,∵四边形ABCD 是矩形,∴∠OBF=∠OCF=30°,∠BFO=60°,∴∠FOC=60°-30°=30°,∴OF=CF ,又∵Rt △BOF 中,BO=12BD=12 ∴OF=tan30°×BO=1,∴CF=1,过H 点O 作OH ⊥BC 于点H ,则OH=132BO = , ∴1133122FOC S CF OH ∆==⨯= ∵四边形ABCD 是矩形, ∴AD//BC ,AO=CO∴∠EAO=∠FCO又∠AOE=∠COF∴△AOE ≌△COF ∴3AOE S ∆= 故答案为:13 【点睛】本题主要考查了矩形的性质以及解直角三角形的运用,解决问题的关键是掌握:矩形的对角线相等且互相平分.15.【分析】首先根据勾股定理求得滑行的水平距离然后根据坡比的定义即可求解【详解】解:滑行的水平距离是:=120(米)故坡道的坡比是:50:120=故答案是:【点睛】本题考查了勾股定理以及坡比的定义正确求解析:512【分析】首先根据勾股定理求得滑行的水平距离,然后根据坡比的定义即可求解.【详解】 2213050-(米),故坡道的坡比是:50:120=512 . 故答案是:512. 【点睛】 本题考查了勾股定理,以及坡比的定义,正确求得滑行的水平距离是关键.16.【分析】根据圆周角定理得由于的直径垂直于弦根据垂径定理得且可判断为等腰直角三角形所以然后利用进行计算【详解】解:∵∴∵的直径垂直于弦∴∴为等腰直角三角形∴∴故答案是:【点睛】本题考查了垂径定理:垂直 解析:42 【分析】 根据圆周角定理得245BOC A ∠=∠=︒,由于O 的直径AB 垂直于弦CD ,根据垂径定理得CE DE =,且可判断OCE △为等腰直角三角形,所以2222CE OC ==,然后利用2CD CE =进行计算.【详解】解:∵22.5A ∠=︒∴245BOC A ∠=∠=︒∵O 的直径AB 垂直于弦CD∴CE DE =∴OCE △为等腰直角三角形∴2222CE OC == ∴242CD CE ==.故答案是:42【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰直角三角形的性质和圆周角定理.17.2+【分析】连接OA 过点A 作AC ⊥OB 于点C 由题意知AC=1OA=OB=2从而得出OC==BC=OB ﹣OC=2﹣在Rt △ABC 中根据tan ∠ABO=可得答案【详解】如图连接OA 过点A 作AC ⊥OB 于点解析:2+3.【分析】连接OA ,过点A 作AC ⊥OB 于点C ,由题意知AC=1、OA=OB=2,从而得出OC=22OA AC -=3、BC=OB ﹣OC=2﹣3,在Rt △ABC 中,根据tan ∠ABO=AC BC 可得答案.【详解】如图,连接OA ,过点A 作AC ⊥OB 于点C ,则AC=1,OA=OB=2,∵在Rt △AOC 中,=∴BC=OB ﹣OC=2∴在Rt △ABC 中,tan ∠ABO=AC BC =故答案是:【点睛】本题考查了解直角三角形,根据题意构建一个以∠ABO 为内角的直角三角形是解题的关键. 18.【分析】探究规律利用规律解决问题即可【详解】解:在中∵∠C=60°∴同理可得:故答案为:【点睛】本题考查了解直角三角形的应用规律型问题解题的关键是学会探究规律的方法解析:n-1⎝⎭【分析】探究规律,利用规律解决问题即可.【详解】解:在12Rt CC C △中,∵∠C=60°,1CC =1,∴121a 1,a CC sin 60==⨯︒=,同理可得:234n 1345n a a a ...a 2222-⎛⎫⎛⎛⎛==== ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝⎭,,,故答案为:n-12⎛ ⎝⎭.【点睛】 本题考查了解直角三角形的应用,规律型问题,解题的关键是学会探究规律的方法. 19.40【分析】如下图利用∠BCA=∠E 可得对应的正切值相等转化为线段比可得BD 长【详解】如下图AB 为乐乐身高BD 是乐乐手臂超出头顶部分AC 是乐乐站立在阳光下的影长AE 是乐乐举起手臂后的影长根据题意AC解析:40【分析】如下图,利用∠BCA=∠E ,可得对应的正切值相等,转化为线段比可得BD 长.【详解】如下图,AB 为乐乐身高,BD 是乐乐手臂超出头顶部分,AC 是乐乐站立在阳光下的影长,AE 是乐乐举起手臂后的影长根据题意,AC=83cm ,AB=166cm ,AE=103cm∵是阳光照射的影长,∴CB ∥ED∴∠BCA=∠E∴tan ∠BCA=tan ∠E ,即:166********BD += 解得:BD=40故答案为:40【点睛】本题考查三角函数的运用,解题关键是将题干抽象成数学模型,然后再利用三角函数的特点求解. 20.【分析】设圆弧与AC 交于F 连接BF 过F 作FH ⊥BC 于H 解直角三角形得到∠BAC =60°求得△ABF 是等边三角形得到∠ABF =60°推出∠FBE =30°然后根据S 阴影=S 扇形BAF +S △BCF−S △A解析:34π 【分析】 设圆弧与AC 交于F ,连接BF ,过F 作FH ⊥BC 于H ,解直角三角形得到∠BAC =60°,求得△ABF 是等边三角形,得到∠ABF =60°,推出∠FBE =30°,然后根据S 阴影=S 扇形BAF +S △BCF −S △ABF −S 扇形BFE =S 扇形BAF −S 扇形BFE 计算即可.2【详解】解:设圆弧与AC 交于F ,连接BF ,过F 作FH ⊥BC 于H ,在矩形ABCD 中,∵∠ABC =90°,AB =BE =3,BC =33 ∴tan ∠BAC 333=∴∠BAC=60°,∵BA=BF=3,∴△ABF是等边三角形,∴∠ABF=60°,∴∠FBH=30°,∴FH=12BF=32,∴S阴影=S扇形BAF+S△BCF−S△ABF−S扇形BFE=S扇形BAF−S扇形BFE 22603303333360360244,故答案为:34π.【点睛】本题考查扇形面积的计算,锐角三角函数,等边三角形的判定和性质,扇形的面积公式等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.三、解答题21.(1)该圆的半径为5m.;(2)2米.【分析】(1)连接OC,延长CO交AB于点D,利用垂径定理求出AD,再利用勾股定理求出圆的半径.(2)过点O作OE⊥AB',利用垂径定理求出A'E的长,再利用勾股定理求出OE的长,然后求出水面上涨的高度.【详解】(1)解:连接OC,延长CO交AB于点D,∴CD⊥AB∴116322AD AB==⨯=,设圆的半径为r,OD=r-1在Rt△AOD中OD2+AD2=AO2即(r-1)2+9=r2.解之:r=5.∴该圆的半径为5m.(2)解:过点O作OE⊥AB'∴A'E=1''2A B=4,∴2222''543OE A O A E,∴水面上涨的高度为5-3=2米.【点睛】此题考查了解直角三角形的应用,垂径定理,以及圆周角定理,熟练掌握各自的性质是解本题的关键.22.(1)4.8;(2)0.6.【分析】(1)在Rt△ABC,根据tan∠ABC=tanα=13,AC=1.6米,即可求出BC的长度;(2)过D作DH⊥BC于H,求出EM的长度,证明△EMN∽△EHD,得到MN EMDH EH=,即可求解.【详解】解:(1)由题意得,∠ABC=∠α,在Rt△ABC中,AC=1.6,tan∠ABC=tanα=13,∴BC=1.64.81tan3ACABC==∠m,答:BC的长度为4.8m;(2)过D作DH⊥BC于H,则四边形ADHC是矩形,∴AD=CH=BE=0.6,∵点M是线段BC的中点,∴BM=CM=2.4米,∴EM =BM ﹣BE =1.8,∵MN ⊥BC ,∴MN ∥DH ,∴△EMN ∽△EHD , ∴MN EM DH EH =, ∴ 1.81.6 4.8MN =, ∴MN =0.6,答:障碍物的高度为0.6米.【点睛】本题考查解直角三角形的应用,理解三角函数的意义,构造直角三角形,得到相似是解题的关键.23.(1)25°;(2)63【分析】(1)由垂径定理可证AD =BD ,再利用圆周角与圆心角的关系求解.(2)由垂径定理可证AC=BC ,△AOC 为直角三角形,由30°的角可求得直角边AC 的长度,从而求得AB 的长度.【详解】(1)∵OD ⊥AB ,∴AD =BD ,∵∠AOD =50°,∴∠DEB=12∠AOD =25°; (2)∵OD ⊥AB , ∴AC=BC ,△AOC 为直角三角形,∵OC=3,∠A=30°, ∴tan 30OC AC ︒=,即3OC AC = ∴AC=33,∴AB=2AC=63【点睛】本题考查了圆周角定理,垂径定理,锐角三角函数.注意:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.24.(1)5;(2)92【分析】 (1)过O 作OH 垂直于AC ,利用垂径定理得到H 为AC 中点,求出AH 的长为4,根据同弧所对的圆周角相等得到tanA =tan ∠BDC ,求出OH 的长,利用勾股定理即可求出圆的半径OA 的长; (2)由AB 垂直于CD 得到E 为CD 的中点,得到EC =ED ,在直角三角形AEC 中,由AC 的长以及tanA 的值求出CE 与AE 的长,由FB 为圆的切线得到AB 垂直于BF ,得到CE 与FB 平行,由平行得比例列出关系式求出AF 的长,根据AF−AC 即可求出CF 的长.【详解】(1)作OH AC ⊥于H ,则142AH AC ==,在Rt AOH ∆中,344AH tanA tan BDC ==∠=,, 3OH ∴=,∴半径225OA AH OH =+=;(2)AB CD ⊥,E ∴为CD 的中点,即CE DE =, 在Rt AEC ∆中,384AC tanA ==,,设3CE k =,则4AE k =, 根据勾股定理得:222AC CE AE =+,即2291664k k +=,解得85k =则2432,55CE DE AE ===, BF 为圆O 的切线,FB AB ∴⊥,又AE CD ⊥,//CD FB ∴,AC AE AF AB ∴=,即328510AF =, 解得:252AF =,则92CF AF AC =-=. 【点睛】 此题考查了切线的性质,垂径定理,锐角三角函数定义,勾股定理,以及平行线的性质,熟练掌握切线的性质是解本题的关键.25.(1)33,4P ⎛⎫ ⎪ ⎪⎝⎭;(2)31,P ⎛⎫ ⎪ ⎪⎝⎭或232,⎛⎫ ⎪ ⎪⎝⎭;(3)存在,(3,3),(23,0)M N【分析】(1)易证点P 是△MON 的自相似点,过点P 作PD ⊥x 轴于D 点根据M 、N 坐标易知∠MNO=90°,再利用三角函数可求出P 点坐标33,44P ⎛⎫ ⎪ ⎪⎝⎭;(2)根据坐标发现ON=MN=2,要找自相似点只能在∠ONM 中做∠ONP=∠OMN 或∠MNP=∠MON,分别画出图形,根据图形性质,结合相似可求出自相似点的坐标;(3)根据前两问可发现,要想有自相似点,其实质就是在大角里面做小角,当三个角都相等时,即△OMN 为等边三角形时,不存在自相似点,因此可得到直线OM 的解析式y=3x ,与33y =的交点就是M ,从而可以求得N 的坐标. 【详解】解:(1)在△ONP 和△OMN 中,∵∠ONP=∠OMN ,∠NOP=∠MON∴△ONP ∽△OMN∴点P 是△MON 的自相似点.过点P 作PD ⊥x 轴于D 点.tan 3MN POD ON∠==∴60MON ∠=︒. ∵△NOP ∽△MON ,M 的坐标是3,3),点N 的坐标是(3,0),∴90MON ∠=︒,∴90OPN ∠=︒.在Rt △OPN 中,3cos 602OP ON =︒=. 313cos 60224OD OP =︒=⨯=. 333sin 60224PD OP ==⨯=. ∴33,44P ⎛⎫ ⎪ ⎪⎝⎭. (2)①如图3,过点M 作MH ⊥x 轴于H 点,∵(3,3),(2,0)M N∴23OM =,直线OM 的表达式为3y x =,2ON = ∵P 是△MON 的自相似点,∴△PON ∽△NOM ,过点P 作PQ ⊥x 轴于Q 点, ∴1,12PO PN OQ ON === ∴P 的横坐标为1, ∴331y =⨯= ∴31,3P ⎛⎫ ⎪ ⎪⎝⎭. 如图4,△PNM ∽△NOM ,∴PN MN ON MO = ∴23PN =. ∵P 的纵坐标为23, ∴233x = ∴2x =, ∴232,P ⎛⎫ ⎪ ⎪⎝⎭. 综上所述,31,3P ⎛⎫ ⎪ ⎪⎝⎭或232,⎛⎫ ⎪ ⎪⎝⎭. (3)存在点M 和点N ,使△MON 无自相似点,(3,3),(23,0)M N .理由如下: (3,3),(23,0)M N ,23,60OM ON MON ∴==∠=︒∴△MON 是等边三角形,∵点P 在△MON 的内部,∴∠PON≠∠OMN ,∠PNO≠∠MON ,∴存在点M 和点N ,使△MON 无自相似点.考点:1相似三角形;2反比例函数;3解直角三角形;4一次函数;5分类思想;6等边三角形.26.∠A=30︒,10c =,53b =【分析】先利用直角三角形两锐角互余计算出∠A ,再利用30°角所对的直角边等于斜边的一半得到c 的值,然后利用勾股定理求出b .【详解】解:由9060C B ∠=︒∠=︒,,可得:180609030A ∠=︒-︒-︒=︒,∴210c a ==,由勾股定理得22221057553b c a =-=-==.【点睛】本题考查了解直角三角形,利用了含30度角的直角三角形的性质以及勾股定理求直角三角形的边,利用直角三角形的性质求直角三角形的角.。
锐角三角函数测试题(含答案)

九年级下册《锐角三角函数》单元测试一、选择题1. 4sin tan 5ααα=若为锐角,且,则为 ( ) 933425543A B C D . . . . 2.在Rt △ABC 中,∠C = 90°,下列式子不一定成立的是( )A .sinA = sinB B .cosA=sinBC .sinA=cosBD .∠A+∠B=90° 3.直角三角形的两边长分别是6,8,则第三边的长为( )A .10B .22C .10或27D .无法确定4.在Rt △ABC 中,∠C=90°,当已知∠A 和a 时,求c ,应选择的关系式是( ) A .c =sin a A B .c =cos a A C .c = a ·tanA D .c = tan aA5、45cos 45sin +的值等于( )A.2B.213+ C.3D. 16.在Rt △ABC 中,∠C=90°,tan A=3,AC 等于10,则S △ABC 等于( )A. 3B. 300C. 503 D. 157.当锐角α>30°时,则cos α的值是( ) A .大于12 B .小于12C .大于32D .小于328.小明沿着坡角为30°的坡面向下走了2米,那么他下降( ) A .1米 B .3米 C .23 D .2339.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,则AB=( )(A )4 (B )5 (C )23 (D )83310.已知Rt △ABC 中,∠C=90°,tanA=43,BC=8,则AC 等于( ) A .6 B .323C .10D .12 二、填空题11.计算2sin30°+2cos60°+3tan45°=_______. 12.若sin28°=cos α,则α=________.13.已知△ABC 中,∠C=90°,AB=13,AC=5,则tanA=______. 14.某坡面的坡度为1:3,则坡角是_______度.15.在△ABC 中,∠C =90°,AB =10cm ,sinA =54,则BC 的长为_______cm . 16.如图,在高楼前D 点测得楼顶的仰角为30︒,向高楼前进60米到C 点,又测得仰角为45︒,则该高楼的高度大约为A.82米B.163米C.52米D.70米17.如图,小鸣将测倾器安放在与旗杆AB 底部相距6m 的C 处,量出测倾器的高度CD =1m ,测得旗杆顶端B 的仰角α=60°,则旗杆AB 的高度为 .(计算结果保留根号)(16题) (17题) 三、解答题18.由下列条件解直角三角形:在Rt △ABC 中,∠C=90°:(1)已知a=4,b=8, (2)已知b=10,∠B=60°.(3)已知c=20,∠A=60°. (4) (2)已知a=5,∠B=35°19.计算下列各题.(1)s in 230°+cos 245°+2sin60°·tan45°; (2)22cos 30cos 60tan 60tan 30︒+︒︒⨯︒+ sin45°(45︒30︒BAD C四、解下列各题20.如图所示,平地上一棵树高为5米,两次观察地面上的影子,•第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长多少米?21.如图,AB是江北岸滨江路一段,长为3千米,C为南岸一渡口,•为了解决两岸交通困难,拟在渡口C 处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?(精确到0.1)22. 如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通,经测得∠ABC=45o,∠ACB=30o,问此公路是否会穿过该森林公园?请通过计算进行说明。
九年级数学下册《锐角三角函数》单元测试卷(含答案解析)

第二十八章达标测试卷一、选择题(每题3分,共30分)1.sin 30°的值为()A.32 B.22 C.12 D.332.在△ABC中,∠C=90°,AC=5,AB=13,则sin B的值是()A.512 B.125 C.1213 D.5133.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为()A.35 B.34 C.105D.14.如图所示,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=45,BC=10,则AB的长是()A.3 B.6 C.8 D.95.如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB 的延长线于点E,若∠A=30°,则sin E的值为()A.12 B.22 C.32 D.336.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知AB=8,BC=10,则tan∠EFC的值为()A.34 B.43 C.35 D.457.如图,若△ABC和△DEF的面积分别为S1,S2,则()A.S1=12S2B.S1=72S2C.S1=85S2D.S1=S28.如图,长4 m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC 的长为()A.2 3 m B.2 6 m C.(23-2)m D.(26-2)m9.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为()A.30°B.50°C.60°或120°D.30°或150°10.如图,在Rt △ABC 中,∠B =90°,∠BAC =30°,以点A 为圆心,BC 长为半径画弧交AB 于点D ,分别以点A ,D 为圆心,AB 的长为半径画弧,两弧交于点E ,连接AE ,DE ,则∠EAD 的余弦值是( ) A.312B.36C.33D.32二、填空题(每题3分,共30分)11.在△ABC 中,∠A ,∠B 都是锐角,若sin A =32,cos B =12,则∠C =________.12.计算:⎝ ⎛⎭⎪⎫13-1-|-2+3tan45°|+(2-1.41)0=________.13.如图,正方形ABCD 的边长为4,点M 在边DC 上,M ,N 两点关于对角线AC 所在的直线对称,若DM =1,则tan ∠ADN =________.14.已知锐角A 的正弦sin A 是一元二次方程2x 2-7x +3=0的根,则sin A=________.15.如图,在菱形ABCD 中,DE ⊥AB ,垂足为点E ,DE =6 cm ,sin A =35,则菱形ABCD 的面积是________cm 2.16.如图,在高度是21 m的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=____________.(结果保留根号)17.如图所示,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的点D′处,那么tan∠BAD′等于________.18.一次函数的图象经过点(tan 45°,tan 60°)和(-cos 60°,-6tan 30°),则此一次函数的解析式为________.19.如图所示,在△ABC中,∠ACB=90°,CD是AB边上的中线,AC=6,CD=5,则sin A等于________.20.如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且CF FD=13.连接AF并延长交⊙O于点E,连接AD,DE.若CF=2,AF=3.下列结论:①△ADF∽△AED;②FG=2;③tan E=52;④S△DEF=45,其中正确的是________.三、解答题(21题12分,23题8分,其余每题10分,共60分) 21.计算:(1)2(2cos 45°-sin 60°)+24 4;(2)(-2)0-3tan 30°-|3-2|.22.在△ABC中,∠C=90°.(1)已知c=83,∠A=60°,求∠B,a,b;(2)已知a=36,∠A=45°,求∠B,b,c.23.如图,已知▱ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.(1)求证:四边形DECF是平行四边形;(2)若AB=13,DF=14,tan A=125,求CF的长.24.如图,大海中某岛C的周围25 km范围内有暗礁.一艘海轮向正东方向航行,在A处望见C在其北偏东60°的方向上,前进20 km后到达B 处,测得C在其北偏东45°的方向上.如果该海轮继续向正东方向航行,有无触礁危险?请说明理由.(参考数据:2≈1.41,3≈1.73)25.如图,拦水坝的横断面为等腰梯形ABCD,坝顶宽BC为6 m,坝高为3.2 m,为了提高水坝的拦水能力需要将水坝加高2 m,并且保持坝顶宽度不变,迎水坡CD的坡度不变,但是背水坡的坡度由原来的1∶2变成1∶2.5(坡度是坡高与坡的水平长度的比).求加高后的坝底HD的长为多少.26.【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=13,求sin 2α的值.小娟是这样给小芸讲解的:如图①,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°. 设∠BAC=α,则sin α=BCAB=13.易得∠BOC=2α.设BC=x,则AB=3x,AC=22x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=CDOC=________.【问题解决】已知,如图②,点M,N,P为⊙O上的三点,且∠P=β,sin β=35,求sin 2β的值.答案一、1.C 2.D 3.B4.B 点拨:因为AD =DC ,所以∠DAC =∠DCA .又因为AD ∥BC ,所以∠DAC =∠ACB ,所以∠DCA =∠ACB .在Rt △ACB 中,AC =BC ·cos ∠ACB =10×45=8,则AB =BC 2-AC 2=6. 5.A 6.A7.D 点拨:如图,过点A 作AM ⊥BC 于点M ,过点D 作DN ⊥EF ,交FE 的延长线于点N .在Rt △ABM 中,∵sin B =AMAB ,∴AM =3×sin 50°,∴S 1=12BC ·AM =12×7×3×sin 50°=212sin 50°.在Rt △DEN 中,∠DEN =180°-130°=50°.∵sin ∠DEN =DN DE ,∴DN =7×sin 50°,∴S 2=12EF·DN =12×3×7×sin 50°=212sin 50°,∴S 1=S 2.故选D.8.B 点拨:在Rt △ABD 中,∵∠ABD =60°,∴AD =4sin 60°=23(m).在Rt △ACD 中,∵∠ACD =45°,∴AC =2AD =2×23=26(m). 9.D 点拨:有两种情况:当顶角为锐角时,如图①,sin A =12,则∠A =30°;当顶角为钝角时,如图②,sin (180°-∠BAC )=12,则180°-∠BAC =30°,所以∠BAC =150°.10.B 点拨:如图所示,设BC =x .在Rt △ABC 中,∠B =90°,∠BAC =30°,∴AC =2BC =2x ,AB =3BC =3x .根据题意,得AD =BC =x ,AE =DE =AB =3x ,过点E 作EM ⊥AD 于点M ,则AM =12AD =12x .在Rt △AEM 中,cos ∠EAD =AM AE =12x3x =36,故选B.二、11.60° 点拨:∵在△ABC 中,∠A ,∠B 都是锐角,sin A =32,cos B=12,∴∠A =∠B =60°,∴∠C =180°-∠A -∠B =180°-60°-60°=60°.12.2+3 点拨:原式=3-|-2+3|+1=4-2+3=2+ 3. 13.43 14.1215.60 点拨:在Rt △ADE 中,sin A =DE AD =35,DE =6 cm ,∴AD =10 cm ,∴AB =AD =10 cm ,∴S 菱形ABCD =AB·DE =10×6=60(cm 2). 16.(73+21)m17.2 点拨:由题意知BD ′=BD =2 2.在Rt △ABD ′中,tan ∠BAD ′=BD′AB =222= 2.18.y =23x -3 点拨:tan 45°=1,tan 60°=3,-cos 60°=-12,-6tan30°=-2 3.设y =kx +b 的图象经过点(1,3),⎝ ⎛⎭⎪⎫-12,-23,则用待定系数法可求出k =23,b =- 3.19.45 点拨:∵CD 是Rt △ABC 斜边上的中线,∴AB =2CD =2×5=10,∴BC =AB 2-AC 2=102-62=8,∴sin A =BC AB =810=45. 20.①②④三、21.解:(1)原式=2×⎝ ⎛⎭⎪⎫2×22-32+62 =2-62+62 =2.(2)原式=1-3+3-2 =-1.22.解:(1)∵∠C =90°,∠A =60°,∴∠B =30°.∵sin A =a c ,sin B =bc , ∴a =c ·sin A =83×32=12.b =c ·sin B =83×12=4 3. (2)∵∠C =90°,∠A =45°, ∴∠B =45°. ∴b =a =3 6. ∴c =a 2+b 2=6 3.23.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC .∴∠ADE =∠DEC .又∵∠AFC =∠DEC ,∴∠AFC =∠ADE ,∴DE ∥FC . ∴四边形DECF 是平行四边形. (2)解:过点D 作DH ⊥BC 于点H ,如图.∵四边形ABCD 是平行四边形, ∴∠BCD =∠A ,AB =CD =13.又∵tan A=125=tan ∠DCH=DHCH,∴DH=12,CH=5.∵DF=14,∴CE=14.∴EH=9.∴DE=92+122=15.∴CF=DE=15.24.解:该海轮继续向正东方向航行,无触礁危险.理由如下:如图,过点C作CD⊥AB,交AB的延长线于点D,∴∠BCD=∠CBM=45°.设BD=x km,则CD=x km.∵∠CAN=60°,∴∠CAD=30°.在Rt△CAD中,tan ∠CAB=tan 30°=CDAD=33,∴AD=3CD=3x(km).∵AB=20 km,AB+BD=AD,∴20+x=3x,解得x=103+10,∴CD=103+10≈27.3(km)>25 km,∴该海轮继续向正东方向航行,无触礁危险.25.解:由题意得BG=3.2 m,MN=EF=3.2+2=5.2(m),ME=NF=BC=6 m.在Rt△DEF中,EFFD=12,∴FD=2EF=2×5.2=10.4(m).在Rt△HMN中,MN HN=12.5,∴HN=2.5MN=13(m).∴HD=HN+NF+FD=13+6+10.4=29.4(m).∴加高后的坝底HD的长为29.4 m.26.解:22x3;429如图,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR ⊥NO于点R.在⊙O中,易知∠NMQ=90°.∵∠Q=∠P=β,∴∠MON=2∠Q=2β.在Rt△QMN中,∵sin β=MNNQ=35,∴设MN=3k,则NQ=5k,∴MQ=QN2-MN2=4k,OM=12NQ=52k.∵S△NMQ=12MN·MQ=12NQ·MR,∴3k·4k=5k·MR.∴MR=125k.在Rt△MRO中,sin 2β=sin ∠MOR=MROM=125k52k=2425.。
新人教版初中数学九年级数学下册第三单元《锐角三角函数》检测卷(包含答案解析)(1)

一、选择题1.已知如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,AD=23,AB=4,连接AC ,若∠CAD=30°,则CD 为( )A .223+B .27C .1033D .123+2.在正方形网格中,小正方形的边长均为1,∠ABC 如图放置,则sin ∠ABC 的值为( )A .52B .55C .33D .13.如图,在正方形ABCD 中,边长为2的等边三角形AEF 的顶点E . F 分别在BC 和CD 上,下列结论:①CE=CF ;②∠AEB=75︒;③BE+DF=EF ;④正方形对角线AC=1+3,其中正确的序号是( )A .①②④B .①②C .②③④D .①③④ 4.如图,在矩形ABCD 中,AB =6,BC =62,点E 是边BC 上一动点,B 关于AE 的对称点为B ′,过B ′作B ′F ⊥DC 于F ,连接DB ′,若△DB ′F 为等腰直角三角形,则BE 的长是( )A .6B .3C .2D .2﹣6 5.如图,ABC 中,6AB AC AE AC DE ==⊥,,垂直平分AB 于点D ,则EC 的长为( )A .23B .43C .22D .426.如图,在ABC ∆中,90ACB ∠=︒,D 是BC 的中点,DE BC ⊥,//CE AD ,若2AC =,30ADC ∠=︒,①四边形ACED 是平行四边形;②BCE ∆是等腰三角形;③四边形ACEB 的周长是10213+;则以上结论正确的是( )A .①②③B .①②C .①③D .②③7.如图,小明想要测量学校操场上旗杆AB 的高度,他作了如下操作:(1)在点C 处放置测角仪,测得旗杆顶的仰角ACE α∠=;(2)量得测角仪的高度CD a =;(3)量得测角仪到旗杆的水平距离DB b =.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )A .tan a b α+B .sin a b α+C .tan b a α+D .sin b a α+ 8.西南大学附中初2020级小李同学想利用学过的知识测量棵树的高度,假设树是竖直生长的,用图中线段AB 表示,小李站在C 点测得∠BCA =45°,小李从C 点走4米到达了斜坡DE 的底端D 点,并测得∠CDE =150°,从D 点上斜坡走了8米到达E 点,测得∠AED =60°,B ,C ,D 在同一水平线上,A 、B 、C 、D 、E 在同一平面内,则大树AB 的高度约为( )米.(结果精确到0.12≈1.413≈1.73)A .24.3B .24.4C .20.3D .20.4 9.若菱形的周长为16,高为2,则菱形两个邻角的比为( ) A .6:1B .5:1C .4:1D .3:1 10.点E 在射线OA 上,点F 在射线OB 上,AO ⊥BO ,EM 平分∠AEF ,FM 平分∠BFE ,则tan ∠EMF 的值为( )A .12B .33C .1D .311.如图,在△ABC 中,∠ACB =60°,∠CAB =45°,BC =4,点D 为AB 边上一个动点,连接CD ,以DA 、DC 为一组邻边作平行四边形ADCE ,则对角线DE 的最小值是( )A .2+6B .1+3C .4D .2+23 12.如图,正方形ABCD 的边长为1,点A 与原点重合,B 在y 轴正半轴上,D 在x 轴负半轴上,将正方形ABCD 绕着点A 逆时针旋转30至AB C D ''',CD 与B C ''相交于点E ,则E 坐标为( )A .3⎛- ⎝⎭B .11,2⎛⎫- ⎪⎝⎭C .31,2⎛- ⎝⎭D .21,3⎛⎫- ⎪⎝⎭ 二、填空题13.如图,矩形ABCD 中,1AB =,3BC =B 为圆心,BD 为半径画弧,交BC 延长线于M 点,以D 为圆心,CD 为半径画弧,交AD 于点N ,则图中阴影部分的面积是________.14.已知菱形ABCD的边长为6,对角线AC与BD相交于点O,OE⊥AB,垂足为点E,AC =4,那么sin∠AOE=_____.15.如果在某建筑物的A处测得目标B的俯角为37°,那么从目标B可以测得这个建筑物的A处的仰角为_____.16.某人沿坡度是1:2的斜坡走了100米,则他上升的高度是_____米.17.如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°,14tan,23BOACBOD∠==,则ABDCBDSS=___.18.已知在矩形ABCD中,AC=12,∠ACB=15°,那么顶点D到AC的距离为_____.19.如图,边长为6的正方形ABCD绕点C按顺时针方向旋转30后得到正方形EFCG,EF交AD于点H,则DH=____________.20.如图:在矩形ABCD中,4AB=,8BC=,对角线AC,BD相交于点O,过点O 作OE AC⊥交AD于点E.求OE的长是.三、解答题21.小明的爸爸准备驾车外出.启动汽车时,车载报警系统显示正前方有障碍物,此时在眼睛点A 处测得汽车前端F 的俯角为α,且tanα=13,若直线AF 与地面l 1相交于点B ,点A 到地面l 1的垂线段AC 的长度为1.6米,假设眼睛A 处的水平线l 2与地面l 1平行. (1)求BC 的长度; (2)假如障碍物上的点M 正好位于线段BC 的中点位置(障碍物的横截面为长方形,且线段MN 为此长方形前端的边),MN ⊥l 1,若小强的爸爸将汽车沿直线l 1后退0.6米,通过汽车的前端F 1点恰好看见障碍物的顶部N 点(点D 为点A 的对应点,点F 1为点F 的对应点),求障碍物的高度.22.定义:如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征轴三角形”.显然,“特征轴三角形”是等腰三角形.(1)抛物线y =x 2﹣23x 对应的“特征轴三角形”是 ;抛物线y =12x 2﹣2对应的“特征轴三角形”是 .(把下列较恰当结论的序号填在横线上:①腰与底边不相等的等腰三角形;②等边三角形;③非等腰的直角三角形;④等腰直角三角形.)(2)若抛物线y =ax 2+2ax ﹣3a 对应的“特征轴三角形”是直角三角形,请求出a 的值. (3)如图,面积为123的矩形ABCO 的对角线OB 在x 轴的正半轴上,AC 与OB 相交于点E ,若△ABE 是抛物线y =ax 2+bx +c 的“特征轴三角形”,求此抛物线的解析式.23.如图1是小明在健身器材上进行仰卧起坐锻炼时的情景,图2是小明锻炼时上半身由ON 位置运动到与底面CD 垂直的OM 位置时的示意图,已知AC 0.66=米,BD 0.26=米,α30=︒(32 1.414==)(1)求AB 的长(2)若ON 0.6=米,求M N 、两点的距离(精确0.01)24.计算:(1)()2222cos30sin 45cos 601tan 60tan 45-+︒+--︒-︒︒︒(2)23260x x --=(3)2(1)5(1)140x x -+--= 25.已知等边三角形ABC .(1)用尺规作图找出ABC ∆外心O .(2)设等边三角形的边长为4,求外接圆的半径.26.如图,PA 是⊙O 的切线,切点为A ,AC 是⊙O 的直径,连接OP 交⊙O 于E .过A 点作AB ⊥PO 于点D ,交⊙O 于B ,连接BC ,PB .(1)求证:PB 是⊙O 的切线;(2)求证:E 为△PAB 的内心;(3)若cos ∠PAB 10BC =1,求PO 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】过C 点作CH ⊥AD 延长线于H 点,由CH=AB=4求出AH 的长,再减去AD 即得到DH 的长,再在Rt △DCH 中使用勾股定理即可求出CD .【详解】解:如图所示,过C 点作CH ⊥AD 延长线于H 点,∵AD ∥BC ,∠B=90°,∴∠BAH=90°,且∠H=90°,∴四边形ABCH 为矩形,∴AB=CH=4,在Rt △ACH 中,3343AHCH AB , ∴DH=AH-AD=23∴在Rt △CDH 中,22121627CDDH CH ,故选:B .【点睛】本题考查了解直角三角形,熟练掌握30°,60°,90°三角形中三边之比为3::是解决本题的关键. 2.B解析:B【分析】作AD ⊥BC 于D ,由勾股定理得出BC 2231+10,AB 2211+2,由△ABC 的面积求出AD =105,由三角函数定义即可得出答案. 【详解】解:作AD ⊥BC 于D ,如图所示:由勾股定理得:BC 2231+10,AB 2211+2,∵△ABC 的面积=12BC×AD =12×3×1−12×1×1, ∴1210×AD =12×3×1−12×1×1, 解得:AD =105, ∴sin ∠ABC =AD AB 10525; 故选:B .【点睛】本题考查了解直角三角形、勾股定理以及三角函数定义;熟练掌握勾股定理和三角函数定义是解题的关键.3.A解析:A【分析】根据三角形的全等的判定和性质可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,根据三线合一的性质,可判定AC ⊥EF ,然后分别求得AG 与CG 的长,继而求得答案.【详解】∵四边形ABCD 是正方形,∴AB=AD= BC=DC ,∵△AEF 是等边三角形,∴AE=AF ,在Rt △ABE 和Rt △ADF 中,AB AD AE AF =⎧⎨=⎩, ∴Rt △ABE ≌Rt △ADF (HL ),∴BE=DF ,AE=AF ,∵BC=DC ,∴BC-BE=CD-DF ,∴CE=CF ,故①正确;∵CE=CF ,∴△ECF 是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,∴∠AEB=180°-60°-45°=75°,故②正确;如图,连接AC ,交EF 于G 点,∵AE=AF ,CE=CF ,∴AC ⊥EF ,且AC 平分EF ,∵∠CAF≠∠DAF ,∴DF≠FG ,∴BE+DF≠EF ,故③错误;∵△AEF 是边长为2的等边三角形,∠ACB=∠ACD=45°,AC ⊥EF ,∴EG=FG=1,∴AG=AE•sin60°323==CG=112EF =, ∴31;故④正确.综上,①②④正确故选:A .【点睛】本题考查了正方形的性质,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,线段垂直平分线的判定和性质以及解直角三角形.注意准确作出辅助线是解此题的关键.4.D解析:D【分析】根据 B 关于 AE 的对称点为 B′,可得22AB AD '=,1AB D ∴等腰直角三角形,可得D B E '、、三点共线,可求出BE 的长.【详解】 解:26,62,2AB AB AB AD AD ==='∴=',又△DB′F 为等腰直角三角形,045FDB ∴∠=,又在矩形 ABCD ,090ADF ∠=,045ADB ∴='∠,又AB AD '= AB D ∴'等腰直角三角形, 090AB D ∴='∠,090AB E ∠=',D BE ∴'、、三点共线,在等腰直角△RCE ,CE=CD=6,∴BE=BC-CE=6,故选D..【点睛】本题考查三角形的性质及解直角三角形,找出D B E '、、三点共线是解题关键. 5.B解析:B【分析】根据线段垂直平分线的性质得到AE=BE ,由等腰三角形的性质得到∠B=∠BAE ,根据三角形的外角的性质得到∠AEC=∠B+∠BAE=2∠B ,求得∠C=30°,根据三角函数的定义即可得到结论.【详解】∵DE 垂直平分AB 于点D ,∴AE=BE ,∴∠B=∠BAE ,∴∠AEC=∠B+∠BAE=2∠B ,∵AB=AC ,∴∠AEC=2∠C ,∵AE ⊥AC ,∴∠EAC=90°,∴∠C=30°,∴CE=cos30AC ==︒ 故选:B .【点睛】本题考查了线段垂直平分线的性质,等腰三角形的性质,三角形外角的性质以及特殊角的三角函数值.注意掌握数形结合思想的应用.6.A解析:A【分析】证明AC ∥DE ,再由条件CE ∥AD 可证明四边形ACED 是平行四边形;根据线段的垂直平分线证明AE=EB可得△BCE是等腰三角形;首先利用三角函数计算出AD=4,CD=出AB长可得四边形ACEB的周长是10+【详解】①∵∠ACB=90°,DE⊥BC,∴∠ACD=∠CDE=90°,∴AC∥DE,∵CE∥AD,∴四边形ACED是平行四边形,故①正确;②∵D是BC的中点,DE⊥BC,∴EC=EB,∴△BCE是等腰三角形,故②正确;③∵AC=2,∠ADC=30°,AD⋅︒=∴AD=4∵四边形ACED是平行四边形,∴CE=AD=4,∵CE=EB,∴EB=4,DB=∴BC=∴==∴四边形ACEB的周长是10+③正确;综上,①②③均正确,故选:A.【点睛】本题主要考查了平行四边形的判定和性质、等腰三角形的判定和性质、特殊角三角函数、勾股定理、线段的垂直平分线的性质等知识,解题的关键是熟练掌握平行四边形的判定方法.等腰三角形的判定方法.7.A解析:A【分析】延长CE交AB于F,得四边形CDBF为矩形,故CF=DB=b,FB=CD=a,在直角三角形ACF 中,利用CF的长和已知的角的度数,利用正切函数可求得AF的长,从而可求出旗杆AB 的长.【详解】延长CE交AB于F,如图,根据题意得,四边形CDBF 为矩形,∴CF=DB=b ,FB=CD=a ,在Rt △ACF 中,∠ACF=α,CF=b ,tan ∠ACF=AF CF∴AF=tan tan CF ACF b α∠=,AB=AF+BF=tan a b α+,故选:A .【点睛】主要考查了利用了直角三角形的边角关系来解题,通过构造直角三角形,将实际问题转化为数学问题是解答此类题目的关键所在.8.B解析:B【分析】过E 作EG ⊥AB 于G ,EF ⊥BD 于F ,则BG=EF ,EG=BF ,求得∠EDF=30°,根据直角三角形的性质得到EF=12DE=4,33即可得到结论.【详解】过E 作EG ⊥AB 于G ,EF ⊥BD 于F ,则BG =EF ,EG =BF ,∵∠CDE =150°,∴∠EDF =30°,∵DE =8,∴EF =12DE =4,DF =3 ∴CF =CD +DF =3,∵∠ABC =90°,∠ACB =45°,∴AB =BC ,∴GE =BF =AB 3,AG =AB ﹣4,∵∠AED =60°,∠GED =∠EDF =30°,∴∠AEG =30°,∴tan30°=3443AG GE AB ==++ , 解得:AB =14+63≈24.4, 故选:B .【点睛】此题考查解直角三角形的应用-坡度坡角问题,根据题意作出辅助线是解题的关键. 9.B解析:B【分析】由锐角函数可求∠B 的度数,可求∠DAB 的度数,即可求解.【详解】如图,∵四边形ABCD 是菱形,菱形的周长为16,∴AB=BC=CD=DA=4,∵AE=2,AE ⊥BC ,∴sin ∠B=12BE AB = ∴∠B=30° ∵四边形ABCD 是菱形,∴AD ∥BC ,∴∠DAB+∠B=180°,∴∠DAB=150°,∴菱形两邻角的度数比为150°:30°=5:1,故选:B .【点睛】本题考查了菱形的性质,锐角三角函数,能求出∠B 的度数是解决问题的关键. 10.C解析:C【分析】根据三角形外角的性质求得∠AEF+∠BFE=270°,由角平分线定义可求得∠MEF+∠MFE=135°,根据三角形内角和定理可求出∠EMF=45°,从而可得出结论.【详解】如图,∵AO⊥BO∴∠AOB=90°∴∠OEF+∠OFE=90°∵∠AEF和∠BFE是△EOF的外角∴∠AEF=90°+∠OFE,∠BFE=90°+∠OEF∴∠AEF+∠BFE=90°+90°+∠OFE+∠OEF=270°∵EM平分∠AEF,FM平分∠BFE,∴∠MEF+∠MFE=12(∠AEF+∠BFE) =135°,∵∠MEF+∠MFE+∠M=180°∴∠M=180°-(∠MEF+∠MFE)=180°-135°=45°∴tan∠EMF=tan45°=1故选:C.【点睛】此题主要考查了三角形内角和定理、三角形外角的性质及三角函数,求出∠MEF+∠MFE=135°是解答此题的关键.11.A解析:A【分析】设DE交AC于O,作BF⊥AC于F,由直角三角形的性质得出CF=12BC=2,AF=BF=3CF=3,求出AC=CF+AF=3AO=CO=12AC=3DO=EO,当OD⊥AB时,DO的值最小,即DE的值最小,则△AOD是等腰直角三角形,即可得出结果.【详解】解:设DE交AC于O,作BF⊥AC于F,如图所示:则∠BFC=∠BFA=90°,∵∠ACB=60°,∠CAB=45°,∴∠CBF=30°,∠ABF=45°=∠CAB,∴CF=12BC=2,AF=BF3=3∴AC=CF+AF=3∵四边形ADCE是平行四边形,∴AO=CO=12AC=3DO=EO,∴当OD⊥AB时,DO的值最小,即DE的值最小,则△AOD是等腰直角三角形,∴OD=22AO62+∴DE=2OD26故选:A.【点睛】本题主要考查解直角三角形,平行四边形的性质,掌握平行四边形的性质和特殊角的三角函数值是解题的关键.12.A解析:A【分析】连接AE,由旋转性质知AD=AB′=1、∠BAB′=30°、∠B′AD=60°,证Rt△ADE≌Rt△AB′E得∠DAE=12∠B′AD=30°,由DE=ADtan∠DAE可得答案.【详解】如图:连接AE∵将边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB C D ''',∴AD=AB′=1,∠BAB′=30°,∴∠B′AD=60°,在Rt △ADE 和Rt △A B′E 中,∵AD AB AE AE '=⎧⎨=⎩∴Rt △ADE ≌Rt △AB′E (HL ),∴∠DAE=∠B′AE=12∠B′AD=30°, ∴DE=ADtan ∠DAE=1×33=33∴点E 的坐标为(-13 故选:A【点睛】本题考查了正方形的性质、坐标与图形旋转.图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.二、填空题13.【分析】先根据矩形的性质勾股定理可得再利用正弦三角函数可得然后根据即可得【详解】四边形ABCD 是矩形在中则即图中阴影部分的面积是故答案为:【点睛】本题考查了矩形的性质正弦三角函数扇形的面积公式等知识 解析:7312π-【分析】先根据矩形的性质、勾股定理可得1,2,90CD BD ADC BCD ==∠=∠=︒,再利用正弦三角函数可得30CBD ∠=︒,然后根据RtBCD DCN BDM S S S S =+-阴影扇形扇形即可得.【详解】四边形ABCD 是矩形,1AB =,3BC =,1,2,90CD AB BC ADC BCD ∴====∠=∠=︒,在Rt BCD 中,1sin 2CD CBD BD ∠==, 30CBD ∴∠=︒, 则Rt BCDDCN BDM S S S S =+-阴影扇形扇形, 22901302113603602ππ⨯⨯=+-⨯7122π=-,即图中阴影部分的面积是7122π-故答案为:712π- 【点睛】 本题考查了矩形的性质、正弦三角函数、扇形的面积公式等知识点,熟练掌握扇形的面积公式是解题关键.14.【分析】由菱形对角线互相垂直得到AC ⊥BD 根据∠OAE =∠BAO ∠OEA =∠AOB 可以判定△OAE ∽△ABO 进而得到∠AOE =∠BAO 再由AO 和AB 的值即可求得sin ∠AOE 的值【详解】∵菱形对角线 解析:13【分析】由菱形对角线互相垂直得到AC ⊥BD ,根据∠OAE =∠BAO ,∠OEA =∠AOB 可以判定△OAE ∽△ABO ,进而得到∠AOE =∠BAO ,再由AO 和AB 的值即可求得sin ∠AOE 的值.【详解】∵菱形对角线互相垂直,∴∠OEA =∠AOB ,∵∠OAE =∠BAO ,∴△OAE ∽△ABO ,∴∠AOE =∠ABO ,∵AO =12AC =2,AB =6, ∴sin ∠AOE =sin ∠ABO =AO AB =13. 故答案为:13. 【点睛】 考查了相似三角形判定和性质、三角形中正弦函数的计算,解题关键是证明三角形相似再利用其性质得到∠AOE=∠ABO .15.37°【分析】由俯角和仰角的定义和平行线的性质即可得到目标B 可以测得这个建筑物的A 处的仰角为37°【详解】如图∵某建筑物的A 处测得目标B 的俯角为37°∴目标B 可以测得这个建筑物的A 处的仰角为37°故解析:37°【分析】由俯角和仰角的定义和平行线的性质即可得到目标B 可以测得这个建筑物的A 处的仰角为37°.【详解】如图,∵某建筑物的A 处测得目标B 的俯角为37°,∴目标B 可以测得这个建筑物的A 处的仰角为37°,故答案为:37°.【点睛】考查了解直角三角形,解题关键是理解向下看,视线与水平线的夹角叫俯角;向上看,视线与水平线的夹角叫仰角.16.【分析】先画出图形再根据坡度的可得然后设米从而可得米最后利用勾股定理求出x 的值由此即可得出答案【详解】如图由题意得:米设米则米由勾股定理得:即解得(米)则米即他上升的高度是米故答案为:【点睛】本题考 解析:5【分析】 先画出图形,再根据坡度的可得12AC BC =,然后设AC x =米,从而可得2BC x =米,最后利用勾股定理求出x 的值,由此即可得出答案.【详解】如图,由题意得:90C ∠=︒,100AB =米,1tan 2AC B BC ==, 设AC x =米,则2BC x =米, 由勾股定理得:22AB AC BC =+()222100x x +=, 解得205x =(米),则5AC =即他上升的高度是5故答案为:205.【点睛】本题考查了勾股定理、解直角三角形的应用:坡度问题,掌握理解坡度的概念是解题关键.17.【分析】过B 点作BE//AD 交AC 于点E 证明得到再证明利用设利用三角形的面积公式可得答案【详解】解:过B 点作BE//AD 交AC 于点EBE ⊥AD ∴∴由∴设则故答案为:解析:332【分析】过B 点作BE//AD 交AC 于点E ,证明ADO EBO ∽△△,得到3,AO OE =再证明,ABE ACB ∠=∠利用1tan tan ,2BE AE ACB ABE CE BE ∠==∠==设,OE a =利用三角形的面积公式可得答案.【详解】 解:过B 点作BE//AD 交AC 于点E ,90,DAC ∠=︒∴ BE ⊥AD ,ADO EBO ∴∽,∴,AO DO EO BO = 43BO OD = ∴3,4AO DO EO BO == 3,4AO OE ∴= 由1tan 2ACB ∠=, 1,2BE CE ∴= 2,CE BE ∴=90,,ABC BE AC ∠=︒⊥90,ABE CBE CBE ACB ∴∠+∠=︒=∠+∠, ABE ACB ∴∠=∠1tan tan,2AEACB ABEBE∴∠=∠==2,BE AE∴=24,CE BE AE∴==∴OAB OADABDCBD OCB OCDS SSS S S∆∆+=+()()11221122AO AD AO BE AO AD BE AOOC AD BE OCOC AD OC BE•+•+===+•+•设,OE a=则3,4AO a=7,4AE AO OE a∴=+=7,CE a=8.OC OE CE a=+=334.832ABDCBDaS AOS OC a∆∆===故答案为:33218.3【分析】先利用三角函数的值分别求出AB及BC然后利用三角形ADC面积的两种表示形式可求出DE的长【详解】如图过点D作DE⊥AC于点E在这里先推导出sin15°的值:如图设中D是AC上一点则设则由题解析:3【分析】先利用三角函数的值分别求出AB及BC,然后利用三角形ADC面积的两种表示形式可求出DE的长.【详解】如图,过点D作DE⊥AC于点E,在这里先推导出sin15°的值:如图,设Rt ABC 中,A 15,C 90∠=︒∠=︒,D 是AC 上一点,BDC 30∠=︒,则ABD 15∠=︒,AD BD =,设BC x =,则AD BD 2x ==,DC 3x =,AC (32)x =+2222[(32)](62)AB AB BC x x ∴=+=+⨯+=+,BC 62sin15sin A AB 4(62)x x -∴︒====+由题意得:AB =AC sin ∠ACB =36﹣32,BC =36+32,S △ADC =12AD •DC =12AC •DE =9, ∴DE =3.故答案为:3.【点睛】此题考查的是矩形的性质,解答本题的关键是根据∠ACB 的度数求出AB 及AC 的长,这要求我们熟练掌握三角函数值的求解方法.19.【分析】过点F 作FI ⊥BC 于点I 延长线IF 交AD 于J 根据含30°直角三角形的性质可求出FIFJ 和JH 的长度从而求出HD 的长度【详解】解:过点F 作FI ⊥BC 于点BC 延长线AD 交AD 于J 由题意可知:CF解析:23【分析】过点F 作FI ⊥BC 于点I ,延长线IF 交AD 于J ,根据含30°直角三角形的性质可求出FI 、FJ 和JH 的长度,从而求出HD 的长度.【详解】解:过点F 作FI ⊥BC 于点BC ,延长线AD 交AD 于J ,由题意可知:CF=BC=6,∠FCB=30°,∴FI=3,CI=33∵JI=CD=6,∴JF=JI-FI=6-3=3,∵∠HFC=90°,∴∠JFH+∠IFC=∠IFC+∠FCB=90°,∴∠JFH=∠FCB=30°,设JH=x ,则HF=2x ,∴由勾股定理可知:(2x )2=x 2+32,∴∴DH=DJ-JH==故答案为:【点睛】本题考查正方形的性质,涉及正方形的性质,勾股定理,旋转的性质,含30°的直角三角形的性质,本题属于中等题型.20.【分析】利用矩形的性质求解再证明利用锐角三角函数可得答案【详解】矩形矩形故答案为:【点睛】本题考查的是矩形的性质解直角三角形知识掌握以上知识点是解题关键【分析】利用矩形的性质求解AC ,再证明OAE ACB ∠=∠,利用锐角三角函数可得答案.【详解】矩形ABCD ,4AB =,8BC =,90,ABC AC ∴∠=︒==41,82OA OC tan ACB ==∠== 矩形ABCD ,//,AD BC ∴,OAE ACB ∴∠=∠,OE OA ⊥1tan tan ,2OAE ACB ∴∠=∠= 1,2=OE ∴=【点睛】本题考查的是矩形的性质,解直角三角形知识,掌握以上知识点是解题关键.三、解答题21.(1)4.8;(2)0.6.【分析】(1)在Rt △ABC ,根据tan ∠ABC =tanα=13,AC=1.6米,即可求出BC 的长度; (2)过D 作DH ⊥BC 于H ,求出EM 的长度,证明△EMN ∽△EHD ,得到MN EM DH EH=,即可求解.【详解】解:(1)由题意得,∠ABC =∠α, 在Rt △ABC 中,AC =1.6,tan ∠ABC =tanα=13, ∴BC = 1.6 4.81tan 3AC ABC ==∠m , 答:BC 的长度为4.8m ;(2)过D 作DH ⊥BC 于H ,则四边形ADHC 是矩形,∴AD =CH =BE =0.6,∵点M 是线段BC 的中点,∴BM =CM =2.4米,∴EM =BM ﹣BE =1.8,∵MN ⊥BC ,∴MN ∥DH ,∴△EMN ∽△EHD ,∴MN EM DH EH =, ∴ 1.81.6 4.8MN =, ∴MN =0.6,答:障碍物的高度为0.6米.【点睛】本题考查解直角三角形的应用,理解三角函数的意义,构造直角三角形,得到相似是解题的关键.22.(1)②;④;(2)12±;(3)y =﹣x 2+63x ﹣24. 【分析】 (1)根据题意先求出这两个抛物线的顶点及与x 轴的交点坐标,然后进行求解即可; (2)由题意易得抛物线的顶点及与x 轴的交点坐标,然后根据题意列方程求解即可; (3)如图,过点A 作AH ⊥x 轴,交于点H ,由题意易得S △ABE =14ABCD S 矩形=14×123=33,则有3BE 2=33,进而可得A (33,3),E (23,0),B (43,0),然后利用待定系数法求解即可.【详解】解:(1)由抛物线y =x 2﹣23x 可得顶点坐标为:()3,3-,与x 轴的交点坐标为:()()0,0,23,0, ∴抛物线y =x 2﹣23x 对应的“特征轴三角形”是等边三角形;由抛物线y =12x 2﹣2可得顶点坐标为:()0,2-,与x 轴的交点坐标为:()()2,0,2,0-, ∴抛物线y =12x 2﹣2对应的“特征轴三角形”是等腰直角三角形; 故答案为②;④;(2)设抛物线y =ax 2+2ax ﹣3a 与x 轴的交点坐标为A ,B ,顶点为D ,∴A (﹣3,0),B (1,0),D (﹣1,﹣4a ),∵抛物线y =ax 2+2ax ﹣3a 对应的“特征轴三角形”是直角三角形,∴AB 2=AD 2+BD 2,∴16=4+16a 2+4+16a 2,∴a =12±; (3)如图,∵四边形ABCD 是矩形,∴AE =CE =OE =BE ,∴S △ABE =14ABCD S 矩形=143=3∵△ABE是抛物线的“特征轴三角形”,根据抛物线的对称性得,AE=AB,∴AE=AB=BE,∴△ABE是等边三角形,过点A作AH⊥BE,∴AH=AB sin∠ABE,∴2=∴BE=∴AH=3,EH∴A(3),E(,0),B(0),设抛物线解析式为y=a(x﹣)2+3,将点E(0)代入得,a=﹣1,∴y=﹣(x﹣2+3=﹣x2﹣24.∴过点A,B,E三点的抛物线的解析式y=﹣x2x﹣24.【点睛】本题主要考查二次函数的综合及三角函数,熟练掌握二次函数的性质及三角函数是解题的关键.23.(1)0.8;(2)1.04 m【分析】(1)已知AC与BD,求AB,为此过D作BE⊥AC于E,可求AE,由∠ABE已知,利用30角所对直角.边等于斜边的一半,可求AB即可,(2)过N作NF⊥MO交射线MO于F点,则FN∥EB,∠ONF=α=30°,利用外角有∠M=∠MNO=12∠FON=30º,在30 º Rt△OFN 中,OF=12ON,易求MF,利用Rt△MFN中MN=MFcos30即可.【详解】(1)过B作BE⊥AC于E,则四边形CDBE为矩形,CE=BD=0.26米,AC=0.66米,∴AE=AC-EC=0.66-0.26=0.40米,在Rt△AEB中,α=30°,AB=2AE=2×0.40=0.80米,(2)过N作NF⊥MO交射线MO于F点,则FN∥EB,∴∠ONF=α=30°,∵ON=0,6米,∴OF=12ON=0,3米,∵OM=ON=0.6米,∴MF=0.9米,∴∠FON=90º-30º=60º,∴∠M=∠MNO=12∠FON=30º, 在Rt △MFN 中,MN=MF ==1.039 1.04cos303≈︒.【点睛】本题考查求斜面长,MN 长,关键是掌握把要求的线段置于Rt △中,用三角函数来解决问题.24.(1)15342--;(2)11193x =,21193x =;(3)13x =,26x =-; 【分析】(1)原式利用特殊角的三角函数值,以及乘方的意义计算即可得到结果;(2)利用求根公式计算即可;(3)将(x -1)看作整体,然后利用因式分解法解方程即可.【详解】(1)解:()2222cos30sin 45cos 601tan 60tan 45-+︒+-︒︒︒︒ =223214()(13)1222-++⨯- =3131)14--- =1534-- (2)解:23260x x --=,∵3,2,6a b c ==-=-,∴2(2)43(6)472760,∆=--⨯⨯-=+=>∴方程有两个不相等的实根, ∴(2)76119x --±±== ∴11193x =,21193x =;(3)解:2(1)5(1)140x x -+--=,[][](1)7(1)20,x x -+--=∴60x +=或30x -=,∴126,3x x =-=.【点睛】本题考查了特殊角的三角函数值、实数的运算以及一元二次方程的解法,常用的解一元二次方程的方法有直接开平方法、配方法、因式分解法、求根公式法,熟练掌握运算法则是解本题的关键.25.(1)见解析;(2)433【分析】 (1)作AB ,BC 的垂直平分线交于点O ,则点O 即为所求;(2)根据正三角形的每个内角为60°和三角形外接圆的相关知识解答.【详解】(1)如图所示,点O 即为所求ABC ∆外心.(2)如图,O 是等边△ABC 的外接圆,连接OA 、OB 、OC ,延长AO 交BC 于D , ∵OB=OC , ∴点O 在BC 的垂直平分线上,又∵ABC 是等边三角形,4AB BC AC ===,∴点A 在BC 的垂直平分线上,∴AO 是BC 的垂直平分线,∴OD ⊥BC ,BD=BC=2,∴190602ODB BOD BOC ∠=︒∠=∠=︒,, ∴43sin 60332BD OB ===︒.【点睛】本题考查正多边形外接圆的问题,解答此题要明确两点:(1)正多边形的中心和外接圆圆心重合;(2)正三角形每个内角每条边都相等.26.(1)见解析;(2)见解析;(3)5【分析】(1)连结OB ,根据圆周角定理得到∠ABC=90°,证明△AOP ≌△BOP ,得到∠OBP=∠OAP ,根据切线的判定定理证明;(2)连结AE ,根据切线的性质定理得到∠PAE+∠OAE=90°,证明EA 平分∠PAD ,根据三角形的内心的概念证明即可;(3)根据余弦的定义求出OA ,证明△PAO ∽△ABC ,根据相似三角形的性质列出比例式,计算即可.【详解】(1)证明:连结OB ,∵AC 为⊙O 的直径,∴∠ABC =90°,∵AB ⊥PO ,∴PO ∥BC∴∠AOP =∠C ,∠POB =∠OBC ,OB =OC ,∴∠OBC =∠C ,∴∠AOP =∠POB ,在△AOP 和△BOP 中,OA OB AOP POB PO PO =⎧⎪∠=∠⎨⎪=⎩,∴△AOP ≌△BOP (SAS ),∴∠OBP =∠OAP ,∵PA 为⊙O 的切线,∴∠OAP =90°,∴∠OBP =90°,∴PB 是⊙O 的切线;(2)证明:连结AE ,∵PA 为⊙O 的切线,∴∠PAE +∠OAE =90°,∵AD ⊥ED ,∴∠EAD +∠AED =90°,∵OE =OA ,∴∠OAE =∠AED ,∴∠PAE =∠DAE ,即EA 平分∠PAD ,∵PA 、PB 为⊙O 的切线,∴PD 平分∠APB∴E 为△PAB 的内心;(3)解:∵∠PAB +∠BAC =90°,∠C +∠BAC =90°,∴∠PAB =∠C ,∴cos ∠C =cos ∠PAB =10,在Rt △ABC 中,cos ∠C =BC AC =1AC ,∴AC,AO ∵△PAO ∽△ABC , ∴PO AO AC BC=,∴PO =AO ACBC ⋅=215. 【点睛】本题考查的是三角形的内切圆和内心、相似三角形的判定和性质、切线的判定,掌握切线的判定定理、相似三角形的判定定理和性质定理是解题的关键.。
(常考题)人教版初中数学九年级数学下册第三单元《锐角三角函数》测试卷(含答案解析)(2)

一、选择题1.已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为()A.33(3,)22-B.33(3,)22--C.33(,3)22D.(3,33)-2.如图,在矩形ABCD中,G是AB边上一点,连结GC,取线段CG上点E,使ED DC=且90AED∠=︒,AF CG⊥于F,2AF=,1FG=,则EC的长()A.4 B.5 C.163D.833.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道.用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是()A.sin0.2= B.2ndF sin0.2=C.tan0.2= D.2ndF tan0.2=4.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点,C画射线OC,则tan AOC∠的值为()A.12B.33C.32D.35.小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆PA的高度与拉绳PB的长度相等,小明先将PB拉到'PB的位置,测得(''PB C a B C∠=为水平线),测角仪/B D的高度为1米,则旗杆PA的高度为()A.11sin a+米B.11cos a-米C.11sin a-米D.11cos a+米6.如图,将一副三角尺如图所示叠放在一起,则BECE的值是()A.3B.3C.2 D.37.如图,在4×5的正方形网格中,每个小正方形的边长都是1,ΔABC的顶点都在这些小正方形的顶点上,那么cos∠ACB值为()A 35B17C.35D.458.如图,四边形 ABCD中,BD是对角线,AB=BC,∠ABC=60°,CD=4,∠ADC=60°,则△BCD的面积为()A .43B .8C .23+4D .36 9.如图,半径为5的O 中, OA BC ⊥,30ADC ∠=︒,则BC 的长为( )A .52B .53C .522D .53210.如图,在平面直角坐标系中,等边三角形OAB 的边长为4,点A 在第二象限内,将OAB 沿射线AO 平移,平移后点A '的横坐标为43,则点B ′的坐标为( )A .(63,2)-B .(63,23)-C .()6,2-D .(63,2)-11.如图,在扇形OAB 中,120AOB ∠=︒,点P 是弧AB 上的一个动点(不与点A 、B 重合),C 、D 分别是弦AP ,BP 的中点.若33CD =,则扇形AOB 的面积为( )A .12πB .2πC .4πD .24π 12.如图,四边形ABCD 中,AB=AD ,AD ∥BC ,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD 的面积是( )A .3B .32C .3D .934二、填空题13.如图,在边长为10的菱形ABCD 中,AC 为对角线,∠ABC =60°,M 、N 分别是边BC ,CD 上的点,BM =CN ,连接MN 交AC 于P 点,当MN 最短时,PC 长度为_____.14.如图,在矩形ABCD 中,6BC =,4cos 5CAB ∠=, P 为对角线AC 上一动点,过线段BP 上的点M 作EF BP ⊥,交AB 边于点E ,交BC 边于点 F ,点N 为线段EF 的中点,若四边形BEPF 的面积为18,则线段BN 的最大值为 ________ .15.01sin 4513(32018)6tan 302-++︒︒=________. 16.如图,在ABC 中,已知90,4,8C AC BC ∠=︒==,将ABC 绕着点C 逆时针旋转到''A B C 处,此时线段''A B 与BC 的交点D 为BC 的中点,那么'B D 的长度为_________.17.在ABCD 中,若30B ∠=︒,BC 10cm =,6AB cm =,则ABCD 的面积是__________.18.如图,MN 是半径为1的O 的直径,点A 在O 上,30AMN ∠=︒,点B 是AN 的中点,点P 是直径MN 上一个动点,则PA PB +的最小值为______.19.如图,我市在建高铁的某段路基横断面为梯形ABCD ,DC ∥AB ,BC 长为6米,坡角β为45°,AD 的坡角α为30°,则AD 的长为 ________ 米 (结果保留根号)20.如图,∠EFG =90°,EF =10,OG =17,cos ∠FGO =0.6,则点F 的坐标是_______.三、解答题21.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP 上架设测角仪,先在点M 处测得观星台最高点A 的仰角为22°,然后沿MP 方向前进16m 到达点N 处,测得点A 的仰角为45°.测角仪的高度为1.6m 求观星台最高点A 距离地面的高度(结果精确到0.1m .参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.402≈1.41).22.如图,在一次数学课外实践活动中,要求测教学楼的高度AB 、小刚在D 处用高1.5m 的测角仪CD ,测得教学楼顶端A 的仰角为30°,然后向教学楼前进40m 到达E ,又测得教学楼顶端A 的仰角为60°.求这幢教学楼的高度AB .(结果带根号)23.小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD 放在每格宽度为12mm 的横格纸中,恰好四个顶点都在横格线上,已知36a =︒,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm )(参考数据:360.60︒≈sin ,360.80cos ≈,360.75tan ≈)24.计算:(1)()2222cos30sin 45cos 601tan 60tan 45-+︒+-︒︒︒︒(2)23260x x --=(3)2(1)5(1)140x x -+--= 25.已知:如图,在△ABC 中,∠A=30°,点D 是AB 中点,E 在边AC 上,且∠AED=∠ABC ,如果AE=6,EC=2.(1)求边AB 的长;(2)求tan ∠AED 的值.26.平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A,B两点,点A,B的坐标分别为(﹣3,0),(1,0),与y轴交于点C,点D为顶点.(1)求抛物线的解析式和tan∠DAC;(2)点E是直线AC下方的抛物线上一点,且S△ACE=2S△ACD,求点E的坐标;(3)如图2,若点P是线段AC上的一个动点,∠DPQ=∠DAC,DP⊥DQ,则点P在线段AC上运动时,D点不变,Q点随之运动.求当点P从点A运动到点C时,点Q运动的路径长.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】如图,作 DE x 轴于点E ,灵活运用三角函数解直角三角形来求点 D 的坐标.【详解】解:如图,作DE⊥x轴于点E,∵点A的坐标为(0,3),∴OA=3.又∵∠OAB=60°,∴OB =OA•tan ∠OAB =33,∠ABO =30°. ∴BD =BC =OA =3.∵根据折叠的性质知∠ABD =∠ABC =60°,∴∠DBE =30°,∴DE =12BD =32,BE =33 ∴OE =33-33=33, ∴E 33(3,)22-. 故选:A .【点睛】本题考查了矩形的性质、坐标与图形性质以及折叠问题,翻折前后对应角相等,对应边相等;注意构造直角三角形利用相应的三角函数值求解.2.C解析:C【分析】如图,过D 作DP CE ⊥于,P 证明:,EP CP EDP CDP =∠=∠, ,DEC DCE ∠=∠再证明,AEF BCG EDP ∠=∠=∠ 结合矩形的性质证明:,AFG EFA ∽利用相似三角形的性质可得4EF =,再求解,AG AE ,设,BG x = 可得5,2,DE x AD x =+= 利用勾股定理求解,x 再由,BCG EDP ∠=∠可得:1,2EP DP =设,EP m = 则2,DP m = 由勾股定理求解m , 从而可得答案.【详解】解:如图,过D 作DP CE ⊥于,P,DE DC =,EP CP EDP CDP ∴=∠=∠, ,DEC DCE ∠=∠90,AED DCB ∠=︒=∠90,AEF DEC DCE BCG DEC EDP ∴∠+∠=︒=∠+∠=∠+∠,AEF BCG EDP ∴∠=∠=∠,,90AGF CGB AF CG B ∠=∠⊥∠=︒,,FAG BCG ∴∠=∠,FAG AEF ∴∠=∠90AFG EFA ∠=∠=︒,,AFG EFA ∴∽ ,AF FG EF FA ∴= 21AF FG ==,,21,2EF ∴= 4EF ∴=,2225AE AF EF ∴=+=, 225,AG AF FG =+= 设BG x =,则5,AB CD x DE ==+=AEF BCG ∠=∠,1tan tan ,2AF AEF BCG EF ∴∠=∠== 1,2BG BC ∴= 2,BC x AD ∴== ()()()2222255,x x ∴=++235250,x x ∴--=553x ∴=5x = 55855DE ∴== ,EDP BCG ∠=∠1,2EP DP ∴= 设,EP m = 则2,DP m =()22285+2,m m ⎛⎫∴= ⎪ ⎪⎝⎭ 83m ∴=(负根舍去) 162.3EC EP ∴==故选:.C【点睛】 本题考查的是矩形的性质,勾股定理的应用,等腰三角形的性质,三角形相似的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键.3.B解析:B【分析】先利用正弦的定义得到10sin 0.250A ==,然后利用计算器求锐角∠A . 【详解】∵ 10sin 0.250A ==, ∴ 用计算器求值的顺序为20.2ndFsin =,故选:B .【点睛】本题考查了锐角三角函数及计算器的应用,掌握科学计算器的应用是解决本题的关键. 4.D解析:D【分析】由题意可以得到∠AOC 的度数,再根据特殊角的锐角三角函数值可以得解.【详解】解:如图,连结BC ,则由题意可得OC=OB ,CB=OB ,∴OC=OB=BC ,∴△BOC 是等边三角形,∴∠AOC=60°,∴tan ∠AOC=tan60°故选D .【点睛】本题考查尺规作图与三角形的综合应用,由尺规作图的作法得到所作三角形是等边三角形是解题关键.5.C解析:C【分析】设PA=PB=PB′=x ,在RT △PCB′中,根据sin αPC PB =',列出方程即可解决问题. 【详解】解:设PA=PB=PB′=x ,在RT △PCB′中,sin αPC PB ='∴1sin αx x-=∴x 1xsin α-=, ∴(1-sin α)x=1,∴x=11sin α-. 故选C .【点睛】 本题考查解直角三角形、三角函数等知识,解题的关键是设未知数列方程,属于中考常考题型.6.B解析:B【分析】设AC=AB=x,求得tan AC CD D ===,根据相似三角形的性质即可得到结论. 【详解】解:设AC=AB=x ,则tan AC CD D ===, ∵∠BAC=∠ACD=90°,∴∠BAC+∠ACD=180°,∴AB ∥CD ,∴△ABE ∽△DCE , ∴33BE AB CE CD x===, 故选:B .【点睛】本题主要考查相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.7.C解析:C【分析】如图,过点A 作AH BC ⊥于H .利用勾股定理求出AC 即可解决问题.【详解】解:如图,过点A 作AH BC ⊥于H .在Rt ACH ∆中,4AH =,3CH =,2222435AC AH CH ∴=+=+=,3cos 5CH ACH AC ∴∠==, 故选:C .【点睛】本题考查解直角三角形,解题的关键是学会添加常用辅助线,构造直角三角形解决问题. 8.A解析:A【分析】先证明△ABC 是等边三角形,以C 为圆心,CD 为半径作圆,交AD 边与点M ,可得△CDM是等边三角形,进而得到∆BCM ≅∆ACD ,可得到60BMC ∠=︒,得到BM ∥CD ,过点M 作MH CD ⊥,根据△BCD 的面积等于△CDM 的面积求解即可;【详解】∵BD 是对角线,AB=BC ,∠ABC=60°,∴△ABC 是等边三角形,以C 为圆心,CD 为半径作圆,交AD 边与点M ,延长BC ,交C 于点N ,如图所示,∵∠ADC=60°,CM=CD ,∴△CDM 是等边三角形,∴60MCD ∠=︒,∴∠ACB+∠ACM=∠MCD+∠ACM ,即:∠BCM=∠ACD ,∴∆BCM ≅∆ACD ,∴∠BMC=∠ADC=60°,∴∠BMC=∠MCD ,∴BM ∥CD ,根据平行线间的距离相等得到△BCD 的面积等于△CDM 的面积,过点M 作MH CD ⊥,∵CD=4,∴2==CH HD , ∴tan 602MH MH DH ︒==, ∴23MH =, ∴△△1423432BDC CDM S S ==⨯⨯= 故答案选A .【点睛】本题主要考查了四边形综合,结合等边三角形性质,构造等边△CDM 是解题的关键. 9.B解析:B【分析】连接OC ,设BC 与OA 交于点E ,根据圆周角定理即可求出∠AOC ,然后根据垂径定理可得BC=2CE ,利用锐角三角函数求出CE ,即可求出结论.【详解】解:连接OC ,设BC 与OA 交于点E∵30ADC ∠=︒∴∠AOC=2∠ADC=60°∵OA BC ⊥∴BC=2CE ,在Rt △OCE 中,CE=OC·sin ∠AOC=532 ∴BC=53故选B .【点睛】此题考查的是圆周角定理、垂径定理和锐角三角函数,掌握圆周角定理、垂径定理和锐角三角函数是解题关键. 10.D解析:D【详解】如解图,过点A 作AC x ⊥轴,过点A '作A D x '⊥轴,∵AOB 是等边三角形,∴4AO BO ==,60AOB ∠=︒,∴30AOC ∠=︒,∴·cos 23CO OA AOC ==,2AC =,∴(23,2)A -,∵30AOD AOC ∠'=∠=︒,43OD =,∴·t 34343an A D OD A OD ⨯=∠'==',∴(43,4)A '-,∴点A '是将点A 向右平移63个单位,向下平移6个单位得到的,∴点B '也是将点B 向右平移63个单位,向下平移6个单位得到的,∵()0,4B ,∴B '的坐标为(63,2)-.11.A解析:A【分析】如图,作OH ⊥AB 于H .利用三角形中位线定理求出AB 的长,解直角三角形求出OB 即可解决问题.【详解】解:如图作OH ⊥AB 于H .∵C 、D 分别是弦AP 、BP 的中点.∴CD 是△APB 的中位线,∴AB =2CD =63∵OH ⊥AB ,∴BH =AH =33∵OA =OB ,∠AOB =120°,∴∠AOH =∠BOH =60°,在Rt △AOH 中,sin ∠AOH =AH AO, ∴AO =336sin 3AH AOH ==∠, ∴扇形AOB 的面积为:2120612360ππ=, 故选:A .【点睛】本题考查扇形面积公式,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.12.A解析:A【分析】如图,过点A 作AE ⊥BC 于E ,过点D 作DF ⊥BC 于F .构建矩形AEFD 和直角三角形,通过含30度角的直角三角形的性质求得AE 的长度,然后由三角形的面积公式进行解答即可.【详解】解:如图,过点A 作AE ⊥BC 于E ,过点D 作DF ⊥BC 于F .设AB=AD=x .又∵AD∥BC,∴四边形AEFD是矩形,∴AD=EF=x.在Rt△ABE中,∠ABC=60°,则∠BAE=30°,∴BE=12AB=12x,∴22AB BE3,在Rt△CDF中,∠FCD=30°,则CF=DF•cot30°=32 x.又∵BC=6,∴BE+EF+CF=6,即12x+x+32x=6,解得 x=2∴△ACD的面积是:12AD•DF=12x×32x=34×223故选:A.【点睛】此题考查了勾股定理,三角形的面积以及含30度角的直角三角形.解题的关键是作出辅助线,构建矩形和直角三角形,目的是求得△ADC的底边AD以及该边上的高线DF的长度.二、填空题13.【分析】连接AMAN证明△AMB≌△ANC推出△AMN为等边三角形当AM⊥BC时AM最短即MN最短在Rt△ABM中求出AM的长在Rt△AMP中求出AP的长即可解决问题【详解】解:连接AMAN∵ABC解析:5 2【分析】连接AM,AN,证明△AMB≌△ANC,推出△AMN为等边三角形,当AM⊥BC时,AM最短,即MN最短,在Rt△ABM中求出AM的长,在Rt△AMP中求出AP的长,即可解决问题.【详解】解:连接AM,AN,∵ABCD是菱形,∠ABC=60°,∴△ABC为等边三角形,∴∠BAC=60°,AB=AC=10,同理可证∠ACN=60°,在△AMB 和△ANC 中,AB AC B ACN BM NC =⎧⎪∠=∠⎨⎪=⎩,∴△AMB ≌△ANC ,∴AM=AN ,∠BAM+∠MAC=∠MAC+∠NAC=60°,∴∠MAN=60°,∴△AMN 为等边三角形,∴MN=AM ,∠MAN=60°,当AM ⊥BC 时,AM 最短,即MN 最短,∵sinB=AM AB , ∴AM=sin60°×10=53.∵∠ABC=60°,∴∠BAM=30°,∴∠MAC=30°,∴∠NAC=30°,∴AP ⊥MN .∵sin ∠AMN=AP AM, ∴AP=sin60°×53=152, ∴CP=10-152=52. 故答案为:52.【点睛】本题考查了菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,以及锐角三角函数的知识,熟练掌握各知识点是解答本题的关键.14.【分析】在△ABC 中求出AC 与AB 的长点P 在AC 上则6≤BP≤8由点N 为线段EF 的中点∠ABC=90º则EF=2BN 根据四边形BEPF 的面积为18利用对角线乘积的一半求面积得BN 与PB 成反比例PB 最 解析:154【分析】在△ABC 中,6BC =,4cos 5CAB ∠=求出AC 与AB 的长,点P 在AC 上 则6≤BP≤8,由点N 为线段EF 的中点,∠ABC=90º,则EF=2BN ,根据四边形BEPF 的面积为18,EF BP ⊥利用对角线乘积的一半求面积得,PB BN=18,BN 与PB 成反比例, PB 最小时,BN 最大,当PB ⊥AC 时,PB 最小,求出最小值即可.【详解】在△ABC 中,6BC =,4cos 5CAB ∠=, ∵22sin cos 1CAB CAB ∠+∠=,∴3sin 5CAB ∠=, 由正弦函数定义BC sin =ACCAB ∠, ∴AC=BC 6==103sin 5CAB ∠,由勾股定理得8==,点P 在AC 上 则6≤BP≤8,∵点N 为线段EF 的中点,由∠ABC=90º,∴EF=2BN ,∵四边形BEPF 的面积为18,EF BP ⊥,∴S 四边形EBFP =11PB EF=PB 2BN=PB BN=1822⨯, ∴PB BN=18, ∴18BN=PB, 当PB 最小时,BN 最大, 当PB ⊥AC 时,PB 最小,即S △ABC=11AB BC=AC BP 22 BP 最小=AB BC 8624==AC 105⨯ BN 最大=1815=2445故答案为:154.【点睛】本题考查锐角三角函数解直角三角形与点到直线距离最短问题,掌握锐角三角函数及其之间的关系,会用锐角三角函数解直角三角形,掌握垂线段最短,会利用面积或勾股定理求BP的最小值,解题时要理解BP最小,BN最大是解题关键.15.【分析】先计算特殊角的三角函数值化简绝对值零指数幂再计算实数的混合运算即可得【详解】原式故答案为:【点睛】本题考查了特殊角的三角函数值绝对值零指数幂实数的运算熟记各运算法则是解题关键解析:32322+【分析】先计算特殊角的三角函数值、化简绝对值、零指数幂,再计算实数的混合运算即可得.【详解】原式213131)622-++=⨯21312322=++3 23 2=+,故答案为:3232.【点睛】本题考查了特殊角的三角函数值、绝对值、零指数幂、实数的运算,熟记各运算法则是解题关键.16.【分析】根据题意先考虑多种情况①与D重合=AB;②与D不重合过点C 作CE于点E利用的余弦值求出由等腰三角形三线合一得求出再用减去得到【详解】①如图与D重合②如图与D不重合过点C作CE于点E∵旋转∴在解析:125 5,5【分析】根据题意,先考虑多种情况,①A '与D 重合,B D '=AB ;②A '与D 不重合,过点C 作CE ⊥A B ''于点E ,利用CA B ''∠的余弦值求出A E ',由等腰三角形三线合一得2A D A E ''=,求出A D ',再用A B ''减去A D '得到B D '.【详解】①如图,A '与D 重合,45B D AB '==.②如图,A '与D 不重合,过点C 作CE ⊥A B ''于点E , ∵旋转,∴4AC A C '==,8BC B C '==,在Rt A B C ''△中,由勾股定理,22224845A B A C B C ''''=++= 5cos 45A C CA B A B '''∠===', 在Rt A EC '中,5cos 4A E A E CA E A C '''∠===', ∴45A E '=∵D 是BC 中点∴4CD CA '== 在等腰三角形ACD '中,由“三线合一”得852A D A E ''==, ∴8512545B D A B A D ''''=-==故答案是:45或125. 【点睛】 本题考查图形的旋转,等腰三角形三线合一,锐角三角函数,关键在于要画出对应的图象进行分类讨论,把情况考虑全面.17.【分析】连接AC 利用求出的面积再求出的面积【详解】解:连接AC 如图:∵∴;∴故答案为:30【点睛】本题考查了解直角三角形平行四边形的性质以及求三角形的面积解题的关键是利用求出三角形的面积解析:30【分析】连接AC ,利用1sin 2ABC S AB BC B ∆=••求出ABC ∆的面积,再求出ABCD 的面积. 【详解】解:连接AC ,如图:∵30B ∠=︒,BC 10cm =,6AB cm =,∴111sin 61015222ABC S AB BC B ∆=••=⨯⨯⨯=; ∴215230ABCD ABC S S ∆==⨯=.故答案为:30.【点睛】本题考查了解直角三角形,平行四边形的性质,以及求三角形的面积,解题的关键是利用1sin 2ABC S AB BC B ∆=••求出三角形的面积.18.【详解】解:如解图作点关于直线的对称点连接则线段的长就是的最小值作直径连接∵为的中点点关于直线对称∴∴故答案为:【点睛】本题考查了与圆有关的基础知识如直径的性质圆心角及圆周角的性质 解析:2 【详解】解:如解图,作点B 关于直线MN 的对称点B ',连接AB ',则线段AB '的长就是PA PB +的最小值,作O 直径AC ,连接CB ',∵30AMN ∠=︒,B 为AN 的中点,点B 、B '关于直线MN 对称,∴45C ∠=︒, ∴sin 452AB AC '=⋅︒=故答案为:2.【点睛】本题考查了与圆有关的基础知识,如直径的性质、圆心角及圆周角的性质.19.【分析】过C 作CE ⊥AB 于EDF ⊥AB 于F 分别在Rt △CEB 与Rt △DFA 中使用三角函数即可求解【详解】解:过C 作CE ⊥AB 于EDF ⊥AB 于F 可得矩形CEFD 和Rt △CEB 与Rt △DFA ∵BC=6∴解析:62【分析】过C 作CE ⊥AB 于E ,DF ⊥AB 于F ,分别在Rt △CEB 与Rt △DFA 中使用三角函数即可求解.【详解】解:过C 作CE ⊥AB 于E ,DF ⊥AB 于F ,可得矩形CEFD 和Rt △CEB 与Rt △DFA , ∵BC=6,∴CE=2sin 456322BC ︒=⨯= ∴DF=CE=32∴62sin 30DF AD ==︒故答案为:62【点睛】此题考查了解直角三角形的应用-坡度坡角问题,难度适中,解答本题的关键是构造直角三角形和矩形,注意理解坡度与坡角的定义.20.【分析】先过点F 作直线交轴于点过点作于点证明根据cos ∠FGO=06以及勾股定理即可得到答案【详解】过点F 作直线交轴于点过点作于点如图:∴(两直线平行内错角相等)又∵∠EFG=90°∴∠AFE+∠H解析:(8,12)【分析】先过点F 作直线//FA OG 交y 轴于点A ,过点G 作GH FA ⊥于点H ,证明FGO ∠HFG FEA =∠=∠,根据cos ∠FGO =0.6以及勾股定理即可得到答案.【详解】过点F 作直线//FA OG 交y 轴于点A ,过点G 作GH FA ⊥于点H ,如图:∴FGO HFG ∠=∠(两直线平行,内错角相等),又∵∠EFG =90°,∴∠AFE+∠HEG =90°,又∵∠AFE+∠FEA =90°,∴HFG FEA ∠=∠,∴FGO HFG FEA ∠=∠=∠,在Rt AEF ∆中,10EF =,则10cos 100.66AE FEA =⋅∠=⨯= ∴221068AF =-=(勾股定理),∴1789FH =-=,在Rt FGH ∆中,90.615FG =÷=, ∴2215912HG =-=(勾股定理),∴(8,12)F ,故答案为:(8,12).【点睛】本题主要考查了平行的性质(两直线平行,内错角相等)、勾股定理的应用以及三角函数,熟练掌握各知识点并灵活运用是解题的关键.三、解答题21.约为12.3m【分析】过A作AD⊥PM于D,延长BC交AD于E,则四边形BMNC,四边形BMDE是矩形,于是得到BC=MN=16m,DE=CN=BM=1.6m,求得CE=AE,设AE=CE=x,得到BE=16+x,解直角三角形即可得到答案.【详解】过A作AD⊥PM于D,延长BC交AD于E,则四边形BMNC,四边形BMDE是矩形,∴BC=MN=16m,DE=CN=BM=1.6m,∵∠AEC=90°,∠ACE=45°,∴△ACE是等腰直角三角形,∴CE=AE,设AE=CE=x,∴BE=16+x,∵∠ABE=22°,∴tan22°=AEBE =16xx+≈0.40,解得:x≈10.7(m),经检验x≈10.7是原分式方程的解∴AD≈10.7+1.6=12.3(m),答:观星台最高点A距离地面的高度约为12.3m.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.22.3 1.5【分析】利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上1.5即为这幢教学楼的高度AB.【详解】解:在Rt△AFG中,tan∠AFG=AG FG,∴FG=tan AGAFG∠=3=33AG.在Rt△ACG中,tan∠ACG=AG CG,∴CG=tan AGACG∠=3AG.又CG−FG=40,即3AG−33AG=40,∴AG=203,∴AB=203+1.5.答:这幢教学楼的高度AB为(203+1.5)米.【点睛】本题考查了解直角三角形,利用两个直角三角形的公共边求解是常用的解直角三角形的方法.23.200mm【分析】求ABCD的周长就是求AB和AD的长,可分别过B、D作垂线垂直于l,通过构造直角三角形根据α=36°和ABCD的四个顶点恰好在横格线且每个横格宽12mm等条件来求出AB、AD 的长.【详解】作BE⊥m于点E,DF⊥m于点F,∵α+∠DAF=180°-∠BAD=180°-90°=90°,∠ADF+∠DAF=90°,∴∠ADF=α=36°,根据题意,得 BE=24mm,DF=48mm,在Rt△ABE中,BE sinAB α=,∴2440sin 360.60BE AB ===︒( mm), 在Rt △ADF 中,DF cos ADF AD ∠=, ∴4860cos360.80DF AD ===︒( mm), ∴矩形ABCD 的周长=2(40+60)=200( mm).【点睛】本题考查了矩形的性质,解直角三角形的应用,通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中解决.24.(1)1542--;(2)113x =,213x =;(3)13x =,26x =-; 【分析】(1)原式利用特殊角的三角函数值,以及乘方的意义计算即可得到结果;(2)利用求根公式计算即可;(3)将(x -1)看作整体,然后利用因式分解法解方程即可.【详解】(1)解:222cos30sin 45cos 60tan 45-+︒+︒︒︒=214()122-+⨯=14++1)124---=154-- (2)解:23260x x --=,∵3,2,6a b c ==-=-,∴2(2)43(6)472760,∆=--⨯⨯-=+=>∴方程有两个不相等的实根,∴x ==∴1x =2x =; (3)解:2(1)5(1)140x x -+--=,[][](1)7(1)20,x x -+--=∴60x +=或30x -=,∴126,3x x =-=.【点睛】本题考查了特殊角的三角函数值、实数的运算以及一元二次方程的解法,常用的解一元二次方程的方法有直接开平方法、配方法、因式分解法、求根公式法,熟练掌握运算法则是解本题的关键.25.(1)边AB 的长为46;(2)tan ∠AED 的值为21+.【分析】(1)由两个角相等证明△AED ∽△ABC ,利用相似三角形的性质以及线段的和差,解方程求出AB 的长;(2)由等腰三角的判定与性质,勾股定理的应用,解直角三角形求出tan ∠AED 的值.【详解】(1)∵∠AED=∠ABC ,∠A=∠A ,∴△AED ∽△ABC , ∴AE AD AB AC=, ∵点D 是AB 中点, ∴AD=BD=12AB , 又∵AC=AE+EC ,AE=6,EC=2,∴AC=8,∴21682AB =⨯, ∴46AB =(负值已舍),∴边AB 的长为46;(2)过点C 作CH ⊥AB 交AB 于点H ,如图所示:∵CH ⊥AB ,∠A=30°,AC=8,∴CH=12AC=4, ∴22228443AC CH --=∴BH=AB- AH=4643,∵∠AED=∠ABC ,∴tan ∠AED= tan ∠ABC=1CH BH ==. 【点睛】 本题综合考查了相似三角形的判定与性质,等腰三角形的判定与性质,勾股定理的应用,解直角三角形等相关知识,重点掌握相似三角形的判定与性质,难点是构建直角三角形求出三角函数的值.26.(1)y =﹣x 2﹣2x +3,AC =DC ;(2)E (1,0);(3【分析】(1)将点A (﹣3,0),B (1,0)分别代入抛物线y =ax 2+bx +3可解的a ,b 的值,从而得到解析式,tan ∠DAC =DC AC,可根据表达式求出C ,D 的坐标然后计算DC 和AC 的长度计算;(2)可取一点E ,过E 作EF 平行于x 轴,交AC 于F 此时可表示出S △ACE ,根据类方程S △ACE =2S △ACD ,求E 点坐标即可;(3)根据题能得到Q 的运动轨迹为直线,且当P 在A 处时Q 在C 处,当P 运动到C 处时,可以得到△ADC ∽PQD ,根据形似性质可得到PQ 长度即为Q 的运动路径长.【详解】解:(1)将A (﹣3,0),B (1,0)分别代入抛物线y =ax 2+bx +3可得: 093303a b a b =-+⎧⎨=++⎩,解得12a b =-⎧⎨=-⎩; ∴抛物线解析式为y =﹣x 2﹣2x +3,∴D (﹣1,4),C (0,3);∴AC =DC ;∴tan ∠DAC =1=3DC AC . (2)如图1所示,过E 作EF //x 轴交AC 于点F ,设点E (m ,﹣m 2﹣2m +3),直线AC 的表达式为y =kx +n ,将A (﹣3,0),C (0,3)分别代入y =kx +n 可得:033k n n =-+⎧⎨=⎩,解得13k n =⎧⎨=⎩, ∴直线AC 表达式为y =x +3,∴F (﹣m 2﹣2m ,﹣m 2﹣2m +3),∴EF =m +m 2+2m =m 2+3m ,∴S △ACE =12(x C ﹣x A )EF , ∵S △ACD =12AC •CD =3,∴S△ACE=1(x C﹣x A)EF=2S△ACD=6,2∴3(m2+3m)=6,2解得m1=1,m2=﹣4(舍),∴E(1,0).(3)如图2所示当点P与点A重合时,∵∠ADQ=∠DCA=90°,∴∠DAC+∠ADC=90°=∠ADC+∠QDC,∴∠DAC=∠QDC,又∵∠DCA=∠DCQ=90°,∴△ADC∽△DQC,∴DC CQ AC DC=,∴.3CQ ==, 当点P 与点C 重合时,∴∠Q'DC=∠ACD=90°,∴DQ'∥CQ ,∵∠DAC=∠Q'P'D ,∠Q'DP'=∠ACD=90°,∴△ADC ∽△P'Q'D , ∴DQ DC DC AC'=,∴DQ '=, ∴DQ'=CQ ,∴四边形DQ'QC 是平行四边形,∴.【点睛】本题综合性比较强,主要考查二次函数点相关知识,解题的关键在于找出变换后的图形,根据已知条件,建立方程求解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )A .圆锥的底面半径为3B .2tan 2α=C .该圆锥的主视图的面积为82D .圆锥的表面积为12π2.已知,一个小球由桌面沿着斜坡向上前进了10cm ,此时小球距离桌面的高度为5cm ,则这个斜坡的坡度i 为( )A .2B .1:2C .1:2D .1:33.如图,为方便行人推车过天桥,市政府在10m 高的天桥两端分别修建了50m 长的斜道.用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )A .sin0.2=B .2ndF sin0.2=C .tan0.2=D .2ndF tan0.2=4.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8m ,坡面上的影长为4m .已知斜坡的坡角为30,同一时刻,一根长为2m 且垂直于地面放置的标杆在地面上的影长为4m ,则树的高度为( )A .10mB .12mC .(63m +D .(423m -5.如图,O 是ABC 的外接圆,60BAC ∠=︒,若O 的半径OC 为1,则弦BC 的长为( )A .12B .32C .1D .36.在Rt △ABC 中,∠ACB =90°,AB =5,tan ∠B =2,则AC 的长为 ( ) A .1 B .2 C .5 D .25 7.若菱形的周长为16,高为2,则菱形两个邻角的比为( )A .6:1B .5:1C .4:1D .3:18.点E 在射线OA 上,点F 在射线OB 上,AO ⊥BO ,EM 平分∠AEF ,FM 平分∠BFE ,则tan ∠EMF 的值为( ) A .12B .33C .1D .39.在平面直角坐标系中,正方形1111D C B A 、1122D E E B 、2222A B C D 、2343D E E B 、3333A B C D …按如图所示的方式放置,其中点1B 在y 轴上,点1C 、1E 、2C 、3E 、4E 、3C …在x 轴上,已知正方形1111D C B A 的边长为1,1160B C O ∠=︒,112233B C B C B C …则正方形2019201920192019A B C D 的边长是( )A .201812⎛⎫⎪⎝⎭B .201912⎛⎫⎪⎝⎭C .20193⎛⎫ ⎪ ⎪⎝⎭D .20183⎛⎫⎪ ⎪⎝⎭10.如图,正方形ABCD 的边长为1,点A 与原点重合,B 在y 轴正半轴上,D 在x 轴负半轴上,将正方形ABCD 绕着点A 逆时针旋转30至AB C D ''',CD 与B C ''相交于点E ,则E 坐标为( )A.31,3⎛⎫- ⎪⎪⎝⎭B.11,2⎛⎫-⎪⎝⎭C.31,2⎛⎫-⎪⎪⎝⎭D.21,3⎛⎫- ⎪⎝⎭11.如图所示,矩形ABCD的边长AB=2,BC=23,△ADE为正三角形.若半径为R的圆能够覆盖五边形ABCDE(即五边形ABCDE的每个顶点都在圆内或圆上),则R的最小值是()A.23B.4 C.2.8 D.2.512.河堤横断面如图所示,迎水坡10AB=米,迎水坡AB的坡比为1:3(坡比是坡面的铅直高度BC与水平度AC之比),则AC的长是()A.53B.2米C.15米D.10米第II卷(非选择题)请点击修改第II卷的文字说明参考答案二、填空题13.某人顺着山坡沿一条直线型的坡道滑雪,当他滑过130米长的路程时,他所在位置的竖直高度下降了50米,则该坡道的坡比是_________.14.在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,3AB=_____.15.如图 1 的矩形ABCD 中,有一点E 在AD 上,现以BE 为折线将点A 往右折,如图2所示,再过点A 作 AF CD ⊥于点F ,如图3所示,若123,26,60AB BC BEA ︒∠===, 则图3中AF 的长度为____.16.如图, 圆O 的直径AB 垂直于弦CD ,垂足是E ,22.5A ∠=︒,4OC =,CD 的长为__________.17.如图,在2×2的网格中,以顶点O 为圆心,以2个单位长度为半径作圆弧,交图中格线于点A ,则tan ∠ABO 的值为_____.18.如图所示,AOB ∠是放置在正方形网格中的一个角,则sin AOB ∠的值是________.19.如图,已知直线l :y 3,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;…;按此作法继续下去,则点A 4的坐标为_____.20.如图,某建筑物的顶部有一块标识牌CD ,小明在斜坡上B 处测得标识牌顶部C 的仰角为45︒,沿斜坡走下来在地面A 处测得标识牌底部D 的仰角为60°,已知斜坡AB 的坡角为30°,10AB AE ==米. 则标识牌CD 的高度是米__________.三、解答题21.在平面直角坐标系xOy 中,O 的半径为1.对于图形M ,给出如下定义:P 为图形M 上任意一点,Q 为O 上任意一点,如果,P Q 两点之间的距离有最大值,那么称这个最大值为图形M 的“圆距”,记作()d M .如图,已知点()2,0A .(1)直接写出d (点A )的值;(2)设T 是直线24y x =-+上一点,以为T 圆心,1长为半径作T .若()d T 满足()612d O ≤≤,求圆心T 的横坐标x 的取值范围;(3)过点A 画直线2y kx k =-与y 轴交于点B ,当d (线段AB )取最小值时,直接写出k 的取值范围.22.如图,已知⊙O 的直径 AB 与弦 CD 互相垂直,垂足为点 E .⊙O 的切线 BF 与弦 AC 的延长线相交于点 F ,且AC=8,tan ∠BDC=34.(1)求⊙O 的半径长; (2)求线段 CF 长. 23.计算 (1)cos 451-sin60︒︒(2)(12)-2-(π-3.14)0-│tan60°-2│ 24.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30,看这栋高楼底部的俯角为60︒,热气球与高楼的水平距离为66m ,这栋高楼有多高?(结果精确到0.1m ,参考数据:3 1.73≈)25.理解写作如下图1,在探究锐角A ∠的对边与直角三角形斜边之比的数学实验中包含两个环节,一是通过在A ∠的边AB 上取不同的点B ', B '',分别作高B C '',B C ''''利用三角形相似,可以说明B C B C A ABB ''''''=''',即A ∠的对边与斜边的比值固定,与点B '的位置无关. 二是说明A ∠的度数发生变化时,A ∠的对边与斜边的比值也会发生变化.请根据下图2简要说明做法并证明第二个环节的结论,并在图3中再构造一种思路证明此结论.26.如图,O 为ABC 的外接圆,AB 为O 的直径,点D 为BC 的中点.(1)连接OD .求证://OD AC . (2)设OD 交BC 于E ,若43BC=2DE =.求阴影部分面积.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据圆锥的侧面展开图的弧长等于圆锥底面周长,可知2πr =180n lπ,求出r 以及圆锥的母线l 和高h 即可解决问题. 【详解】解:设圆锥的底面半径为r ,高为h . A 选项,由题意:2πr =1206180π⨯⨯,解得r =2,故错误;B 选项,h 226242-=,所以tanα2442=,故错误; C 选项,圆锥的主视图的面积=12×4×4282 D 选项,表面积=4π+2π×6=16π,故错误. 故选:C . 【点睛】本题考查圆锥的有关知识,记住圆锥的侧面展开图的弧长等于圆锥底面周长,即2πr =180n lπ,圆锥的表面积=πr 2+πrl 是解决问题的关键,属于中考常考题型. 2.D解析:D 【分析】过B作BC⊥桌面于C,由题意得AB=10cm,BC=5cm,再由勾股定理得AC=53然后由坡度的定义即可得出答案.【详解】解:如图,过B作BC⊥桌面于C,由题意得:AB=10cm,BC=5cm,∴AC=222210553AB BC-=-=,∴这个斜坡的坡度i=BCAC =53=1:3,故选:D.【点睛】本题考查了解直角三角形的应用-坡度坡角问题以及勾股定理;熟练掌握坡度的定义和勾股定理是解题的关键.3.B解析:B【分析】先利用正弦的定义得到10sin0.250A==,然后利用计算器求锐角∠A.【详解】∵10sin0.250A==,∴用计算器求值的顺序为20.2ndFsin=,故选:B.【点睛】本题考查了锐角三角函数及计算器的应用,掌握科学计算器的应用是解决本题的关键.4.C解析:C【分析】延长AC交BF延长线于D点,则BD即为AB的影长,然后根据物长和影长的比值计算即可.【详解】延长AC交BF延长线于D点,作CE⊥BD于E,则∠CFE=30°,在Rt△CFE中,∠CFE=30°,CF=4m,∴CE=2(m),EF=4cos30°3m),在Rt△CED中,∵同一时刻,一根长为2m、垂直于地面放置的标杆在地面上的影长为4m,CE=2(m),则CE:DE=2:4=1:2,AB:BD=1:2,∴DE=4(m),∴3m),在Rt△ABD中,AB=12BD=1233m),故选:C.【点睛】本题考查了解直角三角形的应用以及相似三角形的性质.解决本题的关键是作出辅助线得到AB的影长.5.D解析:D【分析】先作OD⊥BC于D,由于∠BAC=60°,根据圆周角定理可求∠BOC=120°,又OD⊥BC,根据垂径定理可知∠BOD=60°,BD=12BC,在Rt△BOD中,利用特殊三角函数值易求BD,进而可求BC.【详解】解:如右图所示,作OD⊥BC于D,∵∠BAC=60°,∴∠BOC=120°,又∵OD⊥BC,∴∠BOD=60°,BD=12BC,∴BD=sin60°×OB3∴BC=2BD=3故答案是3【点睛】本题考查了圆周角定理、垂径定理、特殊三角函数计算,解题的关键是作辅助线OD⊥BC,并求出BD.6.B解析:B【分析】根据正切的定义得到BC=12AC,根据勾股定理列式计算即可.【详解】在Rt△ABC中,∠ACB=90°,tan∠B=2,∴ACBC=2,∴BC=12AC,由勾股定理得,AB2=AC2+BC2,即(5)2=AC2+(12AC)2,解得,AC=2,故选B.【点睛】本题考查的是锐角三角函数的定义、勾股定理,掌握锐角A的对边a与邻边b的比叫做∠A的正切是解题的关键.7.B解析:B【分析】由锐角函数可求∠B的度数,可求∠DAB的度数,即可求解.【详解】如图,∵四边形ABCD是菱形,菱形的周长为16,∴AB=BC=CD=DA=4,∵AE=2,AE⊥BC,∴sin ∠B=12BE AB = ∴∠B=30° ∵四边形ABCD 是菱形,∴AD ∥BC ,∴∠DAB+∠B=180°,∴∠DAB=150°,∴菱形两邻角的度数比为150°:30°=5:1,故选:B .【点睛】本题考查了菱形的性质,锐角三角函数,能求出∠B 的度数是解决问题的关键. 8.C解析:C【分析】根据三角形外角的性质求得∠AEF+∠BFE=270°,由角平分线定义可求得∠MEF+∠MFE=135°,根据三角形内角和定理可求出∠EMF=45°,从而可得出结论.【详解】如图,∵AO ⊥BO∴∠AOB=90°∴∠OEF+∠OFE=90°∵∠AEF 和∠BFE 是△EOF 的外角∴∠AEF=90°+∠OFE ,∠BFE=90°+∠OEF∴∠AEF+∠BFE=90°+90°+∠OFE+∠OEF=270°∵EM 平分∠AEF ,FM 平分∠BFE ,∴∠MEF+∠MFE=12(∠AEF+∠BFE) =135°, ∵∠MEF+∠MFE+∠M=180°∴∠M=180°-(∠MEF+∠MFE)=180°-135°=45°∴tan ∠EMF=tan45°=1故选:C .【点睛】此题主要考查了三角形内角和定理、三角形外角的性质及三角函数,求出∠MEF+∠MFE=135°是解答此题的关键.9.D解析:D【分析】利用正方形的性质结合锐角三角函数关系得出正方形的边长,进而得出变化规律即可得出答案.【详解】解:∵∠B 1C 1O=60°,B 1C 1//B 2C 2//B 3C 3,∴∠D 1C 1E 1=∠C 2B 2E 2=∠C 3B 3E 4=30°,∴D 1E 1=C 1D 1sin30°= 12, 则B 2C 2= 2230B E cos= 12= 1, 同理可得:B 3C 3= 13= 2, 故正方形A n B n C n D n的边长是:1n . 则正方形2019201920192019A B C D 的边长是:2018)3. 故选D .【点睛】 此题主要考查了正方形的性质以及锐角三角函数关系,得出正方形的边长变化规律是解题关键.10.A解析:A【分析】连接AE ,由旋转性质知AD=AB′=1、∠BAB′=30°、∠B′AD=60°,证Rt △ADE ≌Rt △AB′E 得∠DAE=12∠B′AD=30°,由DE=ADtan ∠DAE 可得答案. 【详解】如图:连接AE∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB C D''',∴AD=AB′=1,∠BAB′=30°,∴∠B′AD=60°,在Rt△ADE和Rt△A B′E中,∵AD AB AE AE'=⎧⎨=⎩∴Rt△ADE≌Rt△AB′E(HL),∴∠DAE=∠B′AE=12∠B′AD=30°,∴DE=ADtan∠DAE=1×33=3 3∴点E的坐标为(-13故选:A【点睛】本题考查了正方形的性质、坐标与图形旋转.图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.11.C解析:C【分析】连接AC、BE、CE,取BC的中点F,连接EF,根据勾股定理可得AC,根据直角三角形的边角关系可得∠ACB=30°,∠CAD=30°,再根据正三角形的性质可得:∠EAD=∠EDA=60°,AE=AD=DE=3△EAC是直角三角形,由勾股定理可得EC的长.判断△EAB≌△EDC,根据全等三角形的性质可得EB=EC,继而根据题意可判断能够覆盖五边形ABCDE的最小圆的圆心在线段EF上,且此圆只要覆盖住△EBC必能覆盖五边形ABCDE,从而此圆的圆心到△BCE的三个顶点距离相等.根据等腰三角形的判定和性质可得F是BC中点,BF=CF3EF⊥BC,由勾股定理可得EF的长,继而列出关于R的一元二次方程,解方程即可解答.【详解】如图所示,连接AC、BE、CE,取BC的中点F,连接EF,∵四边形ABCD 是矩形,∴∠ABC=∠DAB =∠BCD =∠ADC =90°,AD ∥BC ,AD =BC =AB =CD =2∵BC =AB =2由勾股定理可得:AC 4∴sin ∠ACB =24AB AC ==12,sin ∠CAD =24CD AC ==12∴∠ACB =30°,∠CAD =30°∵△ADE 是正三角形 ∴∠EAD =∠EDA =60°,AE =AD =DE =∴∠EAC =∠EAD +∠CAD =90°,∴△EAC 是直角三角形,由勾股定理可得:EC∵∠EAB =∠EAD +∠BAD =150°∠EDC =∠EDA +∠ADC =150°∴∠EAB =∠EDC∵EA =ED ,AB =DC∴△EAB ≌△EDC∴EB =EC =即△EBC 是等腰三角形∵五边形ABCDE 是轴对称图形,其对称轴是直线EF ,∴能够覆盖五边形ABCDE 的最小圆的圆心在线段EF 上,且此圆只要覆盖住△EBC 必能覆盖五边形ABCDE .从而此圆的圆心到△BCE 的三个顶点距离相等.设此圆圆心为O ,则OE =OB =OC =R ,∵F 是BC 中点∴BF =CF EF ⊥BC在Rt △BEF 中,由勾股定理可得:EF 5 ∴OF =EF -OE =5-R在Rt △OBF 中,222BF OF OB即()2225R R +-= 解得:R =2.8∴能够覆盖五边形ABCDE 的最小圆的半径为2.8.故选C .【点睛】本题考查勾股定理的应用、全等三角形的判定及其性质、等腰三角形的判定及其性质、直角三角形的边角关系.解题的关键是理解圆内接五边形的特点,并且灵活运用所学知识. 12.A解析:A【分析】根据迎水坡AB 的坡比3 设,=3=BC x AC x ,然后根据迎水坡AB=10米,利用勾股定理求出x 的值,即可求解.【详解】∵迎水坡AB 的坡比3 ∴,3==BC x AC x ,在Rt △ABC 中:222BC AC AB += ∴)222x 3x 10+=∴x=5±∵0x >∴=5x ∴33553===AC x (米).故选:A【点睛】本题考查了根据坡度和坡角解直角三角形的知识,解答本题的关键是根据坡比设出各边的长度,然后根据勾股定理求解.二、填空题13.【分析】首先根据勾股定理求得滑行的水平距离然后根据坡比的定义即可求解【详解】解:滑行的水平距离是:=120(米)故坡道的坡比是:50:120=故答案是:【点睛】本题考查了勾股定理以及坡比的定义正确求解析:5 12【分析】首先根据勾股定理求得滑行的水平距离,然后根据坡比的定义即可求解.【详解】(米),故坡道的坡比是:50:120=512.故答案是:5 12.【点睛】本题考查了勾股定理,以及坡比的定义,正确求得滑行的水平距离是关键.14.4【解析】分析:由CE所在直线垂直平分线段AD可得出CE平分∠ACD进而可得出∠ACE=∠DCE由CD平分∠BCE利用角平分线的性质可得出∠DCE=∠DCB结合∠ACB=90°可求出∠ACE∠A的度解析:4【解析】分析:由CE所在直线垂直平分线段AD可得出CE平分∠ACD,进而可得出∠ACE=∠DCE,由CD平分∠BCE利用角平分线的性质可得出∠DCE=∠DCB,结合∠ACB=90°可求出∠ACE、∠A的度数,再利用余弦的定义结合特殊角的三角函数值,即可求出AB的长度.详解:∵CE所在直线垂直平分线段AD,∴CE平分∠ACD,∴∠ACE=∠DCE.∵CD平分∠BCE,∴∠DCE=∠DCB.∵∠ACB=90°,∴∠ACE=13∠ACB=30°,∴∠A=60°,∴AB=60BCsin=︒=4.故答案为4.点睛:本题考查了线段垂直平分线的性质、角平分线的性质以及特殊角的三角函数值,通过角的计算找出∠A=60°是解题的关键.15.8【分析】作AH⊥BC于H则四边形AFCH是矩形AF=CHAH=CF在Rt△ABH 中解直角三角形即可解决问题【详解】解:作AH⊥BC于H则四边形AFCH是矩形AF=CH在Rt△ABE中∠BAE=90解析:8【分析】作AH ⊥BC 于H ,则四边形AFCH 是矩形,AF=CH ,AH=CF. 在Rt △ABH 中,解直角三角形即可解决问题.【详解】解:作AH ⊥BC 于H ,则四边形AFCH 是矩形,AF=CH.在Rt △ABE 中,∠BAE=90°,∠BEA=60°∴∠ABE=180°-∠A-∠BEA=180°-90°-60°=30°由题意得∠ABH=90°-2∠ABE=90°-30°×2=30°在Rt △ABH 中,∠ABH=30°,3,BC=26∴BH=AB cos30°332=18 ∴CH=BC-BH=26-18=8.即AF=8.故答案为8.【点睛】本题考查了翻折变换,矩形的性质及解直角三角形等知识.解题的关键是学会添加辅助线,构造直角三角形来解决问题. 16.【分析】根据圆周角定理得由于的直径垂直于弦根据垂径定理得且可判断为等腰直角三角形所以然后利用进行计算【详解】解:∵∴∵的直径垂直于弦∴∴为等腰直角三角形∴∴故答案是:【点睛】本题考查了垂径定理:垂直 解析:2【分析】根据圆周角定理得245BOC A ∠=∠=︒,由于O 的直径AB 垂直于弦CD ,根据垂径定理得CE DE =,且可判断OCE △为等腰直角三角形,所以222CE ==后利用2CD CE =进行计算.【详解】解:∵22.5A ∠=︒∴245BOC A ∠=∠=︒∵O 的直径AB 垂直于弦CD∴CE DE =∴OCE △为等腰直角三角形∴2222CE OC == ∴242CD CE ==. 故答案是:42 【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰直角三角形的性质和圆周角定理.17.2+【分析】连接OA 过点A 作AC ⊥OB 于点C 由题意知AC=1OA=OB=2从而得出OC==BC=OB ﹣OC=2﹣在Rt △ABC 中根据tan ∠ABO=可得答案【详解】如图连接OA 过点A 作AC ⊥OB 于点解析:2+3.【分析】连接OA ,过点A 作AC ⊥OB 于点C ,由题意知AC=1、OA=OB=2,从而得出OC=22OA AC -=3、BC=OB ﹣OC=2﹣3,在Rt △ABC 中,根据tan ∠ABO=AC BC 可得答案.【详解】如图,连接OA ,过点A 作AC ⊥OB 于点C ,则AC=1,OA=OB=2,∵在Rt △AOC 中,222221OA AC -=-3∴BC=OB ﹣OC=23∴在Rt △ABC 中,tan ∠ABO=23AC BC =-3 故答案是:3【点睛】本题考查了解直角三角形,根据题意构建一个以∠ABO 为内角的直角三角形是解题的关键. 18.【分析】由题意可知要求出答案首先需要构造出直角三角形连接AB 设小正方形的边长为1可以求出OAOBAB 的长度由勾股定理的逆定理可得是直角三角形再根据三角函数的定义可以求出答案【详解】连接AB 如图所示: 2 【分析】由题意可知,要求出答案首先需要构造出直角三角形,连接AB ,设小正方形的边长为1,可以求出OA 、OB 、AB 的长度,由勾股定理的逆定理可得ABO 是直角三角形,再根据三角函数的定义可以求出答案.【详解】连接AB 如图所示:设小正方形的边长为1,∴2OA =23+1=10,22BA =3+1=10,222OB =4+2=20,∴ABO 是直角三角形, ∴BA 102sin AOB=OB 220∠=, 故答案为:22. 【点睛】 本题主要考查了勾股定理的逆定理和正弦函数的定义,熟练掌握技巧即可得出答案. 19.(0256)【分析】利用锐角三角函数分别计算得到的坐标利用规律直接得到答案【详解】解:∵l :y =x ∴l 与x 轴的夹角为30°∵AB ∥x 轴∴∠ABO =30°∵OA =1∴AB =∵A1B ⊥l ∴∠ABA1=6解析:(0,256)【分析】利用锐角三角函数分别计算得到12,A A 的坐标,利用规律直接得到答案.【详解】解:∵l :y 3 ∴l 与x 轴的夹角为30°∵AB ∥x 轴∴∠ABO =30°∵OA =1∴AB 3∵A 1B ⊥l∴∠ABA 1=60°∴AA 1=3∴A 1(0,4)同理可得A 2(0,16)…∴A 4纵坐标为44=256∴A 4(0,256)故答案为:(0,256).【点睛】本题考查的是一次函数综合题,先根据所给一次函数判断出一次函数与x 轴夹角是解决本题的突破点;根据含30°的直角三角形的特点依次得到123,,A A A …的点的坐标是解决本题的关键.20.【分析】过点B 作BM ⊥EA 的延长线于点M 过点B 作BN ⊥CE 于点N 通过解直角三角形可求出BMAMCNDE 的长再结合CD =CN +EN−DE 即可求出结论【详解】解:过点B 作BM ⊥EA 的延长线于点M 过点B 作 解析:1553【分析】过点B 作BM ⊥EA 的延长线于点M ,过点B 作BN ⊥CE 于点N ,通过解直角三角形可求出BM ,AM ,CN ,DE 的长,再结合CD =CN +EN−DE 即可求出结论.【详解】解:过点B 作BM ⊥EA 的延长线于点M ,过点B 作BN ⊥CE 于点N ,如图所示.在Rt △ABM 中,AB =10米,∠BAM =30°,∴AM =AB•cos30°=3BM =AB•sin30°=5(米).在Rt △ADE 中,AE =10(米),∠DAE =60°,∴DE =AE•tan60°=3在Rt △BCN 中,BN =AE +AM =10+3∠CBN =45°,∴CN =BN•tan45°=10+3(米),∴CD =CN +EN−DE =10+33=3故答案为:3【点睛】此题考查解直角三角形−仰角俯角问题及解直角三角形−坡度坡脚问题,通过解直角三角形求出BM ,AM ,CN ,DE 的长是解题的关键.三、解答题21.(1)3;(2)圆心T 的横坐标x 的取值范围1405x -≤≤或1665x ≤≤;(3)33-≤≤k . 【分析】(1)根据“圆距”的定义求解即可;(2)先确定OT 的取值范围,求出T 坐标,根据勾股定理列方程求出x ,进一步确定x 的取值;(3)先求出d (线段AB )的最小值,再求出点B 坐标,代入2y kx k =-求出k 的值,从而确定k 的取值.【详解】解:(1)∵A (2,0),O 的半径为1,∴d (点A )=1+2=3; ()2如图1,由题意可知,410OT ≤≤.过T 作TH y ⊥轴于H ,∵24y x =-+,O 的半径为1∴(),24T x x -+,由222TH OH OT +=得,①当4OT =时,()222244x x +-+=,解得12160,5x x == ②当10OT =时,()2222410x x +-+=,解得12146,5x x ==- ∴圆心T 的横坐标x 的取值范围1405x -≤≤或1665x ≤≤ (3)当AB 与⊙O 相切时,d(线段AB )取最小值=2设切点为M ,连接OM ,则OM=1,∠OMA=90°,∵A (2,0),∴OA=2∴sin ∠BOA=12OM OA = ∴∠BOA=30°, 在Rt AOB 中∴OB=OAtan30°3∴B 点坐标为:(03把B 点坐标代入解得k=3-当B 点在x 轴下方时,k=32; ∴当d(线段AB )取最小值时33≤≤k 【点睛】本题考查了点与圆的位置关系,图形M 的“圆距”的定义等知识,解题的关键是理解题意,学会寻找特殊位置解决数学问题22.(1)5;(2)92【分析】(1)过O 作OH 垂直于AC ,利用垂径定理得到H 为AC 中点,求出AH 的长为4,根据同弧所对的圆周角相等得到tanA =tan ∠BDC ,求出OH 的长,利用勾股定理即可求出圆的半径OA 的长;(2)由AB 垂直于CD 得到E 为CD 的中点,得到EC =ED ,在直角三角形AEC 中,由AC 的长以及tanA 的值求出CE 与AE 的长,由FB 为圆的切线得到AB 垂直于BF ,得到CE 与FB 平行,由平行得比例列出关系式求出AF 的长,根据AF−AC 即可求出CF 的长.【详解】(1)作OH AC ⊥于H ,则142AH AC ==,在Rt AOH ∆中,344AH tanA tan BDC ==∠=,, 3OH ∴=,∴半径225OA AH OH =+=;(2)AB CD ⊥,E ∴为CD 的中点,即CE DE =, 在Rt AEC ∆中,384AC tanA ==,,设3CE k =,则4AE k =, 根据勾股定理得:222AC CE AE =+,即2291664k k +=,解得85k =则2432,55CE DE AE ===, BF 为圆O 的切线,FB AB ∴⊥,又AE CD ⊥, //CD FB ∴, AC AE AF AB ∴=,即328510AF =, 解得:252AF =, 则92CF AF AC =-=. 【点睛】此题考查了切线的性质,垂径定理,锐角三角函数定义,勾股定理,以及平行线的性质,熟练掌握切线的性质是解本题的关键. 23.(1)26+2)3【分析】(1)代入特殊角的三角函数值计算即可;(2)根据负整数指数幂、零次幂、特殊角三角函数值化简然后计算即可.【详解】(1)2cos4522226 1-sin603231︒===+︒--;(2)(12)-2-(π-3.14)0-│tan60°-2│=4-1-(2-3)=1+3【点睛】本题考查实数的混合运算,需要熟记特殊角度的三角函数值是解题的关键.24.152.2【分析】过点A作AD BC⊥于点D,根据仰角和俯角的定义得到BAD∠和CAD∠的度数,利用特殊角的正切值求出BD和CD的长,加起来得到BC的长.【详解】解:如图,过点A作AD BC⊥于点D,根据题意,30BAD∠=︒,60CAD∠=︒,66AD m=,3tan3066223BD AD m=⋅︒=⨯=,tan60663663CD AD m=⋅︒=⨯=,223663883152.2BC m=+=≈.【点睛】本题考查解直角三角形的应用,解题的关键是掌握利用特殊角的三角形函数值解直角三角形的方法.25.答案见解析.【分析】环节一,我们用相似论证了当A∠不变时,A∠的对边与斜边的比值固定不变;环节二,再次为我们论证了当A∠改变时,A∠的对边与斜边的比值也随之变化,不再固定不变;进而从斜边相等,或直角边相等,两个方面论证即可.【详解】解:环节二证明过程如下:(1)如下图所示:过点A 在BAC ∠内部做射线AB ',截取AB AB '=,过点 B '作BC AC ''⊥,此时构造出了B AC ''∠,显然 BAC B AC ''∠≠∠此时sin BC BAC AB ∠=;sin B C B AC AB ''''∠=', 因为AB AB '=,而BC B C ''≠,所以 sin sin BAC B AC ''∠≠∠ 所以当A ∠的度数发生变化时,A ∠的对边与斜边的比值也会发生改变.(2)图3中构造另外一种思路证明:由上题我们自然想到控制变量法.环节二我们使斜边相等,现在我们使直角边BC 与B C ''与相等,如图所示:此时sin BC BAC AB ∠=;sin B C B AC AB ''''∠=';因为 BC B C ''=,而AB AB '≠,所以 sin sin BAC B AC ''∠≠∠.【点睛】本题考查了对边与斜边的比,即正弦值,会随着角度的变化而变化,熟悉相关性质是解题的关键.26.(1)证明见解析;(2)16433π- 【分析】(1)先根据圆周角定理可得90ACB ∠=︒,再根据垂径定理的推论可得OD 垂直平分BC ,然后根据平行线的判定即可得证;(2)设O 的半径为r ,从而可得,2OB r OE r ==-,再根据垂径定理的推论可得1232BE BC ==Rt OBE 中,利用勾股定理可得r 的值,从而可得OBC ∠的度数,最后利用扇形和三角形的面积公式即可得.【详解】(1)AB 为O 的直径, 90ACB ∴∠=︒,即AC BC ⊥,点D 为BC 的中点,OD ∴垂直平分BC ,//OD AC ∴;(2)设O 的半径为r ,则OB OD OC r ===,2DE =,2OE OD DE r ∴=-=-,由(1)已证:OD 垂直平分BC ,1122BE BC ∴==⨯=在Rt OBE 中,222OE BE OB +=,即222(2)r r -+=,解得4r =,4,2OB OE ∴==,在Rt OBE 中,1sin 2OE OBC OB ∠==, 30OBC ∴∠=︒,又OB OC =,30OCB OBC ,180120BOC OCB OBC ∴∠=︒-∠-∠=︒,则阴影部分面积为21204116236023OBC OBC S Sππ⨯-=-⨯=-扇形 【点睛】本题考查了圆周角定理、垂径定理的推论、扇形的面积公式、正弦三角函数等知识点,熟练掌握并灵活运用各定理和公式是解题关键.。
