曲线拟合的最小二乘法讲解
第六章_曲线拟合的最小二乘法

25
24
o
1 2 3 4 5 6 7 8
t
(0 , 0 ) (0 , 1 ) a0 (0 , f ) ( , ) ( , ) a ( , f ) 1 1 1 1 1 0
计算系数
(0 , 0 ) 1 8
bt y
则矛盾方程组为:
1 1 1 1 1 0.669131 0.370370 0.390731 0.500000 a 0.621118 0.121869 b 0.309017 0.833333 0.980392 0.587785
例1. 对彗星1968Tentax的移动在某极坐标系下有如 下表所示的观察数据,假设忽略来自行星的干扰,坐 r 标应满足: 1 e p 其中:p为参数,e为偏心率, cos
试用最小二乘法拟合p和e。
r
2.70 480
2.00 670
1.61 830
1.20 1080
1.02 1260
得正则方程组为:
5.0 0.284929 0.284929 a 3.305214 b 0.314887 1.056242
解得: a 0.688617
b 0.483880
1 则: p 1.452186 e bp 0.702684 a 1.452186 则拟合方程为: r 1 0.702684 cos
第六章 曲线拟合的最小二乘法
§6.1 引言
§6.2 线性代数方程组的最小二乘解
§6.3 曲线最小二乘拟合
§1 引言
如果实际问题要求解在[a,b]区间的每一点都 “很好地” 逼近f(x)的话,运用插值函数有时就要 失败。另外,插值所需的数据往往来源于观察测量, 本身有一定的误差。要求插值曲线通过这些本身有误 差的点,势必使插值结果更加不准确。 如果由试验提供的数据量比较大,又必然使得插 值多项式的次数过高而效果不理想。 从给定的一组试验数据出发,寻求函数的一个近 似表达式y=(x),要求近似表达式能够反映数据的基 本趋势而又不一定过全部的点(xi,yi),这就是曲线拟 合问题,函数的近似表达式y=(x)称为拟合曲线。本 章介绍用最小二乘法求拟合曲线。
最小二乘法拟合原理

最小二乘法拟合原理最小二乘法是一种常用的数学方法,用于寻找一组数据的最佳拟合曲线或者最佳拟合函数。
它的原理是通过最小化实际观测数据与拟合曲线之间的残差平方和,来确定最佳拟合曲线的参数。
这个方法在实际应用以及科学研究中非常常见,下面将详细介绍最小二乘法的拟合原理。
在介绍最小二乘法之前,我们首先需要了解线性回归模型。
线性回归是一种常见的数据拟合手段,它基于以下假设:给定自变量X和因变量Y,存在一个线性关系Y=aX+b。
其中,a称为斜率,b称为截距。
当我们拥有一组数据(X1,Y1),(X2,Y2),(X3,Y3),...,(Xn,Yn)时,最小二乘法通过找到最佳的a和b,使得方程Y=aX+b最好地拟合这组数据。
它通过最小化每个观测点的残差来确定最佳拟合曲线。
残差是指实际观测值与拟合值之间的差异。
对于每一个观测点(Xi,Yi),其拟合值为Yi'=aXi+b,残差为Ri=Yi-Yi',即实际观测值与拟合值的差。
S=∑(Yi-Yi')²=∑(Yi-aXi-b)²为了找到最佳的a和b,我们需要求解方程S对a和b的偏导数,并令其等于0。
求解a和b的偏导数得到以下两个方程:∂S/∂a=0∂S/∂b=0对第一个方程求解可以得到:∂S/∂a=-2∑(Yi-aXi-b)Xi=0进一步整理可以得到:∑YiXi-a∑(Xi)²-b∑(Xi)=0对第二个方程求解可以得到:∂S/∂b=-2∑(Yi-aXi-b)=0进一步整理可以得到:∑Yi - a∑(Xi) - nb = 0其中,n为观测点的数目。
解这个方程组,我们可以得到a和b的值,从而确定最佳拟合曲线的方程Y=aX+b。
最小二乘法还可以用于非线性的数据拟合。
对于非线性拟合,我们可以假设一个非线性的函数模型,例如Y=f(X,θ),其中θ是待拟合的参数。
然后,通过最小化残差平方和来确定最佳的θ值。
方法类似于线性拟合,其中拟合值变为Yi'=f(Xi,θ),残差为Ri=Yi-Yi'。
计算方法 第三章曲线拟合的最小二乘法20191103

§2 多项式拟合函数
例3.1 根据如下离散数据拟合曲线并估计误差
x 1 23 4 6 7 8 y 2 36 7 5 3 2
解: step1: 描点
7
*
step2: 从图形可以看出拟
6 5
*
合曲线为一条抛物线:
4
y c0 c1 x c2 x2
3 2 1
* *
* * *
step3: 根据基函数给出法
法
18
定理 法方程的解是存在且唯一的。
证: 法方程组的系数矩阵为
(0 ,0 ) (1 ,0 )
G
(0
,1
)
(1 ,1 )
(0 ,n ) (1 ,n )
(n ,0 )
(
n
,
1
)
(n ,n )
因为0( x),1( x), ...,n( x)在[a, b]上线性无关,
所以 G 0,故法方程 GC F 的解存在且唯一。
第三章 曲线拟合的最小二乘法
2
最小二乘拟合曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
3
三次样条函数插值曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
4
Lagrange插值曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
5
一、数据拟合的最小二乘法的思想
已知离散数据: ( xi , yi ), i=0,1,2,…,m ,假设我们用函
便得到最小二乘拟合曲线
n
* ( x) a*j j ( x) j0
为了便于求解,我们再对法方程组的导出作进一步分析。
第三章 曲线拟合的最小二乘
曲线拟合 最小二乘法

曲线拟合最小二乘法
曲线拟合是指通过已知数据点来推导出一条函数曲线,使得该曲线尽
可能地贴近这些数据点。
而最小二乘法(Least Squares Method)是求解
这种拟合问题的一种常用方法。
最小二乘法的核心思想是尽量减小误差平方和。
假设已知的数据点为$(x_i, y_i)$,曲线函数为 $y=f(x)$,我们希望找到一组参数 $\theta$,使得 $f(x_i;\theta)$ 与 $y_i$ 的差距最小,即:
$$\min_{\theta}\sum_{i=1}^n [y_i - f(x_i;\theta)]^2$$。
这个式子被称为目标函数,也叫做残差平方和(RSS)。
通过对目标
函数进行求导,可以得到最优参数 $\theta^*$ 的解析解:
$$\theta^* = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T
\mathbf{y}$$。
其中,$\mathbf{X}$ 是一个 $n \times p$ 的矩阵,每一行代表一
个数据点的特征向量,$p$ 是曲线函数的参数个数。
$\mathbf{y}$ 是一
个 $n \times 1$ 的列向量,代表数据点的真实输出值。
最小二乘法在实际应用中有很广泛的应用。
例如,可以用它来构建多
项式回归模型、高斯过程回归模型等。
此外,在机器学习领域,最小二乘
法也被用于求解线性回归模型、岭回归模型等。
最小二乘法与曲线拟合(共24张PPT)

j 1
n
aNj
xj
bN
j1
2a1k
a2k
aNk
(
Ax
b)
Q
故 x1
Q
x2
Q
2
AT
(
Ax
b)
2(
AT
Ax
AT b )
xn
令
Q 0
(k 1,2,, n)
即
ATxAk x
AT b
〔*〕
因为rankA=n,故由引理2知,上式有唯一解。设
解为x1=a1, x2=a2,…, xn=an,记为点P0(a1,a2,…,an),
或写为
其矩阵形式为
a11x1 a12x2 a1n xn b1 a21x1 a22x2 a2n xn b2
aN1x1 aN 2 x2 aNn xn bN
n
aij x j bi ( j 1,2,, N )
j 1
Ax b
当方程组的系数矩阵与增广矩阵的秩不相等时, 方程组无解,此时方程组称为矛盾方程组。对于 rankA=n〔A的秩为n〕的矛盾方程组〔N>n〕,我 们寻求其最小二乘意义下的解。
从给定的一组试验数据出发,寻求函数的一个近似表 达式y= (x),要求近似表达式能够反映数据的根本趋势 而又不一定过全部的点(xi,yi),这就是曲线拟合问题,函 数的近似表达式y= (x)称为拟合曲线。本章介绍用最小 二乘法求拟合曲线。
§5.1 用最小二乘法求解矛盾方程组
一、矛盾方程组的定义
设线性方程组
3.最小二乘法解矛盾方程组
计算步骤:
〔1〕判断方程组的秩是否满足rankA=n?
〔2〕写出正那么方程组;
〔3〕求解正那么方程组,其解就是矛盾方程组 的最小二乘解。
第5章-1 曲线拟合(线性最小二乘法)讲解
求所需系数,得到方程: 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得:
a=0.912605
b=0.174034
所以线性拟合曲线函数为: y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数: y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
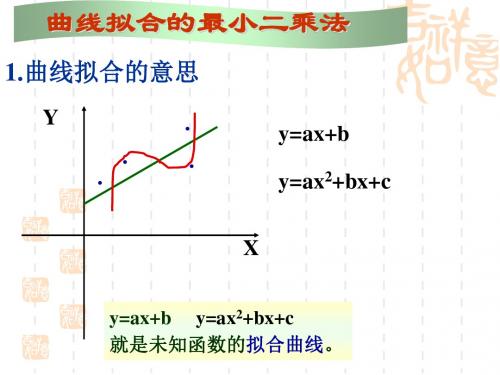
曲线拟合的最小二乘法
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为: y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
曲线拟合的最小二乘法讲解

实验三函数逼近与曲线拟合、问题的提出:函数逼近是指“对函数类A中给定的函数f(x),记作f(x)・A,要求在另一类简的便于计算的函数类B中求函数p(x)・A,使p(x)与f (x)的误差在某中度量意义下最小”函数类A通常是区间[a,b]上的连续函数,记作C[a,b],称为连续函数空间,而函数类B通常为n次多项式,有理函数或分段低次多项式等,函数逼近是数值分析的基础。
主要内容有:(1)最佳一致逼近多项式(2)最佳平方逼近多项式(3 )曲线拟合的最小二乘法实验要求:1、构造正交多项式;2、构造最佳一致逼近;3、构造最佳平方逼近多项式;4、构造最小二乘法进行曲线拟合;5、求出近似解析表达式,打印出逼近曲线与拟合曲线,且打印出其在数据点上的偏差;6、探讨新的方法比较结果。
三、实验目的和意义:1、学习并掌握正交多项式的MATLAB编程;2、学习并掌握最佳一致逼近的MATLAB实验及精度比较;3、学习并掌握最佳平方逼近多项式的MATLAB实验及精度比较;4、掌握曲线拟合的最小二乘法;5、最小二乘法也可用于求解超定线形代数方程组;6、探索拟合函数的选择与拟合精度之间的关系;四、算法步骤:1、正交多项式序列的生成{ \ ( X)}o •:设\ ( X)是[a,b]上首项系数数,如果多项式序列{ \ ( X)}o:满足关系式则称多项式序列{ \(X)}o:为在[a,b]上带权的n次正交多项式。
1 )输入函数「(x)和数据a,b;2) 分别求(x n, j(x)),C j (x), j(x))的内积;. . n 2 (X n,®j(X)), ,3) 按公式①;:o(X)=1, -(X) =X n j j(X)计算;:n(X),生成正交多项式;j鼻Wj(x),W j(x))流程图:开始a n=0的n次多项式,r(x)为[a,b]上权函;Q j秋A 0, jb(j, k)」(x) j(x) k(x)d(X> =a「(x)正交,称;:n (x)为[a,b]上带权「(x)cz>结束2、最佳一致逼近多项式f(x) C[a,b],若存在 R*(x) H n 使得.:(f,P ;^E n ,则称 P ; (x)是 f (x)在[a,b]上的最佳一致逼近多项式或最小偏差逼近多项式,简称最佳逼近多项式。
最小二乘法拟合原理

最小二乘拟合在物理实验中经常要观测两个有函数关系的物理量。
根据两个量的许多组观测数据来确定它们的函数曲线,这就是实验数据处理中的曲线拟合问题。
这类问题通常有两种情况:一种是两个观测量x 与y 之间的函数形式已知,但一些参数未知,需要确定未知参数的最佳估计值;另一种是x 与y 之间的函数形式还不知道,需要找出它们之间的经验公式。
后一种情况常假设x 与y 之间的关系是一个待定的多项式,多项式系数就是待定的未知参数,从而可采用类似于前一种情况的处理方法。
一、最小二乘法原理在两个观测量中,往往总有一个量精度比另一个高得多,为简单起见把精度较高的观测量看作没有误差,并把这个观测量选作x ,而把所有的误差只认为是y 的误差。
设x 和y 的函数关系由理论公式y =f (x ;c 1,c 2,……c m ) (0-0-1)给出,其中c 1,c 2,……c m 是m 个要通过实验确定的参数。
对于每组观测数据(x i ,y i )i =1,2,……,N 。
都对应于xy 平面上一个点。
若不存在测量误差,则这些数据点都准确落在理论曲线上。
只要选取m 组测量值代入式(0-0-1),便得到方程组y i =f (x ;c 1,c 2,……c m ) (0-0-2)式中i =1,2,……,m.求m 个方程的联立解即得m 个参数的数值。
显然N<m 时,参数不能确定。
在N>m 的情况下,式(0-0-2)成为矛盾方程组,不能直接用解方程的方法求得m 个参数值,只能用曲线拟合的方法来处理。
设测量中不存在着系统误差,或者说已经修正,则y 的观测值y i 围绕着期望值 <f (x ;c 1,c 2,……c m )> 摆动,其分布为正态分布,则y i 的概率密度为()()[]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--=22212,......,,;exp 21i mi i i i c c c x f y y p σσπ,式中i σ是分布的标准误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 函数逼近与曲线拟合一、问题的提出:函数逼近是指“对函数类A 中给定的函数)(x f ,记作A x f ∈)(,要求在另一类简的便于计算的函数类B 中求函数A x p ∈)(,使 )(x p 与)(x f 的误差在某中度量意义下最小”。
函数类A 通常是区间],[b a 上的连续函数,记作],[b a C ,称为连续函数空间,而函数类B 通常为n 次多项式,有理函数或分段低次多项式等,函数逼近是数值分析的基础。
主要内容有:(1)最佳一致逼近多项式(2)最佳平方逼近多项式(3)曲线拟合的最小二乘法二、实验要求:1、构造正交多项式;2、构造最佳一致逼近;3、构造最佳平方逼近多项式;4、构造最小二乘法进行曲线拟合;5、求出近似解析表达式,打印出逼近曲线与拟合曲线,且打印出其在数据点上的偏差;6、探讨新的方法比较结果。
三、实验目的和意义:1、学习并掌握正交多项式的MATLAB 编程;2、学习并掌握最佳一致逼近的MATLAB 实验及精度比较;3、学习并掌握最佳平方逼近多项式的MATLAB 实验及精度比较;4、掌握曲线拟合的最小二乘法;5、最小二乘法也可用于求解超定线形代数方程组;6、 探索拟合函数的选择与拟合精度之间的关系;四、 算法步骤:1、正交多项式序列的生成{n ϕ(x )}∞0:设n ϕ(x )是],[b a 上首项系数a ≠n 0的n 次多项式,)(x ρ为],[b a 上权函数,如果多项式序列{n ϕ(x )}∞0满足关系式⎩⎨⎧=>≠==⎰.,0,,0)()()()(),(k j A k j x d x x x kk j bak j ϕϕρϕϕ则称多项式序列{n ϕ(x )}∞0为在],[b a 上带权)(x ρ正交,称n ϕ(x )为],[b a 上带权)(x ρ 的n 次正交多项式。
1)输入函数)(x ρ和数据b a ,;2)分别求))(),(()),(,(x x x x j j j nϕϕϕ的内积; 3)按公式①)())(),(())(,()(,1)(10x x x x x x x x j n j j jj n nn ϕϕϕϕϕϕ∑-=-==计算)(x n ϕ,生成正交多项式;流程图:开始否是结束2、 最佳一致逼近多项式],[)(b a C x f ∈,若存在n n H x P ∈)(*使得n n E P f =∆),(*,则称)(*x P n 是)(x f 在],[b a 上的最佳一致逼近多项式或最小偏差逼近多项式,简称最佳逼近多项式。
现在我们所求的是最佳一次逼近多项式x x P 101)(αα+=,其中)()()(21x f ab b f a f '=--=α ①2)()(2)()(220x a a b a f b f x f a f +--+=α ② 1)输入函数)(x f 和数据b a ,; 2)计算1α和)(x f '; 3)求2x 和)(2x f ; 4)按公式②,计算0α; 5)生成最佳一次逼近多项式;流程图:3、最佳平方逼近多项式对],[)(b a C x f ∈及],[b a C 中的一个子集)}(),...,(),({10x x x span n ϕϕϕϕ=,若存在.)(*ϕ∈x S 使||.)]()()[(min||)()(||min ||)()(2)(22)(22*dx x S x f x x S x f x S x f bax S x S ⎰-=-=-∈∈ρϕϕ则称)(*x S 是)(x f 在子集],[b a C ⊂ϕ中的最佳平方逼近函数。
若取],1,0[)(,1)(,)(C x f x x x kk ∈≡=ρϕ则要在n H 中求n 次最佳平方逼近多项式,...)(**1*0*nn x a x a a x s +++=此时,11))(),((1++==⎰+j k dx x x x j k k j ϕϕk k k d dx x x f x x f ≡=⎰10)())(),((ϕ若用H 表示),...,,1(nn x x G G =对应的矩阵,既⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+++++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)12/(1)2/(1)1/(1)2/(13/12/1)1/(12/11),(),(),(),(),(),(),(),(),(11110101000n n n n n H n n n n n n nϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ称为希尔伯特距阵,记,),...,,(,),...,,(1010Tn T n d d d d a a a a ==则d Ha =的解),...,1,0(*n k a a kk ==即为所求。
平方误差为))(),((||)(||||)(||0*2222x f x a x f x k nk k ϕδ∑=-=;1)输入函数)(x f 和数据b a ,;2)求Tn d d d d ),...,,(10=;3)解方程组 d Ha =,解出 Tn a a a a ),...,,(10=;4)生成最佳平方逼近多项式;流程图:4、曲线拟合的最小二乘法由已知的离散数据点选择与实验点误差最小的曲线)(...)()()(1100x a x a x a x S n n ϕϕϕ+++= 称为曲线拟合的最小二乘法。
若记 ),()()(),(0i k i jmi ik j x x x ϕϕωϕϕ∑==k i k i mi i k d x x f x f ≡=∑=)()()(),(0ϕωϕ上式可改写为),...,1,0(;),(n k d a k j noj j k-=∑=ϕϕ这个方程成为法方程,可写成距阵形式.d Ga =其中,),...,,(,),...,,(1010Tn T n d d d d a a a a ==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=),(),(),()(),(),(),(),(),(101110101000n n n n n n G ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ 。
它的平方误差为:.)]()([)(||||222iimi ix f x S x -=∑=ωδ1) 按照最小二乘法的性质构造Gram 矩阵G ,并求解Ga=d ;构造的时候首先构造一个零矩阵A ;2)然后开始构造Gram 矩阵(在下面程序里我们把克莱姆矩阵用A 来表示)3)然后求列矩阵b ,因为Aa=b ,所以求 a=A\b ;(d 就是列矩阵b ); 4)然后找对应数据的最小二乘拟合方程和画出它的图像;5)在m 文件里制好以上规定的程序后,在matlab 的命令窗口 输入数组x 和数组y 及所选择的拟合多项式次数 m ,然后执行就可以得到曲线二乘拟合方程和它的图像。
流程图:五、Matlab 程序源代码:1、正交多项式序列的生成function gouzaozhengjiaoduoxiangshi 数值例题:1)当区间为]1,1[-,权函数1)(≡x ρ时,由,...},...,,1{nx x 正交化得到的多项式就成为勒让德多项式,它的表达式为1)(0=x P , })1{(!21)(2nnn nn x dxd n x P -=; 递推公式为,...),2,1(),()()12()()1(11=-+=+-+n x nP x xP n x P n n n n 由x x P x P ==)(,1)(10,利用(1)就可推出,8/)33035()(,2/)35()(,2/)13()(2443322+-=-=-=x x x p x x x P x x P…y 12)当权函数21)(x x -=ρ,区间为]1,1[-时,由序列,...},...,,1{nx x 正交化得到的多项式就是切比雪夫多项式,它可表示为.1||),arccos cos()(≤=x x n x T n 若令θcos =x ,则.0,cos )(πθθ≤≤=n x T n递推关系.)(,1)(,...),2,1(,)(2)(1011x x T x T n T x xT x T n n n ===-=-+ 可推出,188)(,34)(),12(2443322+-=-=-=x x x T x x x T x x T2、 最佳一致逼近多项式function yicibijin数值例题:(1)求21)(x x f +=在[0,1]上的最佳一次逼近多项式 ;结果为:x x P 414.0955.0)(1+=;误差限为.045.0|)(1|max 1210≤-+≤≤x P x x3、最佳平方逼近多项式function pingfang● 数值例题:设21)(x x f +=,求]1,0[上的一次最佳平方逼近多项式;结果为:x x S 426.0934.0)(*1+=,0026.0||)(||22=x δ;4、曲线拟合的最小二乘法:function p=nihe(x,y,m)● 数值实例:例1:下面给定的是乌鲁木齐最近1个月早晨7:00左右(新疆时间)的天气预报所得到的温度数据表 ,按照数据找出任意次曲线拟合方程和它的图像.(2006年10月26~11月26)解:x=1:30y=[9 10 11 12 13 14 13 12 11 9 10 11 12 13 14 12 11 10 9 8 7 8 9 11 8 7 6 5 3 1]m=9;(m是任意真整数,但是不要取的太大)运行p=nihe(x,y,m)结果为:p =图形为:或者任意取部分数据也可得到相应得多项式和它的图像m=15时x=1:30y=[9 10 11 12 13 14 13 12 11 9 10 11 12 13 14 12 11 10 9 8 7 8 9 11 8 7 6 5 3 1]运行p=nihe(x,y,m)结果为:p =图形为:如果:m=3x=1:30y=[9 10 11 12 13 14 13 12 11 9 10 11 12 13 14 12 11 10 9 8 7 8 9 11 8 7 6 5 3 1]运行p=nihe(x,y,m)结果为:p =图形为:如果写M文件的时候我们把想得到的多项式的次数直接定义为(m=length(x))跟X的数量一样取得最小二乘法的曲线拟合方程,这样上术问题中的m=30,这时候它的程序代码为:f unction p=nn(x,y)赋值x,y :x=1:30y=[9 10 11 12 13 14 13 12 11 9 10 11 12 13 14 12 11 10 9 8 7 8 9 11 8 7 6 5 3 1];运行p=nn(x,y)解为:p =图像为:结果分析:以上结果可以看到用最小二乘拟合来求解问题时,有时候他的结果很接近实际情况,有时候跟实际情况里的太远,因为所求得多项式次数太小时数据点之间差别很大.次数最大是误差最小但是有时后不符合实际情况,所以用最小二乘法时次数要取合适一点.或采用:function p=duoxiangxi(x,y,m)数值例题:(1)合成纤维抽丝工段中第一导丝盘的速度对丝的质量有很大的影响,第一丝盘的速度和电流周波有重要关系。
