2011-2012学年第一学期期末高二数学(文科)试题及答案
高二上学期期末考试数学(文)试题及答案 (4)

学年第一学期阶段性考试 高二数学(文科)试卷第Ⅰ卷一、选择题:本大题共12小题。
每小题5分,在每小题给出的四个选项中,只有一项符合题目要求. 1.已知命题2015log ,:2=∈∀x R x p ,则p ⌝为( )A .2015log ,2=∉∀x R xB .2015log ,2≠∈∀x R xC .2015log ,020=∈∃x R xD .2015log ,020≠∈∃x R x2.为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为1到50的袋装奶粉中抽取5袋进行检验,用系统抽样方法确定所选取的5袋奶粉的编号可能是( )A .5,10,15,20,25B .2,4,8,16,32C .5,6,7,8,9D .6,16,26,36,46 3.如果一个家庭有两个小孩,则两个孩子是一男一女的概率为( ) A .14 B .13 C .12 D .234.双曲线1222=-y x 的渐近线方程为( ) A. 02=±y x B. 02=±y x C .02=±y x D .02=±y x5.甲、乙两名学生五次数学测验成绩(百分制)如图所示. ①甲同学成绩的中位数大于乙同学成绩的中位数; ②甲同学的平均分与乙同学的平均分相等; ③甲同学成绩的方差大于乙同学成绩的方差. 以上说法正确的是( ) A .①②B .②③C .①③D .①②③6.用秦九韶算法求多项式7234)(234++++=x x x x x f 的值,则)2(f 的值为( ) A .98 B .105 C .112 D .119 7.运行如右图的程序后,输出的结果为( ) A .6053 B .54 C .65 D .76 8.已知椭圆221164x y +=过点)1,2(-P 作弦且弦被P 平分,则此弦 所在的直线方程为( )7 90 1 38 90 1 289甲乙ENDS PRINT WEND i i i i S S i WHILE S i 1))1(/(1601+=+*+=<==A .032=--y xB .012=--y xC .042=--y xD .042=+-y x9.已知)(x g 为函数)0(1232)(23≠--=a ax ax ax x f 的导函数,则它们的图象可能是( )A .B .C .D .10.已知倾斜角为︒45的直线l 过抛物线x y 42=的焦点,且与抛物线交于B A ,两点,则OAB ∆(其中O 为坐标原点)的面积为( ) A .2B .22C .23D .811.已知(),()f x g x 都是定义在R 上的函数,且满足以下条件:①()()xf x ag x =⋅(0,a >1)a ≠且;②()0g x ≠;③)(')()()('x g x f x g x f ⋅<⋅. 若(1)(1)5(1)(1)2f fg g -+=-,则实数a 的值为 ( )A .21 B .2 C .45 D .2或21 12.如图,直线m x =与抛物线y x 42=交于点A ,与圆4)1(22=+-x y 的实线部分(即在抛物线开口内 的圆弧)交于点B ,F 为抛物线的焦点,则ABF ∆的 周长的取值范围是( ) A .()4,2 B .()6,4 C .[]4,2 D . []6,4第Ⅱ卷二、填空题:本大题共四小题,每小题5分.13.将十进制数)10(2016化为八进制数为 . 14.已知变量x 与y 的取值如下表:x 23 5 6y 7a -8 a +9 12从散点图可以看出y 对x 呈现线性相关关系,则y 与x 的线性回归直线方程a bx y+=ˆ必经过的定点为 .15.已知P 为圆4)2(:22=++y x M 上的动点,)0,2(N ,线段PN 的垂直平分线与直线PM 的交点为Q ,点Q 的轨迹方程为 .16.已知函数xxe x f =)(,现有下列五种说法:①函数)(x f 为奇函数;②函数)(x f 的减区间为()-1∞,,增区间为()1+∞,;频率组距50 55 60 65 70 75 80体重(kg)O0.070.060.050.040.030.020.01③函数)(x f 的图象在0x =处的切线的斜率为1; ④函数)(x f 的最小值为1e-. 其中说法正确的序号是_______________(请写出所有正确说法的序号).三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)设命题p :12>-x ;命题q :0)1()12(2≥+++-a a x a x .若p ⌝是q ⌝的必要不充分条件,求实数a 的取值范围.18.(本小题满分12分)某校对高二年段的男生进行体检,现将高二男生的体重()kg 数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[)65,60的人数为200.根据一般标准,高二男生体重超过65kg 属于偏胖,低于55kg 属于偏瘦.观察图形的信息,回答下列问题:(1)求体重在[)6560,内的频率,并补全频率分布直方图;(2)用分层抽样的方法从偏胖的学生中抽取6人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?(3)根据频率分布直方图,估计高二男生的体重的中位数与平均数.19. (本小题满分12分)(1)执行如图所示的程序框图,如果输入的[]3,1-∈t ,若输出的s 的取值范围记为集合A ,求集合A ;(2)命题p :A a ∈,其中集合A 为第(1)题中的s 的取值范围;命题q :函数a x ax x x f +++=2331)(有极值; 若q p ∧为真命题,求实数a 的取值范围.20.(本小题满分12分)已知双曲线C :)00(12222>>=-,b a by a x .(1)有一枚质地均匀的正四面体玩具,玩具的各个面上分别写着数字1,2,3,4.若先后两次投掷玩具,将朝下的面上的数字依次记为b a ,,求双曲线C 的离心率小于5的概率;(2)在区间[]61,内取两个数依次记为b a ,,求双曲线C 的离心率小于5的概率.21.(本小题满分12分)已知椭圆C:)0(12222>>=+b a by a x 的中心在坐标原点O ,对称轴在坐标轴上,椭圆的上顶点与两个焦点构成边长为2的正三角形. (1)求椭圆C 的标准方程;(2)若斜率为k 的直线l 经过点)0,4(M ,与椭圆C 相交于A ,B 两点,且21>⋅OB OA ,求k 的取值范围.22. (本小题满分12分)已知函数)(2ln )(2R a x xa x a x f ∈++-=. (1)当1=a 时,求曲线)(x f y =在点))1(,1(f 处的切线方程;(2)当0>a 时,若函数()f x 在[1,]e 上的最小值记为)(a g ,请写出)(a g 的函数表达式.高二数学(文科)试卷参考答案一、DDCD BBCD ABAB二、13.)8(3740 14.()9,4 15.)0(1322<=-x y x 16.③④ 三、17.解:由p :12>-x 解得1<x 或3>x .……………………………… 3分由q :0)1()12(2≥+++-a a x a x 得[]0)1()(≥+--a x a x ,解得a x ≤或1+≥a x .……………………………… 6分∵p ⌝是q ⌝的必要不充分条件,∴p 是q 的充分不必要条件. …………………… 8分 ∴⎩⎨⎧≤+≥311a a ,则21≤≤a .∴实数a 的取值范围是[]21,.……………………………… 10分 18.解:(1)体重在[)65,60内的频率2.05)01.002.003.007.003.0(1=⨯++++-=04.052.0==组距频率 补全的频率分布直方图如图所示. ……………4分 (2)设男生总人数为n ,由2.0200=n,可得1000=n 体重超过kg 65的总人数为30010005)01.002.003.0(=⨯⨯++在[)70,65的人数为1501000503.0=⨯⨯,应抽取的人数为33001506=⨯, 在[)70,65的人数为1001000502.0=⨯⨯,应抽取的人数为23001006=⨯, 在[)80,75的人数为501000501.0=⨯⨯,应抽取的人数为1300506=⨯. 所以在[)70,65 ,[)75,70,[]80,75三段人数分别为3,2,1.…………………… 8分 (3)中位数为60kg 平均数为(52.50.0357.50.0762.50.0467.50.0372.50.0277.50.01)561.75⨯+⨯+⨯+⨯+⨯+⨯⨯=(kg)…12分19.解:(1)由程序框图可知,当11<≤-t 时,t s 2=,则[)2,2-∈s . 当31≤≤t 时,()322+--=t s组距kg)O0.0.0.0.0.0.0.∵该函数的对称轴为2=t ,∴该函数在[]21,上单调递增,在[]3,2上单调递减. ∴2,3min max ==s s ∴[]3,2∈s综上知,[]3,2-∈s ,集合[]3,2-=A ……………………………… 4分 (1)函数a x ax x x f +++=2331)(有极值,且12)(2'++=ax x x f , 0)('=x f 有两个不相等的实数根,即04)2(2>-=∆a 解得1-<a 或1>a即命题p :1-<a 或1>a .……………………………… 8分q p ∧为真命题,则⎩⎨⎧≤≤->-<3211a a 或a ,解得3112≤<-<≤-a 或a ;∴实数a 的取值范围是[)(]2,113--⋃,.……………………………… 12分20.解:双曲线的离心率22221ab ac a c e +===. 因为5e <a b ab 20422<<∴<∴.……………………………… 2分 (1) 因玩具枚质地是均匀的,各面朝下的可能性相等,所以基本事件),(b a 共有16个:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).设“双曲线C 的离心率小于5”为事件A ,则事件A 所包含的基本事件为(1,1),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共有12个. 故双曲线C 的离心率小于5的概率为431612)(==A P .…………………………… 7分(2) ∵[][]6,1,6,1∈∈b a∴⎪⎩⎪⎨⎧<<≤≤≤≤a b b a 206161 所以以a 为横轴,以b 为纵轴建立直角坐标系,如图所示,21422155=⨯⨯-⨯=阴影S ,由几何概型可知,双曲线C 的离心率小于5的概率为2521=P .……………………………… 12分21.解:(1)∵椭圆的上顶点与两个焦点构成边长为2的正三角形,32,22222=-=∴==∴c a b a c∴椭圆C 的标准方程为13422=+y x .……………………………… 4分 (2) 设直线l 的方程为)4(-=x k y ,设A (x 1,y 1),B (x 2,y 2)联立⎩⎨⎧=+-=1243)4(22y x x k y ,消去y 可得(0126432)43(2222=-+-+k x k x k∵直线l 与椭圆C 相交于A ,B 两点,∴0>∆由0)1264)(43(4)32(2222>-+-=∆k k k 解得412<k 设),(11y x A ,),(22y x B则34322221+=+k k x x ,3412642221+-=k k x x ……………………………… 7分211643324431264)1(16)(4)1()4()4(2222222221221221212121>++-+-+=++-+=--+=+=⋅k k k k k k k k x x k x x k x k x k x x y y x x OB OA解得196272>k ∴41196272<<k所以k 的取值范围是211433143321<<-<<-k 或k .……………………………… 12分22.解:(1)∵)(2ln )(2R a x x a x a x f ∈++-=,∴12)(22'+--=xa x a x f 当1=a 时,121)(,2ln )(2'+--=++-=xx x f x x x x f 2)1(,3)1('-===f k f曲线)(x f y =在点))1(,1(f 处的切线方程为)1(23--=-x y 即052=-+y x .……………………………… 3分(2)222222'))(2(212)(x a x a x x a ax x x a x a x f +-=--=+--=0,0>>x a ,由0)('>x f 得a x 2>,由0)('<x f 得a x 20<<)(x f ∴在(]a 2,0上为减函数,在()+∞,2a 上为增函数.……………………………… 5分①当210120≤<≤<a 即a 时,)(x f 在[]e ,1上为增函数. 12)1()(2+==∴a f a g 在(]a 2,0上为减函数,在()+∞,2a 上为增函数.…………… 7分②当22121ea e 即a <<<<时,)(x f 在[]a 2,1上为减函数,在(]e a ,2上为增函数. a a a a f a g 3)2ln()2()(+-==∴……………………………… 9分③当22ea e 即a ≥≥时,)(x f 在[]e ,1上为减函数. e ea a e f a g ++-==∴22)()(……………………………… 11分综上所述,⎪⎪⎪⎩⎪⎪⎪⎨⎧≥++-<<+-≤<+=)2(2)221(3)2ln()210(12)(22e a e e a a e a a a a a a a g ……………………………… 12分。
浙江省慈溪市2011至2012学年高二上学期期末试题文科扫描版

数学(文科)参考答案及评分标准
(考试时间:120分钟,满分:150分)
一、选择题(本大题共10小2
3
4
5
6
7
8
9
10
答案
D
A
A
B
C
A
C
D
B
D
二、填空题(本大题共7小题,每小题4分,共28分.)
11.若两条直线互相垂直,则这两条直线的斜率互为负倒数;假
解.(1) ……………………2分
(2) ……………………3分
当 时,
当 时,
的增区间为: ,减区间为: ……7分
(3) ,对称轴为
(ⅰ)当 时,
∴由(1)知:当 时,可得: 解得: ………10分
(ⅱ)当 时,
又由(1)同理可得: 递增, 递减
当 时,可得: 解得: ………………14分
故综上所知,所求a的取值范围为 …………15分
……………………7分
(2)连结BG,
为直线BD与平面ABC所成的角,且DG ………………9分
在Rt 中,
在Rt 中,AB=4, ,
……………………10分
在Rt 中, ……………………11分
(3) ……………………12分
……………………14分
19.(本小题满分14分)
解.(1)设圆N的圆心N(a,b),则N(a,b)和点M 关于直线 对称
(3) AB的中点M不在x轴上 AB不垂直于x轴,AB的斜率存在且不为0
……………………10分
可设AB: ……………………11分
由 (*)……………12分
……………………13分
为AB的中点 即 ……………14分
石家庄市2011~2012学年度第一学期期末考试高二数学试卷及答案

石家庄市2011~2012学年度第一学期期末考试试卷高二数学(文科)(时间l20分钟,满分150分)注意事项:1.本试卷分第l 卷(选择题)和第Ⅱ卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第l 卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需 改动,用橡皮擦干净后,再选涂其他答案标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.第1卷(选择题共60分)一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.抛物线y 2=8x 的焦点坐标是A .(2,0)B .(4,0)C .(0,2)D .(0,4)2.“x =1”,是“(x-1)(x +2)=0”的A .充分而不必要条件B .必要而不充分条件c .充要条件 D .既不充分也不必要条件3.曲线Y=x 3—2x+1在点(1,0)处的切线方程为A .Y=x-lB .Y=-x+1C .Y=2x-2D .Y=-2x+24.右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是A .62B .63C .64D .655.由点P(2,3)向圆x 2+y 2=9引切线,则切线长为A .2B .3C .4D .56.先后抛掷硬币三次,则至少一次正面朝上的概率是 A. 81 B.83 c. 85 D .877.执行右图所示的程序框图,输出的S 值是A .13 8.14 C .15 D .168.椭圆5x 2+y 2=5的一个焦点是(0,2),那么k=A .-lB .1c .5 D .-59.从装有2个红球和2个黑球的口袋内任取2个球,那么互斥 而不对立的两个事件是A .至少有一个黑球与都是黑球B .至少有一个黑球与都是红球C .至少有一个黑球与至少有一个红球D .恰有一个黑球与恰有两个黑球 l10.已知样本9,10,11,x ,y 的平均数是l0,标准差是2,则xy=A .95B .96C .97D .9811.若F 1、F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在曲线C 上,∠F 1PF 2 =600,则∣PF 1∣∙∣ PF 2∣=A .2B .4C .6D .812.圆x 2+2x +y 2+4y 一3=0上到直线x+y+1=0的距离等于2的点共有 A .1个 B .2个C .3个D .4个第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.命题“0932,2 +-∈∃ax x R x ”为假命题,则实数a 的取值范围为 .14.某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为 185的样本,已知抽取高一年级学生75人,抽取高二年级学生60人,则高中部共有学生的人数为 .15.函数y=3x+2cosx 在区间[0,2π]上的最大值是 . 16.过抛物线y 2=4x 的焦点F 的直线交抛物线于A 、B 两点,∣AF ∣=2,则∣BF ∣= .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题.(I)在79.5~89.5之间的频率、频数分别是多少?(Ⅱ)估计这次环保知识竞赛的及格率(60分及以上为及格).18.(本小题满分12分)动圆C 截直线3x-y=0和3x+y=0所得弦长分别为8、4,求动圆圆心C 的轨迹方程.19.(本小题满分12分)已知函数c bx ax x f ++=24)(的图象经过点(0,1),且在x=1处的切线方程是y=x-2. (I)求函数)(x f 的解析式;(Ⅱ)求函数)(x f 的单调递增区间.20.(本小题满分12分)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验.收集数据如下:(I)请画出上表数据的散点图;(Ⅱ)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程a x b y +=;(Ⅲ)现需生产20件此零件,预测需用多长时间?(注:用最小二乘法求线性回归方程系数公式x b y a x n x y x n y x b n i i ni i i -=--=∑∑==,1221)21.(本小题满分12分)已知a ∈(0,6),b ∈(0,6)(I)求∣a-b ∣≤1的概率;(Ⅱ)以a ,b 作为直角三角形两直角边的边长,则斜边长小于6的概率.22.(本小题满分12分)已知椭圆C :)0(12222 b a b y a x =+的离心率为36,右焦点为(2,0). (I)求椭圆C 的方程;(Ⅱ)若过原点O 作两条互相垂直的射线,与椭圆C 交于A ,B 两点,求证:点O 到直线AB 的距离为定值.石家庄市2011~2012学年度第一学期期末考试高二数学(文科答案)一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是 符合题目要求的.1~5 AAACA 6~10 DCBDB 11~12 BC二、 填空题:本大题共4小题,每小题5分,共20分..13. [-22,22]; 14.3700; 15. 3π 2; 16.2三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步1.抛17.(本小题满分10分)解:(Ⅰ)频率为0.025×10=0.25;………………3分频数为60×0.25=15.所以在79.589.5 之间的频率、频数分别是0.25和15.……………5分(Ⅱ)0.015×10+0.025×10+0.03×10+0.005×10=0.75所以估计及格率为0.75. …………………10分18. .(本小题满分12分)解:设点C (x ,y ),圆C 的半径为r ,则点C 到直线30x y -=的距离为12331x yd -=+, ……………3分 点C 到直线30x y +=的距离为223+31x yd =+,…………6分依题意 2222331643131x y x y ⎛⎫⎛⎫-++=+ ⎪ ⎪++⎝⎭⎝⎭ ……………9分化简整理,得x y =10.动圆圆心C 的轨迹方程为x y =10. ………………12分19. .(本小题满分12分)解:(Ⅰ)c bx ax x f ++=24)(的图象经过点(0,1),则1c =,………………2分 '3'()42,(1)421,f x ax bx k f a b =+==+=…………4分切点为(1,1)-,则c bx ax x f ++=24)(的图象经过点(1,1)- 得591,,22a b c a b ++=-==-得 4259()122f x x x =-+.……………………6分(Ⅱ)因为'3()109f x x x =-,3109x x -0,>…………………9分 解得3103100,1010x x -<<>或, 所以函数(f x )单调递增区间为310310(,0),(,)1010-+∞.………………12分 20. .(本小题满分12分)解: (Ⅰ)散点图略…………………4分 (Ⅱ)1234 2.54x +++==; 23584.54y +++==…………………6分 41422142+6+15+32-4 2.5 4.5=2(14916)4 2.5 2.54ii i ii x y xy b xx ==-⨯⨯==+++-⨯⨯-∑∑ (). ˆay bx =- =4.5-2×2.5=-0.5 所以ˆ20.5yx =-.……………9分 (Ⅲ)因 2200.539.5y =⨯-=(小时)所以生产20件此零件,预测需用39.5小时.……………12分21. .(本小题满分12分)解:(Ⅰ)若点)6,0(,∈b a ,则点位于正方形OABC 内(不含边界);…………2分 若1≤-b a ,点)6,0(,∈b a 位于直线a -b =1和a +b =1之间(含边界).……………4分 所以满足1≤-b a 的概率为15522511211363636.⨯⨯⨯--=………………6分 (Ⅱ)由已知a 2+b 2<36, )6,0(,∈b a ,则满足题意的点位于阴影部分(不含边界),……………9分 则2164=.364⨯π⨯π 以b a ,作为直角三角形两直角边的边长,斜边长小于6的概率为.4π……………12分 22. .(本小题满分12分) 解:(Ⅰ)由已知222632;.c a c a b c ⎧=⎪⎪⎪=⎨⎪-=⎪⎪⎩; ……………2分 解得3;1.a b ⎧=⎪⎨=⎪⎩ 所以,所求椭圆方程为2213x y +=.…………………4分 (Ⅱ) 设11()A x y ,,22()B x y ,, 若k 存在,则设直线AB :y =kx +m.由2233y kx m x y =+⎧⎨+=⎩,得 222(13)6330k x kmx m +++-=△ >0,12221226133313km x x k m x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩………………7分 有OA ⊥OB 知x 1x 2+y 1y 2=x 1x 2+(k x 1+m ) (k x 2+m ) =(1+k 2) x 1x 2+k m (x 1+x 2)=0 ………………………9分代入,得4 m 2=3 k 2+3 原点到直线AB 的距离d =2321mk =+.………………………10分 当AB 的斜率不存在时,11x y =,可得132x d ==,依然成立. 所以点O 到直线AB 的距离为定值32.………………12分。
惠州市2011-2012学年第一学期高二期末考试文科试题答案

惠州市2011-2012学年第一学期高二期末考试文科数学试题解答一、选择题:本大题共9小题,每小题5分,共45分,在每小题给出的四个选项中,只有一项是符合题目要求的。
2.【解析】基本事件总数为3种,甲被选中的种数为2种,故P =233.【解析】设椭圆的另一焦点为F ,则由椭圆的定义知|BA |+|BF |=23, 且|CF |+|AC |=23,所以△ABC 的周长=|BA |+|BF |+|CF |+|AC |=4 3. 4.【解析】因为p 且q 为假,p 、q 至少有一个为假,故选C. 5.【解析】由椭圆的方程知,a 2=13,b 2=9,焦点在x 轴上,∴c =a 2-b 2=13-9=2,∴抛物线的焦点为(-2,0),∴抛物线的标准方程是y 2=-8x . 6.【解析】函数f (x )=x 2+mx +1的对称轴为x =-m 2,于是-m 2=1,m =-2.7.【解析】在区间[-1,1]上随机取一个数x,即[1,1]x ∈-时,要使cos 2xπ的值介于0到21之间,需使223x πππ-≤≤-或322xπππ≤≤∴213x -≤≤-或213x ≤≤,区间长度为32,由几何概型知cos 2x π的值介于0到21之间的概率为31232=.故选A.8.【解析】由题意得c =3+p 216=p 2,p =4,所以e =c a =23=233.故选C. 9.【解析】这类问题,通常由开始一步一步运行,根据判断条件,要么几步后就会输出结果,要么就会出现规律,如周期性,等差或等比数列型. 程序运行如下:1,x = 2,x =4,x =5,x =6,x =8,x =9,x =10,x =12,x =输出12.二、填空题:本大题共3小题,每小题5分,共15分,把答案填写在答题卷中指定的横线上。
10. 1e 11.m =3. 12. 2910.【解析】k 的最大值即过原点与曲线y =ln x 相切的直线的斜率.设切点P (x 0,y 0),∴y 0=ln x 0.∵y ′=1x ,∴在x 0处的切线斜率为1x 0.∴1x 0=y 0x 0,即1x 0=ln x 0x 0.∴x 0=e.∴1x 0=1e .∴k 的最大值为1e .11.【解析】由题意可知,直线y =0.7x +0.35过点(x ,y ),又x =4.5,代入方程得y =3.5,故m =3.12.【解析】以2颗骰子的点数作为P 点的坐标有36个,其中落在圆x 2+y 2=16内的点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2)共8个.于是所求概率为P =836=29.三、解答题:本大题共3小题,共40分,解答应写出必要的计算过程、推演步骤或文字说明。
江西省南昌市2011—2012学年度第一学期高二年级期末考试(文科乙卷)

— 高二数学(文科乙卷)第1页 —南昌市2011—2012学年度第一学期高二年级期末考试数学(文科乙卷)一、选择题(本大题共10小题,每小题3分,共30分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在答卷的相应表格内)1.设函数()x f y =,当自变量x 由0x 改变到x x ∆+0时,函数的改变量y ∆为 A .()x x f ∆+0 B .()x x f ∆+0C .()xx f ∆⋅0D .()()00x f x x f -∆+2.命题“存在x R ∈,20x≤”的否定是A .不存在x R ∈, 20x> B .对任意的x ∈R, 2x >0 C .存在x R ∈, 20x≥ D .对任意的x ∈R, 2x ≤0 3.一个物体的运动方程为21t t s +-=其中s 的单位是米,t 的单位是秒,那么物体在3秒末的瞬时速度是A .8米/秒B .7米/秒C .6米/秒D . 5米/秒 4.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程是A .430x y --=B .450x y +-=C .430x y -+=D .430x y ++= 5.若()sin cos f x x x =-,则()f a '等于A .sin aB .cos αC .sin cos αα+D .2sin α6.命题“若x =3,则01892=+-x x ”,那么它的的逆命题、否命题与逆否命题这三个命题中,真命题的个数有A . 0 个B . 1个C . 2个D . 3个 7.下列说法正确的是A 、函数的极大值就是函数的最大值B 、函数的极小值就是函数的最小值C 、函数的最值一定是极值D 、在闭区间上的连续函数一定存在最值 8.函数214y x x=+单调递增区间是 A .(0,)+∞ B .(,1)-∞ C .1(,)2+∞ D .(1,)+∞ 9.“2320x x ++>”成立的一个充分不必要条件是A . 21x x <->-或B . 2x >C . 1x ≥-D . x 0< 10.函数2cos y x x =+在π02⎡⎤⎢⎥⎣⎦,上取最大值时,x 的值为A .0B .π6C .π3D .π2— 高二数学(文科乙卷)第2页 —二、填空题(本大题共5小题,每小题4分,共20分,请将正确答案填空在答卷上) 11.已知()221f x x x =+-,则()'0f= .12.全称命题“对任意x Z ∈, x 有一个正因数”的否定是_____________________. 13.一辆汽车从停止时开始加速行驶,并且在5秒内速度)/(s m v 与时间t (s )的关系近似表示为t t t f v 10)(2+-==,则汽车在时刻1=t 秒时的加速度为 2/s m14.曲线32242y x x x =--+在点(1,-3)处的切线方程是 。
陕西省咸阳市2011-2012学年高二数学上学期期末质量检测试题 文 新人教A版
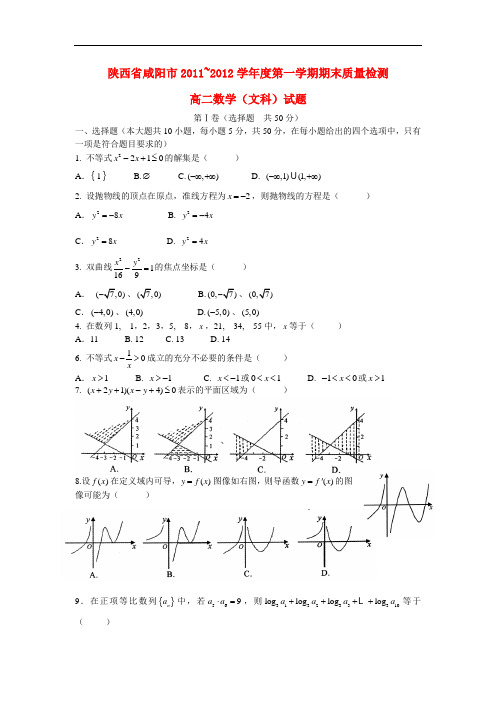
陕西省咸阳市2011~2012学年度第一学期期末质量检测高二数学(文科)试题第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1. 不等式2210x x -+≤的解集是( )A .{}1 B.∅ C.(,)-∞+∞ D. (,1)(1,)-∞+∞2. 设抛物线的顶点在原点,准线方程为2x =-,则抛物线的方程是( ) A .28y x =- B. 24y x =- C .28y x = D. 24y x =3. 双曲线221169x y -=的焦点坐标是( )A . (、 B.(0,、 C .(4,0)-、(4,0) D.(5,0)-、(5,0)4. 在数列1, 1,2,3,5, 8,x ,21, 34, 55中,x 等于( ) A .11 B. 12 C. 13 D. 146. 不等式10x x->成立的充分不必要的条件是( ) A .1x > B. 1x >- C. 1x <-或01x << D. 10x -<<或1x > 7. (21)(4)0x y x y ++-+≤表示的平面区域为( )8.设()f x 在定义域内可导,()y f x =图像如右图,则导函数()y f x '=的图像可能为( )9.在正项等比数列{}n a 中,若569a a ⋅=,则31323331log log log log a a a a ++++等于( )A . 8 B. 10 C.12 D.2log 5a +10.过椭圆22221x y a b+=(0)a b >>的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=,则椭圆的离心率为( ) A.B. C. 12 D. 13第Ⅱ卷 (非选择题 共100分)二、填空题(本大题共5小题,每小题5分,共25分,将答案填在题中的横线上) 11. 命题“存在20,10x R x ∈+<”的否命题是 . 12.函数sin cos y x x =+在2x π=处的切线的倾斜角是 。
2011-2012顺德区期末高二文科数试题

俯视图正视图侧视图2011~2012学年度第一学期 高二年级期末考试数学试题(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1、直线320110x y +-=的倾斜角是A .30oB .120oC .135oD .150o2、直线3x +4y -13=0与圆1)3()2(22=-+-y x 的位置关系是A . 相离B . 相交C . 相切D . 无法判定3、已知△ABC 的三个顶点为A (3,3,2),B (4,-3,7),C (0,5,1),则BC 边上的中线长为 A.2 B.3 C.4 D.54、已知α,β表示两个不同的平面,m 为平面α内的一条直线,则“α⊥β ”是“m ⊥β ”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 5、如图,一个水平放置的平面图形的斜二测直观图是一个底角为45o,腰和上底均为1的等腰梯形,那么原平面图形的面积是A . 22+B . 122+C . 222+D . 12+6、已知命题tan 1p x R x ∃∈=:,使,其中正确的是 A. tan 1p x R x ⌝∃∈≠:,使B. tan 1p x R x ⌝∃∉≠:,使 C.tan 1p x R x ⌝∀∈≠:,使 D.tan 1p x R x ⌝∀∉≠:,使 7、如图,一个简单空间几何体的三视图中,其正视图与侧视图都是边长为2的正三角形,俯视图轮廓为正方形,则其侧面积是A .12B . 8C . 43D . 38、直线330x y +-=与直线610x my ++=平行,则它们之间的距离为A .4B .21313 C .51326D .71020 9、设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是 A.若l m ⊥,m α⊂,则l α⊥ B.若l α⊥,l m //,则m α⊥ C.若l α//,m α⊂,则l m // D.若l α//,m α//,则l m //10、设x 1,x 2∈R ,常数a >0,定义运算“⊙”;x 1⊙x 2=(x 1+x 2)2-(x 1-x 2)2,若x ≥0,则动点P (x ,a ⊙x )的轨迹方程是A .y 2=4axB .y 2=4ax (y ≥0)C .x 2=4ay (x ≥0)D .x 2=4ay二、填空题:本大题共4小题,每小题5分,共20分,将正确答案填在题中横线上。
深圳高级中学2011—2012学年第一学期高二文科数学期末测试

深圳高级中学2011—2012学年第一学期期末考试高二文科数学满分:150分,考试时间:120分钟参考公式:在线性回归方程 y bx a =+中,()1122211()()nni i ii i i nni ii i X Y nXYXX Y Yb X nXXX ====---==--∑∑∑∑, a Y bX =-.一、选择题(每小题5分,共10小题50分)1.设命题甲:三角形ABC 有一个内角是060,命题乙:三角形ABC 三个内角的度数成等差数列,那么A .甲是乙的充分条件,但不是必要条件B .甲是乙的必要条件,但不是充分条件C .甲是乙的充要条件D .甲既不是乙的充分条件,也不是必要条件 2. 复数122,1z i z i =+=-,则复数12z z ⋅对应的点Z 位于 A .第一象限B .第二象限C .第三象限D .第四象限3. 如图1所示,是关于闰年的流程,则以下年份是 闰年的为A .1996年B .1998年C .2010年D .2100年4. 某雷达测速区规定:凡车速大于或等于 70km/h 的汽车视为“超速”,并将受到处罚,如图2是某路段的 一个检测点对200辆汽车的车速进行检测所得结果的频率分布直 方图,则从图中可以看得出将被处罚的汽车大约有 A .30辆 B. 40辆 C. 60辆 D. 80辆5. 从五件正品,一件次品中随机取出两件,则取出的两件产品中 恰好是一件正品,一件次品的概率是A. 1B.21 C.32 D.316. 如图3,在半径为R 的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是0.040.030.020.01频率组距时速8070605040图2图3A .34B .334C .34πD .334π7. 某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日到3日的每天昼夜温差与实验室每天每100颗种子发芽数,得到如下资料:日期 12月1日12月2日12月3日温差x(0C) 11 13 12 发芽数y(颗)253026该农科所确定的研究方案是:先从这3组数据求出线性回归方程,再对12月4日的数据进行推测和检验.则根据以上3天的数据,求出y 关于x 的线性回归方程是A. 23y x ∧=+ B. 39y x ∧=- C. 532y x ∧=- D. 743y x ∧=-8. 图中各正方形图案,每条边上有(2)n n ≥个圆点,第n 个图案中圆点的总数是n S .n=2 n=3 n=4按此规律推断出n S 与n 的关系式为A.n S =2nB. n S =4n-4C. n S =2nD. n S =44n-9. 四个小动物换座位,开始是鼠、猴、兔、猫分别坐1,2,3,4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2005次互换座位后,小兔的座位对应的是A. 编号1B. 编号2C. 编号3D. 编号410. 如图4是二次函数a bx x x f +-=2)(的部分图象,则函数)(ln )(x f x x g '+=的零点所在的区间是A.11(,)42B.1(,1)2C.(1,2)D.(2,3)第三次第二次第一次开始鼠猴猫兔鼠猴猫兔鼠猴猫兔兔猫猴鼠4242424213313131图4二、填空题(每小题5分,共4小题20分)11. 图5给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图,其中判断框内应填入的条件是12. 已知总体的各个体的值由小到大依次为2,3,3,7,a ,b , 12,13.7,18.3,20,且总体的中位数为10.5.若要使该总体的 方差最小,则a 、b 的取值分别是13. 把一根长度为5的铁丝截成任意长的3段,则能构成三角形的 概率为14.抛物线y =ax 2与直线l :y =kx +b (k ≠0)交于A 、B 两点,且此两 点的横坐标分别为x 1,x 2,则直线l 与x 轴交点的横坐标等于 (用x 1,x 2表示,不能出现a, b, k )三、解答题(共6小题,共80分)15.(12分)设命题p :关于x 的不等式101,1)xa a a ><<>(或的解集是{}0|<x x ,命题q :函数)lg(2a x axy +-=的定义域为R .(1)如果“p 且q ”为真,求实数a 的取值范围;(2)如果“p 且q ”为假,“p 或q ”为真,求实数a 的取值范围.16.(12分) 某市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现 从甲、乙两种树苗中各抽测了10株树苗的高度,量出的高度 如下(单位:厘米)甲:37,21,31,20,29,19,32,23,25,33乙:10,30,47,27,46,14,26,10,44,46(Ⅰ)根据抽测结果,完成答题卷中的茎叶图; (Ⅱ)根据你填写的茎叶图,对甲、乙两种树苗 的高度作比较,写出两个统计结论; (Ⅲ)设抽测的10株甲种树苗高度平均值为x ,将 这10株树苗的高度依次输入按程序框图(如图6)进行 的运算,问输出的S 大小为多少?并说明S 的统计学意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
肇庆市中小学教学质量评估 2011—2012学年第一学期统一检测题高二数学(文科)一、选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.在空间中,下列命题正确的是A .垂直于同一平面的两条直线平行B .垂直于同一平面的两个平面平行C .平行于同一直线的两个平面平行D .平行直线的平行投影重合 2.下列是全称命题且是真命题的是A .0,2>∈∀x R xB .0,,22>+∈∀y x R y xC .Q x Q x ∈∈∀2,D .1,200>∈∃x Z x 3.双曲线142522=-yx的渐近线方程是A .xy 52±= B .xy 25±= C .x y 254±= D .x y 425±=4.命题“若a >-3,则a >-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为A .1B .2C .3D .45.已知点P (3,m )在过M (-2,1)和N (-3,4)两点的直线上,则m 的值为A .15B .14C .-14D .-16 6.函数b a x x x f ++=||)(是奇函数的充要条件是A .ab =0B .a +b =0C .a =bD .022=+b a 7.已知平面α和直线l ,则α内至少有一条直线与lA .平行B .相交C .垂直D .异面 8.若焦点在x 轴上的椭圆1222=+kyx的离心率为21,则实数k 等于A .3B .32 C .38D .239.若圆02)1(222=-+-++m my x m y x 关于直线01=+-y x 对称,则实数m 的值为A .-1或3B .-1C .3D .不存在10.如图,某几何体的正视图、侧视图和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体体积为A .34B .32C .4D .2二、填空题:本大题共4小题,每小题5分,满分20分.11.用一个平面截半径为25的球,截面面积是225π,则球心到截面的距离为 ▲ . 12.双曲线14222=-yx的离心率等于 ▲ .13.若动点P 在122+=x y 上,则点P 与点Q (0,-1)连线中点的轨迹方程是 ▲ . 14.如图,在梯形ABCD 中,AB //CD ,AB =4,CD =2. E 、F 分别为AD 、BC 上点,且EF =3, EF //AB ,则梯形ABFE 与梯形EFCD 的面积 比为 ▲ .三、解答题:本大题共6小题,满分80分. 解答须写出文字说明、证明过程和演算步骤.15.(本小题满分12分)求满足下列条件的直线的方程:(1)经过点A (3,2),且与直线4x +y -2=0平行;(2)经过点B (2,-3),且平行于过点M (1,2)和N (-1,-5)的直线; (3)经过点C (3,0),且与直线2x +y -5=0垂直.俯视图正视图侧视图A BCDEF如图,一个高为H 的三棱柱形容器中盛有水. 若侧面AA 1B 1B 水平放置时,液面恰好过AC 、BC 、A 1C 1、B 1C 1的中点E 、F 、E 1、F 1. 当底面ABC 水平放置时,液面高为多少?17.(本小题满分13分)如图,三棱锥V —ABC 中,VO ⊥平面ABC ,O ∈CD ,VA =VB ,AD =BD . (1)证明:平面VAB ⊥平面VCD ; (2)证明:AC =BC .18.(本小题满分14分)求与x 轴相切,圆心在直线3x -y =0上,且被直线x -y =0截得的弦长为72的圆的方程.19.(本小题满分14分)如图,棱长为a 的正方体1111D C B A ABCD -中,M 、N 、E 、F 分别是A 1B 1、A 1D 1、B 1C 1、C 1D 1的中点.(1)求证:B 、D 、E 、F 四点共面; (2)求证:平面AMN //平面BEFD ; (3)求点A 1到平面AMN 的距离.A111A 1A已知F 1、F 2分别为椭圆C 1:)0(12222>>=+b a bx ay 的上、下焦点,其中F 1也是抛物线C 2:y x 42=的焦点,点M 是C 1与C 2在第二象限的交点,且35||1=MF .(1)求椭圆C 1的方程;(2)已知A (b ,0),B (0,a ),直线 y =kx (k >0)与椭圆C 1相交于E 、F 两点. 求四边形AEBF 面积的最大值.2011—2012学年第一学期统一检测题 高二数学(文科)参考答案及评分标准一、选择题二、填空题11.20 12.3 13.24x y = 14.7:5 三、解答题15.(本小题满分12分)解:(1)由直线4x +y -2=0得直线的斜率为-4,(2分) 所以经过点A (3,2),且与直线4x +y -2=0平行的直线方程为y -2=-4(x -3),即4x +y -14=0. (4分) (2)由已知,经过两点M (1,2)和N (-1,-5)的直线的斜率271125=----=k , (6分)所以,经过点B (2,-3),且平行于MN 的直线方程为)2(273-=+x y ,即7x -2y -20=0. (8分)(3)由直线2x +y -5=0得直线的斜率为-2, (9分) 所以与直线2x +y -5=0垂直的直线的斜率为21. (10分)所以,经过点C (3,0),且与直线2x +y -5=0垂直的直线方程为)3(21-=x y ,即x -2y -3=0. (12分)16.(本小题满分13分)解:当侧面AA 1B 1B 水平放置时,水的体积V 等于 四棱柱ABFE —A 1B 1F 1E 1的体积, (2分)HS V V ABFE ∙==梯形四棱柱. (4分)当底面ABC 水平放置时,设水面高为h ,则水的体积h S V ABC ∙=∆. (6分) 因为E 、F 为AC 、BC 的中点,所以ABCCEF S S ∆∆=41, (8分)所以ABCABFE S S ∆=43梯形. (9分)由h S H S ABC ABFE ∙=∙∆梯形,即h S H S ABC ABC ∙=∙∆∆43,得Hh 43=. (12分)故当底面ABC 水平放置时,液面高为H 43. (13分)17.(本小题满分13分)解:(1)因为VO ⊥平面ABC ,且AB ⊂平面ABC , 所以VO ⊥AB . (2分)因为VA =VB ,AD =BD ,即VD 为等腰ΔVAB 底边上中线, 所以VD ⊥AB . (4分)又因为VO ⊂平面VCD ,VD ⊂平面VCD ,且VO ∩VD =V , 所以AB ⊥平面VCD . (6分)A 111A又AB ⊂平面VAB ,所以平面VAB ⊥平面VCD . (8分) (2)由(1),得AB ⊥平面VCD ,且CD ⊂平面VCD ,(9分) 所以AB ⊥CD . (10分) 又AD =BD ,所以CD 为线段AB 的垂直平分线. (12分) 故AD =BD. (13分)18.(本小题满分14分)解:设所求的圆的方程是)0()()(222>=-+-r r b y a x , (2分) 则圆心到直线x -y =0的距离为2||b a -, (4分)所以222)7()2||(+-=b a r ,即14)(222+-=b a r① (6分)因为所求的圆与x 轴相切,所以22b r = ② (8分) 又因为所求圆心在直线3x -y =0上,所以3a -b =0 ③ (10分)联立①②③,解得⎪⎩⎪⎨⎧===,3,3,1r b a 或⎪⎩⎪⎨⎧=-=-=.3,3,1r b a (12分)故所求圆的方程为9)3()1(22=-+-y x 或9)3()1(22=+++y x . (14分)19.(本小题满分14分) (1)证明:如图,连接B 1D 1. 因为E 、F 为B 1C 1、C 1D 1的中点, 所以EF //B 1D 1. (2分) 又因为BD //B 1D 1,所以EF //BD . (3分) 故B 、D 、E 、F 四点共面. (4分) (2)证明:连接EN .因为M 、N 为A 1B 1、A 1D 1的中点,所以MN //B 1D 1.又EF //B 1D 1,所以MN / / EF . (5分)A 1因为EF ⊂平面BEFD ,所以MN //平面BEFD . (6分) 因为E 、N 为B 1C 1、A 1D 1的中点,所以EN //A 1B 1,且EN =A 1B 1. 又AB //A 1B 1,且AB =A 1B 1,所以NE / / AB ,且NE =AB .所以四边形ABEN 为平行四边行,故AN //BE . (7分) 因为BE ⊂平面BEFD ,所以AN //平面BEFD . (8分) 因为MN ⊂平面AMN ,AN ⊂平面AMN ,且MN ∩AN =N ,所以平面AMN //平面BEFD . (9分) (3)证明:设A 1到平面AMN 的距离为d . 在∆AMN 中,a aa AN AM 254122=+==,a aa MN 22414122=+=,所以22283162452221a aa a S AMN =-⨯⨯=∆. (11分)因为MNA A AMNA V V 11--=三棱锥三棱锥, (12分)即aa d a ⨯⨯=⨯⨯2281318331, (13分)解得3a d =,故A 1到平面AMN 的距离为3a. (14分)20.(本小题满分14分) 解:(1)设)0)(,(000<x y x M .由C 2:y x 42=,得F 1(0,1). (1分)因为M 在抛物线C 2上,故0204y x =. ① (2分) 又35||1=MF ,则3510=+y . ② (3分)解①②得⎪⎪⎩⎪⎪⎨⎧=-=.32,36200y x (4分)因为点M 在椭圆上,故1)362()32(2222=-+b a ,即1389422=+ba ③ (5分)又c =1,则122+=b a ④ (6分)解③④得⎪⎩⎪⎨⎧==.3,422b a故椭圆C 1的方程为13422=+xy. (7分)(2)不妨设),(11y x E ,),(22y x F ,且21x x <. 将kx y =代入13422=+xy中,可得431222+=kx, (8分) 即4332212+=-=kx x ,所以4332212+=-=kk y y . (9分)由(1)可得2||,3||==OB OA . (10分) 故四边形AEBF 的面积为22223232212221y x y x S S S AEF BEF +=⨯⨯+⨯⨯=+=∆∆.(11分)所以43341324364334222++∙=+++=kk kk kS (12分)因为k k 34432≥+,所以143342≤+kk . (13分)所以62≤S ,当且仅当332=k 时,等号成立.故四边形AEBF 面积的最大值为62. (14分)。
