经纬度计算最近3个基站最小站间距(快速)(推荐文档)
两个经纬度之间的距离计算公式excel

两个经纬度之间的距离计算公式excel计算两个经纬度之间的距离可以使用"球面余弦定理"。
在Excel 中,可以使用以下公式计算两点之间的距离:Copy code=ACOS(COS(lat1)*COS(long1)*COS(lat2)*COS(long2) + COS(lat1)*SIN(long1)*COS(lat2)*SIN(long2) + SIN(lat1)*SIN(lat2)) * R其中:lat1, long1 是第一个点的纬度和经度(以弧度为单位)lat2, long2 是第二个点的纬度和经度(以弧度为单位)R 是地球半径首先,我们需要把经纬度转换为弧度。
在Excel 中可以使用"RADIANS" 函数进行转换。
例如,将纬度转换为弧度的公式为:Copy code=RADIANS(lat1)经度同理。
然后在用上面给出的公式计算即可。
示例:假设第一个点纬度为A1,经度为B1;第二个点纬度为A2,经度为B2;地球半径为C1那么第一个点纬度转换为弧度的公式为=RADIANS(A1),经度同理。
最后使用公式=ACOS(COS(RADIANS(A1))*COS(RADIANS(B1))*COS(RADIANS(A2))*COS(RADIANS(B2)) + COS(RADIANS(A1))*SIN(RADIANS(B1))*COS(RADIANS(A2))*SIN(RADIANS(B2)) + SIN(RADIANS(A1))*SIN(RADIANS(A2))) * C1 即可计算出两个点之间的距离。
请注意,这个公式的结果是以千米为单位的距离。
如果需要米为单位的距离,可以将地球半径设置为6371即可。
请注意,由于经纬度是按照地球球面来计算的,所以这个公式只能用于近似计算地球上两点之间的距离,如果需要精确计算,可能需要使用其他方法。
计算两经纬度之间的距离的公式

计算两经纬度之间的距离的公式在地理学中,经度和纬度是用来描述地球表面位置的两个重要参数。
经度是指从地球中心到地球表面某一点的线段与本初子午线的夹角,通常用度数来表示;纬度是指从地球中心到地球表面某一点的线段与赤道面的夹角,也通常用度数来表示。
在实际应用中,我们经常需要计算两个地点之间的距离,这时就需要用到计算两经纬度之间的距离的公式。
计算两经纬度之间的距离的公式是基于球面三角学的原理,其基本思想是将地球看作一个球体,然后通过计算球面上两点之间的弧长来确定它们之间的距离。
这个公式的具体形式如下:d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))其中,d表示两点之间的距离,R表示地球的半径,lat1和lat2分别表示两点的纬度,lon1和lon2分别表示两点的经度。
需要注意的是,这个公式中的经纬度需要用弧度来表示,而不是度数。
因此,在计算之前需要将经纬度转换为弧度。
在实际应用中,我们可以使用各种编程语言来实现这个公式,例如Python、Java、C++等。
下面是一个使用Python实现计算两经纬度之间距离的示例代码:import mathdef distance(lat1, lon1, lat2, lon2):R = 6371 # 地球半径,单位为千米lat1, lon1, lat2, lon2 = map(math.radians, [lat1, lon1, lat2, lon2])dlat = lat2 - lat1dlon = lon2 - lon1a = math.sin(dlat / 2) ** 2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2) ** 2c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))d = R * creturn d# 示例lat1, lon1 = 39.9, 116.3 # 北京的经纬度lat2, lon2 = 31.2, 121.5 # 上海的经纬度print(distance(lat1, lon1, lat2, lon2)) # 输出北京和上海之间的距离,单位为千米通过这个示例代码,我们可以很方便地计算出两个地点之间的距离。
坐标计算最近距离计算公式

坐标计算最近距离计算公式在计算机科学和数学领域中,我们经常需要计算两个点之间的距离。
而当这些点的坐标在平面或者三维空间中给出时,我们可以使用最近距离计算公式来进行计算。
这种公式很常见,也是计算几何学和数据挖掘领域的基础知识之一。
1. 平面坐标系中的最近距离计算公式在平面坐标系中,最近距离计算公式可以用来计算两个点之间的欧几里德距离。
假设点A的坐标为 (x1, y1),点B的坐标为 (x2, y2),那么这两个点之间的最近距离可以通过以下公式来计算:距离= √((x1 - x2)^2 + (y1 - y2)^2)这个公式是基于勾股定理推导出来的,它描述了两个点之间的直线距离。
通过将坐标差的平方相加并计算平方根,我们可以得到两个点之间的欧几里德距离。
2. 三维空间中的最近距离计算公式在三维空间中,最近距离计算公式可以用来计算两个点之间的欧几里德距离。
假设点A的坐标为 (x1, y1, z1),点B的坐标为 (x2, y2, z2),那么这两个点之间的最近距离可以通过以下公式来计算:距离= √((x1 - x2)^2 + (y1 - y2)^2 + (z1 - z2)^2)这个公式和平面坐标系中的计算公式非常类似,只是在三维空间中需要考虑坐标的第三个分量。
3. 应用举例最近距离计算公式在很多领域都有广泛的应用,例如:•地理信息系统(GIS):用于计算两个地理坐标点之间的距离,以便进行地理空间分析和路径规划。
•图像处理:用于计算图像中两个像素点之间的距离,以便进行图像分割和目标检测。
•数据挖掘和机器学习:用于计算数据集中样本之间的距离,以便进行聚类分析和异常检测。
这些只是最近距离计算公式的一些应用举例,它在实际问题中的应用非常广泛。
4. 总结在计算机科学和数学领域中,坐标计算最近距离计算公式是非常重要的基础知识。
通过计算两个点之间的欧几里德距离,我们可以获得它们之间的直线距离。
这种公式在平面坐标系和三维空间中都有应用,并且在众多领域中发挥着重要的作用。
python匹配最近经纬度的算法

python匹配最近经纬度的算法Python 匹配最近经纬度的算法引言:在许多应用程序中,需要根据给定的经纬度查找离其最近的位置。
这种需求在地图导航、位置服务、物流规划和其他领域中非常常见。
本文将介绍一种用Python 实现的算法,用于匹配给定的经纬度与一组位置中最近的位置。
算法简介:该算法的核心思想是通过计算两点之间的距离,找到距离给定经纬度最近的位置。
为了实现这一目标,我们将使用Haversine 公式来计算两点之间的距离。
Haversine 公式是一种计算地球上两点之间距离的数学公式,它基于球面三角形的边角关系。
步骤一:导入必要的库和数据首先,我们需要导入Python 中的math 和csv 模块,以及包含位置数据的CSV 文件。
pythonimport mathimport csv# Load location data from CSV filelocations = []with open('locations.csv', 'r') as file:reader = csv.reader(file)for row in reader:locations.append((float(row[0]), float(row[1]), row[2]))在上面的代码中,我们打开包含位置数据的CSV 文件,并将位置信息存储在一个列表中。
每个位置由经度(latitude)、纬度(longitude)和名称(name)组成。
接下来,我们将使用Haversine 公式来计算两点之间的距离。
步骤二:实现Haversine 公式在此步骤中,我们将实现Haversine 公式的计算。
给定两个经纬度点P1 和P2,我们可以通过Haversine 公式计算它们之间的距离。
pythondef haversine(lat1, lon1, lat2, lon2):R = 6371 # 地球半径,单位为千米# 将经纬度转换为弧度lat1 = math.radians(lat1)lon1 = math.radians(lon1)lat2 = math.radians(lat2)lon2 = math.radians(lon2)# Haversine 公式dlon = lon2 - lon1dlat = lat2 - lat1a = math.sin(dlat / 2) 2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2) 2c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))distance = R * creturn distance在上述代码中,我们首先将经纬度转换为弧度,然后使用Haversine 公式计算两点之间的距离。
LTE网络通过经纬度测算距离核查冗余邻区
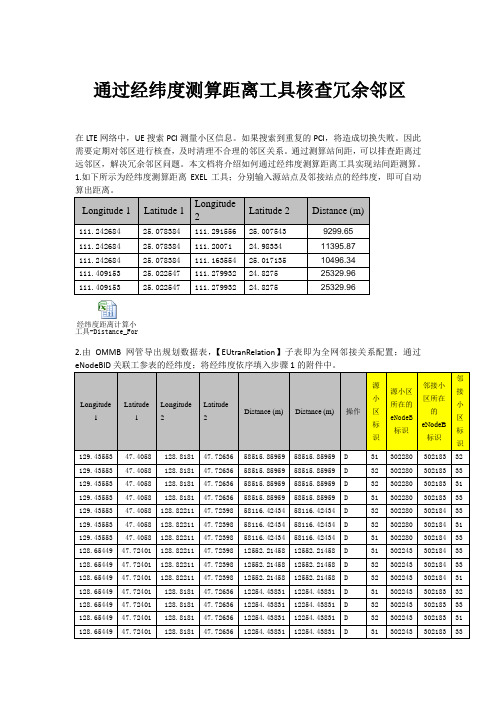
通过经纬度测算距离工具核查冗余邻区
在LTE网络中,UE搜索PCI测量小区信息。
如果搜索到重复的PCI,将造成切换失败。
因此需要定期对邻区进行核查,及时清理不合理的邻区关系。
通过测算站间距,可以排查距离过远邻区,解决冗余邻区问题。
本文档将介绍如何通过经纬度测算距离工具实现站间距测算。
1.如下所示为经纬度测算距离EXEL工具;分别输入源站点及邻接站点的经纬度,即可自动
经纬度距离计算小
工具-Distance_Formul
2.由OMMB网管导出规划数据表,【EUtranRelation】子表即为全网邻接关系配置;通过
经纬度距离计算-伊
春邻接关系.xlsx
3.将源ENODEB 及邻接小区信息按格式复制到规划数据表中,并填写相应操作代码,删除为D。
通过网管规划数据导入执行。
EXCEL0512_删除距
离过远.xlsm。
平均站间距计算方法

平均站间距计算方法
Chalon
2016/5/10
1计算思路
将小区覆盖方向上划分3个角度区间:
1、3个角度区间的划分方法为小区方位角的正负30度范围为第一角度区间。
2、小区方位角负90度至负30度之间为第二角度区间。
3、小区方位角正30度至正90度之间为第三角度区间。
以方位角0度为例,划分3个角度区间如下图,角度划分后在各自角度内搜寻最近基站。
在每个角度区间中计算最近基站距离:
1、第一角度区间内基站距离权重占比为60%。
2、第二角度和第三角度区间内基站距离权重占比各为20%。
3、把每个角度区间查找到基站距离加上权重做平均得出站间距。
以下图的基站分布为例,考虑到主瓣方向的权重较大,因此最终平均站间距的计算结果为300*0.6+500*0.2+700*0.2=420米。
经纬度的距离计算公式

经纬度的距离计算公式
两点距离的计算是日常生活中的一项非常基本的操作,而计算两点经纬度之间的距离更具有技术性和实用性,其中采用的计算装置是基于球面模型的,并以米为单位来表达。
空间直角坐标系(XYZ)本质上是三维中的投影,而地球表面的地球坐标系(LLH)是建立在球形模型的情况下的,其中的经、纬、高度就是它的三个维度坐标。
除此之外,两点之间的距离也可以用平面直角坐标和极坐标系来表达。
球模型的距离计算优势在于可以准确包括了地形和气压的影响,计算所得出的各项结果也更具可信度。
计算两点经纬度之间距离的公式为:d =
2Rarcsin[sqrt{(sin(Δlat/2))^2 + cos(lat1)cos(lat2) (sin(Δlon /2))^2}] 。
其中 2R 是地球
表面球半径,即6,371km;Δlat、Δlon 分别是纬度、经度之间的差分;lat1、lat2、lon1、lon2 是给定的两点的纬度和经度。
除了上述球模型的距离计算,还有多元素模型的方法,它以空间直角坐标系作为其基本模型,通过计算空间两点之间的欧式(Euclidean)距离,即(x1 - x2)2 + (y1 - y2)2 进行计算,但并没有真实反映出地球坐标系中距离的实际大小。
总之,从视角实用性与精确度考虑,当需要计算两个点经纬度之间的距离时,使用基于球模型的计算方法是最可行的。
上述公式的的实用性在工程中日益增加,以便解决交通运输、人口分布、地理信息系统,甚至旅游等行业的实际应用。
地球经纬度计算两点距离

地球经纬度计算两点距离一、经纬度定义:1、纬度是地球上某点与地球球心的连线和赤道面所成的线面角。
在0至90之间。
2、经度是指通过某地的经线面与本子午面所成的二面角。
本初子午线以东叫东经,以西叫西经。
1°=60′,1′=60″。
二、经纬度与距离换算1、纬度1秒的长度:子午线长度约为40008km1度≈40008km/360°≈111km1分≈111km/60′≈1.85km 1秒≈1.85km/60″≈30.9m2、经度1秒的长度:赤道周长约为40075.04km1度≈40075.04km/360°≈111.31955km1分≈111.31955km/60′≈1855.3m1秒≈1855.3m/60″≈30.92m3、特别提醒:经线的距离随纬度的不同而变化,等于111km乘以纬度的余弦。
同一经线上,相差一纬度约为111km,同一纬线上,相差一经度约为111cosα(α为该纬线的纬度) km 。
三、任意两点间距离计算公式为d=111.12cos{1/[sin ΦAsinΦB十 cos ΦAcosΦBcos(λB—λA)]}其中 A 点经度,纬度分别为λA 和ΦA,B 点的经度、纬度分别为λB 和ΦB, d 为距离。
(假设地球是个标准的球体,如下图所示,地球的半径为R,某个纬线圈的纬度为α,且该纬线圈的半径为r,则r=Rcosα,那么纬度为α的纬线圈的周长为2πr=2πRcosα=40000cosα(单位:公里,因为赤道周长2πR=40000 公里),则40000 公里/360 度=111.11公里/度,即赤道每差一个经度长度约为 111 公里,那么纬度为α的纬线每差一个经度的长度就是40000cosα/360度=111c osα公里 /度。
)。
