选 择 排 序 算 法 原 理
排列组合解题方法

排列组合解题方法
排列组合是一个数学问题,也是一个常见的解题方法。
在解决排列组合问题时,可以
按照以下步骤进行操作:
1. 确定问题中的元素个数和要求的组合方式。
例如,给定一组数字,要求按照一定的
规则进行排列或组合。
2. 确定排列或组合的顺序。
排列是指考虑元素的顺序,组合是指不考虑元素的顺序。
3. 根据题目要求确定进行排列或组合的元素个数。
例如,给定一组数字,要求从中选
取特定个数的数字进行排列或组合。
4. 根据排列或组合的特性,确定计算排列或组合的公式。
例如,排列可以使用阶乘来
计算,组合可以使用组合公式来计算。
5. 根据公式计算排列或组合的结果。
6. 根据题目要求,处理计算结果。
例如,将排列或组合的结果进行排序、筛选或统计。
在实际解题时,可以参考以上步骤进行操作。
根据具体的问题,选择合适的方法和公
式进行计算,最终得出满足题目要求的排列组合结果。
第十章排序(可编辑修改word版)

作业布置
10-4(2),(4),(5),10-6,
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
重点难点
希尔的思想,实现,算法分析
要求掌握知识点和
分析方法
1.概念:排序,主(次)关键字,内部(外部)排序,比较排序算法的技术指标2。插入排序的基本思想;3。直接直接插入排序和希尔的思想,实现,算法分析。
教授思路,采 用 的 教学方法和辅助手段,板书设计,重 点 如 何突出,难点如何解决,师 生 互 动等
难点:堆的调整辅助手段:多媒体
作业布置
10-7,10-8
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
章节
10.5归并排序10.6基数排序
讲授主要内容
归并排序 ,基数排序
重点难点
归并排序 ,基数排序的基本思想与算法实现
本章思考题和习题
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
章节
10.1概念10.2插入排序
讲授主要内容
1.概念:排序,主(次)关键字,内部(外部)排序,比较排序算法的技术指标2.
插入排序的基本思想;3。直接直接插入排序和希尔的思想,实现,算法分析。
教授思路,采 用 的 教学方法和辅助手段, 板书设计,重 点 如 何突出,难点如何解决,师 生 互 动等
教学思路:
排列组合的基本原理

排列组合的基本原理尊敬的读者:在数学中,排列组合是一种重要的概念,它用于计算可能性和确定事件发生的方式。
本文将介绍排列组合的基本原理,包括排列和组合的定义、计算方法以及应用。
希望通过本文的阐述,您能够更好地理解和运用排列组合的基本原理。
1. 排列的定义和计算方法在数学中,排列指的是从一个集合中选取若干个元素,按照一定顺序排列的方式。
排列通常用P(n,m)表示,其中n为集合的元素个数,m 为选取的元素个数。
排列的计算方法可分为两种情况:1.1 当选取的元素个数m小于或等于集合的元素个数n时,排列的计算公式为:P(n,m) = n! / (n-m)!1.2 当选取的元素个数m大于集合的元素个数n时,排列的计算公式为0,即不存在这种情况。
2. 组合的定义和计算方法组合指的是从一个集合中选取若干个元素,不考虑顺序的方式。
组合通常用C(n,m)表示,其计算方法可分为两种情况:2.1 当选取的元素个数m小于或等于集合的元素个数n时,组合的计算公式为:C(n,m) = n! / (m! * (n-m)!)2.2 当选取的元素个数m大于集合的元素个数n时,组合的计算公式为0,即不存在这种情况。
3. 排列组合的应用排列组合在实际问题中的应用非常广泛,下面举几个例子来说明:3.1 生日排列问题:假设有5个人,每个人的生日在一年中任意选择。
我们可以用排列来计算不考虑年份的情况下,5个人生日的所有可能排列数量。
根据排列的计算公式,可知P(365,5)即为所求。
3.2 钥匙排列问题:某人有5把钥匙,但只有其中一把能打开家门。
每次进门都尝试一把钥匙,直到能够打开为止。
这个过程中,我们可以用排列来计算需要尝试的所有可能方式的数量。
根据排列的计算公式,可知P(5,5)即为所求。
3.3 选课组合问题:某学校的学生需要选择4门选修课,而学校提供了8门选修课供选择。
我们可以用组合来计算学生选择的所有可能组合的数量。
根据组合的计算公式,可知C(8,4)即为所求。
排列的方法

排列的方法排列是数学中的一个重要概念,它在各个领域都有着广泛的应用。
在数学中,排列是指从给定的元素中按照一定的顺序取出一部分或全部元素,形成一个有序的序列。
在实际生活中,排列也是我们经常会用到的方法之一,比如整理书籍、安排座位等。
本文将介绍排列的方法,以及在实际中如何应用排列。
首先,我们来看一下排列的基本概念。
排列是指从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列。
这个过程可以用数学符号表示为P(n,m),其中n表示总的元素个数,m表示取出的元素个数。
排列的计算公式为P(n,m) = n! / (n-m)!,其中n!表示n的阶乘,即n×(n-1)×(n-2)×…×2×1。
这个公式告诉我们,当我们从n个元素中取出m个元素进行排列时,一共有n! / (n-m)!种不同的排列方法。
接下来,我们来看一下排列的应用。
在实际生活中,排列经常用于解决各种问题。
比如,我们要从8本书中挑选3本书排在书架上,问有多少种不同的排列方法?这个问题就可以用排列的方法来解决。
根据排列的计算公式,我们可以得到答案,P(8,3) = 8! / (8-3)! = 8×7×6 = 336。
所以,从8本书中挑选3本书排列的方法有336种。
除了在实际问题中的应用,排列还在数学领域有着重要的地位。
在组合数学中,排列是一个重要的概念,它与组合、排列组合等概念密切相关。
排列的概念也是许多数学问题的基础,比如排列组合、概率论等。
因此,了解排列的方法对于理解数学问题、解决实际问题都有着重要的意义。
在计算机科学领域,排列也有着广泛的应用。
比如,在算法设计中,排列是一个常见的问题,如全排列、字典序排列等。
排列的方法也经常用于解决搜索、排序等问题。
因此,了解排列的方法对于计算机科学领域的学习和工作也是非常重要的。
总之,排列是数学中的一个重要概念,它在各个领域都有着广泛的应用。
排序算法实验报告
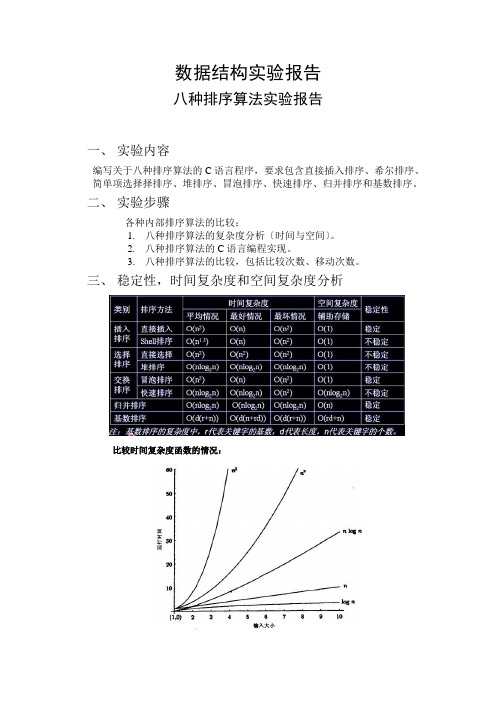
数据结构实验报告八种排序算法实验报告一、实验内容编写关于八种排序算法的C语言程序,要求包含直接插入排序、希尔排序、简单项选择择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。
二、实验步骤各种内部排序算法的比较:1.八种排序算法的复杂度分析〔时间与空间〕。
2.八种排序算法的C语言编程实现。
3.八种排序算法的比较,包括比较次数、移动次数。
三、稳定性,时间复杂度和空间复杂度分析比较时间复杂度函数的情况:时间复杂度函数O(n)的增长情况所以对n较大的排序记录。
一般的选择都是时间复杂度为O(nlog2n)的排序方法。
时间复杂度来说:(1)平方阶(O(n2))排序各类简单排序:直接插入、直接选择和冒泡排序;(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序;(3)O(n1+§))排序,§是介于0和1之间的常数。
希尔排序(4)线性阶(O(n))排序基数排序,此外还有桶、箱排序。
说明:当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O〔n〕;而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O〔n2〕;原表是否有序,对简单项选择择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
稳定性:排序算法的稳定性:假设待排序的序列中,存在多个具有相同关键字的记录,经过排序,这些记录的相对次序保持不变,则称该算法是稳定的;假设经排序后,记录的相对次序发生了改变,则称该算法是不稳定的。
稳定性的好处:排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。
基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。
另外,如果排序算法稳定,可以防止多余的比较;稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序四、设计细节排序有内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
选择法排序

a[0]
9 6 17 2 12
9
9
9 6 17
9 6
k
a[1]
2
k
a[2]
j k
6 17 2 12
k 6
j k
17 2 12
第一轮,i=0; k=i; for(j=i+1;j<5;j++) if(a[k]>a[j]) k=j; if(k!=j) {t=a[k];a[k]=a[i];a[i]=t;}
17 9 12
ቤተ መጻሕፍቲ ባይዱ
17 9
17 9 12
a[3]
{t=a[k];a[k]=a[i];a[i]=t;} 第四轮 I=3;k=I;
j
12 12
for(j=i+1;j<5;j++) if(a[k]>a[j])k=j;
a[4]
j
if(k!=i)
{t=a[k];a[k]=a[i];a[i]=t;}
i从0变到3 for(i=0;i<4;i++) 第i轮 k=I;认为第I个数最小, 从下一个数到最后一个数与 a[k]比较, If(a[k]>a[j]) k=j;k就赋值小数 的下标 If(k!=i) {t=a[k];a[k]=a[i];a[i]=t;}既a[k] 与第I个位置上的数交换位 置。
选择法排序(以5个数为例) 基本思路:
第一轮i=0:认为第一个数a[0]最小,把它的下标赋值给k,k=i;(k=0;) 从下一个数(a[1])到最后一个数a[4]与a[k]比较,如果a[k]大于哪个 数,k就赋值哪个数的下标,一轮结束后,k放最小数的下标,则a[k]与 a[0]交换位置。 第二轮i=1;k=i;认为a[1]最小,下标赋给k,将a[k]从下一个数(a[2]) 开始到最后一个数(a[4])比较,找到最小数,把它的下标赋给k,然后 a[k]与a[1]交换位置。 ……5个数比4轮,第i轮认为第i个位置上的数最小(k=i),将a[k]从 下一个数a[i+1]开始到最后一个数一一比较。找出最小数,把下标赋给 k,将a[k]与第i个位置上的数a[i]交换。
2021-CSP-S(提高组)认证第一轮试题详细解析

iiff tt==11 rreettuurrnn11
eellssee rreettuurrnn 55** ssoollvvee(ቤተ መጻሕፍቲ ባይዱtt--1l,,nn))mmoodd nn 则则 ssoolvlev(e(2233,,2233)) 的的结结果果为为(( ))。。
比比如如 initn t数数组组【[11,,11,,11,6,,64,]中4】a中[0 ]a,【a[01】],,a[a2【]的1】值,相a【等2】,的在值排相序等,时在不排改序变时不其改序变列其,序则列,称则所称用所用的的方方法法
是是稳稳定定的的..((插插入入排排序序、、冒冒泡泡排排序序、、二二叉叉树树排排序序、二路归并排序及其他线形排序是稳定的的;;选 择择排排序序、、希希尔尔排排序序、、快快速速排排序序、、堆堆排排序序是是不不稳稳定定的的))..
BB..系系统统分分配配的的队队列列空空间间溢出
CC.系. 系统统分分配配的的链链表表空空间间溢出
DD.系. 系统统分分配配的的堆堆空空间间溢溢出
【解析】递归需要使使用用到到系系统统堆堆栈栈空空间间,,如如果果递递归归层层数数过过多多,,导导致致系系统统堆堆栈栈空空间间不不足足。。
44.以.以下下排排序序方方法法中中,,(())是是不不稳稳定定的的。。
AA1. 1 B.B.77C.C1. 212 D.D.2222
【解析】程程序序的的运运行行结结果果为为552222mmoodd 2233,,根据费马小定理:∶如如果果是是素素数数,,aa是是一一
个个整整数数,,那那么么 aaPp-11≡=11 mmoodd pp,,可可以以得得 552222mmoodd 2233=≡11mmodo d2233,,结结果果为为11
2.聚合物合成工艺学课后习题全解

。展发有亦 聚缩相固来 年近�聚缩面界和、聚缩液溶、聚缩融熔是要主法方施实的聚缩型 线�中业工成合子分高在 。应反衡平逆可步逐的物聚高型线 成生时同的子分 小去缩在�应反生发间之团能官在�物合化子分低的团能官个两有含是�答 �种几哪有法方施实的合聚型线�合聚型线谓何 .91 。质性的端末链长增响影显明会 同不的类种其在存常 程过合聚子离单 �响影无应反长增链对类种剂发引中程过合聚基由自在 。合聚锁连的子离为心中性活长增�合聚子离 法方续连和法方歇间有法方作操 。制控格严应量水含中料原 他其和体单且并 �合聚液溶和合聚体本 用采能只合聚子离 �合聚液乳和合聚浮悬用采能不即 �质介为作水用能不中 法方施实的合聚子离 �此因 �感敏为极水对剂发引的用所合聚子离 �答 。因原 明说并�同不何有合聚基由自与法方作操和法方合聚中合聚子离在论讨 .81 剂发引元三— iN 是 剂 发 引 的 用 常 合 聚 — a 是 成 组 的 本 基 最 剂 发 引 attaN — relgeiZ 的 烯丙 聚 规 有 产 生于 用 剂 发 引的 合 聚 为 配 烯 丙 ② 法孚美为称常�上铝化氧性活于载钼化氧三。上体载铝化氧三 —硅化氧二于载 铬化氧三 �种两有的用常 。物化氧属金的上体载于载是剂发引的用常法压中 lC2)5H2C(lA+4lCiT 是剂发引的用常法压低 剂发引的合聚为配烯乙①�答 。剂发引的合聚为配的烃烯二和烯丙、烯乙出写 .71 点衡平相三③ �BLH� 值衡平油亲—水亲② �CMC� 度浓束胶界临① �征表来标指个三有 �能性 5.5 于低好最,用使下件条的 7<hP 在是常 通�剂性活面表子离阴 。用使下件条的 7>hP 在是常通�的广最用应中业工合 聚液乳是剂性活面表子离阳�用使 。种四型子离非和性两、型子离阴、型子离 阳�类种的剂化乳 。溶增体单是�束胶成形③ 定稳液乳是�聚凝止防�层护 保成形面表滴液在② 滴液小细成散分体单使�力张面表低降①�用作 。用作化乳为称用 作种这 �液乳的层分以难的定稳 为成系体散分的成组水和体单使能 �用作护保有滴液体单对 �用作溶增有体 单对�力张面界的水低降能质物些某。剂化乳为称质物的用作化乳有具�答 �能性的剂化乳征表来标指些哪有 � 同不 何 有 用 使� 种 几 哪 有 剂 化乳� 么 什 是 用作 剂 化 乳 �剂 化 乳 谓 何 .61 。产生的物 合聚用作合聚用胶橡用以可且而 �产生的物合聚用脂树 成合于用以可仅不合聚液乳⑤ 。高很也量质子分对相的物 合聚 �高很以可料 塑合聚的合聚液乳 �象现速加动自了除消上本基中系体合聚液乳④ 杂复较程 过序工�序工等燥干和洗水、乳破质解电加要需�是物合聚体固用③ 。用利接 直等剂理处面 表或料涂、剂黏胶为作以可胶乳物合聚�作操续连行进以可�良 优性定稳系体散分② 利有分十热传对且�全安廉价�质介为水以①�点特 。易较热散�热比的高 较有�质介散分为作�水质介② 。用作化 乳为称用作种这 �液乳的层分以难 的定稳为成系体散分的成组水和体单使能 �用作护保有滴 液体单对�用作溶 增有体单对�力张面界的水低降能质物些某�用作化乳的剂化乳①�用作 。水质介和剂化乳性溶水、剂发引性溶水、体单性溶油�分组
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选择排序原理证明及Java实现
简单介绍
选择排序是较为简单的排序算法之一,它的原理就是每次把剩余元素中最小的那个挑选出来放在这些剩余元素的首位置,举个栗子:
长度为5的一个数组:3,0,-5,1,8
第一次选择后: -5,0,3,1,8
第二次选择后: -5,0,3,1,8
第三次选择后: -5,0,1,3,8
第四次选择后: -5,0,1,3,8
最后一次选择: -5,0,1,3,8
注:标记红色字体的为发生交换的元素,下划线标记的为剩余元素
简单证明
设数组a共有N个元素,对其进行选择排序:
第一次选择将最小元素放在的位置,即此刻最小
第二次选择将上一步操作后的剩余元素中的最小元素放在?的位置,因此必然小于等于,由于此刻的是从上一步操作后的剩余元素中选出的,必然也大于等于
同理,共经过N次选择后:
Java代码实现
public class SelectionSort {
public static void sort(Comparable[] a){ --排序操作
int min,i,j;
for (i=0;i=a.length-1;i++){ --从头到尾选择length次
for (j=i+1;j=a.length-1;j++){
if (isLess(a[j],a[min]))
} --采用打擂原理获取最小值的索引
exchange(a,i,min);
public static boolean isLess(Comparable x,Comparable y){ return pareTo(y)0;
} --判断x是否小于y
public static void exchange(Comparable[] a,int i,int j){ --交换数组a中索引i和j所指的元素的值
Comparable t=a[i];
a[i]=a[j];
public static boolean isOrdered(Comparable[] a){ --判断数组是否有序
for (int i=0;i=a.length-2;i++){
if (a[i].compareTo(a[i+1])=0)
continue;
return false;
return true;
public static void show(Comparable[] a){ --打印数组
for (int i=0;i=a.length-2;i++){
System.out.print(a[i]+" ");
System.out.println(a[a.length-1]);
import java.util.Scanner;
import java.util.Random;
public class SelectionSortTest {
public static void main(String[] args){
Scanner sb=new Scanner(System.in);
int length;
int choice;
System.out.println("请输入数组元素的个数:");
length=sb.nextInt();
Integer[] a=new Integer[length]; --任意实现Comparable接口的数组皆可为参数,这里以Integer型数组为例
System.out.println("请选择创建数组的方式:1.手动 2.自动");
choice=sb.nextInt();
if (choice==1)
for (int i=0;i=a.length-1;i++){
a[i]=new Integer(sb.nextInt());
Random r=new Random();
for (int i=0;i=a.length-1;i++){
a[i]=new Integer(r.nextInt(length*length)); --随机生成[0,length*length)范围内一个整数
} --并初始化一个Integer对象
SelectionSort.sort(a);
System.out.println("数组是否有序:"+SelectionSort.isOrdered(a));
System.out.println("是否打印数组:1.是 2.否");
choice=sb.nextInt();
if (choice==1)
SelectionSort.show(a);
sb.close();
请输入数组元素的个数:
请选择创建数组的方式:1.手动 2.自动
数组是否有序:true
是否打印数组:1.是 2.否
19 23 47 68 72 99 130 206 248 326 326 338 338 365 403 417 461 466 517 541 555 593 625 626 704 806 833 849 871 873 Process finished with exit code 0
效率分析
通过查看代码我们可以精确地得到,0到N-1(length-1)的任意i都会进行一次交换和N-1-i次比较,因此共有N次交换以及
(N-1)+(N-2)+.+2+1=N(N-1)-2次比较。
算法的时间复杂度为。
用的IDE是IntelliJ IDEA
2? for i ------ length[A] - 1 downto 1
int *parent = new int[size];--父结点子针?
public static void main(String[] args) {
[2] Thomas H.Cormnen ,Charles E.Lesersion et.al .Introduction to Algorithms second Edition.
Scanner sb=new Scanner(System.in);
print(bubbleSort([1, 3, 1, 4, 5, 2, 0]))
for(int i=n-2;i=0;--i){--从第[n-2]个记录开始进行筛选建堆
for (int i = 0; i a.length-1; i++)
swap(array[minpos], array[left]);
实际上当没有数据交换的时候,序列就是完全有序的了,此时我们也可以认为排序已经完成,不用在继续执行后面的冒泡操作了。
