清华大学版理论力学课后习题答案大全 第4章运动分析基础
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
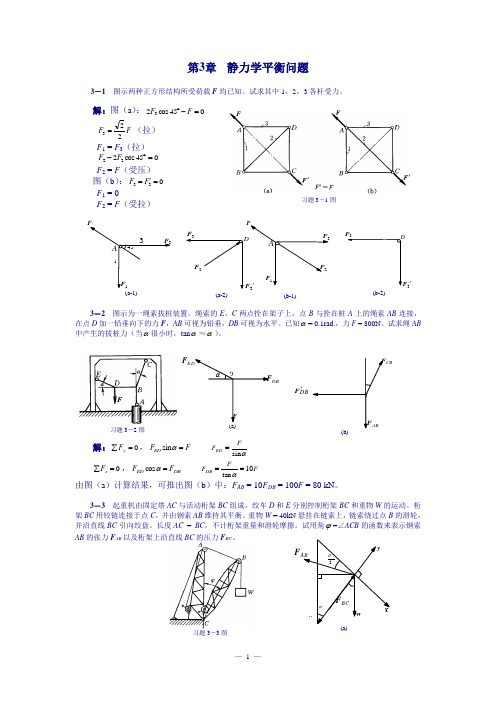
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
理论力学第四章习题答案

理论力学第四章习题答案理论力学第四章习题答案在理论力学的学习过程中,习题是非常重要的一部分。
通过解答习题,我们可以巩固理论知识,加深对概念和原理的理解,并培养解决实际问题的能力。
本文将为大家提供理论力学第四章习题的详细答案,希望能够对大家的学习有所帮助。
1. 一个质点在力F作用下做直线运动,已知力的大小与时间的关系为F = kt,其中k为常数。
求质点的速度与时间的关系。
解答:根据牛顿第二定律F = ma,将力的大小与时间的关系代入,得到ma = kt。
由于质点做直线运动,所以速度的变化率等于加速度,即v = ∫a dt。
将上式代入,得到v = ∫(kt/m) dt = (k/m)∫t dt = (k/m)(t^2/2) + C。
其中C为积分常数。
因此,质点的速度与时间的关系为v = (k/m)(t^2/2) + C。
2. 一个质点在力F作用下做直线运动,已知力的大小与位置的关系为F = -kx,其中k为常数。
求质点的加速度与位置的关系。
解答:根据牛顿第二定律F = ma,将力的大小与位置的关系代入,得到ma = -kx。
由于质点做直线运动,所以加速度的变化率等于速度的变化率,即a =dv/dt。
将上式代入,得到dv/dt = -kx/m。
将变量分离,得到dv = (-kx/m) dt。
对两边同时积分,得到∫dv = ∫(-kx/m) dt。
积分后得到v = (-kx^2/2m) + C1,其中C1为积分常数。
再次对上式积分,得到∫v dx = ∫((-kx^2/2m) + C1) dx。
积分后得到x = (-kx^3/6m) + C1x + C2,其中C2为积分常数。
因此,质点的加速度与位置的关系为a = (-kx/m)。
3. 一个质点在势能函数U(x) = kx^2/2下做直线运动,已知质点的质量为m。
求质点的速度与位置的关系。
解答:根据势能函数U(x) = kx^2/2,可以求得力的大小与位置的关系为F = -dU(x)/dx = -kx。
理论力学课后答案4

魏 魏 魏
后
泳 泳 泳
ww
涛 涛 涛
m
课
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
w.
kh
da
xi (2i 1)a cos , yi a sin 轨迹: xi2 yi2 a 2 2 (2i 1)
w.
co
解:以 A1 为对象研究 x a cos , y a sin 同理, Ai (i 2,3,4) 的运动方程为
kh
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.8 飞轮边缘上一点 M ,随飞轮以匀速 v 10 m s 运动。后因刹车,该点以 at 0.1t m s 2 作减速运动。设轮半径 R 0.4m ,求 M 点在减速运动过程中的运 动方程及 t 2s 时的速度、切向和法向加速度。 解:
魏
at
2 2 v vx vy 2500 4t 2
泳 泳 泳
ww
涛 涛 涛
m
加速度的直角分量 ax 0 , a y 2 切向加速度为
dv 4t dt 2500 4t 2 当 t 0s 时, at 0 ,所以
2 2 an a 2 at2 ax ay at2 2 m s 2
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.1 一动点按 s t 2 6t 1的规律沿直线运动,式中,时间 t 以秒( s )计,坐标 s 以 米( m )计。试求: (1)最初 5s 内的位移; (2)动点改变运动方向的时刻和所在位置; (3)最初 5s 内动点经过的路程; (4) t 5s 时动点的速度和加速度; (5)动点在哪段时间内作加速运动,哪段时间内作减速运动。
理论力学课后题参考答案

1.1 沿水平方向前进的枪弹,通过某一距离s 的时间为t 1,而通过下一等距离s 的时间为2t .试证明枪弹的减速度(假定是常数)为由题可知示意图如题1.1.1图: {{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a .则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得 11021at t s v +=再由此式得 ()()2121122t t t t t t s a +-=1.26一弹性绳上端固定,下端悬有m 及m '两质点。
设a 为绳的固有长度,b 为加m 后的伸长,c 为加m '后的伸长。
今将m '任其脱离而下坠,试证质点m 在任一瞬时离上端O 的距离为解 以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.题1.26.1图设绳的弹性系数为k ,则有 kb mg = ① 当 m '脱离下坠前,m 与m '系统平衡.当m '脱离下坠前,m 在拉力T 作用下上升,之后作简运.运动微分方程为 ()ym a y k mg &&=-- ② 联立①② 得 b b a g y b g y +=+&& ③ 0=+y bg y &&齐次方程通解 t b g A t b g A Y sin cos 211+= 非齐次方程③的特解 b a Y +=0 所以③的通解b a t bg A t b g A Y +++=sin cos 211代入初始条件:0=t 时,,c b a y ++=得0,21==A c A ;故有 b a t b g c y ++=cos 即为m 在任一时刻离上端O 的距离.'1.39 一质点受一与距离23次方成反比的引力作用在一直线上运动。
试证此质点自无穷远到达a 时的速率和自a 静止出发到达4a 时的速率相同。
理论力学课后答案

理论力学课后答案理论力学是力学的基础学科,它主要研究物体的运动与力的关系。
通过学习理论力学,我们可以深入了解物体在不同力的作用下的运动规律,掌握解题方法和技巧。
下面就是一些常见的理论力学问题的答案,希望能对大家的学习有所帮助。
1. 一个质点在匀速直线运动中,如果在t=0时刻位置为x0,速度为v0,则它的位置公式为x = x0 + v0t。
2. 一个质点在匀加速直线运动中,如果在t=0时刻位置为x0,速度为v0,则它的位置公式为x = x0 + v0t + (1/2)at^2。
3. 一个质点在竖直上抛运动中,如果在t=0时刻位置为x0,速度为v0,则它的位置公式为x = x0 + v0t - (1/2)gt^2,其中g为重力加速度。
4. 一个质点做匀速圆周运动,它的速度大小保持不变,但方向不断变化。
当向圆心的向心力为F时,质点的加速度大小为a = v^2 / R,其中v为质点的速度大小,R为圆的半径。
5. 动能定理:物体的动能变化等于物体所受的净功,即ΔK = W,其中ΔK为动能变化量,W为物体所受的净功。
6. 动量定理:物体的动量变化等于物体所受的净冲量,即Δp = FΔt,其中Δp为动量变化量,F为物体受到的净力,Δt为作用时间。
7. 万有引力定律:两个质点之间的引力大小与它们的质量成正比,与它们之间的距离平方成反比。
引力的大小由F = G(m1m2 /r^2)给出,其中F为引力的大小,G为引力常数,m1和m2分别为两个质点的质量,r为两个质点之间的距离。
以上是一些常见的理论力学问题的答案,它们涉及了匀速直线运动、匀加速直线运动、竖直上抛运动、匀速圆周运动、动能定理、动量定理和万有引力定律等内容。
通过学习和掌握这些知识,我们可以更好地理解和解决理论力学的问题。
理论力学是物理学的基础,它不仅在学术研究中有广泛应用,也在工程技术领域中发挥着重要作用。
通过深入研究理论力学,我们可以更好地理解物体的运动规律,为工程设计和科学研究提供有力的理论支持。
理论力学课后习题答案 第4章 运动分析基础

(b)第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环A 的运动规律。
解:Rv a a 2nsin ==θ,θsin 2R v a =θθtan cos d d 2tR v a tv a ===,⎰⎰=t v v t R vv 02d tan 1d 0θ t v R R v t s v 00tan tan d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0tan tan ln tan -=θθθ4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩⎪⎨⎧-=-=225.1324tt y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1) ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得2arccos 213arcsin y x =化简得轨迹方程:2942x y -=(2)轨迹如图(b ),其v 、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt sπ=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π==t ,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ==,12=∴tR a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮以匀角速度ω转动,如图所示。
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解

F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
清华大学版理论力学课后习题答案大全

第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕc o s )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(b)
第2篇 工程运动学基础
第4章 运动分析基础
4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2
π,试确定小环
A 的运动规律。
解:R
v a a 2
n
sin ==θ,θ
sin 2R v a =
θ
θtan cos d d 2t
R v a t
v a =
==,⎰⎰=t v v t R v v 02d tan 1d 0θ t v R R v t s v 00tan tan d d -==θθ
⎰⎰-=t s t t v R R v s 0000d tan tan d θθ
t
v R R R s 0tan tan ln tan -=θθθ
4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩
⎪⎨⎧-=-=225.1324t t y t
t x , 2.⎩⎨⎧==t y t x 2cos 2sin 3
解:1.由已知得 3x = 4y (1) ⎩
⎨⎧-=-=t y t x
3344 t v 55-=
⎩
⎨⎧-=-=34y x
5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得
2arccos 21
3arcsin y x =
化简得轨迹方程:29
4
2x y -=
(2)
轨迹如图(b ),其v
、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为
22
1
Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x
和y 轴上的投影。
解:Rt s v π== ,R v a π== t ,222
n Rt R
v a π==
y 坐标值最大的位置时:R Rt s 2
212ππ== ,12=∴t
R a a x π==t ,R a y 2π-=
A
习题4-1图
习题4-2图
习题4-3图
e e -t (c)
e e -t υ (b)
R t R +υ (a)
习题4-6图
4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮以匀角速度ω转动,如图所示。
试求滑块的速度随距离x 的变化规律。
解:设t = 0时AB 长度为l 0,则t 时刻有:
220
2
20
)arctan arctan (r x l r r x r l r t --=--+ω
对时间求导:
2
22
22r x x x r x x x r r --
=--
ω
2
2
r
x rx x
--=ω
4-5 凸轮顶板机构中,偏心凸轮的半径为R ,偏心距OC = e ,绕轴O 以等角速转动,从而带动顶板A 作平移。
试列写顶板的运动方程,求其速度和加速度,并作三者的曲线图像。
解:(1)顶板A 作平移,其上与轮C 接触点坐标: t e R y sin ω+=(ω为轮O 角速度)
t e y
v cos ωω== t e y a sin 2ωω-== (2)三者曲线如图(a )、(b )、(c )。
4-6 绳的一端连在小车的点A 上,另一端跨过点B 的小滑车车绕在鼓轮C 上,滑车离地面的高度为h 。
若小车以匀速度υ沿水平方向向右运动,试求当θ = 45°时B 、C 之间
绳上一点P 的速度、加速度和绳AB 与铅垂线夹角对时间的二阶导数θ
各为多少。
解:1.∵P 点速度与AB 长度变化率相同
2
221)(d d 2221
22v
x h x x x h t v P =
+⋅=+= (θ= 45°,x = h 时) 2.同样:h
v h x x h x x t v
a P P 2222)(d d 2
222=
=+== (∵0=x
,x = h ) 3.h x =
θtan ,h
x
1tan -=θ
222
211x h x h h
x x h +=+= θ 2222222)(2h
v x h x hx -=+-= θ(顺)
4-7 图示矢径r 绕轴z 转动,其角速度为 ω,角加速度为 α。
试用矢量表示此矢径端点M 的速度、法向加速度和切向加速度。
习题4-4图
习题4-5图
x
y
ωt
解:r ωr v ⨯==t M d d
)(d d r ωωr αv ωr ωv
a ⨯⨯+⨯=⨯+⨯==M M M t
r αa ⨯=t M
v ωr ωωa ⨯=⨯⨯=)(n M
4-8 摩擦传动机构的主动轮I 的转速为n =600r/min ,它与轮II 的接触点按箭头所示的方向移动,距离d 按规律d =10-0.5t 变化,单位为厘米,t 以秒计。
摩擦轮的半径r =5cm ,R =15cm 。
求:(1)以距离d 表示轮II 的角加速度;(2)当d =r 时,轮II 边缘上一点的全加速度的大小。
解:
(1)302nr d πω=,d
nr 302πω=
2
22250305.0560030d d d d nr πππα=⨯⨯=-= rad/s 2 (2)592203025004
4
44242
2
2
=+=+=n r r r a ππωαcm/s 2
4-9 飞机的高度为h ,以匀速度v 沿水平直线飞行。
一雷达与飞机在同一铅垂平面内,
雷达发射的电波与铅垂线成θ 角,如图所示。
求雷达跟踪时转动的角速度ω 和角加速度α与h 、v 、θ 的关系。
解:h vt =θtan
h v =θθ2c o s
,θθ
ω2cos h
v == θθθθωα222
c o s 2s i n 2s i n h
v h v -=-==
4-10 滑座B 沿水平面以匀速v 0向右移动,由其上固连的销钉C 固定的滑块C 带动槽杆OA 绕O 轴转动。
当开始时槽杆OA
求槽杆的转动方程、角速度和角加速度。
解:b
t v 0tan =ϕ,b
t v 0arctan =ϕ rad
2
2020t
v b bv +=
=ϕω rad/s
222023
0)
(2t v b t b v +-==ωα
4-11.设ω 为转动坐标系Axyz 的角速度矢量,i 、j 、k 为动坐标系的单位矢量。
试证明:
习题4-8图
v
习题4-9图
习题4-10图
k j i j i k i k j ω⎪⎭
⎫ ⎝⎛⋅
+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛⋅=t
t t d d d d d d
证:x t ω=⋅=⋅⨯=⋅i ωk j ωk j
)(d d
y t ω=⋅=⋅⨯=⋅j ωi k ωi k
)(d d k t
ω=⋅=⋅⨯=⋅k ωj i ωj i
)(d d ∴等式右侧ωk j i =++=z y x ωωω
证毕。
