高温超导材料的特性测试和低温温度计实验报告
高温超导实验报告步骤(3篇)

第1篇一、实验目的1. 了解高温超导体的基本特性和物理机制。
2. 学习液氮低温技术,掌握低温环境下的实验操作。
3. 测量高温超导体的临界温度(Tc)和临界磁场(Hc)。
4. 研究高温超导体的临界电流(Ic)与磁场、温度的关系。
二、实验原理高温超导现象是指某些材料在液氮温度(约77K)下表现出超导特性。
实验中,通过测量超导体的电阻、临界温度、临界磁场等参数,来研究高温超导体的物理性质。
三、实验仪器与材料1. 高温超导材料(如钇钡铜氧YBCO等)2. 低温冰箱3. 温度计4. 磁场计5. 电阻计6. 磁场发生器7. 数字多用表8. 液氮四、实验步骤1. 样品制备:将高温超导材料制备成合适尺寸的样品,通常为薄片或丝状。
2. 低温环境准备:将低温冰箱预热至液氮温度,并将样品放入冰箱内冷却至液氮温度。
3. 电阻测量:- 使用电阻计测量样品在液氮温度下的电阻。
- 记录电阻值,作为初始数据。
4. 临界温度测量:- 慢慢升温,观察电阻变化。
- 当电阻突然降至零时,记录此时的温度,即为临界温度(Tc)。
5. 临界磁场测量:- 使用磁场计测量样品在液氮温度下的磁场。
- 慢慢增加磁场强度,观察电阻变化。
- 当电阻突然降至零时,记录此时的磁场强度,即为临界磁场(Hc)。
6. 临界电流测量:- 在一定磁场下,逐渐增加电流,观察电阻变化。
- 当电阻突然降至零时,记录此时的电流,即为临界电流(Ic)。
7. 温度与磁场关系研究:- 在不同温度下,重复步骤4和5,研究临界温度(Tc)和临界磁场(Hc)与温度的关系。
- 在不同磁场下,重复步骤6,研究临界电流(Ic)与磁场的关系。
8. 数据整理与分析:- 将实验数据整理成表格,分析高温超导体的物理性质。
- 对比不同高温超导材料的物理性质,总结实验结果。
五、实验注意事项1. 实验过程中,务必保持低温环境,避免样品受热。
2. 在测量电阻、临界温度、临界磁场等参数时,要确保仪器精度。
3. 注意实验安全,防止低温伤害。
实验报告模板

高温超导材料临界转变温度的测定一、实验目的1.通过对氧化物超导材料的临界温度TC 两种方法的测定, 加深理解超导体的两个基本特性2.了解低温技术在实验中的应用3.了解几种低温温度计的性能及Si 二极管温度计的校正方法4.了解一种确定液氮液面位置的方法二、实验原理1.超导现象及临界参数 1)零电阻现象电阻率与温度的关系: 。
式中, 是时的电阻率, 称剩余电阻率。
即使温度趋于绝对零度时, 也总是存在。
超导材料包括金属元素、合金和化合物等。
发生超导转变的温度称为临界温度。
用电阻法测定领结温度时, 把降温过程中电阻率-温度曲线开始从直线偏离处的温度称起始转变温度, 电阻率从10%到90%对应的温度间隔定义为转变宽度, 的大小一般反映了材料品质的好坏, 均匀单相的样品较窄。
临界温度C T 定义为02ρρ=时对应的温度。
2)完全抗磁性当把超导体置于外加磁场中时, 磁通不能穿透超导体, 超导体内的磁感应强度始终保持为0, 超导体的这个特性称为迈斯纳效应。
表示为M=(B/4(。
利用迈斯纳效应, 测量电感线圈中的一个样品在降温时内部磁通被排出的情况, 也可确定样品的超导临界温度, 称电感法。
用电阻法测TC 较简单, 只能测出其中能形成超导通路的临界温度最高的一个超导相的TC 。
用电感法测TC 则可以把不同的超导相同时测出。
3)临界磁场致使超导体有超导态变为正常态的磁场称为超导体的临界磁场, 通常把相应的磁场叫做临界磁场。
第Ⅰ类超导体, 也称软导体。
其与的关系: ;式中, 是时的临界磁场。
当时, 的典型数值为100Gs 。
第Ⅱ类超导体, 也称硬导体。
它存在两个临界磁场和, 的状态为混合类, 磁场进入超导体, 但仍具有零电阻的特性。
高温超导体, 其与的关系不满足。
4)临界电流密度当电流达到某一临界值IC后, 超导体将恢复到正常态。
大多数金属为突变, 超导合金、化合物及高温超导体为渐变。
2.温度的测量1)铂电阻温度计2)温差电偶温度计3)半导体Si二极管温度计3.温度的控制1)恒温器控温法: 定点测量法, 均匀, 精度高2)温度梯度法:连续测量法, 简单易行4.液体位置的确定采用温差电偶的测温差原理来判断液面位置。
高温超导材料特性测试和低温温度计

物理实验研究性报告高温超导材料特性测试和低温温度计高温超导材料特性测试和低温温度计一.实验摘要:采用杜瓦容器和低温恒温器获得从液氮沸点到室温的任意温度,在此条件下,测量高温超导材料电阻,确定其起始转变温度和零电阻温度,并观察记录铂电阻温度计、硅二极管温度计及铜-康铜温差电偶温度计测温参量的变化,进行温度计的比对。
超导体在超导状态具有零电阻现象和完全抗磁性,具有辉煌的应用前景。
一般达到超导状态需要很低的温度,最低为4.15K,大大约束了超导材料的实际应用。
从1911年发现超导现象至今,人们一直为提高超导材料的临界温度而努力。
本实验在液氮沸点到室温范围内测量超导材料电阻特性,相对而言为高温超导,并对各种温度计进行比对,为在不同温区选择合适温度计提供依据。
二.实验原理1.超导体和超导电性.1911 年,卡麦林⋅翁纳斯用液氦冷却水银线并通以几毫安电流,在测量其端电压时发现,当温度稍低于液氦的正常沸点时,水银线的电阻突然跌落到零,这就是所谓的零电阻现象或超导电现象。
通常把具有这种超导电性的物体,称为超导体。
引进起始转变温度T c,onset 、零电阻温度T c0和超导转变(中点)温度T cm来描写高温超导体的特性,如图1 所示。
通常说的超导转变温度T c 指T cm。
2.低温温度计.(1)金属电阻随温度的变化.作为低温物理实验基本工具的各种电阻温度计,是建立在对各种类型材料的电阻−温度关系研究基础上的。
不同类型材料电阻随温度变化性质不同。
合金中,电阻主要由杂质散射引起,因此电子平均自由程对温度变化很不敏感,如锰铜的电阻随温度的变化就很小,实验用标准电阻和电加热器就是用锰铜线绕制而成。
纯金属中,总电阻可近似表达成:R = R i (T ) +R r ,其中,R i为电子运动受到晶格散射出现的电阻,R r为几乎完全由杂质散射造成的剩余电阻,它近似与温度无关。
半导体则具有与金属完全不同的电阻温度关系,在大部分温区中具有负的电阻温度系数。
高温超导材料的特性测试和低温温度计实验报告
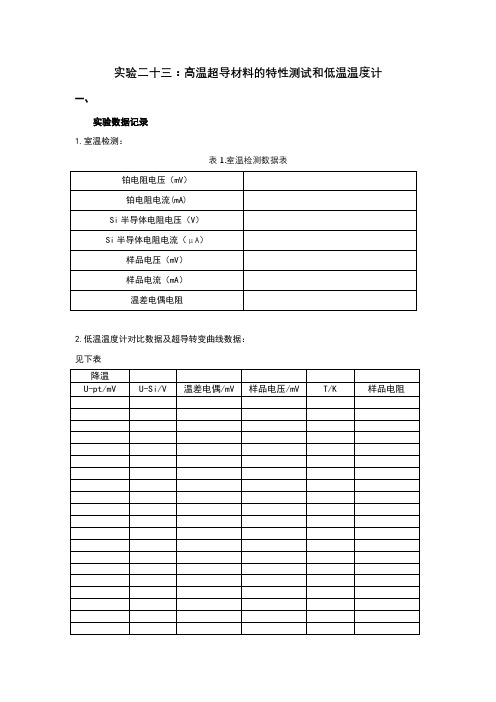
实验二十三:高温超导材料的特性测试和低温温度计一、实验数据记录1.室温检测:表1.室温检测数据表2.低温温度计对比数据及超导转变曲线数据:见下表3.液氮沸点监测数据:表2:液氮沸点监测数据温差电偶电阻二、实验数据分析、处理和结论1.处理室温检测数据,给出三部分测量电路的电流、室温、室温下的超导样品的电阻:(1)电流:铂电阻:Si半导体电阻:μA样品电流:(2)室温:T=*+=(3) 室温下,样品的电阻:R==Ω2.处理低温温度计对比数据,作图给出对比结果,总结三种温度计的特点:图1:Si电压-温度曲线Y=+ R2=图2:温差电偶电压-温度曲线线性拟合:Y= R2=非线性拟合:Y=+ R2=结论:由图1:Si半导体电压随着温度呈线性相关,且是负相关。
由图2:温差电偶与温度成正相关,在拟合过程中发现,二次拟合要比一次的拟合精确的多。
因此温差电偶电压应该与温度成二次关系。
比较两图一直,Si半导体的温敏线性较好,成的是线性关系,温差电偶电压与温度成二次关系,铂电阻R与T成线性关系。
3.作图并用最小二乘法处理超导样品测量数据,给出转变温度。
图3:样品电阻-温度曲线图4:样品电阻-温度电压(最小二乘法)Y=+ R-Square=结论:由图3、4可知:随着温度下降,R首先以直线下降,在到达一定的温度时,斜率发生突变的点为转变温度。
对于高温时的数据进行线性拟合,其近似一条直线。
通过对于突变处的观察,突变温度约为103K。
4.处理液氮沸点检测数据,给出液氮沸点,液氮温度下超导样品的电阻、三部分测量电路的电流,与温室数据对比,评测系统的精确度和稳定性。
Pt 的电阻精确到:Si 半导体电阻精确到: *10^-6A超导样品精确到:Ma温差电偶温度计精确到:铂U最小 mV ,I 最小为,绝对误差为 % 和%硅电压最小:电流:*10^-6A ,绝对误差为 % 和%样品的电流最小为,绝对误差%所以数据中只有样品和电偶可以到0,所以整个系统的精度在于这两个数据的测量。
高温超导实验报告

122.1 118.6 115.5 112.9 110.5 108.5 106.8 105.4 104.1 103.1 102.1 101.4 100.0 96.7 96.2 96.0 95.7 95.5 95.3 94.9 94.6 93.8 92.6 92.4 92.1 91.8 91.6 91.3 77.4
⑴铂电阻温度计: 铂电阻温度关系如下图所示
1
R(T)=AT+B 在液氮沸点到正常室温温度范围内, 其电阻与温度近似成正比: 或 T(R)=aR+b,其中 a,b 都是常数。 ⑵半导体硅电阻温度计: 在较大的温度范围内,半导体具有负的电阻温度系数,这一特性正好弥补 了金属电阻温度计在低温下灵敏度明显降低的缺点。低温物理实验中,常用半 导体温度计。 在小电流下,近似有: U 正向 KT U g 0 。其中 K=-2.3mV/K;硅材料 U g 0 约为 1.20eV ⑶温差电偶温度计: 如果将两种金属材料制成的导线联成回路,并使其两个接触点维持在不同 的温度,则在该闭合回路中就会有温差电动势存在,如果将回路的一个接触点 固定在一个已知的温度,例如液氮的正常沸点 77.4 K,则可以由所测量得到的 温差电动势确定回路的另一接触点的温度,从而构成了温差电偶温度计。这种 温度计十分简便,特别是作为温度敏感部分的接触点体积很小,常用来测量小 样品的温度以及样品各部分之间的温差。 应该注意到,硅二极管 PN 结的正向电压 U 和温差电动势 E 随温度 T 的变化 都不是线性的,因此在用内插方法计算中间温度时,必须采用相应温度范围内 的灵敏度值。
〖实验二十三〗
高温超导材料特性测试和低温温度计
〖目的要求〗
1、了解高临界温度超导材料的基本特性及其测试方法; 2、了解金属和半导体 P-N 结的伏安特性随温度的变化以及温差电效应; 3、 学习几种低温温度计的比对和使用方法, 以及低温温度控制的简便方法。
物理实验报告_高温超导材料的特性

高温超导材料特性测试和低温温度计自1911年荷兰物理学家翁纳斯发现超导现象以后,人们一直在为提高超导临界温度而努力,直到1986年,才有了极大的进展,现在,临界温度已提高到130K 左右。
目前,块状超导体、高温超导导线、大面积超导薄膜等超导材料在磁悬浮输运、强电、弱电等工程领域上的应用已完成了前期实验阶段,现已投入工程开发中。
专家预测,二十年内超导技术将在通讯、交通、军事、电力等领域得到应用。
历史上已有八位科学家因为超导研究方面的成就而荣获诺贝尔物理学奖,可见超导研究的重要性,它是物理学的前沿课题。
本实验的内容是低温的获得和控制、各类温度传感器和液面计的特性应用、电阻的四引线测量法、乱真电动势的判定等。
【目的】1. 了解高临界温度超导材料的基本特性及其测试方法。
2. 了解铂电阻和半导体pn 结的正向电压及温差电偶的电动势随温度的变化情况。
3. 学习几种低温温度计的比对和使用方法,以及低温温度控制的简便方法。
【原理】通常把物体在一定温度下电阻突然跌落到零的现象,称为零电阻现象或超导现象,而把电阻突然变为零的温度称为临界温度,用T C 表示。
利用本实验装置,可用逐点测量的方法得到高温超导体的电阻转变曲线,并可用标准的方法判断零电阻现象是否实现。
除了零电阻现象之外,超导体还具有另一个基本的特征——迈斯纳效应(完全抗磁性),即不论在有或没有外加磁场的情况下,使样品从正常态转变为超导态,只要T <T C ,在超导体内部的磁感应强度总是等于零的。
1. 高临界温度超导特性当超导体温度降到某一温度(T )时,其电阻为零。
本实验中,所用的YBaCuO 样品的零电阻温度大约为90K 左右。
2. 电测量设备及测量原理本实验测量设备主要由铂电阻、硅二极管和超导样品三个电阻测量电路构成,每一电路均包含恒流源、标准电阻、待测电阻、数字电压表和转换开关等五个主要部件。
实验中测量样品电压等采用四引线测量法,其基本原理是:恒流源通过两根电流引线将待测电流I 提供给待测样品,而数字电压表则是通过两根电压引线测量样品上电压U 。
高温超导材料特性测试实验报告

高温超导材料特性测试物理学系0 安宇森【摘要】本次实验,我们利用液氮冷却测量了铜-康温差电偶的超导特性曲线。
通过对Pt电阻温度计的特性曲线的测量,确定超导临界温度。
最后,我们对磁悬浮现象以及抗磁性实验进行了观测。
【关键词】超导临界温度迈斯纳效应【Abstract】In this experiment, we use the liquid nitrogen to cool down the temperature and then we observe the superconductivity of the materials. Through the measurement of the pt thermometers, we find the critical temperature of the superconductor. At last , we observe the resistance of the magnet in the superconductor.【key words】superconductivity critical temperature Misner effect【引言】超导是指某些物质在一定温度条件下(一般为较低温度)电阻降为零的性质。
1911年荷兰物理学家H·卡茂林·昂内斯发现汞在温度降至4.2K 附近时突然进入一种新状态,其电阻小到实际上测不出来,他把汞的这一新状态称为超导态。
以后又发现许多其他金属也具有超导电性。
低于某一温度出现超导电性的物质称为超导体。
1933年,荷兰的迈斯纳和奥森菲尔德共同发现了超导体的另一个极为重要的性质——当金属处在超导状态时,这一超导体内的磁感应强度为零,却把原来存在于体内的磁场排挤出去。
对单晶锡球进行实验发现:锡球过渡到超导态时,锡球周围的磁场突然发生变化,磁力线似乎一下子被排斥到超导体之外去了,人们将这种现象称之为“迈斯纳效应”。
高温超导实验报告仿真(3篇)

第1篇一、实验背景高温超导材料是一种在相对较高的温度下就能表现出超导性的材料,其临界温度(Tc)一般在液氮温度附近。
高温超导材料的发现为电力传输、磁悬浮、医疗成像等领域带来了革命性的变革。
为了深入研究高温超导材料的性质和特点,我们利用仿真软件对高温超导材料进行了实验研究。
二、实验目的1. 研究高温超导材料的临界特性;2. 分析高温超导材料在磁场中的输运特性;3. 仿真高温超导电缆在不同运行条件下的性能;4. 比较高温超导电缆与普通电缆的输电性能。
三、实验原理高温超导材料的临界特性主要包括临界电流密度(Jc)和临界磁场(Hc)。
在临界电流密度以下,高温超导材料表现出零电阻和完全抗磁性;在临界磁场以下,高温超导材料表现出完全抗磁性。
利用仿真软件,我们可以模拟高温超导材料在不同温度、磁场和电流密度下的输运特性。
四、实验方法1. 利用仿真软件建立高温超导材料模型,包括超导芯和绝缘层;2. 设置不同温度、磁场和电流密度,模拟高温超导材料的输运特性;3. 仿真高温超导电缆在不同运行条件下的性能,包括短路容量、功率分布和电压稳定性;4. 比较高温超导电缆与普通电缆的输电性能。
五、实验步骤1. 建立高温超导材料模型,设置模型参数;2. 设置仿真温度、磁场和电流密度,进行仿真;3. 分析仿真结果,包括临界电流密度、临界磁场、输运特性和电缆性能;4. 比较高温超导电缆与普通电缆的输电性能。
六、实验结果与分析1. 临界特性分析在仿真中,我们设置了不同的温度、磁场和电流密度,得到了高温超导材料的临界电流密度和临界磁场。
结果表明,随着温度和磁场的增加,临界电流密度和临界磁场均有所降低。
这与高温超导材料的特性相符。
2. 输运特性分析在仿真中,我们分析了高温超导材料在不同温度、磁场和电流密度下的输运特性。
结果表明,高温超导材料在临界电流密度以下表现出零电阻和完全抗磁性;在临界磁场以下表现出完全抗磁性。
此外,我们还分析了高温超导材料的输运长度和输运时间,发现其与临界电流密度和临界磁场密切相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二十三:高温超导材料的特性测试和低温温度计
2016.12.29
一、实验数据记录
1.室温检测:
表1.室温检测数据表
2.低温温度计对比数据及超导转变曲线数据:
见下表
3.液氮沸点监测数据:
表2:液氮沸点监测数据
二、实验数据分析、处理和结论
1.处理室温检测数据,给出三部分测量电路的电流、室温、室温下的超导样品的电阻:(1)电流:铂电阻:109.03mA
Si半导体电阻:100.00μA
样品电流:10.0165mA
(2)室温:
T=2.4516*109.03+25.736=293.03K
(3) 室温下,样品的电阻:
R=0.162/10.0165=0.0162Ω
2.处理低温温度计对比数据,作图给出对比结果,总结三种温度计的特点:
图1:Si电压-温度曲线
Y=-0.0026x+1.2798 R2= 0.9994
图2:温差电偶电压-温度曲线
线性拟合:Y=0.0279x-2.6711 R2=0.990
非线性拟合:Y=0.000057x2+0.0061x-0.75127 R2=0.9998
结论:由图1:Si半导体电压随着温度呈线性相关,且是负相关。
由图2:温差电偶与温度成正相关,在拟合过程中发现,二次拟合要比一次的拟合精确的多。
因此温差电偶电压应该与温度成二次关系。
比较两图一直,Si半导体的温敏线性较好,成的是线性关系,温差电偶电压与温度成二次关系,铂电阻R与T成线性关系。
3.作图并用最小二乘法处理超导样品测量数据,给出转变温度。
图3:样品电阻-温度曲线
图4:样品电阻-温度电压(最小二乘法)
Y=0.000048x+0.00109 R-Square=0.9994
结论:由图3、4可知:随着温度下降,R首先以直线下降,在到达一定的温度时,斜率发生突变的点为转变温度。
对于高温时的数据进行线性拟合,其近似一条直线。
通过对于突变处的观察,突变温度约为103K。
4.处理液氮沸点检测数据,给出液氮沸点,液氮温度下超导样品的电阻、三部分测量电路
的电流,与温室数据对比,评测系统的精确度和稳定性。
Pt 的电阻精确到:0.01mV 0.01mA
Si 半导体电阻精确到:0.0001V 0.01*10^-6A
超导样品精确到:0.001Mv 0.0001 Ma
温差电偶温度计精确到:0.001Mv
铂U最小 28.39 mV ,I 最小为 99.84mA ,绝对误差为 0.04% 和0.01%
硅电压最小:0.5155mV 电流:100.01*10^-6A ,绝对误差为 0.02% 和0.01%
样品的电流最小为10.0165mA ,绝对误差0.001%
所以数据中只有样品和电偶可以到0,所以整个系统的精度在于这两个数据的测量。
且系统较为灵敏。
稳定性:
I Pt=(100.30-99.84)/99.84=0.5%
I Si=(100.01-100.00)/100.00=0.01%
I样品=(10.173-10.165)/10.165=0.08%
由此可见系统稳定性较好。
三、实验收获
升温时:
曲线轮廓与降温基本一致,但转折点明显提前了,原来大致103K,而升温时大致80K。
.。
