工程管理中数学建模过程
数学建模的基本流程

数学建模的基本流程数学建模是一种通过数学方法来解决现实问题的过程。
它可以应用于各种领域,如物理、经济、生物、环境等。
数学建模的基本流程包括问题描述、建立模型、模型求解以及结果分析与验证。
下面将详细介绍数学建模的基本流程。
首先是问题描述阶段。
在这个阶段,我们需要清楚地了解问题要解决的实际背景和目标,明确问题的详细描述以及需要考虑的限制条件。
这个阶段的目标是对问题进行全面的分析和理解,确保我们对问题的认识是正确的和完整的。
接下来是建立模型阶段。
在这个阶段,我们需要将实际问题转化为数学问题。
具体来说,就是通过数学符号和方程式来表达出问题的关键因素和各种关系。
模型的建立需要结合问题的具体情况和所采取的数学方法,选择适当的数学模型。
通常,数学建模所采用的模型可以分为确定性模型和随机模型两大类。
确定性模型是以确定性的方式描述实际问题的模型,其中的变量和参数都是确定的。
常见的确定性模型包括线性规划模型、非线性规划模型、动态规划模型等。
而随机模型是以概率的方式描述实际问题的模型,其中的变量和参数都是随机的。
常见的随机模型包括马尔可夫链模型、蒙特卡洛模型等。
在这个阶段,我们需要根据实际问题的特点和需求来选择合适的数学模型。
然后是模型求解阶段。
一旦模型建立完毕,我们就需要通过数值计算、优化算法等方法来求解模型。
这个阶段需要使用计算机程序来实现模型求解。
在进行模型求解时,我们还需要对模型的数学方法进行抽象和简化,以便更好地进行计算和求解。
最后是结果分析与验证阶段。
在这个阶段,我们需要对模型的求解结果进行分析和验证。
具体来说,就是对模型的输出进行解释,并与实际问题进行比对。
如果模型的结果与实际问题吻合,那么我们就可以认为模型是有效的。
否则,我们需要对模型进行修正和改进。
这个阶段还可以对模型的灵敏度进行分析,以了解模型对输入数据和参数的变化的响应程度。
总之,数学建模的基本流程包括问题描述、建立模型、模型求解以及结果分析与验证。
数学建模的流程

数学建模的流程一、问题提出。
1.1 这就好比咱们平常生活里啊,遇到个事儿,得先知道是个啥事儿对吧。
数学建模也一样,先得明确问题。
比如说要研究城市交通拥堵,那这就是个大问题,但具体怎么个堵法,哪些地方堵得厉害,这都得搞清楚。
不能稀里糊涂的,就像“丈二和尚摸不着头脑”那样可不行。
1.2 这时候呢,就得去收集各种信息啦。
就像侦探破案似的,到处找线索。
可以去实地考察,看看马路上车流量啥样,也可以查查相关的数据资料,这都是为了把问题的全貌给弄明白。
二、模型假设。
2.1 有了问题和信息之后啊,咱们就得做假设啦。
这假设呢,就像是给这个事儿定个规矩。
比如说研究交通拥堵,咱们假设车的行驶速度是均匀的,这虽然不完全符合实际,但能让这个事儿简单点,先把大框架搭起来嘛。
这就叫“先粗后细”,不能一开始就把事儿想得太复杂,不然根本没法下手。
2.2 假设也不是乱设的,得符合常理。
要是设个车能飞起来的假设,那这模型就乱套了。
咱们得根据实际情况,做一些合理的简化,就像画画一样,先勾勒出个大概的形状。
三、模型建立。
3.1 这时候就开始建立模型啦。
这可是个技术活,就像盖房子一样,得一块砖一块砖地砌。
比如说根据前面的假设,咱们可以用一些数学公式来表示交通流量和拥堵程度的关系。
可能是个很复杂的公式,但是别怕,只要前面的基础打得好,就像“万丈高楼平地起”,总能把这个模型给建起来。
3.2 在建立模型的过程中,还得考虑各种因素的相互作用。
就像一个生态系统似的,每个部分都影响着其他部分。
比如说车流量影响车速,车速又反过来影响车流量,这就得用一些巧妙的数学方法来处理。
四、模型求解。
4.1 模型建好了,就得求解啦。
这就像解一道超级大难题。
有时候可能有现成的数学方法可以用,就像走在一条熟悉的小路上。
但有时候呢,就得自己想办法,这就像在荒野里开辟一条新的道路一样困难。
可能要用到计算机软件来帮忙计算,就像请个小助手似的。
4.2 在求解的过程中,可能会遇到各种各样的问题。
数学建模流程

数学建模流程数学建模是指通过材料、理论、方法等综合分析来获取问题的内在规律及其运行机制,并通过运用数学工具和算法来解决实际问题的过程。
数学建模流程主要包括问题分析、模型建立、模型求解和模型评价四个步骤。
问题分析是数学建模的第一步。
在这一步中,需要准确理解问题陈述,并确定问题的具体要求。
在分析问题时,要对问题的背景、目标、约束条件、变量等因素作适当的调研和分析。
问题分析的关键是抽象问题,即将实际问题转化为数学问题。
模型建立是数学建模的核心步骤之一。
在这一步中,需要根据问题的特点选择合适的数学模型。
数学模型由问题变量、约束条件以及目标函数等要素构成。
建立模型的过程需要运用数学知识和技巧,例如微积分、概率统计、线性代数等。
模型的建立要建立在严格的数学推理基础上,确保模型的合理性和准确性。
模型求解是数学建模的重要步骤之一。
在这一步中,需要确定求解模型的方法和算法。
数学建模常用的求解方法有解析法、数值法和优化算法等。
根据具体问题的特点和难度,在数学分析和计算机编程等方面运用相应的方法和技术进行求解。
求解模型的过程中,需要进行一系列的计算和推理,同时要对求解结果进行判断和验证,确保结果的可靠性。
模型评价是数学建模的最后一步。
在这一步中,需要对模型的结果进行评价和分析。
模型评价的目的是检验和验证模型的有效性和适用性。
评价模型的标准通常有模型拟合度、模拟误差、模拟精度等。
通过评价模型,可以得出结论和建议,为实际问题的决策和解决提供参考。
总体而言,数学建模是一个循序渐进的过程,需要将抽象的实际问题转化为数学问题,并运用数学知识和方法进行建模和求解,最后通过对模型结果进行评价和分析,得出相关结论和建议。
数学建模的流程不仅需要运用严谨的数学思维和逻辑推理,还需要具备良好的问题分析和综合分析能力,以及熟练的数学计算和计算机模拟技术。
只有在完整的数学建模流程中,才能得到准确、有效的问题解决方案。
工程技术中常用的数学建模方法概述

工程技术中常用的数学建模方法概述摘要对目前工程和管理研究领域所涉及的数学建模方法作了简要分析,指出不同的问题所需用到的建模方法,并通过举例说明建模的方法和步骤。
关键词数学建模;建模方法;模型;建模;数学应用在现实社会生产实践中,随着科学研究的进步,多学科交叉运用越来越多。
数学建模就是一种解决实际应用问题的有效方法,当然要在充分了解问题的实际背景的基础上,把实际问题抽象成数学问题,建立起数学模型,利用数学知识对数学模型进行分析探求,得到数学结果,得出应用问题的解。
即通过对问题的数学化,模型构建和求解检验[1]。
其一般步骤可分成如下几点:(1)模型准备:了解问题的实际背景,搜集建模必需的各种信息,明确建模目的。
(2)建模:对问题进行必要合理的简化和假设,根据所作的假设分析对象的因果关系,利用对象的内在规律和适当的数学工具,构造各个量(变量和常量)之间的关系或其他数学结构。
(3)求模:根据数学知识和方法,求解数学模型,得到数学问题的结果。
求模时要注意灵活运用各种数学方法,包括matlab等工程软件[2]。
(4)回归:把数学问题的结果回归到实际问题中,通過分析,判断,验证,得到实际问题的结果。
下面谈谈几种常用的数学建模法,限于篇幅,不便举太多例子。
(1)建立函数模型法有关成本最低,效益最大,用料或费用最省等应用问题,可考虑建立相应函数关系式,并把实际问题转化为求最值的问题。
(2)建立三角形模型法有关涉及几何、测量、航海等应用问题可考虑转化为三角问题来解决[3]。
(3)建立数列模型法对于一些产量增长,细菌繁殖,存款利率,物价调节,人口探测等应用问题,往往需要通过观察分析,归纳抽象,建立出数列模型,然后用数列的有关知识加以解决。
举例:某一信托投资公司,考虑投资1600万元,建造一座星际饭店,经预测,该饭店建成后每年可获利600万元,试问三年内能否把全部投资收回?假设银行每年复利计息,利率为15%,若需要三年内收回全部投资,每年至少应获利多少?建模分析:本例可以建立数列模型,设每年投资额为A,年利率为R,当年投资额为Q,则n年后这笔投资额的实际额为,n年收益的总额为=A,若n年恰好还清投资额,则有数列模型:解:当n=3,A=600,R=15%代入上式,有Q=1370万元,所以三年之后不能全部把投资收回。
数学建模的一般步骤和案例

数学建模的一般步骤和案例数学建模是利用数学方法对实际问题进行描述、分析和求解的过程。
它是一个系统的、多学科的工作过程,可以帮助我们深入了解实际问题,并为问题提供合理的解决方案。
下面将介绍数学建模的一般步骤和一个具体的案例。
一般步骤:1.问题定义:明确研究的问题和要解决的目标。
确定研究的范围、限制和假设条件。
2.建立模型:根据问题的特点和要求,选择适当的数学工具和模型。
常用的数学模型包括数学规划模型、概率统计模型、图论模型等。
3.定义变量:标识出影响因素并对其进行量化。
根据问题的要求,设定需要研究的变量和参数,确定它们的取值范围和关系。
4.假设做法:根据问题背景和可行性,进行必要的简化和假设。
合理简化模型可以简化计算过程并提高求解效率。
5.求解问题:根据所建立的模型,运用数学方法求解问题。
常见的求解方法有解析解法、数值计算法、模拟仿真法等。
6.模型分析和评价:对求解结果进行分析和评价,看是否满足问题的要求。
对模型的合理性和有效性进行检验和验证,对模型的优化和改进提出建议。
7.结果解释和应用:将数学模型的结果解释给问题的决策者,提供相关的建议和策略。
将得到的结果用于实际问题的决策和规划。
案例:假设有一家电子商务公司,想要通过合理的物流网络规划来降低运输成本。
现在给定了各个城市之间的距离、货物的数量、运输的形式和时间要求等信息,要求建立一个模型来确定最佳的物流网络规划,使总运输成本最小。
1.问题定义:研究问题是找到最佳物流网络规划,使运输成本最小。
2.建立模型:选择网络流模型来描述物流网络。
假设各城市之间的运输成本是线性关系,并以各城市之间的距离作为约束条件。
3.定义变量:设定每条路径上的运输量为变量,并对各变量进行量化。
设定各城市之间的距离和运输成本为参数。
4.假设做法:假设各个城市之间的运输量满足需求,并忽略其他可能影响的因素。
5.求解问题:将问题转化为线性规划问题,并运用线性规划方法,如单纯形法等,求解最佳的物流网络规划。
(完整版)数学建模的一般步骤
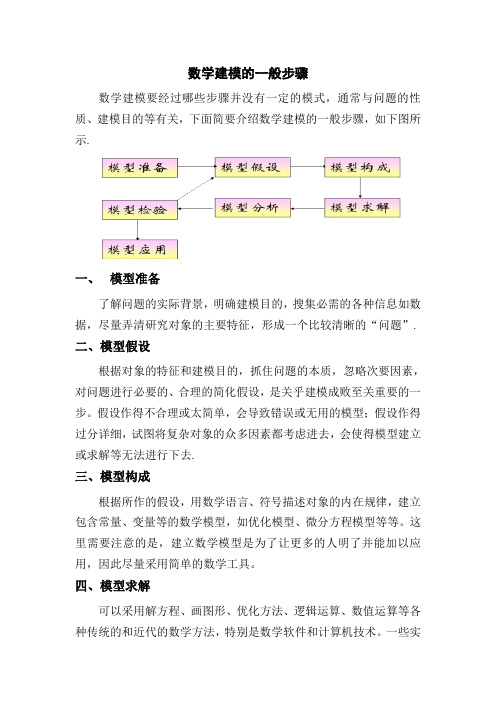
数学建模的一般步骤数学建模要经过哪些步骤并没有一定的模式,通常与问题的性质、建模目的等有关,下面简要介绍数学建模的一般步骤,如下图所示.一、模型准备了解问题的实际背景,明确建模目的,搜集必需的各种信息如数据,尽量弄清研究对象的主要特征,形成一个比较清晰的“问题”.二、模型假设根据对象的特征和建模目的,抓住问题的本质,忽略次要因素,对问题进行必要的、合理的简化假设,是关乎建模成败至关重要的一步。
假设作得不合理或太简单,会导致错误或无用的模型;假设作得过分详细,试图将复杂对象的众多因素都考虑进去,会使得模型建立或求解等无法进行下去.三、模型构成根据所作的假设,用数学语言、符号描述对象的内在规律,建立包含常量、变量等的数学模型,如优化模型、微分方程模型等等。
这里需要注意的是,建立数学模型是为了让更多的人明了并能加以应用,因此尽量采用简单的数学工具。
四、模型求解可以采用解方程、画图形、优化方法、逻辑运算、数值运算等各种传统的和近代的数学方法,特别是数学软件和计算机技术。
一些实际问题的解决往往需要纷繁的计算,许多时候还得将系统运行情况用计算机模拟出来,因此计算机编程和熟悉数学软件能力举足轻重。
五、模型分析对模型求解结果进行数学上的分析。
如结果的误差分析、统计分析、模型对数据的灵敏性分析、对假设的强健性分析等。
六、模型检验将求解和分析结果翻译回到实际问题,与实际的现象、数据比较,检验模型的合理性和适用性.如果结果与实际不符,问题常常出现在模型假设上,应该修改、补充假设,重新建模,如上图中的虚线所示.这一步对于模型是否真的有用非常关键.有些模型要经过几次反复,不断完善,直到检验结果获得某种程度上的满意.七、模型应用将所建立的模型用来解决实际问题.。
数学建模的基本步骤及方法

数学建模的基本步骤及方法数学建模是一种应用数学的方法,通过数学模型来描述、解释和预测现实世界中的问题。
它在科学研究、工程技术、经济管理等领域有着广泛的应用。
本文将介绍数学建模的基本步骤及方法,以帮助读者更好地理解和应用数学建模。
一、问题定义数学建模的第一步是明确问题,并对问题进行定义、限定和分析。
要做到具体明确,确保问题的可行性和实际性。
同时,在问题定义阶段,需要理解问题所处的背景和条件,收集所需的数据和信息。
二、建立数学模型在问题定义的基础上,需要选择合适的数学工具和方法,建立数学模型。
数学模型是通过数学符号和方程来描述问题的规律和关系。
常见的数学模型包括线性模型、非线性模型、动态模型等。
根据实际情况,选择适合的模型形式,并进行相关的假设和简化。
三、模型求解通过数学方法,对建立的数学模型进行求解。
求解的过程中,可以运用数值计算、优化算法、数值逼近等方法。
根据问题的具体要求,选择合适的求解方法,并编写相应的程序进行计算。
四、模型验证模型求解完成后,需要对求解结果进行验证。
验证的目的是检验模型的有效性和准确性。
可以通过与实际数据的对比,对模型的预测能力进行评估。
如果模型与实际结果相符合,说明模型具有较好的预测能力。
五、结果分析与应用在模型验证的基础上,对求解结果进行分析和解释。
通过对结果的分析,可以得到对于问题本质的深刻理解。
同时,根据分析结果,可以制定相应的决策和策略,在实际问题中得到应用和推广。
六、模型优化和调整数学建模是一个循环迭代的过程,在实际应用中,可能会遇到新的情况和问题。
为了提高模型的稳定性和预测能力,需要对模型进行优化和调整。
可以通过改变模型的参数、调整模型的结构、增加新的变量等方式来优化模型。
七、模型评价对建立的数学模型进行评价是数学建模的重要环节。
评价的指标包括模型的准确性、稳定性、可靠性等。
通过评价,可以发现模型的不足和改进的空间,并为进一步应用提供指导和参考。
综上所述,数学建模是一个系统而复杂的过程,需要综合运用数学、计算机、统计学、优化算法等多个学科的知识和方法。
数学建模过程

数学建模过程
数学建模是一种利用数学模型来描述实际问题的方法,常常是对实际问题的抽象思考
及数学化处理,以便做出预测和分析,从而提出合理的结论和决策。
首先,进行问题分析和确定,确定实际问题的目标,明确模型的设计要求。
其次,进行数学模型的构思,建立模型的数学结构,把握系统的各种元素之间的联系,构建一个恰当的数学模型,以反映实际问题客观存在的现象。
之后,进行模型计算,利用计算机对模型中涉及的参数进行计算,得出数学模型的结果,并对计算结果进行分析。
最后,应用模型结果,分析数学模型的解,形成合理的结论,根据模型分析的结论,
提出有效的改进方法,并确定结果的可靠性,从而针对模型提出有效的决策。
总的来说,数学建模的过程主要分为:问题分析、模型构思、模型计算和结果应用四
个步骤。
针对实际问题,从宏观到微观,最终建立一个带有可衡量参数的客观准确的数学
模型,从而帮助决策者指导决策和优化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程管理的马尔可夫骨架过程建模
周 尧
(广深港客运专线有限公司)
侯振挺 薄远超
(中南大学数学学院,长沙,410075)摘 要 在以前,一个工程项目的进程的管理问题在各工段的施工时间为相互独立且都服从负指数分布的假设下通过一个网络图化为对一个马尔可夫链的控制和优化的研究.本文在一般情况下(放弃对各工程段的时间服从负指数分布的假设)把工程项目进程的管理问题化为对一个马尔可夫骨架过程的控制和优化问题.关键词 工程管理 网络图 马尔可夫链 马尔可夫骨架过程
Modeling Project Management Using
Markov Skeleton Processes
Zhou Rao
(Guang shen-Hong Ko ng Passenger Dedicated Lines Co.Limited)
Hou Zhenting
(Schoo l o f M athema tics,Central South U niv er sity ,Cha ng sha ,410075)
Abstract Previo usly ,prog r ess manageme nt pro blem in a pro ject has been studied under the presumptio n that the co nstr uc tio n times fo r each pro ject stag e a re independent o f each other and a lso hav e a neg ativ e ex po nential dist ributio n.And thus this pro blem could be tra nsfo rmed into the study of contr ol and o ptimizatio n fo r a M a rkov chain v ia a new to r k diag ram .This paper ha s r elax ed the restrictio n tha t the constr uction times for each project stag e sho uld hav e a nega tiv e ex ponential distributio n a nd the a bov e pro blem can be tra nsfo rmed into the research o n co ntro l and optimiza tio n o f a M ar ko v skeleton pro cess.Keywords Pro ject M anag ement M ar kov chain M a rkov skeleto n pr ocess
1 引 言
一个工程项目的进程可用一个网络图G =(V ,A )(V 是G 的结点集,A 为孤集)表示出来.例如图1,它的V =(s ,b ,c ,d ,t ),A =(1,2,3,4,5,6)
第27卷第3期
2007年9月 数学理论与应用
M A THEM ATICAL T HEORY AND APPLIC ATION S Vol.27No.3 Sep.2007
李俊平教授推荐 收稿日期:2006年12月10日
图1
这里1,2,3,4,5,6表示每个工段.1,2工段首先开始平行的施工,1成后才能开始工程段3的施工,2完成后才能开始工程段4的施工,3的施工先完成,则需休息待命等完成4工程段的施工后,才能开始5工程段的施工,等等.
在大约四十年前都在每段工程的施工时间是确定的假设下进行研究,如,华罗庚提倡推广的统筹法就属于此.后来,有人把每段工程的施工时间视为遵守负指数分布的随机变量来处理[1],这时工程项目进程就是一个马尔可夫链[2].从而工程项目管理就变成对马尔可夫链的控制和优化问题[3][4][5].如图1,设各工段的施工时间是互相独立的随机变量,工段a (a =1,2,…,6)的施工时间服从以λa 为参数的负指数分布,于是工程项目就是一个马尔可夫链X (t ),这个链共有17个状态:
(1,2),(2,3),(2,3*),(1,4,6),(1,4*,6),(1,4,6*)
(1,4*,6*),(3,4,6),(3*,4,6),(3,4*,6),(3,4,6*)
(3*,4,6*),(3,4*,6*),(5,6),(5*,6),(5,6*),( , )
X (t )=(1,2),表示在时刻t 工程段1和工程段2正在进行施工,X (t )=(3*,4,6)表示在
时刻t 工程段3施工已完成,工段4和6正在施工,X (t )=( , )表示在时刻t 整个工程完成,( , )是一个吸收状态,等等.
这样以来,已把图1所示的工程项目进程化为一个马尔可夫链.
把每个工段的施工时间视为一个服从负指数分布的随机变量后,工程项目进程的研究有了突破性进展.但每段施工时间都服从负指数分布这一假设是缺乏实践的依据,只是为了使问题化为一个马尔可夫链而已.因此,我们有必要在一般情况下考察工程项目进程问题,以找到它的切合实际的数学模型.我们在研究中发现,在一般情况下(对每工段的施工时间的分布不加任何限制),工程项目进程是一个马尔可夫骨架过程,而马尔可夫骨架过程于1997年为侯振挺,刘再明及邹捷中提出的一类新型的随机过程并加以研究
[6].下面我们仍对图1所示的工程
项目进程为例进行讨论.
令
E =[{1}×{2}×[0,∞)×[0,∞)]∪
∪[{2}×{3}×[0,∞)×[0,∞)]∪ ∪[{2}×{3*}×[0,∞)]∪26数学理论与应用 第27卷
∪[{1}×{4}×{6}×[(0,∞)×[0,∞)×[0,∞)]∪
……
∪[{ }×{ }]
设X (t )是以E 为状态空间的随机过程,例如,X (t )={1,2,θ1,θ2}表示在时刻t 工段1正在施工,而且已施工了时间θ1,工段2也正在施工,而且已施工了时间θ2,……
令f 0≡0,f n (n ≥1)表示X (t )的第n 个间断点,显然X (t )是以(f n )为骨架时序列的马尔可夫骨架过程.为了求出X (t )的瞬时分布需要写出并解马尔可夫过程的向后方程.对于我们当前这个例子,不难做到这点.
中南大学数学院研究生张玄,康宁和张希娜以及湖南大工商管理学院博士生吴娟也参与了本文的部分研究工作,特此致谢.
参考文献
[1] A .Char nes ,W .Co pper ,G .Th ompson ,Critical path a naly sis v ia chance co nstr ained and stochastic
pro g ramming ,O perations Research 1964
:12:460-470.[2] V.Kullkarni,V.Adlakha ,M a rkov a nd M a rkov -rege ner ativ e PER T net -w or ks,O pe ratio ns Research 1986:34:769-781.
[3] A .A zar on ,H .Ka tagiri ,M .Sakawa ,K .Kato a nd A .M ema ria ni ,A multi -o bjectiv e resource alloca tio n pro blem in PER T netw o rks,Euro pea n Jour na l o f Opera tio na l Resear ch 2006,172:838-854.
[4] A.Aza ro n,R.Tava kko li-M og hddam,A multi-o bjec tive r eso urce allocatio n pro blem in dy namic PER T netw or ks,Applied Ma thematics and Co mputa tio n 2006,181:163-174.
[5] A .A zaro n ,H .Katagiri ,K .Ka to a nd M .Sakaw a ,L ongest pa th analysis in ne two rk of queues :dyanamic scheduling pro blems,Eur opean J o urnal o f O per atio nal Resea rch 2006:174:132-149.
[6] Zhe nting Ho u and Guoxin Liu,M a rkov Skeleton Pro cesses a nd Their Applica tio ns,Science Press,Beijing ,&Inter na tional Pr ess,Bo ston,2005.27
第3期 工程管理的马尔可夫骨架过程建。
