实验2落球法测定液体的粘滞系数
用落球法测量液体的粘度实验报告

用落球法测量液体的粘度实验报告实验名称:用落球法测量液体的粘度实验目的:通过落球法测量液体的粘度,了解粘度的定义及计算方法。
实验原理:粘度是指液体流动阻力的大小。
通过落球法可以测量液体的粘度。
当一球从管子的上端落下时,由于液体的粘滞力,球不能自由下落,而是随时间逐渐减速直到停止。
落球法利用粘滞力对球体的作用直接测得液体黏度,计算公式如下:η=2(g-ρV)/9c其中,η为液体的粘度,g为重力加速度,V为球体体积,ρ为球体密度,c为液体中球体的附面积所造成的阻力系数。
实验器材:落球仪、不锈钢球、粘度杯、天平、计时器。
实验步骤:1. 将清洗干净的粘度杯放置于水平桌面上,从中心位置向四周倾倒粘度杯内液体,使其液面略高于粘度杯口。
2. 用干净柔软的织物揩干不锈钢球的表面和手指指纹,取适量液体注入粘度杯中。
3. 轻轻放入处理好的不锈钢球,并避免球与粘度杯发生碰撞。
4. 将不锈钢球从杯口自由落下,计时器开始计时。
5. 直到不锈钢球停止落下,记录下时间t。
6. 用天平称出不锈钢球的质量m,以及球的直径D和液体的温度θ。
7. 重复以上步骤3至6,得到不同时间下的球体速度v。
8. 用计算公式计算液体的粘度。
η=2(g-ρV)/(9c)9. 根据实验结果计算液体的平均粘度。
实验数据与结果:实验条件:球体质量m=0.13g,球的直径D=2mm,液体密度ρ=1.207g/cm³,液体表面张力=0.0592N/m,重力加速度g=9.8m/s²。
实验结果如下:实验时间(s)球体速度v(m/s)0 05 0.037310 0.073815 0.106520 0.139225 0.170230 0.1998计算平均粘度:η = 2(g-ρV)/(9c) = 44.478Pa·s实验结论:本实验使用落球法测量液体的粘度,测量结果为Η=44.48Pa·s。
根据测得的粘度,比较不同液体的粘度大小,观察不同温度下同一液体的粘度变化,加深对粘度概念和测量方法的理解。
落球法测液体的粘滞系数

落球法测液体的粘滞系数落球法是一种测定液体粘滞系数的方法,它是通过测量液体小球在垂直于其运动方向的平面上所受阻力来得出液体粘滞系数的。
该方法适用于各种流体,如液体、半固体或高分子体系,可用于研究定量性质,如粘度、流动性、粘滞作用等。
该方法简便易行,不需要特殊设备和条件,适用于实验室教学和科学研究等方面。
实验原理液体粘滞现象是由于粘性阻力的存在而引起的,这种阻力是由分子间的吸引和分子间摩擦力的相互竞争造成的。
落球法是利用这种阻力,通过测量液体小球在垂直于其运动方向的平面上所受的阻力来计算液体的粘滞系数。
实验步骤1.准备实验材料:落球法测定液体粘滞系数所需的材料包括:液体、球体、容器、计时器、温度计等。
2.将球体放入液体中:将球体轻轻地落入液体中,记录球体下落的时间t1。
(球体要保持光滑,不锈钢球较好用)3.测量空气中的自由落体时间:用同样的方法将球体轻轻落入向上的空气中,记录球体上升的时间t2。
4.重复步骤2和步骤3几次,记录其数据,并求其平均值。
5.计算液体的粘滞系数:根据忽略气体粘滞力和重力加速度的条件,在球体下落的过程中,假设液体存在的粘滞阻力是稳定的,则液体的粘滞系数可以通过以下公式进行计算:η = 2(R^2ρgvt) / 9v(1 + 2.4R/d)其中:η为液体粘滞系数;R为球体半径;ρ为液体的密度;g为重力加速度;v为球体的下落速度;d为容器与球体的直径差。
实验注意事项1.实验室环境条件要控制在较稳定的范围内,如温度、湿度、气压等。
2.液体的温度要保持恒定,以便消除温度差异引起的误差。
3.球体的表面要光滑,不锈钢球较好用。
4.实验数据的取值要尽量准确,数据平均值的误差不能超过实验要求的误差范围。
5.仪器要静置一段时间后才开始实验。
6.实验仪器应定期维护保养,并按时校准。
实验结果与分析落球法测定液体粘滞系数的实验结果是根据实验条件和数据计算出的一个值。
对于同一液体,它的粘滞系数往往随着温度的升高而降低,随着浓度的升高而增加,随着分子量的增加而增大。
落球法测液体粘滞系数的研究

表1 落球法测量蓖麻油粘度系数实验数据
d /mm
d 2
/mm
D /mm
D 2
/mm
h /mm
L /mm
t /s
1
2.52
2
2.48
3
2.50
平均值
2.50
1.26
60.82
30.41
295.0
160.0
9.63
1.24
60.62
30.31
297.0
160.0
9.60
1.25
60.80
30.40
296.0
Science and Technology Innovation Herald
速 能 够 和 汽 车发 动 机 所 对应 转 速 相匹配,如 此 才 能 确 保 燃油利用效率得以进一步提升。经验丰富的驾驶人员,还 会 依 照不同的路 况信息,确定合 理的 行驶 速率,尽可能 地 避免出现紧急刹车问题,尽可能地确保汽车的发动机装置 能够一直处在最优的转速空间之中。结合作者实际经验, 通常在市内正常交通条件下驾驶车辆,一般将速度设定在 60km/h相对较为适宜。 2.2 适宜的时机进行换挡操作
用落球法测液体的粘滞系数

用落球法测液体的粘滞系数一、仪器设备:2L 量筒、秒表、蓖麻油、钢珠二、实验目的:1. 观察液体的内摩擦现象。
2. 学会用落球法测量液体的粘滞系数。
三、实验原理:小球在液体中运动时,将受到与运动方向相反的摩擦力的作用,,这种阻力称为粘滞力,它是由于沾附在小球表面的液层与邻近液层的摩擦而产生的。
它不是小球与液体之间的摩擦阻力。
在理想情况下,根据斯托克斯定律,小球受到的粘滞力为:rv f πη6= (注:式中各字母的含义见后面的常数)在装有液体的圆筒形玻璃管中心轴线处让小球自由下落。
小球落入液体后,受到三个力的作用。
即重力、浮力、粘滞力。
在小球刚落入液体时,垂直向下的重力大于垂直向上的浮力与粘滞力之和。
于是小球作加速运动。
随着小球运动速度的增加,粘滞力也增加,当速度增加到某一值v 0时,小球所受到的合力为零。
此后小球就以该速度匀速下落。
当三力平衡时,即rv gV mg πηρ60+=小球作匀速直线运动,得:vrg v m πρη6)(0-= 实验时,待测液体必须盛于容器中,小球沿筒的中心轴线下降。
不是理想的条件,上式需要修正为:)23.31(4.2113()0H d D d rd gV m ++-=πρη四、实验内容:1. 使钢球表面完全被所测量液体浸润后,用镊子夹起一颗钢球沿筒中心轴线放入圆筒,观察钢球在液体中的速度变化及内摩擦现象。
2. 用米尺测量量筒内液体的高度H 和小球下落的距离AB:(1600---600)=s ,并记录。
3. 用镊子夹起被液体完全浸润的钢珠,然后沿量筒中心轴线放入量筒,用秒表测出小球匀速下落通过路程AB 所需要时间T 则:t s v =4. 重复测量三次,然后用磁铁将钢球取出放回盘中。
5. 根据每个小球的数据由公式计算η然后求η的平均值及误差。
误差公式:五、常数重力加速度:=g 9.78 1-⋅Kg N钢球的密度:=ρ78773-⋅m Kg液体的密度:==0ρ11603-⋅m Kg小球的直径:=d 3.00±0.02m圆筒的直径:D = 79.62±0.02m液柱的高度:H=m 下落的距离:S=m。
用落球法测定液体的粘滞系数
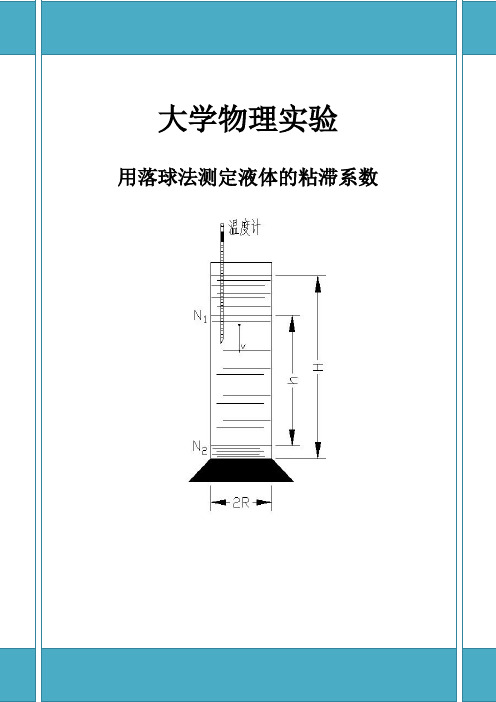
用落球法测定液体的粘滞系数液体的粘滞系数又称为内摩擦系数或粘度。
是描述液体内摩擦力性质的一个重要物理量。
它表征液体反抗形变的能力,只有在液体内存在相对运动时才表现出来。
粘滞系数除了因材料而异之外还比较敏感的依赖温度,液体的粘滞系数随着温度升高而减少,气体则反之,大体上按正比例的规律增长。
研究和测定液体的粘滞系数,不仅在材料科学研究方面,而且在工程技术以及其他领域有很重要的作用。
◆【实验目的】1.学习用落球法测定液体的粘滞系数的原理和方法2.熟悉流动液体中的粘滞现象,掌握粘滞现象的一般规律3.测定蓖麻油的粘滞系数◆【仪器及用具】玻璃量筒、待测液体、游标卡尺、秒表、温度计、米尺、小钢球、读数显微镜◆【实验原理】当流体流动时,各层的流速不同,相邻两层中由于流体分子的热运动,流速慢的流层中的分子进入流速快的流层;同时,流速快的流层中的分子进入流速慢的流层,结果流速快的将变慢,流速慢的将变快。
在宏观上就相当于在两流层间产生了相互作用力,我们称这一对相互作用力为内摩擦力或者粘滞力。
流体中的这一现象称为粘滞现象。
一个半径为r的金属小球在无限广延的粘滞液体中自由下落时,它受到3个力的作用:(1)小球W=ρVg(V为小球体积;ρ为小球密度;g为重力加速度),方向向下;(2)液体作用于小球的浮力F=ρ0Vg(ρ0为液体的密度),方向向上;(3)由于附着于球面的液体与周围其他液层之间的摩擦力,即小球受到的粘滞阻力f,方向向上。
由于液体是无限广延的,而且小球的半径r很小,小球下落的速度v也很小,这由斯托克斯公式可知:f=6πrηv=3πdηv式中,d为小球直径;η为该液体在T℃时的粘滞系数,它只与液体性质和温度有关。
一般的,液体温度越高,η越小。
在CGS制中η的单位是泊(P),1P=1g/(cm•s);在SI制中,η的单位是帕斯卡•秒(Pa•s),1Pa•s=1kg/m•s=10P。
小球在液体中下落时重力ρVg和浮力ρ0Vg为恒力,而粘滞阻力f与小球下落的速度v 成正比。
《大学物理实验》2-02落球法测液体的粘滞系数

蓖 麻 油 密度 ρ1
小 球 质 量m
粘 滞 系 数η
1 2 3
平均值
1 2
3 平均值
六、注意事项
1.实验时,应使油中无气泡;应该彻底清洗小球表面的污渍,小球要圆;油必须要静 止;量筒要铅直放置。 2. 实验时动作仔细,不要让油洒到实验台上。 3.两对激光接收器和发射器之间的距离要适当的大些。 4.将小球放入钢球导管内实验时,如反复数次都没有成功的,有的只有一次挡光,有 的一次都不能挡光,则需检查底盘是否水平,激光是否通过中垂线等。 5.由于小球很小,实验时一定要仔细小球,不能遗失。
60
很快,因此需要标明测量是在什么温度下进行的) 。 7.用公式(9)计算η 值,η 值保留三位有效数据. η 的单位为 kg ⋅ m−1 ⋅ s −1 。
五、数据记录和处理
表一 激光器发射器和接收器的位置
上位置 发射器 接收器 表二 次数 距离 s 时间 t
下位置
高度差
平均高度差 s
球直径 d
量 筒 内 径D
(10)式中 L 为量筒内蓖麻油的深度。
三、实验仪器
落球法粘滞系数测定仪(见图 3) 、小钢球、蓖麻油、量筒、米尺、直流稳压电源计时
59
仪、游标卡尺、电子天平、电子秒表、温度计、密度计等。
四、实验内容和步骤
1.调整粘滞系数测定 仪
9 1 2 5 10
-
(1) 调整底盘水平, 在 底盘横梁上放上小铅锤,调 节底盘旋钮,使铅锤中心对 准底盘中心的圆点。 (2)将实验架上的上, 下两对激光器接通电源,可 看见其发出红光。调节上、 下两个激光发射器,使其红 色激光束平行,并对准铅锤 线, 调节两激光接收器位置, 使能正常接收激光信号,判 别标准是看激光信号指示灯 记下手穿过时间。
实验二 落球法测量液体粘滞系数

实验二落球法测量液体粘滞系数概述当液体流动时,平行于流动方向的各层流体速度都不相同,即存在着相对滑动,于是在各层之间就有摩擦力产生,这一摩擦力称为粘滞力,它的方向平行于两层液体的接触面,其大小与速度梯度及接触面积成正比,比例系数η称为粘度,它是表征液体粘滞性强弱的重要参数。
液体的粘滞性的测量是非常重要的,例如,现代医学发现,许多心血管疾病都与血液粘度的变化有关,血液粘度的增大会使流入人体器官和组织的血流量减少,血液流速减缓,使人体处于供血和供氧不足的状态,这可能引起多种心脑血管疾病和其他许多身体不适症状。
因此,测量血粘度的大小是检查人体血液健康的重要标志之一。
又如,石油在封闭管道中长距离输送时,其输运特性与粘滞性密切相关,因而在设计管道前,必须测量被输石油的粘度。
各种实际液体具有不同程度的粘滞性。
测量液体粘度有多种方法,本实验所采用的落球法是一种绝对法测量液体的粘度。
如果一小球在粘滞液体中铅直下落,由于附着于球面的液层与周围其他液层之间存在着相对运动,因此小球受到粘滞阻力,它的大小与小球下落的速度有关。
当小球作匀速运动时,测出小球下落的速度,就可以计算出液体的粘度。
一、实验目的1、用落球法测液体的粘滞系数;2、研究液体粘滞系数对温度的依赖关系。
二、仪器装置1、YJ-RZT-II数字智能化热学综合实验平台;2、液体粘滞系数实验装置、3、光电转换实验模板;4、连接电缆;5、2mm小钢球;6、甘油(自备);7、直尺;8、千分尺;9、数字温度传感器;10、小磁钢及重锤部件;11、激光器;12、接收器;13、量筒;14、导球管;15、物理天平;16、测温探头。
液体粘滞系数实验仪如图1所示。
三、实验原理1、当金属小球在粘性液体中下落时,它受到三个铅直方向的力:小球的重力mg(mρ(V是小球体积,ρ是液体密度)和粘滞阻力为小球质量);液体作用于小球的浮力gVF(其方向与小球运动方向相反)、如果液体无限深广,在小球下落速度v较小情况下,有rv F πη6= (1)上式称为斯托克斯公式,其中r 是小球的半径;η称为液体的粘度,其单位是s Pa ⋅。
落球法测量液体的粘滞系数实验报告

一、 名称:落球法测量液体的黏滞系数 二、 目的:1.观察小球在液体中的下落过程,了解液体的内摩擦现象。
2.掌握用落球法测定液体粘滞系数的原理和方法。
3.掌握秒表、密度计等基本测量仪器的使用方法。
三、器材:变温黏度测量仪,ZKY PID -温控实验仪,秒表,螺旋测微器,钢球若干。
四、 原理:质量为m 的金属小球在黏滞液体中下落时,它会受到三个力,分别是小球的重力G ,小球受到的液体浮力F 和黏滞阻力ƒ。
如果液体的黏滞性较大,小球的质量均匀、体积较小、表面光滑,小球在液体中下落时不产生漩涡,而起下落速度较小,则小球所受到的黏滞阻力为ƒ =3vd πη (1)式(1)称为斯托克斯公式,其中是η液体的黏度,d 是小球的直径,v 是小球在流体中运动时相对于流体的速度。
当小球开始下落时,速度较小,所受到的黏滞阻力也较小,这时小球的重力大于浮力和黏滞阻力之和,小球做加速运动;随着小球速度的增加,小球所受到的黏滞阻力也随着增加,当小球的速度达到一定的数值0v (称收尾速度)时,三个力达到平衡,小球所受合力为零,小球开始匀速下落,此时+G F =ƒ (2) 即 003mg gV v d ρπη=+ (3)式中m V 、分别表示小球的质量和体积,0ρ表示液体的密度。
如用ρ表示小球的密度,则小球的体积V 为3432d V π⎛⎫= ⎪⎝⎭小球的质量m 为36m V d πρρ==代入式(3)并整理得()20018gd v ρρη-= (4)本实验中,小球在直径为D 的玻璃管中下落,液体在各方向无限广阔的条件不满足,此时黏滞阻力的表达式可加修正系数()1+2.4/d D ,而式(4)可修正为:()()200181 2.4/gd v d D ρρη-=+ (5) 当小球的密度较大,直径不是太小,而液体的黏度值又较小时,小球在液体中的平衡速度0v 会达到较大的值,奥西斯-果尔斯公式反映出了液体运动状态对斯托克斯公式的影响:ƒ20319=31Re Re ......161080v d πη⎛⎫+-+ ⎪⎝⎭(6) 其中Re 称为雷诺数,是表征液体运动状态的无量纲参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二落球法测定液体的粘滞系数
液体(或气体)粘滞系数是表征液体性质的一个物理量,是流体力学中经常接触的问题之一。
在航空航天,船舶研究,水利水力等学科中很有意义。
粘滞系数的测定方法有多种,现仅介绍其中的一种—落球法。
这是根据Stokes定律和方法设计的实验,Stokes是英国著名的物理学家和数学家。
实验方法简单、直观,物理思想清晰明了,在误差处理上应用了合理的数学修正和推理。
希望本实验能对学生们有所启发,实验不在形式的复杂和仪器的排场,而在于它的物理意义和实验思想。
实验目的
1.学习用落球法测定液体的粘滞系数。
2.了解Stokes公式的应用条件,雷诺数及修正。
实验仪器
量筒、直径2.0mm和1.5mm的小钢球、螺旋测微器、秒表、温度计和待测液体(蓖麻油)等,实验装置如图1所示。
实验原理
1.Stokes公式的简单介绍
一个在静止液体中缓慢下落的小球受到三个力的作用:重力、浮力和粘滞阻力的作用。
粘滞阻力是液体密度、温度和运动状态的函数。
如果小球在液体中下落时的速度很小,球的半径也很小,且液体可以看成在各方向上都是无限广阔的,则从流体力学的基本方程出发导出著名的Stokes公式:
vr
fπη
6
=(1)
式中f是小球所受到的粘滞阻力,v是小球
的下落速度,r是小球的半径,η是液体的粘滞系数,它的单位是泊[p]=[0.1牛顿•秒/ 米2]。
Stokes公式是由粘滞液体的普遍运动方程导出的,是在“小球在液体中下落速度很小,球的半径也很小和液体可以看成在各方向上无限广阔”三个假定条件下得到的。
那么,在实验上这些条件如何体现呢?Stokes公式应作如何修正呢?
2、奥西恩-果尔斯公式
温度计
L
V
2R e
h0 N1
N2
图1
小球在液体中下落,速度很小,球的半径也很小,可以归结为雷诺数R e 很小,即: R e η
ρ0
2rv =
(2)
式中0ρ为液体的密度。
当液体相对于小球处于层流运动状态时,解方程过程中可略去R e 的非线性项。
如果考虑R e 的非线性项,Stokes 公式修正为奥西恩-果尔斯公式:
)1080
191631(62
+-
+
=e e R R vr f πη (3)
式中3R e /16项和19R e 2/1080项可以看作Stokes 公式的第一和第二修正项。
如R e =0.1,则零级解(即1式)与一级解(即3式中取一级修正)相差约2%,二级修正项~2×10-4,可略去不计;如R e =0.5,则零级解与一级解相差约10%,二级修正项~0.5%仍可略去不计;但当R e =1时,则二级修正项~2%,随着R e 的增大,高次修正项的影响也变大。
3、容器壁的影响
在一般情况下,小球在容器半径R ,液体的高度为h 的液体内下落,则液体在各方向上都是无限广阔的这一假设条件是不能成立的,因此,必须考虑容器壁的影响,则式(3)变为
)
1080
191633
1)(3
.31)(4
.21(62
⋅⋅⋅+-
+++=e e R R h r R r vr f πη (4)
式(4)等号右边含R 和h 的二项即反映了这一修正
4.η的表示
前面我们讨论了粘滞阻力f 与小球的速度、几何尺寸、液体的密度、雷诺数、粘滞系数等参量之间的关系,但在一般情况下粘滞阻力f 是很难测定的。
因此,还是很难得到粘滞系数η。
这里,我们考虑这么一种情况:
小球在液体中下落时,重力、浮力和粘滞阻力都在铅直方向上,重力方向向下,而浮力和粘滞阻力向上,阻力随着小球的速度增加而增加。
显然,小球从静止开始作加速运动,当小球的下落速度达到一定大小时,这三个力的合力等于零。
然后,小球以匀速下落。
则由式(4)得: )1080
1916
33
1)(3
.31)(4
.21(6)(3
42
03
⋅⋅⋅+-
+++=-e e R R h
r R
r vr g πηρρπγ
(5)
式中ρ是小球的密度,g 为重力加速度,由式(5)得:
)1080
1916
31)(3
.31)(4
.21()(9
22
2
+-
+
++-=
e e o R R h r R
r v gr
ρρη
)1080
1916
31)(23
.31)(24
.21()(18
12
2
+-
+
++-=
e e o R R h d R
d v gd
ρρ (6)
式中d 是小球的直径。
由上面2的讨论,我们得到以下三种情况:
1)当R e <0.1时,可以取零级解,则(6)式就成为:
)23
.31)(24
.21()(18
12
h
d R
d v gd o o ++-=
ρρη (7)
2)0.1<R e <0.5时,可以取一级近似解,式(6)就成为:
)23
.31)(24
.21()(18
1)16
31(2
1h
d R
d v gd R o
e ++-=
+
ρρη
它可以表示成零级近似解的函数:
00116
3ρηηdv -
= (8)
3)R e >0.5时,还必须考虑二级修正,则式(6)的η变成:
)23
.31)(24
.21()(18
1)1080
1916
31(2
2
2h
d R
d v gd R R o
e e ++-=
-
+
ρρη
或 ⎥⎥⎦
⎤⎢⎢⎣
⎡
+
+=2
1
12)(
270
19112
1ηρηηdv (9)
在实验完成后,实验报告中作数据处理时,必须对R e 进行计算。
确定它的范围后,进行相
应修正,得到符合实验要求的粘滞系数值。
实验内容
1.图1的N 1和N 2之间设为匀速下降区,测出其长度L 。
2. 用相应的仪器测出R 和h (至少各测量三次并求平均值)及液体的温度T ,温度T 应取实验开始时的温度和实验结束时的温度的平均值。
3. 用镊子将小球置于量筒中央,尽量接近液面处后放开小球使其下落,测出小球通过匀速下降区L 的时间t ,重复6次,每次间隔5分钟以上。
4. 应用式(7)计算η0。
5. 根据公式(2)计算雷诺数Re ,并根据雷诺数的大小,参照公式(8)或(9)进行相应的修正。
6. 将实验结果与附录的“蓖麻油粘滞系数和温度关系曲线图”作比较。
数据记录
1.匀速下降区L = m; 圆筒的内径R = cm. 液体的高度h = m.
2.小球下落的速度V
T 前= 0C; T 后= 0
C; T 平均= 0
C; d = mm 测量次序
1 2
3
4
5
6
平均值
t 1(s)
V (m/s)
注:钢球密度:33/109.7m Kg ⨯ 蓖麻油密度:3
3/1096.0m Kg ⨯
思考题
1.根据实际情况分析实验中引起测量误差的主要因素是什么?
2.说明雷诺数的物理意义。
附录
蓖麻油
η-θ图
0510********
5
10
15
202530
35
40
θ/℃
η/P。
