matlab电机实例
matlab中关于永磁同步电机的仿真例子

matlab中关于永磁同步电机的仿真例子MATLAB中关于永磁同步电机的仿真例子1. 基本电机参数配置在进行永磁同步电机的仿真前,需要先配置基本的电机参数,包括电机的额定功率、额定电压、额定转速等。
2. 电机模型的建立使用MATLAB中的Simulink模块,可以方便地建立永磁同步电机的模型。
可以利用Simulink库中的电机模块,如Permanent Magnet Synchronous Machine来构建电机模型。
3. 电机控制策略的设计在建立电机模型后,需要设计适合的控制策略来控制电机的运行。
常见的控制策略包括:•PI控制:使用Proportional-Integral (PI) 控制器来调节电机的转速和电流。
•磁场定向控制(FOC):通过测量电机转子位置和速度,将三相交流信号转换为等效直流信号,实现对电机的控制。
4. 电机仿真完成电机模型和控制策略的设计后,可以进行电机的仿真。
使用Simulink中的仿真工具,可以模拟电机的运行情况,并观察电机的转速、电流、转矩等参数的变化过程。
5. 仿真结果分析根据仿真结果,可以分析电机的性能指标,包括:•转速响应:电机在各种工况下的转速响应特性。
•转矩输出:电机在不同负载情况下的转矩输出。
•电流波形:电机的相电流波形及电流变化情况。
•功率因数:电机在运行过程中的功率因数变化。
6. 优化和改进根据仿真结果分析的情况,可以针对电机的性能进行优化和改进,例如:•调整控制策略的参数,提高转速响应和控制精度。
•优化电机的电气设计,提高效率和功率密度。
•添加降噪措施,减少电机的噪声和振动。
7. 结论根据电机仿真的结果和优化改进的情况,得出结论,总结永磁同步电机的特性和性能,并对未来的研究方向进行展望。
以上是关于MATLAB中关于永磁同步电机的仿真例子的一些列举和详细讲解,通过Simulink工具的电机模型建立、控制策略设计、仿真结果分析和优化改进等步骤,可以深入了解和研究永磁同步电机的性能和特性,并为电机控制系统的设计和优化提供有力支持。
matlab电机仿真

学院:机电学院班级:机自09-2班姓名:谢伟学号:03090943报告关于电机互锁的仿真报告我们要先明确什么叫互锁互锁,说的是几个回路之间,利用某一回路的辅助触点,去控制对方的线圈回路,进行状态保持或功能限制。
一般对象是对其他回路的控制.例如:上图是一个很典型的互锁电路图,实现的功能是电机的正反转,当实现正传的时候,关闭断路器Qs,按下正向按钮SB3,SB3的常闭触点断开,是KM2不工作,SB3的常开触点闭合,是电磁铁KM1得电,线圈KM1吸合实现自锁,电机实现正向转动,同时线圈的常闭触点断开,保证KM2不工作,防止电路短路导致的电路故障,当实现反向转动时,按下反向按钮SB2,SB2的常闭触点断开,KM1不得电,电机无法正向转动,SB2的常开触点闭合,KM2得电,线圈KM2吸合实现自锁,电机实现反向转动,同时线圈KM2 的常闭触点断开,保证KM1不工作。
以上当电机正转时保证电机反转电路断开,反转保证正转电路断开的方法叫作互锁。
利用的是两个常闭辅助触点来实现其功能的。
在实际工作中,由于坏境是变化的,负载也随着环境的变化而变化,为了测试电动机在不同负载环境下的运转情况,我们必须测试一系列不同的或者双向的负载加在电机轴上的电机反应。
此外,一个理想的负载应该回归到发电机从电网上吸收的能量。
这样的负载应该有一个有四象限的DC2或者DC4的直流电产生,这测试的时候应该通过刚性轴这两个电动机进行机械耦合连接。
因此,这个仿真实验需要两个电动机模型,AC4电动机和DC2电动机。
其中,AC4电动机是一个直流三相感应异步电动机,DC2是一个直流单向整流电动机。
在这样的系统里,一个电动机负责速度参数的设定,一个电动机负责力矩参数的设定.同时每个电动机可以充当马达或者发电机。
DC2的额定参数一般是3马力,240伏特,1800转每分钟。
AC4电动机的额定参数是3马力,380伏特,60赫兹,4级。
上图为直流电动机的工作原理图上图为桥式整流电路图注意:对于两个电动机的信号控制可以使用用户界面的最下方的机械输入菜单,下图显示了再马达—发电机结构中如何去模拟刚性轴的互相连接。
MATLAB在电机教学中的应用

te s f s a tns J Au i E g S c v14 , o 6 P . 9 h s mui e, . do n . o . o. 0 n . , P 4 7 io c o ” l ,
—
51 6,1 92 9 .
库. 具有 强大 的运算 处理 能力 和方 便 实用 的绘 图功 能 , 尤其 是其 中 的 Sm l k图形界 面环境 .使 各种 工 程 问 i ui n
题 的求解 和仿 真更具 有简 洁性 和直 观性 。将 MA L B TA 应 用于 电机 教学 中 .利用 其 电力 系统 仿 真工 具箱 提供
小 的步 率
参考 文献 :
[】. a ce “ i eadp c a df ao f u i s nl ” 1J Lr h , T m n i hs emo ict no do i a , o t c l i i a g s
i p ia o so g t i n l r c s n o Au i n o s c, n Ap l t n f ci Dii lS g a o e s g t do a d Ac u t s a P i i M . h sa d K. a d n u g E s Kl we,No we , vA, 9 8 Ka r n Brn e b r , d . u r r U /I 1 9 .
个新 的波形 . 波形 是 原本 的两倍 。 音 乐分 为背 景声 该 将
s or—t e Fo ie nayi, I h t i ur r a l ss” EEE Trn .Ac s. pe c ,Sina m as ou t,S e h g l
Pr c si ,v 1 9,n o e ng o .2 o.3, PP.3 74— 3 ,1 81 90 9 .
matlab电机仿真精华50例

matlab电机仿真精华50例Matlab是一种功能强大的仿真软件,它被广泛应用于电机仿真领域。
在这篇文章中,我们将介绍Matlab电机仿真的50个精华例子,帮助读者更好地了解和应用电机仿真技术。
1. 直流电机的仿真:通过Matlab可以模拟直流电机的性能,包括转速、扭矩和电流等。
2. 交流电机的仿真:使用Matlab可以模拟交流电机的工作原理,包括转子和定子的相互作用。
3. 同步电机的仿真:通过Matlab可以模拟同步电机的运行特性,包括电压和频率的控制。
4. 步进电机的仿真:利用Matlab可以模拟步进电机的运行过程,包括步进角度和步进速度等。
5. 无刷直流电机的仿真:通过Matlab可以模拟无刷直流电机的工作原理,包括转子和定子的相互作用。
6. 电机控制系统的仿真:利用Matlab可以模拟电机控制系统的运行过程,包括速度和位置的闭环控制。
7. 电机噪声的仿真:通过Matlab可以模拟电机噪声的产生和传播过程,帮助优化电机的设计。
8. 电机故障诊断的仿真:利用Matlab可以模拟电机故障的发生和诊断过程,提供故障检测和排除的方法。
9. 电机热仿真:通过Matlab可以模拟电机的热传导和散热过程,帮助优化电机的散热设计。
10. 电机振动的仿真:利用Matlab可以模拟电机的振动特性,帮助优化电机的结构设计。
11. 电机效率的仿真:通过Matlab可以模拟电机的能量转换过程,评估电机的效率和能耗。
12. 电机启动过程的仿真:利用Matlab可以模拟电机的启动过程,包括起动电流和启动时间等。
13. 电机负载仿真:通过Matlab可以模拟电机在不同负载条件下的工作特性,帮助优化电机的设计。
14. 电机饱和仿真:利用Matlab可以模拟电机在饱和状态下的工作特性,提供更准确的仿真结果。
15. 电机电磁干扰的仿真:通过Matlab可以模拟电机产生的电磁干扰对其他设备的影响,提供干扰抑制的方法。
16. 电机电磁场的仿真:利用Matlab可以模拟电机内部的电磁场分布,帮助优化电机的设计。
matlab中关于永磁同步电机的仿真例子

matlab中关于永磁同步电机的仿真例子摘要:一、Matlab中永磁同步电机仿真概述二、永磁同步电机仿真模型建立1.参数设置2.控制器设计3.仿真结果分析三、SVPWM算法在永磁同步电机仿真中的应用四、案例演示:基于DSP28035的永磁同步电机伺服系统MATLAB仿真五、总结与展望正文:一、Matlab中永磁同步电机仿真概述Matlab是一款强大的数学软件,其在电机领域仿真中的应用广泛。
永磁同步电机(PMSM)作为一种高效、高性能的电机,其控制策略和性能分析在Matlab中得到了充分的体现。
利用Matlab进行永磁同步电机仿真,可以有效验证控制策略的正确性,优化电机参数,提高系统性能。
二、永磁同步电机仿真模型建立1.参数设置:在建立永磁同步电机仿真模型时,首先需要设定电机的各项参数,如电阻、电感、永磁体磁链等。
这些参数可以根据实际电机的设计值进行设置,以保证模型与实际电机的特性一致。
2.控制器设计:控制器的设计是电机仿真模型的核心部分。
常见的控制器设计包括矢量控制(也称为场导向控制,Field-Oriented Control, FOC)、直接转矩控制(Direct Torque Control, DTC)等。
在Matlab中,可以利用现有的工具箱(如PMSM T oolbox)方便地进行控制器的设计和仿真。
3.仿真结果分析:在完成控制器设计后,进行仿真实验。
通过观察电机的转速、电流、转矩等参数的变化,可以评估控制器的性能。
同时,可以利用Matlab的图像绘制功能,将仿真结果以图表的形式展示,便于进一步分析。
三、SVPWM算法在永磁同步电机仿真中的应用SVPWM(Space Vector Pulse Width Modulation)是一种用于控制永磁同步电机的有效方法。
通过在Matlab中实现SVPWM算法,可以方便地对比不同控制策略的性能。
在仿真过程中,可以观察到SVPWM算法能够有效提高电机的转矩波动抑制能力,减小电流谐波含量,从而提高电机的运行效率。
永磁同步电机矢量控制matlab仿真

永磁同步电机矢量控制matlab仿真永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)的矢量控制(也称为场向量控制或FOC)是一种先进的控制策略,用于优化电机的性能。
这种控制方法通过独立控制电机的磁通和转矩分量,实现了对电机的高性能控制。
在MATLAB中,你可以使用Simulink和SimPowerSystems库来模拟永磁同步电机的矢量控制。
以下是一个基本的步骤指南:1.建立电机模型:使用SimPowerSystems库中的Permanent Magnet SynchronousMachine模型。
你需要为电机提供适当的参数,如额定功率、额定电压、额定电流、极对数、转子惯量等。
2.建立控制器模型:矢量控制的核心是Park变换和反Park变换,用于将电机的定子电流从abc坐标系变换到dq旋转坐标系,以及从dq坐标系变换回abc坐标系。
你需要建立这些变换的模型,并设计一个适当的控制器(如PI控制器)来控制dq轴电流。
3.建立逆变器模型:使用SimPowerSystems库中的PWM Inverter模型。
这个模型将控制器的输出(dq轴电压参考值)转换为逆变器的开关信号。
4.连接模型:将电机、控制器和逆变器连接起来,形成一个闭环控制系统。
你还需要添加一个适当的负载模型来模拟电机的实际工作环境。
5.设置仿真参数并运行仿真:在Simulink的仿真设置中,你需要设置仿真时间、步长等参数。
然后,你可以运行仿真并观察结果。
6.分析结果:你可以使用Scope或其他分析工具来查看电机的转速、定子电流、电磁转矩等性能指标。
这些指标可以帮助你评估控制算法的有效性。
请注意,这只是一个基本的指南,具体的实现细节可能会因你的应用需求和电机参数而有所不同。
在进行仿真之前,建议你仔细阅读相关的文献和教程,以便更好地理解永磁同步电机的矢量控制原理。
MATLAB电机控制综合仿真实验
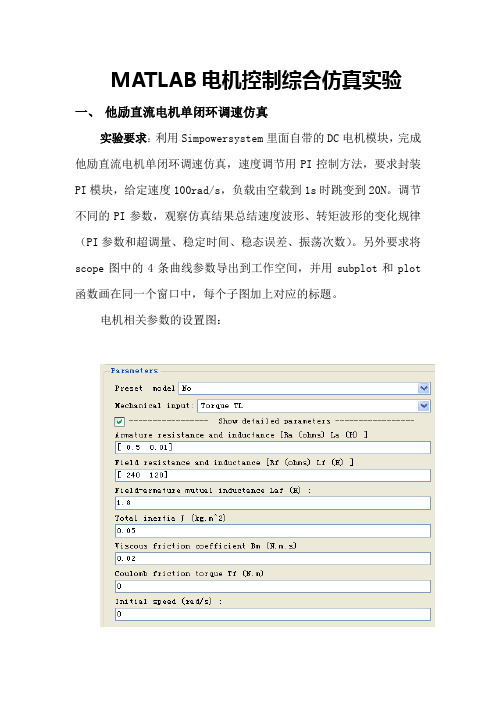
MATLAB电机控制综合仿真实验一、他励直流电机单闭环调速仿真实验要求:利用Simpowersystem里面自带的DC电机模块,完成他励直流电机单闭环调速仿真,速度调节用PI控制方法,要求封装PI模块,给定速度100rad/s,负载由空载到1s时跳变到20N。
调节不同的PI参数,观察仿真结果总结速度波形、转矩波形的变化规律(PI参数和超调量、稳定时间、稳态误差、振荡次数)。
另外要求将scope图中的4条曲线参数导出到工作空间,并用subplot和plot 函数画在同一个窗口中,每个子图加上对应的标题。
电机相关参数的设置图:仿真原理图:在仿真试验中需要按照实验要求对PI控制器子系统进行封装,然后更改Kp、Ki参数值的大小。
封装PI模块图如下:Plot绘图程序:>>subplot(411)>> plot(t,W,'r'),title('转速')>> subplot(412)>> plot(t,Ia,'b'),title('电枢电流')>> subplot(413)>> plot(t,Te,'g'),title('转矩')>> subplot(414)>> plot(t,If,'y'),title('励磁电流')速度调节用PI控制方法,给定速度100rad/s,负载由空载到1s 时跳变到20N,调节不同的PI参数,从PI模块封装中调节,修改不同的参数Ki 、Kp观察仿真结果。
Ki=100, Kp=5;050100w (r a d /s )00.51 1.52 2.53 3.54 4.55-2000200I a (A )-202I f (A )-1000100T e (N .m )Ki=2, Kp=1;w (r a d /s)I a (A)00.51 1.52 2.53 3.54 4.55I f (A)00.51 1.52 2.53 3.54 4.55T e (N .m )二、 他励直流电机闭环调速系统仿真实验要求:利用Simulink 基本模块搭建他励直流电机闭环调速系统直流电机子模块,根据以下电机数学模型搭建:电磁转矩公式:e M a T C I =Φ 动力学平衡方程:e L m d T T B J dtωω--=电机模块要求封装,参数20.05kg m J =⋅,0.02N m s m B =⋅⋅,165m C =,0.01Wb f Φ=,恒定负载T L =20N 点击封装模块时输入。
基于MATLAB的直流电机调速系统

绪论直流调速是指人为地或自动地改变直流电动机的转速,以满足工作机械的要求。
从机械特性上看,就是通过改变电动机的参数或外加工电压等方法来改变电动机的机械特性,从而改变电动机机械特性和工作特性机械特性的交点,使电动机的稳定运转速度发生变化。
直流调速系统,特别是双闭环直流调速系统是工业生产过程中应用最广的电气传动装置之一。
广泛地应用于轧钢机、冶金、印刷、金属切削机床等许多领域的自动控制系统中。
它通常采用三相全控桥式整流电路对电动机进行供电,从而控制电动机的转速,传统的控制系统采用模拟元件,如晶体管、各种线性运算电路等,虽在一定程度上满足了生产要求,但是因为元件容易老化和在使用中易受外界干扰影响,并且线路复杂、通用性差,控制效果受到器件性能、温度等因素的影响,从而致使系统的运行特性也随之变化,故系统运行的可靠性及准确性得不到保证,甚至出现事故。
双闭环直流调速系统是一个复杂的自动控制系统,在设计和调试的过程中有大量的参数需要计算和调整,运用传统的设计方法工作量大,系统调试困难,将SIMULINK 用于电机系统的仿真研究近几年逐渐成为人们研究的热点。
同时,MATLAB软件中还提供了新的控制系统模型输入与仿真工具SIMULINK,它具有构造模型简单、动态修改参数实现系统控制容易、界面友好、功能强大等优点,成为动态建模与仿真方面应用最广泛的软件包之一。
它可以利用鼠标器在模型窗口上“画”出所需的控制系统模型,然后利用SIMULINK提供的功能来对系统进行仿真或分析,从而使得一个复杂系统的输入变得相当容易且直观。
本文采用工程设计方法对转速、电流双闭环直流调速系统进行辅助设计,选择适当的调节器结构,进行参数计算和近似校验,并建立起制动、抗电网电压扰动和抗负载扰动的MATLAB/SIMULINK仿真模型,分析转速和仿真波形,并进行调试,使双闭环直流调速系统趋于完善、合理。
2MATLAB简介MATLAB是一门计算机编程语言,取名来源于Matrix Laboratory,本意是专门以矩阵的方式来处理计算机数据,它把数值计算和可视化环境集成到一起,非常直观,而且提供了大量的函数,使其越来越受到人们的喜爱,工具箱越来越多,应用范围也越来越广泛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
unction [sys,x0,str,ts,simStateCompliance] = BLDC_S(t,x,u,flag) %-----------------------------------------------------------------------% 状态变量:X(1)=ia;X(2)=ib;X(3)=ic;X(4)=SETA;X(5)=OMEGA;% 输入量:u(1)=Ud; u(2)=TL;% 输出量:n, Tem, ia, ib, ic;%------------------------------------------------------------------------%-----------------电动机参数---------------------------------------------R = 0.23;L = 0.00498; M = -0.00005478; J = 0.025;P0=2; % 极对数RR = diag([R R R]); LL = diag([L-M,L-M,L-M]);S = [2,-1,-1;-1,2,-1;-1,-1,2]/3;%-----------------------------------------------------------------------%SFUNTMPL General M-file S-function template% With M-file S-functions, you can define you own ordinary differential% equations (ODEs), discrete system equations, and/or just about% any type of algorithm to be used within a Simulink block diagram.%% The general form of an M-File S-function syntax is:% [SYS,X0,STR,TS,SIMSTATECOMPLIANCE] = SFUNC(T,X,U,FLAG,P1,...,Pn) %% What is returned by SFUNC at a given point in time, T, depends on the% value of the FLAG, the current state vector, X, and the current% input vector, U.%% FLAG RESULT DESCRIPTION% ----- ------ --------------------------------------------% 0 [SIZES,X0,STR,TS] Initialization, return system sizes in SYS,% initial state in X0, state ordering strings% in STR, and sample times in TS.% 1 DX Return continuous state derivatives in SYS.% 2 DS Update discrete states SYS = X(n+1)% 3 Y Return outputs in SYS.% 4 TNEXT Return next time hit for variable step sample% time in SYS.% 5 Reserved for future (root finding).% 9 [] Termination, perform any cleanup SYS=[].%% The state vectors, X and X0 consists of continuous states followed% by discrete states.%% Optional parameters, P1,...,Pn can be provided to the S-function and% used during any FLAG operation.%% When SFUNC is called with FLAG = 0, the following information% should be returned:%% SYS(1) = Number of continuous states.% SYS(2) = Number of discrete states.% SYS(3) = Number of outputs.% SYS(4) = Number of inputs.% Any of the first four elements in SYS can be specified% as -1 indicating that they are dynamically sized. The% actual length for all other flags will be equal to the% length of the input, U.% SYS(5) = Reserved for root finding. Must be zero.% SYS(6) = Direct feedthrough flag (1=yes, 0=no). The s-function% has direct feedthrough if U is used during the FLAG=3% call. Setting this to 0 is akin to making a promise that% U will not be used during FLAG=3. If you break the promise% then unpredictable results will occur.% SYS(7) = Number of sample times. This is the number of rows in TS.%% X0 = Initial state conditions or [] if no states.%% STR = State ordering strings which is generally specified as [].%% TS = An m-by-2 matrix containing the sample time% (period, offset) information. Where m = number of sample% times. The ordering of the sample times must be:%% TS = [0 0, : Continuous sample time.% 0 1, : Continuous, but fixed in minor step% sample time.% PERIOD OFFSET, : Discrete sample time where% PERIOD > 0 & OFFSET < PERIOD.% -2 0]; : Variable step discrete sample time% where FLAG=4 is used to get time of% next hit.%% There can be more than one sample time providing% they are ordered such that they are monotonically% increasing. Only the needed sample times should be% specified in TS. When specifying more than one% sample time, you must check for sample hits explicitly by% seeing if% abs(round((T-OFFSET)/PERIOD) - (T-OFFSET)/PERIOD)% is within a specified tolerance, generally 1e-8. This% tolerance is dependent upon your model's sampling times% and simulation time.%% You can also specify that the sample time of the S-function% is inherited from the driving block. For functions which% change during minor steps, this is done by% specifying SYS(7) = 1 and TS = [-1 0]. For functions which% are held during minor steps, this is done by specifying% SYS(7) = 1 and TS = [-1 1].%% SIMSTATECOMPLIANCE = Specifices how to handle this block when saving and % restoring the complete simulation state of the% model. The allowed values are: 'DefaultSimState',% 'HasNoSimState' or 'DisallowSimState'. If this value% is not speficified, then the block's compliance with% simState feature is set to 'UknownSimState'.% Copyright 1990-2007 The MathWorks, Inc.% $Revision: 1.18.2.3 $%% The following outlines the general structure of an S-function.%switch flag,%%%%%%%%%%%%%%%%%%% Initialization %%%%%%%%%%%%%%%%%%%case 0,[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes; %%%%%%%%%%%%%%%% Derivatives %%%%%%%%%%%%%%%%case 1,sys=mdlDerivatives(t,x,u);%%%%%%%%%%% Update %%%%%%%%%%%case 2,sys=mdlUpdate(t,x,u);%%%%%%%%%%%% Outputs %%%%%%%%%%%%case 3,sys=mdlOutputs(t,x,u);%%%%%%%%%%%%%%%%%%%%%%%% GetTimeOfNextVarHit %%%%%%%%%%%%%%%%%%%%%%%%case 4,sys=mdlGetTimeOfNextVarHit(t,x,u);%%%%%%%%%%%%%% Terminate %%%%%%%%%%%%%%case 9,sys=mdlTerminate(t,x,u);%%%%%%%%%%%%%%%%%%%%% Unexpected flags %%%%%%%%%%%%%%%%%%%%%otherwiseDAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));end% end sfuntmpl%============================================================================= % mdlInitializeSizes% Return the sizes, initial conditions, and sample times for the S-function.%============================================================================= function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes%% call simsizes for a sizes structure, fill it in and convert it to a sizes array.% Note that in this example, the values are hard coded. This is not a% recommended practice as the characteristics of the block are typically% defined by the S-function parameters.%sizes = simsizes;sizes.NumContStates = 5;sizes.NumDiscStates = 0;sizes.NumOutputs = 5;sizes.NumInputs = 2;sizes.DirFeedthrough = 0;sizes.NumSampleTimes = 1; % at least one sample time is neededsys = simsizes(sizes);%% initialize the initial conditionsx0 = [0;0;0;0;0];%% str is always an empty matrixstr = [];%% initialize the array of sample timests = [0 0];% Specify the block simStateComliance. The allowed values are:% 'UnknownSimState', < The default setting; warn and assume DefaultSimState% 'DefaultSimState', < Same sim state as a built-in block% 'HasNoSimState', < No sim state% 'DisallowSimState' < Error out when saving or restoring the model sim statesimStateCompliance = 'UnknownSimState';% end mdlInitializeSizes%============================================================================= % mdlDerivatives% Return the derivatives for the continuous states.%============================================================================= function sys=mdlDerivatives(t,x,u)S = [2,-1,-1;-1,2,-1;-1,-1,2]/3;R = 0.23;L = 0.000498; M = -0.00005478; J = 0.025;P0=2;RR = diag([R R R]); LL = diag([L-M,L-M,L-M]);Ud = u(1);TL = u(2);SETA = mod(abs(x(4)), 2*pi);ea = 0.04*x(5)*(3.30*cos(SETA)+0.388*cos(3*SETA-pi));eb = 0.04*x(5)*(3.30*cos(SETA-2*pi/3)+0.388*cos(3*(SETA-2*pi/3)-pi));ec = 0.04*x(5)*(3.30*cos(SETA+2*pi/3)+0.388*cos(3*(SETA+2*pi/3)-pi));E=[ea eb ec]'; %感应电动势if((0<=SETA)&(SETA<(pi/3))) % 导通顺序AC, BC, BA, CA, CB,AB Uag = Ud/2;Ubg = 1.5*eb;Ucg = -Ud/2;elseif(((pi/3)<= SETA)&(SETA<(2*pi/3)))Uag = 1.5*ea;Ubg = Ud/2;Ucg = -Ud/2;elseif(((2*pi/3)<= SETA)&(SETA<(pi)))Uag = -Ud/2;Ubg = Ud/2;Ucg = 1.5*ec;elseif(((3*pi/3)<= SETA)&(SETA<(4*pi/3)))Uag = -Ud/2;Ubg = 1.5*eb;Ucg = Ud/2;elseif(((4*pi/3)<= SETA)&(SETA<(5*pi/3)))Uag = 1.5*ea;Ubg = -Ud/2;Ucg = Ud/2;elseif(((5*pi/3)<= SETA)&(SETA<(6*pi/3)))Uag = Ud/2;Ubg = -Ud/2;Ucg = 1.5*ec;endU = S*[Uag Ubg Ucg]';sys(1:3) = inv(LL)*(U-RR*x(1:3)-E);ea5 = 0.04*(3.30*cos(SETA)+0.388*cos(3*SETA-pi));eb5 = 0.04*(3.30*cos(SETA-2*pi/3)+0.388*cos(3*(SETA-2*pi/3)-pi));ec5 = 0.04*(3.30*cos(SETA+2*pi/3)+0.388*cos(3*(SETA+2*pi/3)-pi));Tem = 2*(ea5*x(1)+eb5*x(2)+ec5*x(3));sys(4) = x(5);sys(5) = P0*(Tem-TL)/J;%sys = [];% end mdlDerivatives%======================================================================= % mdlUpdate% Handle discrete state updates, sample time hits, and major time step% requirements.%======================================================================== function sys=mdlUpdate(t,x,u)sys = [];% end mdlUpdate%======================================================================== % mdlOutputs% Return the block outputs.%======================================================================== function sys=mdlOutputs(t,x,u)sys(1) = x(5)*60/(2*pi*2);SETA=x(4);ea5 = 0.04*(3.30*cos(SETA)+0.388*cos(3*SETA-pi));eb5 = 0.04*(3.30*cos(SETA-2*pi/3)+0.388*cos(3*(SETA-2*pi/3)-pi));ec5 = 0.04*(3.30*cos(SETA+2*pi/3)+0.388*cos(3*(SETA+2*pi/3)-pi));Tem = 2*(ea5*x(1)+eb5*x(2)+ec5*x(3));sys(2) = Tem;sys(3:5) = x(1:3);%sys = [];% end mdlOutputs%======================================================================== % mdlGetTimeOfNextVarHit% Return the time of the next hit for this block. Note that the result is% absolute time. Note that this function is only used when you specify a% variable discrete-time sample time [-2 0] in the sample time array in% mdlInitializeSizes.%======================================================================= function sys=mdlGetTimeOfNextVarHit(t,x,u)sampleTime = 1; % Example, set the next hit to be one second later.sys = t + sampleTime;% end mdlGetTimeOfNextVarHit%========================================================================% mdlTerminate% Perform any end of simulation tasks.%====================================================================== function sys=mdlTerminate(t,x,u)sys = [];% end mdlTerminate%--------------------------------------------------------------------------% 子程序BLDCfun.m% 状态变量导数计算function DX = BLDCfun(t,X)global Ud TL RR LL J P0 P S;SETA = mod(abs(X(4)), 2*pi);ea = 0.04*X(5)*(3.30*cos(SETA)+0.388*cos(3*SETA-pi));eb = 0.04*X(5)*(3.30*cos(SETA-P(2))+0.388*cos(3*(SETA-P(2))-pi));ec = 0.04*X(5)*(3.30*cos(SETA+P(2))+0.388*cos(3*(SETA+P(2))-pi));E=[ea eb ec]'; %感应电动势%------------------------------------------------------------------------if((0<=SETA)&(SETA<(pi/3))) %导通顺序AC, BC, BA, CA, CB,ABUag = Ud/2;Ubg = 1.5*eb;Ucg = -Ud/2;elseif(((pi/3)<= SETA)&(SETA<(2*pi/3)))Uag = 1.5*ea;Ubg = Ud/2;Ucg = -Ud/2;elseif(((2*pi/3)<= SETA)&(SETA<(pi)))Uag = -Ud/2;Ubg = Ud/2;Ucg = 1.5*ec;elseif(((3*pi/3)<= SETA)&(SETA<(4*pi/3)))Uag = -Ud/2;Ubg = 1.5*eb;Ucg = Ud/2;elseif(((4*pi/3)<= SETA)&(SETA<(5*pi/3)))Uag = 1.5*ea;Ubg = -Ud/2;Ucg = Ud/2;elseif(((5*pi/3)<= SETA)&(SETA<(6*pi/3)))Uag = Ud/2;Ubg = -Ud/2;Ucg = 1.5*ec;end%-------------------------------------------------------------------------U = S*[Uag Ubg Ucg]';I = [X(1) X(2) X(3)]';DX = inv(LL)*(U-RR*I-E);ea5 = 0.04*(3.30*cos(SETA)+0.388*cos(3*SETA-pi));eb5 = 0.04*(3.30*cos(SETA-P(2))+0.388*cos(3*(SETA-P(2))-pi)); ec5 = 0.04*(3.30*cos(SETA+P(2))+0.388*cos(3*(SETA+P(2))-pi)); Tem = P0*(ea5*X(1)+eb5*X(2)+ec5*X(3));DX(4) = X(5);DX(5) = P0*(Tem-TL)/J;n=60*X(5)/(2*pi*P0);fprintf('t=%7.4f',t);fprintf(' n=%7.2F\n',n);SPWM.m%参数输入Ud=390;F1=50;h=0.00001;Tend=1.2/F1;Kf=21;Ka=4/3;F2=Kf*F1;T1=1/F1;T2=1/F2;P(1)=0;P(2)=2*pi/3;P(3)=4*pi/3;% Ö÷³ÌÐòt=0;i=1;while t<=Tendtt2 = mod(t,T2);if tt2<= T2/2A2=Ka*(4*tt2/T2-1);elseA2=Ka*(-4*tt2/T2-1);endfor k=1:3A1=sin(2*pi*t/T1-P(k));if A1>A2S(k)=1;elseS(k)=-1;endend% 逆变器输出线电压Uab=(S(1)-S(2))*Ud/2;Ubc=(S(2)-S(3))*Ud/2;Uca=(S(3)-S(1))*Ud/2;%逆变器输出至直流电源中性点电压Uag=S(1)*Ud/2;Ubg=S(2)*Ud/2;Ucg=S(3)*Ud/2;%负载相电压Ua0=(2*Uag-Ubg-Ucg)/3;Ub0=(-Uag+2*Ubg-Ucg)/3;Uc0=(-Uag-Ubg+2*Ucg)/3;%---------------------------------------------------------------------tx(i)=t;Uaby(i)=Uab;Ubcy(i)=Ubc;Ucay(i)=Uca;Uagy(i)=Uag;Ubgy(i)=Ubg;Ucgy(i)=Ucg;Ua0y(i)=Ua0;Ub0y(i)=Ub0;Uc0y(i)=Uc0;A1y(i)=A1;A2y(i)=A2;t=t+h;i=i+1;endfigure(1); plot(tx, Uaby), title('AB线电压'),xlabel('t(s)');ylabel('Uab');grid;figure(2); plot(tx, Ubcy), title('BC线电压'),xlabel('t(s)');ylabel('Ubc');grid;figure(3); plot(tx, Ucay), title('CA线电压'),xlabel('t(s)');ylabel('Uca');grid;figure(4); plot(tx, Uagy), title('AG电压'),xlabel('t(s)');ylabel('Uag');grid;figure(5); plot(tx, Uagy), title('BG电压'),xlabel('t(s)');ylabel('Ubg');grid;figure(6); plot(tx, Ucgy), title('CG电压'),xlabel('t(s)');ylabel('Ucg');grid;figure(7); plot(tx, Ua0y), title('A相电压'),xlabel('t(s)');ylabel('Ua0');grid;figure(8); plot(tx, Ub0y), title('B相电压'),xlabel('t(s)');ylabel('Ub0');grid;figure(9); plot(tx, Ua0y), title('C相电压'),xlabel('t(s)');ylabel('Uc0');grid;仿真:仿真有称模拟,就是用模型来代替实际的系统,该模型与所有替代的实际系统之间存在某些相对应得量,并能在某些范围内重现实际系统的特征。
