七年级数学下册阶段测评(三)习题课件(新版)华东师大版
七年级数学下册7.3三元一次方程组及其解法课件(新版)华东师大版

◆知识导航(dǎoháng) ◆典例导学 ◆反馈演练 (◎第一阶 ◎第二阶 ◎第三
阶)
第十三页,共24页。
◆知识导航(dǎoháng) ◆典例导学 ◆反馈演练 (◎第一阶 ◎第二阶
◎第三阶)
第十四页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练(yǎn liàn) (◎第一阶 ◎第二阶 ◎第三阶)
三阶)
第二十四页,共24页。
阶 ◎第三阶)
第十八页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练 (◎第一阶 ◎第二(dì èr)阶 ◎第三阶)
第十九页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练 (◎第一(dìyī)阶 ◎第二阶 ◎第
三阶)
第二十页,共24页。
◆知识导航 ◆典例导学 ◆反馈(fǎnkuì)演练 (◎第一阶 ◎第二阶 ◎
◆知识导航 ◆典例导学 ◆反馈演练 (◎第一阶 ◎第二(dì èr)阶 ◎第
三阶)
第十页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练 (◎第一(dìyī)阶 ◎第二阶 ◎第三阶)
第十一页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练 (◎第一阶 ◎第二(dì èr)阶
◎第三阶)
第十二页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练 (◎第一(dìyī)阶 ◎第二阶
◎第三阶)
第四页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练 (◎第一阶 ◎第二(dì èr)阶 ◎第三阶)
第五页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练(yǎn liàn) (◎第一阶 ◎第二阶
◎第三阶)
第六页,共24页。
第三阶)
第二十一页,共24页。
◆知识导航 ◆典例导学 ◆反馈演练(yǎn liàn) (◎第一阶 ◎第二阶 ◎第三阶)
华东师大版数学七年级下7.3-三元一次方程组及其解法-课件(20张PPT)

将③代入①②,得
4y y z 12, 4y 2y 5z 22.
5y z 12, 即 6y 5z 22.
课堂精讲
如何用加减消元法解这个方程组?
x y z 12, ①
x
2
y
5z
22,
②
x 4 y.
③
解:①5②,得 4x 3y 38. ④
③与④组成方程组
x 4 y, 4x 3y
7.3 三元一次方程组及其解法
课程引入
1、解二元一次方程组的方法有_代__入__法__和_加__减__法___ (1)若方程组的其中一个方程的某个未知数的系数为1或-1时,
用 代入 消元比较方便。
(2)若方程组中两个方程的同一个未知数系数相等或互为相反 数时,用 加减 消元比较简单。
2、解二元一次方程组的基本思路是什么?
基本思路: 消元: 二元
一元
学习目标
1.了解三元一次方程、三元一次方程组的概念; 2.会用消元法解三元一次方程组; 3.能运用三元一次方程组解一些简单的实际问题.
自学指导
1.课本P37-P41,《倍速》P51-53; 2.思考云图中的问题; 3.重点学习例题,能解简单的三元一次方程组.
x y z 10...........①
2x+3y+z=9, ②
5x-9y+7z=8. ③
解:②×3+③ ,得11x+10z=35 ④
①与④组成方程组 3x+4z=7, 11x+10z=35.
解这个方程组,得
x=5, z=-2.
把x=5,z=-2代入②,得y= x 5,
1, 3
因此,这个三元一次方程组的解为
y
1, 3
z -2.
课堂小结
七年级数学下学期期末综合测练题(三) 华东师大版
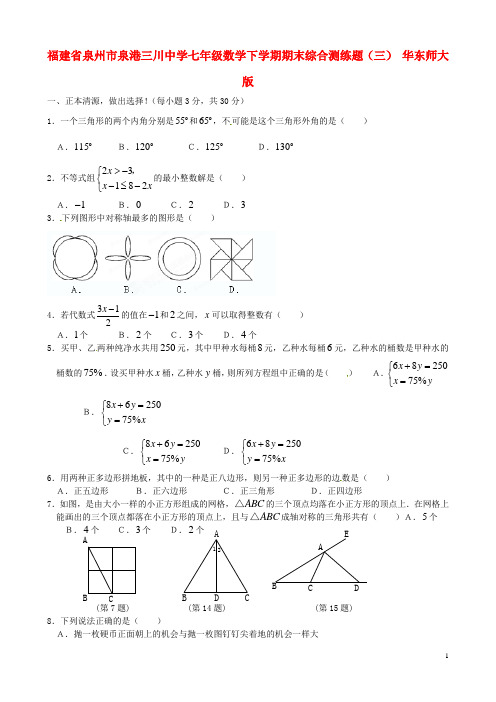
CB A 21D C B A EDC B A 福建省泉州市泉港三川中学七年级数学下学期期末综合测练题(三) 华东师大版一、正本清源,做出选择!(每小题3分,共30分)1.一个三角形的两个内角分别是55和65,不可能是这个三角形外角的是( ) A.115B.120C.125D.1302.不等式组23182x x x>-⎧⎨-≤-⎩,的最小整数解是( )A.1- B.0 C.2 D.3 3.下列图形中对称轴最多的图形是( )4.若代数式312x -的值在1-和2之间,x 可以取得整数有( ) A.1个 B.2个 C.3个 D.4个5.买甲、乙两种纯净水共用250元,其中甲种水每桶8元,乙种水每桶6元,乙种水的桶数是甲种水的桶数的75%.设买甲种水x 桶,乙种水y 桶,则所列方程组中正确的是( ) A.6825075%x y x y+=⎧⎨=⎩B.8625075%x y y x +=⎧⎨=⎩C.8625075%x y x y +=⎧⎨=⎩D.6825075%x y y x +=⎧⎨=⎩6.用两种正多边形拼地板,其中的一种是正八边形,则另一种正多边形的边数是( )A.正五边形 B.正六边形 C.正三角形 D.正四边形7.如图,是由大小一样的小正方形组成的网格,ABC △的三个顶点均落在小正方形的顶点上.在网格上能画出的三个顶点都落在小正方形的顶点上,且与ABC △成轴对称的三角形共有( )A.5个 B.4个 C.3个 D.2个(第7题) (第14题) (第15题)8.下列说法正确的是( )A.抛一枚硬币正面朝上的机会与抛一枚图钉钉尖着地的机会一样大B.如果某种彩票的中奖的机会是25%,买100张这种彩票,就会有25张中奖 C.如果某种彩票的中奖的机会是25%,买4张这种彩票,就会有1张中奖D.抛一枚质量均匀的硬币,每抛一次,朝上的是“正面”还是“反面”无法确定 9.将1,2,3这三个数字全用上写出一个三位数,恰写出一个偶数的机会是( )A.16B.14C.13 D.1210.班级组织有奖知识竞赛,小明用100元班费购买笔记本和钢笔共30件,已知笔记本每本2元,钢笔每支5元,那么小明最多能买钢笔( )A.20支 B.14支 C.13支 D.10支二、有的放矢,圆满填空!(每小题3分,共30分)11.如果正多边形的一个外角为72,那么它的边数是_______.12.关于x 的不等式322x a --≤的解集如图所示,则a 的值是_______.13.某商场计划每月销售900台电脑,5月1日至7日黄金周期限间,商场决定开展促销活动,5月的销售计划又增加了30%.已知黄金周这7天平均每天销售54台,则这个商场本月后24平均每天至少销售_______台才能完成本月计划.14.如图,在ABC △中,AB AC =,AD BC ⊥,D 为垂足.由以上两个条件可得_______.(写出一个结论即可). 15.如图,ABC △中,AC BC =,BAC ∠的外角平分线交BC 的延长线于点D ,若12A D C C A D =∠∠,则ABC =∠_______.16.不等式组1201202x x ->⎧⎪⎨+>⎪⎩,的解集是_______.17.在活动课上,小红已有两根长为4cm ,8cm 的小木棒,现打算拼一个等腰三角形,则小红应取的第三根小木棒长是_______cm . 18.如果221(21)0x y x y --+++=,那么x =_______,y =_______.19.(用x 表示).从这10名女生中任意抽出一名,其身高不低于的事件的机会,可以用图中的点_______表示.(在A B C D E ,,,,五个字母中选择一个符合题意的)20.如图,将标号为AB C D ,,,的正方形沿图形的虚线剪开后得到标号为P Q M N ,,,四组图形,试按照“哪个正方形剪开后得到哪组图形”的对应关系.填空:A与_______对应;B与_______对应;C与_______对应;D与_______对应.三、细心解答,运用自如!(每小题12分,共60分)21.在商品市场经常可以听到小贩的叫卖声和顾客的讨价还价声:“10元一个的玩具赛车打八折,快来买哪!”“能不能再便宜2元?”如果小贩真的让利(便宜)2元卖了,他还能获利20%,根据下列公式求一个玩具赛车进价是多少?(公式=进价⨯利润率=销售价⨯打折数-让利数-进价)22.某校有两种类型的学生宿舍共30间,大的宿舍每间可住8人,小的每间可住5人,该校198人住宿生恰好能住满这30间宿舍.大小宿舍各有多少间?23.如图7的方格纸中,画出了一个“小猪”的图案,已知每个小正方形的边长为1.(1)“小猪”所占的面积为多少?(2)在下面的方格纸中作出“小猪”关于线段DE所在直线对称的图案(只画图,不写作法).24.一对普通骰子,如果掷两骰子正面的点数和为2,11,12,那么甲赢;如果两骰子正面的点数和为7,那么乙赢;如果两骰子正面的点数和为其它数,那么甲乙都不赢.继续下去,直到有一个人赢为止.(1)你认为游戏是否公平,并解释原因;(2)如果你认为游戏公平,那么请你设计一个不公平的游戏;如果你认为游戏不公平,那么请你设计一个公平的游戏.25.某校计划在暑假期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.(1)求外出旅游的学生人数是多少?单租45座客车需多少辆?(2)已知45座客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都能有座,决定同时租用两种客车.使得租车总数可比单租45座客车少一辆,问45座客车和60座客车分别租多少辆才能使得租金最少?参考答案22.大宿舍16间,小宿舍14间.(提示:设学校有大宿舍x 间,小宿舍y 间,依题意,得3085198x y x y +=⎧⎨+=⎩,.解得1614x y =⎧⎨=⎩,.)23.(1)1322; (提示:1114411371332222⨯⨯+⨯⨯+⨯+⨯=.)(2)略.24.解:两骰子正面的点数和共会出现36种情况,出现两骰子正面点数和为2,11,12共有四种可能,则出现和为2,11,12的机会为19;出现和为7的有6种可能,即出现和为7的机会为16,出现的机会不相等,故游戏不公平.(2)游戏规则:一对骰子,如果掷两骰子正面点数和为2,11,12,那么甲赢;如果两骰子正面的点数和为5,那么乙赢.25.解:(1)设学生人数为x 人,单组45座客车需y 辆,由题意,得4560(1)30x y x y =⎧⎨=--⎩,.解得2706x y =⎧⎨=⎩,.所以学生总人数为270人,单租45座客车需6辆.(2)由题意及(1)知:两种客车同时租用共需5辆,设45座客车z 辆,则60座客车为(5)z -辆. 要使每个学生都有座,需有4560(5)270z z +-≥. 解之,得2z ≤. 当2z =时,租金最少为:225033001400⨯+⨯=(元).。
七年级下册数学期末练习试题(三)华东师大新版(有答案)

七年级下册数学期末练习试题(三)华东师大新版(有答案)一.选择题(共12小题,满分48分,每小题4分)1.下列图形中是轴对称图形的是()A.B.C.D.2.解一元一次方程(x﹣1)=2﹣x时,去分母正确的是()A.2(x﹣1)=2﹣5x B.2(x﹣1)=20﹣5xC.5(x﹣1)=2﹣2x D.5(x﹣1)=20﹣2x3.不等式3x≤6的解集在数轴上表示为()A.B.C.D.4.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为()A.16B.14C.12D.105.如果不等式(a﹣3)x>a﹣3的解集是x<1,那么a的取值范围是()A.a>0B.a<0C.a>3D.a<36.下列说法中,①三角形的内角中最多有一个钝角;②三角形的中线将三角形分成面积相等的两部分;③从n边形的一个顶点可以引(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,因此,n边形的内角和是(n﹣2)•180°;④六边形的对角线有7条,正确的个数有()A.4个B.3个C.2个D.1个7.已知关于x,y的方程组和的解相同,则(a+b)2021的值为()A.0B.﹣1C.1D.20218.已知方程mx+2y=﹣2,当x=3时y=5,那么m为()A .B .﹣C .﹣4D .9.用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第n 个图案中,所包含的黑色正三角形和白色正六边形的个数总和是( )A .n 2+4n +2B .6n +1C .n 2+3n +3D .2n +410.如图所示,BD 是△ABC 的角平分线,DE ∥BC 交AB 于点E ,∠A =45°,∠BDC =60°,则∠C 的度数是( )A .100°B .105°C .110°D .115°11.某车间56名工人,每人每天能生产螺栓16个或螺母24个,每个螺栓配两个螺母;设安排x 名工人生产螺栓,才能使每天生产出来的螺栓和螺母刚好配套,下列方程中正确的是( )A .2×16x =24(56﹣x )B .2×24x =16(56﹣x )C .16x =24(56﹣x )D .24x =16(56﹣x )12.如图,△ABC 中,∠A 的平分线交BC 于D ,过点D 作DE ⊥AC ,DF ⊥AB ,垂足为点E 、F ,下面四个结论中:①∠AEF =∠AFE ;②AD 垂直平分EF ;③S △BFD :S △CED =BF :CE ;④EF ∥BC ,正确的是( )A .①②③B .①③④C .①②④D .②③④二.填空题(共6小题,满分24分,每小题4分)13.已知代数式8x﹣7与6﹣2x的值互为相反数,那么x的值等于.14.如图,E是正方形ABCD中CD边上的中点,AB=4,把△ADE绕点A顺时针旋转90°得到△ABF,若连接EF,则EF=.15.《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出十二,盈八;人出十,不足六,问人数、物价各几何?译文:今有人合伙购物,每人出12钱,会多8钱;每人出10钱,又会差6钱,问人数、物价各是多少?设合伙人数为x人,物价为y钱,根据题意可列出方程组.16.不等式组的解是.17.足球比赛的计分规则为:胜一场积3分,平一场积1分,负1场积0分.初三(1)班在校足球联赛中踢了17场,其中负4场,共积31分,那么这支足球队胜了场.18.如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC 绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+;…按此规律继续旋转,直到点P2020为止,则AP2020等于.三.解答题(共7小题,满分78分)19.解方程(组)(1)﹣=1(2).20.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;(2)请画出△ABC关于原点对称的△A2B2C2;(3)P为x轴上一动点,当AP+CP有最小值时,求这个最小值.21.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).(1)∠ABO的度数为°,△AOB.(填“是”或“不是”)“灵动三角形”;(2)若∠BAC=70°,则△AOC(填“是”或“不是”)“灵动三角形”;(3)当△ABC为“灵动三角形”时,求∠OAC的度数.22.疫情期间为了满足口罩需求,某学校决定购进A,B两种型号的口罩.若购进A型口罩10盒,B型口罩5盒,共需1000元;若购进A型口罩4盒,B型口罩3盒,共需550元,(1)求A,B两种型号的口罩每盒各需多少元?(2)若该学校决定购进这两种型号的口罩共计200盒,考虑到实际需求,要求购进A型号口罩的盒数不超过B型口罩盒数的6倍,请为该学校设计出最省钱的方案,并说明理由.23.若关于x,y的二元一次方程组与方程组有相同的解.(1)求这个相同的解;(2)求m﹣n的值.24.阅读理解若在一个两位正整数N的个位数字与十位数字之间添上数字6,组成一个新的三位数,我们称这个三位数为N的“至善数”,如34的“至善数”为364;若将一个两位正整数M加6后得到一个新数,我们称这个新数为M的“明德数”,如34的“明德数”为40.(1)30的“至善数”是,“明德数”是.(2)求证:对任意一个两位正整数A,其“至善数”与“明德数”之差能被9整除;(3)若一个两位正整数B的“明德数”的各位数字之和是B的“至善数”各位数字之和的一半,求B的最大值.25.将锐角△ABC放置在一块正方形卡纸DEFG上,使点B,C在正方形的DG和DE边上.(1)如图①,若∠A=35°,则∠ABC+∠ACB=度.∠DBC+∠DCB=度,∠ABD+∠ACD=度.(2)如图②,改变正方形卡纸DEFG的位置,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论(3)如图③,正方形卡纸的顶点D在△ABC外,且在AB边的左侧,请探究∠ABD,∠ACD,∠A三者之间存在怎样的数量关系,直接写出探究结果,不必验证.参考答案与试题解析一.选择题(共12小题,满分48分,每小题4分)1.解:A、不是轴对称图形,故本选项不符合题意;B、是轴对称图形,故本选项符合题意;C、不是轴对称图形,故本选项不符合题意;D、不是轴对称图形,故本选项不符合题意.故选:B.2.解:解一元一次方程(x﹣1)=2﹣x时,去分母正确的是5(x﹣1)=20﹣2x.故选:D.3.解:不等式解得:x≤2,表示在数轴上,如图所示,.故选:B.4.解:第三边的取值范围是大于4且小于8,又第三边是偶数,故第三边是6.则该三角形的周长是14.故选:B.5.解:∵(a﹣3)x>a﹣3的解集是x<1,∴a﹣3<0,解得a<3,故选:D.6.解:①假设一个三角形有两个钝角,那么这两个钝角的和大于180°,与三角形的内角和为180°相矛盾.故三角形的内角中最多有一个钝角,正确;②三角形的中线把三角形分成的两个三角形的底边相等,高相同,所以面积相等,正确;③因为连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.n边形的一个顶点不能与它本身及左右两个邻点相连成对角线,故从n边形的一个顶点可以引(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,每一个三角形的内角和是180°,因此,n边形的内角和是(n﹣2)•180°,正确;④n边形共有条对角线,所以六边形的对角线有6×3÷2=9条,错误.故选:B.7.解:联立得:,①×5+②×3得:29x=58,解得:x=2,把x=2代入①得:y=1,代入得:,解得:,则原式=(﹣2+2)2021=0.故选:A.8.解:把x=3,y=5代入方程得:3m+10=﹣2,移项合并得:3m=﹣12,解得:m=﹣4,故选:C.9.解:由图形可知图形①的黑色正三角形和白色正六边形的个数总和=4×1+3=7个,图形②的黑色正三角形和白色正六边形的个数总和=4×2+5=13个…依此类推,图形n的黑色正三角形和白色正六边形的个数总和=4n+2n+1=6n+1个.故选:B.10.解:∵∠A=45°,∠BDC=60°,∴∠ABD=∠BDC﹣∠A=15°.∵BD是△ABC的角平分线,∴∠ABC=2∠ABD=30°,∴∠C=180°﹣∠ABC﹣∠A=180°﹣30°﹣45°=105°.故选:B.11.解:设有x 名工人生产螺栓,根据题意可得,2×16x =24(56﹣x ), 故选:A .12.解:∵∠A 的平分线交BC 于D ,DE ⊥AC ,DF ⊥AB , ∴DE =DF ,∴∠DEF =∠DFE ,又∠AED =∠AFD =90°, ∴∠AEF =∠AFE ,①正确; ∵∠AEF =∠AFE , ∴AE =AF ,又DE =DF , ∴AD 垂直平分EF ,②正确;S △BFD :S △CED =×BF ×DF :×CE ×DE =BF :CE ,③正确; EF 与BC 不一定平行,④错误, 故选:A .二.填空题(共6小题,满分24分,每小题4分) 13.解:根据题意得:(8x ﹣7)+(6﹣2x )=0, 即8x ﹣7+6﹣2x =0, 移项合并得:6x =1, 解得:x =. 故答案为: 14.解:连接EF ,∵把△ADE 绕点A 顺时针旋转90°得到△ABF , ∴AE =AF ,∠EAF =90°, ∵四边形ABCD 是正方形, ∴AB =CD =AD =4, ∵E 是CD 的中点,∴DE=CD=2,∴AE===2,∴EF===2,故答案为:2.15.解:依题意,得:.故答案为:.16.解:解不等式2x≤6,得:x≤3,解不等式3x﹣4>2,得:x>2,则不等式组的解集为2<x≤3.故答案为:2<x≤3.17.解:设这支足球队胜了x场,平了y场,依题意,得:,解得:.故答案为:9.18.解:∵∠ACB=90°,∠B=30°,AC=1,∴AB=2,BC=,∴将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=2+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+;…∵2020÷3=673 (1)∴AP2020=673(3+)+2=2021+673,故答案为:2021+673三.解答题(共7小题,满分78分)19.解:(1)﹣=1,去分母得:2(2x+1)﹣(5x﹣1)=6,去括号得:4x+2﹣5x+1=6,移项得:4x﹣5x=6﹣2﹣1,合并同类项得:﹣x=3,系数化为1得:x=﹣3;(2),①+②×4得:9x=63,∴x=7,把x=7代入①得:7﹣4y=﹣1,解得:y=2,∴原方程组的解为.20.解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2B2C2,即为所求;(3)如图所示:P点即为所求,当AP+CP有最小值时,这个最小值为:=.21.解:(1)∵AB⊥OM,∴∠BAO=90°,∵∠AOB=60°,∴∠ABO=90°﹣60°=30°,∵90°=3×30°,∴△AOB是“灵动三角形”.故答案为:30,是.(2)∵∠OAB=90°,∠BAC=70°,∴∠OAC=20°,∵∠AOC=60°=3×20°,∴△AOC是“灵动三角形”.故答案为:是.(3:①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.综上所述,满足条件的值为30°或52.5°或80°.22.解:(1)设购进A型口罩每盒需x元,B型口罩每盒需y元,依题意,得:,解得:.答:购进A型口罩每盒需25元,B型口罩每盒需150元.(2)设购进m盒A型口罩,则购进(200﹣m)盒B型口罩,依题意,得:m≤6(200﹣m),解得:m≤171.设该学校购进这批口罩共花费w元,则w=25m+150(200﹣m)=﹣125m+30000.∵﹣125<0,∴w随m的增大而减小,又∵m≤171,且m为整数,∴当m=171时,w取得最小值,此时200﹣m=29.∴最省钱的购买方案为:购进171盒A型口罩,29盒B型口罩.23.解:(1)∵关于x,y的二元一次方程组与方程组有相同的解,∴解得∴这个相同的解为(2)∵关于x,y的二元一次方程组与方程组有相同的解,∴解得∴m﹣n=3﹣2=1.答:m﹣n的值为1.24.解:(1)30的“至善数”是360;“明德数”是30+6=36故答案为:360;36.(2)证明:设A的十位数字为a,个位数字为b则其“至善数与“明德数”分别为:100a+60+b;10a+b+6它们的差为:100a+60+b﹣(10a+b+6)=90a+54=9(10a+6)∴其“至善数”与“明德数”之差能被9整除.(3)设B的十位数字为a,个位数字为b则B的至善数的各位数字之和是a+6+bB的明德数各位数字之和是a+b+6(当0≤b<4时)或a+1+(6+b﹣10)(当4≤b≤9时)由题意得:0≤b<4时,a+b+6=(a+6+b)∴a+b=﹣6,不符合题意;或者:当4≤b≤9时,a+1+(6+b﹣10)=(a+6+b)∴a+b=12∴当b=4,a=8时,B最大,最大值为84.25.解:(1)∵∠A=35°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣35°=145°,∵四边形DEFG为正方形,∴∠D=90°,∴∠DBC+∠DCB=90°,∴∠ABD+∠ACD=∠ABC+∠ACB﹣(∠DBC+∠DCB)=145°﹣90°=55°.故答案为:145,90,55;(2)∠ABD+∠ACD=90°﹣∠A.证明如下:∵∠ABC+∠ACB=180°﹣∠A,∴∠ABD+∠DBC+∠ACD+∠BCD=180°﹣∠A,∵四边形DEFG为正方形,∴∠BDC=90°,∴∠DBC+∠BCD=90°,∴∠ABD+∠ACD+90°=180°﹣∠A,∴∠ABD+∠ACD=90°﹣∠A.(3)∠ABD=∠A+∠ACD﹣90°.若AB,CD交于点M,∵∠DMB=∠AMC,∠D+∠DBM+∠DMB=180°,∠A+∠ACD+∠AMC=180°,∴∠D+∠ABD=∠A+∠ACD,∵∠D=90°,∴∠ABD=∠A+∠ACD﹣90°.。
