特殊值法解数学题
高考数学复习----《特殊值法、估算法》典型例题讲解

高考数学复习----《特殊值法、估算法》典型例题讲解【典型例题】例1、(2022·全国·高三专题练习)已知3142342,3,log 4,log 5a b c d ====,则a b c d ,,,的大小关系为( )A .b a d c >>>B .b c a d >>>C .b a c d >>>D .a b d c >>>【答案】C【解析】 依题意,314222)a ==,函数y =[0,)+∞上单调递增,而934<<,于是得112232)32<<,即32b a >>, 函数4log y x =在(0,)+∞单调递增,并且有44log 30,log 50>>, 则44442log 16log 15log 3log 5=>=+=2+于是得44log 3log 51⨯<,即4341log 5log 4log 3<=,则c d >, 又函数3log y x =在(0,)+∞单调递增,且4<333log 4log 2<=, 所以32b acd >>>>. 故选:C 例2、(2022·全国·高三专题练习)已知a =142b =,2e log c =,则a ,b ,c 的大小关系为( )A .a b c >>B .a c b >>C .b a c >>D .b c a >>【答案】B【解析】由49a =,42b =,可知1a b >>,又由2e 8<,从而32e 2<,可得23log e 2c a =<<, 因为4461296()205625b −=−<,所以615b <<; 因为565e 2 2.7640−>−>,从而56e 2>,即65e 2>, 由对数函数单调性可知,65226log e >log 25c ==, 综上所述,a c b >>.故选:B.例3、(2023·全国·高三专题练习)若e b a >>b m a =,a n b =,log a p b =,则m ,n ,p 这三个数的大小关系为( ) A .m n p >>B .n p m >>C .n m p >>D .m p n >>【答案】C 【解析】因为e b a >>> 所以取52,2a b ==,则()5225,6b m a ===, 2525 6.2524a n b ⎛⎫=== ⎪⎝⎭=, ()25log log 1,22a pb ==∈,所以n m p >>. 故选:C.。
第六讲 特殊值法的运用技巧
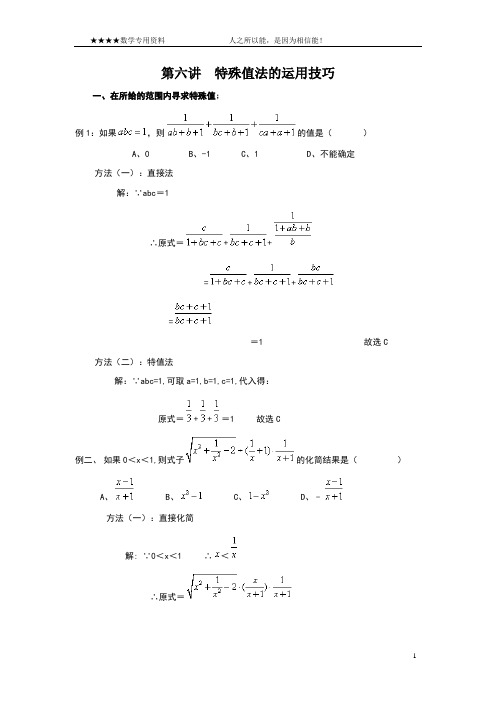
第六讲特殊值法的运用技巧一、在所给的范围内寻求特殊值;例1:如果,则的值是()A、0B、-1C、1D、不能确定方法(一):直接法解:∵abc=1∴原式=++=++==1故选C 方法(二):特值法解:∵abc=1,可取a=1,b=1,c=1,代入得:原式=++=1故选C例二、如果0<x<1,则式子的化简结果是()A、 B、 C、 D、﹣方法(一):直接化简解: ∵0<x<1∴<∴原式======﹣方法(二):特值法解:∵0<x<1,可取=∴原式=××=,∵﹣=﹣=×=∴选D。
例2:若a<﹣1,则3-的最后结果是()A、3-aB、3+aC、-3-aD、a-3方法(一):直接法解:∵解:∵a<﹣1,<﹣1,∴a-3<0∴原式=3-=3-(-)=3+a方法(二):特值法解:∵a<﹣1,可以取a=-4,代入计算:原式=-1,又3+a=-1,∴选B。
二、在隐含的范围内寻求特殊值;例:如果x、y、z是不全相等的实数,且,,则以下结论正确的是()A、a、b、c都不小于0B、a、b、c都不大于0C、a、b、c至少一个小于0D、a、b、c至少一个大于0分析:此题若直接解比较繁杂,可采用特值法,较为简便,由x、y、z是不全相等的实数,可分为两种情况:①x、y、z都不相等;②x、y、z中有两个相等;当x、y、z都不相等时,可取x=1,y=0,z=-1,则a=1,b=1,c=1,可排除B和C;当x、y、z中有两个相等时,可以取x=0,y=z=1,则a=-1,b=1,c=1,可排除A 综合以上情况,所以选D。
三、在选择的结论范围内寻求特殊值例1、如果方程有两个不相等的实数根,则q的取值范围是()A、q≤0B、q<C、0≤q<D、q≥方法(一):直接法解:∵∴y≥0,则y≥q∴q≥0或q<0∴∵△=1-4q>0即q<当q<0时,方程无根,∴0≤q<方法(二):特值法在A、B范围内取q=-6,代入方程化简为,此时方程有一负根,可排除A、B。
【小学数学】北师大版六年级课外拓展第讲特殊值的应用(含答案)

第七讲特殊值的运用“特殊值”的应用是小学数学竞赛中常用的解题方法之一,它主要用来解决表面看来条件不够或没有具体数量的题型。
一般来说,三种相关的量中,要想解决一个问题,必须知道其中的两个量才行,但有的题目,只告诉一种量就要我们去解决相关的问题,这显然是办不到的。
这种情况下,我们可以将所需知道的量设定为一个“特殊值”,这样就多了一个条件,可根据数量关系解决我们想要的问题。
但这种方法不是万能的,使用这种方法解题后,一定要换一个“特殊值”再演算一遍,如果答案没有变化,就说明此方法是可行的,如果答案变了,则说明方法运用不成功。
例1:某剧团举办的“关爱贫困学生”文艺义演门票240元一张,降价后观众增加了13,收入增加了16,则每张门票降价多少元?巩固练习11、演唱会门票150元一张,若降价后观众增加了一半,收入增加了25,每张门票降价多少元?2、某文具店的一种钢笔定价24元,结果无人购买,降价后销量比计划增加了二成,收入增加了一成,每支钢笔售价为多少元?3、一种电瓶车的价格为12021/台,改用新技术后,由于成本降低而使性能更优越,于是降价出售,结果销量增加了2倍,而收入增加了一倍。
每台电瓶车的成本下降了多少元?例2:某工厂生产的灯泡中有15的次品,实际检查时,只发现其中45的被剔除,另有120的正品误以为是次品,也被剔除,其余的灯泡全部上市出售,那么该厂出售的灯泡中次品所占的百分率是多少?巩固练习21、某班一次考试,平均为81分,10%的人不及格,不及格的人的平均分为45分,及格的人平均分是多少分?2、某班同学中男生占47,男生中有15的人喜欢绘画,全班喜欢绘画的人中有23是男生,那么全班女生中有几分之几的人喜欢绘画?3、已知甲校学生人数是乙校学生人数的40%,甲校女生人数是甲校学生人数的30%,乙校男生数是乙校学生数的42%,两校女生总数占两校学生总数的百分比等于多少?例3:某校参加“奥林匹克数学”决赛的同学的平均分是75分,其中参赛中男同学比女同学多80%,而女同学比男同学的平均分数高2021那么女同学的平均分是多少分?巩固练习31、某校全体学生的平均身高是125厘米,其中男生比女生多30%,而女生比男生的平均身高高2021那么女生的平均身高是多少厘米?2、在衔接班招生考试中,只有的考生被录取,没有被录取的同学的平均分比录取分数线低2分,录取的同学的平均分比录取分数线高18分,所有考生的平均分是56分,录取分数线是多少分?3、某县组织数学竞赛,获奖者为前80名,1~10名为一等奖,11~35名为二等奖,36~80名为三等奖;一等奖的平均分比二等奖的平均分多10分,二等奖的平均分比三等奖的平均分多2021这80名的平均分比二等奖的平均分低多少分?综合训练七1、某商品按原价销售,每件获利润12021现降价销售,结果销量增加了一倍,获得的总利润增加了倍,那么每件降价多少元?2、甲乙两种商品,如果甲种商品价格提高25%,乙种商品价格降低2021则两种商品的价格恰好相等,原来甲种商品的价格是乙种商品的价格的百分之几?3、某次考试,衔接班的平均分是88分,其中90%的人得分不低于90分,他们的平均分是91分,那么低于90分的人的平均分是多少分?4、某班买来单价为元的练习本若干,如果将这些练习本只分给女生,平均每人可分得15本,如果将这些练习本只分给男生,平均每人可分得10本。
数学考试技巧附案例习题解题技巧-特殊值法

数学考试技巧附案例习题解题技巧-特殊值法在数学研究中,“从特殊到一般”是重要的思想方法。
数学竞赛题,由于其难度,多少有些研究的性质。
于是对许多竞赛题目,“特殊值法”显得至关重要。
3.1 什么是“特殊值法”特殊值法,又称“和谐法”,就是对题目中所给的表达式,代入特殊值,寻找其规律。
特殊值,就是易于计算、求解的值。
对代数问题,往往是中值(平均值)、边值(最大最小)。
当自变量取特殊值时,函数值往往位于极值点(区间上的最大、最小值)。
对其它问题,就是规模较小,简单的,或具有特殊性质的代入值。
3.2 特殊值法的理论依据若函数f(x)为凸函数,由琴生不等式(导数法证明),有f(a1x1+a2x2+...+a n x n)≤a1 f(x1)+a2 f(x2)+...+a n f(x n). 即:对n个不同变量,他们和的函数与函数的和具有不等关系。
同样,对其他运算,也有类似的不等式存在。
特殊值法的证明,通用方法是导数法。
以3个变量的函数f(x,y,z)为例,设x+y+z=k为常数,x≥y≥z.其中x≥k/3, z≤k/3.先固定x,调整y,z, 即函数f(y,z).又y+z=k-x为常数,则有z=k-x-y,三元函数变为一元函数f(z). 求f(z)含z单项的导数f’(z),可得当z=(k-x)/2时,f’(z)=0; z<(k-x)/2时,f’(z)<0; z>(k-x)/2时,f’(z)>0. 即应用单调性可得,对0<z<k/3, y=z 时f(z)最大。
此时y=z=(k-x)/2. 这次调整使y,z相等。
同理,固定z, 可得x=y. 由此,x=y=z. 这是一种逐步调整的策略。
对于多元函数的情形,可类似的证明。
(详细推导步骤见单墫《利用导数证明不等式》,《中等数学》2006年第2期)由此,我们知道特殊值法的适用范围:当不等式的“一项”为单峰函数(中间值最大或最小)时,可使用特殊值法,此时最值取在均值处,而边值处为另一个最值。
3.2.2代数式——特殊方法求值、规律问题(课件)七年级数学上册(苏科版2024)

84
【分析】第①个图形中,棋子数量为4=2×2+02,
第②个图形中,棋子数量为7=2×3+12,
第③个图形中,棋子数量为12=2×4+22,
…,
第n个图形中,棋子数量为:2(n+1)+(n-1)2,
∴第⑨个图形中,棋子数量为:2×10+82=84。
03
∴3m-4n= ,
∴9m-12n=3(3m-4n)=3× = ,
∴9m-12n+4= +4= 。
∴9m-12n+4= +4= 。
特殊方法求值
——赋值法
01
课堂引入
已知(x+1)2=ax2+bx+c,求代数式a+b+c的值。
【分析】(x+1)2=ax2+bx+c是一个关于x的恒等式,即无论x取何值,
∴20=2(n+1),解得:n=9,∴a=9,b=10,x=10×20+9=209。
03
典例精析
图形类
例4、找出以下图形变化的规律,则第2024个图形中有________个
3036
黑色正方形。
【分析】由图可知:第1个图形中黑色正方形的数量是2,第2个图形
中是3,第3个图形中是5,第4个图形中是6,第5个图形中是8,…,
(3)6x+6y=6(x+y)=6×2=12;
(4)-10x-10y。
(4)-10x-10y=-10(x+y)=(-10)×2=-20。
高三数学选择题解题策略特殊值法

可
6
排除A,故选D
跟踪训练
(2014全国卷)
设
0,
2
,
0,
2
,且
tan
1 sin cos
,则B
(A)3
2
(B )2
2
(C )2
2
(D )3
2
3.特殊位置法
当暗示答案是一个“定值”时,就可以取一个特
殊位置
例30 G为ABC的重心,过点G的直线与AB和AC分别
相交于P、Q两点,若AP m AB,AQ n AC,则 1 1 ( )
x2,x≤0, 若 a=0,则 f(x)=x+1x,x>0,
易知f(0)是f(x)的最小值, 故排除C.D正确.
跟踪训练
1(.2014全国卷)已知函数f x ax 3 3x 2 1,若f x 存在
No 唯一零点x0,且x0 0,则a的取值范围是 B (A)2, (B ) ,2 (C )1,Im(aD )ge,1
ID
4
5
3
5
y
(A) 5
(B) 4
(C) 4
(D) 3
P
M
I
解析:依选项可知,的值与点P的
位置无关,设点P为短轴端点,此时,
F1 o
F2
x
PIM
∽ PF1O,所以
PI ID
PF1 F1 0
a c
5 .故选D. 3
跟踪训练(2015·课标全国Ⅰ)已知 M(x0,y0)是双曲线 C:x22-
y2=1 上的一点,F1,F2 是 C 的两个焦点,若M→F1·M→F2<0, 则 y0 的取值范围是( A )
,
5 4
(B
特殊值法解数学题

用特殊值法解题湖北省公安县斑竹当中学雷学池特殊值法是用满足条件的特殊值(式)代入题目去验证、计算,从而得到正确结论的一种方法.特殊值法在解题中有下列应用.1.解选择题:例1 若a>b>c>0,m>n>0.(m、n为数),则下列各式中成立的是[ ]A.a m b n>b n c m>c n a m B.a m b n>c n a m>b n c mC.c n a m>a m b n>b n c m D.b n c m>c n a m>a m b n解∵a>b>c>0.m>n>0(m、n为整数)取特殊值,a=3,b=2,c=1,m=2,n=1得a mb n=32×21=18b nc m=21×12=2c n a m=11×32=9∴a m b n>c n a m>b n c m故选B.2.确定多项式的系数例2已知当x是任何实数时,x2-2x+5=a(x+1)2+b(x+1)+c都成立,求a、b、c的值.解用特殊值法.当x=-1时,原式为8=c①当x=0时,原式为5=a+b+c②当x=1时,原式为4=4a+2b+c③由①、②、③可知a=1,b=-4,c=8.3.判断命题的真假例3 判断命题“式子a2+(a+1)2+a2(a+1)2=(a2+a-1)2是恒等式”的真假.解取特殊值,当a=1时,原式左边为9,右边为1,因为9≠1,故原命题是假命题.4.解证定值问题例4 若a、b为定值,且无论k取何值时,关于x的一次方程由①、②可得a=3,b=-2.练习用特殊值法解下列各题:2.命题“式子x3+9=(x+2)3-6(x+2)2+12(x+2)是恒等式”是真命题,对吗?值,求a、b应满足的关系式.并求出这个定值.4.已知a+b+c≠0,求证:不论a、b、c取何实数时,三答案2.取x=0,左边为9,右边为8,9≠8.故不对.式得质证明.巧取特殊值解选择题山东省茌平县傅平镇中学初三·一班鲁傅我在解某些选择题时,采用了取特殊值法,使问题简捷,迅速地获得解决,如下面几例.例1 已知a、b、c都是实数,且a>b>c,那么下列式子中正确的是[ ](98年全国初中数学联赛)解:∵a>b>c,∴可取a=1,b=0,c=-1代入各选择支,只有a+b=1>b+c=-1成立.故选(B).例2 设a、b、c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x、y、z[ ]A.都不小于0B.都不大于0C.至少有一个小于0D.至少有一个大于0(94年全国初中数学联赛题)解:若令a=0,b=1,c=-1,则x=y=z=1,故可排除(B)、(C);再令a=0,b=c=1,则x=-1,y=z=1,又可排除(A).故选(D).(94年全国初中数学联赛题)则[ ]A.M<Q<P<N B.M<P<Q<NC.Q<N<P<M D.N<Q<P<M(第六届全国部分省市初中数学通讯赛试题)解:∵x<y<0,∴可取x=-2,y=-1并代入上式,则例5 如果a、b均为有理数,且b<0,则a、a-b,a+b的大小关系是[ ]A.a<a+b<a-b B.a<a-b<a+bC.a+b<a<a-b D.a-b<a+b<a(95年“希望杯”全国数学邀请赛初一试题)解:∵a、b均为有理数,且b<0,∴可取a=1,b=-1并代入上式,得a-b=1-(-1)=2,a+b=1+(-1)=0.∵0<1<2,∴a+b<a<a-b.故选(C).例6二次函数y=ax2+bx+c的图象经过点(-2,1)和(2,3),且与y 轴的交点为P,若P点的纵坐标是小于1的正数,则a的取值范围是[ ](94年山东省初中数学竞赛题)(此文档部分内容来源于网络,如有侵权请告知删除,文档可自行编辑修改内容,供参考,感谢您的配合和支持)。
初一特殊值法例题

初一特殊值法例题题目描述:在初一数学课上,老师出了一个特殊值法例题给同学们解答。
题目如下:如果a +b = 5a -b = 1请你根据题目给出的条件,运用特殊值法,解答下面的问题。
正文:根据题目给出的条件a + b = 5和a - b = 1,我们可以通过特殊值法的思路来解答这个例题。
首先,我们需要找到两个等式中的未知数并进行消元。
将两个等式相加,得到:(a + b) + (a - b) = 5 + 12a = 6解得:a = 3接下来,将这个解作为特殊值代入其中一个等式,解出另一个未知数。
将a = 3代入a + b = 5,得到:3 + b = 5解得:b = 2因此,根据特殊值法的运算过程,我们得出a的值为3,b的值为2。
通过上述步骤,我们成功解答了给定的特殊值法例题。
特殊值法是一种通过设定特殊值来解题的方法,有助于简化问题以及求解未知数。
在解答这个例题的过程中,我们首先根据给定的两个等式相加消元的原理,得到了2a = 6的结果。
由此,我们可以推断出a的值为3。
接着,我们将这个特殊值代入另一个等式,解得b的值为2。
最终,我们成功得到了a和b的值。
特殊值法在初一数学中经常用于解答简单的线性方程组。
通过设定特殊值,我们可以快速求解未知数,从而得到正确的答案。
在实际问题中,特殊值法还可以帮助我们理清思路,简化计算过程,提高解题效率。
总结起来,特殊值法是一种简便有效的解题方法,适用于数学中的各种问题。
通过找到特殊值并代入等式中,我们可以求解未知数,得到正确的答案。
在解答初一特殊值法例题时,我们根据给定条件通过相加消元和代入特殊值的步骤,成功求解出了a和b的值。
通过这个例题的讲解,希望同学们能够掌握特殊值法的使用方法,提高解题的能力。
通过本次特殊值法例题的解答,我们不仅学会了如何运用特殊值法解决问题,也加深了对线性方程组的理解。
希望在今后的数学学习中,同学们能够灵活运用各种解题方法,不断提升自己的数学水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
臧老师辅导课堂之
特殊值法专项训练
特殊值法是用满足条件的特殊值(式)代入题目去验证、计算,从而得到正确结论的一种方法.特殊值法在解题中有下列应用.
1.解选择题:
若a>b>c>0,m>n>0.(m、n为数),则下列各式中成立的是[ ]
A.a m b n>b n c m>c n a m B.a m b n>c n a m>b n c m
C.c n a m>a m b n>b n c m D.b n c m>c n a m>a m b n
2.确定多项式的系数
已知当x是任何实数时,x2-2x+5=a(x+1)2+b(x+1)+c都成立,求a、b、c的值.
3.判断命题的真假
判断命题“式子a2+(a+1)2+a2(a+1)2=(a2+a-1)2是恒等式”的真假.
4.解证定值问题
若a、b为定值,且无论k取何值时,关于x的一次方程
专项练习
1 已知a、b、c都是实数,且a>b>c,那么下列式子中正确的是
[ ]
2.命题“式子x3+9=(x+2)3-6(x+2)2+12(x+2)是恒等式”是真命题,对吗?
值,求a、b应满足的关系式.并求出这个定值.
4.已知a+b+c≠0,求证:不论a、b、c取何实数时,三
5、设a、b、c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x、y、z[]
A.都不小于0B.都不大于0
C.至少有一个小于0D.至少有一个大于0
6、如果a、b均为有理数,且b<0,则a、a-b,a+b的大小关系是
[ ]
A.a<a+b<a-b B.a<a-b<a+b
C.a+b<a<a-b D.a-b<a+b<a
巧取特殊值解选择题
山东省茌平县傅平镇中学初三·一班鲁傅
我在解某些选择题时,采用了取特殊值法,使问题简捷,迅速地获得解决,如下面几例.
例1 已知a、b、c都是实数,且a>b>c,那么下列式子中正确的是
[ ]
(98年全国初中数学联赛)解:∵a>b>c,
∴可取a=1,b=0,c=-1代入各选择支,只有a+b=1>b+c=-1成立.故选(B).
例2 设a、b、c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x、y、z[ ]
A.都不小于0B.都不大于0
C.至少有一个小于0D.至少有一个大于0
(94年全国初中数学联赛题)解:若令a=0,b=1,c=-1,则x=y=z=1,故可排除(B)、(C);
再令a=0,b=c=1,则x=-1,y=z=1,又可排除(A).故选(D).
(94年全国初中数学联赛题)
则[ ]
A.M<Q<P<N B.M<P<Q<N
C.Q<N<P<M D.N<Q<P<M
(第六届全国部分省市初中数学通讯赛试题)解:∵x<y<0,
∴可取x=-2,y=-1并代入上式,则
例5 如果a、b均为有理数,且b<0,则a、a-b,a+b的大小关系是[ ]
A.a<a+b<a-b B.a<a-b<a+b
C.a+b<a<a-b D.a-b<a+b<a
(95年“希望杯”全国数学邀请赛初一试题)解:∵a、b均为有理数,且b<0,
∴可取a=1,b=-1并代入上式,得
a-b=1-(-1)=2,a+b=1+(-1)=0.∵0<1<2,∴a+b<a<a-b.故选(C).
例6二次函数y=ax2+bx+c的图象经过点(-2,1)和(2,3),且与y轴的交点为P,若P点的纵坐标是小于1的正数,则a的取值范围是[ ]
(94年山东省初中数学竞赛题)。
