(完整版)理论力学期末试题及答案
大学期末考试理论力学试卷(含答案详解)

一、选择题(每题2分,共20分)1.若平面力系对一点A 的主矩等于零,则此力系( )。
A .不可能合成为一个力 B .不可能合成为一个力偶C .一定平衡D .可能合成为一个力偶,也可能平衡2.刚体在四个力的作用下处于平衡,若其中三个力的作用线汇交于一点,则第四个力的作用线( )。
A .一定通过汇交点B .不一定通过汇交点C .一定不通过汇交点3.将平面力系向平面内任意两点简化,所得主矢相等,主矩也相等,且主矩不为零,则该力系简化的最后结果为( )。
A .一个力 B .一个力偶 C .平衡4.图1中,已知P =60kN ,F =20kN静摩擦系数f s =0.5,动摩擦系数f d =0.4,则物体所受 摩擦力的大小为( )。
A .25kN B .20kN C .17.3kN5.一点做曲线运动,开始时的速度s m v /100=,恒定切向加速度2/4s m a =τ,则2s 末该点的速度大小为( )。
A .2m/sB .18m/sC .12m/sD .无法确定6.圆轮绕某固定轴O 转动,某瞬时轮缘上一点的速度v 和加速度a 如图2所示,试问哪些情况下是不可能的?( ) A .(a )、(b )运动是不可能的 B .(a )、(c )运动是不可能的 C .(b )、(c )运动是不可能的 D .均不可能7.如图3所示平行四边形机构,在图示瞬时,杆O 1A以角速度ω转动,滑块M 相对AB 杆运动,若取M 动点,动系固联在AB 上,则该瞬时动点M 的牵连速度与杆AB 间的夹角为( )。
A .00 B .300 C .600图28.平面机构如图4所示,选小环M 为动点,动系固联 在曲柄OCD 杆上,则动点M 的科氏加速度的方向( )。
A .垂直于CD B .垂直于AB C .垂直于OM D .垂直于纸面9.如图5所示,两物块A 、B ,质量分别为A m 和B m 初始静止。
如A 沿斜面下滑的相对速度为r v ,设B 向左运动的速度为v ,根据动量守恒定律理有(A .v m v mB r A =θcos B.v m v m B r A=C.v m v v m B r A =+)cos (θD. v m v v m B r A =-)cos (θ10.已知刚体质心C 到相互平行的z '、z 轴之间的距离分别为a 、b ,刚体的质量为m ,对z 轴的转动惯量为z J ,则'z J 的计算公式为( )。
(完整版)武汉理工大学理论力学期末考试试题及答案
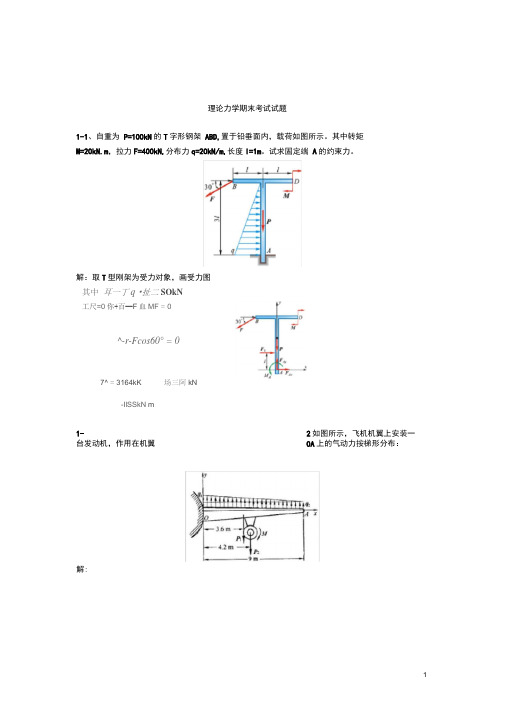
理论力学期末考试试题1-1、自重为P=100kN的T字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m,拉力F=400kN,分布力q=20kN/m,长度l=1m。
试求固定端A的约束力。
解:取T型刚架为受力对象,画受力图其中耳一丁q •扯二SOkN工尺=0你+百—F血MF = 0^-r-Fcos60°= 07^ = 3164kK 场三阿kN-IlSSkN m1-2如图所示,飞机机翼上安装一台发动机,作用在机翼OA上的气动力按梯形分布:解:q! =60kN/m,q2=40kN/m,机翼重p!=45kN,发动机重p2=20kN,发动机螺旋桨的反作用力偶矩M=18kN.m。
求机翼处于平衡状态时,机翼根部固定端O所受的力。
解研究机奧,把梯形號荷分解为一三甬幣戦荷与一矩骼栽荷*其合力甘別为弘=寺(如-q)・9 m 90 kN t ^ = 9*9! = 36Q kN 分别作用圧距再O点3 m与4.5m处,如国所示*曲莎=D,甩=01Y = 0, F® -P t- Pi + F靛 * Fjii = 02M0(F) = Q t M o- 3.6P| - 4.2鬥-M + 3F R1+ 4.$F R1= °解得F® = 0, F佈三-385 kN yM o- 1 626 kN * m1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m , F=50kN ,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
解先研究构架EBD如图(b)*由龙X = 0 F阪-F sin30' = 0SV = 0. F® * F* * F mfiSO = 0EJW R(F)= 0T F.^r U - A4 + 2F sin^ = 0 解得= 25 kN. = 87.3 kN, F* =-44 kN再軒究AB槃如图g).由XX = 0* - * 6 sin30" * F% - = 0XV - 0,為丄 6 ccdtf + F% 二QXM^(F)- 0, - 2 • -j * & * fl CQB3O- “ 0F“ - 40 kN. F A I= 113 3 kN・M A= 575,S kN - m此證也可先無先EBD "琅褂F*之后・再硏究整协・求冲址反力R样所减少平輛方程救*旧计禅轼幷耒测量桟少。
理论力学期末考试试题(卷)(试题(库)带答案解析)

理论力学 期末考试试题1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向作用力F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不D计,求各杆的力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
已知板与斜面的静滑动摩擦因数s f =0.1。
理论力学期末试卷1(带答案)

一.选择题(每题3分,共15分。
请将答案的序号填入划线内。
)1.空间同向平行力系1F 、2F 、3F 和4F ,如图所示。
该力系向O 点简化,主矢为'R F,主矩为OM ,则 (B )(A) 主矢主矩均不为零,且'R F 平行于O M(B) 主矢主矩均不为零,且'RF 垂直于O M(C) 主矢不为零,而主矩为零 (D) 主矢为零,而主矩不为零2.已知点M 的运动方程为ct b s +=,其中b 、c 均为常数,则( C )。
(A) 点M 的轨迹必为直线 (B) 点M 必作匀速直线运动 (C) 点M 必作匀速运动 (D) 点M 的加速度必定等于零3.如图所示若尖劈两侧与槽之间的摩擦角均为m ϕ,则欲使尖劈被打入后不致自动滑出,θ角应为( C )(A) θ≤m ϕ (B) θ≥m ϕ(C) θ≤2m ϕ (D) θ≥2m ϕ4.若质点的动能保持不变,则( D )。
(A) 该质点的动量必守恒 (B)(C) 该质点必作变速运动 (D) 5.直管AB 以匀角速度ω绕过点O 且垂直于管子轴线的定轴转动,小球M 在管内相对于管子以匀速度r v 运动,在如图所示瞬时,小球M 正好经过轴O 点,则在此瞬时小球M 的绝对速度a v 和绝对加速度a a 大小是( D )。
(A)a v =,a a = (B) a rv v =,0a a =(C) 0a v =,2a r a v ω= (D) a r v v =,2a ra v ω=二.填空题(每空2分,共30分。
请将答案填入划线内。
)1.平面汇交力系平衡的几何条件是 各力构成的力多边形自行封闭 ;平面汇交力系平衡的解析条件是0x F =∑、0y F =∑。
2.空间力偶的三个要素是 力偶矩的大小 、 力偶作用面的方位 和 力偶的转向 。
3.如图所示,均质长方体的高度30h cm =,宽度20b cm =,重量600G N =,放在粗糙水平面上,它与水平面的静摩擦系数0.4s f =。
理论力学__期末考试试题(题库_带答案)

理论⼒学__期末考试试题(题库_带答案)理论⼒学期末考试试题1-1、⾃重为P=100kN 的T 字形钢架ABD,置于铅垂⾯内,载荷如图所⽰。
其中转矩M=20kN.m ,拉⼒F=400kN,分布⼒q=20kN/m,长度l=1m 。
试求固定端A 的约束⼒。
解:取T 型刚架为受⼒对象,画受⼒图.1-2 如图所⽰,飞机机翼上安装⼀台发动机,作⽤在机翼OA 上的⽓动⼒按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作⽤⼒偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的⼒。
解:1-3图⽰构件由直⾓弯杆EBD以及直杆AB组成,不计各杆⾃重,已知q=10kN/m,F=50kN,M=6kN.m,各尺⼨如图。
求固定端A处及⽀座C的约束⼒。
1-4 已知:如图所⽰结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束⼒.解:1-5、平⾯桁架受⼒如图所⽰。
ABC 为等边三⾓形,且AD=DB 。
求杆CD 的内⼒。
1-6、如图所⽰的平⾯桁架,A 端采⽤铰链约束,B 端采⽤滚动⽀座约束,各杆件长度为1m 。
在节点E 和G 上分别作⽤载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的内⼒。
解:2-1 图⽰空间⼒系由6根桁架构成。
在节点A上作⽤⼒F,此⼒在矩形ABDC平⾯内,且与铅直线成45o⾓。
ΔEAK=ΔFBM。
等腰三⾓形EAK,FBM和NDB在顶点A,B和D处均为直⾓,⼜EC=CK=FD=DM。
若F=10kN,求各杆的内⼒。
2-2 杆系由铰链连接,位于正⽅形的边和对⾓线上,如图所⽰。
在节点D沿对⾓线LD⽅向F。
在节点C沿CH边铅直向下作⽤⼒F。
如铰链B,L和H是固定的,杆重不计,作⽤⼒D求各杆的内⼒。
2-3 重为1P =980 N ,半径为r =100mm 的滚⼦A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
理论力学考试试题(题库-带答案)

好好1学习理论力学期末考试试题1-1、自重为P=100kN的T字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m,拉力F=400kN,分布力q=20kN/m,长度l=1m。
试求固定端A的约束力。
解:取T型刚架为受力对象,画受力图.1-2如图所示,飞机机翼上安装一台发动机,作用在机翼OA上的气动力按梯形分布:q=60kN/m,1 q=40kN/m,机翼重2p=45kN,发动机1重p2=20kN,发动机螺旋桨的反作用力偶矩M=18kN.m。
求机翼处于平衡状态时,机翼根部固定端O所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4已知:如图所示结构,a,M=Fa, FFF,求:A,D处约束12力.解:1-5、平面桁架受力如图所示。
ABC为等边三角形,且AD=DB。
求杆CD的内力。
1-6、如图所示的平面桁架,A端采用铰链约束,B端采用滚动支座约束,各杆件长度为1m。
在节点E和G上分别作用载荷F=10kN,E F=7 GkN。
试计算杆1、2和3的内力。
解:2-1图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45o角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=D。
M若F=10kN,求各杆的内力。
2-2杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向作用力F。
在节点C沿CH边铅直向下作用力F。
D如铰链B,L和H是固定的,杆重不计,求各杆的内力。
2-3重为P=980N,半径为r=100mm的滚子A与重为1 P=490N 2的板B由通过定滑轮C的柔绳相连。
已知板与斜面的静滑动摩擦因数f=0.1。
滚子A与板B间的滚阻系数为δ=0.5mm,斜面倾角α=30o,s柔绳与斜面平行,柔绳与滑轮自重不计,铰链C为光滑的。
理论力学期末考试试题答案版
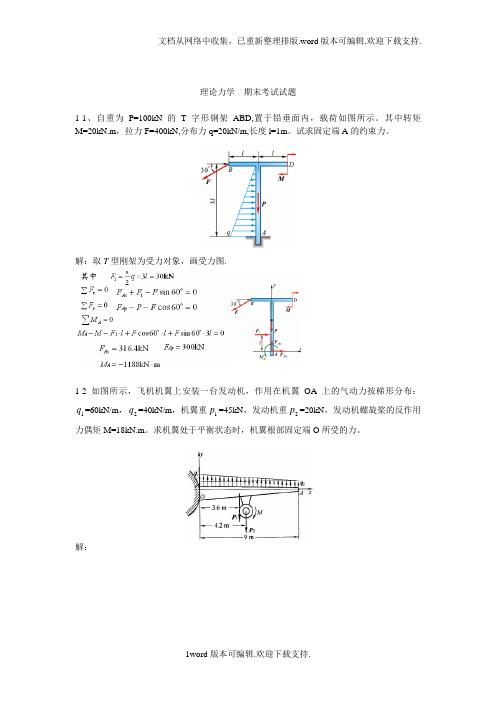
理论力学 期末考试试题1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的内力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不计,作用力D求各杆的内力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
《理论力学》期末考试试卷附答案
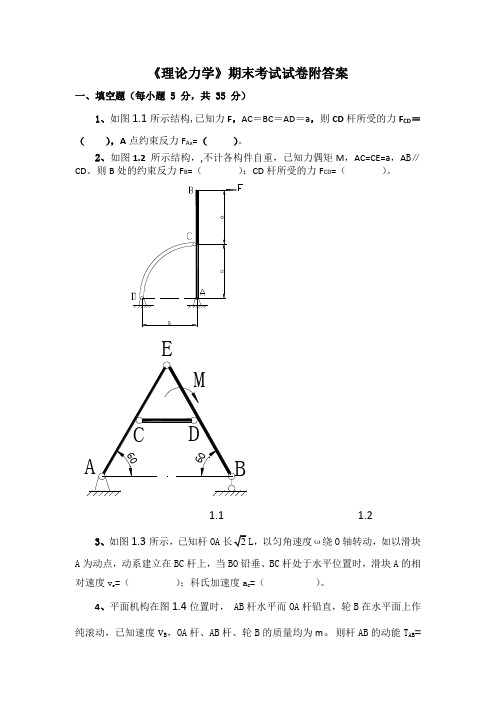
《理论力学》期末考试试卷附答案一、填空题(每小题 5 分,共 35 分)1、如图1.1所示结构,已知力F ,AC =BC =AD =a ,则CD 杆所受的力F CD =( ),A 点约束反力F Ax =( )。
2、如图1.2 所示结构,,不计各构件自重,已知力偶矩M ,AC=CE=a ,A B ∥CD 。
则B 处的约束反力F B =( );CD 杆所受的力F CD =( )。
1.1 1.23、如图1.3所示,已知杆OA L ,以匀角速度ω绕O 轴转动,如以滑块A 为动点,动系建立在BC 杆上,当BO 铅垂、BC 杆处于水平位置时,滑块A 的相对速度v r =( );科氏加速度a C =( )。
4、平面机构在图1.4位置时, AB 杆水平而OA 杆铅直,轮B 在水平面上作纯滚动,已知速度v B ,OA 杆、AB 杆、轮B 的质量均为m 。
则杆AB 的动能T AB =( ),轮B 的动能T B =( )。
1.3 1.45、如图1.5所示均质杆AB 长为L ,质量为m,其A 端用铰链支承,B 端用细绳悬挂。
当B 端细绳突然剪断瞬时, 杆AB 的角加速度 =( ),当杆AB 转到与水平线成300角时,AB 杆的角速度的平方ω2=( )。
6、图1.6所示机构中,当曲柄OA 铅直向上时,BC 杆也铅直向上,且点B 和点O 在同一水平线上;已知OA=0.3m,BC=1m ,AB=1.2m,当曲柄OA 具有角速度ω=10rad/s 时,则AB 杆的角速度ωAB =( )rad/s,BC 杆的角速度ωBC =( )rad/s 。
AB1.57、图1.7所示结构由平板1、平板2及CD 杆、EF 杆在C 、D 、E 、F 处铰接而成,在力偶M 的作用下,在图上画出固定铰支座A 、B 的约束反力F A 、F B 的作用线方位和箭头指向为()(要求保留作图过程)。
1.7二、单项选择题(每小题 5 分,共35 分)1、如图2.1所示,四本相同的书,每本重均为P ,设书与书间的摩擦因数为0.1,书与手间的摩擦因数为0.25,欲将四本书一起抱起,则两侧手应加的压力至少大于( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
lg………密………封………线………以………内………答………题………无………效……一、填空题(共15分,共 5题,每题3 分)1. 如图所示的悬臂梁结构,在图中受力情况下,固定端A 处的约束反力为: M A = ;F Ax =;F Ay =。
2.已知正方形板ABCD 作定轴转动,转轴垂直于板面,A 点的速度v A =10cm/s ,加速度a A =cm/s 2,方向如图所示。
则正方形板的角加速度的大小为。
AA B D题1图题2图3. 图示滚压机构中,曲柄OA = r ,以匀角速度绕垂直于图面的O 轴转动,半径为R 的轮子沿水平面作纯滚动,轮子中心B 与O 轴位于同一水平线上。
则有ωAB = ,ωB =。
4. 如图所示,已知圆环的半径为R ,弹簧的刚度系数为k ,弹簧的原长为R 。
弹簧的一端与圆环上的O 点铰接,当弹簧从A 端移动到B 端时弹簧所做的功为 ;当弹簧从A 端移动到C 端时弹簧所做的功为。
oBC题3图题4图5. 质点的达朗贝尔原理是指:作用在质点上的、和在形式上………密………封………线………以………内………答………题………无………效……组成平衡力系。
二、选择题(共20分,共 5 题,每题4 分)1. 图示机构中,已知均质杆AB 的质量为m ,且O 1A =O 2B =r ,O 1O 2=AB =l ,O 1O =OO 2=l /2,若曲柄转动的角速度为ω,则杆对O 轴的动量矩L O 的大小为( )。
A. L O= mr 2ωB. L O= 2mr 2ωC. L O =mr 2ωD. L O = 0122. 质点系动量守恒的条件是:()A. 作用于质点系上外力冲量和恒为零B. 作用于质点系的内力矢量和为零C. 作用于质点系上外力的矢量和为零D. 作用于质点系内力冲量和为零3. 将质量为m 的质点,以速度 v 铅直上抛,试计算质点从开始上抛至再回到原处的过程中质点动量的改变量:( )A. 质点动量没有改变B. 质点动量的改变量大小为 2m v ,方向铅垂向上C. 质点动量的改变量大小为 2m v ,方向铅垂向下D. 质点动量的改变量大小为 m v ,方向铅垂向下4. 图示的桁架结构,铰链D 处作用一外力F ,下列哪组杆的内力均为零? ()A. 杆CG 与杆GFB. 杆BC 与杆BGC. 杆BG 与杆BFD. 杆EF 与杆AF5. 如图所示,已知均质光球重为Q ,由无重杆支撑,靠在重为P 的物块M 上。
若此时物块平衡开始破坏,则物块与水平面间的静摩擦系数为()。
A.D. 无法确定B………密………封………线………以………内………答………题………无………效……D题4图题5图三、作图题(共15分)1. 如图所示,所有接触均为光滑接触,画出杆AB 与球O 的受力图。
(5分)2. 如图所示,杆与轮的自重不计,各处摩擦不计,作出杆AC 带铰链C 与D 与不带铰链的受力图。
(10分)………密………封………线………以………内………答………题………无………效……三、计算题(说明:第1、2、3题必做。
大班在第4题与第5题选做一题,并在相应的题号标出。
小班学生不做第4题,必做第5题。
)( 共50 分)1.如图所示,结构由T 字梁与直梁铰接而成,结构自重与摩擦不计。
已知:F = 2 kN ,q = 0.5 kN/m ,M = 5 kN ﹒m ,l =2 m 。
试求支座C 及固定端A 的反力。
(12分)ll2.如图所示,圆盘无滑动的沿直线滚动。
长度为l 的AB 杆由铰链连接在圆盘上,圆盘半径为r 。
当机构处于图示位置时,圆盘中心O 的速度为v 0,加速度为a 0。
求此瞬时杆端B 的速度和加速度。
(15分)………密………封………线………以………内………答………题………无………效……3.均质杆长l,质量m,与水平面铰接,杆由与平面成θ角位置静止落下。
用达朗贝尔原理(动静法)求解:刚开始落下时杆AB的角加速度及A支座的约束力。
(其余方法不给分) (8分)4.图示系统中,均质圆盘A、B各重P,半径均为R,两盘中心线为水平线,盘B作纯滚动,盘A上作用矩为M(常量)的一力偶;重物D重Q。
问重物由静止下落距离h时重物的速度与加速度以及AD段、AB段绳拉力。
(绳重不计,绳不可伸长,盘B作纯滚动。
) (15分)………密………封………线………以………内………答………题………无………效……5. 选做题(小班必做):杆AB长l,质量为m,圆轮半径为r,质量为m,地面光滑,杆AB从水平位置无初速释放,圆盘始终与地面接触,求杆AB运动到铅垂位置时:(1)A点的速度和AB杆的角速度。
(2)A点的加速度和AB杆的角加速度。
(15分)一、填空题(共15分,共5题,每题3 分)1. M A = ;F Ax or ;F Ay or2. 1 rad/s2212ql ql-ql3. ωAB = 0,ωB =4. kR2;0。
5. 主动力;约束力;虚加的惯性力ωrR(1二、(共20分) 1. A; 2. C; 3. C; 4. C;5. B三、作图题(共15分)1.(5分)(每个力1分,或每个约束反力1分)2.(10分)(每个力1分)EF杆AC带铰链C与D杆AC不带铰链FAy TCF AxF Ay F Cy………密………封………线………以………内………答………题………无………效……三、计算题(共50 分)1.(12分):分别取BD杆与整体进行受力分析(3分)。
BD杆:, (2分)()0=∑B M F210.522cos3002⨯⨯-⨯=cFkN (1分)0.58==cF(3分)21()0:*0.5*4230*22*cos30*4500:2*cos30sin3000:cos302*sin300⎧=+⎪⎪⎪⎪--=⎨⎪=--=⎪⎪=-+-=⎪⎩∑∑∑A Ax Ax cy Ay cM F MF F FF F F解得:M A = = 10.5 kN/m (1分);F Ax= 2.02 kN (1分);F Ax = = 0.5 kN (1分) 3122.(15分)解:研究圆盘O,其作平面运动。
则圆盘的角速度、角加速度分别为:ωε(1分)ω=0vrarε=(1)求B点的速度(图(1分))因P1为圆轮的速度瞬心,则: (1分)ωω=⋅==A000v AP研究AB杆,该杆作平面运动,v B沿水平方向,由速度投影定理可得:即: (2分οο⋅=⋅A Bv cos0v cos45ο==AB0vv2vcos45(2)求B点的加速度(图(2分))轮和圆盘O作平面运动。
以O为基点求a A,有则nA0AO AOa a a aτ=++(1分)ω=+=+⋅=+2n20Ax0A0000va a a a AO ar(1分)τε==⋅=Ay AO00a a AO a………密………封………线………以………内………答………题………无………效……AB 杆作平面运动,P 2为AB 的速度瞬心,则(1分)ω===B BA2vP B 现以A 为基点,求 a B ,有nB A BA BAa a a a τ=++ (1分)ω=⋅=⋅=22n 200BABA 22v 2v aBA l l l 将上式投影于BA 方向,则:(2分)nB Ax Ay BAa cos 45a cos 45a cos 45a οοο=++即:nB Ax Ay BAa a a =++将、、代入有Aya Ax a nBA a (2分)20B 0a 2a r υ=++3. (8分)解:选杆AB 为研究对象,画受力图。
(2分); ;(2分)tI 2α=Rml F nI n 0 ==R F ma 2I 3αα==A A ml M J 根据动静法,有:(2分)t tt I n nn I I 0 cos 00 sin 0()0 cos /20θθθ=+-=∑=-+=∑=⋅-=∑A R A R A A F F mg F F F mg F M F mg l M ,,,解方程得:(2分)n t 3cos sin cos24αθθθ===-A A g mg F mg F l ,,4. (15分)解:取整个系统为研究对象(1)整个系统所受力的功:τa AxB B αF I Ai nhe ………密………封………线………以………内………答………题………无………效……(2分)12(/)φφ=+=∑WM Qh h R (2)系统的动能:10=T 222221111 ()2222ωω=+++O A C C B Q P T J v v J g g (3分)22222111322222ωω=⋅++⋅A B P Q P R v R g g g其中 于是 (2分),2ωω==A B v v R R 22(87)16=+v T Q P g (3)对系统应用动能定理:2112-=∑T T W(2分)2(87)0() 16+-=+v M Q P Q h g R ⇒=v 上式求导得:从而有:(2分)87d d 2() 16d d +⋅=+Q P v M h v Q g t R t8(/)87+=+M R Q ga Q PAD 段绳拉力:(2分)⋅=-D TAD Q a Q F g ⇒=-⋅+TAD D QF a Q gAB 段绳拉力:, (2分)2P ()2gε⋅=-⋅+A TAD TAB R F F R M τε==A A a a R R P 2g ε⇒=+-TAB TAD A M F F R R 5. 选做题(小班必做)。
(15分)(1) 由圆轮的受力,知圆轮对质心动量矩守恒:, , 圆轮为平动。
(2分)0A A A AO A AO L J L J ωω====0A ω≡(2)当AB 杆运动到铅垂时,设杆的角速度为ωAB ,圆轮A 点的速度为v A ,由C ,A 两点速度关系:, 投影:。
(1分)C A CA v v v =+ 2C A CA AB A lv v v v ω=-+=-(2) 系统整体仅受铅垂方向外力,故系统整体水平方向动量守恒:, ,(2分)00A C p mv mv p =-==()02A AB A lv v ω∴--=4A AB v l ω=(3)系统仅受重力,机械能守恒。
设点A 处为势能零点,则:初始位置:110T V +=b………密………封………线………以………内………答………题………无………效……杆铅垂位置:22l V mg=-222222222222()52222123C C AB AAB A A AB A mv J mv T lm v mv ml mv ωωω=++-=++=⋅ ,。
(2分)222532A l T V mv mg +=-2532A mglmv ∴=, 分)A v =4A AB v l ω∴===(4) 取整体为对象画出受力图:设杆AB 的角加速度为 ,轮心A 加速度为AB α()A a →由两点加速度关系:x y t n C C C A CA CA a a a a a a =+=++ 在x ,y 方向投影:, 2x tC CA A AB Al a a a a α=-=-224122255y n C CA AB l l g a a g l ω===⋅=,, , (2分)()()2xICAB A l F m a α=-→12()5yICmg F =↓212IC AB ml M α=()IA A F ma =←(5) 对整体列达朗贝尔平衡方程:, , (1分)0A m =∑02x IC ICl M F +⋅=2()01222AB AB Aml l lm a αα∴+-⋅=23A AB a l α=, , (1分)0ix F =∑0xIC IA F F -=()02AB A A l m a ma α∴--=14A AB a l α=, , (1分)0iy F =∑20y N IC F F mg --=12205Nmg F mg ∴--=联立得: (2分)0 0A AB a α==。
