机械原理总复习题及解答第五章
孙桓《机械原理》笔记和课后习题(含考研真题)详解(机械的效率和自锁)【圣才出品】

第5章机械的效率和自锁5.1 复习笔记一、机械的效率1.功和效率(1)机械效率①驱动功机械上的驱动功(输入功)为W d,有效功(输出功)为W r,损失功为W f。
则有W d=W r+W f②机械效率a.定义机械的输出功与输入功之比称为机械效率,反映了输入功在机械中的有效利用程度,以η表示。
b.计算方法用功计算时η=W r/W d=1-W f/W d;用功率计算时η=P r/P d=1-P f/P d;式中,P d——输入功率;P r——输出功率;P f——损失功率。
(2)损失率①定义机械的损失功与输入功之比称为损失率,以ξ表示。
②计算方法由定义有ξ=W f/W d=P f/P d。
注:η+ξ=1,由于摩擦损失不可避免,故必有ξ>0和η<1。
(3)效率的简便计算方法为便于效率的计算,可应用下式进行计算η=理想驱动力/实际驱动力=理想驱动力矩/实际驱动力矩①斜面机构正反行程的机械效率分别为η=tanα/tan(α+φ)η′=tan(α-φ)/tanα式中,α——斜面夹角;φ——总反力与法向反力的夹角。
②螺旋机构拧紧和放松螺母时的效率计算式分别为η=tanα/tan(α+φv)η′=tan(α-φv)/tanα式中,α——中径升角;φv——螺旋副的摩擦角。
2.机器(或机组)的效率已知各机构的效率可计算确定整个机构的效率。
常用机构的效率见教材表5-1。
(1)串联①计算公式由k个机器串联组成的机组,设各机器的效率分别为η1、η2、…、ηk,机组的输入功率为P d,输出功率为P r。
则整个串联机组的机械效率为η=P r/P d=(P1/P d)(P2/P1)…(P k/P k-1)=η1η2…ηk②特点a.前一机器的输出功率即为后一机器的输入功率;b.只要串联机组中任一机器的效率很低,就会使整个机组的效率极低;c.串联机器的数目越多,机械效率也越低。
③提高串联机组效率的措施a.减少串联机器的数目;b.优先提高效率最低机器的效率。
西北工业大学机械原理课后答案第5章

第五章 机械的效率和自锁题5-5解: (1)根据己知条件,摩擦圆半径 m r f v 002.001.02.0=⨯==ρ ︒==53.8arctan f φ 计算可得图5-5所示位置︒=67.45α ︒=33.14β (2)考虑摩擦时,运动副中的反力如图5-5所示。
(3)构件1的平衡条件为:()ρα2sin 211+=AB R l F M()[]ρα2sin 2321+==AB R R l M构件3的平衡条件为:034323=++R R 按上式作力多边形如图5-5所示,有()()φβφ--︒=+︒90sin 90sin 323F F R(4)()()()φραφβφφβcos 2sin cos cos 90sin 1233++=--︒=AB R l M F F ()αβs i n c o s 130AB l M F = (5)机械效率:()()91.09889.09688.007553.09214.007153.0cos cos 2sin cos sin 303=⨯⨯⨯=++==φβραφβαηAB AB l l F FF R 12F R 41图5-5F F R 21F R43题5-2解: (1)根据己知条件,摩擦圆半径 22vf d =ρ 11a r c t a n f =φ 22a r c t a n f =φ 作出各运动副中的总反力的方位如图5-2所示。
(2)以推杆为研究对象的平衡方程式如下:∑=0xF 0cos cos sin 232132112=''-'+φφφR RR F F F ∑=0yF0sin sin cos 232132112=''-'--φφφR RR F F G F ∑=0CM()0c o s c o s s i n c o s 2s i n 1122232232112=⋅⋅-⋅''+⋅''+++θφφφφe F d F l F d Gl b F R R R R(3)以凸轮为研究对象的平衡方程式如下:h F M R ⋅=12 ()11cos tan sin cos φφθθρe r e h +++=(4)联立以上方程解得()[]21tan cos 21tan sin cos φθφθθρle e r e G M -+++=θc o s 0Ge M = ()()120tan sin cos tan cos 21cos φθθρφθθηe r e c l e e M M +++-==讨论:由于效率计算公式可知,φ1,φ2减小,L 增大,则效率增大,由于θ是变化的,瞬时效率也是变化的。
考研机械原理复习试题(含答案)总结

考研机械原理复习试题(含答案)2一、正误判断题:(在括号内正确的画“√”,错误的画“×”)1.在平面机构中一个高副引入二个约束。
(×)2.任何具有确定运动的机构都是由机架加原动件再加自由度为零的杆组组成的。
(√)3.运动链要成为机构,必须使运动链中原动件数目大于或等于自由度。
(×)4.平面机构高副低代的条件是代替机构与原机构的自由度、瞬时速度和瞬时加速度必需完全相同。
(√)5.当机构自由度F>0,且等于原动件数时,该机构具有确定运动。
(√)6.若两个构件之间组成了两个导路平行的移动副,在计算自由度时应算作两个移动副。
(×)7.在平面机构中一个高副有两个自由度,引入一个约束。
(√)8.在杆组并接时,可将同一杆组上的各个外接运动副连接在同一构件上。
(×)9.任何机构都是由机架加原动件再加自由度为零的基本杆组组成。
因此基本杆组是自由度为零的运动链。
(√)10.平面低副具有2个自由度,1个约束。
(×)二、填空题1.机器中每一个制造单元体称为零件。
2.机器是在外力作用下运转的,当外力作功表现为盈功时,机器处在增速阶段,当外力作功表现为亏功时,机器处在减速阶段。
3.局部自由度虽不影响机构的运动,却减小了高副元素的磨损,所以机构中常出现局部自由度。
4.机器中每一个独立的运动单元体称为构件。
5.两构件通过面接触而构成的运动副称为低副;通过点、线接触而构成的运动副称为高副。
6.平面运动副的最大约束数为 2 ,最小约束数为1。
7.两构件之间以线接触所组成的平面运动副,称为高副,它产生2 个约束。
三、选择题1.机构中的构件是由一个或多个零件所组成,这些零件间 B 产生任何相对运动。
A.可以B.不能C.变速转动或变速移动2.基本杆组的自由度应为 C 。
A.-1B. +1C. 03.有两个平面机构的自由度都等于1,现用一个带有两铰链的运动构件将它们串成一个平面机构,则其自由度等于 B 。
机械原理第五章答案

5.1解:(1)应满足杆长条件,且AD 必不为最短杆AD 为最长杆:c b d a +≤+,360280120+≤+d ,520360≤≤dAD 不为最长杆:d b c a +≤+,d +≤+280360120,200360≥d 所以,d 的取值范围为200mm ≤d ≤520mm(2)如果满足杆长条件,无论AD 如何取值均有曲柄存在,故本解中必不满足杆长条件 ①AD 为最长杆:(安装条件)c b a d ++≤, 760 dc bd a ++ ,360280120++ d ,520 d因此,760520 d <②AD 不是最长杆也不是最短杆:120=>a dd b c a ++ ,d ++280360120 , 200<d因此,200120<<d5.6解:(1)180180341.46618018034k θθ++===--(2)[]min 33γγ=<死点位置如图示。
5.15 解 1 1.251180180201 1.251k k θ--===++ (1)AC2=269.23mm ,AC1=127.95mm(2)取比例尺mm m L /002.0=μ根据已知条件可作出摇杆DC 的一个极限位置DC1,要进行图解还需找出摇杆的另一极限位置。
(3)以D 点为圆心,DC1为半径作圆弧S 。
连接AC1,作∠C1AC2=360,AC2线与圆弧S 可交于两点C2‘,则DC2(或DC2‘)皆为摇杆的另一极限位置。
(4)取摇杆的极限位置为DC1、DC2时,由图可得AC1=24,AC2=58,则1712=-=AC AC AB 412=-=AB AC BC5.8 解:分析:因为是转动导杆机构,ADP 又是对心的曲柄滑块机构,所以曲柄AD 的两个极位必在AP 线上,那么对于转动导杆机构而言,转动曲柄BC 的极位C1和C2也比在AP 线上。
(1)又因 3018011=+-=k k ϑ,两个极位的实际夹角应该是 150。
机械原理第5章 例题精选及答题技巧

则 ,
3.用范成法加工斜齿轮不发生根切的最小齿数为
而 ,由式 求得
因
故用范成法滚刀加工此斜齿轮时不会发生根切。
4.这两个齿轮的当量齿数
例5-19设计一对外啮合圆柱齿轮机构,用于传递中心距为138mm的两平行轴之间的运动。要求其传动比 ,传动比误差不超过 。已知: , , , ,两轮材质相同。若要求两轮的齿根磨损情况大致相同,重合度 ,顶圆齿厚 ,试设计这对齿轮传动。
小齿轮齿顶厚为
可见上面的设计方案是可用的,但必须指出的是:上面的方案不是唯一的设计方案,更不是最佳方案。
例5-12设一外啮合直齿圆柱齿轮传动, , , , , ,试设计这对齿轮。
解题要点:
故本题只能选择变位齿轮正传动。对于角度变位齿轮传动,其齿数的条件不受限制。
解:1.选择传动类型
标准中心距
安装中心距
例5-13在一对外啮合的渐开线直齿圆柱齿轮传动中,已知: , , , , 。要求小齿轮刚好无根切,试问在无侧隙啮合条件下:
1.实际中心距 时,应采用何种类型的齿轮传动,变位系数 各为多少?
2.实际中心距 时,应采用何种类型的齿轮传动,变位系数 各为多少?
解题要点:
1.当实际中心距 时,由齿数条件确定传动类型和变位系数。
解题要点:
本题设计步骤可分为三步:1.选择传动类型和变位系数;2.齿轮几何尺寸计算;3.验算(包括齿顶不变尖、不根切、重迭系数应大于 等)。
解:1.选择传动类型和变位系数
标准中心距
;
选择传动类型为:高度变位齿轮传动
所以选择变位系数为
2.计算两只齿轮的各部分尺寸
按高度变位齿轮传动计算公式进行计算。
机械原理习题答案第五六章
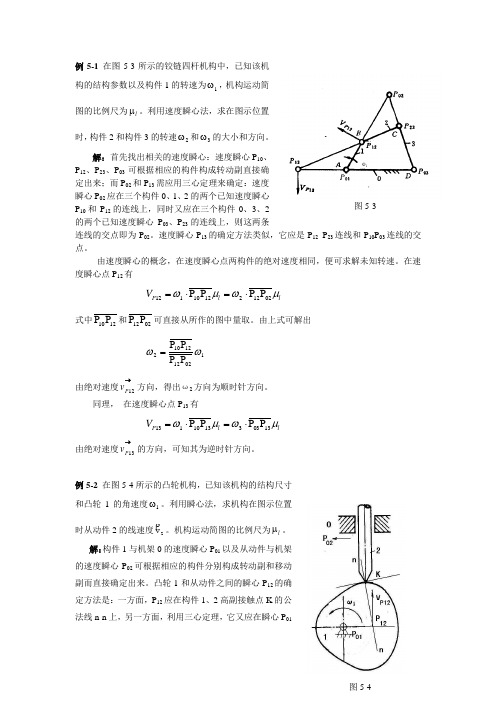
例5-1 在图5-3所示的铰链四杆机构中,已知该机构的结构参数以及构件1的转速为1ω,机构运动简图的比例尺为l μ。
利用速度瞬心法,求在图示位置时,构件2和构件3的转速2ω和3ω的大小和方向。
解:首先找出相关的速度瞬心:速度瞬心P 10、P 12、P 23、P 03可根据相应的构件构成转动副直接确定出来;而P 02和P 13需应用三心定理来确定:速度瞬心P 02应在三个构件0、1、2的两个已知速度瞬心P 10和P 12的连线上,同时又应在三个构件0、3、2的两个已知速度瞬心P 03、P 23的连线上,则这两条连线的交点即为P 02。
速度瞬心P 13的确定方法类似,它应是P 12 P 23连线和P 10P 03连线的交点。
由速度瞬心的概念,在速度瞬心点两构件的绝对速度相同,便可求解未知转速。
在速度瞬心点P 12有l l P V μωμω021*********P P P P ⋅=⋅= 式中1210P P 和0212P P 可直接从所作的图中量取。
由上式可解出1021212102P P P P ωω=由绝对速度→12P v 方向,得出ω2方向为顺时针方向。
同理, 在速度瞬心点P 13有l l P V μωμω130331310113P P P P ⋅=⋅= 由绝对速度→13P v 的方向,可知其为逆时针方向。
例5-2 在图5-4所示的凸轮机构,已知该机构的结构尺寸和凸轮1的角速度1ω。
利用瞬心法,求机构在图示位置时从动件2的线速度2v。
机构运动简图的比例尺为l μ。
解:构件1与机架0的速度瞬心P 01以及从动件与机架的速度瞬心P 02可根据相应的构件分别构成转动副和移动副而直接确定出来。
凸轮1和从动件之间的瞬心P 12的确定方法是:一方面,P 12应在构件1、2高副接触点K 的公法线n-n 上,另一方面,利用三心定理,它又应在瞬心P 01图5-4图5-3和P 02的连线上,即又应在过点P 01而垂直于从动件2与机架移动副导路的直线上。
机械原理课后答案——第五章 凸轮机构及其设计

从动件所受正压力方向: 滚子中心与凸轮几何中心的 连线。
力作用点凸轮从图示位置转过90º 后推杆的位移; 图示位置推杆的位移量S0应 是沿推杆的导路方向(与偏距圆 相切)从基圆开始向外量取。 凸轮从图示位置转过90º 后 推杆的位移等于推杆从图示位 置反转90º 后的位移。 推杆从图示位置反转90º 后 的导路方向仍于与偏距圆相切。 其位移量S1 仍是沿推杆的导路 方向从基圆开始向外量取。 凸轮从图示位置转过90º 后推杆的位移:S=S1 -S0
凸轮机构及其设计
习题9-7 9-8 9-9
9-7 试标出 a 图在图示位置时凸轮机构的压力角,凸轮从 图示位置转过90后推杆的位移;标出图b 推杆从图示位置 升高位移s 时,凸轮的转角和凸轮机构的压力角。
a
b
1) a 图在图示位置时凸轮机构的压力角, 凸轮机构的压力角: 在 不计摩擦的情况下,从动件 所受正压力方向与力作用点 的速度方向之间所夹的锐角。
9-8
作出凸轮的理论 廓线和凸轮的基圆。 以A’为圆心,A到滚子 中心的距离为半径作 圆弧,分别交基圆和 理论廓线于C、C’点, 则C’A’C为所求的位 移角。
过C’作公法线 O’C’,过C’作A’C’的 垂线,则两线的夹角 为所求的压力角。
9-9 解:采用等加速等减速运动规律,可使推杆推程阶段 最大加速度最小。其运动线图如下:
v max 2 h / 0 2 16 1 .5 /( 5 π / 6 ) 18.34mm/s
a 4 h 2 / 02 4 16 1 .5 2 /( 5 π / 6 ) 2 21.03mm/s
2
2) 标出图b 推杆从图示位置升高位移s 时,凸轮的转角和 凸轮机构的压力角。
机械原理复习

第四章 平面机构的力分析
作用在构件上的力
给定力
外加力 惯性力
驱动力 阻抗力 重力
约束反力 法向反力 切向力
静力分析 机构力分析
动态静力分析
静力分析——在不计惯性力的条件下,对机械进行力的 分析称为静力分析。
动态静力分析——将惯性力视为一般外加于相应构件上 的力,再按静力分析的方法进行力分析。
构件组的静定条件
C.运动副的相对位置 D.构件的形状和运动副的结构
(3)有一构件的实际长度L=0.5m,画在机构运动简图中的长度为
20mm,则画此机构运动简图时所取的长度比例尺是( D )。
A.25 B.25mm/m C.1:25 D.0.025m/mm
(4)用一个平面低副连接两个做平面运动的构件所形成的运动链
共有( C )个自由度。
A.0
B.1
C.4
D.6
(5)在机构中,某些不影响机构运动传递的重复部分所带入的约
束为( A )。
A.虚约束 B.局部自由度C.复合铰链 D.真约束
(6)机构具有确定运动的条件是( D )。
A.机构的自由度F≥0 B.机构的构件数N ≥ 4
C.原动件数W ≥ 1 D.机构的自由度F>0,并且F=原动
增加一个齿轮,使机构增加一个虚约束
计算机构的自由度:
局部自由度
n=7, PL=9, pH=2 F=3n-2PL-PH =3×7-2×9-2=1
复合铰链
三、机构具有确定运动的条件
1、F>0,当机构自由度和原动件数相等时, 机构具有确定的运动。 2、 F>0,但F>原动件时,机构的运动不确定。 3、当F>0,但F<原动件时,机构会遭到破坏.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 齿轮机构及其设计5.1填空题5.1.1.按标准中心距安装的渐开线直齿圆柱标准齿轮,节圆与 重合,啮合角在数值上等于 上的压力角。
5.1.2.相啮合的一对直齿圆柱齿轮的渐开线齿廓,其接触点的轨迹是一条线。
5.1.3.渐开线上任意点的法线必定与基圆5.1.4.渐开线齿轮的可分性是指渐开线齿轮中心距安装略有误差时, 。
5.1.5.共轭齿廓是指一对 的齿廓。
5.1.6.用范成法加工渐开线直齿圆柱齿轮,发生根切的原因是 。
5.1.7.一对渐开线直齿圆柱标准齿轮传动,当齿轮的模数m 增大一倍时,其重合度 ,各齿轮的齿顶圆上的压力角a α ,各齿轮的分度圆齿厚s 。
5.1.8.在模数、齿数、压力角相同的情况下,正变位齿轮与标准齿轮相比较,下列参数的变化是:齿厚 ;基圆半径 ;齿根高 。
5.1.9.一个负变位渐开线直齿圆柱齿轮同除变位系数外的其它基本参数均相同的标准齿轮相比较,其 圆及 圆变小了,而 圆及 圆的大小则没有变。
5.1.10.斜齿轮在 上具有标准数和标准压力角。
5.1.11.一对斜齿圆柱齿轮传动的重合度由 两部分组成,斜齿轮的当量齿轮是指 的直齿轮。
5. 2判断题5.2.1.一对外啮合的直齿圆柱标准齿轮,小轮的齿根厚度比大轮的齿根厚度大。
( )5.2.2.一对渐开线直齿圆柱齿轮的正确啮合条件是2b 1b p p =。
( )5.2.3.一对能正确啮合传动的渐开线直齿圆柱齿轮,其啮合角一定为20°。
( )5.2.4.一对直齿圆柱齿轮啮合传动,模数越大,重合度也越大。
( )5.2.5.一对相互啮合的直齿圆柱齿轮的安装中心距加大时,其分度圆压力角也随之加大。
( )5.2.6.标准直齿圆柱齿轮传动的实际中心距恒等于标准中心距。
( )5.2.7.渐开线直齿圆柱齿轮同一基圆的两同向渐开线为等距线。
( )5.2.8.一个渐开线圆柱外齿轮,当基圆大于齿根圆时,基圆以内部分的齿廓曲线,都不是渐开线。
( )5.2.9.对于单个齿轮来说,节圆半径就等于分度圆半径。
( )5.2.10.共轭齿廓就是一对能满足齿廓啮合基本定律的齿廓。
( )5.2.11.在渐开线齿轮传动中,齿轮与齿条传动的啮合角始终与分度圆上的压力角相等。
( )5.2.12.范成法切削渐开线齿轮时,一把模数为m 、压力角为α的刀具可以切削相同模数和压力角的任何齿数的齿轮。
( )5.2.13.一对正传动的渐开线直齿圆柱齿轮传动中,也可以有负变位齿轮。
( )5.2.14.一对渐开线直齿圆柱齿轮在无侧隙传动且中心距a m z z =+1212()时,则必定是一对标准齿轮传动。
( )5.2.15.齿数、模数分别对应相同的一对渐开线直齿圆柱齿轮传动和一对斜齿圆柱齿轮传动,后者的重合度比前者要大。
( )5.2.16.齿数少于17的正常齿制斜齿圆柱齿轮用范成法加工时,一定会发生根切。
( )5.2.17.一对斜齿圆柱齿轮啮合传动时,轮齿接触线平行于齿轮轴线。
( )5.2.18.一对能正确啮合传动的渐开线斜齿圆柱齿轮的端面模数一定相等。
( )5.2.19.斜齿圆柱齿轮不产生根切的最小齿数肯定比相同参数的直齿圆柱齿轮不产生根切的最少齿数要少。
( )5.2.20.一对外啮合斜齿圆柱齿轮正确啮合的条件是两斜齿圆柱齿轮的端面模数和压力角分别相等,螺旋角大小相等,旋向相同。
( )5.2.21.若斜齿圆柱齿轮A 比直齿圆柱齿轮B 的齿数少得多,但轮A 的法面模数、压力角与轮B 的模数、压 力角相同,则这两个齿轮还是可能用同一把齿轮滚刀加工的。
( )5.2.22.在斜齿圆柱齿轮传动中,为满足给定的中心距,只能采用移距变位法。
( )5.2.23.从端面看,渐开线斜齿圆柱齿轮传动是渐开线啮合。
( )5.2.24.斜齿圆柱齿轮法面上的齿廓曲线理论上应该是渐开线。
( )5.2.25.蜗杆的分度圆直径为d mz 1=1,蜗轮的分度圆直径为d mz 22=。
( )5.2.26.蜗轮和蜗杆轮齿的螺旋方向一定相同。
( )5.2.27.和斜齿轮相似,蜗轮的齿向也有螺旋角β,因此蜗轮的法面模数应为标准值。
( )5.2.28.自锁的蜗杆蜗轮机构中,蜗杆不能反向旋转来驱动蜗轮。
( )5.2.29.蜗轮的螺旋角β2一定等于蜗杆的螺旋升角λ 1。
( )5.2.30.蜗杆蜗轮传动中,蜗轮与蜗杆的旋向相同,且它们的螺旋角相等。
( )5.2.31.直齿圆锥齿轮机构可以传递两交错轴之间的运动和动力 。
( )5.2.32.与圆柱直齿轮一样,正常齿制的渐开线直齿圆锥齿轮的齿顶高系数,顶隙系数h *=1a c *.=025。
( ) 5.2.33.直齿圆锥齿轮背锥上的齿廓曲线是球面渐开线。
( )5. 3选择题5.3.1.已知一渐开线标准直齿圆柱齿轮,齿数z =25,齿顶高系数,顶圆直径h a *=1d a =135mm ,则其模数大小应为 。
(A )2mm ;(B )4mm ;(C )5mm ;(D )6mm 。
齿轮齿廓上的渐开线在 上的压力角、曲率半径最小。
(A )根圆;(B )基圆;(C )分度圆。
5.3.2.一对渐开线直齿圆柱齿轮的啮合线切于 。
(A )两分度圆;(B )两基圆;(C )两齿根圆。
5.3.3.一对直齿圆柱齿轮的中心距 等于两分度圆半径之和,但 等于两节圆半径之和。
(A )一定;(B )不一定;(C )一定不。
5.3.4.用标准齿条刀具加工正变位渐开线直齿圆柱外齿轮时,刀具的中线与齿轮的分度圆 。
(A )相切;(B )相割;(C )相离。
5.3.5.渐开线齿轮的标准压力角可通过测量 求得。
(A )分度圆齿厚;(B )齿距;(C )公法线长度。
5.3.6.一对渐开线直齿圆柱齿轮传动,节点附近的滑动速度 。
(A )最大;(B )最小。
5.3.7.在一对渐开线直齿圆柱齿轮传动过程中,齿廓接触处所受的法向作用力 。
(A )不断增大;(B )不断减小;(C )保持不变。
5.3.8.一对渐开线直齿圆柱齿轮传动时,如重合度等于1,这时实际啮合线的长度等于 。
(A )基圆齿距;(B )分度圆齿距;(C )节圆齿距。
5.3.9.用滚刀切制z =90,α½=°20,h a *=1的渐开线直齿圆柱齿轮,变位系数x =−2,则 。
(A )产生根切;(B )不产生根切5.3.10.渐开线斜齿圆柱齿轮分度圆上的端面压力角 法面压力角。
(A )大于; (B )小于; (C )等于。
5.3.11.斜齿圆柱齿轮基圆柱上的螺旋角βb 与分度圆上的螺旋角β相比 。
(A ) βb >β; (B ) βb =β; (C ) βb <β。
5.3.12.一对渐开线斜齿圆柱齿轮在啮合传动过程中,一对齿廓上的接触线长度是变化的。
(A) 由小到大逐渐; (B )由大到小逐渐;(C )由小到大再到小逐渐; (D )始终保持定值。
5.3.13.斜齿圆柱齿轮的模数和压力角之标准值是规定在轮齿的 。
(A )端截面中; (B )法截面中; (C )轴截面中。
5.3.14.增加斜齿轮传动的螺旋角,将引起 。
(A )重合度减小,轴向力增加; (B )重合度减小,轴向力减小;(C )重合度增加,轴向力减小; (D )重合度增加,轴向力增加。
5.3.15.用齿条型刀具加工αn an =°20,=1,β=30°的斜齿圆柱齿轮时不根切的最少齿数是h *(A )17; (B )14; (C )12; (D )26。
5.3.16.一个压力角为αn =°20的正常齿制标准斜齿轮,已知其当量齿轮的基圆半径与斜齿 轮的分度圆 半径相等, 则该斜齿轮的螺旋角β≈ 。
(四舍五入)(A )8°; (B )14°; (C )18°; (D )20°。
5.3.17.阿基米德蜗杆 上的廓线是直线, 上的廓线是阿基米德螺线。
(A )法面; (B )端面; (C )轴面。
5.3.18.在蜗杆蜗轮传动中,轮齿间的啮合是 。
(A )点接触; (B )线接触; (C )面接触。
5.3.19.蜗轮和蜗杆轮齿的螺旋方向 。
(A )一定相同; (B )一定相反; (C )既可相同,亦可相反。
5.3.20.蜗杆蜗轮传动的标准中心距a = 。
(A ))(5.021z z m +; (B ))(5.02z q m +; (C );(D )。
)(5.01z q +)(5.02z q +5.3.21.渐开线直齿圆锥齿轮的当量齿数z v = 。
(A )δcos /z ; (B ); (δ2cos /z C )。
δ3cos /z 5.4简答题5.4.1.什么是齿轮的模数?为什么齿轮的模数,压力角,齿顶高系数和顶隙系数用标准值?5.4.2.渐开线直齿圆柱齿轮的分度圆和节圆有何区别?在什么情况下,标准直齿轮的分度圆和节圆是相等的?5.4.3.为了实现定传动比传动,对齿轮的齿廓曲线有什么要求?传动连续的一对齿廓是否一定满足齿廓啮合基本定律?5.4.4.什么是啮合角?啮合角与压力角有何区别?5.4.5.一对渐开线直齿圆柱齿轮传动中齿廓之间是否有相对滑动?一般在齿廓的什么位置相对滑动较大?什么位置无相对滑动?5.4.6.任意圆上的齿厚公式对齿轮上任意圆上的齿廓都适用吗?5.4.7.与标准齿轮相比较,变位齿轮的哪些参数变了?哪些没变?5.4.8.选择变位系数时要考虑那些因素?5.4.9.试述外啮合渐开线直齿圆柱齿轮传动的传动的可分性。
5.4.10.何谓斜齿轮的当量齿轮?对于螺旋角为β,齿数为Z 的斜齿圆柱齿轮,试写出其当量齿数的表达式。
简述渐开线标准斜齿圆柱齿轮当量齿数是整数吗?5.4.11. 圆锥齿轮的标准参数和压力角在什么地方?正确啮合条件是什么?5.4.12. 何谓圆锥齿轮的当量齿轮?何为背锥?5. 5作图与计算题5.5.1. 齿廓中一条是渐开线,另一条是直线,中心距100mm ,两轮基圆半径如图5.1求:1)若r 1=40mm;r 2=20mm;β=30o ,两轮瞬时的传动比是多少?2)该对齿轮能否恒传动比传动?为什么?5.5.2已知半径为r b =30mm 的基圆所生成的两条渐开线如图5.2所示。
设r k =35mm,kk’=15mm,求:点k’的半径和压力角r k 'α'k2) 以0为圆心,r 为半径画圆交两条渐开线于点k’和k”,则弧长k’k”长多少? k '图5.1题5.5.1图图5.2 题5.5.2图5.5.3.如图5.3是一对正在啮合的标准直齿圆柱齿轮,轮1是主动轮,转向如图,试:1)在图上画出理论和实际啮合线2)量出基圆齿距3)粗估该对齿轮的模数,量出该对齿轮的啮合角和节圆半径4)画出轮2的齿廓工作段。
图5.3 题5.5.3图5.5.4.有一标准直齿圆柱齿轮与齿条传动,已知被加工齿轮毛坯角速度为s rad /1=ω,齿条刀移动线速度s mm v /60=,模数4=m ,刀具中心线与齿轮毛坯圆心的中心距。
