全等三角形二次全等典型习题
二次全等(作业及答案)
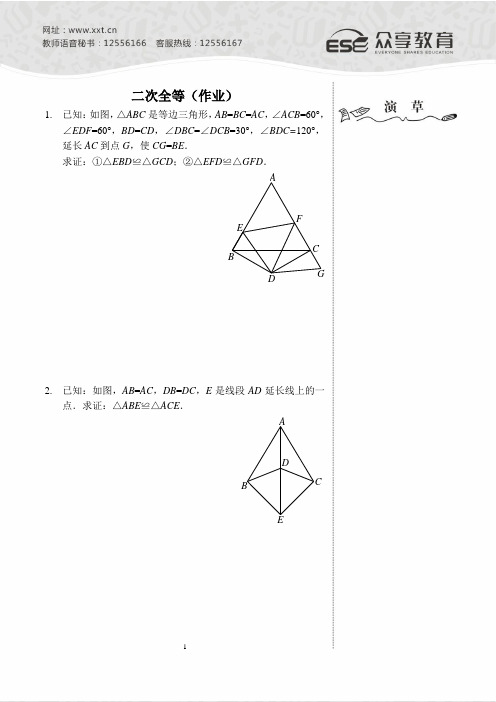
二次全等(作业)1. 已知:如图,△ABC 是等边三角形,AB =BC =AC ,∠ACB =60°,∠EDF =60°,BD =CD ,∠DBC =∠DCB =30°,∠BDC=120°,延长AC 到点G ,使CG =BE .求证:①△EBD ≌△GCD ;②△EFD ≌△GFD .GFE DC BA2. 已知:如图,AB =AC ,DB =DC ,E 是线段AD 延长线上的一点.求证:△ABE ≌△ACE .EDCBA3. 已知:如图,∠ACB =∠ADB =90°,AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别为E ,F .求证:CE =DF .FE DC B A4. 已知:如图,点C ,D 在线段BE 上,且BD =EC ,CA ⊥AB于A ,DF ⊥EF 于F ,且AB =EF .求证:CF =DA .FEDCBA5. 已知:如图,在四边形ABCD 中,AB =CD ,AB ∥CD ,E ,F分别是DA ,BC 延长线上的点,且AE =CF ,连接EF 交BD 于点O ,分别交AB ,CD 于点G ,H .求证:EG =FH .【参考答案】1. 证明:如图,①∵∠ABC =∠ACB =60°,∠DBC =∠DCB =30° ∴∠DBE =∠ABC+∠DBC =90°∠DCG =180°-∠ACB -∠DCB =90°∴∠DBE =∠DCG在△EBD 和△GCD 中,D DBE DC B DCGBE CG ∠=∠=⎧⎪⎨⎪=⎩(已知)(已证)(已知) ∴△EBD ≌△DCG (SAS ) ②∵△DBE ≌△GCD (已证)∴DE =DG (全等三角形对应边相等)∠EDB =∠GDC (全等三角形对应角相等) ∵∠BDC =120°,∠EDF =60° ∴∠EDB +∠CDF =60° ∴∠GDC +∠CDF =60° 即∠GDF =60° ∴∠EDF =∠GDFOHGF EDC BA在△EFD 和△GFD 中,D DE DGEDF GDFF DF =∠=∠⎧⎪⎨⎪=⎩(已证)(已证)(公共边) ∴△EFD ≌△GFD (SAS ) 2. 证明:如图,在△ABD 和△ACD 中,AB ACDB DCAD AD ⎧⎪⎨⎪=⎩==(已知)(已知)(公共边) ∴△ABD ≌△ACD (SSS )∴∠BAD =∠CAD (全等三角形对应角相等) 在△ABE 和△ACE 中,A AB AC BAE CAEE AE =∠=∠⎧⎪⎨⎪=⎩(已知)(已证)(公共边) ∴△ABE ≌△ACE (SAS )3. 证明:如图,在Rt △ACB 和Rt △BDA 中,BC B BAADA ==⎧⎨⎩(公共边)(已知) ∴Rt △ACB ≌Rt △BDA (HL ) ∴AC =BD (全等三角形对应边相等) ∠CAB =∠DBA (全等三角形对应角相等) ∵CE ⊥AB ,DF ⊥AB ∴∠CEA =∠DFB =90° 在△ACE 和△BDF 中,CEA DFBCAE DBFAC BD ⎧⎪⎨∠=∠∠=⎪∠⎩=(已证)(已证)(已证) ∴△ACE ≌△BDF (AAS )∴CE =DF (全等三角形对应边相等) 4. 证明:如图,∵CA ⊥AB ,DF ⊥EF∴∠CAB =∠DFE =90° ∵BD =EC ∴BD +DC =EC +DC 即BC =ED在Rt △ABC 和Rt △FED 中,BC EDAB FE=⎧⎨=⎩(已证)(已知) ∴Rt △ABC ≌Rt △FED (HL ) ∴∠B =∠E (全等三角形对应角相等) 在△ABD 和△FEC 中,AB FEB EBD EC =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已知) ∴△ABD ≌△FEC (SAS )∴CF =DA (全等三角形对应边相等) 5. 证明:如图,∵AB ∥DC∴∠ABD =∠CDB ,∠EAG =∠ADC 在△ABD 和△CDB 中,AB CD ABD CDBBD DB =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(公共边) ∴△ABD ≌△CDB (SAS )∴∠ADB =∠CBD (全等三角形对应角相等) ∴AD ∥BC∴∠E =∠F ,∠ADC =∠FCH ∴∠EAG =∠FCH 在△AEG 和△CFH 中,AE EAG FCH CFE F ⎧⎪=⎨⎪∠=∠=∠⎩∠(已证)(已知)(已证) ∴△AEG ≌△CFH (ASA )∴EG =FH (全等三角形对应边相等)。
全等三角形二次全等典型习题

1. 已知:如图,点C 为线段AB 上一点,△ACM ,△CBN 是等边三角形,AM AC CM ,BC CN BN ,∠ACM ∠BCN ,连接AN 交CM 于点E ,连接BM 交CN 于点F .求证:①△CAN ≌△CMB ;②△CEN ≌△CFB .2. 已知:如图,在正方形ABCD 中,ADAB ,∠D ∠DAB=∠ABC 90°,E ,F 分别为DC ,BC 边上的点,且∠EAF ,延长CB 到点G ,使BG DE ,连接EF ,AG . 求证:①△ADE ≌△ABG ;②△AFE ≌△AFG .第1题图NMCFEBF DECB AG第2题图3. 已知:如图,∠A ∠D ,BE EC .求证:△ABC ≌△DCB .4. 已知:如图,点A ,E ,F ,C 在同一直线上,AE CF ,过E ,F 分别作DE ⊥AC ,BF ⊥AC ,连接AB ,CD ,BD ,BD 交AC 于点G .若AB CD ,求证:△DEG ≌△BFG .5. 已知:如图,AB ,CD 相交于点O ,AOBO ,CO DO ,过点O 作EF 交AC 于点E ,交BD 于点F .求证:OE OF .第4题图A DEG BCF第5题图AD E OBC F6. 已知:如图,ABAC ,BD DC ,AD 与BC 交于点O .求证:AD ⊥BC .7. 已知:如图,在△ABC 中,点D 是BC 的中点,DF ⊥AB ,DE ⊥AC ,垂足分别是F ,E ,DF DE ,试猜想AB 和AC 的数量关系,并证明你的猜想.8. 已知:如图,ABAE ,BC ED ,∠B ∠E ,F 是CD 中点,求证:AF ⊥CD .1.已知:如图,AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F ,且BC =DC .试猜想BE 与DF 有怎样的数量关系?并说明理由.第7题图AD E CF 第6题图AD O BC第8题图AD BCFABCEF D 122.已知:如图,O 是线段AC ,FE 的中点,OE ⊥AB 于E ,OF ⊥CD 于F ,DF =BE . 求证:AD =BC .3.已知:如图,点E 在直线AC 上,ED ⊥CD 于D ,EB ⊥CB 于B ,且CD =CB . 求证:AD =AB .ABCEFDOAB CED4.已知:如图,在四边形ABCD中,AD=BC,AB=DC,E,F分别为AD,CB延长线上一点且DE=BF,试说明∠E =∠F.A B CEFD1.已知:如图,△ABC是等边三角形,AB=BC=AC,∠ACB=∠ABC=60°,∠EDF=60°,DB=DC,∠DBC=∠DCB=30°,∠BDC=120°,延长AC到点G,使CG=BE.求证:①△EBD≌△GCD;②△EFD≌△GFD.AF2. 已知:如图,AB =AC ,DB =DC ,F 是AD 的延长线上的一点.求证:△ABF ≌△ACF .3. 已知:如图,AB =AC ,AD =AE ,AB ,DC 相交于点M ,AC ,BE 相交于点N ,∠DAB =∠EAC .求证:△ADM ≌△AEN .4. 已知:如图,AC ⊥BC ,AD ⊥BD ,AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E ,F . 求证:CE =DF .DABFCDC A5. 已知:如图,点C ,D 在线段BE 上,且BD =EC ,CA ⊥BA 于A ,DF ⊥EF 于F ,且AB =EF .求证:CF =AD .1、已知:如图,AB=CD ,AD=BC ,过AC 的中点O 作直线EF 交AB 的延长线于E ,交CD 的延长线于F.求证:OE=OF.2、已知:如图,∠D=∠E. AM=ME=CN=DN.问:AB 与BC 相等吗?请给予证明.3、已知点A ,C 在直线EF 上,AD =BC ,AB =DC ,AE =CF ,BCDA F AB CDOEFCNDABEM试说明E ∠与∠F 相等的理由.4、如图已知:三角形ABC 中,∠A =90°,AB =AC ,D 为BC 的中点,E ,F 分别是AB ,AC 上的点,且BE =AF ,求证:△DEF 为等腰直角三角形.5、将一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆放成如图的形式,使点B 、F 、C 、D 在同一条直线上。
全等三角形二次全等训练习题
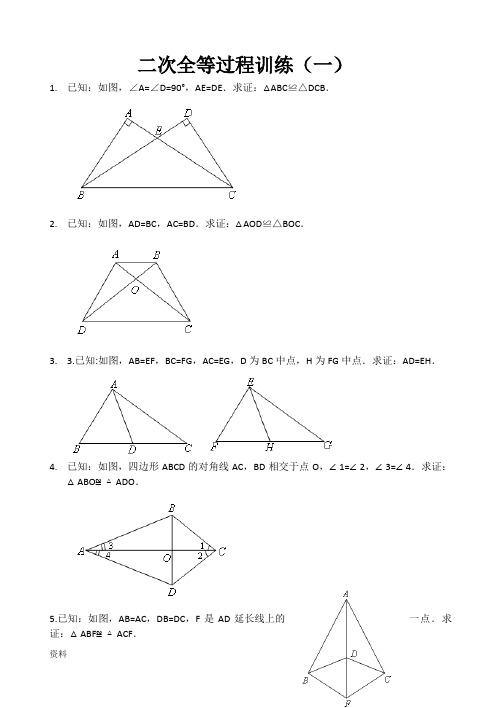
二次全等过程训练(一)1.已知:如图,∠A=∠D=90°,AE=DE.求证:△ABC≌△DCB.2.已知:如图,AD=BC,AC=BD.求证:△AOD≌△BOC.3. 3.已知:如图,AB=EF,BC=FG,AC=EG,D为BC中点,H为FG中点.求证:AD=EH.4.已知:如图,四边形ABCD的对角线AC,BD相交于点O,∠1=∠2,∠3=∠4.求证:△ABO≌△ADO.5.已知:如图,AB=AC,DB=DC,F是AD延长线上的一点.求证:△ABF≌△ACF.6.已知:如图,∠E=∠D,AM=CN,ME=ND.求证:△ABE≌△CBD.二次全等过程训练(二)一、单选题1.已知:如图,AD∥BC,AB,CD相交于点O,AO=BO,过点O作EF交AD于点E,交CB 于点F.求证:△EOD≌△FOC.2.已知:如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且BD=CD.求证:Rt△DEB≌Rt△DFC.3.已知:如图,在四边形ABCD中,AB=CD,AB∥CD,E,F分别是DA,BC延长线上的点,且AE=CF,连接EF交BD于点O.求证:△EOD≌△FOB.4.已知:如图,点C,D在线段BE上,且BD=EC,CA⊥AB于A,DF⊥EF于F,且AB=EF.求证:△ABD≌△FEC.5.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,AB=AC.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.求证:△EAM≌△FAN.二次全等过程训练(三)1.已知:如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DF⊥AB于F,DE⊥AC于E.求证:△BDF≌△CDE.2.已知:如图,点A,E,F,C在同一直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,连接AB,CD,BD,BD交AC于点G,AB=CD.求证:△DEG≌△BFG.3.已知:如图,在Rt△ACD中,∠ADC=90°,BE⊥AC于E,交CD于点F,AE=AD.求证:△CEF≌△BDF.4.已知:如图,在四边形ABCD中,AB=BC=CD=AD,BD平分∠ABC,E为BD上任意一点,连接AE,CE.求证:△ADE≌△CDE.55..已知:如图,在△ABC中,∠ACB=∠ABC=60°,∠EDF=60°,BD=CD,∠DBC=∠DCB=30°,∠BDC=120°,延长AC到点G,使CG=BE.求证:△EFD≌△GFD.二次全等过程训练(四)1.已知:如图,点A,C在直线EF上,BC=AD,AB=CD,AE=CF.求证:∠E=∠F.2.已知,如图,AE=BF,AD=BC,CE=DF.求证:AO=BO.已知:如图,∠D=∠E,AM=ME=CN=DN.试猜想AB和BC的数量关系,并证明你的猜想.4.已知:如图,在△ABC中,点D是BC的中点,DF⊥AB于F,DE⊥AC于E,DF=DE.求证:AB=AC.5.如图,在正方形ABCD中,∠ABC=∠BCD=90°,AB=BC=CD=AD.E为BC边上一点,且AE=DE,AE与对角线BD交于点F,∠ABF=∠CBF,连接CF交DE于点G.求证:DE⊥CF.。
全等三角形经典例题
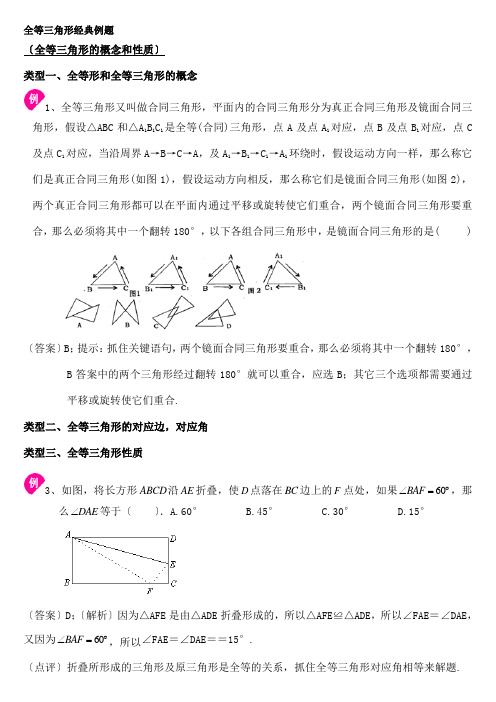
全等三角形经典例题〔全等三角形的概念和性质〕类型一、全等形和全等三角形的概念1、全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形及镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A及点A1对应,点B及点B1对应,点C及点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,假设运动方向一样,那么称它们是真正合同三角形(如图1),假设运动方向相反,那么称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,那么必须将其中一个翻转180°,以下各组合同三角形中,是镜面合同三角形的是( )〔答案〕B;提示:抓住关键语句,两个镜面合同三角形要重合,那么必须将其中一个翻转180°,B答案中的两个三角形经过翻转180°就可以重合,应选B;其它三个选项都需要通过平移或旋转使它们重合.类型二、全等三角形的对应边,对应角类型三、全等三角形性质3、如图,将长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果60BAF∠=︒,那么DAE∠等于〔〕.A.60° B.45° C.30° D.15°〔答案〕D;〔解析〕因为△AFE是由△ADE折叠形成的,所以△AFE≌△ADE,所以∠FAE=∠DAE,又因为60BAF∠=︒,所以∠FAE=∠DAE==15°.〔点评〕折叠所形成的三角形及原三角形是全等的关系,抓住全等三角形对应角相等来解题.举一反三:〔变式〕如图,在长方形ABCD中,将△BCD沿其对角线BD翻折得到△BED,假设∠1=35°,那么∠2=________.〔答案〕35°;提示:将△BCD沿其对角线BD翻折得到△BED,所以∠2=∠CBD,又因为AD∥BC,所以∠1=∠CBD,所以∠2=35°.4、如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,假设∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.〔答案〕∠α=80°〔解析〕∵∠1∶∠2∶∠3=28∶5∶3,设∠1=28x,∠2=5x,∠3=3x,∴28x+5x+3x=36x=180°,x=5°即∠1=140°,∠2=25°,∠3=15°∵△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,∴△ABE≌△ADC≌△ABC∴∠2=∠ABE,∠3=∠ACD∴∠α=∠EBC+∠BCD=2∠2+2∠3=50°+30°=80°“比例〞设未知数x是比拟常用的解题思路.举一反三:〔变式〕如图,在△ABC中,∠A:∠ABC:∠BCA =3:5:10,又△MNC≌△ABC,那么∠BCM:∠BCN等于〔〕A.1:2 B.1:3 C.2:3 D.1:4〔答案〕D;提示:设∠A=3x,∠ABC=5x,∠BCA=10x,那么3x+5x+10x=18x=180°,x=10°. 又因为△MNC≌△ABC,所以∠N=∠B=50°,CN=CB,所以∠N=∠CBN=50°,∠ACB=∠MCN=100°,∠BCN=180°-50°-50°=80°,所以∠BCM:∠BCN=20°:80°=1:4.〔全等三角形判定一〔SSS,SAS〕〕类型一、全等三角形的判定1——“边边边〞1、如图,在△ABC和△ADE中,AB=AC,AD=AE,BD=CE,求证:∠BAD=∠CAE.(答案及解析〕证明:在△ABD和△ACE中,∴△ABD≌△ACE〔SSS〕∴∠BAD=∠CAE〔全等三角形对应角相等〕. (点评〕把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD=∠CAE,先找出这两个角所在的三角形分别是△BDA和△CAE,然后证这两个三角形全等.举一反三:(变式〕:如图,AD=BC,AC=BD.试证明:∠CAD=∠DBC.(答案〕证明:连接DC,在△ACD及△BDC中∴△ACD≌△BDC〔SSS〕∴∠CAD=∠DBC〔全等三角形对应角相等〕类型二、全等三角形的判定2——“边角边〞2、3、举一反三:(变式〕,如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,并且AE=12〔AB+AD〕,求证:∠B+∠D=180°.(答案〕证明:在线段AE上,截取EF=EB,连接FC,∵CE⊥AB,∴∠CEB=∠CEF=90°在△CBE 和△CFE 中,∴△CBE 和△CFE 〔SAS 〕∴∠B =∠CFE∵AE =12〔AB +AD 〕,∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2〔AF +EF 〕-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC 〔SAS 〕∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°. 类型三、全等三角形判定的实际应用4、如图,公园里有一条“Z 字形道路ABCD ,其中AB ∥CD ,在AB ,BC ,CD 三段路旁各有一个小石凳E ,M ,F ,且BE =CF ,M 在BC 的中点.试判断三个石凳E ,M ,F 是否恰好在一条直线上?Why ?(答案及解析〕三个小石凳在一条直线上证明:∵AB 平行CD 〔〕∴∠B =∠C 〔两直线平行,内错角相等〕∵M 在BC 的中点〔〕∴BM =CM 〔中点定义〕在△BME 和△CMF 中∴△BME ≌△CMF 〔SAS 〕∴∠EMB =∠FMC 〔全等三角形的对应角相等〕∴∠EMF =∠EMB +∠BMF =∠FMC +∠BMF =∠BMC =180°〔等式的性质〕∴E ,M ,F 在同一直线上(点评〕对于实际应用问题,首先要能将它化成数学模型,再根据数学知识去解决. 由易证△BME≌△CMF ,可得∠EMB =∠FMC ,再由∠EMF =∠EMB +∠BMF =∠FMC +∠BMF =∠BMC =180°得到E ,M ,F 在同一直线上.〔全等三角形判定二〔ASA ,AAS 〕〕类型一、全等三角形的判定3——“角边角〞1、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.(答案及解析〕证明:∵AD∥BC,∴∠DAC=∠C∵BF平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE及△BCF中∴△DAE≌△BCF〔ASA〕∴DE=BF(点评〕利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.(变式〕:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.(答案〕证明:∵MQ和NR是△MPN的高,∴∠MQN=∠MRN=90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4 ∴∠1=∠2在△MPQ 和△NHQ 中,∴△MPQ ≌△NHQ 〔ASA 〕 ∴PM =HN类型二、全等三角形的判定4——“角角边〞2、:如图,90ACB ∠=︒,AC BC =,CD 是经过点C 的一条直线,过点A 、B 分别作AE CD ⊥、BF CD ⊥,垂足为E 、F ,求证:CE BF =.(答案及解析〕证明:∵ CD AE ⊥,CD BF ⊥ ∴︒=∠=∠90BFC AEC∴︒=∠+∠90B BCF∵,90︒=∠ACB ∴︒=∠+∠90ACF BCF ∴B ACF ∠=∠在BCF ∆和CAE ∆中∴BCF ∆≌CAE ∆〔AAS 〕∴BF CE =(点评〕要证BF CE =,只需证含有这两个线段的BCF ∆≌CAE ∆.同角的余角相等是找角等的好方法.3、平面内有一等腰直角三角板〔∠ACB =90°〕和一直线MN .过点C 作CE ⊥MN 于点E ,过点B 作BF ⊥MN 于点F .当点E 及点A 重合时〔如图1〕,易证:AF +BF =2CE .当三角板绕点A 顺时针旋转至图2的位置时,上述结论是否仍然成立?假设成立,请给予证明;假设不成立,线段AF 、BF 、CE 之间又有怎样的数量关系,请直接写出你的猜测,不需证明.(答案及解析〕解:图2,AF +BF =2CE 仍成立,证明:过B 作BH ⊥CE 于点H ,∵∠CBH +∠BCH =∠ACE +∠BCH =90°∴∠CBH =∠ACE在△ACE 及△CBH 中, 90ACH CBH AEC CHB AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ACE≌△CBH.〔AAS〕∴CH=AE,BF=HE,CE=EF,∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.(点评〕过B作BH⊥CE及点H,易证△ACH≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.正确作出垂线,构造全等三角形是解决此题的关键.举一反三:(变式〕错误!未找到引用源。
全等三角形的判定常考典型例题及练习

全等三角形的判定一、知识点复习①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。
(SAS)图形分析:书写格式: 在△ABC和△DEF中⎪⎩⎪⎨⎧=∠=∠=EFBCEBDEAB∴△ABC≌△DEF(SAS)②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等.(ASA)图形分析:书写格式:在△ABC和△DEF中⎪⎩⎪⎨⎧∠=∠=∠=∠FCEFBCEB∴△ABC≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS)图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧=∠=∠∠=∠EF BC F C E B∴△ABC ≌△DEF (AAS)④“边边边”定理:三边对应相等的两个三角形全等.(SSS )图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。
(HL )图形分析:书写格式:在△ABC 和△DEF 中⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF (HL )一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗?比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗?两个三角形中对应相等的元素两个三角形是否全等 反例SSA ⨯AAA⨯二、常考典型例题分析第一部分:基础巩固1。
下列条件,不能使两个三角形全等的是( )A .两边一角对应相等B .两角一边对应相等C .直角边和一个锐角对应相等D .三边对应相等2.如图,点D ,E 分别在线段AB ,AC 上,CD 与BE 相交于O 点,已知AB=AC ,现添加以下的哪个条件仍不能判定△ABE ≌△ACD( )A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3。
全等三角形练习题(含答案)

全等三角形练习题(含答案)篇一:全等三角形习题选(含)经典三角形证明题选讲(含答案)三角形辅助线做法线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验1.已知:AB=4,AC=2,D是BC中点,AD是整数,求ADD1. 证明:延长AD到E,使DE=AD, 则△ADC≌△EBD ∴BE=AC=2 在△ABE中,AB-BE AE AB+BE ,∴10-2 2AD 10+2 4 AD 6又AD是整数,则AD=5思路点拨:三角形中有中线,延长中线等中线。
2.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠22.证明:连接BF和EF.∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ △BCF≌△EDF(边角边). ∴BF=EF,∠CBF=∠DEF. 连接BE.在△BEF中,BF=EF,∴∠EBF=∠BEF又∵ ∠ABC=∠AED,∴ ∠ABE=∠AEB. ∴ AB=AE在△ABF和△AEF中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF. ∴△ABF≌△AEF∴∠1=∠2.思路点拨:解答本题的关键是能够想到证明AB=AE,而AB、AE在同一个△ABE 中,可利用∠ABE=∠AEB来证明.同一三角形中线段等,可用等角对等边3.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC 证明:过E点,作EG//AC,交AD延长线于G则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴△ADC≌△GDE(AAS)∴EG=AC ∵EF∥AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=EG∴EF=AC 思路点拨:角平分线平行线,等腰三角形来添。
4.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C 证明:延长AC到E使CE=CD,连接 ED,则∠CDE= ∠E∵ AB=AC+CD ∴AB=AC+CE=AE又∵∠BAD=∠EAD,AD=AD∴△BAD≌△EAD ∴∠B=∠E∵∠ACB=∠E+∠CDE,∴∠ACB=2∠B方法二在AC上截取AE=AB,连接ED A∵A D平分∠BAC∴∠EAD=∠BAD又∵AE=AB,AD=AD∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB CBD∵AC=AB+BD ,AC=AE+CE∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C思路点拨:线段等于线段和,理应截长或补短5.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE 证明:过C作CF⊥AD交AD的延长线于F.在△CFA和△CEA中∴∠CFA=∠CEA=90°又∵∠CAF=∠CAE, AC=AC∴△CFA≌△CEA ,∴AE=AF=AD+DF, CE=CF∵∠B+∠ADC=180°,∠FDC+∠ADC=180°∴∠B=∠FDCE在△CEB和△CFD中,CE=CF,∠CEB=∠CFD=90°, ∠B=∠FDCE∴△CEB≌△CFD∴BE=DF∴ AE=AD+BE思路点拨:图中有角平分线,可向两边作垂线。
全等二次证明(含答案)

全等二次证明1.已知:如图,,,是延长线上的一点.求证:.2.如图,,,,、是垂足,.求证:.3.如图,在四边形中,,,,分别是,延长线上的点,且,连接交于点,分别交,于点,.求证:.4.如图,点在线段上,,.求证:.5.如图所示,已知,,,求证:.(1)(2)6.如图,已知中,,、是高,与相交于点;求证:.若,求的度数.7.已知:如图所示,,,,分别是、的中点.求证:.8.已知如图:,,.求证:.9.如图,在中,,为边的中点,,.求证:.10.如图,已知在上,,,那么等于吗?为什么?11.如图,、、、四点在一条直线上,,,,.求证:.12.如图,,,于,于.求证:.13.如图,已知,,试说明:≌.14.如图,已知,,且,,你能证明吗?15.在中,,延长至,使,过作于,交于,求证:平分.16.如图,,.求证:≌.17.已知为等边内一点,且,为三角形外一点,且,,求.18.如图,中,是的中点,是线段延长线上一点,过点作的平行线与线段的延长线交于点,连接,.求证:.19.如图,已知在四边形中,,,于点,交于点,交的延长线于点,且.求证:.20.已知:如图所示,,,,.求证:.21.已知,,,,求的长度.22.已知:如图,点、、、在同一直线上,,过点、分别作,,连接、、,交于点,,求证:≌.23.如图,,,相交于点,且,,.求证:≌.CDOBAFE24.如图,,,于,,求证:平分.25.如图:在中,,于,于,、相交于.求证:平分.(1)(2)26.如图,在中,,延长至,使,过作于,交于.连接.求证:.若,求的度数.(1)(2)27.已知:如图,点、、三点在同一条直线上,平分,,于,于.求证:≌.若,,求的长.(1)(2)28.如图,已知≌,,与相交于点,连接,.图中还有几对全等三角形,请你一一列举.求证:.29.如图,已知:为等边内一点,,,求的度数.30.如图,在的两边、上分别取,,和相交于点,求证:点在的平分线上.EF BCDA(1)(2)31.已知:如图,、、、四点在同一直线上,,且.求证:,(1)(2)32.如图(),、分别为线段的两个动点,且于点,于点,若,,交于点.求证:,.当、两点移动到图()所示的位置时,其余条件不变,上述结论能否成立?若成立,请给予证明;若不成立,请说明理由.全等二次证明1.【解析】【标注】已知:如图,,,是延长线上的一点.求证:.【答案】证明见解析.∵在和中,,∴≌(),∴,在和中,,∴≌(),∴.【知识点】全等三角形之二次全等【备注】【教法指导】引导学生梳理思路如下:①要证,则需证明(或者任选其一都可以);②要证,需找三组条件,其中已有两组边相等,,所以势必需要;③要证,从已知条件出发,发现,,又因为公共边,可证明④由,可得,至此,在和中三组条件找全,利用可以证明全等,从而得出结论.【注意】分析为逆向思维,但是书写过程还是要正向去写≌≌≌≌≌2.【解析】【标注】如图,,,,、是垂足,.求证:.【答案】见解析先证≌,再证≌即可【知识点】全等三角形的对应边与角【备注】【教法指导】例的完整解答如下:∵,,∴,又∵,,∴∴∴,即∴ .∴.≌()≌()3.【解析】如图,在四边形中,,,,分别是,延长线上的点,且,连接交于点,分别交,于点,.求证:.【答案】证明见解析.如图,∵,∴,,在和中,【标注】,∴≌(),∴,∴,∴,,∴,在和中,,∴≌(),∴.【知识点】多解或多种判定混合4.【解析】如图,点在线段上,,.求证:.【答案】证明见解析 .∵,而,,∴,在和中,【标注】,∴≌,∴.在和中,∴≌,∴.【知识点】多解或多种判定混合【备注】【教法指导】练习也可以把、分别当作、的外角,从而可得,同样可以证出.≌5.【解析】如图所示,已知,,,求证:.【答案】证明见解析.∵,∴,即,在和中,∴≌,∴,在和中,【标注】∴≌,∴.【知识点】多解或多种判定混合【备注】【教法指导】练习也可以由得到,从而.≌≌()(1)(2)6.方法一:方法二:(1)【解析】如图,已知中,,、是高,与相交于点;求证:.若,求的度数.【答案】(1)(2)证明见解析..∵,∴,∵、是的两条高线,∴,∴≌,∴,,在和中∵,,,∴≌.∴.∵,、是的两条高线,∴,且.又∵,(2)【标注】∴≌.∴.又∵,∴≌.∴.∵,∴又∵∴∴【知识点】等腰三角形的判定-等角对等边【知识点】三角形内角和的应用【能力】推理论证能力7.【解析】已知:如图所示,,,,分别是、的中点.求证:.【答案】证明见解析.连接,在和中,,∴≌,∴,∵,,分别是,的中点,∴,在和中,【标注】,∴≌,∴.【知识点】多解或多种判定混合8.【解析】已知如图:,,.求证:.【答案】证明见解析.连接,∵,,∴,即,在和中,≌(),∴,在和中,∴≌(),∴.【标注】【知识点】多解或多种判定混合9.【解析】如图,在中,,为边的中点,,.求证:.【答案】证明见解析.连接.在和中,,∴≌(),又∵,为边的中点,∴(三线合一),∴,又∵≌,【标注】∴,∴,,∴.【知识点】全等三角形之二次全等10.【解析】【标注】如图,已知在上,,,那么等于吗?为什么?【答案】.∵,,,∴≌,∴,∵,∴≌,∴.【知识点】多解或多种判定混合11.如图,、、、四点在一条直线上,,,,.求证:.【答案】证明:∵,,∴,【解析】【标注】,∴,即,在和中,∴≌(),∴(全等三角形的对应边相等),(全等三角形的对应角相等),∴,在和中,∴≌(),∴(全等三角形的对应边相等).∵,,∴,,∴,即,在和中,∴≌(),∴(全等三角形的对应边相等),(全等三角形的对应角相等),∴,在和中,∴≌(),∴(全等三角形的对应边相等).【知识点】多解或多种判定混合已证已知已证已证公共边已证已知已证已证公共边12.如图,,,于,于.求证:.【解析】【标注】【答案】证明见解析.在和中,,∴≌,∴,∵,,∴,∴≌,∴.【知识点】HL13.【解析】如图,已知,,试说明:≌.【答案】证明见解析.在和中,,∴≌,∴,【标注】∵,,∴,在和中,,∴≌.【知识点】AAS14.【解析】【标注】如图,已知,,且,,你能证明吗?【答案】证明见解析.∵,,∴,∴.又∵,,∴≌,∴.又∵,,∴≌,∴.【知识点】HL15.在中,,延长至,使,过作于,交于,求证:平分.【解析】【标注】【答案】证明见解析.∵,∴,在和中:∴,∴,在和中:,∴,∴,即平分.【知识点】多解或多种判定混合16.如图,,.求证:≌.【答案】证明:∵,,在和中,,∴≌.∴.又∵,在和中,【解析】【标注】,∴≌.∵,,在和中,,∴≌.∴.又∵,在和中,,∴≌.【知识点】多解或多种判定混合17.【解析】已知为等边内一点,且,为三角形外一点,且,,求.【答案】.∵,又∵为等边三角形,∴,,∴连接,在与中,,【标注】∴≌().∴.又∵,∴.又∵,,∴,在和中,.∴≌().∴.∴.【知识点】多解或多种判定混合18.【解析】如图,中,是的中点,是线段延长线上一点,过点作的平行线与线段的延长线交于点,连接,.求证:.【答案】证明见解析.∵,∴.∵是的中点,∴.在和中,,∴≌,∴.在和中,【标注】,∴≌,∴.∴.【知识点】多解或多种判定混合19.【解析】【标注】如图,已知在四边形中,,,于点,交于点,交的延长线于点,且.求证:.【答案】证明见解析.∵,于点,∴.∵,,∴≌,∴.连接,∵,,∴≌,∴.【知识点】全等三角形之二次全等20.【解析】【标注】已知:如图所示,,,,.求证:.【答案】证明见解析.∵,,∴.在和中,,∴≌().∴.∴.∴.在和中,,∴≌().∴,∴.【知识点】多解或多种判定混合21.已知,,,,求的长度.【答案】.【解析】【标注】∵,∴,在和中,∵,∴≌(),∴,.在和中,∵,∴≌(),∴.【知识点】SAS 【能力】分析和解决问题能力22.【解析】已知:如图,点、、、在同一直线上,,过点、分别作,,连接、、,交于点,,求证:≌.【答案】证明见解析.∵、,∴,∵,,,∴,∵,∴≌,∴,∵,∴≌,【标注】【知识点】AAS 【知识点】全等三角形的性质【能力】推理论证能力【备注】【教法指导】练习注意标答第7行以后,得到、再由(已证)、(对顶角相等)就可以得到.≌()23.【解析】【标注】如图,,,相交于点,且,,.求证:≌.CDOBAFE【答案】证明见解析.在和中,,∴≌(),同理,≌,≌,∴,,,∴≌.【能力】推理论证能力【知识点】SAS【知识点】全等三角形的性质24.如图,,,于,,求证:平分.【解析】【标注】【答案】证明见解析.连接、,在和中:,∴,∴,,∵,∴,在和中:,∴,∴,∴,,即平分.【知识点】多解或多种判定混合25.【解析】如图:在中,,于,于,、相交于.求证:平分.【答案】证明见解析.∵,,∴,∵,,【标注】∴≌,∴,∵,∴≌,∴,∴平分.【知识点】多解或多种判定混合(1)(2)26.(1)(2)【解析】如图,在中,,延长至,使,过作于,交于.连接.求证:.若,求的度数.【答案】(1)(2)证明见解析..在和中,,∴≌(),∴,又∵,,∴.由()知,,∵,在和中,【标注】,∴≌(),∴,∵,∴,设,则,则,∴.【知识点】全等三角形的对应边与角(1)(2)27.(1)(2)【解析】已知:如图,点、、三点在同一条直线上,平分,,于,于.求证:≌.若,,求的长.【答案】(1)(2)证明见解析..∵,,∴.∵平分,∴,在和中,,∴≌.∵≌,【标注】∴,∵,∴.∵平分,∴,∵,,∴,在和中,,∴≌.∴,∴,∵,,∴,∴.【知识点】角分线性质定理【知识点】AAS【知识点】全等三角形的对应边与角【能力】推理论证能力(1)(2)28.如图,已知≌,,与相交于点,连接,.图中还有几对全等三角形,请你一一列举.求证:.【答案】(1)≌,≌(1)(2)【解析】(2)证明见解析.≌,≌证法一:连接,∵≌,∴.∴.又∵≌,∴.∴.即.∴.证法二:∵≌,∴,,,.∴.即,∴≌.∴,.又∵,∴.又∵,【标注】∴≌.∴.证法三:连接.∵≌,∴,,.又∵,∴≌.∴.又∵,∴.即.【知识点】全等三角形的对应边与角29.【解析】如图,已知:为等边内一点,,,求的度数.【答案】.连接,∵等边三角形,∴,∵,【标注】∴,在和中,,∴≌(),∴,在和,,∴≌(),∴,∵,∴.故答案为:.【知识点】多解或多种判定混合30.【解析】如图,在的两边、上分别取,,和相交于点,求证:点在的平分线上.【答案】证明见解析.∵,,,∴≌,∴,【标注】又,,∴≌,∴,易得≌,∴,∴点在的平分线上.【知识点】多解或多种判定混合EFBCD A(1)(2)31.(1)(2)【解析】已知:如图,、、、四点在同一直线上,,且.求证:【答案】(1)(2)证明见解析证明见解析.∵,∴,即.∵,∴,∵,∴在和中,,∴.∵(已证),∴.在和中,,,【标注】,∴.∴【知识点】全等三角形的对应边与角(1)(2)32.(1)【解析】如图(),、分别为线段的两个动点,且于点,于点,若,,交于点.求证:,.当、两点移动到图()所示的位置时,其余条件不变,上述结论能否成立?若成立,请给予证明;若不成立,请说明理由.【答案】(1)(2)证明见解析.结论仍成立.∵,,∴.和是直角三角形,在和中,,∴≌().(2)【标注】∴.在和中,,∴≌().∴,.结论仍成立.∵∵,,∴.和是直角三角形,在和中,,∴≌().∴.在和中,,∴≌().∴,.【知识点】全等三角形的对应边与角。
第二讲全等三角形证明-初一周心仪
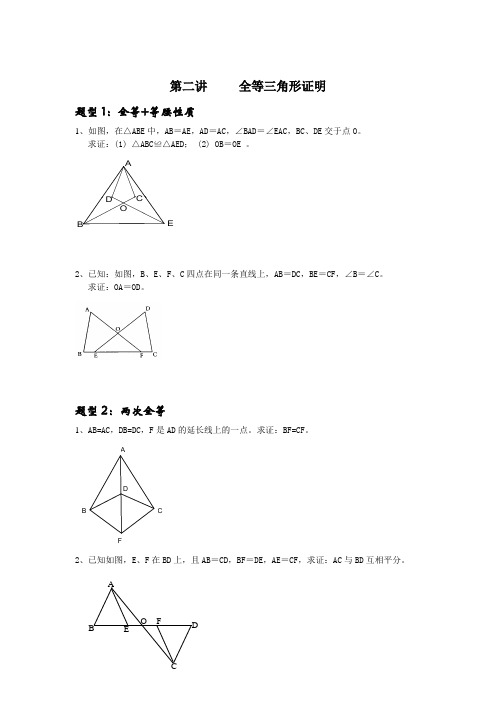
第二讲 全等三角形证明题型1:全等+等腰性质1、如图,在△ABE 中,AB =AE ,AD =AC ,∠BAD =∠EAC ,BC 、DE 交于点O 。
求证:(1) △ABC ≌△AED ; (2) OB =OE 。
2、已知:如图,B 、E 、F 、C 四点在同一条直线上,AB =DC ,BE =CF ,∠B =∠C 。
求证:OA =OD 。
题型2:两次全等1、AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF 。
FDCB A2、已知如图,E 、F 在BD 上,且AB =CD ,BF =DE ,AE =CF ,求证:AC 与BD 互相平分。
E A B E OF D C3、如图,在四边形ABCD 中,AD ∥BC ,∠ABC=90°DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE=AC.求证:BG=FG题型3:直角三角形全等(余角性质)1、如图,在等腰Rt △ABC 中,∠C =90°,D 是斜边上AB 上任一点,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F ,CH ⊥AB 于H 点,交AE 于G 。
求证:BD =CG 。
2、如图,将等腰直角三角形ABC 的直角顶点置于直线l 上,且过A ,B 两点分别作直线的垂线,垂足分别为D ,E ,请你在图中找出一对全等三角形,并写出证明它们全等的过程。
3、如图,∠ABC =90°,AB =BC ,D 为AC 上一点,分别过A 、C 作BD 的垂线,垂足分别为E 、F 求证:EF =CF -AE 。
AFC BDEGAO D C B 4、如图:BE ⊥AC ,CF ⊥AB ,BM=AC ,CN=AB 。
求证:(1)AM=AN ;(2)AM ⊥AN 。
题型4:连接法(构造全等三角形)1、已知:如图所示,AB =AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证:AE =AF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 已知:如图,点C 为线段AB 上一点,△ACM ,△CBN 是等边三角形,AM =AC =CM ,BC =CN =BN ,∠ACM =∠BCN =60°,连接AN 交CM 于点E ,连接BM 交CN 于点F .求证:①△CAN ≌△CMB ;②△CEN ≌△CFB .2. 已知:如图,在正方形ABCD 中,AD =AB ,∠D =∠DAB=∠ABC =90°,E ,F 分别为DC ,BC 边上的点,且∠EAF =45°,延长CB 到点G ,使BG =DE ,连接EF ,AG . 求证:①△ADE ≌△ABG ;②△AFE ≌△AFG .3. 已知:如图,∠A =∠D =90°,BE =EC .求证:△ABC ≌△DCB .第1题图NMCFEBF DECB A G 第2题图4. 已知:如图,点A ,E ,F ,C 在同一直线上,AE =CF ,过E ,F 分别作DE⊥AC ,BF ⊥AC ,连接AB ,CD ,BD ,BD 交AC 于点G .若AB =CD ,求证:△DEG ≌△BFG .5. 已知:如图,AB ,CD 相交于点O ,AO =BO ,CO =DO ,过点O 作EF 交AC于点E ,交BD 于点F .求证:OE =OF .6. 已知:如图,AB =AC ,BD =DC ,AD 与BC 交于点O .求证:AD ⊥BC .第4题图 A DEG BCF 第6题图AD O BC第5题图ADE OBC F7. 已知:如图,在△ABC 中,点D 是BC 的中点,DF ⊥AB ,DE ⊥AC ,垂足分别是F ,E ,DF =DE ,试猜想AB 和AC 的数量关系,并证明你的猜想.8. 已知:如图,AB =AE ,BC =ED ,∠B =∠E ,F 是CD 中点,求证:AF ⊥CD .1.已知:如图,AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F ,且BC =DC .试猜想BE 与DF 有怎样的数量关系?并说明理由.ABCEF D 12第7题图AD E BCF第8题图AD BCF2.已知:如图,O 是线段AC ,FE 的中点,OE ⊥AB 于E ,OF ⊥CD 于F ,DF =BE . 求证:AD =BC .3.已知:如图,点E 在直线AC 上,ED ⊥CD 于D ,EB ⊥CB 于B ,且CD =CB . 求证:AD =AB .ABCEDABCE FDO4.已知:如图,在四边形ABCD 中,AD =BC ,AB =DC ,E ,F 分别为AD ,CB 延长线上一点且DE =BF ,试说明∠E =∠F .ABCE FD1. 已知:如图,△ABC 是等边三角形,AB =BC =AC ,∠ACB =∠ABC =60°,∠EDF =60°,DB =DC , ∠DBC =∠DCB =30°,∠BDC=120°,延长AC 到点G ,使CG =BE .求证:①△EBD ≌△GCD ;②△EFD ≌△GFD .2. 已知:如图,AB =AC ,DB =DC ,F 是AD 的延长线上的一点.求证:△ABF ≌△ACF .AE BDGC FDAB FC3. 已知:如图,AB =AC ,AD =AE ,AB ,DC 相交于点M ,AC ,BE 相交于点N ,∠DAB =∠EAC .求证:△ADM ≌△AEN .4. 已知:如图,AC ⊥BC ,AD ⊥BD ,AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E ,F . 求证:CE =DF .5. 已知:如图,点C ,D 在线段BE 上,且BD =EC ,CA ⊥BA 于A ,DF ⊥EF于F ,且AB =EF .求证:CF =AD .N MCEBD ABDCA1、已知:如图,AB=CD ,AD=BC ,过AC 的中点O 作直线EF 交AB 的延长线于E ,交CD 的延长线于F.求证:OE=OF.2、已知:如图,∠D=∠E. AM=ME=CN=DN.问:AB 与BC 相等吗?请给予证明.3、已知点A ,C 在直线EF 上,AD =BC ,AB =DC ,AE =CF , 试说明E ∠与∠F 相等的理由.4、如图已知:三角形ABC 中,∠A =90°,AB =AC ,D 为BC 的中点,E ,F 分别是AB ,AC 上的点,且BE =AF ,求证:△DEF 为等腰直角三角形.5、将一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆放成如图的形式,使点B 、F 、C 、D 在同一条直线上。
⑴求证:AB ⊥ED⑵若PB=BC ,请找出图中与此条件有关的一对全等三角形,并给予证明。
A B CD OEF CN D ABE MACBDF E N MPFEDCBA6、如图,已知P 点是∠AOB 平分线上一点,PC ⊥OA ,PD ⊥OB ,垂足为C 、D , OP 是CD 的垂直平分线吗? 为什么?7、已知:如图,在梯形ABCD 中,AD ∥BC ,BC=DC ,CF 平分∠BCD ,DF ∥AB ,BF 的延长线交DC 于点E 。
求证: AD=DE、23.如图所示,A ,E ,F ,C 在一条直线上,AE =CF ,过E ,F 分别作DE ⊥AC ,BF ⊥AC ,若AB =CD ,可以得到BD 平分EF ,为什么?若将△DEC 的边EC 沿AC 方向移动,变为图时,其余条件不变,上述结论是否成立?请说明理由.)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MFCO B AD PG DF A C BE G DFA CB E(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.24.如图,△ABC 中,D 是BC 的中点,过D 点的直线GF 交AC 于F ,交AC 的平行线BG 于G 点,DE ⊥DF ,交AB 于点E ,连结EG 、EF .(1)求证:BG =CF . (2)请你判断BE +CF 与EF 的大小关系,并说明理由.1. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE9.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .F EDC B A G F E DCB A巧添辅助线——倍长中线【夯实基础】例:ABC ∆中,AD 是BAC ∠的平分线,且BD=CD ,求证AB=AC 方法1:作D E ⊥AB 于E ,作D F ⊥AC 于F ,证明二次全等 方法2:辅助线同上,利用面积 方法3:倍长中线AD△ABC 中方式1: 延长AD, AD 是BC 边中线 连接方式2:间接倍长作CF ⊥AD 于F ,延长MD作BE ⊥AD 的延长线于使连接BE 连接CN【经典例题】例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围提示:画出图形,倍长中线AD ,利用三角形两边之和大于第三边DFED CBA例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE方法1:过D 作DG ∥AE 交BC 于G ,证明ΔDGF ≌ΔCEF方法2:过E 作EG ∥AB 交BC 的延长线于G ,证明ΔEFG ≌Δ方法3:过D 作DG ⊥BC 于G ,过E 作EH ⊥BC 的延长线于H 证明ΔBDG ≌ΔECH例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 提示:倍长AD 至G ,连接BG ,证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠提示:方法1:倍长AE 至G ,连结DG 方法2:倍长FE 至H ,连结CH1. 正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.第 1 题图ABFDECCC4、如图,在四边形ABCD 中,BC >BA,AD =CD ,BD 平分ABC ∠, 求证: 0180=∠+∠C A2、如图,AC ∥BD ,EA,EB 分别平分∠CAB,∠DBA ,CD 过点E ,求证;AB =AC+BD如图,ABC ∆是边长为3的等边三角形,BDC ∆是等腰三角形,且0120BDC ∠=,以D 为顶点做一个060角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,则AMN ∆的周长为 ;BC如图,在△ABC 中,∠A =90°,且AB=AC ,BE 平分∠ABC 交AC 于F ,过C 作BE的垂线交BE 于E.求证:BF=2CE有以线段中点为端点的线段时,常延长加倍此线段,构造全等三角形。
例::如图2:AD 为△ABC 的中线,且∠1=∠2,∠3=∠4,求证:BE +CF >EFABCE F2图ABCDE FM 1234。
