您的位置：360文档中心› 浙教版中考数学压轴题精选

浙教版中考数学压轴题精选

合集下载

专题4.2 坐标系中平移的几何综合(压轴题专项讲练)(浙教版)(原卷版)

专题4.2 坐标系中平移的几何综合(压轴题专项讲练)(浙教版)(原卷版)

专题4.2 坐标系中平移的几何综合【典例1】如图，在平面直角坐标系中，点A，B的坐标分别为A(0，3)，B(6，3)，现同时将点A，B分别向下平移3个单位，再向左平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．（1）求点C，D的坐标；（2）点M从O点出发，以每秒1个单位的速度向上平移运动．设运动时间为t秒，问：是否存在这样的t使得四边形OMDB的面积为12？若存在，请求出t的值，若不存在，请说明理由．（3）在（2）的条件下，点M从O点出发的同时，点N从D点出发，以每秒2个单位的速度向左平移运动，当点N到达点O时运动停止．设射线BN交y轴于点E．设运动时间为t秒，问：S△EMB−S△OEN的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．（1）根据点的坐标及平移方法即可确定；（2）过B作BH⊥OD的延长线，垂足为H．由（1）中点的坐标得出D=6,DH=2,OD=4，AB=6，设M点坐标为（0，t），连接MB、OB，则四边形OMDB的面积等于△OBD的面积加上△OMD的面积等于12，然后解出t即可；（3）设运动时间为t秒，OM=t，ON=4-2t(0≤t≤2)，过B作BH⊥OD的延长线，垂足为H，连接MB，OB，结合图形可得SΔEMB−SΔOEN=S△ONB+S△OMB，然后代入求解即可．（1）解：∵点A，B的坐标分别为A(0，3)，B(6，3)，将点A，B分别向下平移3个单位，再向左平移2个单位∴C（-2,0），D（4,0）；（2）解：存在；如图，过B作BH⊥OD的延长线，垂足为H．由题意得点C 和点D 的坐标分别为（-2,0）和（4,0）．A (0，3)，B (6，3)，∴CD =6,DH =2,OD =4，AB =6，设M 点坐标为（0，t ），连接MB 、OB ，∴OM =t ．∵S 四边形OMBD =S △OBD +S △OMB =12，∴12OD·BH +12OM·AB =12,即12×4×3+12t ×6=12，解得t =2；（3）解：不变．理由如下：如图所示，设运动时间为t 秒，OM =t ，ON =4-2t (0≤t≤2)，过B 作BH ⊥OD 的延长线，垂足为H ，连接MB ，OB ，∵S ΔEMB −S ΔOEN =S 四边形OMBN ，S 四边形OMBN =S △ONB +S △OMB ，∴S ΔEMB −S ΔOEN =S △ONB +S △OMB=12ON·BH +12OM·AB=12×(4−2t )×3+12t ×6=6-3t+3t=6；∴SΔEMB−SΔOEN为定值6，故其值不会变化．1．（2022春·四川自贡·七年级四川省荣县中学校校考阶段练习）如图，在正方形网格中，横、纵坐标均为整数的点叫做格点，点A、B、C、O均在格点上，其中O为坐标原点，A(﹣3，3)．（1）点C的坐标为 ；（2）将△ABC向右平移6个单位，向下平移1个单位，对应得到△A1B1C1，请在图中画出平移后的△A1B1C1，并求△A1B1C1的面积；（3）在x轴上有一点P，使得△PA1B1的面积等于△A1B1C1的面积，直接写出点P坐标．2．（2022春·广东韶关·七年级统考期中）如图，平面直角坐标系中，已知点A(−3,3)，B(−5,1)，C(−2,0)，P(a,b)是ΔABC的边AC上任意一点，ΔABC经过平移后得到△A1B1C1，点P的对应点为P1(a+6,b−2)．（1）直接写出点A1，B1，C1的坐标．（2）在图中画出△A1B1C1．（3）连接AA1，AO，A1O，求ΔAOA1的面积．（4）连接BA1，若点Q在y轴上，且三角形QBA1的面积为8，请直接写出点Q的坐标．3．（2022春·湖南湘西·七年级统考阶段练习）如图，在平面直角坐标系中，A（-1，-2），B（-2，-4），C （-4，-1）．（1）把△ABC向上平移2个单位长度，再向右平移1个单位长度后得到△A1B1C1，请画出△A1B1C1，并写出点A的对应点的坐标；（2）求△A1B1C1的面积；（3）点P在坐标轴上，且△A1B1P的面积是2，直接写出点P的坐标_____________________．4．（2022春·北京西城·九年级校考期中）如图，在平面直角坐标系中，△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（﹣1，0）．（1）在坐标系中画出△ABC并写出△ABC的面积为．（2）点P（a﹣4，b+2）是△ABC内任意一点．将△ABC平移至△A1B1C1的位置，点A，B，C，P的对应点分别是A1，B1，C1，P1．若点P1的坐标为（a，b）．在坐标系中画出△A1B1C1．（3）若坐标轴上存在一点M，使△BCM的面积等于△ABC的面积，求点M的坐标．5．（2022秋·八年级课时练习）如图（1），在平面直角坐标系中，已知点A(m,0)，B(n,0)，且m，n满足(m+2)2+=0，将线段AB向右平移2个单位长度，再向上平移4个单位长度，得到线段CD，其中点C与点A对应，点D与点B对应，连接AC，BD．（1）求点A、B、C、D的坐标；（2）在x轴上是否存在点P，使三角形PBC的面积等于平行四边形ABDC的面积？若存在，求出点P的坐标；若不存在，请说明理由；（3）如图（2），点E在y轴的负半轴上，且∠BAE=∠DCB．求证：AE//BC．6．（2022秋·八年级单元测试）如图1，在平面直角坐标系中，点A，B的坐标分别是(−2,0)，(4,0)，现同时将点A，B分别向上平移2个单位长度，再向右平移2个单位长度，得到A，B的对应点C，D，连接AC，BD，CD．（1）点C的坐标为_________，点D的坐标为_________，四边形ABDC的面积为_________；（2）在x轴上是否存在一点E，使得△DEC的面积是△DEB面积的2倍？若存在，请求出点E的坐标；若不存在，请说明理由．（3）如图2，点P是线段BD上一动点（B，D两点除外），试说明∠CPO与∠1+∠2的大小关系，并说明理由．7．（2023春·全国·八年级专题练习）在平面直角坐标系中，点A，B的坐标分别为(2,0)，(−2,0)，现将线段AB先向上平移3个单位，再向右平移1个单位，得到线段DC，连接AD，BC．（1）如图1，求点C，D的坐标及四边形ABCD的面积；（2）如图1，在y轴上是否存在点P，连接PA，PB，使S△PAB=S四边形ABCD？若存在这样的点，求出点P的坐标；若不存在，试说明理由；S四边形ABD？若存在这（3）如图2，点E为CD与y轴交点，在直线CD上是否存在点Q，连接QB，使S△QCB=14样的点，直接写出点Q的坐标；若不存在，试说明理由；8．（2022秋·八年级单元测试）规定：如果图形G′是由图形G经过平移所得，那么把图形G′称为图形G的“友好图形”，两个图形上对应点的距离称为图形G′与G的“友好距离”在平面直角坐标系xOy中，已知点A（3，0）．（1）①如图1，若点A的“友好图形”点B（3，6），则点A与点B的“友好距离”是______；②若点A的“友好图形”点A′在y轴上，则点A与点A′的“友好距离”最小值为______；（2）若点A的“友好图形”点C在x轴上，点A与点C的“友好距离”是4，点D在y轴上，且三角形ACD 的面积为10，求点D的坐标；（3）如图3，若点E（0，6），直线AE的“友好图形”直线A′E′恰好过点F（0，－2），且点A的“友好图形”点A′在x轴上，求点A与点A′的“友好距离”．9．（2022秋·八年级单元测试）如图，在长方形ABCD中，AB＝10cm，BC＝6cm，E为DC的中点．（1）以A为原点（即O与A重合），以AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系，则C的坐标为 ；（2）若（1）中长方形以每秒2cm的速度沿x轴正方向移动2秒后，得到长方形A1B1C1D1，则C1的坐标为 ，长方形A1BCD1的面积为 cm2；（3）若（1）中长方形以每秒2cm的速度沿x轴正方向移动，运动时间为t，用含t的式子直接表示出长方形A1BCD1的面积 （线段可以看成是面积为0的长方形）；点E移动后对应点为F，直接写出t为何值时长方形A1BCD1的面积是三角形FBB1的3倍？10．（2023春·全国·八年级专题练习）如图，平面直角坐标系中，A(a,0)，B(0,b)，C(0,c)|2−b| =0，c=1(a−b)．2（1）求△ABC的面积；（2）如图2，点A以每秒m个单位的速度向下运动至A′，与此同时，点Q从原点出发，以每秒2个单位的速度沿x轴向右运动至Q′，3秒后，A′、C、Q′在同一直线上，求m的值；（3）如图3，点D在线段AB上，将点D向右平移4个单位长度至E点，若△ACE的面积等于14，求点D坐标．11．（2022·全国·八年级假期作业）如图，在平面直角坐标系中，点A2，6，B(4,3)，将线段AB进行平移，使点A刚好落在x轴的负半轴上，点B刚好落在y轴的负半轴上，A，B的对应点分别为A′，B′，连接AA′交y轴于点C，BB′交x轴于点D．（1）线段A′B′可以由线段AB经过怎样的平移得到？并写出A′，B′的坐标；（2）求四边形AA′BB′的面积；（3）P为y轴上的一动点（不与点C重合），请探究∠PCA′与∠A′DB′的数量关系，给出结论并说明理由．12．（2022春·福建厦门·七年级统考期末）在平面直角坐标系中，O为坐标原点，将三角形ABC进行平移，平移后点A,B,C的对应点分别是点D,E,F，点A(0,a)，点B(0,b)，点D a,12a，点E m−b,12a+4.（1）若a=1，求m的值；（2）若点C−a,14m+3，其中a>0. 直线CE交y轴于点M，且三角形BEM的面积为1，试探究AF和BF的数量关系，并说明理由.13．（2022春·内蒙古通辽·七年级统考期中）已知点A在平面直角坐标系中第一象限内，将线段AO平移至线段BC，其中点A与点B对应．（1）如图（1），若A(1,3),B(3,0)，连接AB，AC，在坐标轴上存在一点D，使得S△AOD=2S△ABC，求点D 的坐标；（2）如图（2），若∠AOB=60°，点P为y轴上一动点（点P不与原点重合），请直接写出∠CPO与∠BCP 之间的数量关系（不用证明）．14．（2023·全国·七年级专题练习）如图在平面直角坐标系中，点A，B的坐标分别为A(a,0)，B(b,0)．且a，b满足|a+3|+(a−2b+7)2=0，现同时将点A，B分别向左平移2个单位，再向上平移2个单位，分别得到点A、B的对应点C、D，连接AC，BD，CA的延长线交y轴于点K．（1）点P是线段CK上的一个动点，点Q是线段CD的中点，连接PQ，PO，当点P在线段CK上移动时（不与A，C重合），请找出∠PQD，∠OPQ，∠POB的数量关系，并证明你的结论．（2）连接AD，在坐标轴上是否存在点M，使△MAD的面积与△ACD的面积相等？若存在，直接写出点M 的坐标；若不存在，试说明理由．15．（2022春·吉林·七年级统考期中）如图，在平面直角坐标系中，点A，B的坐标分别为（−1，0），（3，0）．现将线段AB向上平移2个单位，再向右平移1个单位，得到线段AB的对应线段CD，连接AC，BD．ABDC；（1）点C，D的坐标分别为_______，________，并求出四边形ABDC的面积S四边形（2）在y轴上存在一点P，连接PA，PB，且S△PAB =S四边形ABDC，求出满足条件的所有点P的坐标．（3）若点Q为线段BD上一点（不与B，D______（填“变”或“不变”）．16．（2022春·福建福州·七年级福建省福州第十六中学校考期中）如图，在平面直角坐标系中，点A，B的坐标分别为（0，1），（0，﹣3），现将点A向右平移2个单位，再向下平移1个单位，得到点C，点D 在点C的下方，CD∥x轴，且CD的长度为4，连接AC，BD，CD．（1）填空：点D的坐标为 ．（2）若P点在直线BD上运动，连接PC、PO．①若P在线段BD上（不与B，D重合），求S△CDP+S△BOP的取值范围．②若P在直线BD上运动，请在考卷的图中画出相应的示意图，并写出∠CPO、∠DCP、∠BOP的数量关系．17．（2022秋·江苏·八年级专题练习）如图，已知点A(a,0)、B(b,0)满足(3a+b)2+|b−3|=0．将线段AB 先向上平移2个单位，再向右平移1个单位后得到线段CD，并连接AC、BD．（1）请求出点A和点B的坐标；（2）点M从O点出发，以每秒1个单位的速度向上平移运动．设运动时间为t秒，问：是否存在这样的t，使得四边形OMDB的面积等于9？若存在，请求出t的值：若不存在，请说明理由；（3）在（2）的条件下，点M从O点出发的同时，点N从点B出发，以每秒2个单位的速度向左平移运动，设射线DN交y轴于点E．设运动时间为t秒，问：SΔEMD−SΔOEN的值是否会发生变化？若不变，请求出它的值：若变化，请说明理由．18．（2023春·全国·七年级专题练习）在平面直角坐标系中，A(a,0)，B(1,b)，a，b满足|a+b−1|+=0，连接AB交y轴于C．（1）直接写出a=______，b=______；（2）如图1，点P是y轴上一点，且三角形ABP的面积为12，求点P的坐标；（3）如图2，直线BD交x轴于D(4,0)，将直线BD平移经过点A，交y轴于E，点Q(x,y)在直线AE上，且，求点Q横坐标x的取值范围．三角形ABQ的面积不超过三角形ABD面积的13。

【玩转压轴题】必考3：相似三角形的综合(原卷版)-浙教版2022年初三数学期末压轴题精选汇编

【玩转压轴题】必考3：相似三角形的综合(原卷版)-浙教版2022年初三数学期末压轴题精选汇编

【玩转压轴题】必考3：相似三角形的综合（原卷版）一、单选题1．如图，C 是线段AB 上的任一点，分别以,,AB AC BC 为直径在线段AB 同侧作半圆，则这三个半圆周围成的图形被阿基米德称为“鞋匠刀形”（即图中阴影部分）．当“鞋匠刀形”的面积等于以BC 为直径的半圆的面积时，过C 作CD AB ⊥，交圆周于点D ，连结BD ，则CD 与BC 的比值为（ ）A ．12B C ．13D 2．如图，在△ABC 中，∠CAB ＝45°，以其三边为边向外作正方形，连接GC 并延长交BH 于点L ，过点C 作CK ⊥DE 于点K ．若L 为BH 中点，则GL CK 的值为（ ）A ．1B ．98C D3．如图，矩形ABCD 中，6,8AB BC ==．点E 、F 分别为边BC 、AD 上一点，连接EF ，将矩形ABCD 沿着EF 折叠，使得点A 落到边CD 上的点A '处，且2DA A C '='，则折痕EF 的长度为（ ）A ．B ．CD 4．如图，在ABC 中，AE 和BD 是高，45ABE ∠=︒，点F 是AB 的中点，BD 与FE AE､分别交于点,G H ，CAE ABD ∠=∠．有下列结论：①FD FE =；②2BH CD =；③22BD BH BE ⋅=；④43ABC BCDFS S =△四边形．其中正确的有（ ）A ．①③B ．②④C ．①②③D ．①②④5．如图，E ，F ，G ，H 分别是矩形ABCD 四条边上的点，连结EG ，HF 相交于点O ，//EG AD ，//FH AB ，矩形BFOE ∽矩形OGDH ，连结AC 交EG ，FH 于点P ，Q ．下列一定能求出BPQ ∆面积的条件是（ ）A ．矩形BFOE 和矩形OGDH 的面积之差B ．矩形ABCD 与矩形BFOE 的面积之差C ．矩形BFOE 和矩形FCGO 的面积之差D ．矩形BFOE 和矩形EOHA 的面积之差6．如图，在ABC 中，90ACB ∠=︒，以ABC 的各边为边分别作正方形ACDE ，正方形BCFG 与正方形ABMN ，AN 与FG 相交于点H ，连结NF 并延长交AE 于点P ，且2NF FP =．记ABC 的面积为1S ，FNH △的面积为2S ，若1221S S -=，则BC 的长为（ ）A ．6B ．C ．8D ．97．如图，将边长为6的正六边形ABCDEF 沿HG 折叠，点B 恰好落在边AF 的中点上，延长B C ''交EF 于点M ，则C M '的长为（ ）A ．1B ．65C ．56D ．958．如图，等腰Rt ABC 中，90BAC AD BC ∠=︒⊥，于D ，ABC ∠的平分线分别交AC AD 、于E F 、两点，M 为EF 的中点，延长AM 交BC 于点N ，连接DM MC 、下列结论：①DF DN =；②ABE MBN ≌；③ CMN 是等腰三角形；④AE CN =，其中正确的是（ ）A ．①②B ．①④C ．①③D ．②③9．勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在Rt ABC 中，()90,,BAC AC a AB b a b ∠=︒==<．如图所示作矩形HFPQ ，延长CB 交HF 于点G ．若正方形BCDE 的面积等于矩形BEFG 面积的3倍，则ab的值为（ ）A B C D 35210．如图，在正方形ABCD 中，对角线AC ，BD 相交于点O ，点E 在DC 边上，且2CE DE =，连接AE 交BD 于点G ，过点D 作DF AE ⊥，连接OF 并延长，交DC 于点P ，过点O 作⊥OQ OP 分别交AE ，AD 于点N ，H ，交BA 的延长线于点Q ，现给出下列结论：①45AFO ∠=︒；②2N P O D H H =⋅；③Q OAG ∠=∠；④OG DG =．其中正确的结论有（ ）A ．①③B ．②④C ．①②③D ．①②③④二、填空题11．如图，在矩形ABCD 中，6AB =，8AD =．连接BD ，DBC ∠的角平分线BE 交DC 于点E ，现把BCE 绕点B 逆时针旋转，记旋转后的BCE 为BC E ''△．当射线BE '和射线BC '都与线段AD 相交时，设交点分别为F ，G ．若BFD △为等腰三角形，则线段DG 长为______．12．如图，点D 是等边ABC 边BC 上一点，将等边ABC 折叠，使点A 与点D 重合，折痕为EF （点E 在边AB 上）．（1）当点D 为BC 的中点时，:AE EB =__； （2）当点D 为BC 的三等分点时，:AE EB =__．13．小明想设计一款如图1所示的喷水壶，于是他绘制了如图2所示的设计图，壶身的主视图呈矩形ABCD ，壶把手呈圆弧状，圆心O 落在AD 上，圆弧交CD 于点E ．支撑架HF 所在直线恰好经过O ．壶嘴GI 的端点I 恰好在AD 所在直线上．已知258cm,4cm,cm, 6.5cm 12AD DE AF HF FG =====，则半径AO 的长为________cm ，壶嘴GI 的长度为________cm ．14．如图，AB 是半圆O 的直径．点C 在半径OA 上，过点C 做CD AB ⊥交半圆O 于点D ．以,CD CA 为边分别向左、下作正方形,CDEF CAGH ．过点B 作GH 的垂线与GH 的延长线交于点I ，M 为HI 的中点．记正方形,CDEF CAGH ，四边形BCHI 的面积分别为123,,S S S ．（1）若:2:3AC BC =，则12S S 的值为_______；（2）若D ，O ，M 在同一条直线上，则123S S S +的值为______．15．四个全等的直角三角形如图摆放成一个风车的形状，形成正方形ABCD 和正方形IJKL ．若BF 平分∠ABK ，AF ：FK ＝5：3，风车周长为面积和是___．16．用一张正方形纸片折成一个“小蝌蚪”图案（如图1）．如图2，正方形ABCD 的边长为2，等腰直角ACE 的斜边AE 过点D ．点F 为CE 边上一点，连结AF 交CD 于点G ，将AEF 沿AF 对称得AE F '，AE '与BC 交于点H ．当//FE CD '时，E FA '∠=______︒；当点G 为CD 的中点时，则CF 的长为______．17．如图，点A C 、分别是x 轴、y 轴正半轴上的点，矩形ABCO 的边,AB BC 分别交函数ky x=（0,0,x k k >≠为常数）的图象于点,P Q ，连接PQ ． （1）若P 为AB 中点，则BQBC=___． （2）若把BPQ ∆沿PQ 翻折，点B 恰好落在x 轴上的点E ，且6,2OE EA ==，则k =___．18．如图，在ABCD 中，E 是BC 边上的中点，AP CD ⊥于点P ，将ABE △沿AE 翻折，点B 的对称点B '落在AP 上，延长EB '恰好经过点D ，若4AB =，则折痕AE 的长为________．19．如图，点A ，B 分别是反比例函数(0,0)a y a x x =>>和(0,0)by b x x=<<图象上的点，且//AB x 轴，点C 在x 轴的正半轴上，连接AC 交反比例函数(0,0)ay a x x=>>的图象于点D ，已知20BOD S =△，8COD S =△，2AD CD =，则-a b 的值为______．20．如图1是护眼台灯，该台灯的活动示意图如图2所示．灯柱6cm BC ，灯臂AC 绕着支点C 可以旋转，灯罩呈圆弧形（即弧AD 和弧EF ）．在转动过程中，AD （EF ）总是与桌面BH 平行．当AC BH ⊥时，51cm AB =．DM MH ⊥，测得42cm DM =（点M 在墙壁MH 上，且MH BH ⊥）；当灯臂AC 转到CE 位置时，FN MH ⊥，测得15cm FN =，则点E 到桌面的距离为______cm ．若此时点C ，F ，M 在同一条直线上，弧EF 的最低点到桌面BH 的距离为31cm ，则弧EF 所在圆的半径为_____cm （保留一位小数）．三、解答题 21．特例感知（1）如图，已知在Rt ABC 中，90BAC ∠=︒，AB AC =，取BC 边上中点D ，连结AD ，点E 为AB 边上一点，连结DE ，作DF DE ⊥交AC 于点F ，求证BE AF =；探索发现（2）如图，已知在Rt ABC 中，90BAC ∠=︒，3AB AC ==，取BC 边上中点D ，连结AD ，点E 为BA 延长线上一点，1AE =，连结DE ，作DF DE ⊥交AC 延长线于点F ，求AF 的长；类比迁移（3）如图，已知在ABC 中，120BAC ∠=︒，4AB AC ==，取BC 边上中点D ，连结AD ，点E 为射线BA 上一点（不与点A 、点B 重合），连结DE ，将射线DE 绕点D 顺时针旋转30°交射线CA 于点F ，当4AE AF =时，求AF 的长．22．（证明体验）（1）如图1，AD 为ABC 的角平分线，60ADC ∠=︒，点E 在AB 上，AE AC =．求证：DE 平分ADB ∠．（思考探究）（2）如图2，在（1）的条件下，F 为AB 上一点，连结FC 交AD 于点G ．若FB FC =，2DG =，3CD =，求BD 的长．（拓展延伸）（3）如图3，在四边形ABCD 中，对角线AC 平分,2BAD BCA DCA ∠∠=∠，点E 在AC上，EDC ABC ∠=∠．若5,2BC CD AD AE ===，求AC 的长． 23．（推理）如图1，在正方形ABCD 中，点E 是CD 上一动点，将正方形沿着BE 折叠，点C 落在点F 处，连结BE ，CF ，延长CF 交AD 于点G ．（1）求证：BCE CDG △△≌． （运用）（2）如图2，在（推理）条件下，延长BF 交AD 于点H ．若45HD HF =，9CE =，求线段DE 的长． （拓展）（3）将正方形改成矩形，同样沿着BE 折叠，连结CF ，延长CF ，BF 交直线AD 于G ，两点，若AB k BC =，45HD HF =，求DEEC的值（用含k 的代数式表示）．24．在Rt ABC 中，90ACB ∠=︒，点D 在直线AC 上，连结BD ，以BD 为边作等腰直角BDE （点E 在直线BD 右侧），连结CE ．（1）如图1，若45A ∠=︒，且点D 在AC 边上，求证：ABD CBE ∽△△； （2）如图2，若045A ︒<∠<︒，且12BC =，5CD =，求CE 的长；（3）如图3，若点D 在AC 的延长线上，BD ，CE 相交于点F ，设CDF 的面积为1S ，BEF 的面积为2S ，BCF △的面积为3S ，则2123122BC S S S =-+，请说明理由．25．如图，四边形ABCD 是矩形，20AB =，10BC =，以CD 为一边向矩形外部作等腰直角CDG ，90G ∠=︒．点M 在线段AB 上，且AM a =，点P 沿折线AD DG -运动，点Q 沿折线BC CG -运动（P ，Q 与点G 不重合），在运动过程中终保持//PQ AB ．设PQ 与AB 之间的距离为x ，四边形AMQP 的面积为y ．（1）若12a =，回答下列问题：①当点P 在线段AD 上时，若四边形AMQP 的面积为48，则x =______． ②求整个运动过程中，y 关于x 的函数解析式，并求出y 的最大值；（2）如图2，若点P 在线段DG 上时，要使四边形AMQP 的面积始终不小于50，求a 的取值范围．26．如图1，在矩形ABCD 中，动点P 沿着边AB 从点A 运动到点B ，同时动点Q 沿着边BC ，CD 从点B 运动到点D ．它们同时到达终点，若点Q 的运动路程x 与线段BP 的长，满足487y x =-+，BD 与PQ 交于点E ． （1）求AB ，BC 的长．（2）如图2．当Q 在CD 上时，求BEDE． （3）将矩形沿着PQ 折叠，点B 的对应点为点F ，连结EF ，当EF 所在直线与BCD △的一边垂直时，求BP 的长．27．如图1，在ABC 中，90A ∠=︒，当点P 从点A 出发，沿着AB 方向匀速运动到点B 时，点Q 恰好从点B 出发，沿着BC 方向匀速运动到点C ，连结PQ ，记,AP x CQ y ==，已知554y x =-+．（1）求AB和BC的长．（2）当BPQ是以PQ为腰的等腰三角形时，求x的值．（3）如图2，直线l是线段PQ的垂直平分线．①若直线l过点B，交AC于点D，请判断四边形BQDP的形状，并说明理由；②A'是点A关于直线l的对称点，若点A'落在ABC的内部，请直接写出x的取值范围．28．如图，四边形ABCD为边长等于7的菱形，其中∠B=60°，点E在对角线AC上，且AE=1，点F在射线CB上运动，连接EF，作∠FEG=60°，交DC延长线于点G．（1）当点F与B点重合时，试判断△EFG的形状，并说明理由；（2）以点B为原点，BC所在的直线为x轴建立平面直角坐标系，当CF=10时，平面内是否存在一点M，使得以点M、E、F、G为顶点的四边形与菱形ABCD相似？若存在，求M的坐标，若不存在，说明理由；（3）记点F关于直线AB的轴对称点为点N，若点N落在∠EDC的内部（不含边界），求CF的取值范围．29．如图，在△ABC中，AC＝BC＝tan∠CAB＝12，P为AC上一点，PD⊥AB交AB于点E，AD⊥AC交PD于点D，连结BD，CD，CD交AB于点Q．（1）若CD⊥BC，求证：△AED∽△QCB；（2）若AB平分∠CBD，求BQ的长；（3）连结PQ并延长交BD于点M．①当点P是AC的中点时，求tan∠BQM的值②当PM平行于四边形ADBC中的某一边时，求BMDM的值．30．如图，已知AB是⊙O的弦，OB＝1，C是弦AB上的任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．设∠B＝α，∠ADC＝β．（1）求∠BOD的度数（用含α，β的代数式表示）；（2）若α＝30°，当AC的长度为多少时，以点A、C、D为顶点的三角形与B、C、O 为顶点的三角形相似？请写出解答过程．（3）若α＝β，连接AO，记△AOD、△AOC、△COB的面积分别为S1，S2，S3，如果S2是S1和S3的比例中项，求OC的长．。

浙江省中考数学真题压轴题分类汇编

浙江省中考数学真题压轴题分类汇编

浙江省中考数学真题压轴题分类汇编一、压轴题--四边形1、（衢州）在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连结OB，D为OB的中点。

点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF。

已知点E从A 点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒。

(1)如图1，当t=3时，求DF的长；(2)如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值；(3)连结AD，当AD将△DEF分成的两部分面积之比为1:2时，求相应t的值。

2、（丽水）如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连结AF，BF，EF，过点F作GF⊥AF交AD于点G，设=n.(1)求证：AE=GE；(2)当点F落在AC上时，用含n的代数式表示的值；(3)若AD=4AB，且以点F，C，G为顶点的三角形是直角三角形，求n的值.二、压轴题--圆3、（•杭州）如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，(1)点点同学通过画图和测量得到以下近似数据：ɑ30°40°50°60°β120°130°140°150°γ150°140°130°120°猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：(2)若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．4、（•温州）如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．(1)当∠APB=28°时，求∠B和的度数；(2)求证：AC=AB．(3)在点P的运动过程中①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比．5、（•宁波）有两个内角分别是它们对角的一半的四边形叫做半对角四边形．(1)如图1，在半对角四边形ABCD中，∠B＝∠D，∠C＝∠A，求∠B与∠C的度数之和；(2)如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．求证：四边形DBCF是半对角四边形；(3)如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当DH＝BG时，求△BGH与△ABC的面积之比．三、压轴题--方程6、（·台州）在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根，比如对于方程，操作步骤是：第一步：根据方程系数特征，确定一对固定点A（0，1），B（5，2）;第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C 的横坐标m即为该方程的一个实数根（如图1）第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D 的横坐标为n即为该方程的另一个实数根。

浙教版中考压轴题精选

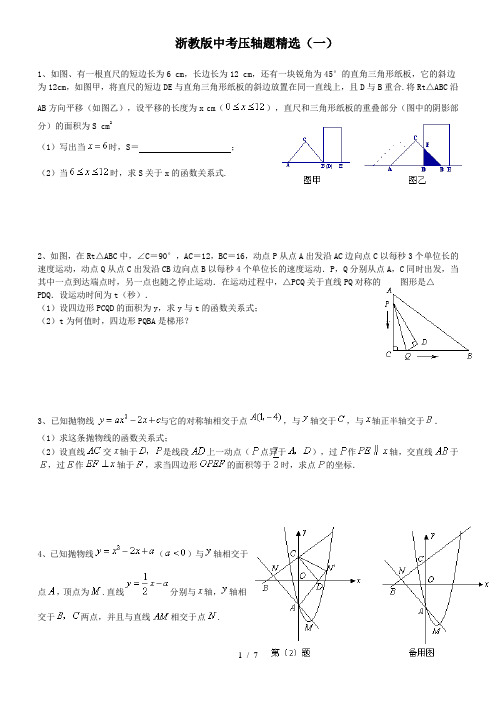
浙教版中考压轴题精选

浙教版中考压轴题精选（一）1、如图、有一根直尺的短边长为6 cm，长边长为12 cm，还有一块锐角为45°的直角三角形纸板，它的斜边为12cm，如图甲，将直尺的短边DE与直角三角形纸板的斜边放置在同一直线上，且D与B重合.将Rt△ABC沿AB方向平移（如图乙），设平移的长度为x cm（），直尺和三角形纸板的重叠部分（图中的阴影部分）的面积为S cm2（1）写出当时，S＝；（2）当时，求S关于x的函数关系式.2、如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝16，动点P从点A出发沿AC边向点C以每秒3个单位长的速度运动，动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动．P，Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ关于直线PQ对称的图形是△PDQ．设运动时间为t（秒）．（1）设四边形PCQD的面积为y，求y与t的函数关系式；（2）t为何值时，四边形PQBA是梯形？3、已知抛物线与它的对称轴相交于点，与轴交于，与轴正半轴交于．（1）求这条抛物线的函数关系式；（2）设直线交轴于是线段上一动点（点异于），过作轴，交直线于，过作轴于，求当四边形的面积等于时，求点的坐标．4、已知抛物线（）与轴相交于点，顶点为.直线分别与轴，轴相交于两点，并且与直线相交于点.(1)填空：试用含的代数式分别表示点与的坐标，则；(2)如图，将沿轴翻折，若点的对应点′恰好落在抛物线上，′与轴交于点，连结，求的值和四边形的面积；(3)在抛物线（）上是否存在一点，使得以为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，试说明理由.6．如图13，二次函数的图像与x轴交于A、B两点，与y轴交于点C（0，-1），ΔABC的面积=（1）求该二次函数的关系式；（2）在该二次函数的图像上是否存在点D，使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。

2024杭州中考数学压轴题

2024杭州中考数学压轴题

中考数学试卷一、单项选择题（共12分）1.如图图形中是中心对称图形的为（）A．B． C． D．2.如图，四边形ABCD是矩形，E是边BC延长线上的一点，AE与CD相交于点F，则图中的相似三角形共有（）A．4对 B．3对C．2对D．1对3.在正方形网格中，△ABC的位置如图所示，则tanB的值为（）A．1B．√22C．√3D．√334.一元二次方程x2﹣3x＝0的根是（）A．x＝3 B．x1＝0，x2＝﹣3C．x1＝0，x2=√3D．x1＝0，x2＝35.一个由相同正方体堆积而成的几何体如图所示，从正面看，这个几何体的形状是（）。

A．B．C．D．6.如图，实数a，b，c，d在数轴上表示如下，则最小的实数为（）A.aB.bC.cD.d二、填空题（共24分）7.把一张半径为2cm，圆心角为120°的扇形纸片卷成一个圆锥的侧面，那么这个圆锥的底面积是。

8．已知方程x2+mx﹣6＝0的一个根为﹣2，则另一个根是。

9.如图，正方形ABCD的面积为4，点E,F,G,H分别为边AB,BC,CD,AD的中点，则四边形EFGH的面积为____.三、解答题（共20分）10.如图，在矩形ABCD中，AB=4，BC=6，M是BC的中点，DE⊥AM于点E。

(1)求证：△ADE∽△MAB；(2)求DE的长。

11.已知△ABC和△DEF中，有ABDE =BCEF=CAFD=23，且△DEF和△ABC的周长之差为15厘米，求△ABC和△DEF的周长。

16.某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件。

（1）当每件的销售价为52元时，该纪念品每天的销售数量为件；（2）当每件的销售价x为多少时，销售该纪念品每天获得的利润y最大？并求出最大利润。

12.如图，D，E分别是△ABC的边AB，AC上的点，DE∥BC，AB＝7，AD＝5，DE＝10，求BC的长．13.如图，一艘渔船正以60海里/小时的速度向正东方向航行，在A处测得岛礁P在东北方向上，继续航行1.5小时后到达B处，此时测得岛礁P在北偏东30∘方向，同时测得岛礁P正东方向上的避风港M在北偏东60∘方向．为了在台风到来之前用最短时间到达M处，渔船立刻加速以75海里/小时的速度继续航行小时即可到达多少？（结果保留根号）14．如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC交BC的延长线于点E。

浙江省初中数学压轴题精选

浙江省初中数学压轴题精选

CBA数学试卷（一）7．已知下列命题：①若00a b >>，，则0a b +>；②若a b ≠，则22a b ≠； ③直角三角形斜边上的中线等于斜边的一半。

④菱形的对角线互相垂直． 其中原命题与逆命题均为真命题的个数是（ ） (A)4个 (B)3个 (C)2个 (D)1个8．如图，在Rt ABC △中，90ACB ∠=°，3BC =，4AC =，AB 的垂 直平分线DE 交BC 的延长线于点E ，则CE 的长为（ ）(A)32 (B)76 (C)256(D)2 9．如图，点A 在双曲线6y x=上，且OA ＝4，过A 作AC ⊥x 轴，垂足为C ，OA 的垂直平分线交OC 于B ，则△ABC 的周长为()(A) 47(B)5 (C) 27 (D)2210．如图，C 为⊙O 直径AB 上一动点，过点C 的直线交⊙O 于D 、E 两点，且∠ACD=45°，DF ⊥AB 于点F,EG ⊥AB 于点G,当点C 在AB 上运动时，设AF=x ，DE=y ，下列中图象中，能表示y 与x 的函数关系式的图象大致是（ ）14．若一边长为40㎝的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过，则铁圈直径的最小值为 ▲ ㎝．(铁丝粗细忽略不计) 15．将一副三角板按如图1位置摆放,使得两块三角板的直角边AC 和MD 重合.已知AB =AC =8 cm,将△MED 绕点A (M )逆时针旋转60°后(图2),两个三角形重叠（阴影）部分的面积是 ▲ cm 216．如图所示，在ABC Rt ∆中，︒=∠90C ，8,6==BC AC ，若以C 为圆心，R 为半径所得的圆与斜边AB 只有一个公共点，则R 的取值范围是： ▲ 。

22．(本小题满分10分)某公司有A 型产品40件，B 型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：AD B EC图2A (M )E DC BDBA M )(第15题)（1）设分配给甲店A 型产品件，这家公司卖出这100件产品的总利润为W （元），求W 关于x 的函数关系式，并求出x 的取值范围；（2）若公司要求总利润不低于17560元，说明有多少种不同分配方案，并将各种方案设计出来；（3）为了促销，公司决定仅对甲店A 型产品让利销售，每件让利a 元，但让利后A 型产品的每件利润仍高于甲店B 型产品的每件利润．甲店的B 型产品以及乙店的A B ，型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大？23．(本小题满分10分)已知一个直角三角形纸片OAB ，其中9024AOB OA OB ∠===°，，．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ． （1）若折叠后使点B 与点A 重合，求点C 的坐标；（2）若折叠后点B 落在边OA 上的点为B '，设OB x '=，OC y=，试写出y 关于x 的函数解析式，并确定y 的取值范围；（3）若折叠后点B 落在边OA 上的点为B '，且使B D OB '∥，求此时点C 的坐标．24．(本小题满分12分)如图，已知抛物线与x 轴交于点(20)A -，，(40)B ，，与y 轴交于点(08)C ，．（1）求抛物线的解析式及其顶点D 的坐标；（2）设直线CD 交x 轴于点E ．在线段OB 的垂直平分线上是否存在点P ，使得点P 到直线CD 的距离等于点P 到原点O 的距离？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）过点B 作x 轴的垂线，交直线CD 于点F ，将抛物线沿其对称轴平移，使抛物线与线段EF 总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？二8．如图，ABC △和的DEF △是等腰直角三角形，90C F ∠=∠=，24AB DE ==，．点B 与点D 重合，点A B D E ，（），在同一条直线上，将ABC △沿D E →方向平移，至点A 与点E 重合时停止．设点B D ，之间的距离为x ，ABC △与DEF △重叠部分的面积为y ，则准确反映y 与x 之间对应关系的图象是A B CO x yBCAE 1 E 2 E 3D 4D 1D 2D 3（第10题图）A EC AB ADAO A（第16题图）F9．已知二次函数2y ax bx c =++中，其函数y 与自变量x 之间的部分对应值如下表所示：x… 0 1 2 3 … y…5212…点A （1x ，1y ）、B （2x ，2y ）在函数的图象上，则当101x <<，223x <<时，1y 与2y 的大小关系正确的是A ．1y ≥2yB ．12y y >C ．12y y <D ．1y ≤2y10．如图，已知Rt ABC △，1D 是斜边AB 的中点，过1D 作11D E AC ⊥于E 1，连结1BE 交1CD 于2D ；过2D 作22D E AC ⊥于2E ，连结2BE 交1CD 于3D ；过3D 作33D E AC ⊥于3E ，…，如此继续，可以依次得到点45D D ，，…，n D ，分别记112233BD E BD E BD E △，△，△，…，n n BD E △的面积为123S S S ，，，…n S ．则A ．n S =14n ABC S △B ．n S =13n +ABC S △ C ．n S =()121n +ABC S △D ．n S =()211n +ABC S △16．如图，矩形纸片ABCD ，点E 是AB 上一点，且BE ∶EA =5∶3，EC =155BCE 沿折痕EC 向上翻折，若点B 恰好落在AD 边上，设这个点为F ，则（1）AB = ，BC = ；（2）若⊙O 内切于以F 、E 、B 、C 为顶点的四边形，则⊙O 的面积= ．yA P M22．（本小题满分10分）如图，以△AOD 的三边为边，在AD 的同侧作三个等边三角形 △AED 、△BOD 、△AOF ，请回答下列问题并说明理由： （1）四边形OBEF 是什么四边形？（2）当△AOD 满足什么条件时，四边形OBEF 是菱形？是矩形？ （3）当△AOD 满足什么条件时，以O 、B 、E 、F 为顶点的四边形不存在？24．(本小题满分12分) 如图，在平面直角坐标系中，已知点A 坐标为（2，4），直线2=x 与x 轴相交于点B ，连结OA ，抛物线2x y =从点O 沿OA 方向平移，与直线2=x 交于点P ，顶点M 到A 点时停止移动．（1）求线段OA 所在直线的函数解析式； （2）设抛物线顶点M 的横坐标为m ，①用m 的代数式表示点P 的坐标； ②当m 为何值时，线段PB 最短；（3）当线段PB 最短时，相应的抛物线上是否存在点Q ，使△QMA 的面积与△PMA 的面积相等，若存在，请求出点Q 的坐标；若不存在，请说明理由．OAFDEB（第22题图）（第10题）三7．Rt △ABC 中，∠C =90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对 边，那么c 等于（ ）A.cos sin a A b B +B.sin sin a A b B +C.sin sin a b A B +D.cos sin a b A B +10．梯形ABCD 中AB ∥CD ，∠ADC +∠BCD =90°，以AD 、AB 、BC 为斜边向形外作等腰直角三角形，其面积分别是S 1、S 2、S 3 ，且S 1 +S 3 =4S 2，则CD =（ ）A. 2.5ABB. 3ABC. 3.5ABD. 4AB14．如图所示，圆锥的母线长OA =8，底面的半径r =2，若一只小虫从A 点出发，绕圆锥的侧面爬行一周后又回到A 点，则小虫爬行的最短路线的长是 .15．将三角形纸片（△ABC ）按如图所示的方式折叠，使点B 落在边AC 上，记为点B ′，折痕为EF ．已知AB ＝AC ＝6，BC ＝8B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是 ．16．如图，已知△OP 1A 1、△A 1P 2A 2、△A 2P 3A 3、……均为等腰直角三角形，直角顶点P 1、P 2、 P 3、……在函数4y x=（x ＞0）图象上，点A 1、A 2、 A 3、……在x 轴的正半轴上，则点P 2010的横坐标为 .EAB ′CF B（第15题）（第14题） P 1OA 1A 2A 3P 3P 2yx510（第16题）24．（本小题满分12分）如图所示，在平面直角坐标系xOy 中，正方形OABC 的边长为2cm ，点A 、C 分别在y 轴的负半轴和x 轴的正半轴上，抛物线y =ax 2+bx +c 经过点A 、B 和D 2(4,)3. （1）求抛物线的解析式.（2）如果点P 由点A 出发沿AB 边以2cm /s 的速度向点B 运动，同 时点Q 由点B 出发沿BC 边以1cm /s 的速度向点C 运动，当其中一点到达终点时，另一点也随之停止运动. 设S =PQ 2(cm 2)①试求出S 与运动时间t 之间的函数关系式，并写出t 的取值范围； ②当S 取54时，在抛物线上是否存在点R ，使得以P 、B 、Q 、R 为顶点的四边形是平行四边形? 如果存在，求出R 点的坐标；如果不存在，请说明理由.（3）在抛物线的对称轴上求点M ，使得M 到D 、A 的距离之差最大，求出点M 的坐标.四16．如图，AB 是半圆O 的直径，C 为半圆上一点，N 是线段BC 上一点（不与B ﹑C 重合），过N 作AB 的垂线交AB 于M ，交AC 的延长线于E ，过C 点作半圆O 的切线交EM 于F ，若NC ∶CF ＝3∶2，则 sinB=_______．（第24题）（第16题）EMNCBAF （第9题）23．（本题10分）如图（1），已知正方形ABCD 在直线MN 的上方，BC 在直线MN 上，E 是线段BC 上一点，以AE 为边在直线MN 的上方作正方形AEFG （1） 连结GD ，求证△ADG ≌△ABE ； （2） 如图（2），将图（1）中正方形ABCD 改为矩形ABCD ，AB=1,BC=2，E 是线段BC 上一动点（不含端点B,C ）,以AE 为边在直线MN 的上方作矩形AEFG ，使顶点G 恰好落在射线CD 上．判断当E 由B 向C 运动时，∠FCN 的大小是否保持不变，若∠FCN 的大小不变，求tan ∠FCN 的值；若∠FCN 的大小发生改变，请举例说明．24．（本题12分）如图①，ABC Rt ∆中，︒=∠90B ︒=∠30CAB ，轴x AC ⊥．它的顶点A 的坐标为)0,10(，顶点B 的坐标为)35,5(，点P 从点A 出发，沿C B A →→的方向匀速运动，同时点Q 从点)2,0(D 出发，沿y 轴正方向以相同速度运动，当点P 到达点C 时，两点同时停止运动，设运动的时间为t 秒． （1）求BAO ∠的度数．(直接写出结果)（2）当点P 在AB 上运动时，OPQ ∆的面积S 与时间t （秒）之间的函数图象为抛物线的一部分（如图②），求点P 的运动速度．（3）求题（2）中面积S 与时间t 之间的函数关系式，及面积S 取最大值时点P 的坐标． （4）如果点Q P ,保持题（2）中的速度不变，当t 取何值时，PO=PQ ，请说明理由．（第24题）(2)E N M F G D A (1)G FDA （第23题）。

解直角三角形与几何综合(压轴题专项)—2023-2024学年九年级数学下册(浙教版)(解析版)

解直角三角形与几何综合(压轴题专项)—2023-2024学年九年级数学下册(浙教版)(解析版)

解直角三角形与几何综合【典例1】如图，在Rt△AEB中，∠AEB=90°，点C在线段BE的延长线上，过点C作CD∥AB，连接AD，再过点A作AF⊥CD于点F；（1）如图1，连接EF，若∠BAE=30°，∠D=45°，DF=6，AE=4，求线段EF的长；（2）如图2，在线段CE上取一点H，连接AH、DH，当AH平分∠BHD，∠ABH=∠DAH时，求证：DH=HC+ 2HE．（3）如图3，在（2）的条件下，连接ED，若AE=12，BE=4，当(ED+DF)取得最小值时，请直接写出线段AH的长．（1）过点E作EM⊥AF于M，利用勾股定理可得EM=√AE2−AM2=2√3，EF=√EM2+MF2=2√7；（2）连接AC，过A作AW⊥HD于，则有∠AWH=∠AWD=90°，可证Rt△AHE≌Rt△AHW(HL)，则HE=HW，然后可得A、H、C、D四点共圆，则可证△AEC≌△AWD(AAS)，进而问题可求证；（3）在线段EB上截取EG=EH，延长AF交BC的延长线于M，连接AG，AC，DM，可证得△AEG≌△AEH(SAS)，，利用解直角三角形可得EM=36，再由勾股定理可得AM=△AGC≌△AHD(SAS)，设∠BAE=α，则tanα=13√AE2+EM2=12√10，作点E关于DM的对称点E′，连接EE′，DE′，EE′交DM于P，则DE=DE′，由于ED+ DF=DE′+DF≥EF，故当且仅当E′、D、F三点共线时，ED+DF=EF为最小值，过点E′作E′N⊥BC于N，过点D作DK⊥CM于K，应用解直角三角形即可求得答案．（1）解：过点E作EM⊥AF于M，如图1，则∠AME=∠EMF=90°，∵AF⊥CD，CD∥AB，∴∠BAF=∠AFD=90°，∵∠BAE=30°，∴∠EAM=60°，∴∠AEM=30°，∵AE=4，AE=2，∴AM=12在Rt△AEM中，EM=√AE2−AM2=√42−22=2√3，在Rt△ADF中，∠D=45°，DF=6，∴AF=DF=6，∴MF=AF−AM=6−2=4，在Rt△EMF中，EF=√EM2+MF2=√(2√3)2+42=2√7，∴线段EF的长为2√7；（2）证明：连接AC，过A作AW⊥HD于W，如图2，则∠AWH=∠AWD=90°，∵∠AEB=90°，∴∠AEH=90°，∵AH平分∠BHD，AE⊥HB，AW⊥HD，∴AE=AW，在Rt△AHE和Rt△AHW中，{AH=AHAE=AW，∴Rt△AHE≌Rt△AHW(HL)，∴HE=HW，∵CD∥AB，∴∠ABH+∠BCD=180°，∵∠ABH=∠DAH，∴∠DAH+∠BCD=180°，∵∠DAH与∠BCD在DH异侧，∴A、H、C、D四点共圆，∴∠ACH=∠ADW，∵AE=AW，∠AEC=∠AWD=90°，∴△AEC≌△AWD(AAS)，∴EC=WD，∴DH=HW+WD=HE+EC=HE+HE+HC，即DH=HC+2HE；（3）解：如图3，在线段EB上截取EG=EH，延长AF交BC的延长线于M，连接AG，AC，DM，则CG=HC+2HE，由（2）得DH=HC+2HE，∴CG=DH，在△AEG和△AEH中，{EG=EH∠AEG=∠AEH=90°AE=AE，∴△AEG≌△AEH(SAS)，∴AG=AH，∠AGC=∠AHE，∵AH平分∠BHD，∴∠AHE=∠AHD，∴∠AGC=∠AHD，∴△AGC≌△AHD(SAS)，∴AC=AD，∵AF⊥CD，∴DF=CF，∴DM=CM，设∠BAE=α，则tanα=BEAE =412=13，∵∠BAE+∠MAE=∠AME+∠MAE=90°，∴∠AME=∠BAE=α，∴AEEM =tanM=13，∴EM=3AE=3×12=36，∴AM=√AE2+EM2=√122+362=12√10，如图4，作点E关于DM的对称点E，连接EE′，DE′，EE′交DM于P，则DE=DE′，∴ED+DF=DE′+DF≥E′F，当且仅当E′、D、F三点共线时，ED+DF=EF为最小值，过点E′作E′N⊥BC于N，过点D作DK⊥CM于K，则∠AMD=∠CE′E=∠CE′N=∠CDK=∠AME=α，设CF=DF=x，则FM=CFtanα=3x，∴CM=√CF2+FM2=√x2+(3x)2=√10x，∵sin∠DCK=DKCD =FMCM，即DK2x=√10x，∴DK=3√105x，∵cos∠DCK=CKCD =CFCM，即CK2x=√10x，∴CK=√105x，∴MK=CM−CK=√10x−√105x=4√105x，∴tan2α=DKMK =3√105x4√105x=34，∴PEPM =tan2α=34，设PE=3y，则PM=4y，∵PE2+PM2=EM2，∴(3y)2+(4y)2=362，∴y=365（负值舍去），∴PE=3×365=1085，PM=4×365=1445，∴EE′=2PE=2165，∵sin2α=ENEE′=PEEM，即EN2165=108536，∴EN=64825，∴MN=EM−EN=36−64825=25225，∴E′N=ENtan2α=6482534=86425，∴CN=E′N⋅tanα=86425×13=28825，∴CM=CN+MN=28825+25225=1085，∴FM=CM⋅cosα=1085×3√1010=162√1025，CF=13FM=54√1025，∴AF=AM−FM=12√10−162√1025=138√1025，在Rt△ADF中，AD=√AF2+DF2=(138√1025)+(54√1025)=12√615，∵∠DAH=∠ABH=∠MAE，∴∠DAH−∠MAH=∠MAE−∠MAH，即∠DAF=∠HAE，∴cos∠DAF=cos∠HAE，∴AFAD =AEAH，即138√102512√615=12AH，∴AH=12√61023．1．（2023·辽宁·中考真题）△ABC是等边三角形，点E是射线BC上的一点（不与点B，C重合），连接AE，在AE的左侧作等边三角形AED，将线段EC绕点E逆时针旋转120°，得到线段EF,连接BF．交DE于点M．（1）如图1，当点E为BC中点时，请直接写出线段DM与EM的数量关系；（2）如图2．当点E在线段BC的延长线上时，请判断（1）中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当BC=6，CE=2时，请直接写出AM的长．【思路点拨】（1）可证得∠BAD=∠BAE=30°，进一步利用等腰三角形的三线合一得出结果；（2）连接BD、DF，可证明△BAD≌△CAE，从而∠ABD=∠ACE=120°，BD=CE，进而得出∠DBE=60°，从而得出∠DBE+∠BEF=60°+120°=180°，从而BD∥EF，结合BD=EF得出四边形BDFE是平行四边形，从而得出DM=EM；（3）分为两种情形∶当点E在BC的延长线上时，作AG⊥BC于G，可得出CG=3，AG=3√3，从而EG=CG+ CE=3+2=5，进而得出AE=2√13，进一步得出结果；当点E在BC上时，作AG⊥BC于G，可得出EG=1，AE=2√7，进一步得出结果．【解题过程】（1）解∶∵△ABC是等边三角形，点E是BC的中点，∠BAC，∴∠BAC=60°，∠BAE=12∴∠BAE=30°，∵△ADE是等边三角形，∴∠DAE=60°，AD=AE，∴∠BAD=∠DAE−∠BAE=60°−30°=30°，∴∠DAE=∠BAE，∴DM=EM；（2）解：如图l，DM=EM仍然成立，理由如下∶连接BD、DF，∵△ABC和△ADE是等边三角形，∴∠ABC=∠BAC=∠DAE=∠ACB=60°，AB=AC，AD=AE，∴∠BAC−∠DAC=∠DAE−∠DAC，∴∠BAD=∠CAE，∴△BAD≌△CAE(SAS)，∴∠ABD=∠ACE=180°−∠ACB=120°，BD=CE，∴∠DBE=∠ABD−∠ABC=120°−60°=60°，∴∠DBE+∠BEF=60°+120°=180°，∴BD∥EF，∵CE=EF，∴BD =EF ，∴四边形BDFE 是平行四边形，∴DM =EM ；（3）解：如图2，当点E 在BC 的延长线上时，作AG⟂BC 于G ，∵∠ACB =60°，∴CG =AC ⋅cos60°=12AC =3，AG =AC ⋅sin60°=√32AC =3√3，∴EG =CG +CE =3+2=5，∴AE =√AC 2+EC 2=√(3√3)2+52=2√13．由（2）知∶DM =EM ，∴AM ⊥DE ，∴∠AME =90°，∴∠AED =60°，∴AM =AE ⋅sin60°=2√13×√32=√39，如图3，当点E 在BC 上时，作AG ⊥BC 于G ，由上知∶AG =3√3，CG =3，∴EG =CG −CE =3−2=1，∴AE=√AG2+EG2=√(3√3)2+12=2√7，∴AM=2√7×√32=√21，综上所述∶AM=√39或√21．2．（22·23下·安徽·专题练习）在△ABC中，∠ACB=90°，ACBC=m，D是边BC上一点，将△ABD沿AD折叠得到△AED，连接BE．（1）特例发现：如图1，当m=1，AE落在直线AC上时．①求证：∠DAC=∠EBC；②填空：CDCE的值为；（2）类比探究：如图2，当m≠1，AE与边BC相交时，在AD上取一点G，使∠ACG=∠BCE，CG交AE于点H．探究CGCE的值（用含m的式子表示），并写出探究过程；（3）拓展运用：在（2）的条件下，当m=√22，D是BC的中点时，若EB⋅EH=6，求CG的长．【思路点拨】（1）①由折叠知，∠AFB=90°=∠ACB，再由等角的余角相等，即可得出结论；②由①知，∠DAC=∠EBC，再判断出AC=BC，进而用ASA判断出，△ACD≌△BCE，即可得出结论；（2）同（1）①的方法，即可得出结论；（3）先判断出DF是△BCE的中位线，得出DF∥CE，进而得出∠BEC=∠BFD=90°，∠AGC=∠ECG，∠GAH=∠CEA，再判断出AG=CE，设CG=x，则AG=√2x，BE=2x，得出AG=CE进而用AAS判断出△AGH≌△ECH，得出GH=12x，再用勾股定理求出AH=32x，即可得出结论．【解题过程】（1）如图1，延长AD交BE于F，由折叠知，∠AFB=90°=∠ACB，∴∠DAC+∠ADC=∠BDF+∠EBC=90°，∵∠ADC=∠BDF，∴∠DAC=∠EBC；②由①知，∠DAC=∠EBC，∵m=1，∴AC=BC，∵∠ACD=∠BCE，∴△ACD≌△BCE(ASA)，∴CD=CE，=1，∴CDCE故答案为1．（2）如图2，延长AD交BE于F，由（1）①知，∠DAC=∠EBC，∵∠ACG=∠BCE，∴△ACG∽△BCE，∴CGCE =ACBC=m；（3）由折叠知，∠AFB=90°，BF=FE，∵点D是BC的中点，∴BD=CD，∴DF是△BCE的中位线，∴DF∥CE，∴∠BEC=∠BFD=90°，∠AGC=∠ECG，∠GAH=∠CEA，由（2）知，△ACG∽△BCE，∴∠AGC=∠BEC=90°，ACCD =AC12BC=2m=√2，∴CGAG =tan∠GAC=DCAC=1√2，设CG=x，则AG=√2x，BE=2x，∴AG=CE，∴△AGH≌△ECH(AAS)，∴AH=EH，GH=CH，∴GH=12x，在Rt△AGH中，根据勾股定理得，AH=√AG2+GH2=32x，∵EB⋅EH=6，∴2x⋅32x=6，∴x=√2或x=−√2（舍)，即CG=√2．3．（22·23·濮阳·一模）数学活动课上，老师组织数学小组的同学们以“正方形折叠”为主题开展数学活动．【动手实践】（1）如图（1），已知正方形纸片ABCD，数学小组将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠使AD与AM重合，折痕为AF，易知点E、M、F共线，则∠EAF=°，EF、BE、DF三条线段的关系为；【拓展应用】（2）解决下面问题：①如图（2）作FN⊥AE于点N，交AM于点P，求证：△ANP≌△FNE；②如图（3），数学小组在图（1）的基础上进行如下操作：将正方形纸片沿EF继续折叠，点C的对应点为点N，他们发现，当点E的位置不同时，点N的位置也不同，若点N恰好落在△AEF边上，AB=3，请直接写出此时BE的长度．【思路点拨】∠BAD=45°．由∠AME=（1）根据折叠的性质可得∠EAM=∠EAB,∠FAM=∠FAD，由此可得∠EAF=12∠B=90°,∠AMF=∠D=90°可得E、M、F三点共线．又由ME=BE,MF=DF可得EF=BE+DF．（2）①由∠ANF=90°，∠EAF=45°可得∠AFN=45°，于是可得AN=FN，由“同角的余角相等”可得∠EAM=∠NFE，最后根据角边角即可证明△ANP≌△FNE．②分两种情况：当点N落在AE上时，当点N落在AF上时，分别利用三角函数解直角三角形即可求得BE的长．【解题过程】（1）∵四边形ABCD是正方形，∴∠BAD=∠B=∠D=90°,AB=AD．∵△ABE沿AE折叠后得△AME，△ADF沿AF折叠后得△AMF，∴△AME≌△ABE,△AMF≌△ADF，∴∠EAM=∠EAB,∠FAM=∠FAD，∠BAD=45°，∴∠EAM+∠FAM=∠EAB+∠FAB=12即∠EAF=45°．∵∠AME=∠B=90°,∠AMF=∠D=90°，∴∠AME+∠AMF=180°．∴E、M、F三点共线．∵ME=BE,MF=DF，∴ME+MF=BE+DF，∴EF=BE+DF．故答案为：45，EF=BE+DF．（2）①∵FN⊥AE，∴∠ANF=∠FNE=90°．∵∠EAF=45°，∴∠AFN=45°，∴AN=FN．∵△AEM中，∠AME=90°，∴∠EAM+∠AEM=90°．∵△FNE中，∠FNE=90°，∴∠NFE+∠AEM=90°，∴∠EAM=∠NFE．在△ANP和△FNE中，{∠NAP=∠NFEAN=FN∠ANP=∠FNE，∴△ANP≌△FNE(ASA)．②如图，当点N落在AE上时，∵四边形ABCD是正方形，∴∠C=∠B=∠D=∠BAD=90°．由折叠的性质可得∠AEB=∠AEM=∠CEF，∵∠AEB+∠AEM+∠CEF=180°，∴∠AEB=∠AEM=∠CEF=60°．∵AB=3，∴BE=ABtan∠AEB =ABtan60°=√3=√3；如图，当N落在AF上时，∵四边形ABCD是正方形，∴∠C=∠B=∠D=∠BAD=90°，由折叠的性质可得∠AFE=∠CFE=∠AFD，又∵∠AFE+∠CFE+∠AFD=180°，∴∠AFE=∠CFE=∠AFD=60°，∴DF=ADtan∠AFD =ADtan60°=3√3=√3，∴CF=CD−DF=3−√3，∴EC=CF⋅tan∠CFE=(3−√3)×√3=3√3−3，∴BE=BC−EC=3−(3√3−3)6−3√3，综上，BE的长为√3或6−3√3．4．（22·23下·泉州·模拟预测）已知：如图1，在矩形ABCD中，AB=4，AD=6，点P是AD的中点，点F是AB上的动点，连接FP并延长交CD的延长线于点M，过点P作PE⊥FM，交直线BC于点E，连接EF．（1）求tan∠PEF的值；（2）如图2，连接EM，点Q是EM的中点．①当∠AFP=2∠BEF时，求PQ的长；②点F从A点运动到B点的过程中，求点Q经过的路径长．【思路点拨】（1）作PG⊥BC于点G，由四边形ABCD是矩形，点P是AD的中点，得∠A=∠B=∠PGB=90°，PA=PD=1 2AD=3，可证明△APF∽△GPE，则tan∠PEF=PFPE=PAPG=34；（2）①作EF的垂直平分线KN交BE于点N，连接FN，则∠BEF=∠NFE，所以∠BNF=2∠BEF，则∠AFP=∠BNF，可证明∠NFP=∠EPM=90°，则FN∥PE，所以∠BEF=∠NFE=∠PEF，则BF=PF，由勾股定理得32+(4−PF)2=PF2，求得PF=258，则FE=12524，再证明PF=PM，则PQ=12FE=12548；②作PG⊥BC于点G，连接AG、PC，取PC的中点I，连接IQ，可证明PC∥AG，则∠DPI=∠PAG，再证明△PFE∽△PAG，得∠PFE=∠PAG，可推导出∠DPI=∠MPQ，则∠IPQ=∠DPM=∠APF，再证明△PIQ∽△PAF，则∠PIQ=∠PAF=90°，可知点Q在线段PC的垂直平分线上运动，延长IQ、PD交于点L，当点F从点A运动到点B，则点Q从点I运动到点L，由ILPI =tan∠DPI=tan∠PAG=PGPA=43，求得IL=43PI=103，则点Q经过的路径长是103．【解题过程】（1）解：作PG⊥BC于点G∵四边形ABCD是矩形，AB=4，AD=6，点P是AD的中点，∴∠A=∠B=∠PGB=90°，PA=PD=12AD=3，∴四边形ABGP是矩形，∴PG=AB=4，∠APG=90°，∵PE⊥FM，交直线BC于点E，∴∠FPE=90°，∴∠APF=∠GPE=90°−∠FPE，∵∠A=∠PGE=90°，∴△APF∽△GPE，∴tan∠PEF=PFPE =PAPG=34，∴tan∠PEF的值是34；（2）解：①作EF的垂直平分线KN交BE于点N，连接FN，则EN=FN，如图2所示：∴∠BEF=∠NFE，∴∠BNF=∠BEF+∠NFE=2∠BEF，∵∠AFP=2∠BEF，∴∠AFP=∠BNF，∴∠AFP+∠BFN=∠BNF+∠BFN=90°，∴∠NFP=∠EPM=90°，∴FN∥PE，∴∠BEF=∠NFE=∠PEF，∵BF⊥EB，PF⊥EP，∴BF=PF，∵AP2+AF2=PF2，AF=4−BF=4−PF，∴32+(4−PF)2=PF2，解得PF=258，设PF=3m，则PE=4m，由3m=258得m=2524，∴FE=√PF2+PE2=√(3m)2+(4m)2=5m=5×2524=12524，∵AF∥DM，∴PFPM =PAPD=1，∴PF=PM，∵点P是FM的中点，点Q是EM的中点，∴PQ=12FE=12×12524=12548，∴PQ的长是12548；②作PG⊥BC于点G，连接AG、PC，取PC的中点I，连接IQ，如图3所示：∵BC=AD=6，GB=PA=3，∴CG=BC−GB=6−3=3=∵CG∥AP，∴四边形APCG是平行四边形，∴PC∥AG，∴∠DPI=∠PAG，∵PFPE =PAPG，∴PFPA =PEPG，∴△PFE∽△PAG，∴∠PFE=∠PAG，∴∠DPI=∠PFE，∵∠MPQ=∠PFE，∴∠DPI=∠MPQ，∴∠DPI−∠DPQ=∠MPQ−∠DPQ，∴∠IPQ=∠DPM=∠APF，∵PC=AG=√PA2+PG2=√32+42=5，∴PI=12PC=12×5=52，∴PIPA =523=56，∵FEPF =53，FE=2PQ，∴2PQPF =53，∴PQPF =56=PIPA，∴△PIQ∽△PAF，∴∠PIQ=∠PAF=90°，∴点Q在线段PC的垂直平分线点上运动，延长IQ、PD交于点L，当点F从点A运动到点B，则点Q从点I运动到点L，∵ILPI =tan∠DPI=tan∠PAG=PGPA=43，∴IL=43PI=43×52=103，∴点Q经过的路径长是103．5．（2023·江苏镇江·中考真题）【发现】如图1，有一张三角形纸片ABC，小宏做如下操作：（1）取AB，AC的中点D，E，在边BC上作MN=DE；（2）连接EM，分别过点D，N作DG⊥EM，NH⊥EM，垂足为G，H；（3）将四边形BDGM剪下，绕点D旋转180°至四边形ADPQ的位置，将四边形CEHN剪下，绕点E旋转180°至四边形AEST的位置；（4）延长PQ ，ST 交于点F ．小宏发现并证明了以下几个结论是正确的： ①点Q ，A ，T 在一条直线上； ②四边形FPGS 是矩形； ③△FQT≌△HMN ；④四边形FPGS 与△ABC 的面积相等． 【任务1】请你对结论①进行证明．【任务2】如图2，在四边形ABCD 中，AD∥BC ，P ，Q 分别是AB ，CD 的中点，连接PQ ．求证：PQ =12(AD +BC )． 【任务3】如图3，有一张四边形纸ABCD ，AD∥BC ，AD =2，BC =8，CD =9，sin∠DCB =45，小丽分别取AB ，CD 的中点P ，Q ，在边BC 上作MN =PQ ，连接MQ ，她仿照小宏的操作，将四边形ABCD 分割、拼成了矩形．若她拼成的矩形恰好是正方形，求BM 的长． 【思路点拨】（1）由旋转的性质得对应角相等，即∠ABC =∠QAD ，∠ACB =∠TAE ，由三角形内角和定理得∠ABC ＋∠BAC ＋∠ACB =180°，从而得∠QAD ＋∠BAC ＋∠TAE =180°，即Q ，A ，T 三点共线；（2）梯形中位线的证明问题常转化为三角形的中位线问题解决，连接AQ 并延长，交BC 的延长线于点E ，证明△ADQ≌△ECQ ，可得AQ =EQ ，AD =CE ，由三角形中位线定理得PQ =12BE =12(AD +BC )；（3）过点D 作DR ⊥BC 于点R ，由DC =9，sin∠DCB =45得DR =365，从而得S 梯形ABCD =12×(2+8)×365=36，由【发现】得S 正方形GEST =S 梯形ABCD ，则GE =6，PE =3，由【任务2】的结论得PQ =5，由勾股定理得EQ =4．过点Q 作QH ⊥BC ，垂足为H ．由CQ=92及sin∠DCB =45得QH =185，从而得CH =2710，证明△PEQ∽△QHM ，得HM =245，从而得BM =BC −HM −CH =12．【解题过程】 [任务1]证法1：由旋转得，∠QAD =∠ABC ，∠TAE =∠ACB ． 在△ABC 中，∠ABC ＋∠BAC ＋∠ACB =180°， ∴∠QAD ＋∠BAC ＋∠TAE =180°， ∴点Q ，A ，T 在一条直线上．证法2：由旋转得，∠QAD =∠ABC ，∠TAE =∠ACB ．∴AQ∥BC，AT∥BC．∴点Q，A，T在一条直线上．[任务2]证明：如图1，连接AQ并延长，交BC的延长线于点E．∵AD∥BC，∴∠DAQ=∠E．∵Q是CD的中点，∴DQ=CQ．在△ADQ和△ECQ中，{∠DAQ=∠E,∠AQD=∠EQC, DQ=CQ,∴△ADQ≌△ECQ(AAS)．∴AQ=EQ，AD=CE．又∵P是AB的中点，∴AP=BP，∴PQ是△ABE的中位线，∴PQ=12BE=12(CE+BC)，∴PQ=12(AD+BC)．[任务3]的方法画出示意图如图2所示．由【任务2】可得PQ ∥BC ，PQ =12(AD +BC )=12×(2+8)=5． 过点D 作DR ⊥BC ，垂足为R ． 在Rt △DCR 中，sin∠DCB =DR CD ，∴DR =CD ⋅sin∠DCB =9×45=365．∴S 正方形GEST =S 梯形ABCD =12×(2+8)×365=36，∴GE =6，PE =3．在Rt △PEQ 中，由勾股定理得EQ =√PQ 2−PE 2= √52−32=4． 过点Q 作QH ⊥BC ，垂足为H ． ∵Q 是CD 的中点， ∴CQ =12CD =12×9=92．在Rt △QHC 中，sin∠DCB =QH CQ，∴QH =CQ ⋅sin∠DCB =92×45=185．又由勾股定理得CH =√CQ 2−QH 2=√(92)2−(185)2=2710．由PQ ∥BC ，得∠PQE =∠QMH ． 又∵∠PEQ =∠QHM =90°， ∴△PEQ∽△QHM ． ∴PE QH =EQ HM ，即3185=4HM ，∴HM =245．∴BM =BC −HM −CH =8−245−2710=12．6．（23·24九年级上·江苏无锡·阶段练习）【基本图形】（1）如图1，在矩形ABCD 中，CE ⊥BD 于点H ，交AD于点E．求证：CEBD =CDBC；【类比探究】（2）如图2，在四边形ABCD中，∠A=∠B=90°,AD=4，BC=9，CD=7．E是边AB上的一动点，过点C作CG⊥ED，交ED的延长线于点G，交AD的延长线于点F．试探究CFDE是否为定值?若是，请求出CFDE的值；若不是，请说明理由；【拓展延伸】（3）如图3，在Rt△ABD中，∠BAD=90°，将△ABD沿BD翻折得到△CBD，点E,F分别在边AB,AD上，连接CF,DE．若∠AED=∠AFC，且CFDE =35，则ADAB的值为______（直接写出结果）．【思路点拨】（1）证明△CED∽△BDC，利用相似三角形的性质即可证明CEBD =CDBC；（2）过点C作CH⊥AF交AF延长线于点H，首先证明四边形ABCH为矩形，易得AB=CH，BC=AH，再证明△DEA∽△CFH，由相似三角形的性质可得CFDE =CHAD，然好由勾股定理解得CH=2√6，即可证明CFDE=CHAD=√62，即可获得答案；（3）过点C作CG⊥AD于点G，交BD于点H，作HM⊥CD于点M，证明CG∥AB，易得∠ABD=∠GHD，再证明△AED∽△GFC，由相似三角形的性质可得CFDE =CGAD=35，由折叠的性质可得AD=CD，∠ADB=∠CDB，设GC=3x，则AD=CD=5x，由勾股定理可得DG=√CD2−CG2=4x，然后由角平分线的性质定理可得HG=HM，结合S△HDG+S△CHD=S△CDG，可求得HG=4x3，然后可推导tan∠ABD=tan∠DHG=DGHG=3，即可获得ADAB得值．【解题过程】解：（1）∵四边形ABCD为矩形，∴∠ADC=∠DCB=90°，∵CE⊥BD，∴∠DBC+∠BCH=∠BCH+∠ECD=90°，∴∠DBC=∠ECD，∴△CED∽△BDC，∴CE BD =CDBC；（2）CFDE是否为定值，如下图，过点C作CH⊥AF交AF延长线于点H，∴∠A=∠B=∠H=90°，∴四边形ABCH为矩形，∴AB=CH，BC=AH，∵∠GFD=∠HFC，∠GDF=∠ADE，又∵∠GFD+∠GDF=∠HFC+∠HCF，∴∠ADE=∠HCF，∵∠A=∠H，∴△DEA∽△CFH，∴CF DE =CHAD，∵BC=9，CD=7，AD=4，∴DH=AH−AD=BC−AD=5，∴CH=√CD2−DH2=2√6，∴CF DE =CHAD=2√64=√62，∴CF DE 为定值√62；（3）如下图，过点C作CG⊥AD于点G，交BD于点H，作HM⊥CD于点M，∴∠CGF=∠A=90°，∴CG∥AB，∴∠ABD=∠GHD，∵∠AED=∠AFC，∠CGF=∠A，∴△AED∽△GFC，∴CF DE =CGAD=35，∵将△ABD沿BD翻折得到△CBD，∴AD=CD，∠ADB=∠CDB，设GC=3x，则AD=CD=5x，∴DG=√CD2−CG2=4x，∵HG⊥AD，HM⊥CD，∠ADB=∠CDB，∴HG=HM，∵S△HDG+S△CHD=S△CDG，即12×4x×HG+12×5x×HM=12×3x×4x，∴HG=4x3，∴tan∠ABD=tan∠DHG=DGHG =4x43x=3，∴ADAB=3．7．（21·22九年级下·辽宁盘锦·期中）如图，在矩形ABCD中，AB=3,BC=5，BE平分∠ABC交AD于点E．连接CE，点F是BE上一动点，过点F作FG∥CE交BC于点G．将△BFG绕点B旋转得到△BF′G′，（1）如图1，连接CG′,EF′，求证：△BEF′∽△BCG′；（2）当点G′恰好落在直线AE上时，若BF=3，求EG′的值；（3）如图3，连接GG′，当GG′与BE交于点F时，猜想FG与FG′的数量关系，并证明．【思路点拨】（1）平行得到△BFG∽△BEC，得到BFBE =BGBC，旋转得到BF=BF′,BG=BG′,∠GBF=∠G′BF′，进而得到BF′BE =BG′BC，∠FBF′=∠GBG′，即可得证；（2）分点G′在线段AE和在线段EA的延长线上，两种情况进行讨论求解；（3）过点F作FH⊥BG于点H，过点B作BP⊥GG′于点P，易得BH=FH，根据矩形的性质，平行线的性质，得到∠FGB=∠ECB=∠CED，进而得到tan∠FGB=tan∠CED=CDDE =32，cos∠FGB=cos∠CED=EDCE=2√1313，推出tan∠FGB=FHGH =32，cos∠FGB=PGBG=2√1313，设FH=3a,HG=2a，分别求出FG,FG′，即可得解．【解题过程】（1）证明：∵FG∥CE，∴△BFG∽△BEC，∴BF BE =BGBC，∵将△BFG绕点B旋转得到△BF′G′，∴BF=BF′,BG=BG′,∠GBF=∠G′BF′，∴BF′BE =BG′BC，∠FBF′=∠GBG′，∴BF′BG′=BEBC，∴△BEF′∽△BCG′；（2）解：∵矩形ABCD中，AB=3,BC=5，∴AD∥BC，∠A=∠ABC=90°，∴∠AEB=∠EBC，∵BE 平分∠ABC ， ∴∠ABE =∠EBC =45°， ∴∠ABE =∠AEB =45°， ∴AE =AB =3，BE =3√2， 由（1）知：BFBE =BGBC ，即：3√2=BG 5，∴BG =5√22， ∴BG ′=BG =5√22， ①当点G ′在线段AE 上时，在Rt △BAG ′中，AG ′=√G ′B 2−AB 2=√142， ∴EG ′=AE −AG ′=3−√142； ②当点G ′在线段EA 的延长线上时，在Rt △BAG ′中，AG ′=√G ′B 2−AB 2=√142， ∴EG ′=AE +AG ′=3+√142；综上：EG ′=3−√142或3+√142； （3）FGFG ′=137；证明如下：过点F 作FH ⊥BG 于点H ，过点B 作BP ⊥GG ′于点P ，由（2）知，∠FBC =45°，AE =3， ∴BH =FH ， ∵矩形ABCD ，∴AD ∥BC,AD =BC =5,CD =AB =3,∠D =90°， ∴DE =5−3=2，∠CED =∠ECB ，∴CE=√DE2+CD2=√13，∵FG∥CE，∴∠FGB=∠ECB=∠CED，∴tan∠FGB=tan∠CED=CDDE =32，cos∠FGB=cos∠CED=EDCE=2√1313，∴tan∠FGB=FHGH =32，cos∠FGB=PGBG=2√1313，设FH=3a,HG=2a，则：FG=√FH2+HG2=√13a，BH=FH=3a，∴BG=BH+HG=5a，∴PG=10√1313a，∵旋转，∴BG=BG′，∴GG′=2PG=20√1313a，∴FG′=GG′−FG=7√1313a，∴FG FG′=√13a7√13a13=137．8．（21·22下·沧州·二模）如图1，在一平面内，线段AB=20，M，N是线段AB上两点，且AM=BN=2，点C从点M开始向终点N AC，BC为边在线段AB同侧作等边△ACD和等边△BCE，设AC=x．（1）直接写出CD和BE位置关系：______；（2）如图2，连接AE，BD，求证：AE=BD；（3）如图3，点G，点H分别是CD，BE的中点，①求当x为何值时，线段GH取得最小值？最小值是多少？②当线段GH取得最小值此时，求△ACE的面积；（4）如图4，设DE的中点为P，则点P移动路径的长为______．【思路点拨】（1）根据平行线的判定即可；（2）证明△ACE≌△DCB(SAS)即可；（3）①连接AG并延长交直线BE于F，连接CH、CF，先证明四边形CGFH是矩形，得FC=GH，当FC⊥AB 时GH最小即可，②过E作EK⊥AB于K，∠ECB=60°，再根据三角函数及三角形的面积公式即可；（4）以点A为原点，直线AB为x轴，过点A垂直于直线AB的直线为y轴，建立平面直角坐标系，过点D作DG⊥AC于点G，过点E作EH⊥AC于点H，再表示出点P的坐标即可．【解题过程】（1）解：在等边△ACD和等边△BCE中，∴∠ACD=∠B=60°，∴CD∥BE．故答案为：平行．（2）解：∵△ACD和△BCE是等边三角形，∴AC=CD，CE=CB，∠ACD=∠BCE=60°，∴∠ACD+∠DCE=∠BCE+∠DCE，即：∠ACE=∠DCB，∴△ACE≌△DCB(SAS)，∴AE=BD；（3）解：①连接AG并延长交直线BE于F，连接CH、CF，∵△ACD和△BCE是等边三角形，∴∠ACD=∠B=60°，∴CD∥BE，∴∠DCH=∠CHB，∵点G，点H分别是CD，BE的中点，∴∠AGC=∠CHE=∠CHB=90°，∠BAF=30°∴∠CGF=∠AGC=∠DCH=90°，∴∠CGF=∠CHE=∠DCH=90°，∴四边形CGFH是矩形，∴FC=GH，∴当FC⊥AB时GH最小，在△ABF中，AF=ABsin60°=在△AFC中，AC=AFcos30°=15，FC=AF⋅sin30°=5√3，∵2≤AC≤18，∴当x=15时，线段GH取得最小值，最小值是5√3；②过E作EK⊥AB于K，∠ECB=60°，在△CEK中，∠ECB=60°，CB=AB−AC=5，EK=CE⋅sin60°=5√3，2∴S △ACE =12⋅AC ⋅EK =754√3；（4）解：如图，以点A 为原点，直线AB 为x 轴，过点A 垂直于直线AB 的直线为y 轴，建立平面直角坐标系，过点D 作DG ⊥AC 于点G ，过点E 作EH ⊥AC 于点H ，则M(2,0),B(20,0),N(18,0),C(x,0)， AC =x,BC =20−x ，∵△ACD,△BCE 均为等边三角形，∴∠DAC =∠ECH =60°，AG =12AC =x2,CH =12BC =20−x 2，∴AH =AC +CH =x +20−x 2=x2+10，∴DG =OG ⋅tan60°=x 2×√3=√3x2，EH =CH ⋅tan60°=(10−x2)×√3=−√3x2+10√3，∴D(x 2,√3x 2)，E(x2+10,−√3x 2+10√3)，则DE 的中点为P 的坐标为P(x2+5,5√3)(2≤x ≤18)， ∵P 的纵坐标为定值，即点P 在平行于x 轴的直线上运动， x =2时，P 1(6,5√3)， x =18时，P 2(14,5√3)，点P 移动路径的长为P 1P 2=14−6=8， 故答案为：8．9．（23·24九年级上·吉林长春·阶段练习）如图①，在▱ABCD 中，∠A =60°，AB =4，AD =6，点E 在边BC 上，且BE =2，动点P 从点E 出发，沿折线EB −BA −AD 以每秒2个单位长度的速度运动．作∠PEQ =60°，EQ 交边AD 或边DC 于点Q ，连接PQ ．当点Q 与点C 重合时，点P 停止运动．设点P 的运动时间为t 秒．（t >0）（1）当点P和点B重合时，线段PQ的长为______；（2）当点Q和点D重合时，求tan∠PQE．（3）如图②，当点Q在边DC上运动时，证明：PD=CQ．（4）作点E关于直线PQ的对称点F，连接PF、QF，当四边形EPFQ和▱ABCD重叠部分图形为轴对称四边形时，直接写出t的值．【思路点拨】（1）首先证明四边形ABEQ是平行四边形，取QE中点M,连接BM，则△AQP是直角三角形，利用勾股定理解题即可；（2），过点D作DN⊥BC于点N,在Rt△QNC中,CN=2，EN=2，在Rt△QCN中,利用勾股定理求出QN= 2√3，然后根据tan∠PQE=tan∠QEC=DN解题即可；EN（3）连接DE,过点D作DG⊥BC于点G,利用ASA证明△PED≌△QEC解题即可；（4）当Q点位于CD中点时.四边形EPFQ与ABCD重叠部分四边形为轴对称四边形，根据题意求出t的值．【解题过程】（1）)解: ∵四边形ABCD是平行四边形，∴AQ∥BE，∴∠A+∠ABC=180°，∵∠A=60°，∴∠ABC=120°，又∵∠PEQ=60°，∴∠ABE+∠PEQ=180°，∴AB∥QE，∴四边形ABEQ是平行四边形.∴QE=AB=4,AQ=BE=2，取QE中点M,连接BM，∴QM=ME=2，又∵∠PEQ=60°，∴△BME是等边三角形，∴QM=BM=ME，∴∠MBE=60°，∴∠MQP=∠QPM=30°,∴∠QPE=90°，∵AQ∥BE，∴∠AQP=90°，∴△AQP是直角三角形，∴在Rt△AQP中QP=√AB²−AQ²=√42−22=2√3，∴当P点和B点重合时,PQ的长为2故答案为：2√3；（2）)解:∴四边形ABCD是平行四边形. ∴AD∥BC,∠A=∠C=60°∴∠PQE=∠QEC∵BC=AD=6,BE=2.∴CE=4如图2，过点D作DN⊥BC于点N,在Rt△QNC中,∠QNC=90°,∠C=60°∴∠NQC=30°∴CN=12CD=12×4=2，∴EN=EC−CN=4−2=2∴在Rt△QCN中,∴QN=√CQ²−CN²=√42−22=2√3，∴tan∠PQE=tan∠QEC=DNEN =2√32=√3，∴当Q点和D点重合时,tan∠PQE=√3；（3）证明:连接DE,过点D作DG⊥BC于点G,如图3由(2)知EC=CD=4,∠C=60°，∴△CDE是等边三角形∴DE=EC=CD=4又∵四边形ABCD是平行四边形.∴∠ADC=120°又∵∠PEQ=60°，∠DEC=∠C=∠EDC=60°，∴∠PED+∠DEQ=∠QEC+∠DEQ，∴∠PDE=∠QCE=60°，∠PED=∠QEC，∴△PED≌△QEC(ASA)，∴PD=QC，（4）解:由题意得，当Q点位于CD中点时.四边形EPFQ与ABCD重叠部分四边形为轴对称四边形.理由如下：如图4，连接DE，由(3)知△CDE是等边三角形,∵Q点为CD的中点，∴QD=QC=1CD=22∴QE⊥CD，∴∠CQE=90°，又∵∠C=60°∴∠CEQ=30°∴∠PEQ=60°∴∠PEC=90°∴PE⊥BC，又∵AD∥BC，∴PE⊥AD∴DE=4,PE=2√3，PD=2，∴PD=QD，∴Rt△PDE≌Pt△QDE(HL).∴四边形EPFQ与ABCD的重叠部分为EPDQ为轴对称四边形，∴P点的运动轨迹为EB+BA+AP=2+4+4=10，∵P点的速度为2个单位长度每秒，∴2t=10∴t=5∴t的值为5．10．（21·22·武汉·模拟预测）问题背景：如图（1），在四边形ABCD中，P是BC上一点，∠ABC=∠BCD=∠APD，求证：△ABP∽△PCD；尝试运用：如图（2），D,E,F三点分别在等边△ABC边BC,AB,AC上，∠ABC=∠EDF,BD=CD．已知BC=4，设EF=x,△DEF的面积为y，求y关于x的函数关系式（不求自变量x的取值范围）；拓展创新：如图（3），D是等边△ABC边BC上一点，连接AD,E是AD上一点，CD=2BD,∠BEC=120°，请用一个等式直接写出BE与CE的数量关系．【思路点拨】问题背景：如图（1），根据三角形相似的判定定理：两角对应相等的两个三角形相似证明即可；尝试运用：过点D分别作DG⊥AB,DH⊥AC，垂足分别为G,H，如图所示，D，E，F三点分别在等边ΔABC边BC，AB，AC上，∠ABC=∠EDF，BD=CD．已知BC=4，设EF=x，ΔDEF的面积为y，根据相似三角形判定与性质，再结合解直角三角形即可得到答案；拓展创新：将ΔBCE绕点C顺时针旋转60°，作DF∥CE，如图所示，可得DF∥CE∥AE′，证得△BDF∽△BCE，设BE=m，EC=x，可得EF的长，由△DFE∽△AE′E，利用相似三角形的性质可得结果．【解题过程】问题背景：证明：如图所示：∵∠ABC=∠APD，∴∠BAP+∠BPA=∠CPD+∠BPA，∴∠BAP=∠CPD，又∵∠ABP=∠PCD，∴△ABP∽△PCD；尝试运用：解：过点D分别作DG⊥AB,DH⊥AC，垂足分别为G,H，如图所示：∵△ABC是等边三角形，∠ABC=∠EDF，∴∠ABC=∠EDF=∠C=60°，由（1）知△BDE∽△CFD，∴BECD =DEFD，∵BD=CD，∴BEBD =DEFD，又∵∠ABC=∠EDF，∴△BDE∽△DFE，∴∠BED=∠DEF，∴DG=DH，在Rt△BDG中，∠ABC=60°，BD=2，则sinB=DGBD =DG2，即DG=2×√32=√3，∴DH=√3，∴y=√32x；拓展创新：解：CE=√2BE．将△BCE绕点C顺时针旋转60°，作DF∥CE，如图所示：∵将△BCE绕点C顺时针旋转60°得到△ACE′，∴BE=AE′，∠AE′C=120°，CE=CE′，∵DF∥CE，∠BEC=120°，∴∠CEE′=60°，∴△CEE′为等边三角形，∴∠CE′E=60°，EE′=CE，∴∠AE′B=60°，∴CE∥AE′，∵DF∥CE，∴DF∥AE′，∴△BDF∽△BCE，∴BFBE =DFCE=BDBC=13，设BE=m，∴BF=13m，EF=23m，设CE=x，∴DF=x3，∵△DFE∽△AE′E，∴EFEE′=DFAE′，∴23mx=13xm，∴x2=2m2，∵x>0，m>0，∴x=√2m，∴EC=√2BE．11．（22·23·信阳·三模）综合与实践【问题情境】在△ABC中，AB=AC，∠BAC=α，点D为BC边上一动点（不与B，C重合），连接AD，以AD为始边顺时针作∠ADE=β(α+β=180°)，DF平分∠ADE．【初步探究】（1）如图1，DE与AC的延长线交于点E，若α=60°，β=120°，CD=2BD，则BDCF的值为_____，∠CDF与∠E的数量关系是_________．【类比探究】（2）如图2，DE与AC的延长线交于点E，若α=β=90°，CD=2BD，求出BDCF的值及∠CDF与∠E的数量关系．【拓展应用】（3）如图3，DE与AC交于点E，α=β=90°，∠CAD=15°，AB=6√2，将△ADF绕点在平面内自由旋转，当B，A，F三点共线时，直接写出AFBD的值．【思路点拨】（1）可证得△ABD∽△DCF，从而BDCF =ABCD，进而得出BDCF=32，由∠BAD+∠DAE=60°可得出∠CDF=∠E；（2）可证得△ABD∽△DCF，从而得出BDCF =ABCD，进而得出BDCF=3√24，根据∠BAD+∠DAE=90°可推出∠CDF=∠E；（3）作AH⊥BC于H，作AR⊥DF，交DF的延长线于R，解直角三角形ABH求得AH=6，解Rt△ADH求得AD的值，解Rt△ADR求得AR和BR的值，解Rt△ARF求得AF和RF，进而求得AF，当F在BA的延长线上时，解Rt△DFX求得FX和DX的值，解Rt△ADX求得BD，进一步得出结果；当F在AB上时，作DV⊥AB于V，同样的方法得出结果．【解题过程】解：（1）∵AB=AC，∠BAC=60°，∴△ABC是等边三角形，∴∠B=∠C=60°，∴∠BAD+∠ADB=120°，∵∠ADF=12∠ADE=60°，∴∠DB+∠CDE=120°，∴∠BAD=∠CDF，∴△ABD∽△DCF，∴BDCF =ABCD，∵CD=2BD，∴AB=BC=32CD，∴BDCF =32，∵∠BAD+∠DAE=60°，∴∠CDF+60°−∠E=60°，∴∠CDF=∠E，故答案为：32，相等；（2）∵AB=AC，∠BAC=90°，∴∠B=∠C=45°，∴∠BAD+∠ADB=135°，∵∠ADF=12∠ADE=45°，∴∠DB+∠CDE=135°，∴∠BAD=∠CDF，∴△ABD∽△DCF，∴BDCF =ABCD，∵CD=2BD，∴BC=32CD，∵AB=√22BC，∴BDCF =3√24，∵∠BAD+∠DAE=90°，∴∠CDF+90°−∠E=90°，∴∠CDF=∠E；（3）如图1，作AH⊥BC于H，作AR⊥DF，交DF的延长线于R，∵AB=AC，∠BAC=90°，∴∠B=∠C=45°，BH=CH，∴AH=√22AB=6，在Rt△ADH中，∠ADH=∠DAC+∠C=60°，AH=6，∴AD=6 sin60°=4√3，在Rt△ADR中，AD=4√3，∠ADF=45°，∴AR=DR=√22AD=2√6，在Rt△ARF中，AR=2√6，∠AFR=∠DAC+∠ADF=15°+45°=60°，∴AF=2√6 sin60°=√6√32=4√2，RF=2√6=√6√3=2√2，∴AF=2FR=DF=DR−RF=2√6−2√2，如图2，当F在BA的延长线上时，作DX⊥AF于X，在Rt△DFX中，DF=2√6−2√2，∠DFX=60°，∴FX=12DF=√6−√2，DX=DF⋅sin60°=3√2−√6，在Rt△ADX中，BX=AB+AF+FX=6√2+4√2+√6−√2=9√2+√6，DX=3√2−√6，∴BD=√(9√2+√6)2+(3√2−√6)2=2√48+6√3，∴ AFBD =√22√48+6√3=√24+3√324+3√3，如图3，当F在AB上时，作DV⊥AB于V，由上知：FV=√6−√2，DV=3√2−√6，∴BV=AB−AF−FV=6√2−4√2−(√6−√2)=3√2−√6，∴BD=√2BV=√2(3√2−√6)，∴AFBD =√2√2(3√2−√6)=3√2+√63，综上所述： AFBD =√24+3√324+3√3或3√2+√63．12．（23·24九年级上·辽宁沈阳·阶段练习）在平面直角坐标系中，已知点A(0，6)，点B在线段AO上，且AB=2BO，若点P在x轴的正半轴上，连接BP，过点P作PQ⊥PB．（1）如图1，点E是射线PQ上一点，过点E作EC⊥x轴，垂足为点C．①点B的坐标__________．②求证：△BOP∼△PCE；（2）在（1）的条件下，如图2，若点C坐标为(8，0)．过点A作DA⊥y轴，且和CE的延长线交于点D．若点C关于直线PQ的对称点C′正好落在线段AD上．连接PC，则点P的坐标__________．（3）如图3，若∠BPO=60°，点E在直线PQ上，EC⊥x轴，垂足为点C．若以点E，P，C为顶点的三角形和△BPE相似，请直接写出点E的坐标__________．【思路点拨】（1）①根据OA=6,AB=2OB求解即可.②根据两角对应相等，两三角形相似证明即可.（2）如图2中, 过点C′作C′G⊥OC于G, 延长PB交DA的延长线于F.设OP=x,则PC=4−x.在Rt△EBC′中，根据C′P2=PG2+C′G2,构建方程求解即可.（3）如图3中, 由题意∠PBQ=∠ECP=90°, 分四种情形, 当∠PE1B=30°时, 以点E,P,C为顶点的三角形和△BPE相似, 当∠PBE2=30°时, 以点E,P,C为顶点的三角形和△BPE相似, 当∠PE3B=30°时, 以点E,P,C 为顶点的三角形和△BPE相似，当∠PBE4=30°时, 以点E,P,C为顶点的三角形和△BPE相似, 分别求解即可.【解题过程】（1）①∵A(0,6)，∴OA=6,∵AB=2BO,∴AB=4, OB=2,∴B(0,1)；故答案为：(0,1)②证明: 如图1中,∵PQ⊥PB,EC⊥OC,∴∠ECP=∠BPE=∠POB=90°,∴∠OPB+∠EPC=90°,∠EPC+∠CEP=90°,∴∠OPB=∠PEC,∴△BOP∽△PCE.（2）如图2中, 过点C′作C′G⊥OC于G, 延长PB交DA的延长线于F.设OP=x, 则PC=4−x.∵AF∥OP,∴∠F=∠BPO，∠FAB=∠BOP，∴△FBA∽△PBO,∴FAOP =ABOB=2，∴AF=2x,∵∠EPC+∠OPB=90°,∠EPC′+∠C′PF=90°∵∠EPC=∠EPC′，∴∠C′PF=∠OPB，∵∠OPB=∠F,∴∠F=∠C′PF，∴C′F=C′P=PC=8−x,∴AC′=8−3x，∴C′D=3x，∴PG=PC−CG=8−4x,在Rt△EBC′中,∵C′P2=PG2+C′G2，∴(8−x)2=(8−4x)2+62,解得x=65或x=2,∴P(65，0) 或(2,0).故答案为：(65，0) 或(2,0)；（3）如图3中,∵OB=2,∠POB=90°,∠OPB=60°,∴∠PBO=30°,∴OP=OB⋅tan30°=2√33，PB=2OP=4√33，∵∠BPQ=90°,∴∠QPC=30°,∵∠PBQ=∠ECP=90°,∴当∠PE1B=30°时, 以点E,P,C为顶点的三角形和△BPE相似,∴PE1=√3PB=4,∴E1C=12PE1=2,PC=2√3∴OC=8√33,∴E1(8√33，2)，当∠PBE2=30°时, 以点E,P,C为顶点的三角形和△BPE相似,，同法可得E2(4√33，23).当∠PE3B=30°时, 以点E,P,C为顶点的三角形和△BPE相似,同法可得E3(−4√33，−2).当∠PBE4=30°时, 以点E,P,C为顶点的三角形和△BPE相似,同法可得E4(0，−23).综上所述，满足条件的点E的坐标为(8√33，2)或(4√33，23)或(−4√33，−2)或(0，−23).13．（23·24·全国·专题练习）（1）如图①，在矩形ABCD的AB边上取一点E，将△ADE沿DE翻折，使点A落在BC上A′处，若AB=6,BC=10，求AEEB的值；（2）如图②，在矩形ABCD的BC边上取一点E，将四边形ABED沿DE翻折，使点B落在DC的延长线上B′处，若BC⋅CE=24,AB=6，求BE的值；（3）如图③，在△ABC中，∠BAC=45°，AD⊥BC，垂足为点D，AD=10,AE=6，过点E作EF⊥AD交AC于点F，连接DF，且满足∠DFE=2∠DAC，直接写出BD+53EF的值．【思路点拨】（1）由矩形性质和翻折性质、结合勾股定理求得A′B=2，设AE=A′E=x则BE=AB−AE=6−x，Rt△A′BE中利用勾股定理求得x=103，则AE=103，BE=6−103=83，进而求解即可；（2）由矩形的性质和翻折性质得到∠EBC=∠BDA，证明△EBC∽△BDA，利用相似三角形的性质求得BC= 4，则BD=10，在Rt△ABD中，利用勾股定理求得AD=8，进而求得BC=8,CE=3可求解；（3）证明△AEF∽△ADC得到CD=53EF，则BD+53EF=BD+CD=BC；设EF=3k，CD=5k，过点D作DH⊥AC于H，证明△CHD≌△FHD(ASA)得到DF=CD=5k，在Rt△EFD中，由勾股定理解得k=1，进而可求得AC=5√5．过B作BG⊥AC于G，证明∠CBG=∠CDH=∠DAC，则sin∠CBG=sin∠DAC=√55，cos∠CBG=cos∠DAC=2√55，再证明AG=BG，在Rt△BCG中利用锐角三角函数和AG+CG=BG+CG= AC，求得BC，即可求解．【解题过程】解：（1）∵四边形ABCD是矩形，∴AD=BC=10,CD=AB=6,∠A=∠B=∠C=90°，由翻折性质得AD=A′D=10,AE=A′E，在Rt△A′CD中，A′C=√A′D2−CD2=√102−62=8，∴A′B=BC−AC=2，。

浙江省中考数学一轮复习 专题练习10 压轴题(1) 浙教版-浙教版初中九年级全册数学试题

浙江省中考数学一轮复习 专题练习10 压轴题(1) 浙教版-浙教版初中九年级全册数学试题

压轴题（1）班级某某学号一、选择题1.在△ABC中，AB＝10，AC＝210，BC边上的高AD＝6，则另一边BC等于( )A．10 B．8 C．6或10 D．8或102.若x0是方程ax2+2x+c=0（a≠0）的一个根，设M=1﹣ac，N=（ax0+1）2，则M与N的大小关系正确的为（）A．M＞N B．M=N C．M＜N D．不确定3.如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E．若BC=3，则DE的长为（）A．1 B．2 C．3 D．44.如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（）A．6 B．6C．2D．35.二次函数y=ax2+bx+c（a≠0）和正比例函数y=x的图象如图所示，则方程ax2+（b﹣）x+c=0（a≠0）的两根之和（）A ．大于0B ．等于0C ．小于0D ．不能确定6.如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC ，垂足为点F ，连接DF ，分析下列四个结论：①△AEF ∽△CAB ；②CF ＝2AF ；③DF ＝DC ；④tan∠CAD ＝2．其中正确的结论有( ) A.4个 B ．3个 C ．2个 D ．1个第10题图FEDB CA7.如图，在Rt △AOB 中，两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上，将△AOB 绕点B 逆时针旋转90°后得到△A ′O ′B．若反比例函数的图象恰好经过斜边A ′B 的中点C ，S △ABO =4，tan ∠BAO =2，则k 的值为（ ）A ．3B ．4C ．6D ．88.有3个正方形如图所示放置，阴影部分的面积依次记为S 1，S 2，则S 1：S 2等于（ ）A ．1：B ．1：2C ．2：3D ．4：99.如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第n 个图案中有2017个白色纸片，则n 的值为（ ）A ．671B ．672C ．673D ．67410.如图，抛物线y =ax 2+bx +c （a ≠0）的对称轴为直线x =1，与x 轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论： ①4ac ＜b 2；②方程ax 2+bx +c =0的两个根是x 1=﹣1，x 2=3； ③3a +c ＞0④当y ＞0时，x 的取值X 围是﹣1≤x ＜3 ⑤当x ＜0时，y 随x 增大而增大 其中结论正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个 二、填空题11.如图，在Rt△ABC 中，∠B ＝90°，AB ＝4，BC ＞AB ，点D 在BC 上，以AC 为对角线的所有平行四边形ADCE 中，DE 的最小值是_____________．第14题图EOBCD12.如图，直线y ＝x ＋b 与直线y ＝kx ＋6交于点P (3，5)，则关于x 的不等式x ＋b ＞kx ＋6的解集是_____________．13.在矩形ABCD中，∠B的角平分线BE与AD交于点E，∠BED的角平分线EF与DC交于点F，若AB=9，DF=2FC，则BC=．（结果保留根号）14.如图，已知点A（1，2）是反比例函数y=图象上的一点，连接AO并延长交双曲线的另一分支于点B，点P是x轴上一动点；若△PAB是等腰三角形，则点P的坐标是．15.如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=2，OC=1．在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2…，以此类推，得到的矩形A n OB n的对角线交点的坐标为．三、解答题16.如图，在Rt△ABC中，∠C=90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．（1）求证：AC是⊙O的切线；（2）若OB=10，CD=8，求BE的长．17.某段工程建设中，甲队单独完成这项工程需要150天，甲队单独施工30天后增加乙队，两队又共同工作了15天，共完成总工程的．（1）求乙队单独完成这项工程需要多少天？（2）为了加快工程进度，甲、乙两队各自提高工作效率，提高后乙队的工作效率是，甲队的工作效率是乙队的m倍（1≤m≤2），若两队合作40天完成剩余的工程，请写出a关于m的函数关系式，并求出乙队的最大工作效率是原来的几倍？18.已知在关于x的分式方程①和一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0②中，k、m、n 均为实数，方程①的根为非负数．（1）求k的取值X围；（2）当方程②有两个整数根x1、x2，k为整数，且k=m+2，n=1时，求方程②的整数根；（3）当方程②有两个实数根x1、x2，满足x1（x1﹣k）+x2（x2﹣k）=（x1﹣k）（x2﹣k），且k为负整数时，试判断|m|≤2是否成立？请说明理由．19.如图，直线y=﹣x+2与x轴，y轴分别交于点A，点B，两动点D，E分别从点A，点B同时出发向点O运动（运动到点O停止），运动速度分别是1个单位长度/秒和个单位长度/秒，设运动时间为t秒，以点A为顶点的抛物线经过点E，过点E作x轴的平行线，与抛物线的另一个交点为点G，与AB相交于点F．（1）求点A，点B的坐标；（2）用含t的代数式分别表示EF和AF的长；（3）当四边形ADEF为菱形时，试判断△AFG与△AGB是否相似，并说明理由．（4）是否存在t的值，使△AGF为直角三角形？若存在，求出这时抛物线的解析式；若不存在，请说明理由．20.阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线经过B、C两点，顶点D在正方形内部．（1）直接写出点D（m，n）所有的特征线；（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？21.如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．（1）求抛物线的解析式及点C的坐标；（2）求证：△ABC是直角三角形；（3）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．22.已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别是(0，4)、（－1，0），将此平行四边形绕点O顺时针旋转90°，得到平行四边形A′B′OC′．(1)若抛物线过点C、A、A′，求此抛物线的解析式；(2)点M是第一象限内抛物线上的一动点，问：当点M在何处时，△AMA′的面积最大？最大面积是多少？并求出此时M的坐标；(3)若P为抛物线上的一动点，N为x轴上的一动点，点Q坐标为(1，0)，当P、N、B、Q构成平行四边形时，求点P的坐标，当这个平行四边形为矩形时，求点N的坐标．24.如图1，△ABC是等腰直角三角形，∠BAC＝90°，AB＝AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD＝CF，BD⊥CF成立．(1)当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD＝CF成立吗？若成立，请证明；若不成立，请说明理由．(2)当△ABC绕点A逆时针旋转45°时，如图3，延长DB交CF于点H.①求证：BD⊥CF；②当AB＝2，AD＝32时，求线段DH的长．答案详解一、选择题【考点】一元二次方程的解．【分析】把x0代入方程ax2+2x+c=0得ax02+2x0=﹣c，作差法比较可得．【解答】解：∵x0是方程ax2+2x+c=0（a≠0）的一个根，∴ax02+2x0+c=0，即ax02+2x0=﹣c，则N﹣M=（ax0+1）2﹣（1﹣ac）=a2x02+2ax0+1﹣1+ac=a（ax02+2x0）+ac=﹣ac+ac=0，∴M=N，故选：B．3.如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E．若BC=3，则DE的长为（）A．1 B．2 C．3 D．4【分析】由角平分线和线段垂直平分线的性质可求得∠B=∠CAD=∠DAB=30°，【解答】解：∵DE垂直平分AB，∴DA=DB，∴∠B=∠DAB，∵AD平分∠CAB，∴∠CAD=∠DAB，∵∠C=90°，∴3∠CAD=90°，∴∠CAD=30°，∵AD平分∠CAB，DE⊥AB，CD⊥AC，∴CD=DE=BD，∵BC=3，∴CD=DE=1，故选A．4.如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（）A．6 B．6C．2D．3【考点】翻折变换（折叠问题）．【分析】根据折叠的性质判定△EDB是等腰直角三角形，然后再求BE．【解答】解：根据折叠的性质知，CD=ED，∠CDA=∠ADE=45°，∴∠CDE=∠BDE=90°，∵BD=CD，BC=6，∴BD=ED=3，即△EDB是等腰直角三角形，∴BE=BD=×3=3，故选D．5.二次函数y=ax2+bx+c（a≠0）和正比例函数y=x的图象如图所示，则方程ax2+（b﹣）x+c=0（a≠0）的两根之和（）A ．大于0B ．等于0C ．小于0D ．不能确定【考点】抛物线与x 轴的交点．【分析】设ax 2+bx +c =0（a ≠0）的两根为x 1，x 2，由二次函数的图象可知x 1+x 2＞0，a ＞0，设方程ax 2+（b ﹣）x +c =0（a ≠0）的两根为a ，b 再根据根与系数的关系即可得出结论．【解答】解：设ax 2+bx +c =0（a ≠0）的两根为x 1，x 2，∵由二次函数的图象可知x 1+x 2＞0，a ＞0，∴﹣＞0．设方程ax 2+（b ﹣）x +c =0（a ≠0）的两根为a ，b ，则a +b =﹣=﹣+，∵a ＞0，∴＞0， ∴a +b ＞0．故选C ．6.如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC ，垂足为点F ，连接DF ，分析下列四个结论：①△AEF ∽△CAB ；②CF ＝2AF ；③DF ＝DC ；④tan∠CAD ＝2．其中正确的结论有( )A.4个 B ．3个 C ．2个 D ．1个第10题图F D B A【知识点】特殊平行四边形——矩形的性质、相似三角形——相似三角形的判定与性质、锐角三角函数——锐角三角函数值的求法【答案】B. 【解析】∵矩形ABCD 中，∴AD ∥BC .∴△AEF ∽△CAB ….......................①正确；∵△AEF ∽△CAB ，∴AF CF ＝AE BC ＝12，∴CF ＝2AF ……………………………②正确；过点D 作DH ⊥AC 于点H .易证△ABF ≌△CDH (AAS ).∴AF ＝CH .∵EF ∥DH ,∴AF FH ＝AEED ＝1.∴AF ＝FH .∴FH ＝CH .∴DH 垂直平分CF .∴DF ＝DC . ……………………………………………③正确；第10题答案图G HF E D ACB设EF ＝1，则BF ＝2.∵△ABF ∽△EAF .∴AF EF ＝BFAF .∴AF ＝EF •BF ＝1×2＝ 2.∴tan∠ABF ＝AF BF ＝22.∵∠CAD ＝∠ABF ，∴tan∠CAD ＝tan∠ABF ＝22.…………④错误. 故选择B.7.如图，在Rt △AOB 中，两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上，将△AOB 绕点B 逆时针旋转90°后得到△A ′O ′B．若反比例函数的图象恰好经过斜边A ′B 的中点C ，S △ABO =4，tan ∠BAO =2，则k 的值为（ ）A ．3B ．4C ．6D ．8【分析】先根据S △ABO =4，tan ∠BAO =2求出AO 、BO 的长度，再根据点C 为斜边A ′B 的中点，求出点C 的坐标，点C 的横纵坐标之积即为k 值．【解答】解：设点C 坐标为（x ，y ），作CD ⊥BO ′交边BO ′于点D ，∵tan ∠BAO =2，∴=2，∵S△ABO=•AO•BO=4，∴AO=2，BO=4，∵△ABO≌△A′O′B，∴AO=A′0′=2，BO=BO′=4，∵点C为斜边A′B的中点，CD⊥BO′，∴CD=A′0′=1，BD=BO′=2，∴x=BO﹣CD=4﹣1=3，y=BD=2，∴k=x•y=3•2=6．故选C．．8.有3个正方形如图所示放置，阴影部分的面积依次记为S1，S2，则S1：S2等于（）A．1：B．1：2 C．2：3 D．4：9【考点】正方形的性质．【分析】设小正方形的边长为x，再根据相似的性质求出S1、S2与正方形面积的关系，然后进行计算即可得出答案．【解答】解：设小正方形的边长为x，根据图形可得：∵=，∴=，∴=，∴S1=S正方形ABCD，∴S1=x2，∵=，∴=，∴S2=S正方形ABCD，∴S2=x2，∴S1：S2=x2：x2=4：9；故选D．9.如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第n个图案中有2017个白色纸片，则n的值为（）A．671 B．672 C．673 D．674【分析】将已知三个图案中白色纸片数拆分，得出规律：每增加一个黑色纸片时，相应增加3个白色纸片；据此可得第n个图案中白色纸片数，从而可得关于n的方程，解方程可得．【解答】解：∵第1个图案中白色纸片有4=1+1×3X；第2个图案中白色纸片有7=1+2×3X；第3个图案中白色纸片有10=1+3×3X；…∴第n个图案中白色纸片有1+n×3=3n+1（X），根据题意得：3n+1=2017，解得：n=672，故选：B．10.如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c＞0④当y＞0时，x的取值X围是﹣1≤x＜3⑤当x＜0时，y随x增大而增大其中结论正确的个数是（）A．4个B．3个C．2个D．1个【考点】二次函数图象与系数的关系．【分析】利用抛物线与x轴的交点个数可对①进行判断；利用抛物线的对称性得到抛物线与x轴的一个交点坐标为（3，0），则可对②进行判断；由对称轴方程得到b=﹣2a，然后根据x=﹣1时函数值为负数可得到3a+c＜0，则可对③进行判断；根据抛物线在x轴上方所对应的自变量的X围可对④进行判断；根据二次函数的性质对⑤进行判断．【解答】解：∵抛物线与x轴有2个交点，∴b2﹣4ac＞0，所以①正确；∵抛物线的对称轴为直线x=1，而点（﹣1，0）关于直线x =1的对称点的坐标为（3，0），∴方程ax 2+bx +c =0的两个根是x 1=﹣1，x 2=3，所以②正确；∵x =﹣=1，即b =﹣2a ，而x =﹣1时，y ＜0，即a ﹣b +c ＜0，∴a +2a +c ＜0，所以③错误；∵抛物线与x 轴的两点坐标为（﹣1，0），（3，0），∴当﹣1＜x ＜3时，y ＞0，所以④错误；∵抛物线的对称轴为直线x =1，∴当x ＜1时，y 随x 增大而增大，所以⑤正确．故选B ．二、填空题11.如图，在Rt△ABC 中，∠B ＝90°，AB ＝4，BC ＞AB ，点D 在BC 上，以AC 为对角线的所有平行四边形ADCE 中，DE 的最小值是_____________．第14题图EO B A CD【知识点】直线射线和线段——垂线段最短、图形的相似——平行线分线段成比例定理、平行四边形——平行四边形的性质、【答案】4.【解析】根据“垂线段最短”，可知：当OD ⊥BC 时，OD 最短，DE 的值最小.当OD ⊥BC 时，OD ∥AB .∴CD BD ＝CO OA ＝1.∴OD 是△ABC 的中位线.∴OD ＝12AB ＝2.∴DE 的最小值＝2OD ＝4.第14题答案图EOCABD12.如图，直线y＝x＋b与直线y＝kx＋6交于点P(3，5)，则关于x的不等式x＋b＞kx＋6的解集是_____________．【知识点】一次函数——一次函数与一元一次不等式【答案】x＞3.【解析】由图象得到直线y＝x＋b与直线y＝kx＋6的交点P(3，5)，在点P(3，5)的右侧，直线y ＝x＋b落在直线y＝kx＋6的上方，该部分对应的x的取值X围为x＞3,即不等式x＋b＞kx＋6的解集是x＞3．13.在矩形ABCD中，∠B的角平分线BE与AD交于点E，∠BED的角平分线EF与DC交于点F，若AB=9，DF=2FC，则BC=．（结果保留根号）【考点】矩形的性质；等腰三角形的判定；相似三角形的判定与性质．【分析】先延长EF和BC，交于点G，再根据条件可以判断三角形ABE为等腰直角三角形，并求得其斜边BE的长，然后根据条件判断三角形BEG为等腰三角形，最后根据△EFD∽△GFC得出CG与DE的倍数关系，并根据BG=BC+CG进行计算即可．【解答】解：延长EF和BC，交于点G∵矩形ABCD中，∠B的角平分线BE与AD交于点E，∴∠ABE=∠AEB=45°，∴AB=AE=9，∴直角三角形ABE中，BE==，又∵∠BED的角平分线EF与DC交于点F，∴∠BEG=∠DEF∵AD∥BC∴∠G=∠DEF∴∠BEG=∠G∴BG=BE=由∠G=∠DEF，∠EFD=∠GFC，可得△EFD∽△GFC∴设CG=x，DE=2x，则AD=9+2x=BC∵BG=BC+CG∴=9+2x+x解得x=∴BC=9+2（﹣3）=故答案为：14.如图，已知点A（1，2）是反比例函数y=图象上的一点，连接AO并延长交双曲线的另一分支于点B，点P是x轴上一动点；若△PAB是等腰三角形，则点P的坐标是（﹣3，0）或（5，0）或（3，0）或（﹣5，0）．【考点】反比例函数图象上点的坐标特征；等腰三角形的性质．【分析】由对称性可知O为AB的中点，则当△PAB为等腰三角形时只能有PA=AB或PB=AB，设P点坐标为（x，0），可分别表示出PA和PB，从而可得到关与x的方程，可求得x，可求得P点坐标．【解答】解：∵反比例函数y=图象关于原点对称，∴A、B两点关于O对称，∴O为AB的中点，且B（﹣1，﹣2），∴当△PAB为等腰三角形时有PA=AB或PB=AB，设P点坐标为（x，0），∵A（1，2），B（﹣1，﹣2），∴AB==2，PA=，PB=，当PA=AB时，则有=2，解得x=﹣3或5，此时P点坐标为（﹣3，0）或（5，0）；当PB=AB时，则有=2，解得x=3或﹣5，此时P点坐标为（3，0）或（﹣5，0）；综上可知P点的坐标为（﹣3，0）或（5，0）或（3，0）或（﹣5，0），故答案为：（﹣3，0）或（5，0）或（3，0）或（﹣5，0）．15.如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=2，OC=1．在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2…，以此类推，得到的矩形A n OB n的对角线交点的坐标为（﹣，）．【考点】位似变换；坐标与图形性质；矩形的性质．【分析】根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k，即可求得B n的坐标，然后根据矩形的性质即可求得对角线交点的坐标．【解答】解：∵在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，∴矩形A1OC1B1与矩形AOCB是位似图形，点B与点B1是对应点，∵OA=2，OC=1．∵点B的坐标为（﹣2，1），∴点B1的坐标为（﹣2×，1×），∵将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2…，∴B2（﹣2××，1××），∴B n（﹣2×，1×），∵矩形A n OB n的对角线交点（﹣2××，1××），即（﹣，），故答案为：（﹣，）．三、解答题16.如图，在Rt△ABC中，∠C=90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．（1）求证：AC是⊙O的切线；（2）若OB=10，CD=8，求BE的长．【考点】切线的判定．【专题】计算题；与圆有关的位置关系．【分析】（1）连接OD，由BD为角平分线得到一对角相等，根据OB=OD，等边对等角得到一对角相等，等量代换得到一对内错角相等，进而确定出OD与BC平行，利用两直线平行同位角相等得到∠ODA 为直径，即可得证；（2）由OD与BC平行得到三角形OAD与三角形BAC相似，由相似得比例求出OA的长，进而确定出AB的长，连接EF，过O作OG垂直于BC，利用勾股定理求出BG的长，由BG+GC求出BC的长，再由三角形BEF与三角形BAC相似，由相似得比例求出BE的长即可．【解答】（1）证明：连接OD，∵BD为∠ABC平分线，∴∠1=∠2，∵OB=OD，∴∠1=∠3，∴∠2=∠3，∴OD∥BC，∵∠C=90°，∴∠ODA=90°，则AC为圆O的切线；（2）解：过O作OG⊥BC，∴四边形ODCG为矩形，∴GC=OD=OB=10，OG=CD=8，在Rt△OBG中，利用勾股定理得：BG=6，∴BC=BG+GC=6+10=16，∵OD∥BC，∴△AOD∽△ABC，∴=，即=，解得：OA=，∴AB=+10=，连接EF，∵BF为圆的直径，∴∠BEF=90°，∴∠BEF=∠C=90°，∴EF∥AC，∴=，即=，解得：BE=12．17.某段工程建设中，甲队单独完成这项工程需要150天，甲队单独施工30天后增加乙队，两队又共同工作了15天，共完成总工程的．（1）求乙队单独完成这项工程需要多少天？（2）为了加快工程进度，甲、乙两队各自提高工作效率，提高后乙队的工作效率是，甲队的工作效率是乙队的m倍（1≤m≤2），若两队合作40天完成剩余的工程，请写出a关于m的函数关系式，并求出乙队的最大工作效率是原来的几倍？【考点】一次函数的应用；分式方程的应用．【分析】（1）设乙队单独完成这项工程需要x天，根据题意得方程即可得到结论；（2）根据题意得（+）×40=，即可得到a=60m+60，根据一次函数的性质得到=，即可得到结论．【解答】解：（1）设乙队单独完成这项工程需要x天，根据题意得×（30+15）+×15=，解得：x=450，经检验x=450是方程的根，答：乙队单独完成这项工程需要450天；（2）根据题意得（+）×40=，∴a=60m+60，∵60＞0，∴a随m的增大增大，∴当m=1时，最大，∴=，∴÷=7.5倍，18.已知在关于x的分式方程①和一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0②中，k、m、n 均为实数，方程①的根为非负数．（1）求k的取值X围；（2）当方程②有两个整数根x1、x2，k为整数，且k=m+2，n=1时，求方程②的整数根；（3）当方程②有两个实数根x1、x2，满足x1（x1﹣k）+x2（x2﹣k）=（x1﹣k）（x2﹣k），且k为负整数时，试判断|m|≤2是否成立？请说明理由．【分析】（1）先解出分式方程①的解，根据分式的意义和方程①的根为非负数得出k的取值；（2）先把k=m+2，n=1代入方程②化简，由方程②有两个整数实根得△是完全平方数，列等式得出关于m的等式，由根与系数的关系和两个整数根x1、x2得出m=1和﹣1，分别代入方程后解出即可．（3）根据（1）中k的取值和k为负整数得出k=﹣1，化简已知所给的等式，并将两根和与积代入计算求出m的值，做出判断．【解答】解：（1）∵关于x的分式方程的根为非负数，∴x≥0且x≠1，又∵x=≥0，且≠1，∴解得k≥﹣1且k≠1，又∵一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0中2﹣k≠0，∴k≠2，综上可得：k≥﹣1且k≠1且k≠2；（2）∵一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0有两个整数根x1、x2，且k=m+2，n=1时，∴把k=m+2，n=1代入原方程得：﹣mx2+3mx+（1﹣m）=0，即：mx2﹣3mx+m﹣1=0，∴△≥0，即△=（﹣3m）2﹣4m（m﹣1），且m≠0，∴△=9m2﹣4m（m﹣1）=m（5m+4），∵x1、x2是整数，k、m都是整数，∵x1+x2=3，x1•x2==1﹣，∴1﹣为整数，∴m=1或﹣1，∴把m=1代入方程mx2﹣3mx+m﹣1=0得：x2﹣3x+1﹣1=0，x2﹣3x=0，x（x﹣3）=0，x1=0，x2=3；把m=﹣1代入方程mx2﹣3mx+m﹣1=0得：﹣x2+3x﹣2=0，x2﹣3x+2=0，（x﹣1）（x﹣2）=0，x1=1，x2=2；（3）|m|≤2不成立，理由是：由（1）知：k≥﹣1且k≠1且k≠2，∵k是负整数，∴k=﹣1，（2﹣k）x2+3mx+（3﹣k）n=0且方程有两个实数根x1、x2，∴x1+x2=﹣==﹣m，x1x2==，x1（x1﹣k）+x2（x2﹣k）=（x1﹣k）（x2﹣k），x12﹣x1k+x22﹣x2k=x1x2﹣x1k﹣x2k+k2，x12+x22═x1x2+k2，（x1+x2）2﹣2x1x2﹣x1x2=k2，（x1+x2）2﹣3x1x2=k2，（﹣m）2﹣3×=（﹣1）2，m2﹣4=1，m2=5，m=±，∴|m|≤2不成立．19.如图，直线y=﹣x+2与x轴，y轴分别交于点A，点B，两动点D，E分别从点A，点B同时出发向点O运动（运动到点O停止），运动速度分别是1个单位长度/秒和个单位长度/秒，设运动时间为t秒，以点A为顶点的抛物线经过点E，过点E作x轴的平行线，与抛物线的另一个交点为点G，与AB相交于点F．（1）求点A，点B的坐标；（2）用含t的代数式分别表示EF和AF的长；（3）当四边形ADEF为菱形时，试判断△AFG与△AGB是否相似，并说明理由．（4）是否存在t的值，使△AGF为直角三角形？若存在，求出这时抛物线的解析式；若不存在，请说明理由．【考点】二次函数综合题．【分析】（1）在直线y=﹣x+2中，分别令y=0和x=0，容易求得A、B两点坐标；（2）由OA、OB的长可求得∠ABO=30°，用t可表示出BE，EF，和BF的长，由勾股定理可求得AB 的长，从而可用t表示出AF的长；（3）利用菱形的性质可求得t的值，则可求得AF=AG的长，可得到=，可判定△AFG与△AGB 相似；（4）若△AGF为直角三角形时，由条件可知只能是∠FAG=90°，又∠AFG=∠OAF=60°，由（2）可知AF=4﹣2t，EF=t，又由二次函数的对称性可得到EG=2OA=4，从而可求出FG，在Rt△AGF中，可得到关于t的方程，可求得t的值，进一步可求得E点坐标，利用待定系数法可求得抛物线的解析式．【解答】解：（1）在直线y=﹣x+2中，令y=0可得0=﹣x+2，解得x=2，令x=0可得y=2，∴A为（2，0），B为（0，2）；（2）由（1）可知OA=2，OB=2，∴tan∠ABO==，∴∠ABO=30°，∵运动时间为t秒，∴BE=t，∴在Rt△BEF中，EF=BE•tan∠ABO=BE=t，BF=2EF=2t，在Rt△ABO中，OA=2，OB=2，∴AB=4，∴AF=4﹣2t；（3）相似．理由如下：当四边形ADEF为菱形时，则有EF=AF，即t=4﹣2t，解得t=，∴AF=4﹣2t=4﹣=，OE=OB﹣BE=2﹣×=，如图，过G作GH⊥x轴，交x轴于点H，则四边形OEGH为矩形，∴GH=OE=，又EG∥x轴，抛物线的顶点为A，∴OA=AH=2，在Rt△AGH中，由勾股定理可得AG2=GH2+AH2=（）2+22=，又AF•AB=×4=，∴AF•AB=AG2，即=，且∠FAG=∠GAB，∴△AFG∽△AGB；（4）存在，∴∠GFA=∠BAO=60°，又G点不能在抛物线的对称轴上，∴∠FGA≠90°，∴当△AGF为直角三角形时，则有∠FAG=90°，又∠FGA=30°，∴FG=2AF，∵EF=t，EG=4，∴FG=4﹣t，且AF=4﹣2t，∴4﹣t=2（4﹣2t），解得t=，即当t的值为秒时，△AGF为直角三角形，此时OE=OB﹣BE=2﹣t=2﹣×=，∴E点坐标为（0，），∵抛物线的顶点为A，∴可设抛物线解析式为y=a（x﹣2）2，把E点坐标代入可得=4a，解得a=，∴抛物线解析式为y=（x﹣2）2，即y=x2﹣x+．20.阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线经过B、C两点，顶点D在正方形内部．（1）直接写出点D（m，n）所有的特征线；（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？【分析】（1）根据特征线直接求出点D的特征线；（2）由点D的一条特征线和正方形的性质求出点D的坐标，从而求出抛物线解析式；（2）分平行于x轴和y轴两种情况，由折叠的性质计算即可．【解答】解：（1）∵点D（m，n），∴点D（m，n）的特征线是x=m，y=n，y=x+n﹣m，y=﹣x+m+n；（2）点D有一条特征线是y=x+1，∴n﹣m=1，∴n=m+1∵抛物线解析式为，∴y=（x﹣m）2+m+1，∵四边形OABC是正方形，且D点为正方形的对称轴，D（m，n），∴B（2m，2m），∴（2m﹣m）2+n=2m，将n=m+1带入得到m=2，n=3；∴D（2，3），∴抛物线解析式为y=（x﹣2）2+3（3）如图，当点A′在平行于y轴的D点的特征线时，根据题意可得，D（2，3），∴OA′=OA=4，OM=2，∴∠A′OM=60°，∴∠A′OP=∠AOP=30°，∴MN==，∴抛物线需要向下平移的距离=3﹣=．乳头，当点A′在平行于x轴的D点的特征线时，∵顶点落在OP上，∴A′与D重合，∴A′（2，3），设P（4，c）（c＞0），由折叠有，PD=PA，∴=c，∴c=，∴P（4，）∴直线OP解析式为y=，∴N（2，），∴抛物线需要向下平移的距离=3﹣=，即：抛物线向下平移或距离，其顶点落在OP上．21.如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．（1）求抛物线的解析式及点C的坐标；（2）求证：△ABC是直角三角形；（3）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．【考点】二次函数综合题．【分析】（1）可设顶点式，把原点坐标代入可求得抛物线解析式，联立直线与抛物线解析式，可求得C点坐标；（2）分别过A、C两点作x轴的垂线，交x轴于点D、E两点，结合A、B、C三点的坐标可求得∠ABO=∠CBO=45°，可证得结论；（3）设出N点坐标，可表示出M点坐标，从而可表示出MN、ON的长度，当△MON和△ABC相似时，利用三角形相似的性质可得=或=，可求得N点的坐标．【解答】解：（1）∵顶点坐标为（1，1），∴设抛物线解析式为y=a（x﹣1）2+1，又抛物线过原点，∴0=a（0﹣1）2+1，解得a=﹣1，∴抛物线解析式为y=﹣（x﹣1）2+1，即y=﹣x2+2x，联立抛物线和直线解析式可得，解得或，∴B（2，0），C（﹣1，﹣3）；（2）如图，分别过A、C两点作x轴的垂线，交x轴于点D、E两点，则AD=OD=BD=1，BE=OB+OE=2+1=3，EC=3，∴∠ABO=∠CBO=45°，即∠ABC=90°，∴△ABC是直角三角形；（3）假设存在满足条件的点N，设N（x，0），则M（x，﹣x2+2x），∴ON=|x|，MN=|﹣x2+2x|，由（2）在Rt△ABD和Rt△CEB中，可分别求得AB=，BC=3，∵MN⊥x轴于点N∴∠ABC=∠MNO=90°，∴当△ABC和△MNO相似时有=或=，①当=时，则有=，即|x||﹣x+2|=|x|，∵当x=0时M、O、N不能构成三角形，∴x≠0，∴|﹣x+2|=，即﹣x+2=±，解得x=或x=，此时N点坐标为（，0）或（，0）；②当=时，则有=，即|x||﹣x+2|=3|x|，∴|﹣x+2|=3，即﹣x+2=±3，解得x=5或x=﹣1，此时N点坐标为（﹣1，0）或（5，0），综上可知存在满足条件的N点，其坐标为（，0）或（，0）或（﹣1，0）或（5，0）．22.已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．【考点】四边形综合题．【分析】（1）结论AE=EF=AF．只要证明AE=AF即可证明△AEF是等边三角形．（2）欲证明BE=CF，只要证明△BAE≌△CAF即可．（3）过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，根据FH=CF•cos30°，因为CF=BE，只要求出BE即可解决问题．【解答】（1）解：结论AE=EF=AF．理由：如图1中，连接AC，∵四边形ABCD是菱形，∠B=60°，∴AB=BC=CD=AD，∠B=∠D=60°，∴△ABC，△ADC是等边三角形，∴∠BAC=∠DAC=60°∵BE=EC，∴∠BAE=∠CAE=30°，AE⊥BC，∵∠EAF=60°，∴∠CAF=∠DAF=30°，∴AF⊥CD，∴AE=AF（菱形的高相等），∴△AEF是等边三角形，∴AE=EF=AF．（2）证明：如图2中，∵∠BAC=∠EAF=60°，∴∠BAE=∠CAE，在△BAE和△CAF中，，∴△BAE≌△CAF，∴BE=CF．（3）解：过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，∵∠EAB=15°，∠ABC=60°，∴∠AEB=45°，在RT△AGB中，∵∠ABC=60°AB=4，∴BG=2，AG=2，在RT△AEG中，∵∠AEG=∠EAG=45°，∴AG=GE=2，∴EB=EG﹣BG=2﹣2，∵△AEB≌△AFC，∴AE=AF，EB=CF=2﹣2，∠AEB=∠AFC=45°，∵∠EAF=60°，AE=AF，∴△AEF是等边三角形，∴∠AEF=∠AFE=60°∵∠AEB=45°，∠AEF=60°，∴∠CEF=∠AEF﹣∠AEB=15°，在RT△EFH中，∠CEF=15°，∴∠EFH=75°，∵∠AFE=60°，∴∠AFH=∠EFH﹣∠AFE=15°，∵∠AFC=45°，∠CFH=∠AFC﹣∠AFH=30°，在RT△CHF中，∵∠CFH=30°，CF=2﹣2，∴FH=CF•cos30°=（2﹣2）•=3﹣．∴点F到BC的距离为3﹣．，平行四边形ABOC如图放置，点A、C的坐标分别是(0，4)、（－1，0），将此平行四边形绕点O 顺时针旋转90°，得到平行四边形A′B′OC′．(1)若抛物线过点C、A、A′，求此抛物线的解析式；(2)点M是第一象限内抛物线上的一动点，问：当点M在何处时，△AMA′的面积最大？最大面积是多少？并求出此时M的坐标；(3)若P为抛物线上的一动点，N为x轴上的一动点，点Q坐标为(1，0)，当P、N、B、Q构成平行四边形时，求点P的坐标，当这个平行四边形为矩形时，求点N的坐标．【知识点】平行四边形——平行四边形的性质、旋转——旋转的性质、二次函数——确定二次函数的表达式（待定系数法）、函数与几何动态——运动产生的面积问题及运动产生的特殊四边形问题、分类讨论思想、实际问题与数学建模——函数模型【思路分析】（1）先由OA ′＝OA 得到点A ′的坐标，再用点C 、A 、A ′的坐标即可求此抛物线的解析式；（2）连接AA ′, 过点M 作MN ⊥x 轴，交AA ′于点N ,把△AMA ′分割为△AMN 和△A ′MN , △AMA ′的面积＝△AMA ′的面积＋△AMN 的面积＝12OA ′•MN ,设点M 的横坐标为x ，借助抛物线的解析式和AA ′的解析式，建立MN 的长关于x 的函数关系式，再据此建立△AMA ′的面积关于x 的二次函数关系式，再求△AMA ′面积的最大值以及此时M 的坐标；（3）在P 、N 、B 、Q 这四个点中，B 、Q 这两个点是固定点，因此可以考虑将BQ 作为边、将BQ 作为对角线分别构造符合题意的图形，再求解.【解答】解：(1)∵ ABOC 绕点O 顺时针旋转90°，得到平行四边形A ′B ′OC ′，点A 的坐标是(0，4)，∴点A ′的坐标为(4，0)，点B 的坐标为(1，4).∵抛物线过点C ，A ，A ′，设抛物线的函数解析式为y ＝ax 2＋bx ＋c (a ≠0),可得： ⎩⎪⎨⎪⎧a －b ＋c ＝0c ＝416a ＋ 4b ＋c ＝0. 解得：⎩⎪⎨⎪⎧a ＝－1b ＝3c ＝4.∴抛物线的函数解析式为y ＝－x 2＋3x ＋4.(2)连接AA ′，设直线AA ′的函数解析式为y ＝kx ＋b ，可得⎩⎨⎧0＋b ＝414k ＋b ＝0.解得：⎩⎨⎧k ＝－1b ＝4.∴直线AA '的函数解析式是y ＝－x ＋4.设M (x ，－x 2＋3x ＋4)，S △AMA ′＝12×4×[－x 2＋3x ＋4一(一x ＋4)]＝一2x 2＋8x ＝一2(x －2)2＋8.∴x ＝2时，△AMA ′的面积最大S △AMA ′＝8．∴M (2，6).(3)设P 点的坐标为（x ，－x 2＋3x ＋4），当P 、N 、B 、Q 构成平行四边形时，①当BQ 为边时，PN ∥BQ 且PN ＝BQ ，∵BQ ＝4，∴一x 2＋3x ＋4＝±4.当一x 2＋3x ＋4＝4时，x 1＝0，x 2＝3，即P 1(0,4)，P 2(3，4)；当一x 2＋3x ＋4＝一4时，x 3＝3＋412，x 4＝3－412，即P 3(3＋412,－4)，P 4(3－412，－4)； ②当BQ 为对角线时，PB ∥x 轴，即P 1(0，4)，P 2(3，4);当这个平行四边形为矩形时，即P l (0，4)，P 2(3，4)时，N 1(0，0)，N 2(3，0).综上所述，当P 1(0，4)，P 2(3，4)，P 3(3＋412,－4)，P 4(3－412，－4)时，P 、N 、B 、Q 构成平行四边形；当这个平行四边形为矩形时，N 1(0，0)，N 2(3，0).24.如图1，△ABC 是等腰直角三角形，∠BAC ＝ 90°，AB ＝AC ，四边形ADEF 是正方形，点B 、C 分别在边AD 、AF 上，此时BD ＝CF ，BD ⊥CF 成立．(1)当△ABC 绕点A 逆时针旋转θ（0°＜θ＜90°）时，如图2，BD ＝CF 成立吗？若成立，请。

浙教版中考数学压轴题

浙教版中考数学压轴题

55．如图，抛物线y ＝－x2－2x ＋3与x 轴相交于点A 、B （A 在B 的左侧），与y 轴交于点C ．（1）求线段AC 所在直线的解析式；（2）点M 是第二象限内抛物线上的一点，且S △MAC＝12S △MAB，求点M 的坐标；（3）点P 以每秒1个单位长度的速度，沿线段BA 由B 向A 运动，同时，点Q 以每秒2个单位长度的速度，从A 开始沿射线AC 运动，当P 到达A 时，整个运动随即结束．设运动的时间为t 秒．①求△APQ 的面积S 与t 的函数关系式，并求当t 为何值时，△APQ 的面积最大，最大面积是多少？ ②在整个运动过程中，以PQ 为直径的圆能否与直线BC 相切？若能，请直接写出相应的t 值；若不能，请说明理由；③直接写出线段PQ 的中点在整个运动过程中所经过路径的长．56．如图，在平面直角坐标系中，直线AC ：y ＝43x ＋8与x 轴交于点A ，与y 轴交于点C ，抛物线y ＝ax2＋bx ＋c 过点A 、点C ，且与x 轴的另一交点为B （x 0，0）（x 0＞0），点P 是抛物线的对称轴l 上一动点．（1）求点A 的坐标，并在图1中的l 上找一点P 0，使P 0到点A 与点C 的距离之和最小； （2）若△P AC 周长的最小值为10＋241，求抛物线的解析式及顶点N 的坐标；（3）如图2，在线段CO 上有一动点M 以每秒2个单位的速度从点C 向点O 移动（M 不与端点C 、O 重合），过点M 作MH ∥CB 交x 轴于点H ．设M 移动的时间为t 秒，试把△P 0HM 的面积S 表示成时间t 的函数，当t 为何值时，S 有最大值，并求出最大值；（4）在（3）的条件下，当S ＝ 7532时，过M 作x 轴的平行线交抛物线于E 、F 两点，问：过E 、F 、C三点的圆与直线CN 能否相切于点C ？请证明你的结论．（用图3解答）抛物线的对称轴与x 轴交于点D ． 图1 图3图2（1）求此抛物线的解析式；（2）动点P从点B出发，沿线段BD向终点D作匀速运动，速度为每秒1个单位长度，运动时间为t s，过点P作PM⊥BD交BC于点M，过点M作MN∥BD，交抛物线于点N．①当t为何值时，线段MN最长；②在点P运动的过程中，是否有某一时刻，使得以O、P、M、C为顶点的四边形为等腰梯形？若存在，求出此刻的t值；若不存在，请说明理由．48．如图，对称轴为直线x＝－1的抛物线经过点A（－3，0）和点C（0，3），与x轴的另一交点为B．点P、Q同时从B点出发，均以每秒1个单位长度的速度分别沿BA、BC边运动，其中一个点到达终点时，另一点也随之停止运动．设运动时间为t（秒）．（1）求抛物线的解析式；（2）连接PQ，将△BPQ沿PQ翻折，所得的△B′PQ与△ABC重叠部分的面积记为S，求S与t之间的函数关系式，并求S的最大值；（3）若点D的坐标为（－4，3），当点B′恰好落在抛物线上时，在抛物线的对称轴时是否存在点M，使四边形MADB′的周长最小，若存在，求出这个最小值；若不存在，请说明理由．46．如图，抛物线y＝ax2＋bx＋4与x轴交于A（－2，0）、B（4，0）两点，与y轴交于C点．（1）求抛物线的解析式；（2）T是抛物线对称轴上的一点，且△ATC是以AC为底的等腰三角形，求点T的坐标；（3）M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行，当点M到达原点时，点Q立刻掉头并以每秒32个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动．过点M的直线l⊥x轴交AC或BC于点P．求点M的运动时间t与△APQ面积S的函数关系式，并求出S的最大值．43．已知抛物线y＝ax2＋bx＋c经过O（0，0），A（4，0），B（3，3）三点，连接AB，过点B作BC∥x轴交抛物线于点C．动点E、F分别从O、A两点同时出发，其中点E沿线段OA以每秒1个单位长度的速度向A点运动，点F沿折线A→B→C以每秒1个单位长度的速度向C点运动．设动点运动的时间为t（秒）．（1）求抛物线的解析式；（2）记△EF A的面积为S，求S关于t的函数关系式，并求S的最大值，指出此时△EF A的形状；（3）是否存在这样的t值，使△EF AF两点的坐标；若不存在，请说明理由．40．如图，直线y＝－43x＋4与x轴交于点B，与y轴交于点C，二次函数的图象经过A（－1，0）、B、C三点．（1）求二次函数的表达式；（2）设二次函数图象的顶点为D，求四边形OCDB的面积；（3）若动点E、F同时从O点出发，其中点E以每秒32个单位长度的速度沿折线OBC按O→B→C的路线运动，点F 以每秒4个单位长度的速度沿折线OCB 按O →C →B 的路线运动，当E 、F 两点相遇时，整个运动随之结束．设运动时间为t （秒），△OEF 的面积为S （平方单位）．①在E 、F 两点运动过程中，是否存在EF ∥OC ？若存在，求出此时t 的值；若不存在，请说明理由； ②求S 关于t 的函数关系式，并求S 的最大值．34．已知二次函数y ＝ax2＋bx －2的图象与x 轴交于A 、B 两点，与y 轴交于点C ，点A 的坐标为（4，0），且当x ＝－2和x ＝5时二次函数的函数值y 相等． （1）求实数a 、b 的值；（2）如图1，动点E 、F 同时从A 点出发，其中点E 以每秒2个单位长度的速度沿AB 边向终点B 运动，点F 以每秒 5个单位长度的速度沿射线AC 方向运动．当点E 停止运动时，点F 随之停止运动．设运动时间为t 秒．连接EF ，将△AEF 沿EF 翻折，使点A 落在点D 处，得到△DEF ． ①当t 为何值时，线段DF 平分△ABC 的面积？②是否存在某一时刻t ，使得△DCF 为直角三角形？若存在，求出t 的值；若不存在，请说明理由． ③设△DEF 与△ABC 重叠部分的面积为S ，求S 关于t 的函数关系式；（3）如图2，点P 在二次函数图象上运动，点Q 在二次函数图象的对称轴上运动，四边形PQBC 能否成为以PQ 为底的等腰梯形？如果能，直接写出P 、Q 两点的坐标；如果不能，请说明理由．1．已知直线y ＝、B O 向点A（1）当k ＝－1向点点P① ② 若以Q （2）当k ＝－3 4时，设以C 为顶点的抛物线y ＝(x ＋m)2＋n 与直线AB 的另一交点为D （如图2）．① 求CD 的长；② 设△COD 的OC 边上的高为h ，当t 为何值时，h 的值最大？图1 图22．已知二次函数的图象经过A（2，0）、C（0，12）两点，与x轴的另一交点为点B，且对称轴为直线x＝4，设顶点为点D．（1）求二次函数的解析式及顶点D的坐标；（2）如图1，在直线y＝2x上是否存在点E，使四边形ODBE为等腰梯形？若存在，求出点E的坐标；若不存在，请说明理由；（3）如图2，点P是线段OD上的一个动点（不与O、D重合），以每秒2个单位长度的速度由点D 向点O运动，过点P作直线PQ∥x轴，交BD于点Q，将△DPQ沿直线PQ对折，得到△D1PQ．在点P运动的过程中，设△D1PQ与梯形OPQB的重叠部分的面积为S，运动时间为t秒，求S关于t的函数关系式．56．如图，二次函数y＝ax2＋bx（a＞0）与反比例函数y＝kx的图象相交于A，B两点，且点A的坐标为（1，4），点B在第三象限，△AOB的面积为3．（1）求二次函数的表达式；（2）过点A作x轴的平行线，交二次函数y＝ax2＋bx的图象于另一点C，连接CO，在坐标平面内求点P，使△POC∽△AOB（点P与点A对应）．57．已知直线y＝12x和y＝－x＋m，二次函数y＝x2＋bx＋c图象的顶点为M．（1）若M恰好是直线y＝12x与y＝－x＋m的交点，试证明：无论m取何实数值，二次函数y＝x2＋bx＋c的图象与直线y＝－x＋m总有两个不同的交点；（2）在（1）的条件下，若直线y＝－x＋m过点D（0，－3），求二次函数y＝x2＋bx＋c的表达式；（3）在（2）的条件下，若二次函数y＝x2＋bx＋c的图象与y轴的交点为C，与x轴的左交点为A．①在直线y＝12x上求异于M的点P，使点P在△ CM的外接圆上；②在二次函数图象的对称轴上是否存在点Q，使得△QAC为等腰三角形？若存在，直接写出点Q 的坐标；若不存在，请说明理由．58．已知二次函数y＝x2＋(m－1)x＋m－2的图象与x轴相交于A（x1，0），B（x2，0）两点，且x1＜x2．（1）若x1x2＜0，且m为正整数，求该二次函数的表达式；y＝x2－1（2）若x1＜1，x2＞1，求m的取值范围；（3）是否存在实数m，使得过A、B两点的圆与y轴相切于点C（0，2），若存在，求出m的值；若不存在，请说明理由；（4）若过点D（0，12）的直线与（1）中的二次函数图象相交于M、N两点，且MDDN＝13，求该直线的表达式．53．已知抛物线F1：y＝ax2－2amx＋am2＋2m＋1（a＞0，m＞0）的顶点为A，抛物线F2的顶点B在y轴上，且抛物线F1和F2关于点M（1，3）成中心对称．（1）求m的值和抛物线F2的解析式；y＝-ax2 +1 m=2（2）设抛物线F2与x轴正半轴的交点为C，当△ABC为等腰三角形时，求a的值．。

九年级数学压轴题精选(填空题,解答题最后一题)

九年级数学压轴题精选(填空题,解答题最后一题)

浙教版九上数学压轴题精选（填空，解答题最后一题）26．如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A，B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上．（1）求∠ACB的大小；（2）写出A，B两点的坐标；（3）试确定此抛物线的解析式；（4）在该抛物线上是否存在一点D，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．解：（1）作CH⊥x轴，H为垂足，∵CH=1，半径CB=2，∵∠BCH=60°，∴∠ACB=120°．（2）∵CH=1，半径CB=2∴HB= 3 ，故A（1- 3 ，0），B（1+ 3 ，0）．（3）由圆与抛物线的对称性可知抛物线的顶点P的坐标为（1，3）设抛物线解析式y=a（x-1）2+3，把点B（1+ 3 ，0）代入上式，解得a=-1；∴y=-x2+2x+2．（4）假设存在点D使线段OP与CD互相平分，则四边形OCPD是平行四边形∴PC∥OD且PC=OD．∵PC∥y轴，∴点D在y轴上．又∵PC=2，∴OD=2，即D（0，2）．又D（0，2）满足y=-x2+2x+2，∴点D在抛物线上所以存在D（0，2）使线段OP与CD互相平分．18．如图，在反比例函数y=2x（x＞0）的图象上，有点P1，P2，P3，P4，它们的横坐标依次为1，2，3，4．分别过这些点作x 轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，则S1+S2+S3= （）10．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，则该半圆的半径为（）根据题意，因为P10Q10∥X轴，所以P10和Q10的纵坐标相同．根据数列1，3，6，10，15，21…，的排列规律，第10个数为1+2+3+4+5+6+7+8+9+10=55，代入y=3 x 得，y=3 55 ，代入y=-6 x ，得3 55 =-6 x ，x=-110．如图，在平面直角坐标系中，点A1是以原点O为圆心，半径为2的圆与过点（0，1）且平行于x 轴的直线l1的一个交点；点A2是以原点O为圆心，半径为3的圆与过点（0，2）且平行于x轴的直线l2的一个交点；…按照这样的规律进行下去，点An的坐标为（——）某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=-x2+4x（单位：米）的一部分，则水喷出的最大高度是（）下．。

专题4.2 坐标规律问题(压轴题专项讲练)(浙教版)(原卷版)

专题4.2 坐标规律问题(压轴题专项讲练)(浙教版)(原卷版)

专题4.2 坐标规律问题【典例1】如图，在平面直角坐标系中，有若干个横、纵坐标均为整数的点，按如图顺序依次排列为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…，根据这个规律，第2021个点的坐标为（ ）A．（46，4）B．（46，3）C．（45，4）D．（45，5）观察图形可知，以最外边的矩形边长上的点为准，点的总个数等于x轴上右下角的点的横坐标的平方，并且右下角的点的横坐标是奇数时最后以横坐标为该数，纵坐标为0结束，当右下角的点横坐标是偶数时，以横坐标为1，纵坐标为右下角横坐标的偶数减1的点结束，根据此规律解答即可．解：根据图形，以最外边的矩形边长上的点为准，点的总个数等于x轴上右下角的点的横坐标的平方，例如：右下角的点的横坐标为1，共有1个，1＝12，右下角的点的横坐标为2时，共有4个，4＝22，右下角的点的横坐标为3时，共有9个，9＝32，右下角的点的横坐标为4时，共有16个，16＝42，…右下角的点的横坐标为n时，共有n2个，∵452＝2025，45是奇数，∴第2025个点是（45，0），第2021点是（45，4）．故选：C．1．（2021秋•碑林区校级月考）如图，动点P从（0，3）出发，沿所示的方向运动，每当碰到边时反弹，反弹时反射角等于入射角，第1次碰到长方形的边时的位置P1（3，0），当点P第2021次碰到长方形的边时，点P2021的坐标是（ ）A．（1，4）B．（5，0）C．（0，3）D．（7，4）2．（2021秋•柯桥区期末）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第一次从原点O 运动到点P1（1，1），第二次运动到点P2（2，0），第三次运动到P3（3，﹣2），…，按这样的运动规律，第2022次运动后，动点P2022的坐标是（ ）A．（2022，1）B．（2022，2）C．（2022，﹣2）D．（2022，0）3．（2021春•蓬江区校级月考）如图，将边长为1的正方形OABC沿x轴正方向连续翻转2020次，点A依次落在点A1、A2、A3、A4…A2021的位置上，则点A2021的坐标为（ ）A．（2019，0）B．（2019，1）C．（2020，0）D．（2020，1）4．（2021秋•沙坪坝区校级期中）如图，在平面直角坐标系中，有若干个整点，按图中a→“方向排列，即（0，0）→（0，1）→（1，1）→（2，2）→（2，3）→（3，3）→（4，4），……，则按此规律排列下去第20个点的坐标为（ ）A．（13，14）B．（13，13）C．（12，13）D．（12，12）5．（2021春•珠海期中）如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一条长为2021个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（ ）A．（﹣1，0）B．（0，2）C．（﹣1，﹣2）D．（0，1）6．（2021春•嘉祥县期末）如图，长方形BCDE的各边分别平行于x轴、y轴，物体甲和物体乙由点A（2，0）同时出发，沿长方形BCDE的边做环绕运动，物体甲按逆时针方向以每秒1个单位长度的速度匀速运动，物体乙按顺时针方向以每秒2个单位长度的速度匀速运动，则两个物体运动后的第2021次相遇地点的坐标是（ ）A．（﹣1，﹣1）B．（2，0）C．（1，﹣1）D．（﹣1，1）7．（2021春•九龙坡区期中）在平面直角坐标系内原点O（0，0）第一次跳动到点A1（0，1），第二次从点A1跳动到点A2（1，2），第三次从点A2跳动到点A3（﹣1，3），第四次从点A3跳动到点A4（﹣1，4），…，按此规律下去，则点A2021的坐标是（ ）A．（673，2021）B．（674，2021）C．（﹣673，2021）D．（﹣674，2021）8．（2021春•抚顺期末）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0）；（2，0）；（2，1）；（3，2）、（3，1），（3，0）、（4，0），…，根据这个规律探索可得，第20个点的坐标为（ ）A．（6，4）B．（6，5）C．（7，3）D．（7，5）9．（2021春•海拉尔区期末）如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2021秒时，点P的坐标是（ ）A．（2020，0）B．（2021，﹣1）C．（2021，1）D．（2022，0）10．（2021春•福州期末）如图，一个粒子从原点出发，每分钟移动一次，依次运动到（0，1）→（1，0）→（1，1）→（1，2）→（2，1）→（3，0）→…则2021分钟时粒子所在点的横坐标为（ ）A．886B．903C．946D．99011．（2021春•东港区校级期末）如图，在平面直角坐标系上有点A（1，0），第一次点A跳动至点A1（﹣1，1），第二次点A1跳动至点A2（2，1），第三次点A2跳动至点A3（﹣2，2），第四次点A3跳动至点A4（3，2），依此规律跳动下去，则点A2021与点A2022之间的距离是 ．12．（2021•潍坊）在直角坐标系中，点A1从原点出发，沿如图所示的方向运动，到达位置的坐标依次为：A2（1，0），A3（1，1），A4（﹣1，1），A5（﹣1，﹣1），A6（2，﹣1），A7（2，2），…．若到达终点A n（506，﹣505），则n的值为 ．13．（2021春•龙岩期末）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排行，如（0，1），（0，2），（1，2），（1，3），（0，3），（﹣1，3），…根据这个规律探索可得，第40个点的坐标为 ．14．（2021秋•同安区期末）如图，点A（0，1），点A1（2，0），点A2（3，2），点A3（5，1）…，按照这样的规律下去，点A2021的坐标为 ．15．（2021春•新余期末）如图，在平面直角坐标系中，一电子蚂蚁按照设定程序从原点O出发，按图中箭头所示的方向运动，第1次从原点运动到点（1，2），第2次接着运动到点（2，0），第3次接着运动到点（2，﹣2），第4次接着运动到点（4，﹣2），第5次接着运动到点（4，0），第6次接着运动到点（5，2）．…按这样的运动规律，经过2021次运动后，电子蚂蚁运动到的位置的坐标是 ．16．（2021秋•即墨区期中）如图，一个粒子在第一象限内及x轴、y轴上运动，在第一分钟，它从原点运动到点（1，0），第二分钟它从点（1，0）运动到点（1，1），而后它接着按图中箭头所示在与x轴，y轴平行的方向上来回运动，且每分钟移动1个单位长度，那么在第2022分钟时，这个粒子所在位置的坐标是 ．17．（2021秋•长丰县月考）在平面直角坐标系中，一只蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次只移动1个单位长度，其行走路线如图所示．（1）填写下列各点的坐标：A4 ，A8 ，A12 ．（2）写出点A4n的坐标（n为正整数） ．（3）蚂蚁从点A2020到点A2021的移动方向是 ．（填“向上”、“向右”或“向下”）18．（2020春•新丰县期中）如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0）…（1）填写下列各点的坐标：P9（ ），P12（ 、 ），P15（ 、 ）（2）写出点P3n的坐标（n是正整数）；（3）点P60的坐标是（ 、 ）；（4）指出动点从点P210到点P211的移动方向．19．（2021春•饶平县校级期中）如图，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知：A（1，3）、A1（2，3）、A2（4，3）、A3（8，3）、B（2，0）、B1（4，0）、B2（8，0）、B3（16，0）．求：（1）A4、B4点的坐标；（2）A n、B n点的坐标．20．（2021春•自贡期末）综合与实践问题背景：（1）已知A（1，2），B（3，2），C（1，﹣1），D（﹣3，﹣3）．在平面直角坐标系中描出这几个点，并分别找到线段AB和CD中点P1、P2，然后写出它们的坐标，则P1 ，P2 ．探究发现：（2）结合上述计算结果，你能发现若线段的两个端点的坐标分别为（x1，y1），（x2，y2），则线段的中点坐标为 ．拓展应用：（3）利用上述规律解决下列问题：已知三点E（﹣1，2），F（3，1），G（1，4），第四个点H（x，y）与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．。

2024年浙江中考数学最后一卷终极押题卷及答案

2024年浙江中考数学最后一卷终极押题卷及答案

2024年浙江中考最后一卷数学注意事项：1．本试卷共有三个大题，分为单项选择题、填空题、解答题，满分120分，考试时间100分钟。

2．本试卷上不要答题，请按答题卡上注意事项的要求直接把答案填写在答题卡上，答在试卷上的答案无效。

一、单选题（本大题共有10小题，每小题3分，共30分）1．下列各数中最大的数是（）A．5−B．0 C．1−D2．下面计算正确的是（）A．3a﹣2a＝1 B．2a2+4a2＝6a4C．（x3）2＝x5D．x8÷x2＝x63．今年春节电影《热辣滚烫》《飞驰人生2》《熊出没•逆转时空》《第二十条》在网络上持续引发热议，根据国家电影局2月18日发布数据，我国2024年春节档电影票房达80.16亿元，创造了新的春节档票房纪录．其中数据80.16亿用科学记数法表示为（）A．8×80.16108.01610×B．9C．10×80.1610×D．100.8016104．下列立体图形中，主视图是三角形的是（）A．B．C．D．5．在数轴上表示不等式x﹣2≤0的解集，正确的是（）A．B．C ．D ．6．随着自动驾驶技术的不断发展，某知名汽车制造公司近期对研发的自动驾驶汽车进行了一次大规模的路测，有45辆自动驾驶汽车参与了这次测试．测试结束后，技术部门对每辆汽车的性能进行评估（车辆的自动驾驶技术、安全性、反应速度等综合表现），得分如下：得分（分） 75 80 85 90车辆（辆） 5 16 14 10得分的中位数和众数分别是（ ）A ．80，80B ．82.5，80C ．80，85D ．85，807．如图，线段CD 是O 的直径，CD AB ⊥于点E ，若8AB =，3OE =，则CE 的长是（ ）A ．8B ．7C ．6D ．58．《九章算术》中曾记载：“今有牛五羊二，直金十两；牛二羊五，直金八两．问牛、羊各直金几何？”译文：“假设有5头牛，2只羊，值金10两；2头牛、5只羊，值金8两．问：每头牛、每只羊各值金多少两？若设每头牛值金x 两，每只羊值金y 两，则可列方程组为（ ）A ．5210258x y x y += +=B ．2510528x y x y += +=C ．51058x y x y += +=D ．21028x y x y += +=9．二次函数2y =的图象如图所示，点O 为坐标原点，点A 在y 轴的正半轴上，点B ，C 在函数图象上，四边形OBAC 为菱形，且120ABO ∠=°，则点C 的坐标为（ ）A ．14 −B ．14 −C ． −D ．(− 10．如图，四边形ABCD 是一张矩形纸片．折叠该矩形纸片，使AB 边落在AD 边上，点B 的对应点为点F ，折痕为AE ，展平后连接EF ；继续折叠该纸片，使FD 落在FE 上，点D 的对应点为点H ，折痕为FG ，展平后连接HG ．若矩形HECG ∽矩形ABCD ，1AD =，则CD 的长为（ ）．A ．0.5B 1−C D二、填空题（本大题共有6小题，每小题4分，共24分）11．因式分解： 34t t −=12．实现中国梦，必须弘扬中国精神．在如图所示除正面图案不同外，其余无差别的四张不透明卡片上分别写有“红船精神”、“长征精神”、“延安精神”、“特区精神”，将卡片置于暗箱摇匀后随机抽取一张，则所抽取卡片为“特区精神”的概率为 ．13x 的值可以是 ．（写出一个即可） 14．如图，《掷铁饼者》是希腊雕刻家米隆于约公元前450年雕刻的青铜雕塑，掷铁饼者张开的双臂与肩宽可以近似看像一张拉满弦的弓，若弧长为2π3米，“弓”所在圆的半径1．2米，则“弓”所对的圆心角θ的度数为 ．15．如图，点A 为反比例函数(0,0)k y k x x=<<的图象上一点，AB x ⊥轴于点B ，点C 是y 轴正半轴上一点，连接BC ，AD BC ∥交y 轴于点D ，若0.5ABCD S =四边形，则k 的值为 ．16．如图，正方形ABCD 的边长为2，以AB 边上的动点O 为圆心，OB 为半径作圆，将AOD △沿OD 翻折至A OD ′ ，若O 过A OD ′ 一边上的中点，则O 的半径为 ．三、解答题（本大题共有8小题，共66分）（共66分）17．（本题6分）计算或化简：(1)()201253π− +−−+−； (2)()()()2m n n m m n +−−−．18．（本题6分）如图，在平面直角坐标系中，ABC 的顶点坐标分别为()2,4A ，()3,1B ，()5,3C ．(1)作ABC 关于y 轴对称的111A B C △；(2)将ABC 绕原点O 顺时针旋转90°，得到222A B C △，作出222A B C △并求点C 旋转到点2C 所经过的路径长．19．（本题6分）2023年全国教育工作会议提出要把开展读书活动作为一件大事来抓．引导学生爱该书．读好书，善读书，贵阳市某校为了推进这项工作，对全校学生一周内平均读书时间进行抽样调查．将调查结果的数据分成A 、B 、C 、D 、E 五个等级并绘制成表格和扇形统计图如下．等级 周平均读书时间t （单位：小时） 人数A01t ≤< 4 B12t ≤< a C23t ≤< 20 D34t ≤< 15 E 4t ≥5 每个等级人数扇形统计图(1)求统计图表中=a ______，m =______．(2)已知该校共有2800名学生，试估计该校每周读书时间至少3小时的人数为______．(3)请写出一条你对读书的建议．20．（本题8分）我国是世界上最早发明历法的国家之一，《周礼》中记载：垒土为圭，立木为表，测日影，正地中，定四时，如图1，圭是地面上一根水平标尺，指向正北，表是一根垂直于地面的杆，正午，表的日影（即表影）落在圭上，根据表影的长度可以测定节气．在一次数学活动课上，要制作一个圭表模型，如图2，地面上放置一根长2米的杆AB ，向正北方向画一条射线BC ，在BC 上取点D ，测得 1.5m BD =， 2.5m AD =．(1)判断：这个模型中AB 与BC 是否垂直．答：______（填“是”或“否”）；你的理由是：______．(2)利用这个圭表模型，测定某市冬至正午阳光与日影夹角30°，夏至正午阳光与日影夹角为60°，请求出这个模型中该市冬至与夏至的日影的长度差（结果保留根号）．21．（本题8分）如图，在矩形ABCD 中，沿EF 将矩形折叠，使A 、C 重合，AC 与EF 交于点H ．(1)求证：AE ＝AF ；(2)若AB ＝4，BC ＝8，求△ABE 的面积．22．（本题10分）我市某镇组织20辆汽车装运完A 、B 、C 三种脐橙共100吨到外地销售．按计划，20辆车都要装运，每辆汽车只能装运同一种脐橙．且必须装满，根据下表组织的信息，解答以下问题．脐橙品种A B C 每辆汽车运载量（吨） 6 5 4每吨脐橙获利（元） 1200 1600 1000(1)设转运A 种脐橙的车辆数为x ，转运B 种脐橙的车辆数为y ，求y 与x 的函数表达式；(2)如果转运每种脐橙的车辆数都不少于4，那么车辆的安排方案有几种？(3)若要使此次销售获利最大，应采用哪种安排方案？并求出此时最大利润的值．23．（本题10分）定义：平面直角坐标系xOy 中，当点N 在图形M 的内部，或在图形M 上，且点N 的横坐标和纵坐标相等时，则称点N 为图形M 的“梦之点”．(1)如图①，矩形ABCD 的顶点坐标分别是(1,2)A −，(1,1)B −−，(3,1)C −，(3,2)D ，在点1(2,2)P −−，2(0,0)P ，3(1,1)P ，4(2,2)P 中，是矩形ABCD “梦之点”的是________；(2)如图②，已知A 、B 是抛物线21922y x x =−++上的“梦之点”，点C 是抛物线的顶点： ①求出AC ，AB ，BC 三条线段的长度；②判断ABC 的形状，并说明理由．24．（本题12分）如图，ABC 内接于圆O ，AD 是ABC 的高线，9AD =，12CD =，tan 3ABD ∠=，连接OC ．(1)求证：ABC 是等腰三角形；(2)求证：BCO BAD ∠=∠；(3)若点E 是OC 上一动点，EF AB ∥交BC 于点F ．①若OEF 与ABD △相似，求EF 的长；②当OEF 的面积与CEF △的面积差最大时，直接写出此时CF 的长．2024年浙江中考最后一卷数学解析及参考答案一、单选题1．D【分析】此题考查了实数的大小比较法则：正数大于零，零大于负数，两个负数绝对值大的反而小，据此判断．【详解】∵510−<−<<故选：D ．2．D【分析】根据各个选项中的式子可以计算出正确的结果，本题得以解决．【详解】解：∵3a ﹣2a ＝a ，故选项A 错误；∵2a 2+4a 2＝6a 2，故选项B 错误；∵（x 3）2＝x 6，故选项C 错误；∵x 8÷x 2＝x 6，故选项D 正确；故选D ．【点睛】本题考查整式的混合运算，解答本题的关键是明确整式混合运算的计算方法．3．B【分析】此题考查科学记数法的表示方法．科学记数法的表示形式为10n a ×的形式，其中110a ≤<，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值10≥时，n 是正数；当原数的绝对值1<时，n 是负数．【详解】解：80.16亿98.01610×，故选：B ．4．B【分析】本题考查立体几何的三视图．根据题意，逐项判断即可．【详解】解：A.主视图为长方形，此项不符合题意；B.主视图为三角形，此项符合题意；C.主视图为圆，此项不符合题意；D.主视图为长方形，此项不符合题意．故选：B ．5．C【分析】先解不等式，求出解集，然后在数轴上表示出来．【详解】解：不等式x ﹣2≤0，得：2x ≤ ，把不等式的解集在数轴上表示出来为：．故选：C【点睛】本题主要考查了解不等式，并在数轴上表示解集，解题的关键是熟练掌握解不等式的步骤，不等式的解集在数轴表示时空心圈不包含该点，实心圈包含该点．6．D【分析】本题为统计题，考查众数与中位数的意义，根据众数的定义，找到该组数据中出现次数最多的数即为众数；根据中位数定义，将该组数据按从小到大依次排列，处于中间位置的两个数的平均数即为中位数．【详解】有45辆自动驾驶汽车参与了这次测试，45个分数，按大小顺序排列最中间的数据是第23个数：85，故得分的中位数是85（分），得80分的人数最多，有16人，故众数为80，故选D ．7．A【分析】本题考查了垂径定理和勾股定理的应用，根据垂径定理求出AE 的长是解此题的关键．连接OA ，根据垂径定理求出AE ，再根据勾股定理求出OA ，最后根据线段的和差求解即可．【详解】解：如图，连接OA ，线段CD 是O 的直径，CD AB ⊥于点E ，∴12AE AB =，8AB =， ∴4AE =，3OE =，∴5OA ，∴5OC OA ==，∴8CE OC OE =+=，故选：A ．8．A【分析】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是设每头牛、每只羊分别值金x 两、y 两，根据“5头牛，2只羊，值金10两；2头牛，5只羊，值金8两”列出方程组即可得答案．【详解】解：设每头牛值金x 两，每只羊值金y 两，则可列方程组为5210258x y x y += +=， 故选A ．9．B【分析】本题考查了菱形的性质、二次函数图象上点的坐标特征，根据二次函数图象上点的坐标性质得出BD 的长是解题关键．连接BC 交OA 于D ，如图，根据菱形的性质得BC OA ⊥，60OBD ∠=°，利用含30度的直角三角形三边的关系得OD =，设BD t =，则OD =，()B t ，利用二次函数图象上点的坐标特征得2=，得出14BD =，OD =C 点坐标． 【详解】解：连接BC 交OA 于D ，如图，四边形OBAC 为菱形，BC OA ，120ABO ∠=° ，60OBD ∴∠=°，OD ∴，设BD t =，则OD =，()B t ∴，把()B t 代入2y =,得2=，解得10t =（舍去）， 214t =，14BD ∴=，OD =故C 点坐标为：14 − ．故答案为：B ．10．C【分析】本题考查的是矩形的性质、翻折的性质及相似多边形性质，熟练应用矩形和相似多边形性质是解题关键，设CD x =，则()1,1EC x CG x x =-=--，根据两矩形相似求出即可．【详解】解：在矩形ABCD 中，设CD x =，则ABCD x ==，1AD BC ==， 由翻折得,90AB AF x AFE B BAF ==∠=∠=∠=︒，∴四边形ABEF 是正方形，同理，四边形DFHG 是正方形，,1BE AB x DF DG x ∴====-，()1,121CE x CG x x x ∴=-=--=-，矩形HECG ∽矩形ABCD ，EC CG BC CD∴=，即1211x x x --=，解得：x =，经检验，xCD ∴ 故选：C ．二、填空题11．()()22t t t +−【分析】本题考查了因式分解，先提取公因式，再利用公式法即可求解，熟练掌握提公因式法及公式法分解因式是解题的关键．【详解】解：()()()324422t t t t t t t −=−=+−，故答案为：()()22t t t +−．12．14/0.25 【分析】本题考查了概率公式的应用，用到的知识点为：概率所求情况数与总情况数之比．全部情况的总数是四种，符合条件的情况的是一种，二者的比值就是其发生的概率．【详解】由于概率为所求情况数与总情况数之比，而抽取卡片为“特区精神”的情况数只有一种，从暗箱随机抽取一张的情况数为四种，故抽取卡片为“特区精神”的概率为14， 故答案为14． 13．0（答案不唯一）【分析】本题主要考查了二次根式有意义的条件，分式有意义的条件，根据二次根式有意义的条件的条件是被开方数大于等于0，分式有意义的条件是分母不为0进行求解即可．∴10x −>，解得1x <．∴x 的值可以是0，故答案为：0（答案不唯一）．14．100°/100度【分析】本题考查的是已知弧长与半径求解弧所对的圆心角，熟记弧长公式是解本题的关键．直接利用弧长公式计算即可．【详解】解： 设“弓”所在的圆的弧长圆心角度数是n °， 则1.2π2π1803n =， 解得：100n =，故答案为：100°．15．0.5−【分析】本题考查了反比例函数k 值的几何意义，熟练掌握k 值的几何意义是解答本题的关键.根据反比例函数k 值的几何意义进行解答即可.【详解】AB x ⊥ 轴于点B ，CD x ⊥轴，∴AB CD ，又 AD BC ，∴四边形ABCD 是平行四边形，过点作AM y ⊥轴，则四边形ABOM 是矩形， ∴0.5,ABOMABCD S S k ===矩形平行四边形∵反比例函数图象在第二象限，0.5k ∴=−，故答案为：0.5−.16．23、54【分析】本题考查了折叠的性质，正方形的性质，勾股定理，圆的定义；分三种情况讨论，设O 的半径为r ，分别根据勾股定理，即可求解．【详解】设O 的半径为r ，当O 经过A O ′的中点，即经过AO 的中点， ∴1233r AB =，当O 经过OD 的中点，则12r OB OD ==， ∴2OD r =，2AO AB OB r =−=−， 在Rt AOD 中，222AD AO OD +=∴()()222222r r +−=解得：r = 当O 经过A D ′的中点，即经过AD 的中点，设AD 的中点为M ，∴2,1,AO r AM OM r =−== ∴()22221r r −+= 解得：54r =综上所述，半径为23、54故答案为：23、54 三、解答题17．(1)5(2)222m mn −+【分析】此题考查了实数的运算以及整式的混合运算，熟练掌握运算法则是解本题的关键．（1）原式利用零指数幂、绝对值的代数意义以及负整数指数幂法则计算即可求出值；（2）根据平方差公式和完全平方公式化简，再合并同类项即可．【详解】（1）解：原式159=-+5=；（2）原式()22222n m m mn n =−−−+22222n m m mn n =−−+−222m mn =−+18．(1)图见解析(2)【分析】本题考查作图-轴对称变换，旋转变换，以及求弧长，熟练掌握相关作图方法是解题关键； （1）根据点关于y 轴对称的性质分别找到对应的点1A ，1B ，1C ，然后进一步连接即可；（2）利用旋转变换的性质分别作出A ，B ，C 的对应点2A ，2B ，2C ，再顺次连接即可，利用弧长公式求得点C 经过的路径长．【详解】（1）解：如图，111A B C △即为所求；（2）如图，222A B C △即为所求，由题意可知，OC∴点C 旋转到点2C =． 19．(1)6，40(2)1120(3)全校学生一周内平均读书时间23t ≤<(答案不唯一)【分析】本题考查了扇形统计图，样本估计总体等知识．（1）由等级得到学生总数，即可得出a ，再求C 等级的占比即可；（2）用样本估计总体即可得出结果；（3）根据表格可题建议合理即可．【详解】（1）解：由等级D 得到学生总数1530%50÷=人， ∴504201556a −−−−，()%2050100%40%m =÷×=，40m =，故答案为：6，40．（2）1552800112050+×=人， 故该校2800名学生每周读书时间至少3小时的人数为1120人．故答案为：1120．（3）根据表格可建议：全校学生一周内平均读书时间23t ≤<．20．(1)是；222AB BD AD +=，由勾股定理的逆定理可知AB BC ⊥．(2)．【分析】本题考查的勾股定理的逆定理的应用，解直角三角形的应用，理解题意是解本题的关键． （1）利用勾股定理的逆定理判断即可；（2）先画图，利用三角函数再计算BE=BF =，从而可得答案． 【详解】（1）解：是， 理由：由测量结果可知得 1.5m BD =， 2.5m AD =，而2m AB =，∴2226.25AB BD AD +==，∴90ABD ，∴AB BC ⊥．故答案是：是；222AB BD AD +=，由勾股定理的逆定理可知AB BC ⊥．（2）如图，由题意可得：90ABC ∠=°，2AB =，30AFB ∠=°，60AEB ∠=°，∴tan tan 60AB AEB BE∠=°=，∴BE =， 同理：tan tan 30AB AFBBF ∠=°=，∴BF =，∴FE BF BE =−==． 21．(1)证明见解析(2)6【分析】（1）依据平行线的性质以及矩形的性质，即可得到∠AFE =∠AEF ，进而得出AE =AF ．（2）设BE =x ，则AE =EC =8-x ，在Rt △ABE 中，根据勾股定理可得方程，即可得到BE 的长，再根据三角形面积计算公式求解．【详解】（1）证明：∵四边形ABCD 矩形，∴AD ∥BC ，∴∠AFE =∠FEC ，由折叠的性质得：∠AEF =∠FEC ，∴∠AFE =∠AEF ，∴AE =AF ．（2）解：根据折叠的性质可得AE =EC ，设BE =x ，则AE =EC =8-x ，在Rt △ABE 中，根据勾股定理可得：222AB BE AE +=，即()22248x x +=−，解得：x =3，∴BE =3，∴ABE S = 12AB •BE =12×4×3=6． 【点睛】本题主要考查了折叠问题以及矩形的性质的运用，解题的方法是设要求的线段长为x ，然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．22．(1)220y x =−+ (2)5种(3)当转运A 种脐橙的车4辆，转运B 种脐橙的车12辆，转运C 种脐橙的车4辆时，利润最大为140800元【分析】（1）根据题意列式：()20651040x x y y −−=++，整理后即可得到220y x =−+； （2）根据装运每种水果的车辆数都不少于4辆，4x ≥，2204x −+≥，解不等式组即可；（3）设利润为W 元，则()480016000048W x x =−+≤≤，根据一次函数的增减性求解即可． 【详解】（1）根据题意，装运A 种水果的车辆数为x ，装运B 种水果的车辆数为y ，∴装运C 种水果的车辆数为()20x y −−，∴()20651040x x y y −−=++， 整理得220y x =−+． （2）由（1）知，装运A ，B ，C 三种水果的车辆数分别为x ，220x −+，x ，由题意得2204x −+≥，解得8x ≤，∵4x ≥，∴48x ≤≤．∵x 为整数，∴x 的值为4，5，6，7，8，∴安排方案共有5种．（3）设利润为W 元，∴()612005220160041000W x x x =×+−+×+× 4800160000x =−+，因为48000−<，且x 的值为4，5，6，7，8，∴W 的值随x 的增大而减小，∴当4x =时，销售利润最大．当装运A 种水果4车，B 种水果12车，C 种水果4车，销售获利最大．最大利润48004160000140800W =−×+=（元）．【点睛】主要考查利用一次函数的模型解决实际问题的能力．要先根据题意列出函数关系式，再代数求值．解题的关键是要分析题意根据实际意义求解．注意要根据自变量的实际范围确定函数的最值．23．(1)2(0,0)P ，3(1,1)P ，4(2,2)P(2)①AC =BC =AB =ABC 是直角三角形，理由见解析【分析】本题考查了二次函数的图象与性质、勾股定理以及勾股定理逆定理：（1）根据“梦之点”的定义判断这几个点是否在矩形的内部或者边上即可得到答案；（2）①根据“梦之点”的定义求出A ，B 的坐标，再求出顶点的坐标，计算出AC ，AB ，BC 的长； ②根据勾股定理逆定理，即可求解．【详解】（1）解：∵矩形ABCD 的顶点坐标分别是(1,2)A −，(1,1)B −−，(3,1)C −，(3,2)D ，∴矩形ABCD 的“梦之点”(),x y 满足2,131x y −−≤≤≤≤，∴点2(0,0)P ，3(1,1)P ，4(2,2)P 是矩形ABCD 的“梦之点”，1(2,2)P −−不是矩形的“梦之点”．故答案为：2(0,0)P ，3(1,1)P ，4(2,2)P（2）解：①A 、B 是抛物线21922y x x =−++上的“梦之点”， ∴21922x x x =−++， 解得：123,3x x ==−，当3x =时，3y =，当3x =−时，=3y −，∴()()3,3,3,3A B −−， ∵()2219115222y x x x =−++=−−+， ∴顶点坐标为()1,5C ，∴AC =BC =AB =； ②ABC 是直角三角形，理由如下：∵AC =BC =AB =∴((2222280AB AC BC +=+==，∴ABC 是直角三角形．24．(1)证明见解析(2)证明见解析(3)①EF =253CF =【分析】本题考查了圆的性质，等腰三角形的判定与性质，相似三角形的判定与性质，锐角三角函数等知识，掌握相关知识是解题的关键．（1）利用勾股和锐角三角函数求得AC BC =即可证明；（2）连接,OA OB ，延长CO 交AD 于点M ，交AB 于点N ，先证明CO 是ACB ∠的角平分线，再证明ANM CDM ∽即可得出结论；（3）①过O 点作OH BC ⊥交BC 于点H ，点E 是OC 上一动点，EF AB ∥交BC 于点F ，先证明CHO CFB ∽，设EF x =3x =即可求解，②要使OEF 的面积与CEF △的面积差最大，必须使EF 和()CE OE −最大，当E 点与O 点重合时，EF 最大，CE OE OC −=最大，先求得EF =即可求出CF ． 【详解】（1）证明：∵AD 是ABC 的高线，∴90ADC ADB ∠=∠=°， ∵9AD =，12CD =，∴15AC ===，∵tan 3ABD ∠=， ∴tan 3AD ABD BD∠==， ∴3BD =，∴31215BC BD CD =+=+=， ∴AC BC =，∴ABC 是等腰三角形．（2）证明：连接,OA OB ，延长CO 交AD 于点M ，交AB 于点N ，如图：∵AC BC =，∴CAB CBA ∠=∠， ∵OA OB =，∴OAB OBA ∠=∠， ∴CAO CBO ∠=∠， ∵OA OC =，∴CAO ACO ∠=∠， ∵OB OC =，∴BCO CBO ∠=∠， ∴ACO BCO ∠=∠， ∴CO 是ACB ∠的角平分线， 又∵ AC BC =，∴CN AB ⊥，∴90ANC BNC ∠=∠=°， ∴90MDC ANE ∠=∠=°， 又∵AMN CMD ∠=∠， ∴ANM CDM ∽，∴DCM NAM ∠=∠， ∴BCO BAD ∠=∠． （3）解：①过O 点作OH BC ⊥交BC 于点H ，点E 是OC 上一动点，EF AB ∥交BC 于点F ，如图：∵,,15OB OC OH BC BC =⊥=， ∴17.52CH BC ==，90CHO CFB ∠=∠=°， ∴CHO CFB ∽，∴COH CBF ∠=∠， ∵tan 3ABD ∠=， ∴tan tan 3CH COH CBF OH∠=∠==， ∴ 2.5OH =，∴OC =， ∵EF AB ∥，90BNC ∠=°， ∴CEF CNB ∽，∴90CEF CNB ∠=∠=°， 设EF x =，∴tan tan 3CE CE CFE CBN EF x∠=∠===， ∴3CE x =，∵OEF ADB ∽，∴OE EF AD BD=， ∵OEOC CE =−， 3x =， 解得：x =∴EF ②∵90CEF ∠=°，即EF OC ⊥， ∴12CEF S CE EF =⋅ ，12OEF S OE EF =⋅ ， ∴()111222CEF OEF S S CE EF OE EF EF CE OE −=⋅−⋅=⋅− ， 由题知，要使OEF 的面积与CEF △的面积差最大，必须使EF 和()CE OE −最大，∴当E 点与O 点重合时，EF 最大，CE OE OC −=最大，如图：∵EF AB ∥，∴CEF CNB ∽，∴CFE CBN ∠=∠，CE OC ==，∴tan tan 3CE CFE CBN EF ∠=∠==，∴EF∴253CF =．。

二次函数 压轴题(八大题型)(原卷版)—2024-2025学年九年级数学上学期期中冲刺卷(浙教版)

二次函数 压轴题(八大题型)(原卷版)—2024-2025学年九年级数学上学期期中冲刺卷(浙教版)

二次函数 压轴题（八大题型）目录：题型1：存在性问题题型2：最值问题题型3：定值问题题型4：定点问题题型5：动点问题综合题型6：对称问题题型7：新定义题题型8：二次函数的代数（综合）应用题型1：存在性问题1．如图，抛物线26y ax x c =++与x 轴交于A 、()5,0B 两点，与y 轴交于点()0,5C -，点(),P t s 是抛物线上的一动点．(1)求该抛物线所对应的函数解析式；(2)如图，当点(),P t s 在直线BC 上方的抛物线时，过点P 作y 轴的平行线交直线BC 于点E ．求PBC △面积的最大值；(3)如图，当点(),P t s 在直线BC 上方的抛物线时，过点P 作y 轴的平行线交直线BC 于点E ．点M 是平面直角坐标系内一点，是否存在点P ，使得以点B ，E ，P ，M 为顶点的四边形是菱形，若存在，请求出所有点M 的坐标；若不存在，请说明理由．2．如下图，抛物线24y ax bx =+-与x 轴相交于(2,0)A ，0()6,B -两点，与y 轴相交于点C ．连接BC ，过点A 作AD BC ∥交抛物线于点D ．(1)求抛物线的解析式；(2)如下图，点M 为直线BC 下方抛物线上一点，连接DM 交BC 于N ，连接AM 、AN ，求AMN V 面积的最大值及此时点M 的坐标；(3)将抛物线沿DA 方向平移个单位，点P 为平移后的抛物线对称轴上一点，是否存在点P ，使得BCP V 为等腰三角形，若存在，写出点P 的坐标，并写出其中一个点的求解过程；若不存在，说明理由．3．如图，已知抛物线24y ax bx =++与x 轴交于(),40A B ，两点，与y 轴交于点C ，与直线BD 交于点51,2D æö-ç÷èø，其对称轴与直线BD 交于点E ，点F 是此抛物线上的一个动点．(1)求此抛物线的解析式并直接写出直线BD 的解析式；(2)如图1，若点F 是直线BD 上方抛物线上的一点，连接DF 、BF 和OD ，当BDF V 与BDO △面积相等时，求点F 的横坐标；(3)如图2，连接EF ，在此抛物线对称轴右侧的抛物线上是否存在点F 使得线段EF 最小？若存在，请求出点F 的坐标；若不存在，请说明理由．题型2：最值问题4．在平面直角坐标系中，O 为坐标原点，抛物线23y ax bx =+-与x 轴交于()1,0A -，()3,0B 两点，与y 轴交于点C ，连接BC ．(1)求a ，b 的值；(2)点M 为线段BC 上一动点（不与B ，C 重合），过点M 作MP x ^轴于点P ，交抛物线于点N ．（ⅰ）如图1，当3PA PB=时，求线段MN 的长；（ⅱ）如图2，在抛物线上找一点Q ，连接AM ，QN ，QP ，使得PQN V 与APM △的面积相等，当线段NQ 的长度最小时，求点M 的横坐标m 的值．5．已知抛物线(2)(4)(y a x x a =+-为常数，且0)a <与x 轴交于A ，B 两点（点A 在点B 的右侧），与y 轴交于点C ，经过点B 的直线12y x b =+与抛物线的另一交点为点D ，与y 轴的交点为点E ．(1)如图1，若点D 的横坐标为3，试求抛物线的函数表达式；(2)如图2，若DE BE =，试确定a 的值；(3)如图3，在（1）的情形下，连接AC ，BC ，点P 为抛物线在第一象限内的点，连接BP 交AC 于点Q ，当APQ BCQ S S -△△取最大值时，试求点P 的坐标．6．在平面直角坐标系中，抛物线23y ax bx =++交x 轴于点(1,0)A -、(3,0)B ，交y 轴于点C ，连结AC 、BC ．点D 在该抛物线上，过点D 作∥D E A C ，交直线BC 于点E ，连结AD 、AE 、BD ．设点D 横坐标为(0)m m >，DAE V 的面积为1S ，DBE V 的面积为2S ．(1)求a ，b 的值；(2)设抛物线上D 、B 两个点和它们之间的部分为图象G ，当图象G 的最高点的纵坐标与m 无关时，求m 的取值范围；(3)当点D 在第一象限时，求1S ＋2S 的最大值；(4)当12:2:1S S =时，直接写出m 的值．7．如图1，在平面直角坐标系xOy 中，O 为坐标原点，已知抛物线2y x bx c ¢=-++的顶点坐标为()3,4C -，与x 轴分别交于点A ，B ．连接AC ，点D 是线段AC 上方抛物线上的一动点．(1)求抛物线的解析式；(2)如图1，在点D 运动过程中，连接AD CD 、，求ADC △面积的最大值；(3)如图2，在点D 运动过程中，连接OD 交AC 于点E ，点F 在线段OA 上，连接OC DF EF 、、，若ACO FDO DFE Ð=Ð+Ð，求点F 横坐标的最大值．题型3：定值问题8．已知抛物线()²30y ax bx a =+-¹与x 轴交于点(1,0)A -，点(3,0)B ，与y 轴交于点C ．(1)求抛物线的表达式；(2)如图，若直线BC 下方的抛物线上有一动点M ，过点M 作y 轴平行线交BC 于N ，过点M 作BC 的垂线，垂足为H ，求HMN △周长的最大值；(3)若点P 在抛物线的对称轴上，点Q 在x 轴上，是否存在以B ，C ，P ，Q 为顶点的四边形为平行四边形，若存在，求出点Q 的坐标，若不存在，请说明理由；(4)将抛物线向左平移1个单位，再向上平移4个单位，得到一个新的抛物线，问在y 轴正半轴上是否存在一点F ，使得当经过点F 的任意一条直线与新抛物线交于S ，T 两点时，总有2211FS FT +为定值？若存在，求出点F 坐标及定值，若不存在，请说明理由．9．已知抛物线()212y x a x a =+-+-．(1)对于任意实数a ，该抛物线都会经过一个定点，求此定点的坐标．(2)当1a =-时，该抛物线与x 轴交于点A ，B （点A 在点B 的左侧），与y 轴交于点C ，顶点为点D ．①如图（1），若点P 是x 轴上的动点，当PD PC -取最大值时，求PBD △的面积；②小聪研究发现：如图（2），E ，F 是抛物线上异于B ，C 的两个动点，若直线CE 与直线BF 的交点始终在直线29y x =-上，那么在直线EF 存在点Q ，使得QCE V ，QAC △，QAF △中必存在定值的三角形，请直接写出其中面积为定值的三角形及其面积，不必说明理由．题型4：定点问题10．如图，在平面直角坐标系中，抛物线2y x bx c =++与x 轴交于点()2,0A -，()1,0B ．(1)求抛物线的函数表达式；(2)直线43y x h =-+经过点B ，交抛物线于另一点C ．P 是线段BC 上一点，过点P 作直线PQ y ∥轴交抛物线于点Q ，且PB PQ =，求点P 的坐标；(3)M ，N 是抛物线上的动点（不与点B 重合），直线BM ，BN 分别交y 轴于点E ，F ，若EBF EOB ∽△△，求证：直线MN 经过一个定点．11．已知二次函数2y x bx c =++图象1C 交x 轴于点()1,0-和()3,0两点；(1)求抛物线的解析式；(2)将抛物线1C 向上平移n 个单位得抛物线2C ，点P 为抛物线2C 的顶点，()0,4C ，过C 点作x 轴的平行线交抛物线2C 于点A ，点B 为y 轴上的一动点，若存在90ABP Ð=°有且只有一种情况，求此时n 的值；(3)如图2，恒过定点()1,1的直线QN 交抛物线1C 于点Q ,N 两点，过Q 点的直线2y x t =-+的直线交抛物线1C 于M 点，作直线MN ，求MN 恒过的定点坐标．题型5：动点问题综合12．如图，在平面直角坐标系中，抛物线2y x bx c =++与x 轴交于点A B ，（点A 在点B 的左侧），与y 轴交于点()0,3C -，其对称轴为直线1x =．(1)求该抛物线的函数解析式；(2)如图1，已知点D 为第三象限抛物线上一点，连接AC ，若90ABD BAC Ð+Ð=°，求点D 的坐标；(3)(),P m n 和点Q 分别是直线y x =--24和抛物线上的动点，且点Q 的横坐标比点P 的横坐标大4个单位长度，分别过P Q ，作坐标轴的平行线，得到矩形PMQN ．设该抛物线在矩形PMQN 内部（包括边界）的图象的最高点与最低点的纵坐标的差为t ．①如图2，当12m =-时，请直接写出t 的值；②请直接写出t 关于m 的函数关系式．13．如图， 抛物线2y x bx c =++与x 轴交于()1,0A -，()3,0B 两点，直线l 与抛物线交于A ，C 两点，其中点C 的横坐标为2．(1)求抛物线的解析式；(2)P 是线段AC 上的一个动点（P 与A ， C 不重合），过 P 点作y 轴的平行线交抛物线于点 E ，求ACE △面积的最大值；(3)点H 是抛物线上的动点，在x 轴上是否存在点F ，使A 、C 、F 、H 四个点为顶点的四边形是平行四边形？如果存在，请求出所有满足条件的F 点坐标；如果不存在，请说明理由．(4)若直线PE 为抛物线的对称轴，抛物线与y 轴交于点 D ，直线AC 与y 轴交于点Q ，点M 为直线PE 上一动点，则在x 轴上是否存在一点N ，使四边形DMNQ 的周长最小？若存在，请直接写出点N 的坐标；若不存在，请说明理由．14．如图，在平面直角坐标系中，抛物线21322y x x =--与x 轴正半轴交于点A ，过点A 的直线y =kx +b (k ≠0)与该抛物线的另一个交点B 的横坐标为2，P 是该抛物线上的任意一点，其横坐标为1m +，过点P 作x 轴的垂线，交直线AB 于点C ，在该垂线的点P 上方取一点D ，使1PD =，以CD 为边作矩形CDEF ，设点E 的横坐标为2m ．(1)写出抛物线21322y x x =--的顶点坐标______．(2)当点P 与点A 重合时，求点E 的坐标；(3)当点E 在该抛物线上时，求抛物线的顶点到EF 的距离；(4)当矩形CDEF 的一组邻边与该抛物线相交，且该抛物线在矩形CDEF 内的部分所对应的函数值y 随x 的增大而增大时，直接写出m 的取值范围．15．如图1，抛物线²y x bx c =-++过点()()1,0,3,0A B -．(1)求抛物线的解析式；(2)设点P 是第一象限内抛物线上的一个动点，①当P 为抛物线的顶点时，求证：PBC △是直角三角形；②求出PBC △的最大面积及此时P 点的坐标；③如图2，过点P 作PN x ^轴，垂足为N ，PN 与BC 交于点E ．当PE 的值最大时，求点P 的坐标．题型6：对称问题16．如图1，二次函数214y x bx c =-++与x 轴交于A 、B 两点，与y 轴交于点C ．点B 坐标为(6,0)，点C 坐标为(0,3)，点P 是第一象限内抛物线上的一个动点，过点P 作PD x ^轴，垂足为D ，PD 交直线BC 于点E ，设点P 的横坐标为m ．(1)求该二次函数的表达式；(2)如图2，过点P 作PF BC ^，垂足为F ，当m 为何值时，PF 最大？最大值是多少？(3)如图3，连接CP ，当四边形OCPD 是矩形时，在抛物线的对称轴上存在点Q ，使原点O 关于直线CQ 的对称点O ¢恰好落在该矩形对角线所在的直线上，请直接写出满足条件的点Q 的坐标．17．如图1，已知抛物线23y ax bx =++与x 轴交于点()1,0A -，()3,0B ，与y 轴交于点C ，连接BC ．(1)求a ，b 的值及直线BC 的解析式；(2)如图1，点P 是抛物线上位于直线BC 上方的一点，连接AP 交BC 于点E ，过P 作PF x ^轴于点F ，交BC 于点G ，(ⅰ)若EP EG =，求点P 的坐标，(ⅱ)连接CP ，CA ，记PCE V 的面积为1S ，ACE V 的面积为2S ，求12S S 的最大值；(3)如图2，将抛物线位于x 轴下方面的部分不变，位于x 轴上方面的部分关于x 轴对称，得到新的图形，将直线BC 向下平移n 个单位，得到直线l ，若直线l 与新的图形有四个不同交点，请直接写出n的取值范围．题型7：新定义题18．定义：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于直线x n =（n 为常数）对称，则称该函数为“()X n 函数”．(1)在下列函数中，是“()X n 函数”的有 （填序号）．①y x =；②20241y x =+；③1y x =；④2y x =(2)若关于x 的函数()2y x h k =-+是“()0X 函数”，且图象与直线4y =相交于A ，B 两点，函数()2y x h k =-+图象的顶点为P ，当45PBA Ð=°时，求h ，k 的值．(3)若关于x 的函数()240y ax bx a =++¹是()1X 函数，且过点()3,1，当1t x t -££时，函数的最大值1y 与最小值2y 的差为2，求t 的值．19．以x 为自变量的两个函数y 与g ，令h y g =-，我们把函数h 称为y 与g 的“相关函数”例如：以x 为自变量的函数2y x =与21g x =-，则它们的“相关函数”为221h y g x x =-=-+．因为()222110h x x x =-+=-³恒成立．所以借助该“相关函数”可以证明：不论自变量x 取何值，y g ³恒成立．(1)已知函数2y x mx n =++与函数41g x =+相交于点()1,3--、()3,13．①此时m ，n 的值分别为：m =______，n =______；②求此时函数y 与g 的“相关函数”h ；(2)已知以x 为自变量的函数3y x t =+与2g x =-，当1x >时，对于x 的每一个值，函数y 与g 的“相关函数”0h >恒成立，求t 的取值范围；(3)已知以x 为自变量的函数2y ax bx c =++与2g bx c =--（,,a b c 为常数且0a >，0b ¹）．点1,02A æöç÷èø，点()12,B y -，()21,C y 是它们的“相关函数”h 的图象上的三个点．且满足212c y y <<，求函数h 的图象截x 轴得到的线段长度的取值范围．题型8：二次函数的代数（综合）应用20．二次函数2y x bx c =++的图象与x 轴交于点()1,0A x ，()2,0B x 且12x x ¹．(1)当12x =，且6b c +=-时，①求b ，c 的值②当2x t -££时，二次函数2y x bx c =++的最大值与最小值的差为4，求t 的值；(2)若123x x =，求证：332b c -£．21．在平面直角坐标系中，已知抛物线()2233y mx m x m =--+-（m 是常数，且0m ¹）经过点()2,4，且与y 轴交于点A ，其对称轴与x 轴交于点B ．(1)求出二次函数的表达式．(2)垂直于y 轴的直线l 与抛物线交于点(),P a p 和(),Q b q ，与直线AB 交于点(),c n ，若a c b <<，直接写出a b c ++的取值范围．(3)当13x t =-，2x t =，33x t =+时，对应的函数值分别为1y ，2y ，3y ．求证：123454y y y ++³．22．已知y 关于x 的两个函数y ax a =+（a 为常数，0a ¹，0x £）与22y ax ax a =-+（a 为常数，0a ¹，0x >）的图像组成一个新图形N ．图形N 与x 轴交于A ，B 两点（点A 在点B 左边），交y 轴于点C ．(1)求点A ，B 坐标；(2)若ABC V 为直角三角形；①求实数a 的值；②若直线(0)y kx b k =+¹与图形N 有且只有两个交点()11,x y ，()22,x y ，满足12202x x -<<<<，求实数k 满足条件．。

浙教版九年级上册压轴题数学精品模拟试卷

浙教版九年级上册压轴题数学精品模拟试卷

浙教版九年级上册压轴题数学精品模拟试卷一、压轴题1．如图，正方形ABCD 中，对角线AC 、BD 交于点O ，E 为OC 上动点(与点O 不重合)，作AF ⊥BE ，垂足为G ，交BO 于H ．连接OG 、CG ．(1)求证：AH=BE ；(2)试探究：∠AGO 的度数是否为定值？请说明理由；(3)若OG ⊥CG ，BG=32，求△OGC 的面积．2．某校开展了一次综合实践活动，参加该活动的每个学生持有两张宽为6cm ，长足够的矩形纸条．探究两张纸条叠放在一起，重叠部分的形状和面积．如图1所示，一张纸条水平放置不动，另一张纸条与它成45°的角，将该纸条从右往左平移．（1）写出在平移过程中，重叠部分可能出现的形状．（2）当重叠部分的形状为如图2所示的四边形ABCD 时，求证：四边形ABCD 是菱形． （3）设平移的距离为cm(0662)x x <≤+，两张纸条重叠部分的面积为2cm s ．求s 与x 的函数关系式，并求s 的最大值．3．如图，过原点的抛物线y=﹣12x 2+bx+c 与x 轴交于点A （4，0），B 为抛物线的顶点，连接OB ，点P 是线段OA 上的一个动点，过点P 作PC ⊥OB ，垂足为点C ．（1）求抛物线的解析式，并确定顶点B 的坐标；（2）设点P 的横坐标为m ，将△POC 绕着点P 按顺利针方向旋转90°，得△PO′C′，当点O′和点C′分别落在抛物线上时，求相应的m 的值；（3）当（2）中的点C′落在抛物线上时，将抛物线向左或向右平移n （0＜n ＜2）个单位，点B 、C′平移后对应的点分别记为B′、C″，是否存在n ，使得四边形OB′C″A 的周长最短？若存在，请直接写出n 的值和抛物线平移的方向，若不存在，请说明理由．4．如图，A 是以BC 为直径的圆O 上一点，AD ⊥BC 于点D ，过点B 作圆O 的切线，与CA 的延长线相交于点E ，G 是AD 的中点，连接并延长CG 与BE 相交于点F ，连接并延长AF 与CB 的延长线相交于点P ．（1）求证：BF ＝EF ；（2）求证：PA 是圆O 的切线；（3）若FG ＝EF ＝3，求圆O 的半径和BD 的长度．5．如图1，在平面直角坐标系中，抛物线与x 轴交于点 A (-1，0) ，B （点A 在点B 的左侧），交y 轴与点(0，-3)，抛物线的对称轴为直线x ＝1，点D 为抛物线的顶点． （1）求该抛物线的解析式；（2）已知经过点A 的直线y ＝kx +b (k >0)与抛物线在第一象限交于点E ，连接AD ，DE ，BE ，当2ADE ABE S S ∆∆=时，求点E 的坐标．（3）如图2，在（2）中直线AE 与y 轴交于点F ，将点F 向下平移233+个单位长度得到Q ，连接QB ．将△OQB 绕点O 逆时针旋转一定的角度α（0°<α<360°）得到OQ B ''，直线B Q ''与x 轴交于点G ．问在旋转过程中是否存在某个位置使得OQ G '是等腰三角形？若存在，请直接写出所有满足条件的点Q '的坐标；若不存在，请说明理由．6．直线m∥n，点A、B分别在直线m，n上（点A在点B的右侧），点P在直线m上，AP＝13AB，连接BP，将线段BP绕点B顺时针旋转60°得到BC，连接AC交直线n于点E，连接PC，且ABE为等边三角形．（1）如图①，当点P在A的右侧时，请直接写出∠ABP与∠EBC的数量关系是，AP 与EC的数量关系是．（2）如图②，当点P在A的左侧时，（1）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由．（3）如图②，当点P在A的左侧时，若△PBC的面积为934，求线段AC的长．7．（问题发现）（1）如图①，在△ABC中，AC＝BC＝2，∠ACB＝90°，D是BC边的中点，E是AB边上一动点，则EC+ED的最小值是．（问题研究）（2）如图②，平面直角坐标系中，分别以点A（﹣2，3），B（3，4）为圆心，以1、3为半径作⊙A、⊙B，M、N分別是⊙A、⊙B上的动点，点P为x轴上的动点，试求PM+PN的最小值．（问题解决）（3）如图③，该图是某机器零件钢构件的模板，其外形是一个五边形，根据设计要求，边框AB长为2米，边框BC长为3米，∠DAB＝∠B＝∠C＝90°，联动杆DE长为2米，联动杆DE的两端D、E允许在AD、CE所在直线上滑动，点G恰好是DE的中点，点F可在边框BC上自由滑动，请确定该装置中的两根连接杆AF与FG长度和的最小值并说明理由．8．如图，在平面直角坐标系中，抛物线与轴交于点，与轴交于点，的解析式为，若将抛物线平移，使平移后的抛物线经过点， 对称轴为直线，抛物线与轴的另一个交点是，顶点是，连结.（1）求抛物线的解析式；（2）求证：∽（3）半径为的⊙的圆心沿着直线从点运动到，运动速度为1单位/秒，运动时间为秒，⊙绕着点顺时针旋转得⊙，随着⊙的运动，求的运动路径长以及当⊙与轴相切的时候的值.9．将抛物线2:(2)C y x =-向下平移6个单位长度得到抛物线1C ，再将抛物线1C 向左平移2个单位长度得到抛物线2C ．（1）直接写出抛物线1C ，2C 的解析式；（2）如图（1），点A 在抛物线1C 对称轴l 右侧上，点B 在对称轴l 上，OAB 是以OB 为斜边的等腰直角三角形，求点A 的坐标；（3）如图（2），直线y kx =（0k ≠，k 为常数）与抛物线2C 交于E ，F 两点，M 为线段EF 的中点；直线4y x k=-与抛物线2C 交于G ，H 两点，N 为线段GH 的中点．求证：直线MN 经过一个定点．10．对于⊙C 与⊙C 上的一点A ，若平面内的点P 满足：射线．．AP 与⊙C 交于点Q （点Q 可以与点P 重合），且12PA QA≤≤，则点P 称为点A 关于⊙C 的“生长点”． 已知点O 为坐标原点，⊙O 的半径为1，点A （-1，0）．（1）若点P 是点A 关于⊙O 的“生长点”，且点P 在x 轴上，请写出一个符合条件的点P 的坐标________；（2）若点B 是点A 关于⊙O 的“生长点”，且满足1tan BAO 2∠=，求点B 的纵坐标t 的取值范围；（3）直线3y x b =+与x 轴交于点M ，与y 轴交于点N ，若线段MN 上存在点A 关于⊙O 的“生长点”，直接写出b 的取值范围是_____________________________．11．如图，在平面直角坐标系中，四边形ABCD 的顶点A 、B 在函数(0)m y x x =>的图象上，顶点C 、D 在函数(0)n y x x=>的图象上，其中0m n <<，对角线//BD y 轴，且BD AC ⊥于点P ．已知点B 的横坐标为4．（1）当4m =，20n =时，①点B 的坐标为________，点D 的坐标为________，BD 的长为________．②若点P 的纵坐标为2，求四边形ABCD 的面积．③若点P 是BD 的中点，请说明四边形ABCD 是菱形．（2）当四边形ABCD 为正方形时，直接写出m 、n 之间的数量关系．12．小聪与小明在一张矩形台球桌ABCD 边打台球，该球桌长AB =4m ，宽AD =2m ，点O 、E 分别为AB 、CD 的中点，以AB 、OE 所在的直线建立平面直角坐标系。

浙教版九年级中考压轴题练习

浙教版九年级中考压轴题练习

1.在平面直角坐标系xOy中，抛物线y = x2– 2mx + m2– 1与x轴交于A，B两点（点A在点B左侧）（1）求抛物线的顶点坐标（用含m的代数式表示）；（2）求线段AB的长；（3）抛物线与y轴交于点C（点C不与原点O重合），若△OAC的面积始终小于△ABC 的面积，求m的取值范围2.在平面直角坐标系中xOy 中，抛物线2211222y x mx m m =-++-的顶点在x 轴上． （1）求抛物线的表达式；（2）点Q 是x 轴上一点， ①若在抛物线上存在点P ，使得∠POQ =45°，求点P 的坐标；②抛物线与直线y =2交于点E ，F （点E 在点F 的左侧），将此抛物线在点E ，F （包含点E 和点F ）之间的部分沿x 轴平移n 个单位后得到的图象记为G ，若在图象G 上存在点P ，使得∠POQ =45°，求n 的取值范围．1.解：（1）y = x2 – 2mx + m2 – 1 = （x – m）2 – 1 ，∴顶点为（m，-1）………………………………………………1分（2）令y = 0∴x2 – 2mx + m2 – 1 = 0解得x1 = m – 1 ，x2 = m + 1 ……………………………………2分∵点A在点B的左侧∴A（m – 1，0），B（m + 1，0）∴AB = （m + 1）– ( m – 1 ) = 2…………………………………3分（3）∵△OAC与△ABC等高△OAC的面积小于△ABC的面积∴OA < AB…………………………………………4分①当点A在x轴的正半轴上时m – 1 < 2m < 3……………………………………………………5分②当点A在x轴的负半轴上时1 – m < 2m > – 1…………………………………………………6分又∵点C不与原点O重合∴m 2 – 1≠0，m≠±1∴– 1< m <3且m≠1…………………………………7分2.解：（1）222111-2()2222y x mx m m x m m =++-=-+-. 由题意，可得m -2=0．∴2m =．∴21(2)2y x =-． （2）①由题意得，点P 是直线y x =与抛物线的交点. ∴21-222x x x =+.解得 13x =23x =.∴P 点坐标为(3+或 (3--.②当E 点移动到点（2,2）时，n =2.当F 点移动到点（-2,2）时，n =-6.由图象可知，符合题意的n 的取值范围是26-≤≤n .。

压轴题综合练习2021--2022学年浙教版九年级数学上册 含答案

压轴题综合练习2021--2022学年浙教版九年级数学上册 含答案

压轴题综合1．如图，在等边三角形ABC 中，点E 、F 分别是边AB 、AC 上两点，将△ABC 沿EF 翻折，点A 正好落在线段BC 上的点D 处，若BD ＝3CD ．若AE ＝13，则点C 到线段DF 的距离是____．2．如图，在矩形ABCD 中，AB =2，BC =3，点E 是边AB 的中点，连接CE ，将△BCE 沿CE 折叠得到△FCE ，CF 与BD 交于点P ，则DP 的长为 ___．3．如图在Rt ABC 中，△BAC =90°，AB = AC =10，等腰直角三角形ADE 绕点A 旋转，△DAE =90°，AD = AE =4，连接DC ，点M 、P 、N 分别为DE 、DC 、BC 的中点，连接MP 、PN 、MN ，则△PMN 面积的最小值是_______．4．如图，在正方形ABCD 中，点E 为BC 边上一点，且2CE BE =，点F 为对角线BD 上一点，且2BF DF =，连接AE 交BD 于点G ，过点F 作FH AE ⊥于点H ，若2HG cm =，则正方形ABCD 的边长为_______cm ．5．问题发现：（1）如图△，点A 和点B 均在△O 上，且△AOB ＝90°，点P 和点Q 均在射线AM 上，若△APB ＝45°，则点P 与△O 的位置关系是 ；若△AQB ＜45°，则点Q 与△O 的位置关系是 ． 问题解决：如图△、图△所示，四边形ABCD 中，AB △BC ，AD △DC ，△DAB ＝135°，且AB ＝1，AD ＝22，点P 是BC 边上任意一点．（2）当△APD ＝45°时，求BP 的长度．（3）是否存在点P ，使得△APD 最大？若存在，请说明理由，并求出BP 的长度；若不存在，也请说明理由．6．已知抛物线()()213y x m x m =--+-（m 为常数，1m ）．()14,A m y +，()22,B m y 是该抛物线上不同的两点，现将抛物线的对称轴绕坐标原点O 逆时针旋转90︒得到直线a ，过抛物线顶点P 作PH a ⊥于H ． （1）当3m =时，求出这条抛物线的顶点坐标；（2）若无论m 取何值，抛物线与直线34m y x m k m ⎛⎫=-++ ⎪⎝⎭（k 为常数）有且仅有一个公共点，求k 的值；（3）当24PH <≤时，试比较1y ，2y 之间的大小．7．已知△ABC 和△ADE 都是等腰三角形，AB ＝AC ，AD ＝AE ，△DAE ＝△BAC ．（初步感知）（1）特殊情形：如图△，若点D ，E 分别在边AB ，AC 上，则DB EC ．（填＞、＜或＝）（2）发现证明：如图△，将图△中△ADE 的绕点A 旋转，当点D 在△ABC 外部，点E 在△ABC 内部时，求证：DB ＝EC ． （深入研究）（3）如图△，△ABC 和△ADE 都是等边三角形，点C ，E ，D 在同一条直线上，则△CDB 的度数为 ；线段CE ，BD 之间的数量关系为 ．（4）如图△，△ABC 和△ADE 都是等腰直角三角形，△BAC ＝△DAE ＝90°，点C 、D 、E 在同一直线上，AM 为△ADE 中DE 边上的高，则△CDB 的度数为 ；线段AM ，BD ，CD 之间的数量关系为 ．8．已知抛物线y ＝ax 2＋bx ＋c ，a 、b 、c 为实数，且a ≠0（1）当a ＝1且b ＝c ＋1时，在－1＜x ＜3中，恒有y ＜0，求c 的取值范围；（2）抛物线与x 轴交于A 、B 两点，与y 轴交于点C ，顶点D 的纵坐标为－1，若△ABC 是直角三角形，当Rt △ABC 面积取得最大值时，求抛物线的解析式；（3）若抛物线与x 轴只有一个公共点M （2，0），与y 轴交于（0，：直线l ：y ＝kx ＋2k 与抛物线交于点P 、Q ，过点P 且与y 轴平行的直线与直线MQ 相交于点N ，求证：对于每个给定的实数k ，点N 的纵坐标均为定值． 9．如图，在△ABC 中，AB ＝AC ，△是△ABC 的外接圆，连接BO 并延长交边AC 于点D ． （1）如图1，求证：△BAC ＝2△ABD ；（2）如图2，过点B 作BH △AC 于点H ，延长BH 交△O 于点G ，连接OC ，CG ，OC 交BG 于点F ，求证：BF ＝2HG ； （3）如图3，在（2）的条件下，若AD ＝2，CD ＝3，求线段BF 的长．10．如图，菱形ABCD 与菱形EBGF 的顶点B 重合，顶点F 在射线AC 上运动，且120BCD BGF ∠=∠=︒，对角线AC 、BD 相交于点O ．（1）如图1．当点F 与点O 重合时，直接写出AEFD的值为 ； （2）当顶点F 运动到如图2的位置时，连接CG ，CG BG ⊥，且CG BC =，试探究CG 与DF 的数量关系，说明理由，并直接写出直线CG 与DF 所夹锐角的度数；（3）如图3，取点P 为AD 的中点，若B 、E 、P 三点共线，且当CF ＝2时，请直接写出BP 的长．11．已知一个矩形纸片OACB ，将该纸片放置在平面直角坐标系中，点A （11，0），点B （0，6），点P 为BC 边上的动点（点P 不与点B 、C 重合），经过点O 、P 折叠该纸片，得点B ′和折痕OP ．设BP ＝t ．（1）如图△，当△BOP ＝30°时，直接写出点B ′的坐标为 ；（2）如图△，经过点P 再次折叠纸片，使点C 落在直线PB ′上，得点C ′和折痕PQ ，若AQ ＝m ，试用含有t 的式子表示m ；（3）如图△，在（2）的条件下，当点C ′恰好落在边OA 上时，求点P 的坐标．12．在Rt △ABC 中，△ACB ＝90°，D 是BC 上一点，BD ＝AC ，F 是AC 上一点，连接BF 交AD 于E ． （1）如图1，若AC ＝5，CD ＝2，△CAD ＝△CBF ，求EF ：DE 的值； （2）如图2，若△DEB ＝45°，求证：AF ＝CD ；（3）如图3，在（2）问条件下，过B 作AD 的垂线，交AD 延长线于H ，过C 点作CG △AD 垂足为G ，若DH ＝a，BH ＝b ，直接写出DGAE的值（用a ，b 的式子表示）13．函数2223y x mx m =+-+（m 为常数）的顶点为点P ，设其图象为G ． （1）若点()3,2在图象G 上，求m 的值．（2）设直线y m =-与图象G 交于A 、B 两点，当6AB =时，求m 的值． （3）当02x ≤≤时，该函数的最大值为5，求m 的值．（4）若图象G 在直线12x m =+和直线2x m =-间的部分的满足y 随x 的增大而增大时，且点()21,1Q m m --在直线12x m =+和直线2x m =-以及图象G 、x 轴围城的封闭区域内，直接写出m 的取值范围．14．如图，在等腰Rt ABC 中，90BAC ∠=︒，AD BC ⊥，垂足为D ，点E 为AC 边上一点，连接ED 并延长至F ，使ED FD =，以EF 为底边作等腰Rt EGF ．（1）如图1，若30ADE ∠=︒，4AE =，求CE 的长；（2）如图2，连接BF ，DG ，点M 为BF 的中点，连接DM ，过D 作DH AC ⊥，垂足为H ，连接AG 交DH 于点N ，求证：=DM NG ；（3）如图3，点K 为平面内不与点D 重合的任意一点，连接KD ，将KD 绕点D 顺时针旋转90︒得到K D '，连接K A '，KB ，直线K A '与直线KB 交于点P ，D 为直线BC 上一动点，连接AD '并在AD '的右侧作C D AD '''⊥且C D AD '''=，连接AC '，Q 为BC 边上一点，3CD CQ =，122AB =，当QC C P ''+取到最小值时，直线C P '与直线BC 交于点S ，请直接写出BPS △的面积．15．以BC 为斜边在它的同侧作Rt△DBC 和Rt△ABC ，其中△A ＝△D ＝90°，AB ＝AC ，AC 、BD 交于点P ． （1）如图1，BP 平分△ABC ，求证：BC ＝AB +AP ；（2）如图2，过点A 作AE △BP ，分别交BP 、BC 于点E 、点F ，连接AD ，过A 作AG △AD ，交BD 于点G ，连接CG ，交AF 于点H ，△求证：△ABG △△ADC ；△求证：GH ＝CH ；（3）如图3，点M 为边AB 的中点，点Q 是边BC 上一动点，连接MQ ，将线段MQ 绕点M 逆时针旋转90°得到线段MK ，连接PK 、CK ，当△DBC ＝15°，AP ＝2时，请直接写出PK +CK 的最小值．16．已知抛物线22y ax bx =++与x 轴交于(1,0)A -和B 两点，且5AB =，与y 轴交于C ，且对于该二次函数图象上的任意两点()111,P x y ，()222,P x y ，当121x x <≤-时，总有12y y <． （1）求抛物线的解析式；（2）过点A 的直线:l y kx b =+与该抛物线交于另一点E ，与线段BC 交于点F ． △若45EFB ∠=︒，求点E 的坐标；△当14t k t ≤≤+时，AFEF 的最小值是52，求t 的值．17．如图1，等腰△ABC 中，AB ＝AC ，D 为AB 上一点，等腰△CDE ，CD ＝DE ，△BAC ＝△EDC ，DE 交BC 于点M ，连接BE ．（1）如图1，若△BAC ＝30°，AC ＝3，AD 32=，求DE 的长度； （2）如图2．若DM △BC 求证：2MB +EB ＝BC ．（3）如图3，△A ＝30°，AC △DE ，CN △AB ，EF △CE ，延长DB 至点H ，使得DH ＝DE ，试判断FM 与FN 的数量关系，并写出证明过程．18．如图，在平面直角坐标系中，抛物线215222y x x =-+交x 轴于A 、B ，交y 轴于点C ．（1）求ABC 的面积；（2）D 为抛物线的顶点，连接BD ，点P 为抛物线上点C 、D 之间一点，连接CP ，DP ，过点P 作//PM BD 交直线BC 于点M ，连接DM ，求四边形CPDM 面积的最大值以及此时P 点的坐标：（3）将抛物线沿射线BC 方向平移35个单位后得到新的抛物线2(0)y ax bx c a '=++≠），新抛物线'y 与原抛物线的交点为E ，在原抛物线上是否存在点Q ，使得以B ，E ，Q 为顶点的三角形为直角三角形？若存在，请直接写出点Q 的坐标：若不存在，请说明理由．19．如图，已知AB 是△O 的弦，OB ＝1，C 是弦AB 上的任意一点（不与点A 、B 重合），连接CO 并延长CO 交△O 于点D ，连接AD ．设△B ＝α，△ADC ＝β．（1）求△BOD 的度数（用含α，β的代数式表示）；（2）若α＝30°，当AC 的长度为多少时，以点A 、C 、D 为顶点的三角形与B 、C 、O 为顶点的三角形相似？请写出解答过程．（3）若α＝β，连接AO ，记△AOD 、△AOC 、△COB 的面积分别为S 1，S 2，S 3，如果S 2是S 1和S 3的比例中项，求OC 的长．20．如图，在Rt ABC 中，90BAC ∠=︒，AB AC =，点D 是AB 外一动点，连接AD ，把AD 绕点A 逆时针旋转90°，得到AE ，连接CE ，DE ，BC 与DE 交于点F ，且AB BD ⊥． （1）如图1，若102,CB =6CE =，求DE 的长；（2）如图2，若点H 、G 分别为线段CF 、AE 的中点，连接HG ，求证：12HG BF =； （3）如图3，在（2）的条件下，若22,CE =4CF =，将BDF 绕点F 顺时针旋转角3(060)αα︒<≤︒，得到B D F ''，连接B G '，取B G '中点Q ，连接BQ ，当线段BQ 最小时，请直接写出BQB '的面积．21．已知直线10y kx =+与x 轴相交于B 两点，交y 轴于点A ，且ABO 的面积为45．（1）求直线AB 的解析式；（2）若(),0D t ，点()0,4E ，连接DE ，将线段DE 绕点E 逆时针转90︒得到线段EK ，连接OK ，KD ，设ODK 的面积为S ，求S 与t 的函数关系式；（3）在（2）的条件下，点F 为OB 上一点，过F 作OB 的垂线交AB 于点G ，在AE 上取点C ，使得CE ED =，连接CG 、GE ，EF ，且2180FEO EDO ∠+∠=︒，当20CEG S =△时，求CK 的长．22．类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．（1）如图1，在四边形ABCD 中，DB 平分ABC ∠，180A C ∠+∠=︒，请说明四边形ABCD 是“等邻边四边形”； （2）如图2，在Rt ABC 中，90ABC ∠=︒，2AB =，4BC =，并将Rt ABC 沿ABC ∠的平分线'BB 方向平移得到'''A B C ，连接'AA ，'BC ，要使平移后的四边形''ABC A 是“等邻边四边形”，应平移多少距离？（即线段'BB 的长）？请直接写出平移的距离；（3）如图3，“等邻边四边形”ABCD 中，AB BC =，90ABC ADC ∠+∠=︒，BD nBC =，试探究AD ，AC ，CD 之间的数量关系（用含n 的等式表示）．23．ABC 内接于O ，点D 在BC 边上，射线AD 交O 于点E ，点F 在弧BE 上，连接AF ，ADB AFE ∠=∠．（1）如图1，求证：AB AC =；（2）如图2，BE 交弦AF 于点G ，BC 经过O 点，2AGE EAF ∠=∠，求证：AF BE =；（3）如图3，在（2）的条件下，H 为EG 的中点，连接OH 、CH ，若2180ACH ABE ∠+∠=︒，26AB =，求线段OH 的长．24．如图，函数y ＝﹣x 2＋bx ＋c 的图象经过点A （m ，0），B （0，n ）两点，m ，n 分别是方程x 2﹣2x ﹣3＝0的两个实数根，且m ＜n ．（1）求m ，n 的值以及函数的解析式；（2）设抛物线y ＝﹣x 2＋bx ＋c 与x 轴的另一个交点为C ，抛物线的顶点为D ，连接AB ，BC ，BD ，CD ．求证：△BCD △△OBA ；（3）对于（1）中所求的函数y ＝﹣x 2＋bx ＋c ，连接AD 交BC 于E ，在对称轴上是否存在一点F ，连接EF ，将线段EF 绕点E 顺时针旋转90°，使点F 恰好落在抛物线上？若存在，请求出点F 的坐标；若不存在，请说明理由． 25．已知矩形ABCD 中，AB ＝4，AD ＝10，点E 是AD 边上一动点，连接BE 、CE ，以BE 为直径作△O ，交BC 于点F ，过点F 作FH △CE 于H ．（1）当F 为BC 中点时，求证EB ＝EC ； （2）当FH △BE 时，求AE 的长；（3）若线段FH 交△O 于点G ，在点E 运动过程中，如果△FOG ＝90°，请求出此时AE 的长．26．如图，在等边ABC 的AC ，BC 边上各取一点E ，D ，使AE ＝CD ，AD ，BE 相交于点O ． （1）求证：AD ＝BE ；（2）若BO ＝6OE =，求CD 的长． （3）在（2）的条件下，动点P 在CE 上从点C 向终点E 匀速运动，点Q 在BC 上，连结OP ，PQ ，满足△OPQ ＝60°，记PC 为x ，DQ 的长为y ，求y 关于x 的函数表达式．27．已知，点A 是平面直角坐标系内的一点，将点A 绕坐标原点O 逆时针旋转90︒得到点B ，经过A 、O 、B 三点的二次函数的图象记为G ． （1）若点A 的坐标为()1,2． △点B 的坐标为___________． △求图象G 所对应的函数表达式．（2）若点A 的坐标为()(),20m m m ≠，图象G 所对应的函数表达式为2y ax bx =+（a 、b 为常数，0a ≠）．写出b 的值，并用含m 的代数式表示a ．（直接写出即可）（3）在（2）的条件下，直线2x =-与图象G 交于点P ，直线1x =与图象G 交于点Q ．图象G 在P 、Q 之间的部分（包含P 、Q 两点）记为1G ．△当图象G 在21x -≤≤上的函数值y 随自变量x 的增大而增大时，设图象1G 的最高点的纵坐标为1h ，最低点的纵坐标为2h ，记12h h h =-，求h 的取值范围．△连结PQ ，当PQ 与图象1G 围成的封闭图形与x 轴交于点D （点D 不与坐标原点重合）．当12OD ≥时，直接写出m 的取值范围．28．已知抛物线y ＝ax 2+bx +c （a ＞0）与x 轴交于A (﹣1，0)，B 两点，与y 轴交于点C (0，﹣3a )． （1）求点B 的坐标；（2）若a ＝12，点M 和点N 在抛物线上，且M 的横坐标为4，点N 在第二象限，若△AMN ＝2△OAM ，求点N 的坐标； （3）P 是第四象限内抛物线上的一个动点，直线P A 、PB 分别交y 轴于点M 、N ，判断CM 与CN 的数量关系，并说明理由．29．已知，在ABC 中，AB AC =，1902D BCD B ∠+∠=︒+∠．（1）如图1，求证：AD DC =（2）如图2，连接BD ，交AC 于点E ，若60ADC ∠=︒，求CBD ∠的度数（3）如图3，在（2）的条件下，延长BA 、CD 交于点F ，若1AE =，3DF =，求BF 的长．30．如图，AB 是△O 的直径，C 、D 是△O 上两点．AE 与过点C 的切线垂直，垂足为E ，直线EC 与直径AB 的延长线相交于点P ，弦CD 交AB 于点F ，连接AC 、AD 、BC 、BD ． （1）若△ABC ＝△ABD ＝60°，判断△ACD 的形状，并证明你的结论； （2）若CD 平分△ACB ，求证：PC ＝PF ；（3）在（2）的条件下，若AD ＝52，PF ＝53，求由线段PC 、CB 和线段BP 所围成的图形（阴影部分）的面积．31．如图，在△ABC 中，AC ＝BC ＝25，tan△CAB ＝12，P 为AC 上一点，PD △AB 交AB 于点E ，AD △AC 交PD 于点D ，连结BD ，CD ，CD 交AB 于点Q ．（1）若CD △BC ，求证：△AED △△QCB ； （2）若AB 平分△CBD ，求BQ 的长； （3）连结PQ 并延长交BD 于点M ． △当点P 是AC 的中点时，求tan△BQM 的值△当PM 平行于四边形ADBC 中的某一边时，求BMDM的值．32．如图1，已知抛物线2y x bx c =-++过点(1,0)A ，(3,0)B -． （1）求抛物线的解析式及其顶点C 的坐标；（2）设点D 是x 轴上一点，当CDO ACO ∠=∠时，求点D 的坐标；（3）如图2，抛物线与y 轴交于点E ，点P 是该抛物线上位于第二象限的点，线段P A 交BE 于点M ，交y 轴于点N ，BMP 和EMN 的面积相等时，求P 的坐标．33．在ABC 中，3AC BC ==，120ACB ∠=︒，在ADE 中，90DAE ∠=︒，30AED ∠=︒，1AD =，连接BD ，BE ，点F 是BD 的中点，连接CF ．（1）如图1，当顶点D 在边AB 上时，线段BE 与线段CF 的数量关系是______，线段BE 与线段CF 的位置关系是 ；（2）将ADE 绕点A 旋转，转到图2的位置时，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由；（3）在ADE 绕点A 旋转的过程中，线段AF 的最大值为______；当//DE CF 时，线段CF 的长为______． 34．已知抛物线y ＝ax 2＋bx ＋c （a 、b 、c 为常数，且a ≠0）（1）若抛物线的对称轴为x ＝3，若抛物线与x 轴的两个交点的横坐标比为1：2，求这两个交点的坐标； （2）抛物线的顶点为点C ，抛物线与x 轴交点分别为A 、B ，若△ABC 为等边三角形，求证：b 2—4ac ＝12； （3）若当x ＞—1时，y 随x 的增大而增大，且抛物线与直线y ＝ax —1a ＋c 相切于点D ，若OD ≥22恒成立，求c 的取值范围．参考答案1 【分析】过点C 作CN △FD 于点N ，过点E 作EM △BC 于点M ，首先证明BED CDF △△，得到BE ED BD CD DF CF==，设=CD x ，通过计算用x 表示出相关线段，根据相似比解出x 的值，再证明EMD CNF △△，得到EM ED CN CF=，代入数值计算即可． 【详解】解：过点C 作CN △FD 于点N ，过点E 作EM △BC 于点M ，作图如下：△ABC 为等边三角形△60A B ACB ∠=∠=∠=△折叠△160A ∠=∠=△2+1801120FDC ∠∠=-∠=又△60FCD ∠=△3+=180120FDC FCD ∠∠-∠=△2=3∠∠又△=60B FCD ∠∠=△BED CDF △△ △BE ED BD CD DF CF== 又△3BD CD =△设=CD x ，则3,4BD x BC x ==△=13,AE AE BE AB +=△413BE x =- △4133x x x CF-= △23413x CF x =- △折叠△AF FD =，13AE ED == △234413x AF DF x x ==-- △13413x DF x-= 即：21341334413x x x x x -=-- 化简得：213650x x -=解得：12=5=0x x ，（舍）△1341320137BE AB x =-=-=-=，3257577CF ⨯== 在Rt BME △中，60B ∠= △1722BM BE ==,ME == △7723315222MD BD BM x =-=-=-= 又△2390EMD N ∠=∠∠=∠=，△EMD CNF △△ △EM ED CN CF=即：132=757CN△CN =【点睛】本题考查三角形的相似性质和判定，等边三角形的性质，含30︒的直角三角等知识点，牢记定理内容是解题关键．2 【分析】由勾股定理可求出BD 、EC 的长，连接BF 交CE 于点G ，作FH △BC 于点H ，PQ △BC 于点Q ，根据相似三角形的性质求出BG 的长，再根据面积等式列方程求出FH 的长，再根据相似三角形的性质求出BQ 与CQ 的比，进而求出DP 的长．【详解】解：如图，连接BF 交CE 于点G ，作FH △BC 于点H ，PQ △BC 于点Q ，△四边形ABCD 是矩形，△AB =DC =2，△ABC =△BCD =90°，△BC =3，△.BD =△AE =BE =12AB =12×2=1，△EC =由折叠得，CE 垂直平分BF ，△△BGC =△EBC =90°，△△GCB =△BCE ，△△BGC △△EBC ， △GB BC BE EC=，△BC BE GB EC ⋅==△22BF GB ===，CG =由12BC•FH=12BF•CG得，12×3FH=12解得，FH=95；△△CHF=90°，FC=BC=3，△125CH=；△PQ△FH，△△CPQ△△CFH，△CQ PQCH FH=，△1245935CQ CHPQ FH===，△CQ=43PQ，△△BQP=△BCD=90°，△PQ△DC，△△BPQ△△BDC，△BQ PQBC DC=，△32BQ BCPQ DC==，△BQ=32PQ，△392483PQBP BQDP CQ PQ===，△881717DP BD==，．【点睛】本题重点考查矩形的性质、轴对称的性质、相似三角形的判定与性质、勾股定理、二次根式的化简以及用面积等式列方程等知识与方法，解题的关键是正确地作出所需要的辅助线，此题难度较大，计算烦琐，应注意检验所求的结果是否正确．3．92【分析】通过ABC 和ADE 为等腰直角三角形，判定出ADB AEC ≅，得到,,DB EC ABD ACE =∠= 通过已知条件，再设,,ACE x ACD y ∠=︒∠=︒得到PMN 为等腰直角三角形，所以2211,28PMN S PN BD ==当BD 最小时，PMN 的面积最小，D 是以A 为圆心，AD =4为半径的圆上的点，所以点D 在AB 上时，BD 最小，即可得到最终结果．【详解】 Rt ABC 中，△BAC =90°，AB = AC =10，∴ABC 为等腰直角三角形， 又△DAE =90°，AD = AE =4，∴ADE 为等腰直角三角形，(),,,,,BAC DAC DAE DAC BAD CAE ADB AEC SAS DB EC ABD ACE ∴∠-∠=∠-∠∴∠=∠∴≅∴=∠= 点M 、P 、N 分别为DE 、DC 、BC 的中点，11//,,//,,22,,,MP EC MP EC NP BD NP BD MP NP DPM DCE PNC DBC ∴==∴=∠=∠∠=∠ 设,,ACE x ACD y ∠=︒∠=︒,45,45,90,,90,ABD x DBC x PNC DCB y DPN DCB PNC x y DPM DCE x y MPN DPM DPN ∴=︒∠=︒-︒=∠∠=︒-︒∴∠=∠+∠=︒-︒-︒∠=∠=︒+︒∴∠=∠+∠=︒ PMN ∴△是等腰直角三角形，2211,28PMN S PN BD ∴== ∴当BD 最小时，PMN 的面积最小， D 是以A 为圆心，AD =4为半径的圆上的点，∴点D 在AB 上时，BD 最小，1046,BD AB AD =-=-=221196,882PMN S BD ∴==⨯=∴△PMN 面积的最小值是92． 故答案为：92． 【点睛】本题主要考查了旋转的性质，涉及全等三角形的性质和判定，等腰直角三角形的性质等知识，有一定难度和综合性，属于压轴题，熟练掌握这些性质，利用旋转解题是关键．4【分析】如图，过F 作FI BC ⊥于I 点，连接FE 和F A ，得到BIF BCD ，设23BE EI IC acm CE FI acm AB acm ======，，，求出FE ，AH ，AG ，证明BEG DAG ， 得到1122)33cm c GE AG GE HE GH m ⎫==+=-=-⎪⎪⎝⎭，， 最后求值即可． 【详解】如图，过F 作FI BC ⊥于I 点，连接FE 和F A ，FI BC ⊥，四边形ABCD 为正方形，//FI CD ∴，BIF BCD ∴，2BF DF =，23BI BF BC BD ∴==， I ∴ 为BC 的三等分点，2CE BE =，E ∴为 BC 的三等分点，BE EI IC ∴==，∴设BE EI IC acm ===，∴3AB BC acm ==， BFI 为等腰直角三角形，2BI FI acm ∴==，FE FC FA ∴==， H ∴ 为AE 的中点，AE AB ===，122)AH HE AE AG AH GH cm ∴===∴=+=+，， 四边形ABCD 为正方形，∴//BE AD ， BEG DAG ∴，13112332)122)33GE BE AG AD GE AG G cm cm cm c E HE GH a m AB a ∴==⎫∴==+⎪⎪⎝⎭=-=-⎫∴+=-⎪⎪⎝⎭∴=∴==，，，，． 【点睛】 本题属于四边形综合题，是填空题压轴题，考查了正方形的性质，相似三角形的判定与性质，等腰三角形的性质，勾股定理，解决本题的关键是CE= 2BE ，BF=2DF 的利用以及这些性质的熟记．5．（1）点P 在△O 上，点Q 在△O 外；（2）PB2（3−1【分析】（1）如图△中，根据圆周角与圆心角的关系即可判断；（2）如图2中，造等腰直角三角形△AOD，与O为圆心作△O交BC于P、P′，易知△APD ＝△AP′D＝45°．求出BP′和BP的长即可解决问题；（3）作线段AD的垂直平分线，交AD于E，交BC于F，点O在EF上，以OA为半径作△O，当△O与BC相切于点P时，△APD最大，求出此时BP的值即可；【详解】解：（1）如图△中，△AOB＝45°，△△APB＝12△点P在△O上，△△AQB＜45°，△点Q在△O外．故答案为点P在△O上，点Q在△O外．（2）如图2中，如图构造等腰直角三角形△AOD，与O为圆心，OA为半径作△O交BC于P、P′，易知△APD＝△AP′D＝45°．延长DO交BC于H，△△DAB＝135°，△DAO＝45°，△△OAB＝△B＝90°，△OA△BC，△△DOA＝△OHB＝90°，△四边形ABHO是矩形，△AB＝OH＝1，OA＝BH，△AD＝△OA＝OD＝OP＝OP′＝2，在Rt△OPH和Rt△OP′H中，易知HP＝HP′=，△BH＝OA＝2，△BP′＝，PB＝2（3）如图△中，存在．作线段AD的垂直平分线，交AD于E，交BC于F，点O在EF上，以OA为半径作△O，当△O与BC相切于点P时，△APD最大，理由：在BC上任意取一点M，连接MA、MD，MD交△O于N，连接AN．△△AND＞△AMD，△APD＝△AND，△△APD＞△AND，连接OP，延长DA交CB的延长线于点G．△AB△BC，△DAB＝135°，△△G＝△EFG＝45°，△△ABG，△EFG都是等腰直角三角形，△AB＝BG＝1，△AG△AD＝OE△AD，△AE＝ED△EG＝EF＝GF EG＝4，设OP ＝PF ＝r ，则OF，OE ＝EF −OF ＝， 在Rt △AOE 中，AE 2＋OE 2＝OA 2，△()222+r =，解得r ＝或4（舍弃）， △BP ＝GF −GB −PF ＝4−1−r−1． 【点睛】本题考查圆综合题、圆周角与圆心角的关系、点与圆的位置关系、矩形的判定和性质、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，利用辅助圆解决问题．6．（1）()1,1-；（2）1k =-;（3）当34m <<时，12y y >，当4m =时，12y y =当45m <≤时，12y y >【分析】（1）将m 3=代入解析式，进而化为顶点式即可求得抛物线的顶点坐标；（2）联立抛物线与直线解析式，根据题意，令0∆=，根据结果与m 无关，令m 的系数为0，即可求得k 的值；（3）先根据顶点公式求得抛物线的顶点为21613,24m m m ⎛⎫--+- ⎪⎝⎭，根据旋转可得四边形ODHC 是正方形，进而根据坐标与图形的关系求得24114m m PH -+=，根据24PH <≤，又1m ，求得m 的范围，由()14,A m y +，()22,B m y 是抛物线()()213y x m x m =--+-上不同的两点，求得12,y y ，进而根据函数图像比较1y ，2y 之间的大小． 【详解】 （1）3m =()22211y x x x ∴=-=--∴这条抛物线的顶点坐标为()1,1-；（2）()()21334y x m x m m y x m k m ⎧=--+-⎪⎨⎛⎫=-++ ⎪⎪⎝⎭⎩即()2313()4m x m x m x m k m--+-=-++ ()22104m x mx k m -+++=若无论m 取何值，抛物线与直线34m y x m k m ⎛⎫=-++ ⎪⎝⎭（k 为常数）有且仅有一个公共点，∴0∆=()224104m m k m ⎡⎤∴-⨯++=⎢⎥⎣⎦即1k =- （3）122b m a --=， ()2224(3)14613444m m ac b m m -----+-==， ∴抛物线的顶点为21613,24m m m ⎛⎫--+- ⎪⎝⎭将抛物线的对称轴绕坐标原点O 逆时针旋转90︒得到直线a ，过抛物线顶点P 作PH a ⊥于H ，如图，设PH 交x 轴于点C ，a 交y 轴于点D ，设点P 旋转后的对应点为P '，根据旋转的性质可得 OCP ODP '△≌△，则OC OD =，PH a ⊥，PH x ⊥轴，90DOC ∠=︒∴四边形ODHC 是矩形OC OD=∴四边形ODHC是正方形，∴PH HC CP=+,2161324m m mPH--+-∴=-24114m m-+=()22411270m m m-+=-+≥24114m mPH-+∴=24PH<≤，又1m∴224304501m mm mm⎧-+>⎪--≤⎨⎪>⎩即3,1151m mmm><⎧⎪-≤≤⎨⎪>⎩35m∴<≤()14,A m y+，()22,B m y是抛物线()()213y x m x m=--+-上不同的两点，()()()()214413617y m m m m m∴=+-+-+-=+()()()2222213233y m m m m m m=--+-=+-223332()48y m=+-即当34m≥-时，y随m的增大而增大，∴当35m<≤，y随m的增大而增大，当42m m+=，即4m=时，,A B两点重合，根据图像可知，4m <时，12y y > 当4m =时，12y y = 当4m >时，12y y >35m <≤∴当34m <<时，12y y >，当4m =时，12y y =当45m <≤时，12y y >【点睛】本题考查了二次函数综合，求抛物线顶点坐标，二次函数与一元二次方程的关系，与不等式的关系，二次函数的性质，正方形的性质，熟练掌握二次函数图象的性质是解题的关键． 7．（1）=；（2）见解析；（3）60︒，DB CE =；（4）90︒，2AM BD CD += 【分析】（1）根据等腰三角形的性质即可得到DB EC =；（2）由旋转得到的结论判断出DAB EAC ∆≅∆，得到DB CE =；（3）根据等边三角形的性质和全等三角形的判定定理证明DAB EAC ∆≅∆，根据全等三角形的性质求出结论；（4）根据全等三角形的判定和性质和等腰直角三角形的性质即可得到结论． 【详解】解：（1）AD AE =，AB AC =，AB AD AC AE ∴-=-，即BD CE =故答案为：=， （2）成立．理由：由旋转性质可知DAB EAC ∠=∠，在DAB ∆和EAC ∆中AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩，()DAB EAC SAS ∴∆≅∆，DB CE ∴=；（3）如图△，设AB ，CD 交于O ， ABC ∆和ADE ∆都是等边三角形，AD AE ∴=，AB AC =，60∠∠︒DAE BAC ==，DAB EAC ∴∠=∠，在DABDAB ∆和EAC ∆中AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩，()DAB EAC SAS ∴∆≅∆，DB CE ∴=，ABD ACE ∠=∠， BOD AOC ∠=∠，60CDB BAC ∴∠=∠=︒；故答案是：60︒，DB CE =； （4）DAE ∆是等腰直角三角形，45AED ∴∠=︒， 135∴∠=︒AEC ，在DAB ∆和EAC ∆中AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩，()DAB EAC SAS ∴∆≅∆，135ADB AEC ∴∠=∠=︒，BD CE =，45ADE ∠=︒，90BDC ADB ADE ∴∠=∠-∠=︒，ADE ∆都是等腰直角三角形，AM 为ADE ∆中DE 边上的高，AM EM MD ∴==， 2AM BD CD ∴+=；故答案为：90︒，2AM BD CD +=； 【点睛】本题是几何变换综合题，主要考查了旋转和全等三角形的性质和判定，旋转过程中面积变化分析，解题的关键是掌握三角形全等的判定． 8．（1）3c ≤-；（2）21y x =-；（3）见解析 【分析】（1）由－1＜x ＜3中，恒有y ＜0，得出1x =-或3x =时，函数值不大于0，列不等式组即可求得c 的范围；（2）令0y =，设12,x x 是方程20ax bx c ++=的两根，则()()()12,0,00,A x B x C c ，，，根据题意，90C ∠=︒，120x x <<，证明AOC COB ∽，可得212c x x =-，根据根与系数的关系可得2c c a =-，即1ac =-，由顶点D 的纵坐标为－1，2241144b b a +==+≥，计算121=2ABC S c x x ⨯⋅-，根据1a ≥可得1ABC S ≤，进而确定,,a b c 的值，即可求得解析式；（3）根据已知条件，设抛物线的解析式为()22y a x =-，将（0，解析式)22y x =-，设直线2y kx k =+与抛物线交于点P 、Q ，()(),,,P P Q Q P x y Q x y ，联立直线与抛物线解析式，利用根与系数的关系求得,P Q P Q x x x x +=，根据题意求得直线MQ 的直线解析式，进而求得N 的纵坐标，将)22Q Q y x =-，代入N y ，根据,P Q P Q x x x x +=计算即可求得N 的纵坐标为一定值，进而即可得证． 【详解】（1）当1a =且1b c =+时，()21y x c x c =+++，－1＜x ＜3中，恒有y ＜0，1x ∴=-或3x =时，函数值不大于0，即()()()()2211103310c c c c ⎧-++⨯-+≤⎪⎨+++≤⎪⎩3c ∴≤-（2）令0y =，设12,x x 是方程20ax bx c ++=的两根，则()()()12,0,00,A x B x C c ，， 抛物线与x 轴交于A 、B 两点，与y 轴交于点C ，△ABC 是直角三角形，90C ∴∠=︒，120x x <<如图，90AOC BOC ACB ∴∠=∠=∠=︒ 90,90ACO A A B ∴∠+∠=︒∠+∠=︒B ACO ∴∠=∠ AOC COB ∴∽OC AOOB CO∴= 2CO AO BO ∴=⋅12,,OA x OB x OC c =-==- 212c x x ∴=-1212,b cx x x x a a +=-=2cc a∴=-0c ≠1c a∴=-即1ac =-顶点D 的纵坐标为－1，2414ac b a -∴=-244a b ∴=+2241144b b a +∴==+≥121=2ABCS c x x ∴⨯⋅-=====1ABCS∴≤此时1,0,1a b c ===-∴抛物线的解析式为21y x =-（3）抛物线与x 轴只有一个公共点M （2，0），与y 轴交于（0，∴设抛物线的解析式为()22y a x =-，将（0，得()202a -解得a =∴抛物线的解析式为)222y x =-=-+设直线2y kx k =+与抛物线交于点P 、Q ， 设()(),,,P P Q Q P x y Q xy联立得22kx k x +=-+()2240k x k -+=,P Q P Q x x x x ∴+= 设MQ 的直线解析式为y mx n =+，将()2,0M ，(),Q Q Q x y 代入得20Q Q m n mx n y +=⎧⎨+=⎩解得222Q Q Q Q y m x y n x ⎧=⎪-⎪⎨⎪=-⎪-⎩∴直线MN 的解析式为222Q Q Q Q y y y x x x =---过点P 且与y 轴平行的直线与直线MQ 相交于点N ， 当P x x =时， N y =222Q Q P Q Q y y x x x ---()22Q P Q y x x =--)2322Q Qy x =-))()222222P N Q Q P Q x y x x x x -∴=---- ()24P Q P Q x x x x⎤=-++⎦24⎤⎛⎫=-+⎥ ⎪⎪⎢⎥⎝⎭⎣⎦ =-∴对于每个给定的实数k ，点N的纵坐标均为定值-【点睛】本题考查了二次函数综合，待定系数法求解析式，一次函数与抛物线交点，不等式组的应用，一元二次方程根与系数的关系，直角三角形的性质，相似三角形的性质与判定，二次函数最值问题，综合运用以上知识是解题的关键． 9．（1）证明见解析；（2）证明见解析，（3）BF =． 【分析】（1）连接OA 并延长AO 交BC 于E ，证明△BAC =2△BAE 和△ABD =△BAE 即可得结论， （2）利用直角三角形两锐角互余、圆周角定理进行导角，得出MCG △和△FCG 是等腰三角形，得出BM =MC =FG =CG ，MH =HG ，进而由BF =BM +MH -FH =FG -FH +HG ，得出结论； （3）过O 点作OP △AC ，由垂径定理得出12PD =，再由52ABO ADOS AB BO S AD OD ===和平行线分线段成比例定理求出7724DH DP ==，由勾股定理进而可求BH ，再利用相似三角形对应边成比例求出HG ，即可得BF 长． 【详解】解：（1）连接OA 并延长AO 交BC 于E ，△AB =AC ， △AB AC =， △AE 过圆心O ， △AE BC ⊥，BE EC =， △△BAC =2△BAE ， △OA =OB ， △△ABD =△BAE ， △△BAC =2△ABD ；（2）如解图（2），连接OA 并延长AO 交BC 于E ，AE 交BF 于M ，连接MC ， 设2BAC α∠=，则ABD BAE EAC α∠=∠=∠=△AE =EC ，AE △BC ，△BM =MC ，△△MBC =△MCB ，△BG △AC ，AE △BC ，△△EAC +△ACE =90°，△HBC +△ACE =90°，△EAC HBC MCB α∠=∠=∠=，△2CMG MBC MCB α∠=∠+∠=，△BC BC =，△2G BAC α∠=∠=，△△G =△CMG ，△CG =CM =BM ，△AC △BG ，△MH =HG ，△OA =OC ，△ACO EAC α∠=∠=△9090CFG ACO α∠=︒-∠=︒-，△180FCG CFG G ∠=︒-∠-∠，即180(90)290FCG ααα∠=︒-︒--=︒-，△FCG CFG ∠=∠，△FG =CG ，△BM =MC =FG =CG ，又△MH =HG ，△BF =BM +MH -FH =FG -FH +HG ，△BF =2HG ．（3）过O 点作OP △AC ，如解图（3）△AO 是△BAC 的角平分线，△点O 到AB 、AC 的距离相等， △ABO ADO SAB BO S AD OD==， △AD =2，CD =3，△AB =AC =5， △5=2BO OD ，即：2=7OD BD ， △OP △AC ，△52AP PC ==，12PD =， △BH AC ⊥， △OP //BH ，△27DP OP OD DH BH BD ===， △7724DH DP ==， △154AH AD DH =+=，5-4HC DC DH ==，△在Rt ABH中，BH == △BAH G ∠=∠，AHB GHC ∠=∠， △AHB GHC △△，△AH BH HG CH = 即：AH HC BHHG =， 51544=⨯， △HG =， 由（2）得BF =2HG ，△BF =【点睛】本题是圆的综合题，主要考查了圆周角定理，涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点，解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系，从而利用相似或勾股定理解题．10．（1（2）FD ，30；（3）【分析】（1）设菱形ABCD 边长=2AB a ，由菱形性质和已知得出30ABD ∠=︒，60BAO ∠=︒，=BF FD AB =，再由含30度角的直角三角形的性质求出=BF FD AB =，1=2AE EF BE AB a ===，进而求得AE FD 的值；（2）菱形ABCD 的边长为2a ，由BGC 是等腰直角三角形CG ==，再已知菱形的条件，求出BOF 是等腰直角三角形，继而得出BF DF ==，从而求出FD =，由B 、D 是关于AC 的轴对称可知15CDF CBF ∠=∠=︒，再由三角形外角的性质可得直线CG 与DF 所夹锐角的度数为30；（3）利用半角模型将BCF △逆时针旋转60°到BAM 位置，从而得出BNF BNM ≅（SAS ），得到一个由CF 、NF 、AN 三条线段长组成的三角形，而且有内角为120°，从而确定三条线段关系，再利用中位线定理和三角形相似在菱形中得出NF 、AN 与菱形边长关系，求出菱形边长即可解答．【详解】解：（1）设菱形ABCD 边长=2AB a ，△在菱形ABCD 中，120BCD BGF ∠=∠=︒，△AC BD ⊥， 60ABC ∠=︒，120BAD ∠=︒，△30ABD ∠=︒，60BAO ∠=︒，=BF FD AB =， △在四边形EBGF 是菱形，120BGF ∠=︒，BE EF =，∴30EBH EFH ∠=∠=︒，60AFE ∴∠=︒，△=60AFE EAO ∠=∠︒，△AE EF =，△1=2AE EF BE AB a ===，AE FD ∴==（2）FD =，直线CG 与DF 所夹锐角的度数为30．理由如下，如图，连接BF ，延长GC 交FD 于N ，设菱形ABCD 的边长为2a ，△CG BG ⊥，且CG BG =，△=45GBC GCB ∠=∠︒，CG == △60GBE ∠=︒，△四边形EBGF 是菱形， 120BGF ∠=︒，1=302GBF BFG GBE ∴∠=∠∠=︒， △15CBF GBC GBF ∠=∠-∠=︒，△301545OBF OBC CBF ∠=∠+∠=︒+︒=︒，△AC BD ⊥，BO DO =，△45BFO OBF ∠=∠=︒，BF DF =，由（2）可知：BO =，△BF DF ==，△DF ，由B 、D 是关于AC 的轴对称可知，15CDF CBF ∠=∠=︒，又△18015DCN BCG BCD ∠=︒-∠-∠=︒，△30GNF CDF DCN ∠=∠+∠=︒，即直线CG 与DF 所夹锐角的度数为30；（3）BP =过程如下：依题意，作出图形，此时B 、E 、P 三点共线，连接BF ，并将线段BF 绕点B 逆时针旋转60°到BM 位置，连接MG 、MA ，△=60CBA FBM ∠=∠︒，BC BA =△BCF BAM ≅（SAS ）△AM=CF=2，60MAB FCB ∠=∠=︒， △1302EBF GBE ∠=∠=︒， △-30MBN FBM FBN ∠=∠∠=︒，△30MBG FBG ∠=∠=︒，△BNF BNM ≅（SAS ），△=FN MN过M 点作MH △CH ，△60BAO ∠=︒，△60MAH ∠=︒，30HMA ∠=︒，△112AH AM ==，MH == 取OD 的中点Q ，连接QP ，△AP =PD ，△12PQ OA =，//PQ OA ， △BNO BPQ ~， △2233NO BO OQ PQ BQ OQ ===， △2133NO PQ OA ==， 设菱形ABCD 的边长为2a ，则12AO CO AB a ===， △1233AN AO ON a a a =-=-=， 142233MN FN CO ON CF a a a ==+-=+-=-， 213NH NA AH a =+=+， 在Rt MGH 中，222NH MH MN +=，△222241233a a ⎛⎫⎛⎫++=- ⎪ ⎪⎝⎭⎝⎭， 解得1=0a （舍去），2=3a ，△1322PQ a ==，32BQ OD ===， △在Rt BPQ 中，222BQ PQ BP +=，△223)2BP += 【点睛】本题是几何旋转综合题，主要考查了菱形的性质、旋转全等、30°直角三角形性质和勾股定理解三角形等，解题关键是利用特殊角进行计算得出其他角度数，利用旋转得到由CF 、NF 、AN 三条线段长组成的三角形，而且有内角为120°，从而通过已知计算．11．（1）()；（2）()2111601166m t t t =-+<<；（3）⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭ 【分析】(1)根据题意得，△OBP =90°，OB =6，在Rt △OBP 中，由△BOP =30°，如图，过点B ′作B M OA '⊥于M 点，根据折叠可得30,6,B OP BOP OB OB ''∠=∠=︒==推出30,B OM ∠=︒'得到13,2B M OB ''==再利用勾股定理求出OM 的长，即可求得答案； (2）由△O B 'P 、△QC 'P 分别是由△OBP 、△QCP 折叠得到的，可知△O B 'P ≅△OBP ，△Q C '。

(完整版)浙江中考数学压轴题汇编

(完整版)浙江中考数学压轴题汇编

压轴汇编1。

某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下:第k 棵树种植在点)(k k k y x P ，处，其中11=x ，11=y ，当k ≥2时，⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ，［a ]表示非负实数a 的整数部分，例如［2。

6］=2，[0.2］=0。

按此方案，第2009棵树种植点的坐标为A 。

(5，2009） B.（6，2010) C 。

（3，401） D(4，402） 2。

以正方形ABCD 的BC 边为直径作半圆O , 过点D 作直线切半圆于点F , 交AB 边于点E . 则三角形ADE 和直角梯形EBCD 周长之比为（A) 3:4 （B) 4:5 (C) 5:6 (D ） 6：73。

设1x ，2x 是关于x 的方程02=++q px x 的两根,11+x ，12+x 是关于x 的方程02=++p qx x 的两根，则p ，q 的值分别等于（ ）（A ）1，—3 (B ）1，3 （C ）—1,—3 （D ）-1，34. 如图，在Rt ΔABC 中,AF 是斜边上的高线,且BD=DC=FC=1,则AC 的长为 （A ）32 （B ）3 （C ）2 (D)334 4 55。

如图,在等腰Rt ABC 中，AC=BC,以斜边AB 为一边作等边ABD ,使点C,D 在AB 的同侧;再以CD 为一边作等边CDE ，使点C ，E 落在AD 的异侧.若AE=1,则CD 的长为 ( ）（A)31- (B)312- (C)62- （D ）622-填空1。

如图，矩形ABCD （AD ＞AB ）中,AB ＝a ，∠BDA ＝θ，作AE 交BD 于E ，且AE ＝AB ,试用a 与θ表示：AD ＝______，BE ＝_______．2。

根据指令［s,A](s ≥0,0º〈A<180º），机器人在平面上能完成下列动作：先在原地逆时针旋转角度A ，再朝其面对的方向沿直线行走距离s.现机器人在直角坐标系的坐标原点，且面对x 轴正方向。

2024年中考数学考前押题密卷(浙江卷)(全解全析)

2024年中考数学考前押题密卷(浙江卷)(全解全析)

2024年中考考前押题密卷（浙江卷）数学·全解全析第Ⅰ卷一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）1．下列手机中的图标是轴对称图形的是（）A．B．C．D．【答案】C【分析】根据轴对称图形的概念，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，进行判断即可．【解析】解：A．不是轴对称图形，故此选项不合题意；B．不是轴对称图形，故此选项不合题意；C．是轴对称图形，故此选项符合题意；D．不是轴对称图形，故此选项不合题意．故选：C．【点睛】本题考查的是轴对称图形的概念，正确掌握相关定义是解题关键．2．已知，则的值为（）A．B．C．12D．18【答案】B【分析】根据二次根式的被开方数是非负数，由非负数的性质列式求出x的值；然后将x的值代入求出y的值，最后代入待求式，进行计算即可．【解析】解：由题意得：，解得x＝3，把x＝3代入，可得y＝3，所以＝＝．故选：B．【点睛】本题考查二次根式有意义的条件，关键是掌握二次根式有意义的条件以及求代数式的值的方法．3．下列运算结果正确的是（）A．m2+m2＝2m4B．a2•a3＝a5C．（mn2）3＝mn6D．m6÷m2＝m3【答案】B【分析】直接利用合并同类项法则、同底数幂的乘除运算法则、积的乘方运算分别计算，进而判断得出答案．【解析】解：A．m2+m2＝2m2，故此选项不合题意；B．a2•a3＝a5，故此选项符合题意；C．（mn2）3＝m3n6，故此选项不合题意；D．m6÷m2＝m4，故此选项不合题意．故选：B．【点睛】此题主要考查了合并同类项、同底数幂的乘除运算、积的乘方运算，正确掌握相关运算法则是解题关键．4．在五边形ABCDE中，∠A＝∠E＝120°，∠B＝130°，∠C＝70°，则∠D＝（）A．100°B．110°C．120°D．130°【答案】A【分析】根据多边形内角和公式解题即可．【解析】解：多边形的内角和为180°×（n﹣2），∴五边形ABCDE的内角和为180°×（5﹣2）＝540°，∴∠D＝540°﹣∠A﹣∠B﹣∠C﹣∠E＝540°﹣120°﹣130°﹣70°﹣120°＝100°．故选：A．【点睛】本题主要考查了多边形的内角和求法，关键是多边形内角和公式的应用．5．下列调查适合做普查的是（）A．调查游客对我市景点的满意程度B．调查我省中小学生的身高情况C．调查九年级（3）班全班学生本周末参加社区活动的时间D．调查我市中小学生保护水资源的意识【答案】C【分析】全面调查是对需要调查的对象逐个调查，这种调查能够收集全面、广泛、可靠的资料，但调查费用较高，时间延续较长，适合于较小的调查范围，抽样调查适合于较广的调查范围，据此可得到结．【解析】解：A、调查游客对我市景点的满意程度，范围较广，适合于抽样调查，该选项不符合题意；B、调查我省中小学生的身高情况，人数多，范围广，适合于抽样调查，该选项不符合题意；C、调查九年级（3）班全班学生本周末参加社区活动的时间，人数少，范围小，适合于全面调查，即普查，该选项符合题意；D、调查我市中小学生保护水资源的意识，人数多，范围广，适合于抽样调查，该选项不符合题意；故选：C．【点睛】本题考查了判断全面调查与抽样调查，了解全面调查与抽样调查的区别是解题的关键．6．一个正棱柱的正（主）视图和俯视图如图所示，则该三棱柱的侧（左）视图的面积为（）A．8B．16C．8D．8【答案】A【分析】求出正三棱锥底面边长的高，然后求解侧视图的面积．【解析】解：由题意可知，底面三角形是正三角形，边长为4，高为2，所以侧视图的面积为：4×＝8．故选：A．【点睛】本题考查三视图求解几何体的侧视图，求解底面三角形的高是解题的关键，是基础题．7．如图，为做好疫情防控，小航同学在超市帮妈妈买回一袋纸杯，他把纸杯整齐地叠放在一起，请根据图中信息，如果把这50个纸杯整齐叠放在一起时，它的高度为（）A．56cm B．57cm C．58cm D．59cm【答案】B【分析】根据题中所给图形，求出一个杯子高度及叠放后每个杯子漏出部分的高度即可得到答案．【解析】解：由图可知，右边8个杯子叠放高度比左边3个杯子高15﹣10＝5（cm），∴杯子叠放后每个杯子漏出来部分的高度为5÷5＝1cm，则一个杯子高度为10﹣2＝8（cm），∴把这50个纸杯整齐叠放在一起时，它的高度为8+49＝57（cm），故选：B．【点睛】本题考查数学知识解决实际问题，读懂题意，数形结合，分析出叠放后每个杯子漏出来部分的高度是解决问题的关键．8．将一副三角板如图放置，则下列结论中正确的是（）①如果∠2＝30°，则有AC∥DE；②∠BAE+∠CAD＝180°；③如果BC∥AD，则有∠2＝45°；④如果∠CAD＝150°，必有∠4＝∠C．A．①②③B．③④C．①②④D．①②③④【答案】D【分析】根据平行线的性质与判定，余角的性质，等逐项分析并选择正确的选项即可．【解析】解：①∵∠2＝30°，∴∠1＝60°，∴∠1＝∠E，∴AC∥DE，故①正确；②∵∠1+∠2＝90°，∠2+∠3＝90°，∴∠BAE+∠CAD＝∠2+∠1+∠2+∠3＝90°+90°＝180°，故②正确；③∵BC∥AD，∴∠1+∠2+∠3+∠C＝180°，又∵∠C＝45°，∠1+∠2＝90°，∴∠3＝45°，∴∠2＝90°﹣45°＝45°，故③正确；④∵∠CAD＝150°，∠DAE＝90°，∴∠1＝∠CAD﹣∠DAE＝150°﹣90°＝60°，∵∠E＝60°，∴∠1＝∠E，∴AC∥DE，∴∠4＝∠C，故④正确；故选：D．【点睛】本题考查三角板中的角度计算，平行线的性质与判定，能够掌握数形结合思想是解决本题的关键．9．在学习勾股定理时，甲同学用四个相同的直角三角形（直角边长分别为a，b，斜边长为c）构成如图所示的正方形；乙同学用边长分别为a，b的两个正方形和长为b，宽为a的两个长方形构成如图所示的正方形，甲、乙两位同学给出的构图方案，可以证明勾股定理的是（）A．甲B．乙C．甲，乙都可以D．甲，乙都不可以【答案】A【分析】由图形中的面积关系，应用完全平方公式即可解决问题．【解析】解：甲同学的方案：∵大正方形的面积＝小正方形的面积+直角三角形的面积×4，∴（a+b）2＝c2+ab×4，∴a2+b2+2ab＝c2+2ab，∴a2+b2＝c2，因此甲同学的方案可以证明勾股定理；乙同学的方案：∵大正方形的面积＝矩形的面积×2+两个小正方形的面积，∴（a+b）2＝a2+2ab+b2，∴得不到a2+b2＝c2，因此乙同学的方案不可以证明勾股定理．故选：A．【点睛】本题考查勾股定理的证明，关键是应用面积法，完全平方公式．10．如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边分别作正方形BAHI，正方形BCFG与正方形CADE，延长BG，FG分别交AD，DE于点K，J，连结DH，IJ．图中两块阴影部分面积分别记为S1，S2．若S1：S2＝1：4，S四边形边BAHE＝18，则四边形MBNJ的面积为（）A．5B．6C．8D．9【答案】B【分析】先证△CAB≌△DAH（SAS），得∠ADH＝90°，则H、D、E三点共线，再证＝，则BC ＝FC＝FG＝BG＝2GJ，AC＝AD＝DE＝CE＝BC+GJ＝3GJ，然后由S四边形BAHE＝S△ADH+S梯形ADEB＝18，求出GJ＝，证△FAN≌△EBM（ASA），则S△FAN＝S△EBM，最后由S四边形MBNJ ＝S矩形CFJE﹣S四边形BCFN﹣S△EBM＝S矩形CFJE﹣S△ABC，即可得出结果．【解析】解：∵四边形BAHI和四边形CADE都是正方形，∴AC＝AD，AB＝AH，∠CAD＝∠ABI＝∠BAH＝∠ADE＝90°，∴∠CAB+∠BAD＝∠DAH+∠BAD，∴∠CAB＝∠DAH，在△CAB和△DAH中，，∴△CAB≌△DAH（SAS），∴∠ADH＝∠ACB＝90°，∵∠ADE＝90°，∴H、D、E三点共线，∵四边形BCFG和四边形CADE都是正方形，延长BG、FG分别交AD、DE于点K、J，∴四边形ADJF和四边形BEDK都是矩形，且AF＝BE，∠AFN＝∠BEM＝90°，四边形DKGJ是正方形，四边形CFJE是矩形，∵S1：S2＝1：4，∴＝，∴BC＝FC＝FG＝BG＝2GJ，∵四边形CADE是正方形，∴∠ADE＝90°，AC＝AD＝DE＝CE＝BC+GJ＝3GJ，在Rt△ACB中，由勾股定理得：AB＝＝＝GJ，在Rt△ADH中，由勾股定理得：DH＝＝＝2GJ，∵S四边形BAHE＝S△ADH+S梯形ADEB＝18，∴AD•DH+（AD+BE）•DE＝×3GJ×2GJ+（3GJ+GJ）×3GJ＝18，解得：GJ＝（负值已舍去），∵∠ABC+∠EBM＝180°﹣∠ABI＝180°﹣90°＝90°，∠ABC+∠CAB＝90°，∴∠CAB＝∠EBM，即∠FAN＝∠EBM，在△FAN和△EBM中，，∴△FAN≌△EBM（ASA），∴S△FAN＝S△EBM，∴S△ABC＝S四边形BCFN+S△FAN＝S四边形BCFN+S△EBM，∴S四边形MBNJ＝S矩形CFJE﹣S四边形BCFN﹣S△EBM＝S矩形CFJE﹣S△ABC＝FC•CE﹣AC•BC＝2GJ×3GJ﹣×3GJ×2GJ＝3GJ2＝3×（）2＝6，故选：B．【点睛】本题考查了勾股定理、正方形的判定与性质、矩形的判定与性质、全等三角形的判定与性质、矩形面积、梯形面积与三角形面积的计算等知识，证明△FAN≌△EBM是解题的关键．第Ⅱ卷二、填空题（本大题共6个小题，每小题4分，共24分）11．分解因式6xy2﹣3x2y＝．【答案】3xy（2y﹣x）【分析】原式提取公因式3xy即可．【解析】解：原式＝3xy（2y﹣x）．故答案为：3xy（2y﹣x）．【点睛】此题考查了因式分解﹣提公因式法，熟练掌握提取公因式的方法是解本题的关键．12．如图，▱ABCD的对角线AC、BD相交于点O，AC+BD＝22，AB＝9．则△OCD的周长为．【答案】20【分析】由平行四边形的性质得OC＝AC，OD＝BD，CD＝AB＝9，则OC+OD＝（AC+BD）＝11，即可求出OC+OD+CD的值．【解析】解：∵四边形ABCD是平行四边形，对角线AC与BD交于点O，∴OC＝OA＝AC，OD＝OB＝BD，CD＝AB＝9，∵AC+BD＝18，∴OC+OD＝（AC+BD）＝×22＝11，∴OC+OD+CD＝11+9＝20，∴△OCD的周长为20，故答案为：20．【点睛】此题重点考查平行四边形的性质、三角形的周长等知识，证明OC＝AC，OD＝BD，并且求得OC+OD＝11是解题的关键．13．如图，将等腰△ABC（∠A是锐角）沿BD对折，使得点A落在射线BC上的E点处，再将△DCE沿CD 对折得到△DCF，若DF刚好垂直于BC，则∠A的大小为°．【答案】45【分析】由等腰三角形的性质可得∠ABC＝∠ACB，由折叠的性质可得∠A＝∠E＝∠F，∠DCE＝∠DCF，由外角性质可求∠BCF＝∠A＝∠E＝∠F，由直角三角形的性质可求解．【解析】解：∵AB＝AC，∴∠ABC＝∠ACB，∵将等腰△ABC（∠A是锐角）沿BD对折，使得点A落在射线BC上的E点处，∴∠A＝∠E，∵将△DCE沿CD对折得到△DCF，∴∠E＝∠F，∠DCE＝∠DCF，∵∠DCE＝∠ABC+∠A，∠DCF＝∠ACB+∠BCF，∴∠BCF＝∠A，∴∠BCF＝∠A＝∠E＝∠F，∵DF⊥BC，∴∠BCF＝∠F＝45°，∴∠A＝45°，故答案为：45．【点睛】本题考查了翻折变换，等腰三角形的性质，外角的性质，灵活运用折叠的性质是本题的关键．14．已知一组数据x1，x2，x3，x4，x5的方差是，那么x1﹣5，x2﹣5，x3﹣5，x4﹣5，x5﹣5的方差是．【答案】【分析】方差是用来衡量一组数据波动大小的量，每个数都减去5所以波动不会变，方差不变．【解析】解：由题意知，原数据的平均数为，新数据的每一个数都减去了5，则平均数变为﹣5，则原来的方差＝[（x1﹣）2+（x2﹣）2+…+（x5﹣）2]＝，现在的方差＝[（x1﹣5﹣+5）2+（x2﹣5﹣+5）2+…+（x5﹣5﹣+5）2]＝[（x1﹣）2+（x2﹣）2+…+（x5﹣）2]＝，所以方差不变．故答案为：．【点睛】本题考查了方差，本题说明了当数据都加上一个数（或减去一个数）时，方差不变，即数据的波动情况不变．15．直线y＝kx+6k交x轴于点A，交y轴于点B，以原点O为圆心，3为半径的⊙O与l相交，则k的取值范围为．【答案】﹣＜k＜【分析】根据题意得到A（﹣6，0），B（0，6k），设⊙O于AB相切于C，连接OC，求得∠OAC＝30°，于是得到结论．【解析】解：∵直线y＝kx+6k交x轴于点A，交y轴于点B，∴A（﹣6，0），B（0，6k），设⊙O与AB相切于C，连接OC，∴OA＝6，OC＝3，∠ACO＝90°，∴OC＝OA，∴∠OAC＝30°，当⊙O与l相交时，OB＝|6k|＜2，∴﹣＜k＜，故答案为﹣＜k＜．【点睛】本题考查了直线与圆的位置关系，一次函数图象与系数的关系，正确的作出图形是解题的关键．16．在二次函数y＝x2﹣2tx+3中，t为大于0的常数．（1）若此二次函数的图象过点（2，1），则t等于；（2）如果A（m﹣2，a），B（4，b），C（m，a）都在此二次函数的图象上，且a＜b＜3，则m的取值范围是．【答案】（1）；（2）3＜m＜4或m＞6【分析】（1）将（2，1）代入y＝x2﹣2tx+3计算得出t值即可；（2）先根据点AC的纵坐标相等，可得对称轴x＝t＝m﹣1，再分两种情况讨论得出结果即可．【解析】解：（1）将（2，1）代入y＝x2﹣2tx+3得：1＝4﹣4t+3，解得：t＝，故答案为：．（2）∵A（m﹣2，a），C（m，a）都在二次函数图象上，∴二次函数y＝x2﹣2tx+3的对称轴为直线x＝t＝＝m﹣1，∵t＞0，∴m﹣1＞0，解得m＞1，∵m﹣2＜m，∴A点在对称轴左侧，C点对称轴右侧，在二次函数y＝x2﹣2tx+3中，令x＝0，y＝3，∴抛物线与y轴的交点坐标为（0，3），∴点（0，3）关于对称轴对称点的坐标为（2m﹣2，3），∵b＜3，∴4＜2m﹣2，解得m＞3，①当点A（m﹣2，a），B（4，b）都在对称轴左侧时，∵y随x的增大而减小，且a＜b，∴4＜m﹣2，解得m＞6，此时m满足的条件为：m＞6；②当点A（m﹣2，a）在对称轴左侧，点B（4，b）在对称轴右侧时，∵a＜b，∴点B（4，b）到对称轴的距离大于点A到对称轴的距离，∴4﹣（m﹣1）＞m﹣1﹣（m﹣2），解得：m＜4，此时，m满足的条件是：3＜m＜4，综上分析，3＜m＜4或m＞6．故答案为：3＜m＜4或m＞6．【点睛】本题考查了二次函数的性质，解题的关键是分类讨论．三、解答题（本大题共8个小题，共66分．解答应写出文字说明，证明过程或演算步骤）17．以下是某同学化简分式的部分运算过程：解：原式＝……第一步＝第二步＝．……第三步……（1）上面第二步计算中，中括号里的变形的依据是通分；（2）上面的运算过程中第三步出现了错误；（3）请你写出完整的正确解答过程，并从﹣2，2，0中选一个作为x的值代入求值．【分析】（1）根据分式的性质，即可求解；（2）根据分式的运算法则：先乘方，再加减，最后乘除，有括号先算括号里面的计算即可；（3）取x＝0，代入计算即可．【解析】解：（1）上面第二步计算中，中括号里的变形是通分，通分的依据是分式的基本性质，故答案为：通分；（2）第三步出现错误，原因是分子相减时未变号，原式＝[﹣]×，＝[﹣]×，＝×，＝×，＝．故答案为：三．（3）当x＝0时，上式＝＝．【点睛】本题主要考查了分式的混合运算，熟练掌握分式的运算法则是解决本题的关键．18．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（﹣1，5），B（﹣4，3），C（﹣2，2）．（1）△A1B1C1与△ABC关于原点O成中心对称，画出△A1B1C1，并写出点A1，B1，C1的坐标；（2）将△ABC绕原点O顺时针旋转90°得到△A2B2C2，画出△A2B2C2；（3）求（2）的旋转过程中点C经过的路径长．【分析】（1）利用中心对称的性质分别作出A，B，C的对应点A1，B1，C1，再顺次连接，写出点A1，B1，C1的坐标即可．（2）利用旋转变换的性质分别作出A，B，C的对应点A2，B2，C2，再顺次连接即可．（3）利用弧长公式求得点C经过的路径长．【解析】解：（1）如图1，△A1B1C1即为所求．A1（1，﹣5），B1（4，﹣3），C1（2，﹣2）；（2）如图2，△A2B2C2即为所求；（3），点C经过的路径长为．【点睛】本题考查作图﹣平移变换，旋转变换，解题的关键是掌握平移变换，旋转变换的性质，属于中考常考题型．19．如图，在△ABC中，AB＝AC，点D，E，F分别在AB，BC，AC边上，且BE＝CF，BD＝CE．（1）求证：∠BED＝∠CFE；（2）当∠BAC＝44°时，求∠DEF的度数．【分析】利用边角边定理证明△DBE≌△CEF，利用三角形内角和定理即可求出∠DEF的度数．【解析】（1）证明：∵AB＝AC，∴∠ABC＝∠ACB，在△DBE和△CEF中，，∴△DBE≌△CEF（SAS），∴∠BED＝∠CFE；（2）解：由（1）知：△DBE≌△CEF，∴∠1＝∠3，∵∠A+∠B+∠C＝180°，∠B＝∠C，∴∠B＝（180°﹣44°）＝68°，∴∠1+∠2＝180°﹣68°＝112°，∴∠3+∠2＝112°，∴∠DEF＝180°﹣112°＝68°．【点睛】本题考查了全等三角形的判定和性质，证明三角形全等是解题的关键．20．跳绳是驿城区某校体育活动的特色项目．体育组为了了解八年级学生1分钟跳绳次数情况，随机抽取20名八年级学生进行1分钟跳绳测试（单位：次），数据如下：100110114114120122122131144148152155156165165165165174188190对这组数据进行整理和分析，结果如下：平均数众数中位数145a b请根据以上信息解答下列问题：（1）填空：a＝165，b＝150．（2）学校规定1分钟跳绳165次及以上为优秀，请你估计七年级500名学生中，约有多少名学生能达到优秀．（3）某同学1分钟跳绳152次，请推测该同学的1分钟跳绳次数是否超过年级一半的学生？说明理由．【分析】（1）根据众数和中位数的定义解答即可；（2）用总人数乘样本中1分钟跳绳165次及以上所占比例即可；（3）根据中位数的意义解答即可．【解析】解：（1）在被抽取20名八年级学生进行1分钟跳绳测试成绩中，165出现的次数最多，故众数a＝165；把被抽取20名八年级学生进行1分钟跳绳测试成绩从小到大排列，排在中间的两个数分别是148，152，故中位数b＝＝150．故答案为：165；150；（2）500×＝175（名），答：估计八年级500名学生中，约有175名学生能达到优秀；（3）超过年级一半的学生，理由如下：∵152＞150，∴推测该同学的1分钟跳绳次数超过年级一半的学生．【点睛】本题考查众数、中位数以及用样本估计总体等知识，解题的关键是熟练掌握基本概念．21．A、B两地相距120km，甲车从A地驶往B地，乙车从B地以80km/h的速度匀速驶往A地，乙车比甲车晚出发m h．设甲车行驶的时间为x（h），甲、乙两车离A地的距离分别为y1（km）、y2（km），图中线段OP表示y1与x的函数关系．（1）甲车的速度为60km/h；（2）若两车同时到达目的地，在图中画出y2与x的函数图象，并求甲车行驶几小时后与乙车相遇；（3）若甲、乙两车在距A地60km至72km之间的某处相遇，直接写出m的范围．【分析】（1）甲车的速度为120÷2＝60（km/h）；（2）求出乙车比甲车晚出发0.5h，即可画出图象，再求出y1＝60x，y2＝﹣80x+160，联立解析式解方程组即可得到答案；（3）求得y1＝60x，y2＝120﹣80（x﹣m）＝﹣80x+120+80m，联立解方程组可得y1＝y2＝60（+m），根据甲、乙两车在距A地60km至72km之间的某处相遇，可列60＜60（+m）＜72，即可解得答案．【解析】解：（1）由图可得，甲车的速度为120÷2＝60（km/h），故答案为：60；（2）∵乙车从B地以80km/h的速度匀速驶往A地，两车同时到达目的地，∴乙车行驶时间为120÷80＝1.5（h），∵2﹣1.5＝0.5（h），∴乙车比甲车晚出发0.5h，画出y2与x的函数图象如下：图象CD即为y2与x的函数图象，由题意得y1＝60x，设CD的函数表达式为y2＝﹣80x+b，将（2，0）代入y2＝﹣80x+b，得b＝160，∴y2＝﹣80x+160，由﹣80x+160＝60x，解得x＝，∴甲车出发后h与乙车相遇，答：甲车出发后h与乙车相遇；（3）根据题意得y1＝60x，y2＝120﹣80（x﹣m）＝﹣80x+120+80m，由60x＝﹣80x+120+80m得：x＝+m，当x＝+m时，y1＝y2＝60（+m），∵甲、乙两车在距A地60km至72km之间的某处相遇，∴60＜60（+m）＜72，解得＜m＜，∴m的范围是＜m＜．【点睛】本题考查一次函数的应用，涉及待定系数法，解题的关键是数形结合数形的应用．22．某校八年级学生在数学课上进行了项目化学习研究，某小组研究如下：【提出驱动性问题】机场监控问题．【设计实践任务】选择“素材1”“素材2”，设计了“任务1”“任务2”“任务3”的实践活动．请你尝试帮助他们解决相关问题．机场监控问题的思考素材1如图是某机场监控屏显示两飞机的飞行图象，1号指挥机（看成点P）始终以3km/min的速度在离地面5km高的上空匀速向右飞行．素材22号试飞机（看成点Q）一直保持在1号机P的正下方从原点O处沿45°角爬升，到高4km 的A 处便立刻转为水平飞行，再过1min 到达B 处开始沿直线BC 降落，要求1min 后到达C（10，3）处．问题解决任务1求解析式和速度求出OA 段h 关于s 的函数解析式，直接写出2号机的爬升速度；任务2求解析式和坐标求出BC 段h 关于s 的函数解析式，并预计2号机着陆点的坐标；任务3计算时长通过计算说明两机距离PQ 不超过3km 的时长是多少．【分析】（1）设OA 段h 关于s 的函数解析式为正比例函数的一般形式，根据OA 与水平方向的夹角求出k 值，从而求出对应函数解析式；根据勾股定理，求出点O 与A 的距离，1号机与2号机在水平方向的速度相同，由速度＝路程÷时间求出2号机的爬升速度即可；（2）先求出点B 的坐标，再利用待定系数法求出BC 段h 关于s 的函数解析式；当h ＝0时对应s 的值，从而求得2号机着陆点的坐标；（3）分别求出2号机在OA 段和BC 段PQ ＝3时对应的s 的值，根据图象，当s 处于这两者之间时PQ 不超过3km ，根据时间＝路程÷速度求解即可．【解析】解：任务1：设OA 段h 关于s 的函数解析式为h ＝ks ，∴k ＝＝tan45°＝1，∴h ＝s ，∴当h ＝4时，s ＝4，∴OA 段h 关于s 的函数解析式为h ＝s （0≤s ≤4）；2号机从O 点到达A 点飞行的路程为OA ＝＝4（km ），所用时间为min ，∴2号机的爬升速度为4÷＝3（km /min ）．任务2：B 点的横坐标为4+1×3＝7，∴B点的坐标为（7，4）．设BC段h关于s的函数解析式为h＝k1s+b（k1、b为常数，且k1≠0）．将坐标B（7，4）和C（10，3）分别代入h＝k1s+b，得，解得，∴BC段h关于s的函数解析式为h＝﹣s+．当h＝0时，0＝﹣s+，解得s＝19，∴预计2号机着陆点的坐标为（19，0）．任务3：当2号机在OA段，且PQ＝3时，5﹣s＝3，解得s＝2；当2号机在BC段，且PQ＝3时，5﹣（﹣s+）＝3，解得s＝13，根据图象可知，当2≤s≤13时，两机距离PQ不超过3km，∴两机距离PQ不超过3km的时长是（13﹣2）÷3＝（min）．【点睛】本题考查一次函数的应用，理解题意并利用待定系数法求出函数关系式是解题的关键．23．【操作与发现】如图①，在正方形ABCD中，点N，M分别在边BC、CD上．连接AM、AN、MN．∠MAN＝45°，将△AMD 绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而可得：DM+BN＝MN．（1）【实践探究】在图①条件下，若CN＝6，CM＝8，则正方形ABCD的边长是12．（2）如图②，在正方形ABCD中，点M、N分别在边DC、BC上，连接AM、AN、MN，∠MAN＝45°，若tan∠BAN＝，求证：M是CD的中点．（3）【拓展】如图③，在矩形ABCD中，AB＝12，AD＝16，点M、N分别在边DC、BC上，连接AM、AN，已知∠MAN＝45°，BN＝4，则DM的长是8．【分析】（1）先证△AMN≌△EAN（SAS），得MN＝EN．则MN＝BN+DM．再由勾股定理得MN＝10，则BN+DM＝10，设正方形ABCD的边长为x，则BN＝BC﹣CN＝x﹣6，DM＝CD﹣CM＝x﹣8，得x﹣3+x ﹣4＝5，求解即可；（2）设BN＝m，DM＝n，由（1）得MN＝BN+DM＝m+n，再由锐角三角函数定义得AB＝3BN＝3m，则CN＝BC﹣BN＝2m，CM＝CD﹣DM＝3m﹣n，然后在Rt△CMN中，由勾股定理得出方程，得3m＝2n，即可解决问题；（3）延长AB至P，使BP＝BN＝4，过P作BC的平行线交DC的延长线于Q，延长AN交PQ于E，连接EM，则四边形APQD是正方形，得PQ＝DQ＝AP＝AB+BP＝16，设DM＝a，则MQ＝16﹣a，证△ABN∽△APE，得PE＝BN＝，则EQ＝，然后在Rt△QEM中，由勾股定理得出方程，求解即可．【解析】（1）解：∵四边形ABCD是正方形，∴AB＝CD＝AD，∠BAD＝∠C＝∠D＝90°，由旋转的性质得：△ABE≌△ADM，∴BE＝DM，∠ABE＝∠D＝90°，AE＝AM，∠BAE＝∠DAM，∴∠BAE+∠BAM＝∠DAM+∠BAM＝∠BAD＝90°，即∠EAM＝90°，∵∠MAN＝45°，∴∠EAN＝90°﹣45°＝45°，∴∠MAN＝∠EAN，在△AMN和△AEN中，，∴△AMN≌△AEN（SAS），∴MN＝EN，∵EN＝BE+BN＝DM+BN，∴MN＝BN+DM，在Rt△CMN中，由勾股定理得：MN＝＝＝10，则BN+DM＝10，设正方形ABCD的边长为x，则BN＝BC﹣CN＝x﹣6，DM＝CD﹣CM＝x﹣8，∴x﹣6+x﹣8＝10，解得：x＝12，即正方形ABCD的边长是12；故答案为：12；（2）证明：设BN＝m，DM＝n，由（1）可知，MN＝BN+DM＝m+n，∵∠B＝90°，tan∠BAN＝，∴tan∠BAN＝＝，∴AB＝3BN＝3m，∴CN＝BC﹣BN＝2m，CM＝CD﹣DM＝3m﹣n，在Rt△CMN中，由勾股定理得：（2m）2+（3m﹣n）2＝（m+n）2，整理得：3m＝2n，∴CM＝2n﹣n＝n，∴DM＝CM，即M是CD的中点；（3）解：延长AB至P，使BP＝BN＝4，过P作BC的平行线交DC的延长线于Q，延长AN交PQ于E，连接EM，如图③所示：则四边形APQD是正方形，∴PQ＝DQ＝AP＝AB+BP＝12+4＝16，设DM＝a，则MQ＝16﹣a，∵PQ∥BC，∴△ABN∽△APE，∴＝＝＝，∴PE＝BN＝，∴EQ＝PQ﹣PE＝16﹣＝，由（1）得：EM＝PE+DM＝+a，在Rt△QEM中，由勾股定理得：（）2+（16﹣a）2＝（+a）2，解得：a＝8，即DM的长是8；故答案为：8．【点睛】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、锐角三角函数定义、相似三角形的判定与性质等知识；本题综合性强，熟练掌握正方形的性质和矩形的性质，证明三角形全等和三角形相似是解题的关键，属于中考常考题型．24．如图1，E点为x轴正半轴上一点，⊙E交x轴于A、B两点，交y轴于C、D两点，P点为劣弧上一个动点，且A（﹣1，0）、E（1，0）．（1）的度数为120°；（2）如图2，连结PC，取PC中点G，连结OG，则OG的最大值为；（3）如图3，连接AC、AP、CP、CB．若CQ平分∠PCD交PA于Q点，求AQ的长；（4）如图4，连接PA、PD，当P点运动时（不与B、C两点重合），求证：为定值，并求出这个定值．【分析】（1）由已知条件可以得到CD垂直平分AE，所以CA＝CE，由于CE＝AE，所以可以证得三角形ACE为等边三角形，得到∠CEB＝120°；（2）由于直径AB⊥CD，根据垂径定理，可以得到O是CD的中点，又G是CP的中点，连接PD，则OG∥PD，OG＝，要求OG最大值，只需要求PD最大值，由于P是劣弧上的一动点，故当P，E，D三点共线，即PD为直径时，PD最大，此时OG最大；（3）由于直径AB⊥CD，根据垂径定理，可以得到，所以∠ACD＝∠CPA，又CQ平分∠DCP，所以∠PCQ＝∠DCQ，可以证明∠ACQ＝∠AQC，所以AC＝AQ，由（1）可得，AC＝AE＝2，所以AQ ＝2；（4）由直径AB⊥CD，可以得到AB垂直平分CD，所以AC＝AD，∠CAD＝2∠CAE＝120°，将△ACP 绕A点顺时针旋转120°至△ADM，可以证明M，D，P三点共线，所以PC+PD＝PM，可以证明△PAM 是顶角为120°的等腰三角形，过A做AG⊥PM于G，由于∠APM＝30°，可以通过勾股定理或者三角函数证明PM＝PA，所以＝．【解析】解：（1）连接AC，CE，∵A（﹣1，0）、E（1，0），∴OA＝OE＝1，∵OC⊥AE，∴AC＝CE，∵AE＝CE，∴AC＝CE＝AE，∴∠CAE＝60°，∴∠BEC＝2∠CAB＝120°，∴的度数为120°，故答案为：120；（2）由题可得，AB为⊙E直径，且AB⊥CD，由垂径定理可得，CO＝OD，连接PD，如图2，又∵G为PC的中点，∴OG∥PD，且OG＝，当D，E，P三点共线时，此时DP取得最大值，且DP＝AB＝2AE＝4，∴OG的最大值为2，故答案为：2；（3）连接AC，BC，∵直径AB⊥CD，∴，∴∠ACD＝∠CPA，∵CQ平分∠DCP，∴∠DCQ＝∠PCQ，∴∠ACD+∠DCQ＝∠CPA+∠PCQ，∴∠ACQ＝∠AQC，∴AQ＝AC，∵∠CAO＝60°，AO＝1，∴AC＝2，∴AQ＝2；（4）由题可得，直径AB⊥CD，∴AB垂直平分CD，如图4，连接AC，AD，则AC＝AD，由（1）得，∠DAC＝120°，将△ACP绕A点顺时针旋转120°至△ADM，∴△ACP≌△ADM，∴∠ACP＝∠ADM，PC＝DM，∵四边形ACPD为圆内接四边形，∴∠ACP+∠ADP＝180°，∴∠ADM+∠ADP＝180°，∴M、D、P三点共线，∴PD+PC＝PD+DM＝PM，过A作AG⊥PM于G，则PM＝2PG，⋅∠APM＝∠ACD＝30°，在Rt△APG中，∠APM＝30°，设AG＝x，则AP＝2x，∴，∴∴，∴∴为定值．【点睛】本题是一道圆的综合题，重点考查了垂径定理在圆中的应用，最后一问由“共顶点，等线段”联想到旋转，是此题的突破口，同时，要注意顶角为120度的等腰三角形腰和底边比是固定值．。

历年浙教版杭州地区初三数学中考压轴题精选及答案

历年浙教版杭州地区初三数学中考压轴题精选及答案

杭州地区中考数学压轴题精选25.(本小题满分10分)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为2y x c =-+,正方形ABCD 的边长和正方形EFGH 的边长之比为5:1,求:(1)抛物线解析式中常数c 的值;(2)正方形MNPQ 的边长.26.(本小题满分12分)在三角形ABC 中,60,24,16O B BA cm BC cm ∠===.现有动点P 从点A 出发,沿射线AB 向点B 方向运动;动点Q 从点C 出发,沿射线CB 也向点B 方向运动.如果点P 的速度是4cm /秒,点Q 的速度是2cm /秒,它们同时出发,求:(1)几秒钟后,ΔPBQ 的面积是ΔABC 的面积的一半?(2)在第(1)问的前提下,P,Q 两点之间的距离是多少?２４、（本题１２分）如图，在矩形ABCD 中，AD=8,点E 是AB 边上的一点，AE=22,过D,E 两点作直线PQ ，与BC 边所在的直线MN 相交于点F 。

（１）求tan ∠ADE 的值；（２）点G 是线段AD 上的一个动点（不运动至点A,D ），GH ⊥DE 垂足为H ，设DG 为x ，四边形AEHG 的面积为y ，请求出y 与x 之间的函数关系式；（３）如果AE=2EB ，点O 是直线MN 上的一个动点，以O 为圆心作圆，使⊙O 与直线PQ相切，同时又与矩形ABCD 的某一边相切。

问满足条件的⊙O 有几个？并求出其中一个圆的半径。

２５（本题１４分）如图，抛物线2y ax bx c =++经过点O(0,0),A(4,0),B(5,5)，点C 是y 轴负半轴上一点，直线l 经过B,C 两点，且5tan 9OCB ∠=（１）求抛物线的解析式；（２）求直线l 的解析式；（３）过O,B 两点作直线，如果P 是直线OB 上的一个动点，过点P 作直线PQ 平行于y轴，交抛物线于点Q 。

动点的函数图象问题(压轴题专项讲练)原卷版—2024-2025学年九年级数学上册压轴题专项(浙教版)

动点的函数图象问题(压轴题专项讲练)原卷版—2024-2025学年九年级数学上册压轴题专项(浙教版)

动点的函数图象问题数形结合思想：所谓数形结合，就是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的思想，实现数形结合，常与以下内容有关：（1）实数与数轴上的点的对应关系；（2）函数与图象的对应关系；（3所给的等式或代数式的结构含有明显的几何意义。

【典例1】如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD=2，CD⊥AB于点D，点E、F、G分别是边CD、CA、AD的中点，连接EF、FG，动点M从点B出发，以每秒2个单位长度的速度向点A方向运动（点M运动到AB的中点时停止）；过点M作直线MP∥BC与线段AC交于点P，以PM为斜边作Rt△PMN，点N在AB 上，设运动的时间为t(s)，Rt△PMN与矩形DEFG重叠部分的面积为S，则S与t之间的函数关系图象大致为（）A．B．C．D．本题考查几何动点问题的函数图象，正确分段并分析是解题的关键．根据题意先分段，分为0≤t≤0.5，0.5<t≤1，1<t≤2三段，分别列出三段的函数解析式便可解决，本题也可只列出0≤t≤0.5，1<t≤2两段，用排除法解决．解：分析平移过程，①从开始出发至PM与点E重合，由题意可知0≤t≤0.5，如图，则BM=2t，过点M作MT⊥BC于点T，∵∠B=60°，CD⊥AB，∴BC=2BD=4，CD==BT=12BM=t，∵∠ACB=90°，MP∥BC，∴∠ACB=∠MPA=90°，∴四边形CTMP为矩形，∴PM=CT=BC―BT=4―t，∵∠PMN=∠B=60°，PN⊥AB，∴MN=PM2=4―t2，∴DN=MN―MD=MN―BD+BM=3t2，∵E为CD中点，∴DE=CD2=∴S=DE⋅DN=∴S与t的函数关系是正比例函数；②当0.5<t≤1，即从PM与E重合至点M与点D重合，如图，由①可得QN=ED=DM=2―2t，DN=32t，S矩形EDNQ=∵∠PMN=∠B=60°，CD⊥AB，∴SD==，∴ES=ED―SD=∴ER ==2t ―1，∴S =S 矩形EDNQ ―S △ERS =12(2―2t ―1)=―2+此函数图象是开口向下的二次函数；③当1<t ≤2，即从点M 与点D 重合至点M 到达终点，如图，由①可得DN =32t ，MN =4―t 2，∵AD ==6， DG =12AD =3，∴NG =DG ―DN =3―32t ，∴QF =NG =3―32t ，∴PQ==，∴HQ ==1―12t ，∴S =(HQ+MN )×QN 2==―∴S 与t 的函数关系是一次函数，综上，只有选项A 的图象符合，故选：A ．1．（2024·四川广元·二模）如图，在矩形ABCD 中，AB =4cm ,AD =2cm ，动点M 自点A 出发沿AB 方向以每秒1cm 的速度向点 B 运动，同时动点N 自点A 出发沿折线AD －DC －CB 以每秒2cm 的速度运动，到达点B 时运动同时停止．设△AMN的面积为y (cm2)，运动时间为x （秒），则下列图象中能大致反映y 与x 之间的函数关系的是（ ）A ．B ．C ．D ．2．（22-23九年级上·安徽合肥·期中）如图，在△ABC 中，∠C =135°，AC =BC =P 为BC 边上一动点，PQ∥AB 交AC 于点Q ，连接BQ ，设PB =x ，S △BPQ =y ，则能表示y 与x 之间的函数关系的图象大致是（ ）A ．B ．C ．D ．3．（2024·河北石家庄·二模）如图所示，△ABC 和△DEF 均为边长为4的等边三角形，点A 从点D 运动到点E 的过程中，AB 和DF 相交于点G ，AC 和EF 相交于点H ，(S △BGF +S △FCH )为纵坐标y ，点A 移动的距离为横坐标x，则y与x关系的图象大致为（）A．B．C．D．4．（2023·辽宁铁岭·模拟预测）如图，矩形ABCD中，AB=8cm，AD=12cm，AC与BD交于点O，M是BC 的中点．P、Q两点沿着B→C→D B、点M同时出发，并都以1cm/s的速度运动，当点Q到达D点时，两点同时停止运动．在P、Q两点运动的过程中，与△OPQ的面积随时间t变化的图象最接近的是（）A．B．C．D．5．（2023·江苏南通·模拟预测）如图，在矩形ABCD中，AB=4，BC=6，E为AB中点，动点P从点B开始沿BC方向运动到点C停止，动点Q从点C开始沿CD→DA方向运动，与点P同时出发，同时停止；这两点的运动速度均为每秒1个单位；若设他们的运动时间为x（s），△EPQ的面积为y，则y与x之间的函数关系的图像大致是（）A．B．C．D．6．（2024·河南开封·一模）如图1，在△ABC中，∠B=60°，点D从点B出发，沿BC运动，速度为1cm/s．点P在折线BAC上，且PD⊥BC于点D．点D运动2s时，点P与点A重合．△PBD的面积S(cm2)与运动时间t(s)的函数关系图象如图2所示，E是函数图象的最高点．当S(cm2)取最大值时，PD的长为（）A．B．(1+cm C．(1+cm D．(2+cm7．（2024·安徽·一模）如图，在四边形ABCD中，∠A=60°，CD⊥AD，∠BCD=90°,AB=BC=4，动点P，Q同时从A点出发，点Q以每秒2个单位长度沿折线A―B―C向终点C运动；点P以每秒1个单位长度沿线段AD向终点D运动，当其中一点运动至终点时，另一点随之停止运动.设运动时间为x秒，△APQ的面积为y 个平方单位，则y随x变化的函数图象大致为（）A．B．C．D．8．（23-24九年级上·浙江温州·期末）某兴趣小组开展综合实践活动：在Rt△ABC中，∠C=90°，CD=，D为AC上一点，动点P以每秒1个单位的速度从C点出发，在三角形边上沿C→B→A匀速运动，到达点A时停止，以DP为边作正方形DPEF，设点P的运动时间为t s，正方形DPEF的面积为S，当点P由点C运动到点A 时，经探究发现S是关于t的二次函数，并绘制成如图2所示的图象，若存在3个时刻t1，t2，t3(t1<t2<t3)对应的正方形DPEF的面积均相等，当t3=5t1时，则正方形DPEF的面积为（）A．3B．3499．（22-23九年级上·浙江嘉兴·期中）如图，在Rt△ABC中，∠C=90°，∠ABC=60°，BC=6，点O为AC中点，点D为线段AB上的动点，连接OD，设BD＝x，OD2＝y，则y与x之间的函数关系图像大致为（ ）A．B．C．D．10．（2024·广东深圳·三模）如图，在Rt△ABC中，∠C=90°，AC=12，BC=8，点D和点E分别是AB和AC的中点，点M和点N分别从点A和点E出发，沿着A→C→B方向运动，运动速度都是1个单位/秒，当点N到达点B时，两点间时停止运动．设△DMN的面积为S，运动时间为t，则S与t之间的函数图象大致为（）A．B．C．D．11．（2024·河南南阳·二模）如图是一种轨道示意图，其中A、B、C、D分别是菱形的四个顶点，∠A=60°．现有两个机器人(看成点)分别从A，C两点同时出发，沿着轨道以相同的速度匀速移动，其路线分别为A→B→C和C→D→A．若移动时间为t，两个机器人之间距离为d．则d²与t之间的函数关系用图象表示大致为（）A．B．C．D．12．（2024·山东聊城·二模）如图，等边△ABC与矩形DEFG在同一直角坐标系中，现将等边△ABC按箭头所指的方向水平移动，平移距离为x，点C到达点F为止，等边△ABC与矩形DEFG重合部分的面积记为S，则S关于x的函数图象大致为（）A．B．C．D．13．（2024·河南·模拟预测）如图，在等腰直角三角形ABC中，∠ABC=90°，BD是AC边上的中线，将△BCD 沿射线BA方向匀速平移，平移后的三角形记为△B1C1D1，设△B1C1D1与△ABD重叠部分的面积为y，平移距离为x，当点B1与点A重合时，△B1C1D1停止运动，则下列图象最符合y与x之间函数关系的是（）A．B．C．D．14．（23-24九年级上·安徽滁州·期末）如图，菱形ABCD的边长为3cm，∠B=60°，动点P从点B出发以3cm/ s的速度沿着边BC―CD―DA运动，到达点A后停止运动；同时动点Q从点B出发，以1cm/s的速度沿着边BA 向A点运动，到达点A后停止运动．设点P的运动时间为x(s)，△BPQ的面积为y(cm2)，则y关于x的函数图象为（）A．B．C．D．15．（2023·辽宁盘锦·中考真题）如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴的正半轴上，顶点B、C在x轴的正半轴上，D，P(―1,―1)．点M在菱形的边AD和DC上运动（不与点A，C重合），过点M作MN∥y轴，与菱形的另一边交于点N，连接PM，PN，设点M的横坐标为x，△PMN的面积为y，则下列图象能正确反映y与x之间函数关系的是（）A．B．C．D．16．（22-23九年级上·安徽蚌埠·期末）如图，在平面直角坐标系中，点A(2,0)，点B，点C(―，点P从点O出发沿O→A→B路线以每秒1个单位的速度运动，点Q从点O出发沿O→C→B的速度运动，当一个点到达终点时另一个点随之停止运动，设y=PQ2，运动时间为t秒，则正确表达y与t的关系图象是（）A．B．C．D．17．（2022·辽宁·中考真题）如图，在等边三角形ABC中，BC＝4，在Rt△DEF中，∠EDF＝90°，∠F＝30°，DE＝4，点B，C，D，E在一条直线上，点C，D重合，△ABC沿射线DE方向运动，当点B与点E重合时停止运动．设△ABC运动的路程为x，△ABC与Rt△DEF重叠部分的面积为S，则能反映S与x之间函数关系的图象是（ ）A ．B ．C ．D ．18．（2023·山东聊城·三模）如图（1）所示，E 为矩形ABCD 的边AD 上一点，动点P ，Q 同时从点B 出发，点P 沿折线BE ―ED ―DC 运动到点C 时停止，点Q 沿BC 运动到点C 时停止，它们运动的速度都是1cm/秒，设P ，Q 同时出发t 秒时，△BPQ 的面积为y cm 2．已知y 与t 的函数关系图像如图（2）（曲线OM 为抛物线 ）A ．AB:AD =4:5B ．当t =2.5秒时，PQ =C ．当t =294时，BQ PQ =53D ．当△BPQ 的面积为4cm 2时，t 或475秒19．（2023·辽宁·中考真题）如图，∠MAN =60°，在射线AM ，AN 上分别截取AC =AB =6，连接BC ，∠MAN 的平分线交BC 于点D ，点E 为线段AB 上的动点，作EF ⊥AM 交AM 于点F ，作EG∥AM 交射线AD 于点G ，过点G作GH⊥AM于点H，点E沿AB方向运动，当点E与点B重合时停止运动．设点E运动的路程为x，四边形EFHG与△ABC重叠部分的面积为S，则能大致反映S与x之间函数关系的图象是（）A．B．C．D．20．（22-23九年级上·安徽滁州·期末）如图，在平面直角坐标系中，菱形ABCD的边长为4，且点A与原点O 重合，边AD在x轴上，点B的横坐标为―2，现将菱形ABCD沿x轴以每秒1个单位长度的速度向右平移，设平移时间为t（秒），菱形ABCD位于y轴右侧部分的面积为S，则S关于t的函数图像大致为（）A．B．C．D．。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

浙教版中考压轴题精选
1、如图、有一根直尺的短边长为6 cm，长边长为12 cm，还有一块锐角为45°的直角三角形纸
板，它的斜边为12cm，如图甲，将直尺的短边DE与直角三角形纸板的斜边放置在同一直线上，
且D与B重合.将Rt△ABC沿AB方向平移（如图乙），设平移的长度为x cm（），直尺
和三角形纸板的重叠部分（图中的阴影部分）的面积为S cm2
（1）写出当时，S＝；
（2）当时，求S关于x的函数关系式.
2、如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝16，动
点P从点A出发沿AC边向点C以每秒3个单位长的速度运动，动
点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动．P，Q分别从点A，C同时出发，当
其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ关于直线PQ对称的图形是
△PDQ．设运动时间为t（秒）．
（1）设四边形PCQD的面积为y，求y与t的函数关系式；
（2）t为何值时，四边形PQBA是梯形？
3、已知抛物线与它的对称轴相交于点，与轴交
于，与轴正半轴交于．
（1）求这条抛物线的函数关系式；
（2）设直线交轴于是线段上一动点（点异于），过作轴，交直
线于，过作轴于，求当四边形的面积等于时，求点的坐标．
4、已知抛物线（）与轴相交于点
，顶点为.直线分别与轴，轴
相交于两点，并且与直线相交于点.
(1)填空：试用含的代数式分别表示点与的坐标，则；
(2)如图，将沿轴翻折，若点的对应点′恰好落在抛物线上，′与轴交于点，连结，求的值和四边形的面积；
(3)在抛物线（）上是否存在一点，使得以为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，试说明理由.
6．如图13，二次函数的图像与x轴交于A、B两点，与y
轴交于点C（0，-1），ΔABC的面积=
（1）求该二次函数的关系式；
（2）在该二次函数的图像上是否存在点D，使四边形ABCD为直角梯形？若存在，
求出点D的坐标；若不存在，请说明理由。

6、如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，
0）、D（8，8）.抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标，并求出抛物线的解析式；
(2)动点P从点A出发．沿线段AB向终点B运动，同时点Q从
点C出发，沿线段CD
向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P
作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线
段EG最长?
②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值.
参考答案
1、（1）18cm2
（2）如图，当时
BE=x-6，AD=12-x
∴
=
2、（1）由题意知 CQ＝4t，PC＝12－
3t，
∴S△PCQ =．
∵△PCQ与△PDQ关于直线PQ对称，
∴y=2S△PCQ ．
（2）当时，有PQ∥AB，而AP与BQ不平行，这时四边形PQBA是梯形，∵CA=12，CB=16，CQ＝4t， CP＝12－3t，
∴，解得t＝2．
∴当t＝2秒时，四边形PQBA是梯形
3、解：（1）由题意，知点是抛物线的顶点，
，，抛物线的函数关系式为．
（2）由（1）知，点的坐标是．设直线的函数关系式为，则，，．
由，得，，点的坐标是．
设直线的函数关系式是，
则解得，．
直线的函数关系式是．
设点坐标为，则．
轴，点的纵坐标也是．
设点坐标为，
点在直线上，，．
轴，点的坐标为，
，，，
，，，当时，，而，，
点坐标为和．
4、（1）
（2）由题意得点与点′关于轴对称，
，
将′的坐标代入得，（不合题意，舍去），.
，点到轴的距离为3.
，，直线的解析式为，它与轴的交点为点到轴的距离为.
.
（3）当点在轴的左侧时，若是平行四边形，则平行且等于，把向上平移个单位得到，坐标为，代入抛物线的解析式，
得：
（不合题意，舍去），，
.
当点在轴的右侧时，若是平行四边形，则与互相平分，
．
与关于原点对称，，
将点坐标代入抛物线解析式得：，
（不合题意，舍去），，．
存在这样的点或，能使得以为顶点的四边形是平行四边形．5、解：（1）OC=1,所以,q=-1,又由面积知0.5OC×AB=,得AB=
设A（a,0）,B(b,0)
AB=b-a==，解得p=,但p<0,所以p=。

所以解析式为：
（2）存在，AC⊥BC,①若以AC为底边，则BD//AC,易求AC的解析式为y=-2x-1,可设BD的解析式为y=-2x+b，把B(2,0)代入得BD解析式为y=-2x+4，解方程组得D（,9）
②若以BC为底边，则BC//AD,易求BC的解析式为y=0.5x-1,可设AD的解析式为y=0.5x+b，把 A(,0)代入得AD解析式为y=0.5x+0.25，解方程组得D()
综上，所以存在两点：（,9）或()。

6、(1)点A的坐标为（4，8）
将A (4,8)、C（8，0）两点坐标分别代入y=ax2+bx
解得a =-,b=4
∴抛物线的解析式为：y=-x2+4x
（2）①在Rt△APE和Rt△ABC中，tan∠PAE==,即=
∴PE=AP=t．PB=8-t．
∴点Ｅ的坐标为（4+t，8-t）.
∴点G的纵坐标为：-（4+t）2+4(4+t）=-t2+8. ∴EG=-t2+8-(8-t)
=-t2+t.
∵-＜0，∴当t=4时，线段EG最长为2.
②共有三个时刻.
t1=，t2=，t3= ．。

相关文档
最新文档