(完整版)2018中考数学:几何证明题
2018年中考数学-----几何综合题汇总3

2018年中考数学-----几何综合题汇总31.如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现:①当α=0°时,= ;②当α=180°时,= .(2)拓展探究:试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决:当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.2.在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E.DF 与线段AC(或AC的延长线)相交于点F.(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC 的延长线相交于点F,作DN⊥AC于点N,若DN⊥AC于点N,若DN=FN,求证:BE+CF=(BE﹣CF).3.如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.(1)直接写出∠NDE的度数;(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.4.已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系:.(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.5.【问题提出】如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF;试证明:AB=DB+AF。
上海市各区2018届中考二模数学分类汇编:几何证明专题(含答案)

上海市各区2018届九年级中考二模数学试卷精选汇编几何证明专题宝山区、嘉定区23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图6,在正方形ABCD 中,点M 是边BC 上的一点(不与B 、C 重合),点N 在CD 边的延长线上,且满足︒=∠90MAN ,联结MN 、AC ,MN 与边AD 交于点E . (1)求证;AN AM =;(2)如果NAD CAD ∠=∠2,求证:AE AC AM ⋅=2.23.证明:(1)∵四边形ABCD 是正方形∴AD AB =,︒=∠=∠=∠=∠90BCD ADC B BAD ……1分 ∴︒=∠+∠90MAD MAB ∵︒=∠90MAN∴︒=∠+∠90MAD NAD ∴NAD MAB ∠=∠………1分 ∵︒=∠+∠180ADC ADN ∴︒=∠90ADN ……1分 ∴ADN B ∠=∠……………………1分 ∴△ABM ≌△ADN ………………………1分 ∴AN AM = ……………………………1分(2)∵四边形ABCD 是正方形 ∴AC 平分BCD ∠和BAD ∠ ∴︒=∠=∠4521BCD BCA ,︒=∠=∠=∠4521BAD CAD BAC ……1分 ∵NAD CAD ∠=∠2 ∴︒=∠5.22NAD∵NAD MAB ∠=∠ ∴︒=∠5.22MAB ………1分 ∴︒=∠5.22MAC ∴︒=∠=∠5.22NAE MAC ∵AN AM =,︒=∠90MAN ∴︒=∠45ANE图6图6∴ANE ACM ∠=∠…………………1分 ∴△ACM ∽△ANE …………1分 ∴ANACAE AM =……1分 ∵AN AM =∴AE AC AM ⋅=2…………1分长宁区23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,在四边形ABCD 中,AD //BC ,E 在BC 的延长线,联结AE 分别交BD 、CD 于点 G 、F ,且AG GF BE AD =. (1)求证:AB //CD ;(2)若BD GD BC ⋅=2,BG =GE ,求证:四边形ABCD 是菱形.23.(本题满分12分,第(1)小题5分,第(2)小题7分)证明:(1)∵BC AD // ∴BG DG BE AD = (2分)∵AG GFBE AD =∴AGGF BG DG = (1分) ∴ CD AB // (2分) (2)∵BC AD //,CD AB //∴四边形ABCD 是平行四边形 ∴BC=AD (1分) ∵ BD GD BC ⋅=2∴ BD GD AD ⋅=2即ADGDBD AD =又 ∵BDA ADG ∠=∠ ∴ADG ∆∽BDA ∆ (1分) ∴ABD DAG ∠=∠∵CD AB // ∴BDC ABD ∠=∠ ∵BC AD // ∴E DAG ∠=∠∵BG =GE ∴E DBC ∠=∠ ∴DBC BDC ∠=∠ (3分)ACDEF GB第23题图∴BC=CD (1分) ∵四边形ABCD 是平行四边形 ∴平行四边形ABCD 是菱形. (1分)崇明区23.(本题满分12分,第(1)、(2)小题满分各6分)如图,AM 是ABC △的中线,点D 是线段AM 上一点(不与点A 重合).DE AB ∥交BC 于点K ,CE AM ∥,联结AE .(1)求证:AB CMEK CK=; (2)求证:BD AE =.23.(本题满分12分,每小题6分) (1)证明:∵DE AB ∥∴ ABC EKC =∠∠ ……………………………………………………1分∵CE AM ∥∴ AMB ECK =∠∠ ……………………………………………………1分∴ABM EKC △∽△ ……………………………………………………1分 ∴AB BMEK CK=………………………………………………………1分 ∵ AM 是△ABC 的中线∴BM CM = ………………………………………………………1分∴AB CMEK CK=………………………………………………………1分 (2)证明:∵CE AM ∥ ∴DE CMEK CK=………………………………………………………2分 (第23题图)ABK MCDE又∵AB CMEK CK=∴DE AB = ………………………………………………………2分 又∵DE AB ∥∴四边形ABDE 是平行四边形 …………………………………………1分 ∴BD AE = ………………………………………………………1分奉贤区23.(本题满分12分,每小题满分各6分)已知:如图7,梯形ABCD ,DC ∥AB ,对角线AC 平分∠BCD , 点E 在边CB 的延长线上,EA ⊥AC ,垂足为点A . (1)求证:B 是EC 的中点;(2)分别延长CD 、EA 相交于点F ,若EC DC AC ⋅=2,求证:FC AC AF AD ::=.黄浦区23.(本题满分12分)如图,点E 、F 分别为菱形ABCD 边AD 、CD 的中点. (1)求证:BE =BF ;(2)当△BEF 为等边三角形时,求证:∠D =2∠A .ACD E图7B23. 证:(1)∵四边形ABCD为菱形,∴AB=BC=AD=CD,∠A=∠C,——————————————————(2分)又E、F是边的中点,∴AE=CF,——————————————————————————(1分)∴△ABE≌△CBF———————————————————————(2分)∴BE=BF. ——————————————————————————(1分)(2)联结AC、BD,AC交BE、BD于点G、O. ——————————(1分)∵△BEF是等边三角形,∴EB=EF,又∵E、F是两边中点,∴AO=12AC=EF=BE.——————————————————————(1分)又△ABD中,BE、AO均为中线,则G为△ABD的重心,∴1133OG AO BE GE===,∴AG=BG,——————————————————————————(1分)又∠AGE=∠BGO,∴△AGE≌△BGO,——————————————————————(1分)∴AE=BO,则AD=BD,∴△ABD是等边三角形,———————————————————(1分)所以∠BAD=60°,则∠ADC=120°,即∠ADC=2∠BAD. —————————————————————(1分)金山区23.(本题满分12分,每小题6分)如图7,已知AD 是△ABC 的中线, M 是AD 的中点, 过A 点作AE ∥BC ,CM 的延 长线与AE 相交于点E ,与AB 相交于点F . (1)求证:四边形AEBD 是平行四边形; (2)如果AC =3AF ,求证四边形AEBD 是矩形.23.证明:(1)∵AE //BC ,∴∠AEM =∠DCM ,∠EAM =∠CDM ,……………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,…………………………(1分) ∵BD=CD ,∴AE =BD .……………………………………………………(1分) ∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………(2分)(2)∵AE //BC ,∴AF AEFB BC=.…………………………………………………(1分) ∵AE=BD=CD ,∴12AF AE FB BC ==,∴AB=3AF .……………………………(1分) ∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分) 又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分) ∴四边形AEBD 是矩形.……………………………………………………(1分)静安区23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分) 已知:如图,在平行四边形ABCD 中, AC 、DB 交于点E , 点F 在BC 的延长线上,联结EF 、DF ,且∠DEF =∠ADC .EAFMD图7CC第23题图ABDE F(1)求证:DBABBF EF =; (2)如果DF AD BD ⋅=22,求证:平行四边形ABCD 是矩形.23.(本题满分12分,第(1)小题6分,第(2)小题6分) 证明:(1)∵平行四边形ABCD ,∴AD //BC ,AB //DC∴∠BAD +∠ADC =180°,……………………………………(1分) 又∵∠BEF +∠DEF =180°, ∴∠BAD +∠ADC =∠BEF +∠DEF ……(1分) ∵∠DEF =∠ADC ∴∠BAD =∠BEF , …………………………(1分) ∵AB //DC , ∴∠EBF =∠ADB …………………………(1分)∴△ADB ∽△EBF ∴DB ABBF EF = ………………………(2分) (2) ∵△ADB ∽△EBF ,∴BFBEBD AD =, ………………………(1分) 在平行四边形ABCD 中,BE =ED =BD 21∴221BD BE BD BF AD =⋅=⋅∴BF AD BD ⋅=22, ………………………………………(1分) 又∵DF AD BD ⋅=22∴DF BF =,△DBF 是等腰三角形 …………………………(1分) ∵DE BE =∴FE ⊥BD , 即∠DEF =90° …………………………(1分) ∴∠ADC =∠DEF =90° …………………………(1分) ∴平行四边形ABCD 是矩形 …………………………(1分)闵行区23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)如图,已知在△ABC 中,∠BAC =2∠C ,∠BAC 的平分线AE 与∠ABC 的平分线BD 相交于点F ,FG ∥AC ,联结DG .(1)求证:BF BC AB BD ⋅=⋅; (2)求证:四边形ADGF 是菱形.AB第23题图DE FABEGCFD(第23题图)23.证明:(1)∵AE 平分∠BAC ,∴∠BAC =2∠BAF =2∠EAC .∵∠BAC =2∠C ,∴∠BAF =∠C =∠EAC .…………………………(1分) 又∵BD 平分∠ABC ,∴∠ABD =∠DBC .……………………………(1分) ∵∠ABF =∠C ,∠ABD =∠DBC ,∴ABF CBD ∆∆∽.…………………………………………………(1分) ∴AB BFBC BD=.………………………………………………………(1分) ∴BF BC AB BD ⋅=⋅.………………………………………………(1分) (2)∵FG ∥AC ,∴∠C =∠FGB ,∴∠FGB =∠FAB .………………(1分)∵∠BAF =∠BGF ,∠ABD =∠GBD ,BF =BF ,∴ABF GBF ∆∆≌.∴AF =FG ,BA =BG .…………………………(1分) ∵BA =BG ,∠ABD =∠GBD ,BD =BD ,∴ABD GBD ∆∆≌.∴∠BAD =∠BGD .……………………………(1分) ∵∠BAD =2∠C ,∴∠BGD =2∠C ,∴∠GDC =∠C ,∴∠GDC =∠EAC ,∴AF ∥DG .……………………………………(1分) 又∵FG ∥AC ,∴四边形ADGF 是平行四边形.……………………(1分) ∴AF =FG .……………………………………………………………(1分) ∴四边形ADGF 是菱形.……………………………………………(1分)普陀区23.(本题满分12分)已知:如图9,梯形ABCD 中,AD ∥BC ,DE ∥AB ,DE 与对角线AC 交于点F ,FG ∥AD ,且FG EF =.(1)求证:四边形ABED 是菱形; (2)联结AE ,又知AC ⊥ED ,求证:212AE EF ED = .ABC DE FG图923.证明:(1)∵ AD ∥BC ,DE ∥AB ,∴四边形ABED 是平行四边形. ··························· (2分)∵FG ∥AD ,∴FG CFAD CA=. ·················································································· (1分) 同理EF CFAB CA = . ··································································································· (1分) 得FG AD =EF AB∵FG EF =,∴AD AB =. ··················································································· (1分) ∴四边形ABED 是菱形. ························································································· (1分) (2)联结BD ,与AE 交于点H .∵四边形ABED 是菱形,∴12EH AE =,BD ⊥AE . ····································· (2分) 得90DHE ∠= .同理90AFE ∠= .∴DHE AFE ∠∠=. ······························································································· (1分) 又∵AED ∠是公共角,∴△DHE ∽△AFE . ··················································· (1分)∴EH DEEF AE =. ········································································································ (1分) ∴212AE EF ED = . ······························································································ (1分) 青浦区23.(本题满分12分,第(1)、(2)小题,每小题6分)如图7,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点M ,点E 在边 BC 上,且DAE DCB ∠=∠,联结AE ,AE 与BD 交于点F . (1)求证:2DM MF MB =⋅; (2)联结DE ,如果3BF FM =,求证:四边形ABED 是平行四边形.23.证明:(1)∵AD //BC ,∴∠=∠DAE AEB , ····························································· (1分)∵∠=∠DCB DAE ,∴∠=∠DCB AEB , ··········································· (1分)MFE DBA图7∴AE //DC , ···································································································· (1分)∴=FM AMMD MC. ························································································· (1分) ∵AD //BC ,∴=AM DMMC MB, ····································································· (1分) ∴=FM DMMD MB, ························································································· (1分) 即2=⋅MD MF MB .(2)设=FM a ,则=3BF a ,=4BM a . ························································· (1分)由2=⋅MD MF MB ,得24=⋅MD a a ,∴2=MD a , ································································································ (1分) ∴3==DF BF a . ························································································ (1分) ∵AD //BC ,∴1==AF DFEF BF, ····································································· (1分) ∴=AF EF , ································································································· (1分) ∴四边形ABED 是平行四边形. ······································································ (1分)松江区23.(本题满分12分,第(1)小题满分7分,第(2)小题满分5分)如图,已知梯形ABCD 中,AB ∥CD ,∠D =90°,BE 平分∠ABC ,交CD 于点E , F 是AB 的中点,联结AE 、EF ,且AE ⊥BE .求证:(1)四边形BCEF 是菱形;(2)2BE AE AD BC ⋅=⋅.23.(本题满分12分,第(1)小题满分7分,第(2)小题满分5分) 证明:(1) ∵BE 平分∠ABC ,∴∠ABE =∠CBE …………………………………………………1分 ∵AE ⊥BE(第23题图)FACD EB∴∠AEB =90°∵F 是AB 的中点 ∴12EF BF AB ==………………………………………………1分 ∴∠FEB =∠FBE …………………………………………………1分∴∠FEB =∠CBE …………………………………………………1分∴EF ∥BC …………………………………………………1分∵AB ∥CD∴四边形BCEF 是平行四边形…………………………1分∵EF BF =∴四边形BCEF 是菱形……………………………………1分(2) ∵四边形BCEF 是菱形,∴BC =BF ∵12BF AB = ∴AB =2BC ………………………………………………1分∵ AB ∥CD∴ ∠DEA =∠EAB∵ ∠D =∠AEB∴ △EDA ∽△AEB ………………………………………2分∴AD AE BE AB = …………………………………………1分 ∴ BE ·AE =AD ·AB∴ 2BE AE AD BC ⋅=⋅…………………………………1分徐汇区23. 在梯形ABCD 中,AD ∥BC ,AB CD =,BD BC =,点E 在对角线BD 上,且DCE DBC ∠=∠.(1)求证:AD BE =;(2)延长CE 交AB 于点F ,如果CF AB ⊥,(第23题图)F A C D E⋅=⋅.求证:4EF FC DE BD杨浦区23、(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图7,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD 于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN。
中考复习初中数学几何证明 试题(含答案)
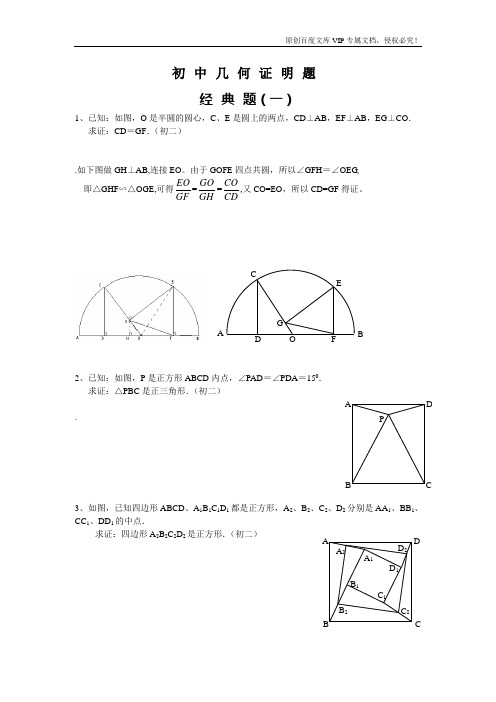
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.BF求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
陕西省2018年中考数学复习课件:第二编:陕西中考十年真题精讲第19题:几何证明(解答题).pptx

《中考内参(数学)2018》配套课件
陕西中考十年真题精讲第19题:几何证明(解答题)
5.(陕西省,2016年)如图,在□ABCD中, 连接BD,在BD的延长线上取一点E,在DB的延 长线上取一点F,使BF=DE,连接AF、CE. 求证:AF∥CE.
《中考内参(数学)2018》配套课件
陕西中考十年真题精讲第19题:几何证明(解答题)
•早在人类文化发展的上古时期,文化的发展就不是一个模式,而是形成多个文化体系,呈现多样形态。此后,不同文化并不是孤立地、互不联系地发展,而是在相互交流、对话、学习、碰撞中前行,逐渐形成“你中有我、我中有你”的格局。而不同文明的接触,常常成为人类进步的里程碑: 希腊学习埃及,罗马学习希腊,阿拉伯学习罗马帝国,中世纪欧洲学习阿拉伯,文艺复兴时期的欧洲又学习东罗马帝国。欧洲文化的发展状况是这样,东亚也是如此:日本明治维新之前,日本学习借鉴中国;明治维新之后,中国通过日本学习世界。中国从印度引入佛教,之后中国佛教影响东 亚、东南亚大片区域。人类文化发展史表明,一种本土文化、民族文化或地域文化与外来文化进行交流互鉴时,只要坚持科学方法,保持自己文化的特性,就能不断吸收改造外来文化并使其成为自己的一部分。这种处于变化发展中的文化,其民族性往往更为鲜明突出,更符合民族文化发展的 需要。以中国绘画为例,“六朝以来,就大受印度美术的影响”。内容与形式发生较大人类文化发展史表明,一种本土文化、民族文化或地域文化与外来文化进行交流互鉴时,只要坚持科学方法,保持自己文化的特性,就能不断吸收改造外来文化并使其成为自己的一部分。这种处于变化发展 中的文化,其民族性往往更为鲜明突出,更符合民族文化发展的需要。以中国绘画为例,“六朝以来,就大受印度美术的影响”。内容与形式发生较大人类文化发展史表明,一种本土文化、民族文化或地域文化与外来文化进行交流互鉴时,只要坚持科学方法,保持自己文化的特性,就能不断
最新2018重庆中考数学25题几何证明

2017年12月04日月之恒的初中数学组卷一.解答题(共 小题).( 贵港)已知: 是等腰直角三角形,动点 在斜边 所在的直线上,以 为直角边作等腰直角三角形 ,其中 ,探究并解决下列问题:( )如图 ,若点 在线段 上,且 , ,则:线段 , ;猜想: , , 三者之间的数量关系为;( )如图 ,若点 在 的延长线上,在( )中所猜想的结论仍然成立,请你利用图 给出证明过程;( )若动点 满足 ,求的值.(提示:请利用备用图进行探求).( 保亭县模拟)如图 ,在 和 中, , , 与 交于 , 与 、 分别交于 、.( )试说明 ;( )如图 , 不动,将 从 的位置绕点 顺时针旋转,当旋转角 为多少度时,四边形 是平行四边形,请说明理由;( )当 时,在( )的条件下,求四边形 的面积..( 春 嘉兴期末)如图,菱形 中, ,有一度数为 的 绕点 旋转.( )如图 ,若 的两边 , 分别交 , 于点 , ,则线段 , 的大小关系如何?请证明你的结论;( )如图 ,若 的两边 , 分别交 , 的延长线于点 , ,则线段 ,还有( )中的结论吗?请说明你的理由..( 营口)【问题探究】( )如图 ,锐角 中分别以 、 为边向外作等腰 和等腰 ,使 , , ,连接 , ,试猜想 与 的大小关系,并说明理由.【深入探究】( )如图 ,四边形 中, , , ,求 的长.( )如图 ,在( )的条件下,当 在线段 的左侧时,求 的长..( 菏泽)如图,已知 , 是直线 上的点, .( )如图 ,过点 作 ,并截取 ,连接 、 、 ,判断 的形状并证明;( )如图 , 是直线 上一点,且 ,直线 、 相交于点 , 的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由..( 春 重庆校级期末)如图 , 中, 于点 , 于点 ,连接.( )若 , , ,求 的周长;( )如图 ,若 , , 的角平分线 交 于点 ,求证: ;( )如图 ,若 , ,将 沿着 翻折得到 ,连接 、 ,请猜想线段 、 、 之间的数量关系,并证明你的结论..( 于洪区一模)如图 ,在 中, 为锐角,点 为射线 上一点,连接 ,以 为一边且在 的右侧作正方形 .( )如果 , ,当点 在线段 上时(与点 不重合),如图 ,线段 、 所在直线的位置关系为,线段 、 的数量关系为;当点 在线段 的延长线上时,如图 , 中的结论是否仍然成立,并说明理由;( )如果 , 是锐角,点 在线段 上,当 满足什么条件时, (点 、 不重合),并说明理由..( 绍兴)( )如图 ,正方形 中,点 , 分别在边 , 上, ,延长 到点 ,使 ,连结 , .求证: .( )如图,等腰直角三角形 中, , ,点 , 在边 上,且 ,若 , ,求 的长..( 东营)( )如图( ),已知:在 中, , ,直线 经过点 , 直线 , 直线 ,垂足分别为点 、 .证明: .( )如图( ),将( )中的条件改为:在 中, , 、 、 三点都在直线 上,并且有 ,其中 为任意锐角或钝角.请问结论 是否成立?如成立,请你给出证明;若不成立,请说明理由.( )拓展与应用:如图( ), 、 是 、 、 三点所在直线 上的两动点( 、 、 三点互不重合),点 为 平分线上的一点,且 和 均为等边三角形,连接 、 ,若 ,试判断 的形状..( 昭通)已知 为等边三角形,点 为直线 上的一动点(点 不与 、 重合),以 为边作菱形 ( 、 、 、 按逆时针排列),使 ,连接 .( )如图 ,当点 在边 上时,求证: ; ;( )如图 ,当点 在边 的延长线上且其他条件不变时,结论 是否成立?若不成立,请写出 、 、 之间存在的数量关系,并说明理由;( )如图 ,当点 在边 的延长线上且其他条件不变时,补全图形,并直接写出 、 、 之间存在的数量关系..( 常德)已知两个共一个顶点的等腰 , , ,连接 , 是 的中点,连接 、 .( )如图 ,当 与 在同一直线上时,求证: ;( )如图 ,若 , ,求 , 的长;( )如图 ,当 时,求证: ..( 庐阳区校级模拟)如图,将两个全等的直角三角形 、 拼在一起(图 ). 不动,( )若将 绕点 逆时针旋转,连接 , 是 的中点,连接 、 (图 ),证明: .( )若将图 中的 向上平移, 不变,连接 , 是 的中点,连接 、 (图 ),判断并直接写出 、 的数量关系.( )在( )中,若 的大小改变(图 ),其他条件不变,则( )中的 、 的数量关系还成立吗?说明理由..( 武汉模拟)已知 中, .( )如图 ,在 中,若 ,且 ,求证: ;( )如图 ,在 中,若 ,且 垂直平分 , , ,求 的长;( )如图 ,在 中,当 垂直平分 于 ,且 时,试探究 , , 之间的数量关系,并证明..( 长春)感知:如图 ,点 在正方形 的边 上, 于点 , 于点 ,可知 .(不要求证明)拓展:如图 ,点 、 分别在 的边 、 上,点 、 在 内部的射线 上, 、 分别是 、 的外角.已知 , ,求证: .应用:如图 ,在等腰三角形 中, , > .点 在边 上, ,点 、 在线段 上, .若 的面积为 ,则 与 的面积之和为..( 昌平区模拟)( )如图,在四边形 中, , , 、 分别是边 、 上的点,且 .求证: ;( )如图,在四边形 中, , , 、 分别是边 、 上的点,且 ,( )中的结论是否仍然成立?( )如图,在四边形 中, , , 、 分别是边 、 延长线上的点,且 ,( )中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明..( 哈尔滨模拟)已知 是等腰三角形, , 为边 上任意一点, 于 , 于 ,且 , 分别在边 , 上.( )如图 ,当 是等边三角形时,证明: .( )如图 ,若 中, ,探究线段 , , 之间的数量关系,并对你的猜想加以证明.( )如图 ,若 中, , , ,利用你对( ),( )两题的解题思路计算出线段 ( > )的长..( 绍兴)数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:( )特殊情况 探索结论当点 为 的中点时,如图 ,确定线段 与的 大小关系.请你直接写出结论:(填 > , < 或 ).( )特例启发,解答题目解:题目中, 与 的大小关系是: (填 > , < 或 ).理由如下:如图 ,过点 作 ,交 于点 ,(请你完成以下解答过程)( )拓展结论,设计新题在等边三角形 中,点 在直线 上,点 在直线 上,且 .若 的边长为 , ,求 的长(请你直接写出结果)..( 沈阳)已知, 为等边三角形,点 为直线 上一动点(点 不与 、 重合).以 为边作菱形 ,使 ,连接 .( )如图 ,当点 在边 上时,求证: ; 请直接判断结论 是否成立;( )如图 ,当点 在边 的延长线上时,其他条件不变,结论 是否成立?请写出 、 、 之间存在的数量关系,并写出证明过程;( )如图 ,当点 在边 的延长线上时,且点 、 分别在直线 的异侧,其他条件不变,请补全图形,并直接写出 、 、 之间存在的等量关系..( 梅州)如图 ,已知线段 的长为 ,点 是 上的动点( 不与 , 重合),分别以 、 为边向线段 的同一侧作正 和正 .( )当 与 的面积之和取最小值时, ;(直接写结果)( )连接 、 ,相交于点 ,设 ,那么 的大小是否会随点 的移动面变化?请说明理由;( )如图 ,若点 固定,将 绕点 按顺时针方向旋转(旋转角小于 ),此时 的大小是否发生变化?(只需直接写出你的猜想,不必证明).( 抚顺)如图 ,在 中, , , 为斜边 上的中线,将 绕点 顺时针旋转 ( < < ),得到 ,点 的对应点为点 ,点 的对应点为点 ,连接 、 .( )判断 与 的位置、数量关系,并说明理由;( )若连接 、 ,请直接写出在旋转过程中四边形 能形成哪些特殊四边形;( )如图 ,将 中 改成 时,其他条件不变,直接写出 为多少度时( )中的两个结论同时成立..( 安徽模拟)如图,在 中, , ,且 > , 于 , 于 , 于 .( )在图( )中, 是 边上的中点,计算 和 的长(用 , 表示),并判断 与 的关系.( )在图( )中, 是线段 上的任意一点, 与 的关系是否仍然成立?如果成立,证明你的结论;如果不成立,请说明理由.( )在图( )中, 是线段 延长线上的点,探究 、 与 的关系.(不要求证明).( 丹东)如图,已知等边三角形 中,点 , , 分别为边 , , 的中点, 为直线 上一动点, 为等边三角形(点 的位置改变时, 也随之整体移动).( )如图 ,当点 在点 左侧时,请你判断 与 有怎样的数量关系?点 是否在直线 上?都请直接写出结论,不必证明或说明理由;( )如图 ,当点 在 上时,其它条件不变,( )的结论中 与 的数量关系是否仍然成立?若成立,请利用图 证明;若不成立,请说明理由;( )若点 在点 右侧时,请你在图 中画出相应的图形,并判断( )的结论中 与 的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由..( 铁岭) 是等边三角形,点 是射线 上的一个动点(点 不与点 、 重合), 是以 为边的等边三角形,过点 作 的平行线,分别交射线 、 于点 、 ,连接 .( )如图( )所示,当点 在线段 上时.求证: ;探究四边形 是怎样特殊的四边形?并说明理由;( )如图( )所示,当点 在 的延长线上时,直接写出( )中的两个结论是否成立;( )在( )的情况下,当点 运动到什么位置时,四边形 是菱形?并说明理由.。
2018年中考数学总复习经典(几何)试题(含答案)

中考数学总复习经典题(几何)(二)几何试题1、 如图,正方形ABCD 的边长为2,点E 在AB 边上.四边形EFGB 也为正方形,设△AFC 的面积为S ,则 ( )A .S=2B .S=2.4C .S=4D .S 与BE 长度有关2、正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图4所示,点G 在线段DK 上,正方形BEFG 的边长为4,则DEK △的面积为: (A)10 (B)12 (C)14 (D)163、如图,矩形ABCD 中,3AB =cm ,6AD =cm ,点E 为AB 边上的任意一点,四边形EFGB 也是矩形,2EF BE =,则AFC S =△ 2cm .4、 如图,在△ABC 中, ο70=∠CAB . 在同一平面内, 将△ABC 绕点A 旋转到△//C AB 的位置, 使得AB CC ///, 则=∠/BAB ( )A. ο30 B. ο35 C. ο40 D. ο50 5、如图,1P 是一块半径为1的半圆形纸板,在1P 的左下端剪去一个半径为12的半圆后得到图形2P ,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆1的半径)得图形34,,,,n P P P L L ,记纸板n P 的面积为n S , 试计算求出2S = ;3S = ;并猜想得到1n n S S --= ()2n ≥。
6、如图,在四边形ABCD 中,P 是对角线BD 的中点,E F ,分别是AB CD ,的中点,18AD BC PEF =∠=o ,,则PFE ∠的度数是 .(第16题)CFD BE A P (第6题)ADCEF GB 3题图 D ABRP F CGK图4E8题10题 12题7、如图,点G 是ABC △的重心,CG 的延长线交AB 于D ,5cm GA =,4cm GC =,3cm GB =,将ADG △绕点D 旋转180o得到BDE △,则DE = cm ,ABC △的面积= cm 2.8、如图,已知梯形ABCD ,AD BC ∥,4AD DC ==,8BC =,点N 在BC 上,2CN =,E 是AB 中点,在AC 上找一点M 使EM MN +的值最小,此时其最小值一定等于( ) A .6B .8C .4D .439、将一副直角三角板按图示方法放置(直角顶点重合),则AOB DOC ∠+∠= o.10、已知:如图,在正方形ABCD 外取一点E ,连接AE 、BE 、DE .过点A 作AE 的垂线交DE 于点P .若AE=AP =1,PB = 5 .下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为 2 ;③EB ⊥ED ;④S △APD +S △APB =1+ 6 ;⑤S 正方形ABCD =4+ 6 .其中正确结论的序号是()A .①③④B .①②⑤C .③④⑤D .①③⑤11、如图,直角梯形ABCD 中,∠BCD =90°,AD ∥BC ,BC =CD ,E 为梯形内一点,且∠BEC =90°,将△BEC 绕C 点旋转90°使BC 与DC 重合,得到△DCF ,连EF 交CD 于M .已知BC =5,CF =3,则DM:MC 的值为 ( ) A.5:3 B.3:5 C.4:3 D.3:412、如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD=2,将腰CD 以D 为中心逆时针旋转90°至ED ,AE 、DE ,△ADE 的面积为3,则BC 的长为 . 13、如图,四边形OABC 为菱形,点B 、C 在以点O 为为圆心的上,若OA = 3,∠1 = ∠2,则扇形OEF 的面积为_________.14、 如图,点P 是∠AOB 的角平分线上一点,过点P 作PC ∥OA 交OB 于点C.若∠AOB = 60o,OC = 4,则点P 到OA 的距离PD 等于__________. 15、如图,在Rt ABC △中,90ACB ∠=°,3BC =,4AC =,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( )A .32 B .76 C .256D .2B AC D O P (第14题) AD B EC (第15题) ABE G CD(第7题)C D AO B30°45°A D EM(第11题(第13题)O A B C F 1 2 E E D(第20题)16、如图,⊙P 内含于⊙O ,⊙O 的弦AB 切⊙P 于点C ,且OP AB //.若阴影部分的面积为π9,则弦AB 的长为( )A .3B .4C .6D .917、如图,等腰△ABC 中,底边a BC =,︒=∠36A ,ABC ∠的平分线交AC 于D ,BCD ∠的平分线交BD 于E ,设215-=k ,则=DE ( )A .a k 2B .a k 3C .2k aD .3ka18、如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BD 、CD 、AC 的中点,要使四边形EFGH 是菱形,四边形ABCD 还应满足的一个条件是19、如图,把矩形纸条ABCD 沿EF 、GH 同时折叠,B 、C 两点恰好落在AD 边的P 点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD 的边BC 长为 . 20、.梯形ABCD 中AB ∥CD ,∠ADC +∠BCD =90°,以AD 、AB 、BC 为斜边向形外作等腰直角三角形,其面积分别是S 1、S 2、S 3 ,且S 1 +S 3 =4S 2,则CD =( )A. 2.5ABB. 3ABC. 3.5ABD. 4AB21、如图,在□ABCD 中,AB =3,AD =4,∠ABC =60°,过BC 的中点E 作EF ⊥AB ,垂足为点F ,与DC 的延长线相交于点H ,则△DEF 的面积是 .22、如图,已知a ∥b ,∠1=70°,∠2=40°,则∠3= __________。
精品上海市各区2018届精品中考二模数学分类汇编:几何证明专题(含答案)

上海市各区2018届九年级中考二模数学试卷精选汇编几何证明专题宝山区、嘉定区23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图6,在正方形ABCD 中,点M 是边BC 上的一点(不与B 、C 重合),点N 在CD 边的延长线上,且满足︒=∠90MAN ,联结MN 、AC ,MN 与边AD 交于点E . (1)求证;AN AM =;(2)如果NAD CAD ∠=∠2,求证:AE AC AM ⋅=2.23.证明:(1)∵四边形ABCD 是正方形∴AD AB =,︒=∠=∠=∠=∠90BCD ADC B BAD ……1分 ∴︒=∠+∠90MAD MAB ∵︒=∠90MAN∴︒=∠+∠90MAD NAD ∴NAD MAB ∠=∠………1分 ∵︒=∠+∠180ADC ADN ∴︒=∠90ADN ……1分 ∴ADN B ∠=∠……………………1分 ∴△ABM ≌△ADN ………………………1分 ∴AN AM = ……………………………1分(2)∵四边形ABCD 是正方形 ∴AC 平分BCD ∠和BAD ∠∴︒=∠=∠4521BCD BCA ,︒=∠=∠=∠4521BAD CAD BAC ……1分 ∵NAD CAD ∠=∠2 ∴︒=∠5.22NAD∵NAD MAB ∠=∠ ∴︒=∠5.22MAB ………1分 ∴︒=∠5.22MAC ∴︒=∠=∠5.22NAE MAC ∵AN AM =,︒=∠90MAN ∴︒=∠45ANE∴ANE ACM ∠=∠…………………1分图6图6∴△ACM ∽△ANE …………1分 ∴ANACAE AM =……1分 ∵AN AM =∴AE AC AM ⋅=2…………1分长宁区23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,在四边形ABCD 中,AD //BC ,E 在BC 的延长线,联结AE 分别交BD 、CD 于点 G 、F ,且AG GF BE AD =. (1)求证:AB //CD ;(2)若BD GD BC ⋅=2,BG =GE ,求证:四边形ABCD 是菱形.23.(本题满分12分,第(1)小题5分,第(2)小题7分)证明:(1)∵BC AD // ∴BG DG BE AD = (2分)∵AG GFBE AD =∴AGGF BG DG = (1分) ∴ CD AB // (2分) (2)∵BC AD //,CD AB //∴四边形ABCD 是平行四边形 ∴BC=AD (1分) ∵ BD GD BC ⋅=2∴ BD GD AD ⋅=2即ADGDBD AD =又 ∵BDA ADG ∠=∠ ∴ADG ∆∽BDA ∆ (1分) ∴ABD DAG ∠=∠∵CD AB // ∴BDC ABD ∠=∠ ∵BC AD // ∴E DAG ∠=∠∵BG =GE ∴E DBC ∠=∠ ∴DBC BDC ∠=∠ (3分) ∴BC=CD (1分) ∵四边形ABCD 是平行四边形 ∴平行四边形ABCD 是菱形. (1分)ACDEF GB第23题图崇明区23.(本题满分12分,第(1)、(2)小题满分各6分)如图,AM 是ABC △的中线,点D 是线段AM 上一点(不与点A 重合).DE AB ∥交BC 于点K ,CE AM ∥,联结AE . (1)求证:AB CMEK CK=; (2)求证:BD AE =.23.(本题满分12分,每小题6分) (1)证明:∵DE AB ∥∴ ABC EKC =∠∠ ……………………………………………………1分∵CE AM ∥∴ AMB ECK =∠∠ ……………………………………………………1分∴ABM EKC △∽△ ……………………………………………………1分 ∴AB BMEK CK=………………………………………………………1分 ∵ AM 是△ABC 的中线∴BM CM = ………………………………………………………1分∴AB CMEK CK=………………………………………………………1分 (2)证明:∵CE AM ∥∴DE CMEK CK =………………………………………………………2分 又∵AB CMEK CK=∴DE AB = ………………………………………………………2分 又∵DE AB ∥(第23题图)ABK MCDE∴四边形ABDE 是平行四边形 …………………………………………1分 ∴BD AE = ………………………………………………………1分奉贤区23.(本题满分12分,每小题满分各6分)已知:如图7,梯形ABCD ,DC ∥AB ,对角线AC 平分∠BCD , 点E 在边CB 的延长线上,EA ⊥AC ,垂足为点A . (1)求证:B 是EC 的中点;(2)分别延长CD 、EA 相交于点F ,若EC DC AC ⋅=2,求证:FC AC AF AD ::=.黄浦区23.(本题满分12分)如图,点E 、F 分别为菱形ABCD 边AD 、CD 的中点. (1)求证:BE =BF ;(2)当△BEF 为等边三角形时,求证:∠D =2∠A .23. 证:(1)∵四边形ABCD 为菱形,∴AB =BC =AD =CD ,∠A =∠C ,——————————————————(2分)ACD E图7B又E、F是边的中点,∴AE=CF,——————————————————————————(1分)∴△ABE≌△CBF———————————————————————(2分)∴BE=BF. ——————————————————————————(1分)(2)联结AC、BD,AC交BE、BD于点G、O. ——————————(1分)∵△BEF是等边三角形,∴EB=EF,又∵E、F是两边中点,∴AO=12AC=EF=BE.——————————————————————(1分)又△ABD中,BE、AO均为中线,则G为△ABD的重心,∴1133OG AO BE GE===,∴AG=BG,——————————————————————————(1分)又∠AGE=∠BGO,∴△AGE≌△BGO,——————————————————————(1分)∴AE=BO,则AD=BD,∴△ABD是等边三角形,———————————————————(1分)所以∠BAD=60°,则∠ADC=120°,即∠ADC=2∠BAD. —————————————————————(1分)金山区23.(本题满分12分,每小题6分)如图7,已知AD是△ABC的中线,M是AD的中点,过A点作AE∥BC,CM的延长线与AE相交于点E,与AB相交于点F.(1)求证:四边形AEBD是平行四边形;(2)如果AC=3AF,求证四边形AEBD是矩形.E AFM23.证明:(1)∵AE //BC ,∴∠AEM =∠DCM ,∠EAM =∠CDM ,……………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,…………………………(1分) ∵BD=CD ,∴AE =BD .……………………………………………………(1分) ∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………(2分)(2)∵AE //BC ,∴AF AEFB BC=.…………………………………………………(1分) ∵AE=BD=CD ,∴12AF AE FB BC ==,∴AB=3AF .……………………………(1分) ∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分) 又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分) ∴四边形AEBD 是矩形.……………………………………………………(1分)静安区23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分) 已知:如图,在平行四边形ABCD 中, AC 、DB 交于点E , 点F 在BC 的延长线上,联结EF 、DF ,且∠DEF =∠ADC .(1)求证:DBABBF EF =; (2)如果DF AD BD ⋅=22,求证:平行四边形ABCD 是矩形.23.(本题满分12分,第(1)小题6分,第(2)小题6分) 证明:(1)∵平行四边形ABCD ,∴AD //BC ,AB //DC∴∠BAD +∠ADC =180°,……………………………………(1分) 又∵∠BEF +∠DEF =180°, ∴∠BAD +∠ADC =∠BEF +∠DEF ……(1分)C第23题图AB DEFA DE∵∠DEF =∠ADC ∴∠BAD =∠BEF , …………………………(1分) ∵AB //DC , ∴∠EBF =∠ADB …………………………(1分)∴△ADB ∽△EBF ∴DB ABBF EF = ………………………(2分) (2) ∵△ADB ∽△EBF ,∴BFBEBD AD =, ………………………(1分) 在平行四边形ABCD 中,BE =ED =BD 21∴221BD BE BD BF AD =⋅=⋅∴BF AD BD ⋅=22, ………………………………………(1分) 又∵DF AD BD ⋅=22∴DF BF =,△DBF 是等腰三角形 …………………………(1分) ∵DE BE =∴FE ⊥BD , 即∠DEF =90° …………………………(1分) ∴∠ADC =∠DEF =90° …………………………(1分) ∴平行四边形ABCD 是矩形 …………………………(1分)闵行区23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)如图,已知在△ABC 中,∠BAC =2∠C ,∠BAC 的平分线AE 与∠ABC 的平分线BD 相交于点F ,FG ∥AC ,联结DG .(1)求证:BF BC AB BD ⋅=⋅; (2)求证:四边形ADGF 是菱形.23.证明:(1)∵AE 平分∠BAC ,∴∠BAC =2∠BAF =2∠EAC .∵∠BAC =2∠C ,∴∠BAF =∠C =∠EAC .…………………………(1分) 又∵BD 平分∠ABC ,∴∠ABD =∠DBC .……………………………(1分) ∵∠ABF =∠C ,∠ABD =∠DBC ,∴ABF CBD ∆∆∽.…………………………………………………(1分) ∴AB BFBC BD=.………………………………………………………(1分) ∴BF BC AB BD ⋅=⋅.………………………………………………(1分) (2)∵FG ∥AC ,∴∠C =∠FGB ,∴∠FGB =∠FAB .………………(1分)ABEGCFD(第23题图)∵∠BAF =∠BGF ,∠ABD =∠GBD ,BF =BF ,∴ABF GBF ∆∆≌.∴AF =FG ,BA =BG .…………………………(1分) ∵BA =BG ,∠ABD =∠GBD ,BD =BD ,∴ABD GBD ∆∆≌.∴∠BAD =∠BGD .……………………………(1分) ∵∠BAD =2∠C ,∴∠BGD =2∠C ,∴∠GDC =∠C ,∴∠GDC =∠EAC ,∴AF ∥DG .……………………………………(1分) 又∵FG ∥AC ,∴四边形ADGF 是平行四边形.……………………(1分) ∴AF =FG .……………………………………………………………(1分) ∴四边形ADGF 是菱形.……………………………………………(1分)普陀区23.(本题满分12分)已知:如图9,梯形ABCD 中,AD ∥BC ,DE ∥AB ,DE 与对角线AC 交于点F ,FG ∥AD ,且FG EF =. (1)求证:四边形ABED 是菱形; (2)联结AE ,又知AC ⊥ED ,求证:212AE EF ED =.23.证明:(1)∵ AD ∥BC ,DE ∥AB ,∴四边形ABED 是平行四边形. ··························· (2分)∵FG ∥AD ,∴FG CFAD CA=. ·················································································· (1分) 同理EF CFAB CA = . ··································································································· (1分) 得FG AD =EF AB∵FG EF =,∴AD AB =. ···················································································· (1分) ∴四边形ABED 是菱形. ························································································· (1分) (2)联结BD ,与AE 交于点H .ABC DE FG图9∵四边形ABED 是菱形,∴12EH AE =,BD ⊥AE . ····································· (2分) 得90DHE ∠= .同理90AFE ∠=.∴DHE AFE ∠∠=.································································································ (1分) 又∵AED ∠是公共角,∴△DHE ∽△AFE . ··················································· (1分)∴EH DEEF AE =. ········································································································· (1分) ∴212AE EF ED =. ······························································································ (1分) 青浦区23.(本题满分12分,第(1)、(2)小题,每小题6分)如图7,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点M ,点E 在边 BC 上,且 DAE DCB ∠=∠,联结AE ,AE 与BD 交于点F .(1)求证:2DM MF MB =⋅; (2)联结DE ,如果3BF FM =,求证:四边形ABED 是平行四边形.23.证明:(1)∵AD //BC ,∴∠=∠DAE AEB , ····························································· (1分)∵∠=∠DCB DAE ,∴∠=∠DCB AEB , ··········································· (1分) ∴AE //DC , ···································································································· (1分)∴=FM AMMD MC.·························································································· (1分) ∵AD //BC ,∴=AM DMMC MB, ····································································· (1分) ∴=FM DMMD MB, ························································································· (1分) 即2=⋅MD MF MB .(2)设=FM a ,则=3BF a ,=4BM a . ························································· (1分)由2=⋅MD MF MB ,得24=⋅MD a a ,∴2=MD a , ································································································ (1分) ∴3==DF BF a . ························································································ (1分) ∵AD //BC ,∴1==AF DFEF BF, ····································································· (1分) MFE DCBA图7∴=AF EF , ································································································· (1分) ∴四边形ABED 是平行四边形. ······································································ (1分)松江区23.(本题满分12分,第(1)小题满分7分,第(2)小题满分5分)如图,已知梯形ABCD 中,AB ∥CD ,∠D =90°,BE 平分∠ABC ,交CD 于点E , F 是AB 的中点,联结AE 、EF ,且AE ⊥BE .求证:(1)四边形BCEF 是菱形;(2)2BE AE AD BC ⋅=⋅.23.(本题满分12分,第(1)小题满分7分,第(2)小题满分5分) 证明:(1) ∵BE 平分∠ABC ,∴∠ABE =∠CBE …………………………………………………1分 ∵AE ⊥BE ∴∠AEB =90° ∵F 是AB 的中点 ∴12EF BF AB ==………………………………………………1分 ∴∠FEB =∠FBE …………………………………………………1分 ∴∠FEB =∠CBE …………………………………………………1分 ∴EF ∥BC …………………………………………………1分 ∵AB ∥CD∴四边形BCEF 是平行四边形…………………………1分 ∵EF BF =∴四边形BCEF 是菱形……………………………………1分(2) ∵四边形BCEF 是菱形, ∴BC =BF∵12BF AB =(第23题图)FACD E(第23题图)FACD EB∴AB =2BC ………………………………………………1分∵ AB ∥CD∴ ∠DEA =∠EAB∵ ∠D =∠AEB∴ △EDA ∽△AEB ………………………………………2分∴AD AE BE AB = …………………………………………1分 ∴ BE ·AE =AD ·AB∴ 2BE AE AD BC ⋅=⋅…………………………………1分徐汇区23. 在梯形ABCD 中,AD ∥BC ,AB CD =,BD BC =,点E 在对角线BD 上,且DCE DBC ∠=∠.(1)求证:AD BE =;(2)延长CE 交AB 于点F ,如果CF AB ⊥,求证:4EF FC DE BD ⋅=⋅.杨浦区23、(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图7,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G 的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN。
河北省2018年中考数学总复习 几何证明专题

河北中考复习之几何证明1、如图1,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是【】A.22B.21 C.23 D.322、如图2,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线长是A.10 B.212C.152D.123、小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图3所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料A.15匹B.20匹C.30匹D.60匹4、如图4,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于.5、一个正方形和两个等边三角形的位置如图5所示,若∠3=50°,则∠1+∠2=()A.90° B.100° C.130° D.180°6、把三张大小相同的正方形卡片A,B,C叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图6-1摆放时,阴影部分的面积为S1;若按图6-2摆放时,阴影部分的面积为S2,则S1 S2(填“>”、“<”或“=”).7、如图7-1,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A’B’D’的位置,得到图7-2,则阴影部分的周长为.8、用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图8-1,用n个全等的正六边形按这种方式拼接,如图8-2,若围成一圈后中间也形成一个正多边形,则n的值为.9、如图10,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是()A.7 B.8 C.9 D.10、平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图10,则∠3+∠1-∠2= .BCDEF GHA图3AB CD图4图2AB CDABDCERPQ图1图5 图6-1 图7-1 图8-2图6-2 图7-2 图8-1图14 图10 图11 图12 图1312、如图12,边长为a 的正六边形内有两个三角形(数据如图),则空白阴影s s A . 3 B.4 C .5 D . 613、如图13,M 是铁丝AD 的中点,将该铁丝首尾相接折成△ABC ,且∠B=30°,∠C=100°,如图13.则下列说法正确的是( )A .点M 在AB 上 B .点M 在BC 的中点处 C .点M 在BC 上,且距点B 较近,距点C 较远D .点M 在BC 上,且距点C 较近,距点B 较远14、如图14,将长为8cm 的铁丝首尾相接围成半径为2cm 的扇形.则扇形s =15、小宇同学在一次手工制作活动中,先把一张矩形纸片按图9—1的方式进行折叠,使折痕的左侧部分比右侧部分短1cm ;展开后按图9—2的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm ,再展开后,在纸上形成的两条折痕之间的距离是A .0.5cmB .1cmC .1.5cmD .2cm16、如图15,等边△ABC 的边长为1cm ,D 、E 分别是AB 、AC 上的点,将△ADE 沿直线DE 折叠,点A 落在点A ′处,且点A ′在△ABC 外部,则阴影部分图形的周长为 cm .17、如图16,△ABC 中,D ,E 分别是边AB ,AC 的中点.若DE=2,则BC=( )A .2 B .3 C .4 D .5 18、如图17,将长为2、宽为1的矩形纸片分割成n 个三角形后,拼成面积为2的正方形,则n ≠( ) A .2 B .3 C .4 D .519、如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A ,B 围成的正方体上的距离是( )A .0 B .1 C .2 D . 320、如图14,已知△ABC (AC <BC ),用尺规在BC 上确定一点P ,使PA+PC=BC ,则符合要求的作图痕迹是( )A .B .C .D .20、嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD ,并写出了如下不完整的已知和求证. 已知:如图1,在四边形ABCD 中,BC=AD ,AB= 求证:四边形ABCD 是 四边形. (1)在方框中填空,以补全已知和求证; (2)按嘉淇的想法写出证明;(3)用文字叙述所证命题的逆命题为 . 21、如图,△ABC 中,AB=AC ,∠BAC=40°,将△ABC 绕点A 按逆时针方向旋转100°.得到△ADE ,连接BD ,CE 交于点F .左 右左 右 第二次折叠 第一次折叠 图9-1 图9-2 图15 图16 图17 图14(1)求证:△ABD≌△ACE;(2)求∠ACE的度数;(3)求证:四边形ABFE是菱形.22、如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,又知∠EFD=∠BCD,请问你能推出什么结论?(直接写出一个结论,要求结论中含有字母E)23、如图,在▱ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.(1)求证:△AED≌△CFB;(2)若∠A=30°,∠DEB=45°,求证:DA=DF.22.在▱ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.23、在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是3 km和2 km,AB= a km(a>1).现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.方案设计某班数学兴趣小组设计了两种铺设管道方案:图13-1是方案一的示意图,设该方案中 管道长度为d 1,且d 1=PB+BA (km )(其中BP ⊥ l 于点P );图13-2是方案二的示意图,设该方案中管道长度为d 2 ,且d 2=PA +PB (km )(其中点A '与点A 关于l 对称,A 'B 与l 交于点P ).观察计算(1)在方案一中,d 1= km (用含a的式子表示);(2)在方案二中,组长小宇为了计算d 2的长,作了如图13-3所示的辅助线,请你按小宇同学的思路计算,d 2=km (用含a 的式子表示). 探索归纳(1)①当a = 4时,比较大小: d 1 d 2(填“>”、“=”或“<”);②当a = 6时,比较大小: d 1 d 2(填“>”、“=”或“<”);(2)请你参考右边方框中的方法指导,就a (当a >1时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?24、在正方形ABCD 中,点E 是AD 上一动点,MN ⊥AB 分别交AB ,CD 于M ,N ,连接BE 交MN 于点O ,过O 作OP ⊥BE 分别交AB ,CD 于P ,Q .探究:(1)如图①,当点E 在边AD 上时,请你动手测量三条线段AE ,MP ,NQ 的长度,猜测AE 与MP+NQ 之间的数量关系,并证明你所猜测的结论;探究:(2)如图②,若点E 在DA 的延长线上时,AE ,MP ,NQ 之间的数量关系又是怎样请直接写出结论; 再探究:(3)如图③,连接并延长BN 交AD 的延长线DG 于H ,若点E 分别在线段DH 和射线HG 上时,请在图③中完成符合题意的图形,并判断AE ,MP ,NQ 之间的数量关系又分别怎样?请直接写出结论.25、在图14-1至图14-3中,点B 是线段AC 的中点,点D 是线段CE 的中点.四边形BCGF 和CDHN 都是正方形.AE 的中点是M .(1)如图14-1,点E 在AC 的延长线上,点N 与点G 重合时,点M 与点C 重合,求证:FM = MH ,FM ⊥MH ;∵22()()m n m n m n -=+-,m +n >0, ∴(22m n -)与(m n -)的符号相同. 当22m n ->0时,m n ->0,即m >n ; 当22m n -= 0时, m n -= 0,即m =n 当22m n -<0时,m n -<0,即m <n . 方法指导 当不易直接比较两个正数m 与n 的 大小时,可以对它们的平方进行比较:A l 图13 -1 A B l A ' 图13 -2 A B P C 图13 -3 K l A ' BPC(2)将图14-1中的CE 绕点C 顺时针旋转一个锐角,得到图14-2,求证:△FMH 是等腰直角三角形; (3)将图14-2中的CE 缩短到图14-3的情况,△FMH 还是等腰直角三角形吗?(不必说明理由)26、操作示例 对于边长均为a 的两个正方形ABCD 和EFGH ,按图11—1所示的方式摆放,再沿虚线BD ,EG 剪开后,可以按图中所示的移动方式拼接为图11—1中的四边形BNED .从拼接的过程容易得到结论:①四边形BNED 是正方形; ②S 正方形ABCD +S 正方形EFGH =S 正方形BNED .实践与探究(1)对于边长分别为a ,b (a >b )的两个正方形ABCD 和EFGH ,按图11—2所示的方式摆放,连结DE ,过点D 作DM ⊥DE ,交AB 于点M ,过点M 作MN ⊥DM ,过点E 作EN ⊥DE ,MN 与EN 相交于点N .①证明四边形MNED 是正方形,并用含a ,b 的代数式表 示正方形MNED 的面积;②在图11—2中,将正方形ABCD 和正方形EFGH 沿虚线剪开后,能够拼接为正方形MNED .请简略说明你的拼接方法(类比图11—1,用数字表示对应的图形).(2)对于n (n 是大于2的自然数)个任意的正方形,能否通过若干次拼接,将其拼接为一个正方形?请简要说明你的理由.27、如图14—1,14—2,四边形ABCD 是正方形,M 是AB 延长线上一点.直角三角尺的一条直角边经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点A ,B 重合),另一条直角边与∠CBM 的平分线BF 相交于点F .(1)如图14—1,当点E 在AB 边的中点位置时: ①通过测量DE ,EF 的长度,猜想DE 与EF 满足的数量关系是 ;②连接点E 与AD 边的中点N ,猜想NE 与BF 满足的数量关系是 ;③请证明你的上述两个猜想.(2)如图14—2,当点E 在AB 边上的任意位置时,请你在AD 边上找到一点N ,使得NE =BF ,进而猜想此时DE 与EF 有怎样的数量关系.28、如图13-1,一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转. (1)如图13-2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 满足的数量关系,并证明你的猜想;A B C D E F GM图11—2(H ) A CDF图14—1 N A B C D E M F 图14—2 43 2 1 A B C D E F (H ) 图11—1 (G ) 5 6图14(2)若三角尺GEF 旋转到如图13-3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.29、在图14-1—14-5中,正方形ABCD 的边长为a ,等腰直角三角形FAE 的斜边AE =2b ,且边AD 和AE 在同一直线上.操作示例 当2b <a 时,如图14-1,在BA 上选取点G ,使BG =b ,连结FG 和CG ,裁掉△FAG 和△CGB 并分别拼接到△FEH 和△CHD 的位置构成四边形FGCH .思考发现小明在操作后发现:该剪拼方法就是先将△FAG 绕点F 逆时针旋转90°到△FEH 的位置,易知EH 与AD 在同一直线上.连结CH ,由剪拼方法可得DH =BG ,故△CHD ≌△CGB ,从而又可将△CGB 绕点C 顺时针旋转90°到△CHD 的位置.这样,对于剪拼得到的四边形FGCH (如图14-1),过点F 作FM ⊥AE 于点M (图略),利用SAS 公理可判断△HFM ≌△CHD ,易得FH =HC =GC =FG ,∠FHC =90°.进而根据正方形的判定方法,可以判断出四边形FGCH 是正方形.实践探究(1)正方形FGCH 的面积是 ;(用含a ,b 的式子表示)(2)类比图14-1的剪拼方法,请你就图14-2—图14-4的三种情形分别画出剪拼成一个新正方形的示意图.联想拓展小明通过探究后发现:当b ≤a 时,此类图形都能剪拼成正方形,且所选取的点G 的位置在BA 方向上随着b 的增大不断上移.当b >a 时,如图14-5的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图;若不能,简要说明理由.图E 图图(2b =a ) (a <2b <2a ) (b图14-1 (2b <a )图(b >a ) 图13-2 G图13-3图13-1 A ( E )D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018中考数学:几何证明题答题思路总结几何证明题重点考察的是学生的逻辑思维能力,能通过严密的”因为”、”所以”逻辑将条件一步步转化为所要证明的结论。
这类题目出法相当灵活,不像代数计算类题目容易总结出固定题型的固定解法,而更看重的是对重要模型的总结、常见思路的总结。
所以对中考中最常出现的若干结论做了一个思路总结。
一、证明两线段相等
1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
12.两圆的内(外)公切线的长相等。
13.等于同一线段的两条线段相等。
二、证明两角相等
1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。
7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8.相似三角形的对应角相等。
9.圆的内接四边形的外角等于内对角。
10.等于同一角的两个角相等
三、证明两直线平行
1.垂直于同一直线的各直线平行。
2.同位角相等,内错角相等或同旁内角互补的两直线平行。
3.平行四边形的对边平行。
4.三角形的中位线平行于第三边。
5.梯形的中位线平行于两底。
6.平行于同一直线的两直线平行。
7.一条直线截三角形的两边(或延长线)所得的线段对应成比例,则这条直线平行于第三边。
四、证明两直线互相垂直
1.等腰三角形的顶角平分线或底边的中线垂直于底边。
2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。
3.在一个三角形中,若有两个角互余,则第三个角是直角。
4.邻补角的平分线互相垂直。
5.一条直线垂直于平行线中的一条,则必垂直于另一条。
6.两条直线相交成直角则两直线垂直。
7.利用到一线段两端的距离相等的点在线段的垂直平分线上。
8.利用勾股定理的逆定理。
9.利用菱形的对角线互相垂直。
10.在圆中平分弦(或弧)的直径垂直于弦。
11.利用半圆上的圆周角是直角。
五、证明线段的和、差、倍、分
1.作两条线段的和,证明与第三条线段相等。
2.在第三条线段上截取一段等于第一条线段,证明余下部分等于第二条线段。
3.延长短线段为其二倍,再证明它与较长的线段相等。
4.取长线段的中点,再证其一半等于短线段。
5.利用一些定理(三角形的中位线、含30度的直角三角形、直角三角形斜边上的中线、三角形的重心、相似三角形的性质等)。
六、证明角的和、差、倍、分
1.作两个角的和,证明与第三角相等。
2.作两个角的差,证明余下部分等于第三角。
3.利用角平分线的定义。
4.三角形的一个外角等于和它不相邻的两个内角的和。
七、证明两线段不等
1.同一三角形中,大角对大边。
2.垂线段最短。
3.三角形两边之和大于第三边,两边之差小于第三边。
4.在两个三角形中有两边分别相等而夹角不等,则夹角大的第三边大。
5.同圆或等圆中,弧大弦大,弦心距小。
6.全量大于它的任何一部分。
八、证明两角不等
1.同一三角形中,大边对大角。
2.三角形的外角大于和它不相邻的任一内角。
3.在两个三角形中有两边分别相等,第三边不等,第三边大的,两边的夹角也大。
4.同圆或等圆中,弧大则圆周角、圆心角大。
5.全量大于它的任何一部分。
九、证明比例式或等积式
1.利用相似三角形对应线段成比例。
2.利用内外角平分线定理。
3.平行线截线段成比例。
4.直角三角形中的比例中项定理即射影定理。
5.与圆有关的比例定理--相交弦定理、切割线定理及其推论。
6.利用比利式或等积式化得。
以上九项是中考几何证明题中最常出现的内容,只要掌握了对应的方法,再根据题目中的条件进行合理选择,攻克难题不再是梦想!。
