(完整word版)初中平面几何经典练习题
人教版七年级上册数学同步精炼第四章 几何图形初步复习题(word版,含答案解析)

第四章几何图形初步复习题一、选择题(共15小题;共75分)1. 下列几何体没有曲面的是( )A. 圆锥B. 圆柱C. 球D. 棱柱2. 如图所示,该几何体的俯视图是( )A. B.C. D.3. 把弯曲的道路改直,就能缩短路程,其中蕴含的数学原理是( )A. 过一点有无数条直线B. 两点确定一条直线C. 两点之间线段最短D. 线段是直线的一部分4. 如图,直角三角形绕直线l旋转一周,得到的立体图形是( )A. B.C. D.5. 下列说法正确的是( )A. 射线PA和射线AP是同一条射线B. 射线OA的长度是12cmC. 直线ab,cd相交于点MD. 两点确定一条直线6. 钟面上12点30分,时针与分针的夹角是( )A. 150∘B. 165∘C. 170∘D. 175∘7. 下面平面图形经过折叠不能围成正方体的是( )A. B.C. D.8. 下列关系式正确的是( )A. 35.5∘=35∘5ʹB. 35.5∘=35∘50ʹC. 35.5∘<35∘5ʹD. 35.5∘>35∘5ʹ9. 设时钟的时针与分针所成角是α,则正确的说法是( )A. 八点一刻时,∠α是平角B. 十点五分时,∠α是锐角C. 十一点十分时,∠α是钝角D. 十二点一刻时,∠α是直角10. 如图,已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )A. 12β B. 12(α−β) C. 12α D. α−12β。
(完整word版)初中几何最值问题
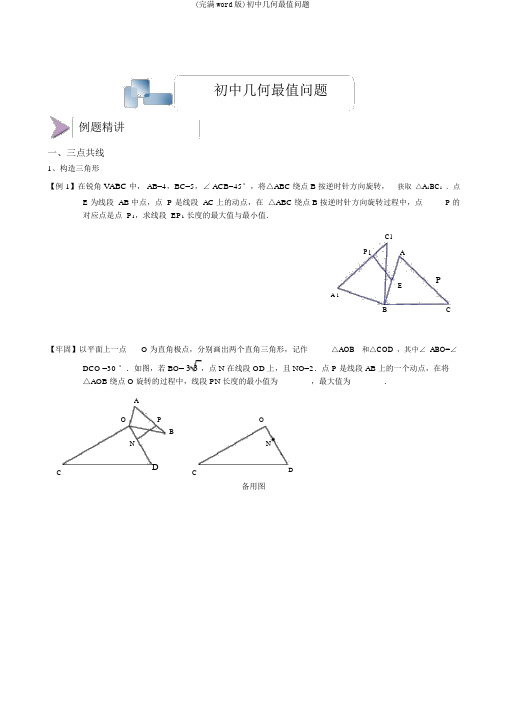
初中几何最值问题例题精讲一、三点共线1、构造三角形【例 1】在锐角VABC中, AB=4,BC=5,∠ ACB=45°,将△ABC 绕点 B 按逆时针方向旋转,获取△A1BC1.点E 为线段 AB 中点,点 P 是线段 AC 上的动点,在△ABC 绕点 B 按逆时针方向旋转过程中,点P 的对应点是点 P1,求线段 EP1长度的最大值与最小值.C1P1 AEPA 1B C 【牢固】以平面上一点O 为直角极点,分别画出两个直角三角形,记作△AOB和△COD,其中∠ ABO=∠DCO =30 °.如图,若 BO= 3 3,点 N 在线段 OD 上,且 NO=2.点 P 是线段 AB 上的一个动点,在将△AOB 绕点 O 旋转的过程中,线段 PN 长度的最小值为 _______,最大值为 _______.AO P OBN NC DC D备用图【例 2】如图,MON 90°,矩形ABCD 的极点 A. B 分别在边OM , ON 上,当 B 在边 ON 上运动时, A 随之在边 OM 上运动,矩形ABCD 的形状保持不变,其中AB=2, BC=1,运动过程中,点 D 到点O 的最大距离为 __________【牢固】已知:△AOB 中, AB OB 2 ,△COD 中,CD OC 3 ,∠ABO ∠DCO .连接AD 、BC ,点 M 、N、 P 分别为OA、OD、BC的中点.若 A 、O、C三点在同素来线上,且∠ ABO 2 ,固定△AOB ,将△ COD 绕点 O 旋转,则PM的最大值为____________B AMOP NDC【牢固】在平面直角坐标系xOy 中,点 A 、 B 分别在x轴、y轴的正半轴上,点M为线段AB的中点.点D 、E 分别在x轴、y轴的负半轴上,且DE AB 10 .以 DE 为边在第三象限内作正方形DGFE ,央求出线段MG 长度的最大值,并直接写出此时直线MG 所对应的函数的剖析式.yBMD O A xGEF【例 3 】如图,已知 A( 1, y ) ,B(2, y 2 ) 为反比率函数1P(x,0) 在x正半轴上运y图像上的两点,动点2 1 x动,当线段AP与线段BP之差达到最大时,点P的坐标是 _________yABO P x2、轴对称【例 1】求x 3 2 2 1 的最小值4x【例 2】ABE ,CD CD 是半径为5的MN 于点F,P为e O 的两条弦,EF 上任意一点,则AB 8 ,PA+PCCD 6 ,的最小值为MN 为直径,_________AB MN 于点ACM NE O P FDB【牢固】设半径为 1 的半圆的圆心为O ,直径为AB , C、 D 是半圆上两点,若弧AC 的度数为96 °,弧 BD的度数为36°,动点P在直径AB上,则CP+PD的最小值是 _______【牢固】设正三角形 ABC 的边长是2, M 是 AB 边上的中点, P 是边 BC 上任意一点,则PA+PM 的最大值为 _______,最小值为 ________【例 3】如图,已知等边△ABC 的边长为1, D、E、 F 分别是 AB、 BC、 AC 边上的点(均不与点A、 B、 C 重合),记△ DEF的周长为p .若D、E、F分别是AB、BC、AC边上任意点,则p的取值范围是.ADFB EC【例 4】如图 1,在平面直角坐标系中,抛物线y=— x2+ 2x+ 3 与 x 轴交于 A.B 两点,与y 轴交于点C,点D 是抛物线的极点.(1)求直线 AC 的剖析式及 B. D 两点的坐标;( 2)请在直线AC 上找一点M,使△BDM 的周长最小,求出点M 的坐标.图 1【例 5】如图,直线y 3 分别交 x 轴、 y 轴于 C、A 两点,将射线 AM 绕点 A 顺时针旋转 45°获取射x 23线A N, D 为 AM 上的动点, B 为 AN 上的动点,点 C 在∠ MAN 的内部.(1)当 AM∥ x 轴,且四边形 ABCD 为梯形时,求△ BCD 的面积;(2)求△BCD 周长的最小值;( 3)当△BCD 的周长获取最小值,且BD 5 2时,求△ BCD 的面积.3yA yAyA2 2 2D1 M 1 1O 123C 4x O 123C 4x O 12 3 C 4x BN备用图备用图【例 6】在直角坐标系中, A 1, 2 , B 4, 1 , C m,0 , D n, n 为四边形的 4 个极点,当四边形ABCD 的周长最短时,m_________nyODC xBA【牢固】如图1,抛物线 y= ax2+ bx+ c( a≠0)的极点为 C( 1, 4),交 x 轴于 A、 B 两点,交 y 轴于点 D,其中点 B 的坐标为( 3, 0)。
平面几何练习题

平面几何练习题题一:求三角形边长和周长已知一个三角形的两边长分别为a和b,夹角为C°,求第三边c的长度和三角形的周长P。
解:根据余弦定理可知,余弦公式为:c² = a² + b² - 2ab·cos(C)。
根据上述公式,可以计算得到c的长度。
根据三角形的定义可知,三角形的周长P等于三边之和,即P = a + b + c。
题二:求三角形的面积已知一个三角形的底边长为b,高为h,求三角形的面积S。
解:根据三角形的面积公式可知,S = 0.5 * b * h。
题三:判断点是否在三角形内部已知一个三角形的三个顶点坐标分别为A(x₁,y₁),B(x₂,y₂),C(x₃,y₃),以及一个待判断的点D(x,y),判断点D是否在三角形ABC的内部。
解:利用行列式的性质可以判断点D是否在三角形ABC内部。
设点D的坐标为(x,y),则点D在三角形ABC内部的条件为:|(x₁ - x) (y₁ - y) 1||(x₂ - x) (y₂ - y) 1| > 0|(x₃ - x) (y₃ - y) 1|如果等式左侧的行列式结果大于0,则点D在三角形ABC内部;如果等式左侧的行列式结果小于0,则点D在三角形ABC的外部;如果等式左侧的行列式结果等于0,则点D在三角形ABC所在的边界上。
题四:求矩形的面积和周长已知一个矩形的长为L,宽为W,求矩形的面积S和周长P。
解:矩形的面积公式为S = L * W,周长公式为P = 2 * (L + W)。
题五:求圆的面积和周长已知一个圆的半径为r,求圆的面积S和周长C(circumference)。
解:圆的面积公式为S = π * r²,其中π取近似值3.14159;圆的周长公式为C = 2 * π * r。
题六:判断点是否在圆内部已知一个圆的圆心坐标为O(x₀,y₀),半径为r,以及一个待判断的点P(x,y),判断点P是否在圆O内部或者在圆的边界上。
2024年数学九年级上册平面几何基础练习题(含答案)

2024年数学九年级上册平面几何基础练习题(含答案)试题部分一、选择题:1. 在平面几何中,下列哪个图形既是轴对称图形又是中心对称图形?()A. 矩形B. 等腰三角形C. 梯形D. 正五边形2. 下列各角中,哪个角是补角?()A. 30°B. 45°C. 60°D. 120°3. 在直角坐标系中,点A(2, 3)关于原点对称的点是()A. (2, 3)B. (2, 3)C. (2, 3)D. (2, 3)4. 下列哪个条件能判定两个三角形全等?()A. 两边和其中一边的对角相等B. 两角和其中一边相等C. 两边和它们的夹角相等D. 两边和其中一边的对角相等5. 若平行线l1和l2之间的距离为5cm,直线l3与l1、l2均相交,且l3与l1、l2的夹角均为45°,则l3与l1、l2之间的距离为()A. 5cmB. 5√2 cmC. 2.5cmD. 2.5√2 cm6. 下列哪个图形是正多边形?()A. 边长为1,内角为108°的多边形B. 边长为1,内角为120°的多边形C. 边长为1,内角为135°的多边形D. 边长为1,内角为140°的多边形7. 在直角三角形中,若一个锐角的度数为30°,则另一个锐角的度数为()A. 30°B. 45°C. 60°D. 90°8. 下列哪个比例式成立?()A. a² : b² = (a+b)² : (ab)²B. a² : b² = (a+b) : (ab)C. a : b = (a+b)² : (ab)²D. a : b = (a+b) : (ab)9. 若等腰三角形的底边长为8cm,腰长为5cm,则该三角形的面积为()A. 20cm²B. 40cm²C. 30cm²D. 24cm²10. 在平面几何中,下列哪个说法是正确的?()A. 对角线互相垂直的四边形一定是矩形B. 对角线互相平分的四边形一定是平行四边形C. 对角线相等的四边形一定是矩形D. 对角线互相垂直平分的四边形一定是菱形二、判断题:1. 平行线的性质是:同位角相等,内错角相等,同旁内角互补。
初二平面几何练习题及答案

在△ABC中,AB=AC,P是△ABC内部的一点,且∠APB﹥∠APC。
求证:PB<PC由于AB=AC,可将△ABP旋转至AP'C。
∵AP‘=AP,∴∠APP'=∠AP'P∵∠AP’C = ∠APB > ∠APC∴∠PP'C > ∠P'PC∴ BP=CP' < PC在△ABC中,∠C=90°,M在BC上,且BM=AC,N在AC上,且AN=MC,AM与BN相交于点P,求证:∠BPM=45°在直角三角形ABC中,∠C=90°,M在BC上,N在AC上,且BM=AC,AN=MC,求证∠BPM=45°。
证明设AC=b,BC=a, 则CM=AM=a-b,CN=2b-a。
过N点作NH∥AM,过M点作MH∥AC,交于H.连BH.则四边形ANHM是平行四边形,所以 MH=AN=CM=a-b,AM=NH.由勾股定理得:BN^2=BC^2+CN^2=a^2+(2b-a)^2=2(a^2-2ab+2b^2);AM^2=AC^2+CM^2=b^2+(a-b)^2= a^2-2ab+2b^2;BH^2=BM^2+MH^2=b^2+(a-b)^2= a^2-2ab+2b^2.所以得 AM=BH,AM^2+BH^2=BN^2。
故三角形BHN是等腰直角三角形。
因此∠BPM=∠BNH=45°。
这里的O 点相当于你们作业上的G 点 将边长为1+n/2(n=1,2,3,……)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次为A1A2A3,……2011-2-19 10:16提问者: 兔兔漂亮吗 | 浏览次数:1369次(1)若摆放前6个正方形纸片,则被遮盖的线段长度和为( ),(2)若摆放前n (n 为大于1的正整数)个正方形纸片,则被遮盖的线段长度之和为( )答案为:10 1/4*(n+2)(n-1)①过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D ,根据正方形的性质推出∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D ,求出∠AA 1B=∠DA A C ,证△BAA 1≌△CDA 1,得到AB=DC ,求出虚线部分的线段之和是1,依次求出其它虚线之和,相加即可;②根据①的结论求出12×(2+3+4+…+n )即可.①解:过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D ,∵正方形EFGH ,∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D ,∴∠AA 1D=∠BA 1C=90°,∴∠AA 1B=∠DA A C ,∴△BAA 1≌△CDA 1,∴AB=DC ,∴BF+FC=FA+FD=1+12=1,同理第2个虚线之和是1+22=3,同理第3个虚线之和是2,同理第4个虚线之和是5同理第5个虚线之和是3,∴1+32+2+52+3=12×(2+3+4+5+6)=10,②若摆放前n个(n为大于1的正整数)个正方形纸片,则图中被遮盖的线段(虚线部分)之和为12×(2+3+4+…+n)=n2+n-24,故答案为:10,n2+n-24.S△DEF+S△CEF= 12S△ABC 仍然成立.证明:当∠EDF绕点D旋转到DE⊥AC于E时,连接CD.∵Rt△ABC中,AC=BC,即△ABC为等腰直角三角形.又∵D为AB边的中点,∴CD=BD,∠ECD=∠FBD=45°,∠CDB=90°,又∵∠EDF=90°,∴∠EDF-∠CDF=∠CDB-∠CDF,即∠CDE=∠BDF,∴△CDE≌△BDF,∴S△CDE=S△BDF,∴S△DEF+S△CEF=S△CDE+S△CDF=S△BDF+S△CDF=S△BCD= 12S△ABC,得证.当∠EDF绕点D旋转到DE和AC不垂直时:猜想 S△DEF+S△CEF= 1/2S△ABC,证明:连接CD,同理易得△CDE≌△BDF,∴S△CDE=S△BDF,∴S△DEF+S△CEF=S四边形DECF=S△CDE+S△CDF=S△DBF+S△CDF=S△BCD,又S△BCD= 12S△ABC,则S△DEF+S△CEF= 12S△ABC.故答案是:S△DEF+S△CEF= 12S△ABC,S△DEF+S△CEF=12S△ABC.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M 放在△ABC的斜边AB的中点处,设AC=BC=a.解:(1),(1+)a;(2),2a;(3)猜想:重叠部分的面积为。
初二平面几何基础练习题

初二平面几何基础练习题1. 问题描述:在平面上给定一个等边三角形ABC,边长为10cm。
求三角形ABC的高和面积。
解答:设三角形ABC的高为h,由于ABC是等边三角形,所以三角形ABC也是等腰三角形。
连接AB的中点M与C,可得到三角形AMC。
由于AM与CM分别垂直于BC和AB,所以AM和CM就是三角形ABC的高。
根据勾股定理,三角形AMC的斜边AC等于三角形ABC的边长,即AC = 10cm。
由于三角形AMC是直角三角形,所以AM和CM相等,记为AM = CM = h。
根据勾股定理,有AC² = AM² + CM²,即10² = h²+ h² = 2h²。
解方程2h² = 100,可以得到h = √50 ≈ 7.07 cm。
三角形ABC的面积S可以通过底乘高的公式计算,即S = 0.5 × 10× h = 0.5 × 10 × 7.07 ≈ 35.35 cm²。
所以,三角形ABC的高为7.07 cm,面积为35.35 cm²。
2. 问题描述:在平面上给定一个矩形ABCD,已知AB = 12cm,BC = 8cm。
求矩形ABCD的对角线长度和周长。
解答:设矩形ABCD的对角线长度为d。
根据勾股定理,可以得到d² = AB² + BC² = 12² + 8² = 144 + 64 = 208。
解方程d² = 208,可以得到d = √208 ≈ 14.42 cm。
矩形ABCD的周长可以通过将四条边的长度相加得到,即周长 =AB + BC + CD + DA = 12 + 8 + 12 + 8 = 40 cm。
所以,矩形ABCD的对角线长度约为14.42 cm,周长为40 cm。
3. 问题描述:在平面上给定一个圆O,半径为6cm。
初中平面几何经典专题之绝配角问题,详细分析讲解,练习题含参考答案

绝配角问题绝配关系一个角度的一半的余角和它本身之间的关系我们称之为绝配,例如之间就是绝配关系.总结来说:半角的余角和其本身称之为绝配.当然:ɑ和90°+21ɑ之间也可是绝配关系,因为90°-21ɑ和90°+21ɑ一般成对出现。
(邻补角的角平分线所形成的角度关系)若∠AOC=α,OD 平分∠COB 则∠BOD=∠COD=90°-21α(镜面角的形式出现)若∠BOC=α,∠DOB=∠COA 则∠BOD=∠COA=90°-21α(三角形外角平分线交点形成的角)△ABC 的外角平分线相交于一点F 若∠DAE=α,则BFC=90°-(1/2)α(等腰三角形顶角和底角的关系)AB=AC ,∠A=α则∠B=∠C=90°-21α思路:当α与90°-21α两个角共顶点且共边时;常见的绝配角关系顶角2ɑ180°-2ɑ90°+2ɑ90°-2ɑ底角90°-ɑɑ45°-ɑ45°+ɑ顶角60°+2ɑ60°-2ɑ120°+2ɑ120°-2ɑ底角60°-ɑ60°+ɑ30°-ɑ30°+ɑ例1如图,在正△ABC 中,D 在BC 延长线上,E 在AD 边上,且∠CAD=2∠DBE ,BE 、AC 交于点F 若CF=1,DE=2,则CD 的长为_________方法一:把∠ADB 看作顶角构等腰,在DB 上取一点G ,使DG=DE=2方法二:把∠ABD 看作顶角构等腰;在AD 上取一点G ,使DG=DC方法三:把∠ADB 看作顶角构等腰;在DB 上取一点G ,使DG=DA方法四:把∠AFB 看作底角构等腰;延长FA 至G ,使BG=FG方法五:把AFB 看作底角构等腰,延长AF 至G 点,连接EG ,使得FG=EG练习题1.如图,在△ABC 中,AD ⊥BC ,垂足为D ,E 在AB 边上,CE 平分∠ACB ,且∠AEC=45°,若BD=6,CD=4,则BE 的长为______2.如图,在△ABC 中,AB=AC ,D 在△ABC 外,且∠ADB=90°-21∠BDC ;(1)求证:∠DBC=∠DAC(2)若∠ACD=60°,BD=5,CD=3,求AD 的长3.如图,正方形ABCD 中,E 为BC 边上一点,F 在AE 上,且AF=AD ,过点F 作FG ⊥FDFG 交AB 于点G ,若AG=2,EF=1,则FG 的长为______4.如图,在正△ABC 中,D 在BC 延长线上,E 在AD 边上,且∠DBE=21∠CAD ,BE 、AC 相交于点F,若CF=1,DE=2,则AB 的长为______5.如图△ABC 中,AB=AC ,CD ⊥AB ,垂足为D ,E 在CA 的延长线上,且∠BEC=90°+21∠ABC ,若AE=2,AD=7,则BC 的长为_______6.如图,△ABC 中,∠ACB=90°,D 在BC 边上,且∠CAD=21∠B ,E 在AB 边上,且∠ADE=∠ADC,若CD=5,BE=12,则BD 的长为______7.如图,正方形ABCD 中,AF=5,BE=8,∠AFB=2∠BCE ,求AE8.阅读下面材料:小明遇到这样一个问题:在Rt △ABC 中,∠ACB=90°,AC=BC ,点D 在BC 上,点E 在AC 上,∠ADC=2∠EBC ,若CD=mCE ,求ADCE 的值(用含m 的代数式表示)小明通过探究发现,将△ACD 绕点C 顺时针旋转90°得到△BCM ,再证出EM=BM ,问题就得到解决(1)请你根据小明的思路解决这个问题;参考小明解决问题的方法,解决下面的问题;(2)如图3,在等边△ABC 中,D 为边AB 上一点,E 为CD 上一点,∠EBC=2∠ACD ,F 为BE 上一点且∠FDE=60°,若EF=k BF,求DFDE 的值.(用含有k 的代数式表示)9.如图,在四边形ABCD 中,连接AC ,DE ⊥AC 于点E ,∠ACB=90°,21∠EDC+∠BAC=45°AC=DE ,AB=6,CD=5,则线段DE 的长为______参考答案1.解:过点B 作BF ⊥AC 于点F ,设∠ACE=α则∠BAF=∠BAD=45°+α,AB=AB ,∠AFB=∠ADB=90°故△ABF ≌△ABD ,BF=6,得CF=10,设AD=x 则AC=10-x ,由勾股定理222)8(4x x -=+,解得x =3故AD=32.解:(1)将△ABD 沿AD 向右折叠,得到△ADE 则∠ADB=∠ADE ,故∠ADB+∠ADE+∠BDC=2∠ADB+∠BDC=180°,故点C 、D 、E 共线AE=AB ,而AB=AC ,故AC=AE ,得∠AEC=∠ACE 而∠AEC=∠ABD ,故∠ABD=∠ACD 故点A 、B 、C 、D 四点共圆,所以∠CAD=∠CBD(2)过A 作AF ⊥CE 于点F ,DF=BD=5,故CE=8,而∠ACD=60°,AC=AE ,故△ACE 为等边三角形AF=43,CF=1,AF=73.解:由已知易得点A 、D 、F 、G 共圆,并引入圆交CD 于点H 则AG=DH=2,连接AH 、FH ,并延长DF 交BC 于点Q 而△ADH ≌△AFH ,FH=DH=2,又EF=1,故tan ∠FHE=21故AD=AF=4,FH 2=FA ·FE ,得∠AHE=90°,故∠FHE=α,tan ∠AFI=34,FI=512,AG=516,故GI=56,得FG=5564.见前面解析;5.解:过点B 作BG ⊥CE 于点G ,在CG 延长线上取一点I 使GI=GE,设∠ACB=∠ABC=α则∠BEC=90°-α=∠BIA △AGB ≌△ADC ,AG=AD=7,AB=AI=12,BG=85,故BC=11426.解:在BC 延长线上取一点F ,使CF=CD ,设∠B=2α,则∠DAC=α,∠F=90°-α=∠FAB 作EG ⊥BC 于点G ,则∠EDB=∠EBD=2α设DG=x,BG=x,则AE=2x-2,EG||AC 得CG BG AE BE =,52-212+=x x x ,x =10,故BC=107.解:在DA 延长线上取一点G ,使FG=FB 设∠BCE=α,则∠AFB=2α,∠AGB=90°-α故△BCE ≌△ABG ,得AG=BE=8,GF=BF=13,故AB=128.解:(1)∠M=2α,∠MEB=∠MBE=90°-α得EM=BM ,设AD=x,则BD=x,MC=x-1,AC(^2)=x(^2)-m(^2),在△BCM 中,由勾股定理可得222)1(x m x =+-,212+=m x ,故12AD CE 2+=m (2)延长DG 至点M ,使DM=DC ,连接MB 、MC 作正△MNB 连接MN ∠ACD=∠MDN=α,∠EBC=2α,易证△ACD ≌△DNM ∠BED=∠BDE=60°+α,设BF=1,则EF=k ,BD=k +1而∠BFM=∠BMF=60°-α,故BM=1,故AB=k+2;而△DEF~△DGC ,GC EF ==DC DF DG DE ,故21DM DG DC DG DF DE ++===k k ,故21DF DE ++=k k 9.解:延长AC 至F 使CF=CD ,设∠BAC=α,则∠BAC=90°-2α∠F=∠CDF=α,CF=CD=5,而△FCG~△ABC 设AC=x ,则DF=35x ,故EF=34x ,△FDE~△ABC 得x =524。
(word完整版)人教版八年级上册数学几何练习题

人教版八年级上册数学几何练习题1、已知:在⊿ABC中,∠A=90,AB=AC,在BC上任取一点P,作PQ∥AB交AC于Q,作PR∥CA交BA于R,D是BC的中点,求证:⊿RDQ是等腰直角三角形。
2、已知:在⊿ABC中,∠A=90,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
B3、已知:在⊿ABC中BD、CE是高,在BD、CE或其延长线上分别截取BM=AC、CN=AB,求证:MA⊥NA。
C4、已知:如图,在△ABC中,BP、CP分别平分∠ABC 和∠ACB,DE过点P交AB于D,交AC于E,且DE∥BC.求证:DE-DB=EC. APE DBC图⑴5、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
写出点O到△ABC的三个顶点A、B、C的距离的大小关系;如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
A M B6、如图,△ABC为等边三角形,延长BC到D,延长BA到E,AE=BD,连结EC、ED,求证:CE=DE7、如图,等腰三角形ABC中,AB=AC,∠A=90°,BD平分∠ABC,DE⊥BC且BC=10,求△DCE的周长。
几何证明习题答案1. 连接AD,由△ABC为等腰直角三角形可得AD垂直AC,且AD=BD,∠DAQ=∠DBR=45度, 又由平行关系得,四边形RPQA为矩形,所以AQ=RP, △BRP也是等腰直角三角行,即BR=PR,所以AQ=BR由边角边,△BRD全等于△AQD,所以∠BDR=∠ADQ,DR=DQ, ∠RDQ=∠RDA+∠ADQ=∠RDA+∠BDR=90度, 所以△RDQ是等腰RT△。
2. 作AG平分∠BAC交BD于G ∵∠BAC=90° ∴∠CAG= ∠BAG=45° ∵∠BAC=90° AC=AB ∴∠C=∠ABC=45°∴∠C=∠BAG ∵AE⊥BD ∴∠ABE+∠BAE=90°∵∠CAF+∠BAE=90° ∴∠CAF=∠ABE ∵ AC=AB ∴△ACF ≌△BAG ∴CF=AG ∵∠C=∠DAG =45°CD=AD ∴△CDF ≌△ADG ∴∠CDF=∠ADB3. 易证△ABM≌△NAC.∠NAM=∠NAE+∠BAM=∠NAE+ANE=90°4. 略5.因为直角三角形的斜边中点是三角形的外心,所以O到△ABC的三个顶点A、B、C距离相等;△OMN是等腰直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中平面几何经典练习题
1如图,在⊙O 中,弦CD 垂直于直径AB ,M 是OC 的中点,AM 的延长线交⊙O 于点E ,DE 与BC 交于点N.求证:BN=CN.
2.如图,直角梯形OABC 中,AB ∥OC ,O 为坐标原点,点A 在y 轴正半轴上,点C 在x 轴正半轴
上,点B 坐标为(2,2
3),∠BCO = 60°,BC OH ⊥于点H .动点P 从点H 出发,沿线段HO
向点O 运动,动点Q 从点O 出发,沿线段OA 向点A 运动,两点同时出发,速度都为每秒1个单位长度.
设点P 运动的时间为t 秒. (1) 求OH 的长;
(2)
若OPQ ∆的面积为S (平方单位). 求S 与t 之间的函数关系式.并求t 为何值时,OPQ
∆的面积最大,最大值是多少? (3)
设PQ 与OB 交于点M .①当△OPM 为等腰三角形时,求(2)中S 的值.
②探究线段OM 长度的最大值是多少?(直接写出答案).
3.已知实数x 、y 、z 满足4=+y x 及42+=z xy ,求z y x 32++的值。
6
4. 已知半径为R 的⊙O ′经过半径为r 的⊙O 的圆心,⊙O 与⊙O•′交于E 、F 两点.
(1)如图甲,连结OO ′交于⊙O 于点C ,并延长交⊙O ′于点D ,过点C 作⊙O•的切线交⊙O ′于A 、B 两点,求OA ·OB 的值; (2)若点C 为⊙O 上一动点..
, ①当点C 运动到⊙O ′内时,如图乙,过点C 作⊙O ′的切线交⊙O 于A 、B 两点,则OA ·OB 的值与(1)中的结论相比较有无变化?请说明理由.
②当点C 运动到⊙O ′外时,过点C 作⊙O 的切线,若能交⊙O ′于A 、B 两点,如图丙,则OA ·OB 的值与(1)中的结论相比较有无变化?请说明理由.
5.(1)在正方形ABCD 中,∠MAN=45°,∠MAN 绕点A 顺时针旋转,它的两边分别交CB 、DC(或它们的延长线)于点M 、N .如果∠MAN 在如图1所示的位置时,有BM+DN=MN 成立(不必证明).请问当∠MAN 绕点A 旋转到如图2所示的位置时,线段BM 、DN 和MN 之间又有怎样的数量关系?请说明理由.
(2)如图3,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,连接AD 与内切圆相交于另一点P,连接PC、PE、PF、FD,且PC⊥PF.
求证:(1)△PFD ∽△PDC;
(2)EP PD DE DC
6.如图,四边形ABCD中,∠A=∠C=90°,AB=AD,BC+CD=10.
(1)求四边形ABCD的面积;
(2)若∠ADC=60°,求四边形ABCD的周长
7.如图:⊙O的直径AB=12,AM和BM是它的两条切线,DE切⊙O于E,交AM于D,交BN于C,设AD=X,BC=Y,求Y与X的函数关系式,并画出它的大致图象.y=36/x
.
8.已知Rt△ABC中,∠ACB=90°,AC=6,BC=8.
(Ⅰ)如图①,若半径为r1的⊙O1是Rt△ABC的内切圆,求r1;
(Ⅱ)如图②,若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2;
(Ⅲ)如图③,当n大于2的正整数时,若半径rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、BC相切,⊙On与BC、AB相切,⊙O1、⊙O2、⊙O3、…、⊙On-1均与AB边相切,求rn.
9.已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的弧AB 所在圆的圆心为O′时,求O′A的长度;2
②如图2,当折叠后的弧AB 经过圆心为O时,求弧AOB 的长度;4π/ 3
③如图3,当弦AB=2时,求圆心O到弦AB的距离;3
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的弧AB 与弧CD 所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值;2
②如图5,当AB与CD不平行,折叠后的弧AB 与弧CD 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.平行四边形
与第八题类似
......
10.在Rt△ABC中,BC=3,AC=4,AB=5,
(1)如图1,D、E、F为切点,求△ABC内切圆⊙O的半径r1的值.r1=1
(2)如图2△ABC中放置两个互相外切的等圆⊙O1、⊙O2,⊙O1与AC、AB相切,⊙O2与BC、AB相切,求它们的半径r2时,小李同学是这样思考的:如果将⊙O2连同BC边向左平移2r2,使⊙O2与⊙O1重合、BC移到DE,则问题转化为第(1)问中的情况,于是可用同样的方法算出r2,你认为小李同学的想法对吗?请你求出r2的值(不限于上述小李同学的方法).r2=5/ 7
(3)如图3,n个排成一排的等圆与AB边都相切,又依次外切,前后两圆分别与AC、BC边相切,求这些等圆的半径rn.rn=5/ 3+2n
简略答案除证明题外附在各题后面,打字能力有限,见谅.。
