《圆的证明与计算》专题讲解
圆的相关证明与计算(复习讲义)(原卷版)-中考数学重难点题型专题汇总
题型五--圆的相关证明与计算(复习讲义)【考点总结|典例分析】考点01圆的有关概念1.与圆有关的概念和性质(1)圆:平面上到定点的距离等于定长的所有点组成的图形.(2)弦与直径:连接圆上任意两点的线段叫做弦,过圆心的弦叫做直径,直径是圆内最长的弦.(3)弧:圆上任意两点间的部分叫做弧,小于半圆的弧叫做劣弧,大于半圆的弧叫做优弧.(4)圆心角:顶点在圆心的角叫做圆心角.(5)圆周角:顶点在圆上,并且两边都与圆还有一个交点的角叫做圆周角.(6)弦心距:圆心到弦的距离.考点02垂径定理及其推论1.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.关于垂径定理的计算常与勾股定理相结合,解题时往往需要添加辅助线,一般过圆心作弦的垂线,构造直角三角形.2.推论(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.考点03圆心角、弧、弦的关系1.定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.圆心角、弧和弦之间的等量关系必须在同圆等式中才成立.2.推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.考点04圆周角定理及其推论1.定理一条弧所对的圆周角等于它所对的圆心角的一半.2.推论(1)在同圆或等圆中,同弧或等弧所对的圆周角相等.(2)直径所对的圆周角是直角.考点05与圆有关的位置关系1.点与圆的位置关系设点到圆心的距离为d.(1)d<r⇔点在⊙O内;(2)d=r⇔点在⊙O上;(3)d>r ⇔点在⊙O 外.判断点与圆之间的位置关系,将该点的圆心距与半径作比较即可.2.直线和圆的位置关系位置关系相离相切相交图形公共点个数0个1个2个数量关系d>r d=r d<r考点06切线的性质与判定1.切线的性质(1)切线与圆只有一个公共点.(2)切线到圆心的距离等于圆的半径.(3)切线垂直于经过切点的半径.利用切线的性质解决问题时,通常连过切点的半径,利用直角三角形的性质来解决问题.2.切线的判定(1)与圆只有一个公共点的直线是圆的切线(定义法).(2)到圆心的距离等于半径的直线是圆的切线.(3)经过半径外端点并且垂直于这条半径的直线是圆的切线.切线判定常用的证明方法:①知道直线和圆有公共点时,连半径,证垂直;②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.考点07三角形与圆1.三角形外接圆外心是三角形三条垂直平分线的交点,它到三角形的三个顶点的距离相等.2.三角形的内切圆内心是三角形三条角平分线的交点,它到三角形的三条边的距离相等.1.如图,点,,,,A B C D E 在O 上,,42AB CD AOB =∠=︒,则CED ∠=()A.48︒B.24︒C.22︒D.21︒2.如图,A,B,C 是半径为1的⊙O 上的三个点,若,∠CAB=30°,则∠ABC 的度数为()A.95°B.100°C.105°D.110°3.如图,AB 是⊙O 的直径,AC,BC 是⊙O 的弦,若20A ∠=︒,则B Ð的度数为()A.70°B.90°C.40°D.60°4.如图,Rt ABC 中,90ACB ∠=︒,AC =3BC =.点P 为ABC ∆内一点,且满足22PA PC +2AC =.当PB 的长度最小时,ACP ∆的面积是()A.3B.C.4D.25.如图,已知在⊙O 中, AB BCCD ==,OC 与AD 相交于点E.求证:(1)AD∥BC(2)四边形BCDE 为菱形.6.如图,A,B 是O 上两点,且AB OA =,连接OB 并延长到点C,使BC OB =,连接AC.(1)求证:AC 是O 的切线.(2)点D,E 分别是AC,OA 的中点,DE 所在直线交O 于点F,G,4OA =,求GF 的长.7.如图,Rt ABC 中,90ABC ∠=︒,以点C 为圆心,CB 为半径作C ,D 为C 上一点,连接AD 、CD ,AB AD =,AC 平分BAD ∠.(1)求证:AD 是C 的切线;(2)延长AD 、BC 相交于点E,若2EDC ABC S S = ,求tan BAC ∠的值.8.如图,在O 中,AB 是直径,弦CD AB ⊥,垂足为H ,E 为 BC上一点,F 为弦DC 延长线上一点,连接FE 并延长交直径AB 的延长线于点G ,连接AE 交CD 于点P ,若FE FP =.(1)求证:FE 是O 的切线;(2)若O 的半径为8,3sin 5F =,求BG 的长.9.如图,ABC 是O 的内接三角形,AC 是O 的直径,点D 是 BC的中点,//DE BC 交AC 的延长线于点E .(1)求证:直线DE 与O 相切;(2)若O 的直径是10,45A ∠=︒,求CE 的长.10.如图,已知点C 是以AB 为直径的圆上一点,D 是AB 延长线上一点,过点D 作BD 的垂线交AC 的延长线于点E ,连结CD ,且CD ED =.(1)求证:CD 是O 的切线;(2)若tan 2DCE ∠=,1BD =,求O 的半径.11.如图,AB 是⊙O 的直径,C 为⊙O 上一点,连接AC,CE⊥AB 于点E,D 是直径AB 延长线上一点,且∠BCE=∠BCD.(1)求证:CD 是⊙O 的切线;(2)若AD=8,BE CE=12,求CD的长.12.如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.(1)求证:∠CAD=∠CBA.(2)求OE的长.13.如图,⊙O的半径OA=6,过点A作⊙O的切线AP,且AP=8,连接PO并延长,与⊙O 交于点B、D,过点B作BC∥OA,并与⊙O交于点C,连接AC、CD.(1)求证:DC∥AP;(2)求AC的长.=CD =DB ,连接AD,过点D作14.如图,AB为⊙O的直径,C、D为⊙O上的两个点,ACDE⊥AC交AC的延长线于点E.(1)求证:DE是⊙O的切线.(2)若直径AB=6,求AD的长.15.如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AD=BC,AC与BD相交于点F.BE是半圆O所在圆的切线,与AC的延长线相交于点E.(1)求证:△CBA≌△DAB;(2)若BE=BF,求证:AC平分∠DAB.16.如图,AB为⊙O的直径,C为⊙O上一点,AD与过C点的直线互相垂直,垂足为D,AC 平分∠DAB.(1)求证:DC为⊙O的切线.(2)若AD=3,DC=3,求⊙O的半径.17.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若⊙O的半径为5,BC=16,求DE的长.。
中考数学题型专题复习题型2圆的证明与计算课件

即(7+x)2-72=42-x2,
解得x=1或-8(舍去).
∴AC=8,BD=
=
∴S菱形ABFC=AC·BD=8 . ∴S半圆= ×π×42=8π.
5.[2018·无锡]如图,四边形ABCD内接于圆
O,AB=17,CD=10,∠A=90°,cosB=
3 ,求AD的长.
5
解:如图,延长AD,BC交于点E.
题型2 圆的证明与计算
考查类型
与圆的性质 有关的证明
与计算
年份 2015
2018
2017
与圆的切线 有关的证明
与计算
2016
2014
2013
与扇形有关 的计算
2018
考查形式
题型
以圆内接四边形为背景,判断三角形的形状 ,结合全等三角形探究线段间关系,通过图
形分割探究四边形最大面积
解答
已知圆的切线,根据圆的性质证明两线垂直 ,并求出线段长度及弧长
∴EA=
∴AD=EA-DE=
类型②与圆的位置关系有关的证明与计算
例2►[2018·黄冈]如图,AD是⊙O的直径,AB为⊙O的弦, OP⊥AD,OP与AB的延长线交于点P,过点B的切线交OP于点C. (1)求证:∠CBP=∠ADB;
(2)若OA=2,AB=1,求线段BP的长.
规范解答:(1)证明:如图,连接OB. ∵BC是⊙O的切线. ∴OB⊥BC, ∴∠OBC=90°,即∠OBD+∠DBC=90°. ∵AD为⊙O的直径, ∴∠ABD=90°, ∴∠DBP=90°,即∠CBP+∠DBC=90°, ∴∠OBD=∠CBP. ∵OB=OD, ∴∠OBD=∠ADB, ∴∠CBP=∠ADB.…………………………………………(5分)
中考数学 第二部分 专题综合强化 专题三 圆的相关证明与计算实用课件

4
(3)利用相似三角形求解:圆的综合题中往往会涉及切线的性质与圆周角定理推 论的结合,因此利用等角之间的等量代换找出与要求线段相关的两个三角形相似是 解题关键,另外对圆周角定理的灵活运用也非常重要;
(4)运用等面积公式,也可求解点到直线距离类题.
5
例1 (2018·泰州)如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交 ⊙O于点D,DE⊥BC于点E.
12
(2)若AE=1,ED=3,求⊙O的半径.
思路点拨 设⊙O的半径为R,则OE=R+1,在Rt△ODE中,利用勾股定理列出方程,求
解即可. 【解答】 设⊙O的半径为R,则OD=R,OE=R+1, ∵CD是⊙O的切线,∴∠EDO=90°, ∴ED2+OD2=OE2,∴32+R2=(R+1)2, 解得R=4,∴⊙O的半径为4.
13
类型3 与圆有关的弦切角问题
例3 如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于
点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EF是⊙O的切线;
14
思路点拨
连 接 EO , 由 ∠ EOG = 2∠C , ∠ ABG = 2∠C 知 ∠ EOG = ∠ ABG , 从 而 得 AB∥EO,根据EF⊥AB得EF⊥OE,即可得证.
2
(2)直线与圆没有已知的公共点时,通常过圆心作直线的垂线段,证明垂线段的 长等于圆的半径,可简述为:“无切点,作垂直,证半径”.证明垂线段的长等于 半径常用的方法是利用三角形全等或者利用角平分线上的点到角两边的距离相等.
2.圆中求角度或证明角相等的几种思路 (1)利用切线的性质,构造直角三角形,由两锐角和等于90°进行角度转化求 解; (2)利用圆周角定理及其推论,通常圆中相等的角代换可得角的大小; (3)利用圆周角定理的推论、勾股定理等得到一组平行线,通常圆中相等的角代 换可得角的大小.
第40讲 与圆有关的计算与证明题 课件(共74张ppt) 2024年中考数学总复习专题突破.ppt

复习讲义
(2)若 = 5 , cos ∠ =
4
,求 的长.
5
∘
解: ∵ ∠ = 90∘ , ∴ ∠ + ∠ = 90 .
由(1)知, = 2 = 10 , ∠ = 90∘ ,
∴ ∠ + ∠ = 90∘ .
图3
∴ ∠ = ∠.
4
.
5
∴ cos = cos ∠ =
复习讲义
(2)若 = 10 , = 12 , = 2 ,求 ⊙ 的半径.
思路点拨 由(1)知 ⊥ ,因此可在 Rt △
中利用勾股定理列方程求解.
解: ∵ = , ⊥ , ∴ = =
1
2
= 6.
图1
∴ = 2 − 2 = 102 − 62 = 8.
∴ = 6 .
目录导航
9
第40讲 与圆有关的计算与证明题
复习讲义
2.(2022·鄂尔多斯)如图3,以 为直径的
⊙ 与 △ 的边 相切于点 ,且与 边
交于点 ,点 为 的中点,连接 , ,
.
(1)求证: 是 ⊙ 的切线.
1.(2022·衡阳)如图2, 为 ⊙ 的直径,过圆上一
点 作 ⊙ 的切线 交 的延长线于点 ,过点
作 // 交 于点 ,连接 .
(1)直线 与 ⊙ 相切吗?请说明理由.
图2
目录导航
7
第40讲 与圆有关的计算与证明题
复习讲义
解:直线 与 ⊙ 相切.
, 的点,连接 , ,点 在 的延长线
上,且 ∠ = ∠ ,点 在 的延长线上,
陕西中考圆的证明与计算(2023版)

陕西中考圆的证明与计算(2023版)知识总结1.切线的性质:垂直于过切点的半径.(连半径,得垂直)2.切线的判定:(1)定义法:和圆只有一个交点的直线是圆的切线;(2)距离法:到圆心距离等于半径的直线是圆的切线;证明d =r 即可,常用于已知数据的计算,比如动圆相切问题.(3)判定定理:经过半径外端且垂直于这条半径的直线是圆的切线.换个说法:⎧⎨⎩有交点:连半径,证垂直无交点:作垂直,证半径,多用于几何证明.多数情况为有交点,重点考虑如何证垂直:①证明和已知垂线平行;②证明夹角为直角.3.常见相切图(1)角分+等腰得平行:点C 在以AB 为直径的圆O 上,AH ⊥CH ,且AC 平分∠HAB .【证明】连接OC,则OC=OA,∴∠OCA=∠OAC,又∠OAC=∠HAC,∴∠OCA=∠HAC,∴OC∥AH,∴OC⊥CH,∴CH是圆O的切线.(2)证明和已知直角相等.证明△PCO≌△PAO,可得∠PCO=∠PAO=90°.(3)证明夹角为直角.(弦切角定理)如图,若∠BAC=∠D,则AB是圆O切线.如图,连接AO并延长交圆O于点P,则∠P=∠D=∠BAC,∵∠P+∠PAC=90°,∴∠BAC+∠PAC=90°,即AB⊥AP,∴AB是圆O的切线.1.如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC 于点E.(1)求证:DE=AE;(2)若AD=8,DE=5,求BC的长度.2.如图,在Rt△ABC中,∠ABC=90°,以BC为直径的⊙O交AC于点E,⊙O的切线DE交AB于点D.(1)求证:DA=DB;(2)连接BE,OD,交点为F,若cos A=,BC=6,求OF的长.3.如图,AB是⊙O的直径,经过⊙O上一点D,作⊙O的切线EF,交AB的延长线于点F,AE⊥EF,交BD的延长线于点C.(1)求证:AB=AC.(2)若⊙O的半径为3,,求BF的长.4.如图,AB为⊙O的直径,C、E为⊙O上的两点,过点E的切线交CB的延长线于点D,且CD⊥DE,连接CE,AE.(1)求证:∠ABC=2∠A;(2)若⊙O半径为,AB:BD=5:1,求AE的长.5.已知:如图,AB为⊙O的直径,CD与⊙O相切于点C,交AB延长线于点D,∠D=30°,连接AC、BC,CE平分∠ACB交⊙O于点E,过点B作BF⊥CE,垂足为F.(1)求证:CA=CD;(2)若AB=12,求线段BF的长.6.已知:如图,⊙O过正方形ABCD的顶点A,B,且与CD边相切于点E.点F是BC与⊙O的交点,连接OB,OF,AF,点G是AB延长线上一点,连接FG,且∠G+∠BOF=90°.(1)求证:FG是⊙O的切线;(2)如果正方形边长为8,求⊙O的半径.7.如图,在△AOB中,以点O为圆心的⊙O与AB相切于点D,延长AO交⊙O于点C,连接CD,过点A作AF⊥BO,交BO的延长线于点H,交⊙O于点F,∠B=∠C.求证:(1)AF∥CD;(2)AH2=OH⋅BH.8.如图,AB是⊙O的直径,已知点D是弧BC的中点,连接DO并延长,在延长线上有一点E,连接AE,且∠E=∠B.(1)求证:AE是⊙O的切线;(2)连接AC,若AC=6,CF=4,求OE的长.9.如图,AB是⊙O的直径,C在AB的延长线上,⊙O与CD相切于点D,过点A作AE ⊥CD,垂足为E.(1)求证:AD平分∠EAC.(2)若BC=3,,求⊙O的半径以及线段ED的长.10.如图,AB是⊙O的直径,点D是直径AB上不与A,B重合的一点,过点D作CD⊥AB,且CD=AB,连接BC交⊙O于点F,在CD上取一点E,使EF=EC.(1)求证:EF是⊙O的切线;(2)当D是OA的中点时,AB=4,求BF的长.11.如图,△ABC内接于⊙O,AB=AC,过点A作BC平行线AM,连接BO并延长,交AM于点D,连接AO、CO.(1)求证:AM是⊙O的切线;(2)若BC=10,AD=8,求⊙O的半径.12.如图,已知△ABC的边AB所在的直线是⊙O的切线,切点为B,AC经过圆心O并与圆交于点D、C,E为AB延长线上一点,连接CE交⊙O于点F,且∠BCE=∠ACB.(1)求证:CE⊥AB;(2)若⊙O的半径是6,AB=8,求EF的长.13.如图,在△ABC中,∠C=90°,以FB为直径作⊙O,⊙O与直角边AC相切,切点为E.(1)求证:∠DBE=∠EBA;(2)若AB=10,DB=4,求EB的长.14.如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC,垂足为D,连接AD,过点A作⊙O的切线与DO的延长线相交于点E.(1)求证:∠B=∠E;(2)若⊙O的半径为4,OE=6,求AD的长.15.如图,AB是⊙O的直径,点D、E均在⊙O上,连接AD、BD、BE、DE,过点D作⊙O的切线,交AB的延长线于点C.(1)求证:∠DEB=∠CDB;(2)若BD=DE=6,BE=9.6,求⊙O的半径.16.如图,△ABC是⊙O的内接三角形,BC为⊙O的直径,点E是⊙O上一点,连接OE 并延长交过点C的切线CD于点D,∠B=∠D.(1)求证:OD∥AC;(2)延长EO交AB于点F,AF=2,⊙O的直径为2,求OD的长.17.如图,已知△ABC的外接圆直径是AB,点O是圆心,点D在⊙O上,且=,过点D作⊙O的切线,与CA、CB的延长线分别交于点E、F.(1)求证:AB∥EF;(2)若⊙O的半径为5,BC=8,求DF的长度.18.如图,AB为⊙O的直径,C为⊙O上一点,AD⊥CE,垂足为D,AC平分∠DAB.(1)判定直线CE与⊙O的位置关系,并说明你的理由;(2)若AD=3,AC=4,求圆的半径.19.如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,与AC边的交点为F,过点D作DE⊥AC于点E.(1)求证:直线DE是⊙O的切线;(2)若AB=5,tan∠ACB=2,求弦AF的长度.20.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作DE⊥AC,垂足为E,延长CA交⊙O于点F.(1)求证:DE是⊙O的切线;(2)若tan B=,⊙O的半径为5,求线段CF的长.21.如图,AB为⊙O的直径,OD为⊙O的半径,⊙O的弦CD与AB相交于点F,⊙O的切线CE交AB的延长线于点E,EF=EC.(1)求证:OD垂直平分AB;(2)若⊙O的半径长为3,且BF=BE,求OF的长.22.如图,AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,BD⊥CD,DB的延长线与⊙O交于点E.(1)求证:∠ABE=2∠A;(2)若,BD=4,求BE的长.23.如图,在△ABC中,AC=AB,以AB为直径的⊙O交BC于点D,过点D作ED⊥AC 点E,交AB延长线于点F.(1)求证:EF是⊙O的切线;(2)若DF=4,tan∠BDF=,求AC的长.24.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.(1)求证:CF是⊙O的切线;(2)若直径AD=10,cos B=,求FD的长.25.如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O 于点D,连接BD并延长交线段AC于点E.(1)求证:∠CAD=∠CDE;(2)若CD=6,tan∠BAD=,求⊙O的半径.26.如图,四边形ABCD是⊙O的内接四边形,且对角线BD为⊙O的直径,过点A作AE ⊥CD,与CD的延长线交于点E,且DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)若⊙O的半径为5,CD=6,求AD的长.27.如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B是的中点,过点B的切线与AC的延长线交于点D.①求证:BD⊥AD;②若AC=9,tan∠ABC=,求⊙O的半径.28.如图,△ABC中,∠C=90°,点O在AB上,⊙O经过点A,且与BC相切于点D.(1)求证:AD平分∠BAC;(2)若AC=6,cos∠BAC=,求⊙O的半径.29.如图,AB是⊙O的直径,点C为⊙O上一点,CD平分∠ACB,交AB于点E,交⊙O 于点D,延长BA到点P,使得PE=PC.(1)求证:PC与⊙O相切;(2)若⊙O的半径3,PC=4,求CD的长.30.如图,AB是⊙O的直径,点C、D是⊙O上两点,CE与⊙O相切,交DB延长线于点E,且DE⊥CE,连接AC,DC.(1)求证:∠ABD=2∠A;(2)若DE=2CE,AC=8,求⊙O的半径.31.如图,AB是⊙O的直径,AC是弦,且OD⊥AC于点E,OD交⊙O于点F,连接CF、BF,若∠BFC=∠ODA.(1)求证:AD是⊙O的切线:(2)若AB=10,AC=8,求AD的长.32.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接OD,过点D作⊙O的切线DE,交AC于点E,延长CA交⊙O于点F,连接BF.(1)求证:DE⊥AC;(2)若⊙O的直径为5,cos C=,求CF的长.33.如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.(1)求证:HB是⊙O的切线;(2)若HB=4,BC=2,求⊙O的半径.34.如图,AB是⊙O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB,与⊙O交于点F,在CD上取一点E,使得EF=EC.(1)求证:EF是⊙O的切线;(2)若D是OA的中点,AB=4,求CF的长.35.如图,四边形ABCD是⊙O的内接四边形,且对角线BD为直径,过点A作⊙O的切线AE,与CD的延长线交于点E,已知DA平分∠BDE.(1)求证:AE⊥DE;(2)若⊙O的半径为5,CD=6,求AD的长.36.如图,在Rt△ACD中,∠ACD=90°,点O在CD上,作⊙O,使⊙O与AD相切于点B,⊙O与CD交于点E,过点D作DF∥AC,交AO的延长线于点F,且∠OAB=∠F.(1)求证:AC是⊙O的切线;(2)若OC=3,DE=2,求DF的长.37.如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,以CD为直径作⊙O,与BC交于点E,过点E作⊙O的切线EF,交AB于点F.(1)求证:EF⊥AB;(2)若⊙O的半径是,cos∠ACD=,求DF的长.38.如图,⊙O是△ABC的外接圆,=,过点A作AD∥BC交⊙O于点D,连接CD,延长DA到点E,连接CE,∠D=∠E.(1)求证:CE是⊙O的切线;(2)若CE=8,AE=5,求⊙O半径的长.39.如图,BD为⊙O的直径,∠ABE=∠BCA,过点A的直线与⊙O分别交于点E,C,与BD交于点F,连接BE,BC.(1)求证:AB为⊙O的切线.(2)若∠A=∠ABE,BE=5,BC=8,求⊙O的半径.40.如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O 于点D,连接BD并延长交线段AC于点E.(1)求证:∠CDE=∠CAD;(2)若CD=4,tan B=,求⊙O的半径.。
2021届湘教版九年级数学下册课件:第2章 微专题4 与圆有关的证明和计算(共27张PPT)

类型 2 与切线相关的证明与计算 4. (2018·昆明)如图,AB 是⊙O 的直径,ED 切⊙O 于点 C,AD 交⊙O 于点 F,AC 平分∠BAD,连接 BF. (1)求证:AD⊥ED; (2)若 CD=4,AF=2,求⊙O 的半径.
解:证明:连接 OC,交 BF 于点 H,如图,∵AC 平分∠BAD,
解:(1)过点 O 作 OE⊥AB 于点 E, ∵AD⊥BO 于点 D,∴∠D=90°, ∴∠BAD+∠ABD=90°, ∠AOD+∠OAD=90°, ∵∠AOD=∠BAD, ∴∠ABD=∠OAD, 又∵BC 为⊙O 的切线,∴AC⊥BC, ∴∠BCO=∠D=90°,
∵∠BOC=∠AOD,∴∠OBC=∠OAD=∠ABD,
∵四边形 ABCO 是菱形,∴AM=MC=12AC, ∴AC=2AM=6 3 mm.故扳手张开的开口 b 至少 为 6 3 mm.
第2章 圆 微专题4 与圆有关的证明和计算
专题解读 1.在圆中求解线段长度有以下常用的四种方法: (1)勾股定理,适用于已知两边的直角三角形,其中 多涉及到垂径定理知识的运用,通常可以构造直角三角 形并利用 l= r2-d2来求圆中某些弦的长度; (2)三角函数法,适用于存在特殊角及特殊线段长的 三角形,如已知含有 30°,45°,60°角或含有 2, 3 的线段长,均可借助切线的性质构造直角三角形,列出 三角函数关系来求解;
解:如图所示,设正六边形 ABCDEF 的中心是 O, 连接 OA,OB,OC,AC,AC 与 BO 交于 M.易知∠AOB =∠BOC=60°,∴OA=OB=AB=OC=BC,∴四边形 ABCO 是菱形,∴BO⊥AC,∠BAC=12∠BAO=30°,
在 Rt△ABM 中,AB=6 mm,cos∠BAC=AAMB , ∴AM=6× 23=3 3(mm).
初中三:圆的证明与计算
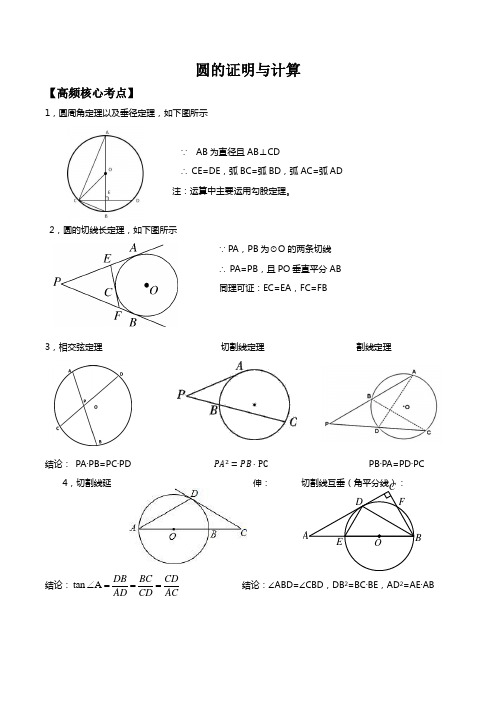
圆的证明与计算【高频核心考点】1,圆周角定理以及垂径定理,如下图所示∵ AB 为直径且AB ⊥CD∴ CE=DE ,弧BC=弧BD ,弧AC=弧AD 注:运算中主要运用勾股定理。
2,圆的切线长定理,如下图所示∵ PA,PB 为⊙O 的两条切线∴ PA=PB ,且PO 垂直平分AB 同理可证:EC=EA ,FC=FB3,相交弦定理 切割线定理 割线定理结论: PA ·PB=PC ·PD PA 2=PB ·PC PB ·PA=PD ·PC4,切割线延伸: 切割线互垂(角平分线):结论:tan A DB BC CDAD CD AC∠===结论:∠ABD=∠CBD ,DB 2=BC ·BE ,AD 2=AE ·ABOFE DC BA【精题精讲精练】◆例1:《角平分线模型》1,如图,在Rt ABC∆中,90C∠=︒,AD平分BAC∠交BC于点D,O为AB上一点,经过点A,D的O⊙分别交AB,AC于点E,F,连接OF交于点G.(1)求证:BC是O⊙的切线;(2)设AB x=,AF y=,试用含,x y的代数式表示线段AD的长;(3)若8BE=,5sin13B=,求DG的长.2,如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点C作∠BCD=∠ACB交⊙O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.(1)求证:ED=EC;(2)求证:AF是⊙O的切线;(3)如图2,若点G是△ACD的内心,BC·BE=25,求BC的长.AD【变式练习】已知:如图,△ABC 内接于⊙O ,AB 为直径,∠CBA 的平分线交AC 于点F ,交⊙O 于点D ,DE ⊥AB 于点E ,且交AC 于点P ,连结AD. (1)求证:2AC DE =;(2)若tan∠CBD =12,AP·AC=5,求AC 的长; (3)若65AD =,⊙O 的半径为152,延长DE 交⊙O 于点M ,且DP :DM=1:3,求CM 的长.◆例2:《母子型相似》1,如图,AB 为⊙O 的直径,C,D 为圆上的两点,OC∥BD,弦AD ,BC 相交于点E.(1)求证:弧AC=弧CD ;(2)若CE=1,EB=3,求⊙O 的半径;(3)在(2)的条件下,过点C 作⊙O 的切线,交BA 的延长线于点P,过点P 作PQ∥CB 交⊙O 于F,Q 两点(点F 在线段PQ 上),求PQ 的长。
中考《圆》有关的证明和计算

中考《圆》有关的证明和计算圆是数学中的重要概念,它在几何学和代数学中都有广泛的应用。
本文将围绕圆的性质、定理和计算等方面展开,旨在帮助读者更好地理解和掌握圆的相关知识。
一、圆的定义和性质1.定义:平面上的圆是由一组与给定点的距离相等的点组成的几何体。
这个给定点称为圆心,与圆心距离相等的线段称为半径。
2.性质:(1)所有点到圆心的距离相等;(2)圆上的任意两点与圆心的距离相等;(3)半径相等的圆互为同心圆;(4)圆的直径是通过圆心的线段,且长度等于半径的两倍;(5)圆的周长是圆周上所有点之间的距离之和,用2πr表示(r为半径);(6)圆的面积是圆所包围的平面区域的大小,用πr²表示。
二、圆的计算1.计算周长:圆的周长公式为:C=2πr,其中C表示周长,r表示半径。
例如,如果一个圆的半径为5,则周长C=2π×5=10π。
2.计算面积:圆的面积公式为:S=πr²,其中S表示面积,r表示半径。
例如,如果一个圆的半径为5,则面积S=π×5²=25π。
三、圆的相关定理1.弧长与圆心角的关系:在圆上,如果两个弧所对的圆心角相等,那么这两个弧的弧长也相等。
2.弦和弧对应角的关系:在圆上,如果两个弦所对的弧相等,那么这两个弦所对应的圆心角也相等;反之亦成立。
3.正交弦的性质:在圆上,如果一条弦和一条半径相交且相互垂直,那么这条弦被分成的两个弧是相等的。
4.切线与半径的垂直性:在圆上,从圆外一点引一条切线,这条切线与半径的连线相互垂直。
5.弦切角定理:在圆上,切线和半径之间的夹角等于所对的弦所对应的圆心角的一半。
6.切线定理:从圆外一点引两条切线,这两条切线的切点与该点连结的线段平分该点外接圆所对应的弦。
7.弦的垂直平分线:圆上一条弦与它的垂直平分线所在的直径垂直。
四、圆的证明1.圆心角相等的证明:设AB和CD是圆上的两条弧,且它们所对的圆心角相等。
要证明的是,这两条弧的弧长也相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《圆的证明与计算》专题讲解
圆的有关证明
一、圆中的重要定理:
(1) 圆的能义:主要是用来证明四点共圆.
(2) 垂径定理:主要是用来证明一一弧相等、线段相等、垂直关系等等.
(3) 三者之间的关系圧理:主要是用来证明一一弧相等、线段相等、圆心角相等.
(4) 圆周角性质泄理及其推轮:主要是用来证明一一直角、角相等、弧相等.
(5) 切线的性质定理:主要是用来证明一一垂直关系.
(6) 切线的判定眾理:主要是用来证明直线是圆的切线.
(7) 切线长定理:线段相等、垂直关系、角相等.
2.圆中几个关键元素之间的相互转化:弧、弦、圆心角、圆周角等都可以通过相等来互相转化•这在圆中的证明和讣算中经常用到.
知识点一:判定切线的方法:
(1>若切点明确,则“连半径,证垂直”。
常见手法有:全等转化:平行转化:直径转化:中线转化等:有时可通过计算结合相似、勾股定理证垂直:
(2)若切点不明确,则“作垂直,证半径”。
常见手法:角平分线泄理;等腰三角形三线合一,隐藏角平分线:
总而言之,要完成两个层次的证明:①直线所垂直的是圆的半径(过圆上一点);②直线与半径的关系是互相垂直。
任证明中的关键是要处理好弧、弦、角之间的相互转化,要善于进行由此及彼的联想、要总结常添加的辅助线•例:
方法一:若直线1过OO上某一点A,证明I是OO的切线,只需连OA,证明OA丄1就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.
例1如图,在Z\ABC中,AB=AC,以AB为直径的00交BC于D,交AC于E, B为切点的切线交0D延长线于F.
求证:EF与OO相切.
例2如图,已知:AB是的直径,点C在€)0上,且ZCAB=30°, BD=0B, D在AB 的延长线上.
求证:DC是00的切线
例3如图,AB是0O的直径,CD丄AB, ji OA2=OD・OP.求证:PC是OO的切线.
方法二若直线1与OO没有已知的公共点,又要证明1是OO的切线,只需作OA丄1, A 为垂足,证明OA是QO的半径就行了,简称:“作垂直;证半径”(一般用于函数与几何综合题)
例1:已知:如图,AC, BD与OO切于A、B,且AC〃BD,若ZCOD=90°.
求证:CD是00的切线.
知识点二:与圆有关的计算
计算圆中的线段长或线段比,通常与勾股泄理、垂径圧理与三角形的全等、相似等知识的结合,形式复杂,无规律性。
分析时要重点注意观察已知线段间的关系,选择左理进行线段或者角度的转化。
特别是要借助圆的相关定理进行弧、弦、角之间的相互转化,找岀所求线段与已知线段的关系,从而化未知为已知,解决问题。
其中重要而常见的数学思想方法有:
(1)构造思想:如:①构建矩形转化线段;②构建“射影泄理”基本图研究线段(已知任意两条线段可求其它所有线段长):
射影左理:所谓射影,就是正投影。
其中,从一点到一条直线所作垂线的垂足,叫做这点在这条直线上的正投影。
一条线段的两个端点在一条直线上的正投影之间的线段,叫做这条线段在这直线上的正投影。
由三角形相似的性质:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每
一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式RtA ABC中,ZBAC=90c.AD是斜边BC上的髙,则有射影左理如下::(1)(AD)2;=BD DC.
⑵(AB)2;=BD・BC,(3)(AC)2;=CD・BC。
等积式(4)ABXAC=BCXAD(可用而积来证明)
③构造垂径泄理模型:弦长一半、弦心距、半径;
④构造勾股立理模型(已知线段长度):
⑤构造三角函数(已知有角度的情况);
⑥找不到,找相似
(2) 方程思想:设岀未知数表示关键线段,通过线段之间的关系,特別是发现英中的相等关系建立方程,解决问题。
(3) 建模思想:借助基本图形的结论发现问题中的线段关系,把问题分解为若干基本图形的问题,通过基本图形的解题模型快速发现图形中的基本结论,进而找出隐藏的线段之间的数量关系。
例讲解:
例题1:中,,以M为直径作00交汕于Q点,狐CF二CB,过C作府的
垂线,垂足为M, MC的延长线交肿于ZZ
(1) 求证:〃为00的切线:
EF
M P
(2) 连BF交AP于E,若於6, E&2,求——的值。
例题2:直角梯形個刃中,ZBCE90。
, AB二AD+BC,月万为直径的圆交氏于伐连&\加交于F.
⑴求证:G?为<9。
的切线
例题3:如图,初为直径,丹为切线,点Q在00上,AC//OP.
(1) 求证:FC为O0的切线。
(2) 过。
点作加丄E为垂足,连初交庞于G CQ3, D&4,求——的值。
例题4(2009调考):如图,已知△月庞中,以边證为直径的00与边M交于点以点卍为的中点,处为△磁的角平分线,且护丄应;
(1) 求证:EQ与QO相切:
(2) 若AC=6. BC=8.求比的长
家庭练习:
1. 如图,Rt/\ABC.以AB为直径作。
0交AC于点D, 为垂足.
(1) 求证:DF为0O的切线:
(2) 若DF=3, OO的半径为5,求tailZfiAC的值.
2. 如图,为QO的直径,C. D为0O上的两点, 交直线AB于
点& F为垂足.
(1) 求证:EF为00的切线;
(2) 若AC=6, BD=5,求sinE 的值.
3•如图,AB为00的直径,半径0C丄AB. D为AB延长线上
一点,过D作的切线, E为切点,连结CE交AB于点F.
(1)求证:DE=DF:
(2)连结A& 若OF" BF=3,求tanZA 的值.
,过D作直线BC的垂线
4・如图,RtAABC中,ZC=90°, BD平分ZABC,以AB上一点0为圆心过反D两点作00, 00交AB于点一点E, EF丄AC于点E
(1)求证:OO与AC相切;
(2)若EF=3, BC=4,求tanZA 的值.
5. 如图,等腰ZVIBC中,AB=AC.以AB为直径作00交BC于点D, DE丄AC于E
(1)求证:为。
0的切线:
(2)若BC=4$ AE=1,求cosZAQ的值.
6. 如图,BD为00的直径,A为的中点,AD交BC于点E, F为BC延长线上一
点,且FD=FE.
(1)求证:DF为0O的切线:
(2)若AE=2. DE=4, ABDF的面积为8丁5\ 求tanZQF 的值.
7、如图,AB是OO的直径,M是线段OA上一点,过M作AB的垂线交AC于点N,交BC 的延长线于点E,直线CT交EN于点F,且ZECF=ZE.
(1)求证:CF是00的切线:
(2)设OO的半径为1,且AC=CE=氐求AM的长.
8、如图,AB是0O的直径,BC丄AB,过点C作。
O的切线CE,点D是CE延长线上一点,连结AD, RAD+BC=CD・
(1)求证:AD是00的切线:
(2)设0E交AC于F.若0F=3, EF=2,求线段BC的长.
9、如图,AABC中,AB=BC,以AB为直径的0O交AC于点D,且CD二BD
(1)求证:BC是00的切线;
(2)已知点M、N分别是AD. CD的中点,BM延长线交00于E, EF//AC,分别交BD、DV 的延长线于H. F,若DH=2,求£F的长.
10、如图,AB是半00上的直径,E是匿的中点,OE交弦BC于点D,过点C作交AD 的平行线交OE的延长线于点F. ZADO=ZB.
(1) 求证:CF为00的00切线;
(2) 求sinZBAD的值.
1K如图,MBC中,AB=AC,以AC为直径的与AB相交于点&点F是BE的中点・
(1) 求证:DF是0O的切线.
(2) 若A£=14, BC=12,求BF的长。
