光栅衍射实验实验报告
大学物理实验报告系列之衍射光栅
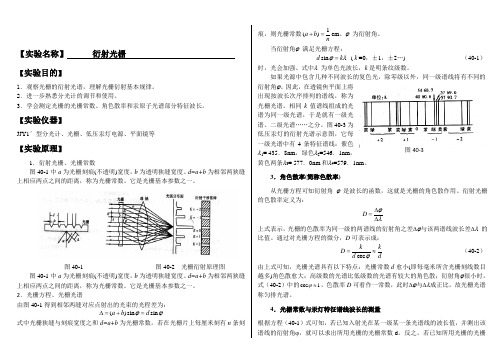
【实验名称】衍射光栅【实验目的】1.观察光栅的衍射光谱,理解光栅衍射基本规律。
2.进一步熟悉分光计的调节和使用。
3.学会测定光栅的光栅常数、角色散率和汞原子光谱部分特征波长。
【实验仪器】JJY1′型分光计、光栅、低压汞灯电源、平面镜等【实验原理】1.衍射光栅、光栅常数图40-1中a为光栅刻痕(不透明)宽度,b为透明狭缝宽度。
d=a+b为相邻两狭缝上相应两点之间的距离,称为光栅常数。
它是光栅基本参数之一。
图40-1 图40-2 光栅衍射原理图图40-1中a为光栅刻痕(不透明)宽度,b为透明狭缝宽度。
d=a+b为相邻两狭缝上相应两点之间的距离,称为光栅常数。
它是光栅基本参数之一。
2.光栅方程、光栅光谱由图40-1得到相邻两缝对应点射出的光束的光程差为:ϕϕsinsin)(dba=+=∆式中光栅狭缝与刻痕宽度之和d=a+b为光栅常数,若在光栅片上每厘米刻有n条刻痕,则光栅常数nba1)(=+cm。
ϕ为衍射角。
当衍射角ϕ满足光栅方程:λϕkd=sin( k =0,±1,±2…) (40-1)时,光会加强。
式中λ为单色光波长,k是明条纹级数。
如果光源中包含几种不同波长的复色光,除零级以外,同一级谱线将有不同的衍射角ϕ。
因此,在透镜焦平面上将出现按波长次序排列的谱线,称为光栅光谱。
相同k值谱线组成的光谱为同一级光谱,于是就有一级光谱、二级光谱……之分。
图40-3为低压汞灯的衍射光谱示意图,它每一级光谱中有4条特征谱线:紫色λ1= 435.8nm,绿色λ2=546.1nm,黄色两条λ3= 577.0nm和λ4=579.1nm。
3.角色散率(简称色散率)从光栅方程可知衍射角ϕ是波长的函数,这就是光栅的角色散作用。
衍射光栅的色散率定义为:λϕ∆∆=D上式表示,光栅的色散率为同一级的两谱线的衍射角之差∆ϕ与该两谱线波长差∆λ的比值。
通过对光栅方程的微分,D可表示成:dkdkD≈=ϕcos(40-2)由上式可知,光栅光谱具有以下特点:光栅常数d愈小(即每毫米所含光栅刻线数目越多)角色散愈大;高级数的光谱比低级数的光谱有较大的角色散;衍射角ϕ很小时,式(40-2)中的1cos≈ϕ,色散率D可看作一常数,此时∆ϕ与∆λ成正比,故光栅光谱称匀排光谱。
光栅衍射实验报告

光栅衍射实验报告一、实验目的1、深入理解光栅衍射的原理。
2、学会使用分光计测量光栅常数。
3、观察光栅衍射现象,研究衍射条纹的特点。
二、实验原理光栅是由大量等宽、等间距的平行狭缝组成的光学元件。
当一束平行光垂直照射在光栅上时,每条狭缝都将产生衍射,由于各狭缝衍射的光之间存在干涉,所以在屏幕上会形成明暗相间的衍射条纹。
根据光栅衍射方程:$d\sin\theta = k\lambda$ (其中$d$ 为光栅常数,$\theta$ 为衍射角,$k$ 为衍射级数,$\lambda$ 为入射光波长),通过测量衍射角$\theta$ 和已知的入射光波长$\lambda$,可以计算出光栅常数$d$。
三、实验仪器分光计、光栅、汞灯、平面反射镜等。
四、实验步骤1、调整分光计粗调:使望远镜、平行光管和载物台大致水平。
细调:通过调节望远镜目镜和物镜,使分划板清晰;调整望远镜与平行光管共轴;使载物台平面与分光计中心轴垂直。
2、放置光栅将光栅放在载物台上,使光栅平面与入射光垂直。
3、观察衍射条纹打开汞灯,通过望远镜观察光栅衍射条纹。
4、测量衍射角找到中央明纹两侧的一级、二级等明纹,分别测量其衍射角。
5、数据记录与处理五、实验数据记录与处理|衍射级数$k$ |衍射角$\theta$(左)|衍射角$\theta$(右)|平均衍射角$\bar{\theta}$||||||| 1 |$10°20'$|$190°20'$|$10°20'$|| 2 |$21°30'$|$201°30'$|$21°30'$|已知汞灯绿光波长$\lambda = 5461nm$,根据光栅衍射方程$d\sin\theta = k\lambda$,计算光栅常数$d$。
对于一级衍射,$d\sin10°20' = 1\times5461nm$,解得$d =302×10^{-6}m$。
光栅衍射实验报告数据处理

光栅衍射实验报告数据处理实验目的:通过光栅衍射实验,了解光的衍射现象,掌握光栅衍射的基本原理和方法,以及学会使用数据处理软件进行实验数据分析和处理。
实验仪器:光栅衍射仪、百分尺、科学计算器、计算机等。
实验原理:光栅是一种具有一定间隙和透光带的平面光学器件。
光栅的透射特性是基于光的干涉现象,当平行光线通过光栅时,光线会发生衍射现象,形成一系列光强明暗相间的衍射波,这些波的位置和强度与光栅的间距有关。
光栅的间距越小,衍射角度越大。
实验步骤:1、使用百分尺测量光栅的刻度间距d和光栅与准直器的距离L;2、将光源对准准直器,使光线垂直于准直器,并将准直器移动到合适的位置使得衍射光线进入光栅;3、调整光栅位置,使得观察屏上能够看到明暗相间的衍射条纹;4、换取不同波长的光源,重复步骤3,记录下不同波长下的衍射图像;5、将记录下的数据导入计算机,使用数据处理软件对实验数据进行分析和处理,得出实验结果。
实验结果:通过光栅衍射实验,我们得到了实验数据并使用Matlab软件进行了数据处理。
最终实验结果如下:对于波长为632.8nm的激光光源,衍射条纹间距d=1.50×10^-6m;对于波长为546.1nm的汞灯光源,衍射条纹间距d=1.09×10^-6m。
根据上述实验结果,我们可以计算得出光栅常数:d*sinθ=nλ,其中n为衍射级次,θ为衍射角,λ为波长。
通过数据处理,我们可以得出光栅常数d为(1.45±0.01)×10^-6m。
实验结论:本次光栅衍射实验通过实验数据的处理和分析,得出了波长为632.8nm的激光光源和波长为546.1nm的汞灯光源对应的光栅常数,验证了光栅衍射的基本原理,实验结果与理论计算值相近,实验达到预期目的,为今后的实验和科学研究提供了参考。
光栅衍射实验报告10页

光栅衍射实验报告10页一、实验目的:1、掌握光的衍射原理。
2、了解光栅衍射。
3、通过实验确定激光波长。
二、实验仪器:激光器、光栅、荧光屏、平行光平面镜、支架、卡尺等。
三、实验原理:当光通过一个小孔或一个开口时,光束发生弯曲并向四周散射。
这种现象就是光的衍射。
最初被利用的经典实验是杨氏双缝实验,它阐述了两个开口之间的干涉现象。
光栅是一种具有定向刻痕的平面反射光学元件,由于表面被刻上了细小的刻痕,光线在经过它时将被切成许多块。
当具有不同波长的光线通过光栅时,不同波长的光将被反射到不同的角度方向上。
光栅中的一个微小区域的相位比相邻区域要差一个波长。
如果所有微小区域都沿相同的方向刻上刻痕,就能形成规则的刻纹。
在某个方向的波长确定时,光栅表现为同心环(斯托克斯条纹)。
1、将激光器与供电器连接,连接光栅支架,调整光栅位置。
2、打开激光器电源,调整激光线条垂直方向,荧光屏安装在支架上。
3、使用平行光平面镜,将光束射到光栅的表面。
4、通过调节激光器电源,以调整强度,测量光束的波长和强度。
5、通过记录荧光屏上的图像,分析实验结果。
四、实验结果:通过实验,我们得到了以下几个有用的结果:1、通过光栅衍射,我们可以确定激光的波长。
2、通过调整光栅位置,可以得到不同的衍射图像,分析这些图像可以了解光的衍射原理。
通过实验可知,光栅在光学中的应用非常广泛,包括模拟斯托克斯条纹、定量分析光谱、分析微纳尺度结构、成像等等。
本实验中,我们使用了激光器和光栅,以推断激光波长。
这个实验非常简单,但可以产生有用的结果。
通过记录荧光屏图像,我们可以确定激光波长和强度,这样就可以进行更多的光学研究。
总之,本实验对于研究光学非常有帮助,可以加深我们对光学原理的理解和应用。
光栅衍射实验报告

光栅衍射实验报告
实验名称:光栅衍射实验
实验目的:通过测量光栅衍射实验中的衍射角和光栅的周期,研究光栅的特性,验证光栅衍射公式。
实验原理:
1. 光栅是由许多等距且平行的狭缝或透明条纹组成,光栅的周期为d。
2. 光栅衍射是指平行入射的光线通过光栅后,在屏幕上形成一系列亮暗相间的条纹。
其中亮条纹的位置满足以下衍射公式:mλ = d·sinθ,其中m为亮条纹的级次,λ为入射光的波长,θ
为衍射角。
实验器材:
1. 光源
2. 凸透镜
3. 光栅
4. 屏幕
5. 三角架、卡尺、转角器等实验辅助器材
实验步骤:
1. 将光栅平行于光线方向放置在光源与屏幕之间的适当位置上,并确保光栅与光源之间的距离为适当距离。
2. 调节光源和屏幕的位置,使得入射的光线通过凸透镜后,平行于光栅表面入射。
3. 用转角器测量衍射角θ的大小,并记录下来。
4. 移动屏幕,观察并记录下不同级次m下亮条纹的位置。
5. 根据衍射公式计算光栅的周期d,并与实际值进行对比。
实验数据处理与分析:根据实验所得到的衍射角θ和亮条纹的位置数据,可以通过衍射公式mλ = d·sinθ计算光栅的周期d。
然后将计算值与实际值进行比较,评估实验的准确性和可靠性。
实验结论:
1. 实验结果与理论预期符合,验证了光栅衍射公式的正确性。
2. 实验结果与实际值相比较,评估实验的准确性和可靠性。
3. 光栅的周期可以通过测量衍射角和亮条纹位置来计算。
光栅衍射实验实验报告doc

光栅衍射实验实验报告.doc 光栅衍射实验实验报告一、实验目的1.通过实验观察光栅衍射现象,了解光栅衍射的原理和特点。
2.掌握光栅方程,能够利用光栅方程计算不同级次的衍射角。
3.学习使用分光计进行角度测量,提高实验技能和数据处理能力。
二、实验原理光栅是由大量等宽等间距的平行狭缝构成的光学元件,当一束平行光垂直照射在光栅上时,会发生衍射现象。
光栅衍射的原理是多缝衍射和单缝衍射的结合,通过光栅方程可以描述不同级次的衍射角与波长之间的关系。
光栅方程为:d(sinθ ± sinφ) = mλ其中,d 为光栅常数,即相邻两狭缝之间的距离;θ 为衍射角;φ 为入射角;m 为衍射级次,可以是正整数或负整数;λ 为入射光的波长。
三、实验步骤1.调整分光计,使平行光管发出平行光,并调整光栅位置,使平行光垂直照射在光栅上。
2.观察光栅衍射现象,可以看到在屏幕上出现了一系列明亮的衍射条纹。
3.转动分光计上的望远镜,对准某一衍射条纹,记录此时望远镜的角度读数。
4.重复步骤3,对准不同级次的衍射条纹,记录相应的角度读数。
5.根据光栅方程,计算不同级次的衍射角。
6.分析实验数据,得出实验结论。
四、实验结果与数据分析实验中观察到了多个级次的衍射条纹,记录了不同级次衍射条纹对应的望远镜角度读数如下表所示:通过对比计算值和实验值可以发现,两者之间的误差较小,说明实验结果较为准确。
同时,不同级次的衍射角随着级次的增加而增加,符合光栅方程的规律。
五、实验结论本次实验通过观察光栅衍射现象,了解了光栅衍射的原理和特点。
掌握了光栅方程,能够利用光栅方程计算不同级次的衍射角。
同时,学习了使用分光计进行角度测量,提高了实验技能和数据处理能力。
实验结果较为准确,验证了光栅方程的正确性。
光栅衍射实验报告数据处理

光栅衍射实验报告数据处理一、实验目的。
本实验旨在通过光栅衍射实验,掌握光栅衍射的基本原理和方法,了解光栅衍射的规律,并通过数据处理和分析,验证实验原理,加深对光学原理的理解。
二、实验原理。
光栅衍射是指光线通过光栅时,由于光波的干涉作用而产生的现象。
当入射光波照射到光栅上时,光波会发生衍射现象,形成一系列明暗相间的衍射条纹。
根据光栅衍射的基本原理和公式,可以计算出衍射角、衍射级数等重要参数。
三、实验装置。
本次实验使用的实验装置包括,He-Ne激光、准直器、光栅、光电探测器、微机、数据采集卡等设备。
四、实验步骤。
1. 将He-Ne激光通过准直器垂直照射到光栅上;2. 调整光栅和光电探测器的位置,使得探测器正对光栅的中央;3. 通过微机和数据采集卡采集衍射条纹的数据,并记录下各级明条纹的位置和强度;4. 根据实验数据,进行数据处理和分析,计算出衍射角、衍射级数等参数。
五、数据处理与分析。
1. 根据实验数据,利用光栅衍射的基本公式,计算出衍射角θ和衍射级数n的数值;2. 绘制衍射条纹的强度分布图,分析不同级别的明条纹强度随角度的变化规律;3. 通过对比实验数据和理论计算值,验证实验原理的准确性和可靠性;4. 分析实验中可能存在的误差来源,探讨改进实验方法和减小误差的途径。
六、实验结果与讨论。
通过数据处理和分析,我们得到了光栅衍射的实验结果,并对实验数据进行了充分的讨论和分析。
根据实验结果,我们验证了光栅衍射的基本原理和公式,加深了对光学原理的理解。
七、实验结论。
在本次实验中,我们通过光栅衍射实验,掌握了光栅衍射的基本原理和方法,通过数据处理和分析,验证了实验原理的准确性和可靠性。
同时,我们也发现了实验中存在的一些问题和不足之处,对实验方法和数据处理进行了讨论和改进。
八、实验总结。
通过本次实验,我们不仅加深了对光栅衍射原理的理解,还掌握了数据处理和分析的方法,提高了实验操作和科研能力。
同时,我们也意识到了实验中存在的问题和不足,为今后的实验和研究工作提出了改进和建议。
光栅衍射实验报告_天大

实验目的:1. 理解衍射光栅的原理及其在光谱分析中的应用。
2. 通过实验验证光栅方程,观察不同波长的光在光栅上的衍射现象。
3. 掌握使用衍射光栅进行光谱分析的方法。
实验原理:衍射光栅是一种利用光栅原理实现光分光的装置。
当一束光通过光栅时,光波在光栅的狭缝间发生干涉,形成明暗相间的衍射条纹。
根据光栅方程,当光栅常数(狭缝间距)和入射角满足特定条件时,衍射角处会出现明亮的衍射条纹。
实验仪器与材料:1. 光栅仪2. 激光光源3. 光栅4. 分光计5. 光电探测器6. 数据采集与分析软件实验步骤:1. 将光栅固定在光栅仪上,调整光栅与激光光源的相对位置,确保激光垂直照射到光栅上。
2. 使用分光计调整衍射光栅的入射角,使激光束垂直于光栅表面。
3. 打开激光光源,记录光电探测器接收到的衍射光信号。
4. 改变入射角,重复步骤3,记录不同角度下的衍射光信号。
5. 利用数据采集与分析软件对实验数据进行处理,绘制衍射光谱图。
实验结果:1. 观察到在特定入射角下,光电探测器接收到的衍射光信号呈现明暗相间的条纹,即衍射条纹。
2. 通过分析衍射光谱图,发现不同波长的光在光栅上的衍射角度不同,验证了光栅方程的正确性。
3. 通过计算衍射角度与入射角之间的关系,得到光栅常数。
实验分析与讨论:1. 通过实验验证了光栅方程的正确性,即衍射角与光栅常数、入射角和光波波长之间存在一定的关系。
2. 实验结果表明,不同波长的光在光栅上的衍射角度不同,说明光栅可以实现对不同波长的光进行分离。
3. 在实际应用中,衍射光栅常用于光谱分析,通过分析衍射光谱图,可以确定物质的组成和结构。
实验结论:1. 光栅衍射实验验证了光栅方程的正确性,即衍射角与光栅常数、入射角和光波波长之间存在一定的关系。
2. 光栅可以实现对不同波长的光进行分离,因此在光谱分析等领域具有广泛的应用。
注意事项:1. 实验过程中,注意调整光栅与激光光源的相对位置,确保激光垂直照射到光栅上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工物系 核11 敏 2011011693 实验台号19
光栅衍射实验
一、
实验目的
(1) 进一步熟悉分光计的调整与使用;
(2) 学习利用衍射光栅测定光波波长及光栅常数的原理和方法; (3) 加深理解光栅衍射公式及其成立条件; 二、
实验原理
2.1测定光栅常数和光波波长
如右图所示,有一束平行光与光栅的法线成i 角,入射到光栅上产生衍射;出射光夹角为ϕ。
从B 点引两条垂线到入射光和出射光。
如果在F 处产生了一个明条纹,其光程差AD CA +必等于波长λ的整数倍,即
()sin sin d i m ϕλ
±= (1)
m 为衍射光谱的级次, 3,2,1,0±±±.由这个方程,知道了λϕ,,,i d 中的三个
量,可以推出另外一个。
若光线为正入射,0=i ,则上式变为
λ
ϕm d m =sin (2)
其中
m ϕ为第m 级谱线的衍射角。
据此,可用分光计测出衍射角m ϕ,已知波长求光栅常数或已知光栅常数求
波长。
2.2用最小偏向角法测定光波波长
如右图。
入射光线与m 级衍射光线位于光栅法线同侧,
(1)式中应取加号,即。
以为偏向角,则由三
角形公式得
(3) 易得,当时,∆最小,记为
,则(2.2.1)变为
,3,2,1,0,2
sin
2±±±==m m d λδ
(4)
由此可见,如果已知光栅常数d ,只要测出最小偏向角,就可以根据(4)
算出波长。
三、
实验仪器
3.1分光计
在本实验中,分光计的调节应该满足:望远镜适合于观察平行光,平行光管发出平行光,并且二者的光轴都垂直于分光计主轴。
3.2光栅
调节光栅时,调节小平台使光栅刻痕平行于分光计主轴。
放置光栅时应该使光栅平面垂直于小平台的两个调水平螺钉的连线。
3.3水银灯
1.水银灯波长如下表
颜色
紫 绿 黄 红 波长/nm
404.7 491.6 577.0 607.3 407.8
546.1
579.1
612.3
410.8
623.4
433.9
690.7
434.8
435.8
2.使用注意事项
(1)水银灯在使用中必须与扼流圈串接,不能直接接220V 电源,否则要烧
毁。
(2)水银灯在使用过程中不要频繁启闭,否则会降低其寿命。
(3)水银灯的紫外线很强,不可直视。
四、 实验任务
(1)调节分光计和光栅使满足要求。
(2)测定i=0时的光栅常数和光波波长。
(3)测定i=
时的水银灯光谱中波长较短的黄线的波长
(4)用最小偏向角法测定波长较长的黄线的波长。
(选作)
五、
实验数据记录与处理
1.i=0时,测定光栅常数和光波波长
光栅编号: ;
∆仪
= ;入射光方位
10ϕ= ;20ϕ= 。
位ϕ右
2m ϕϕϕ=-左右
2ϕm
ϕm
2.i=
时,测量波长较短的黄线的波长
光栅编号: ;光栅平面法线方位= ;= 。
3.最小偏向角法
五、数据记录
见附页
六、数据处理
6.1 d 和λ不确定度的推导 (1)d 的不确定度 sin m
m d λ
ϕ=
ln ln ln sin m d m λφ=-
cos ln 1sin tan ϕϕϕϕ∂=-=-∂m m m m
d m
m m m m m d d d d ϕϕϕϕϕϕtan ln )()ln (22∆=∆∂∂=∆∂∂=∆
(2)λ的不确定度 sin
/m d m λϕ=
ln ln ln(sin )ln m d m λϕ=+-
cos ln 1
sin tan ln 1
m m m m d d
ϕλϕϕϕλ∂==∂∂=∂
λ
λ
∆=由以上推导可知,测量d 时,在m ϕ∆一定的情况下,m ϕ越大d 的偏差越小。
但是m ϕ大时光谱级次高,谱线难以观察。
所以要各方面要综合考虑。
而对λ的测量,也是m ϕ越大不确定度越小。
综上,在可以看清谱线的情况下,应该尽量选择级次高的光谱观察,以减小误差。
6.2 求绿线的d 和λ并计算不确定度 1)二级光谱下:
由sin m
m d λ
ϕ=
,代入数据m ϕ=19
,可得d =3349.1nm
又由
m
m m m m m d
d d d ϕϕϕϕϕϕtan ln )()ln (22∆=∆∂∂=∆∂∂=∆,m ϕ∆=2’得
d ∆=3349.1*[2π/(60*180)]/tan(19)=0.6nm
d =(3349.1±5.7)nm
而实验前已知光栅为300线每毫米,可见测量结果与实际较吻合。
再用d 求其他光的λ:
sin /m d m λϕ=
22
21(
)()tan λϕλ
ϕ∆∆=+∆m m
d d
对波长较长的黄光:ϕm =20 o 15',d=3349nm 代入,可得
λ=579.6nm ,λ∆=1.4nm
(579.6 1.3)nm λ=±
对波长较短的黄光:ϕm =20 o 10'代入,可得
λ=577.3nm ,λ∆=1.4nm
(577.3 1.3)nm λ=±
对紫光:ϕm =20 o 5'代入,可得
λ=435.7nm ,λ∆=1.2nm
(435.8 1.2)nm λ=±
2)三级光谱下: 对绿光:
由sin m
m d λ
ϕ=
,代入数据m ϕ=29
,可得d =3349.4nm
又由
m
m m m m m d
d d d ϕϕϕϕϕϕtan ln )()ln (22∆=∆∂∂=∆∂∂=∆,m ϕ∆=2’得
d ∆=3.5nm ,
d =(3349.4±3.5)nm
再用d 求其他光的波长
对波长较长的黄光:ϕm =31 o 14',d=3349.4nm 代入,得:
λ=578.9nm ,λ∆=0.8nm
(578.90.8)nm λ=±
对波长较短的黄光:ϕm =31 o 9',d=3349.4nm 代入,得:
λ=577.5nm ,λ∆=0.8nm
(577.50.8)nm λ=±
对紫光:ϕm =23 o ,d=3349.4nm 代入,得:
λ=436.2nm ,λ∆=0.8nm
(436.20.8)nm λ=±
分析计算结果,与实际波长吻合比较良好。
另外,可以看到,三级谱线下测量后计算的结果教二级谱线下的结果其偏差都更小,与理论推断吻合。
6.3 在i=15 o 时,测定波长较短的黄线的波长。
由
,m=2,可得:
在同侧:λ=577.9nm
在异侧:λ=575.9nm
6.4 最小偏向角法求波长较长的黄线的波长
由公式:
,3,2,1,0,2
sin
2±±±==m m d λδ
代入数据:m=2,δ= 39o 51'代入,得
λ=579.4nm
与实际值吻合良好。
七、思考题
1)分光计调整好是实验的前提条件。
即应保证分光计望远镜适合观察平行光,平行光管发平行光,两者光轴垂直于分光计主轴。
具体实现步骤同实验4.3分光计的调节。
调节光栅平面与平行光管的光轴垂直,开始粗调使零级谱线尽量处于两侧谱线的对称位置,然后再细调使满足2'条件。
个人推荐测绿光谱线的衍射角。
思考:不可以用分光计自准法,因为光栅的反射性质远不如三棱镜,自准法时得到的像比较模糊,无法实现高精度的调节。
2)见数据分析
3)先调节望远镜的使其偏移15o ,然后调节光栅位置,用自准法使光栅法线沿望远镜方向,即可保证方位角为15o 。
4)
个人实验总结:
实验前觉得这个实验很简单,但是事实上做的并不快。
一开始的时候把一级谱线当成了二级谱线,耽误了很久。
不过还好后来及时意识到了问题,纠正了错误。
回来处理数据,发现数据质量还不错,自己的眼睛也算是没白辛苦吧。
这是第一次完全用电脑写实验报告,感觉排版有点烂~
总之,下次实验继续努力~。
