信号与系统课后习题答案汇总
信号与系统 陈后金 第二版 课后习题答案(完整版)
（1） f (t) = 3sin 2t + 6 sinπ t
（2） f (t) = (a sin t) 2
（8）
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解：（1）因为 sin 2t 的周期为π ，而 sin πt 的周期为 2 。
显然，使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示，绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
（3） f (5 − 3t) （7） f ′(t) 解：（3）将 f (t) 表示成如下的数学表达式
（5） f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
（7）方法 1：几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变，所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理，在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号（方向向下，因为是负跳变），而在 0 < t < 2 的区间内有 f ′(t) = −0.5 （由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》（陈后金等编）作业参考解答
（2）显然，该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统课后习题答案(金波 华中科技大学出版社)
1-3 解 周期 T=7 ，一个周期的能量为 信号的功率为
P
E 56 8W T 7
1-5 解 (a) (3t 2 2) ( ) 4 (t ) ； (b) e
3t
t 2
(5 2t ) 0.5e 3t (t 2.5) 0.5e 7.5 (t 2.5)
2
1-10 已知一线性非时变系统，系统的初始状态为零，当输入信号为 f1 (t ) ，其输出信号为
y1 (t ) ，对应的波形如题图 1.10(a)(b)所示。试求： (a) 当输入信号为 f 2 (t ) 时，其波形如题图 1.15(c)所示，画出对应的输出 y 2 (t ) 的波形。 (b) 当输入信号为 f 3 (t ) 时，其波形如题图 1.10(d)所示，画出对应的输出 y 3 (t ) 的波形。
(b) 波形如图1.2(b)所示。显然是能量信号。
E 1 1 6 2 1 37 J
(c) 能量信号
E lim (e 5t ) 2 dt e 10t dt
T 0 0
T
1 10t e 0.1 J 10 0
(d) 功率信号，显然有
P 1W
习
基本练习题
题 一
1-1 判断下列信号是否是周期的，如果是周期的，求出它的基频和公共周期。 (a) f (t ) 4 3 sin(12 t ) sin(30 t ) ； (b) f (t ) cos(10 t ) cos(20 t ) ; (c) f (t ) cos(10 t ) cos(20t ) ; (d) f (t ) cos(2t ) 2 cos(2t
2
信号与系统陈后金版答案
第二步:求差分方程的齐次 解： 2 求差分方程的齐次 第二步 h [ 0 ] = C 1 + C 2 r −5r /6 +1/ 6 = 0 1 k1 1 k 1 特征方程为: [ ( + 特征方程为=hCk1 ] = )[3 (C 2) ( −) 2 ( 求 ] u [ C ] = 3, C 2 = − 2 h [1] ⇒ ) 出 k1 ∴r =1/ 2, r2 =1/3 2 3 3 1 2
(3) 计算固有响应与强迫响应 计算固有响应与强迫响应:
1 7 1 k 4 1 k y[k ] = [ − ( ) + ( ) ]u[k ] 完全响应: 完全响应 2 2 2 3 3 7 1 k 4 1 k 固有响应: yh [k ] = [− ( ) + ( ) ]u[ k ] 固有响应 2 2 3 3 1 强迫响应: 强迫响应 y p [k ] = u[k ] 2 (4) 计算瞬态响应与稳态响应 计算瞬态响应与稳态响应:
特征根为 s1 = -2, s2 = -5, 又因为 n > m , 所以： 则 h ( t ) = K 1e − 2 t u ( t ) + K 2 e − 5 t u ( t )
h '(t ) = − 2 K 1e −2 t u (t ) + K 1δ (t ) − 5 K 2 e −5 t u (t ) + K 2δ (t ) = − 2 K 1e −2 t u (t ) − 5 K 2 e −5 t u (t ) + ( K 1 + K 2 )δ (t ) h ''(t ) = 4 K 1e −2 t u (t ) − 2 K 1δ (t ) + 25 K 2 e −5 t u (t ) − 5 K 2δ (t ) + ( K 1 + K 2 )δ '(t ) 代入方程有： = K 1 + K 2 = '( t ) = 2 K 2δ ( t ) + 5 K∴K2 + (7/3; K1 )δ −1/3; 2δ '( t ) + 3δ ( t ) 1δ ( t )
信号与系统课后答案(全)
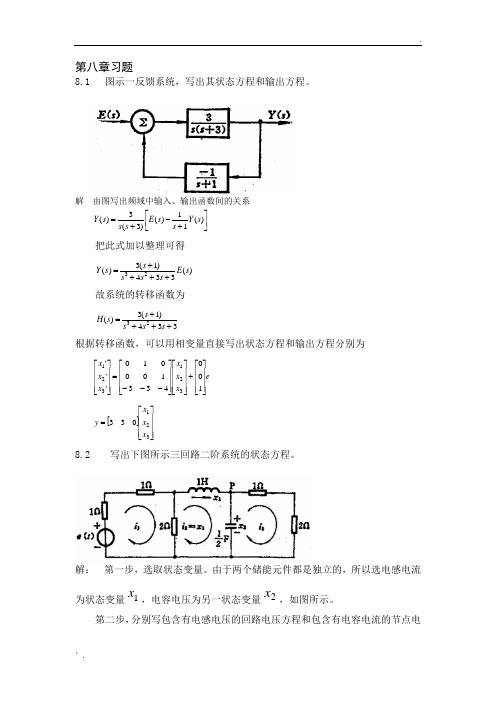
第八章习题8.1 图示一反馈系统，写出其状态方程和输出方程。
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数，可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。
解：第一步，选取状态变量。
由于两个储能元件都是独立的，所以选电感电流为状态变量1x，电容电压为另一状态变量2x，如图所示。
第二步，分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。
根据第二个回路的回路方程，并代入元件参数，则有112122'ixxx+--=312'21ixx-=第三步，上两式中1i和3i不是状态变量，要把它们表为状态变量。
由第一个回路有1124xie-=，即112141xei+=由第三个回路有323ix=，即2331xi=把1i和3i分别代入第二步中两式，并经整理，最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路，这里的激励函数)(t e是一压控电流源，输出电压)(t y由耦合电路的电阻L R上取得。
要求写出此电路的状态方程和输出方程。
解：第一步，选状态变量。
因为电感电流和电容电压等三个变量都是独立的，所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。
第二步，分别写回路方程或节点方程。
由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步，消去非状态变量。
信号与系统课后习题答案
习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。
因此，公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。
因此，公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的，基频 =0f 1/π Hz 。
因此，公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统课后习题参考答案.pdf
-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
（e）[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 （-1/2）
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 （-1/2）
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则：整个信号的周期为：T = LCM{T1,T2} = π
1.11
j 4πn
解： e 7
→
ω1
=
4πn 7
，则：
2π ω1
=
2π 4π
=7= 2
N1 k
，⇒
N1
=
7
7
j 2πn
e5
→ ω2
信号与系统版课后答案 郑君里 高等教育出版社
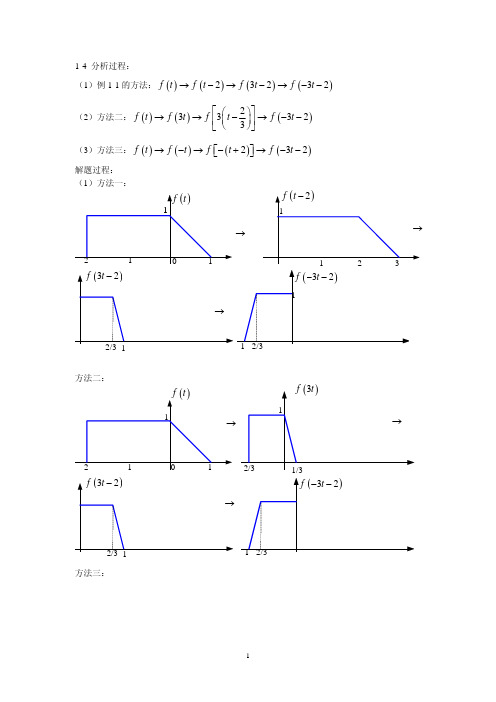
（1）例 1-1 的方法： f (t ) → f (t − 2) → f (3t − 2) → f (−3t − 2)
（2）方法二：
f
(t) →
f
(3t ) →
f
⎡⎢⎣3⎛⎜⎝ t −
2 ⎞⎤ 3 ⎟⎠⎥⎦
→
f
(−3t − 2)
（3）方法三： f (t ) → f (−t ) → f ⎡⎣− (t + 2)⎤⎦ → f (−3t − 2)
(R2
+
2L) C
d2 dt 2
v0 (t)
+
2R C
d dt
v0 (t)
+
1 C2
v0 (t)
=
MR
d3 dt 3
e(t)
∫ v0 (t)
图(c)微分方程：
=
L1i
' 1
=
1 C1
i2 dt
⇒
d
dt d2 dt 2
i1 i1
= =
1 L1 1 L1
v0 (t) v '0 (t)
∫
i1
=
1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即
f (t) = fe (t) + fo (t)
(1)
其中， fe (t ) 为偶分量， fo (t ) 为奇分量，二者性质如下：
fe (t ) = fe (−t )
(2)
fo (t ) = − fo (−t )
(3)
(1) ∼ (3) 式联立得
5t −∞
e2
(τ
)
dτ
= c1r1 (t ) + c2r2 (t )
信号与系统课后题解第一章
（6） f (2 − t ) （8） f (− 2 − t )ε (− t )
图 1.14
【知识点窍】本题考察信号的绘制及自变量变换导致信号变换的概念 【逻辑推理】本题用到信号的时域运算与变换。 解： （1） f (2t ) 信号的波形如图 1.15 所示。 （2） f (t )ε (t ) 信号的波形如图 1.16 所示。
t
ε [sin π t ]
1 … -2 -1 1 2 3 …
t
（b） 图 1.8 （9） 2 −n ε [n ] 函数式的信号的波形如图 1.9（c ）所示. 。
ε [n]
1 0 1 … 2 1
2−n
-1
n
-1 （a） 0 1 2
…
n
（b）
2 −n ε [n ]
1 … -1 0 1 2 （c ）
7
n
4
cos ω (t − t 0 )
1 … …
t0பைடு நூலகம்
-1 （a）
t
cos [ω (t − t 0 )]ε (t )
1 …
t0
-1
t
（b） 图 1.3
cos ω (t − t 0 )
1 …
t0
-1
t
图 1.4 （5） ε (t 0 − t ) （6） ε (t 0 − 2t )
t 0 > 0 函数式的信号的波形如图 1.5（b）所示. 。 t 0 > 0 函数式的信号的波形如图 1.6 所示. 。
T
2
（4） 3 cos (ω 0t + θ ) 是功率信号，其平均功率为：
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
信号与系统第三版郑君里课后习题答案
信号与系统第三版郑君里课后习题答案第一章习题参考解1，判刑下列信号的类型解：()sin [()];y t A x t = 连续、模拟、周期、功率型信号 。
()()tt y t x ed τττ--∞=⎰连续、模拟、非周期、功率型信号。
()(2y n x n =） 离散、模拟、非周期、功率型信号。
()()y n n x n = 离散、模拟、非周期、功率型信号。
1－6，示意画出下列各信号的波形，并判断其类型。
(1) 0()s in ()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()t x t A e -= 连续、模拟、非周期、只是一个函数，不是物理量。
(3) ()c o s 0tx t ett -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5k x k k =≥ 离散、模拟、非周期、能量型(6) 0().j kx k eΩ= 离散、模拟、周期、功率型()s i n [()];()()()(2);()()tt y t A x t y t x ed y n x n y n n x n τττ--∞====⎰1－6题，1－4图。
t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1－6 5－6题n=0:pi/10:2*pi;y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill'),title('(0.8)^n'),gridn1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill'),title('exp[2*pi*n1'),gridsubplot(4,1,4),stem(n1,sin(2*pi*n1),'fill'),title('sin2pin1'),gridsubplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1－8，判断下列系统的类型。
信号与系统课后习题附参考答案
1-1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。
题图1-3t)(2t x )(b 12112t)(1t x )(a 121123122T T2TEt)(t x )(a t)(t x )(b 13124023412t)(t x )(c n)(n x )(d 2213012112344⑴)2(1t x ⑵)1(1t x ⑶)22(1t x ⑷)3(2tx ⑸)22(2t x ⑹)21(2t x ⑺)(1t x )(2t x ⑻)1(1t x )1(2tx ⑼)22(1t x )4(2tx 1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴)12(1n x ⑵)4(1n x ⑶)2(1n x ⑷)2(2n x ⑸)2(2n x ⑹)1()2(22n x n x ⑺)2(1nx )21(2n x ⑻)1(1n x )4(2nx ⑼)1(1nx )3(2nx 1-5 已知信号)25(t x 的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。
题图1-5t)25(t x 110232523n)(2n x )(b 2213121124n)(1n x )(a 22131142134212321231-6 试画出下列信号的波形图：⑴)8sin()sin()(t t t x ⑵)8sin()]sin(211[)(t t t x ⑶)8sin()]sin(1[)(t t t x ⑷)2sin(1)(t tt x 1-7 试画出下列信号的波形图：⑴)(1)(t u e t x t⑵)]2()1([10cos )(t u t u t e t x t⑶)()2()(t u e t x t⑷)()()1(t u et x t ⑸)9()(2tu t x ⑹)4()(2tt x 1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。
信号与系统课后习题答案
信号与系统课后习题答案《低频电⼦线路》⼀、单选题（每题2分，共28分：双号做双号题，单号做单号题）1.若给PN结两端加正向电压时，空间电荷区将（）A变窄B基本不变C变宽D⽆法确定2.设⼆极管的端电压为 U，则⼆极管的电流与电压之间是（）A正⽐例关系B对数关系C指数关系D⽆关系3.稳压管的稳压区是其⼯作（）A正向导通B反向截⽌C反向击穿D反向导通4.当晶体管⼯作在饱和区时，发射结电压和集电结电压应为 ( ) A前者反偏，后者也反偏B前者反偏，后者正偏C前者正偏，后者反偏D前者正偏，后者也正偏5.在本征半导体中加⼊何种元素可形成N型半导体。
（）A五价B四价C三价D六价6.加⼊何种元素可形成P 型半导体。
（）A五价B四价C三价D六价7.当温度升⾼时，⼆极管的反向饱和电流将（）。
A 增⼤B 不变C 减⼩ D不受温度影响8. 稳压⼆极管两端的电压必须（）它的稳压值Uz 才有导通电流，否则处于截⽌状态。
A 等于 B ⼤于 C ⼩于 D与Uz ⽆关9. ⽤直流电压表测得放⼤电路中某三极管各极电位分别是2V 、6V 、2.7V ，则三个电极分别是（） A （B 、C 、E ） B （C 、B 、E ） C （E 、C 、B ） D（B 、C 、E ）10. 三极管的反向电流I CBO 是由（）形成的。
A 多数载流⼦的扩散运动 B 少数载流⼦的漂移运动 C 多数载流⼦的漂移运动D少数载流⼦的扩散运动11. 晶体三极管⼯作在饱和状态时，集电极电流Ci 将（）。
A 随B i 增加⽽增加 B 随B i 增加⽽减少C 与Bi ⽆关，只决定于eR 和CEuD不变12. 理想⼆极管的正向电阻为( )A A.零 B.⽆穷⼤ C.约⼏千欧 D.约⼏⼗欧13. 放⼤器的输⼊电阻⾼，表明其放⼤微弱信号能⼒（）。
A 强B 弱C ⼀般 D不⼀定14. 某两级放⼤电路，第⼀级电压放⼤倍数为5，第⼆级电压放⼤倍数为20，该放⼤电路的放⼤倍数为（）。
信号与系统课后答案
与奇分量的波形，相应如图题 1.12 中所示。
1-13 已知信号 f(t)的偶分量 fe(t)的波形如图题 1-13(a)所示， 信号 f(t+1)×U(-t-1)的波形如图题 1-13(b) 所示。求 f(t)的奇分量 fo(t)，并画出 fo(t)的波形。
解 因
f (t ) = f e (t ) + f 0 (t )
∫
t
−∞
δ (τ )dτ ，故根据现行系统的积分性有
y (t ) = ∫ h(τ (dτ = ∫ [δ (τ ) − δ (τ − 1) − δ (τ − 2) + δ (τ − 3)]dτ = u (t ) − u (t − 1) − u (t − 2) + u (t − 3)
1-2 已知各信号的波形如图题 1-2 所示，试写出它们各自的函数式。
解： f 1 (t ) = t[u (t ) − u (t − 1)] + u (t − 1)
f 2 (t ) = −(t − 1)[u (t ) − u(t − 1)]
f 3 (t ) = (t − 2)[u(t − 2) − u(t − 3)]
y 2 (t ) 的波形如图题 1.17(c)所示.
1-18 图题 1-18(a)所示为线性时不变系统，已知 h1(t)=δ(t)-δ(t-1), h2(t)=δ(t-2)-δ(t-3)。（1）求响 应 h(t)； （2） 求当 f(t)=U(t)时的响应 y(t)（见图题 1-18(b))。
解（1） h(t ) = h1 (t ) − h2 (t ) = δ (t ) − δ (t − 1) − δ (t − 2) + δ (t − 3) (2) 因 f (t ) = u (t ) =
信号与系统课后习题与解答第一章
1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解 信号分类如下：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 （a ）连续信号（模拟信号）； （b ）连续（量化）信号； （c ）离散信号，数字信号； （d ）离散信号；（e ）离散信号，数字信号； （f ）离散信号，数字信号。
1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问） （1）)sin(t e at ω-； （2）nT e -； （3）)cos(πn ；（4）为任意值）（00)sin(ωωn ；（5）221⎪⎭⎫⎝⎛。
解由1-1题的分析可知： （1）连续信号； （2）离散信号；（3）离散信号，数字信号； （4）离散信号； （5）离散信号。
1-3 分别求下列各周期信号的周期T ： （1）)30t (cos )10t (cos -； （2）j10t e ；（3）2)]8t (5sin [；（4）[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。
（1）对于分量cos (10t )其周期5T 1π=；对于分量cos (30t )，其周期15T 2π=。
由于5π为21T T 、的最小公倍数，所以此信号的周期5T π=。
（2）由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
信号与系统(郑君里)课后答案 第一章习题解答
1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。
注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。
1-9 解题过程： （1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。
信号与系统的课后答案
(b)根据(t)的特点，则
f1(t) *f2(t) =f1(t) *[(t)+(t2)+(t+ 2)]
=f1(t)+f1(t2)+f1(t+ 2)
结果见图p2-10(b)所示。
图p2-10
2-11试求下列卷积。
(a)
(b)
解(a)因为 ，故
2-10对图示信号，求f1(t) *f2(t)。
题2-10图
解(a)先借用阶跃信号表示f1(t)和f2(t)，即
f1(t)= 2(t)2(t1)
f2(t)=(t)(t2)
故
f1(t) *f2(t) = [2(t)2(t1)] * [(t)(t2)]
因为
(t) *(t)= =t(t)
故有
f1(t) *f2(t) = 2t(t)2(t1)(t1)2(t2)(t2)+ 2(t3)(t3)
题2-14图
解由KCL和KVL，可得电路方程为
代入数据得
特征根
1,2=1j1
故冲激响应uC(t)为
2-15一线性时不变系统，在某起始状态下，已知当输入f(t)=(t)时，全响应y1(t)= 3e3t(t)；当输入f(t)=(t)时，全响应y2(t)= e3t(t)，试求该系统的冲激响应h(t)。
解因为零状态响应
1-2给定题1-2图示信号f(t)，试画出下列信号的波形。[提示：f( 2t)表示将f(t)波形压缩，f( )表示将f(t)波形展宽。]
(a)2f(t2)
(b)f(2t)
(c)f( )
(d)f(t+1)
题1-2图
解以上各函数的波形如图p1-2所示。
信号与系统课后习题参考答案
题图2-10
2-11已知系统得微分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-12已知系统得差分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-13已知系统得微分方程,试求系统得单位冲激响应。
⑴
⑵
⑶
2-14已知系统得差分方程,试求系统得单位样值响应。
1-1试分别指出以下波形就是属于哪种信号？
题图1-1
1-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所示,试作出下列各信号得波形图,并加以标注。
题图1-3
⑴⑵⑶
⑷⑸⑹
⑺⑻⑼
1-4已知信号与波形如题图1-4中所示,试作出下列各信号得波形图,并加以标注。
题图1-4
⑴⑵⑶
⑷⑸⑹
⑵
⑶
⑷
⑸
⑹
2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)
⑵
⑶
⑷
⑸
⑹
2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-3
2-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-4
2-5已知,试求:
⑴⑵⑶
并作出她们得图形。
2-6系统如题图2-6所示,试求系统得单位冲激响应。已知其中各子系统得单位冲激响应分别为:
3-5设有一周期信号x(t),其复振幅为:
⑴x(t)就是实函数吗？⑵x(t)就是偶函数吗？⑶就是偶函数吗？
3-6设x(t)就是一基波频率为Ω得周期信号,其复振幅为,试用表示以下周期信号得复振幅。
⑴⑵
信号与系统课后答案(西南交大)
y x (t ) = 3e −2 t − 2 e−3 t t ≥ 0 y f ( t ) = te−2 t − e−2 t + e −3 t t ≥ 0
自由响应 2 e−2 t − e −3 t 强迫响应 te−2 t 稳态响应 0
暂态响应 te−2 t + 2e −2 t − e− 3t t ≥ 0
2.19 y f ( t ) =
2.22① t 3 u( t ) ④(
②∞
③( t−
1 2
1 1 −2 t + e )u( t ) 4 4
sin t + cost 1 −t − e )u( t ) ⑤ eu (t − 3) + e t − 2 u( 3 − t ) ⑥ cos(ωt + 45° ) 2 2 1 − cosπt cosπt − 1 1 1 2.23① u( t ) + u( t − 2) ② t 2 u( t ) − ( t − 1)2 u( t − 1) π π 2 2
3.6 f (t ) =
1 − j 3 ω0 t 3 − j 2 ω 0 t 3 1 e + e + e − jω 0 t + 1 + e jω 0 t + e j 2 ω0 t + e j 3 ω 0t 2 2 2 2
3.7 f (t ) = cos( 4ω0 t + 20°) + 2 cos( 2ω0 t + 30 °) + 3 cos(ω 0 t + 10° ) + 2
p2 + p +1 2.3 H ( p ) = 3 p + 2 p2 + 3p + 2 p2 + 3 p + 2 2.4 H ( p ) = 2p2 +3p +2
《信号与系统》习题参考答案
《信号与系统》习题参考答案（1）2—1（1） 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ （2） 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰（3） 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= （4） 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ （5） 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ （6）()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2（1） [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--（2） 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑（3） 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ （4） 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑（5） 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3（1） 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- （2） 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---（3） 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5（1） 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰（2） 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质，先对()x t 积分，对()h t 微分，'()()()y t x t dt h t =*⎰（3） 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰（4） 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰（5） 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7（1） 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =（2） 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- （3） 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8（1） 0()3()y t y t =（2） 00()()(2)y t y t y t =-- （3） 0()(1)y t y t =- （4） 0()()y t y t =-（5） 0()()dy t y t dt=（6） 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10（1） 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ （2） 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ （3） 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11（1） 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ （2） 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---（1）'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- （2）当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13（1）213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--（2）1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14（1）因果、稳定 （2）非因果、非稳定 （3）非因果、稳定 （4）非因果、稳定 （5）非因果、稳定 （6）因果、稳定 （7）因果、非稳定 2—15（1）因果、稳定 （2）非因果、稳定 （3）非因果、非稳定 （4）非因果、稳定 （5）因果、非稳定 （6）非因果、稳定 （7）因果、稳定 2—16（1）对 （2）对()h t dt ∞-∞=+∞⎰（3）错 例如单位冲激响应(1)t δ-是因果的，但LTI 系统的逆系统(1)t δ+不是因果的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为：(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列，周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知，在),(∞-∞区间上n 4sin π的功率为1/2，因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sinn n επ在),0(∞区间上的功率，其功率为1/2。
(7) te t x -=3)(解 非功率、非能量信号。
考虑其功率： 上式分子分母对T 求导后取极限得∞→P 。
(8) )(3)(t e t x tε-=解 能量信号。
信号能量为：1.3 已知)(t x 的波形如题图1.3所示，试画出下列函数的波形。
(3) )2(t x(4) (x(5) )(t x -(6) )2(+-t x11 -1/2 0 1 1 -2 -1 0 1 23 4(7) )2(--t x(8) )22(+-t x(9) )221(-t x)221(--t x (10)(11) )221()(-+t x t x(12) )21()2(t x t x ⋅(13)d(14)⎰∞-t d x ττ)(=⎪⎪⎪⎩⎪⎪⎪⎨⎧-<≥<≤+<≤-++=122320210121221t t t t t t t1.4 已知)(1t x 及)(2t x 的波形如题图1.4所示，试分别画出下列函数的波形，并注意它们的区别。
(1) )2(1t x1.5已知)(n x 序列的波形。
(1))4(+n x(3)x (4) )3(+-n x(5))3(--n x +)3(+-n x(7) )1()()(--=∇n x n x n x(8)∑-∞=nm m x )(1-2 -1 0 110 1 2 31 -4 -3 -3 -1 010 1 3/21 -8 -4 -2 010 1 2 3 4 5 6 7 81-1 0 1 2 3 4 5 6 7 81-1/2 0 11-1 03/21/2-1 0 1 2 t2 1-1/2 1/22 2 22 2 21.6 任何信号可以分解为奇分量和偶分量的和：)()()(t x t x t x o e += 或 )()()(n x n x n x o e += 其中e x 为偶分量；o x 为奇分量。
偶分量和奇分量可以由下式确定：)]()([21)(t x t x t x e -+=， )]()([21)(t x t x t x o --=)]()([21)(n x n x n x e -+=， )]()([21)(n x n x n x o --=(1) 试证明)()(t x t x e e -=或)()(n x n x e e -=；)()(t x t x o o --=或)()(n x n x o o --=。
(2) 试确定题图1.6(a)和(b)所示信号的偶分量和奇分量，并绘出其波形草图。
(1) 证明 根据偶分量和奇分量的定义：离散序列的证明类似。
(2) 根据定义可绘出下图nn x 2)(=，试求)(),(),(),(22n x n xn x n x ∆∇∆∇。
11222122)1()()(--=⋅=-=--=∇n nn n n x n x n x 解1.8 判断下列信号是否为周期信号，若是周期的，试求其最小周期。
(1) )64cos()(π+=t t x解 周期信号，21π=T(2) )()2sin()(t t t x επ=解 非周期信号。
(3) )2cos()(t et x tπ-=解 非周期信号。
(4) )3(4)(-=t j et x π解 周期信号，81=T 。
(5) )cos()5sin()(t b t a t x π+= 解 若,0,0≠=b a 则)(t x 为周期信号，21=b T ；若,0,0=≠b a 则)(t x 为周期信号，π521=a T ；若,0,0≠≠b a 则)(t x 为非周期信号。
(6) )38cos()(+=n n x π解 周期信号，161=N 。
(7) )97cos()(n n x π= 解 周期信号，181=N 。
(8) )16()(n con n x =解: 非周期信号。
1 18 8 8 642 11-2 -1 01/2-2 -1 0 1 2 1/2-2 -10 1 2 t2-3 3-3/2 2 n(9) n jen x 152)(π=解: 周期信号，151=N 。
(10) )34sin(2)3sin()6cos(3)(ππππ+-+=n n n n x 解: 周期信号，最小公共周期为241=N 。
1.9 计算下列各式的值。
(1)⎰∞∞--dt t t t x )()(0δ解: 原式dt t t x )()(0δ⎰∞∞--==).(0t x -(2)⎰∞--td t x ττδτ)()(0解: 原式ττδd t x t)()(0⎰∞--=)()(0t t x ε⋅-=(3)⎰∞∞--dt t t t x )()(0δ解: 原式dt t t x )()(0δ⎰∞∞-=)(0t x =(4)⎰∞∞--dt t t t x )(')(0δ解: 原式)(')(000't x t t x t --=--==(5)⎰∞∞---dt t t t t )2()(00εδ 解: 原式dt t t t t )()2(000-⋅-=⎰∞∞-δε)2(0t ε=(6)⎰∞---td t t ττετδ)2()(00解: 原式=⎰∞---td t t t τετδ)2()(000=⎰∞---t d t t ττδε)()(00)()(00t t t --=εε=⎩⎨⎧<->0)(00000t t t t ε (7)⎰∞∞-dt t )(δ解: 原式1= (8)⎰-∞-0)(dt t δ解: 原式0= (9)⎰∞+)(dt t δ解 原式0= (10)⎰+-00)(dt t δ解 原式1= (11)⎰∞∞--+-dt t tt )12)(33(2δ解 令t v 3=得：原式dv v vv 31]132)3)[(3(2-+-=⎰∞∞-δ32]132)3[(31=-+=x v v 32=(12)⎰∞∞-+dt t x t )()1('δ 解: 原式)1()('1'--=-=-=x t x t(13) ⎰∞∞--dt et t)('δ解: 原式1][0'=-==-t t e (14)⎰--3131)()32(dt t x t δ解: 令t v 2=得：原式dv v x v 21)2()3(3232⋅-=⎰-δ＝dv v x v 21)2()3(3232⋅-=⎰-δ因为0)3(3232=-⎰-dv v δ，所以: 原式＝01.10 设)(t x 或)(n x 为系统的输入信号，)(t y 或)(n y 为系统的输出信号，试判定下列各函数所描述的系统是否是：(a) 线性的 (b) 时不变的 (c) 因果的 (d) 稳定的 (e) 无记忆的? (1) )4()(+=t x t y 解 )(a 线性的.Θ若 );4()()(111+=→t x t y t x )4()()(222+=→t x t y t x则: )()()4()4()()()(212121t by t ay t bx t ax t y t bx t ax +=+++=→+)(b 时不变的.Θ若 )4()()(+=→t x t y t x则: )4()(ττ-+→-t x t x)(c 非因果的.t Θ时刻的响应取决于0t 以后时刻(即40+t 时刻)的输入. )(d 稳定的.Θ若|M t x ≤|)(<∞ 则:∞<≤M t y |)(| )(e 有记忆的Θ若系统的输出仅仅取决当前时刻的输入，则称此系统为无记忆系统。
题给系统显然不满足此条件。
(2) )()()(τ-+=t x t x t y (0>τ，且为常数)解 )(a 线性的.Θ若 )()()()(1111τ-+=→t x t x t y t x ，)()()()(2222τ-+=→t x t x t y t x则: )]()([)]()([)()()(221121ττ-++-+=→+t x t x b t x t x a t y t bx t ax =)()(21t by t ay +)(b 时不变的.Θ 若 )()()()(τ-+=→t x t x t y t x则: )()()()(0000t t y t t x t t x t t x -=--+-→-τ )(c 当0>τ时为因果的.Θ 当0>τ时:系统0t 时刻的输出仅与0t 及0t 以前时刻的输入有关. 当0<τ时:系统0t 时刻的输出与0t 以后时刻的输入有关. )(d 稳定的.Θ若|)(|t x ∞<， 则∞<|)(|t y )(e 有记忆的.Θ 系统0t 时刻的输出与0t 时刻以前的输入有关. (3) )2/()(t x t y =解:)(a 线性的. (说明略) )(b 时变的Θ若)2()()(t x t y t x =→ 则: )2()2()(τττ-≠-→-t x t x t x )(c 非因果的.)21()1(-=-x y Θ. 即1-=t 时刻的输出与1-=t 时刻以后)21(-=t 的输入有关.)(d 稳定的. (说明略))(e 有记忆的.Θ)21()1(x y =. 即1=t 时刻的输入与1=t 时刻以前)21(=t 的输入有关.(4) )()(2t x t y =解:)(a 非线性的.Θ 若 )()()(2111t x t y t x =→， )()()(2222t x t y t x =→则: )()()()()]()([)()(21222122121t by t ay t bx t ax t bx t ax t bx t ax +=+≠+→+)(b 时不变的.Θ若)()()(2t x t y t x =→ 则: )()()(2τττ-=-→-t y t x t x)(c 因果的. (说明略) )(d 稳定的. (说明略) )(e 无记忆的.Θ 0t 时刻的输出仅取决于0t 时刻的输入.(5) )(2)(t x et y =解:)(a 非线性的. (说明略))(b 时不变的. (说明略) )(c 因果的. (说明略)(d)稳定的.Θ 若 |)(t x |∞<≤M , 则∞<≤M e t y 2|)(|(e)无记忆的. (说明略) (6) t t x t y π2sin )()(=解: (a)线性的.Θ 若 )(]2[sin )()(111t x t t y t x π=→，)(]2[sin )()(222t x t t y t x π=→ 则: )()()]()([2sin )()(212121t by t ay t bx t ax t t bx t ax +=+→+π (b)时变的.Θ 若 )()(t y t x →则: )()](2[sin )()()2(sin )(ττπττπτ--=-≠-→-t x t t y t x t t x (c)因果的. (说明略)(d)稳定的.Θ 若∞<≤M t x |)(|， 则∞<≤≤M t M t y |2sin ||)(| (e)无记忆的. (说明略) (7) ⎩⎨⎧>=0)()()(t x t x t y解: (a)非线性的.Θ 若 0)()0()(1≠→<t y t x而0<a 时: )(0)()0)((12t ay t y t ax ≠=→<，即不满足均匀性. (b)时不变的.Θ若 )()(t y t x → 则: )(0)(00)()()(00000t t y t t x t t x t t x t t x -=⎩⎨⎧<->--→-(c)因果的.Θ0t 时刻的输出仅与0t 以后时刻的输入无关. (d)稳定的. (说明略) (e)无记忆的. (说明略) (8) dtt dx t y )()(=解:(a) 线性的. Θ 若 dt t dx t y t x )()()(111=→，dtt dx t y t x )()()(222=→ 则: )()()]()([)()(212121t by t ay t bx t ax dtdt bx t ax +=+→+ (b)时不变的.Θ若: dtt dx t y t x )()()(=→ 则: )()()()()(τττττ-=--=-→-t y t d t dx dt t dx t x(c)因果的. (说明略) (d)非稳定的.(e)无记忆的 (说明略) (9) ⎰∞-=td x t y ττ)()(解: (a)线性的. (说明略) (b)时不变的.Θ 若: ⎰∞-=→td x t y t x ττ)()()(则: )()()()(0000t t y dv v x d t x t t x t t t-==-→-⎰⎰-∞-∞-ττ(c)因果的. (说明略)(d)非稳定的.Θ 若∞<=|)(||)(|t u t x 1，但∞→|)(|t y (e)有记忆的. (说明略) (10) )1()()(-⋅=n x n x n y解: (a)非线性的Θ若 )1()()()(1111-⋅=→n x n x n y n x ，)1()()()(2222-⋅=→n x n x n y n x则: )()()]1()1()][()([)()(2122121n by n ay n bx n ax n bx n ax n bx n ax +≠-+-+→+(b)时不变的.Θ若 )1()()()(-⋅=→n x n x n y n x则: )()1()()(N n y N n x N n x N n x -=--⋅-→- (c)因果的.0n Θ时刻的输出与0n 时刻以后的输入无关. (d)稳定的.Θ 若 |∞<≤M n x |)(, 则: |∞<≤2|)(M n y(e)有记忆的.0n Θ时刻的输出与0n 时刻以前的输入有关.(11) )()(n nx n y =解: (a)线性的.Θ若 )()()(11n nx n y n x =→，)()()(222n nx n y n x =→ 则: )()()]()([)()(212121n by n ay n bx n ax n n bx n ax +=+→+ (b)时不变的.Θ若 )()()(n nx n y n x =→则: )()()()(N n y N n x N n N n x -=--→- (c)因果的. (说明略)(d)非稳定的.Θ 即使M n x <|)(|，∞→n 时，∞→)(n y (e)无记忆的. (说明略) (12) 6)(5)(+=n x n y解: (a)非线性的.Θ若 6)(5)()(111+=→n x n y n x ，6)(5)()(222+=→n x n y n x 则: )(6)(6)]()([5)()()(212121n y n ay n bx n ax n y n bx n ax +≠++=→+ (b)时不变的. (说明略) (c)因果的. (说明略) (d)稳定的. (说明略) (e)无记忆的. (说明略)(13) )()(n x n y -=解: (a)线性的. (说明略) (b)时变的.Θ若 )()()(n x n y n x -=→则: )]([)()()(N n x N n y N n x N n x --=-≠--→-(c)非因果的.)1()1(x y =-Θ. 即 1-=n 时刻的输出与 1-=n 以后时刻(1=n 时刻)的输入有关. (d)稳定的. (说明略)(e)有记忆的.).1()1(-=x y Θ 即 1=n 时刻的输出与1=n 以前时刻(1-=n 时刻)的输入有关.*1.11 已知)22(t x -的波形如题图1.11所示，试画出)(t x 的波形。