运筹学课件第九章_网络计划
运筹学网络计划
A
拆迁
/
2
B
工程设计
/
3
C
土建工程设计
B
2.5
D
采购设备
B
6
E
厂房土建
C、A
20
F
设备安装
D、E
4
G
设备调试
F
2
A(2)
1
B (3)
2
C (2.5)
3
D (6)
E (20)
G (2)
F (4)
4
5
6
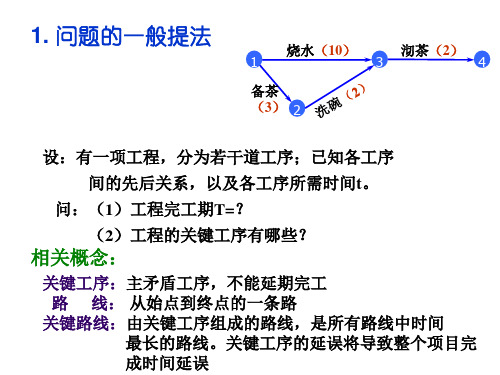
用箭秆删除法标号(保证箭尾号大于箭头号)
工序
A
B
C
D
EFGHIJKL
M
N
紧前工序
_
_
_
_
D
E
A
F
G
B
由本例可见:关键工序 头尾皆有
=
关键工序时间之和=工期T。
,但反之未必。
二、工程完工期的概率分析
(计划评审技术PERT)
1、PERT与 CPM的区别:
CPM工序时间是确定的
工程工期的概率分析是是时间不确定情况下PERT
的主要工作
确定平均工序时间的三点估计法:
设工序最乐观时间为aij,最悲观时间为bij,最可能时间为m ij ,
t ij
a ij 4m ij bij
- 给任意点 i 标 Li ,
Li=Min{以 i 为箭尾的各箭之 “箭头
- 箭长tij”}
16
(3)求关键路(用标号法)
6
2
8
0
0 1
3
B '(0)
3
2)计算各工序 i
华中科技大学运筹学课件!!!network

175
220
80
支行 4
270 215 120 175 - 310
支行 5
160 50 220 80 310 -
管理者希望确定哪两个银行之间应该用特殊的电话线直接相连,使得将每一 个支行和总行(直接或间接)相连的总费用最小。
a. 请解释为什么这个问题符合最小支撑树问题的网络描述。 b. 运用 7.5 节中介绍的贪婪算法求解这个问题。这种特殊电话线的总成本是
这种特殊电话线的费用是每英里 100 美元。银行之间的距离如下表所示(单 位:英里):
总行 支行 1 支行 2 支行 3 支行 4 支行 5
总行
- 190 70 115 270 160
支行 1
190 - 100 110 215 50
银行间的距离
支行 2
支行 3
70
115
100
110
-
140
140
-
120
表 1 货币汇率
比 日元 卢比 林吉特 美元 加拿大 欧元
英镑
比索
由
元
4
日本日元
1
印度尼西亚卢比
马来西亚林吉特
美元
加拿大元
欧元
英镑
墨西哥比索
50
0.04
0.008 0.01
0.0064 0.0048 0.0768
1
0.0008 0.00016 0.0002 0.000128 0.000096 0.001536
4.在一个不断扩建的小弄飞机场里,一家本地的航空公司购买了一辆新的牵引 车作为拖车,在飞机场之间搬运行李。因为机场在三年后将安装一个新的机械化 行李搬运系统,所以到那时候牵引车将被淘汰。然而,由于高负荷工作,其使用 与维护成本地随着年份急剧增加。因此使用一两年后进行重置可能更加经济。下 面的表格(0 表示现在)给出了第 I 年末购买的拖车在第 j 年末卖出的总净折现 成本(美元,购买价格减去交易抵偿,加上使用和维护费用)。
运筹学网络计划-PPT精选文档

Ch7 网络计划 Network Programming
2019/3/21
Page 3
• 网络还是进行计划工作的有效工具
Ch7 网络计划 Network Programming
2019/3/21
Page 4
优点:直观、易懂、便于检查 缺点:不能反映相互之间联系和影响, 无法找出关键工作。
2019/3/21
Page 11
网络图 由工序、事件及标有完成各道工序所需时间所构成的连 通有向图。 箭示网络图 用箭条表示工序的计划网络图。本章讲的就是箭示图 节点网络图 用节点表示工序的计划网络图 路 从起点沿箭头方向到终点的有向路。 紧前工序 紧接某项工序的先行工序 紧后工序 紧接某项工序的后续工序 前道工序 某工序之前的所有工序
表7-1 工序明细表
序 号 1 2 3 代 号 A B C 工序名称 基础工程 构件安装 屋面工程 A B 紧前工序 时间 (天 ) 40 50 30 序 号 5 6 7 代 号 E F G 工序名称 装修工程 地面工程 设备安装 紧前工序 C D B 时间 (天 ) 25 20 50
横道图
5月 6月
时间
开题报告
3月
4月
英文翻译
文献查阅 论文撰写 论文答辩
7.1 绘制网络图 Draw network plot
Ch7 网络计划 Network Programming
2019/3/21
Page 5
7.1.1项目网络图的基本概念 用网络图编制的计划称为网络计划,网络计划技术由计划协 调技术(Program Evaluation and Review Technique 简写为 PERT)与关键路径法(Critical Path Method 简写为CPM)组 成。 PERT主要针对完成工作的时间不能确定而是一个随机变量 时的计划编制方法,活动的完成时间通常用三点估计法,注重 计划的评价和审查。 CPM以经验数据确定工作时间,看作是确定的数值, 主要研究项目的费用与工期的相互关系。通常将这两种方 法融为一体,统称为网络计划、网络计划技术 (PERT/CPM)。
运筹学课件第九章网络计划

运筹学
1
2
3
4
5
6
24
22
26
24
30
18
18
上图为一个项目的网络计划,已知用于该项目的直接成本为47800元,间接成本为18000元,该项目原订74日完成,现要缩短工期,每缩短一天,间接费用可以节省330元,试求出工期较短而成本最少的最优方案。箭线下的数字为正常持续时间,括弧内为最短持续时间。相关数据见下表。 1→3→4→6为关键线路。
工作的最迟可能开工时间与最迟可能结束的时间
02
总时差
在不影响任务总工期的条件下,某工作(i,j)可以延迟其开工时间的最大幅度称为工作的总时差R(i,j) R(i,j) =tLF(i,j)-tEF(i,j)=tLS(i,j)-tES(i,j)
工作单时差
在不影响紧后工作的最早开工时间条件下,此工作可以延迟其开工时间的最大服务,r(i,j) r(i,j)= tES(j,k)-tEF(i,j)
本工作
紧后工作
紧前工作
紧后工作
双代号网络计划
双代号网络图是以箭线及其两端节点的编号表示工作的网络图
支模2
支模1
扎筋2
扎筋1
混凝土2
混凝土1
1.双代号网络图的基本符号
运筹学
工作i—j的持续时间 -------- D i—j 节点最早时间:earliest time -------- ETi 节点最迟时间:latest time -------- LTi 工作最早开始时间earliest star time -------- ES i—j 工作最早结束时间earliest finish time -------- EF i—j 工作最迟开始时间 latest star time -------- LS i—j 工作最迟结束时间 latest finish time ------- LF i—j i—j工作的自由时差 -------- FF i—j i—j工作的总时差 -------- TF i—j
第九章-网络图分析

最大流问题的目标是使得从源到收点 的总流量最大。这个流量的大小可以 用两种等价的方法来衡量,分别叫作 从源点出发的流量和进入收点的流量。
最大流问题标号法
基本思想:从任一初始可行流出发, 寻找这个可行流的一条可增路,利用 这条可增路使原可行流增加一个尽可 能大的流量,一直这样下去直到再也 找不到新的可增路为止。
最短路问题的Dijkstra标号法
步骤3:某临时标号点的所有可能标 号的最小值即是其最终标号,此时 将该临时标号点标记为已标号点, 并记录其前一节点
P(vl ) min {P(vi ) d (vi , vl )}
i
vl为零时标号点,vi是已标号点
最短路问题的Dijkstra标号法 步骤4:重复步骤2和3直至找到最 短路线,此时得到的最终标号即 为其最短路线的长度
摩登公司决定铺设最先进的光纤网络 系统以便在其主要中心之间提供高速 通信,包括数据、声音和视频等。
为了充分利用光纤技术在中心之间高 速通信的优势,不需要在每两个中心 之间都用一条光缆把它们直接连接起 来。可供选择的铺设光纤的线路如图。
应该铺设哪些光纤以 便在每两个中心之间 提供高速通信?
图的基本概念介绍
最小支撑树问题
练习
B
6 2 3 1 1
E
6 4 3
2 6
H
3
A
C
2
G
10
D
F
2
4
I
最小支撑树问题-破圈法
破圈法:任取一个圈,从圈 中去掉权最大的边(如果有两 条或两条以上的边都是权最 大的边,则任意去掉其中一 条)。在余下的图中,重复这 个步骤,一直到图中不含圈 为止。去边的同时必须保证 图的连通性
运筹学9网络计划

关键路线的特征:在线<a name=baidusnap0></a>路上</B>从起点到终点都由关键工作组成。
在确定型网络计划中是指线路中工作总持续时间最长的线路。
在关键线路上</B>无机动时间,工作总时差为零。
在非确定型网络计划中是指估计工期完成可能性最小的线路。
课堂练习:某机械厂管理信息系统开发活动清单见下表,试绘制网络计划图、计算时间参数并确定关键路线。
某机械厂管理信息系统开发网络计划图事件时间参数计算表项目的关键路线:1-2-4-5-7-8-9-10,或A-C-F-H-I-J-L。
第3节时标网络计划图时间坐标,简称时标。
在网络计划图的上方或下方,用以表示工程进度时间的坐标轴。
根据需要规定时间单位为:小时、天、周、月或季。
标注有时间坐标的网络计划图称为时标网络计划图。
在该图中箭线的长度就表示工作持续时间的长度。
在图中可以用实粗箭线或实红色的箭线表示关键工作和关键线路。
并且可用不同的线型表示出工作的总时差和自由时差。
例1的时标网络计划图如图所示。
回本章目录图9-8 第4节网络计划的优化绘制网络计划图,计算时间参数和确定关键线路,仅得到一个初始计划方案。
然后根据上级要求和实际资源的配置,需要对初始方案进行调整和完善。
即进行网络计划优化。
目标是综合考虑进度,合理利用资源,降低费用等。
包括:4.1 工期优化。
4.2 资源优化 4.3 时间-费用优化回本章目录4.1 工期优化(技术-时间优化、组织-时间优化)若网络计划图的计算工期大于上级要求的工期,就必须根据要求计划的进度,缩短工程项目的完工工期。
主要采取以下措施,增加对关键工作的投入,以便缩短关键工作的持续时间,实现工期缩短。
采取技术措施,提高工效,缩短关键工作的持续时间,使关键线路的时间缩短。
采取组织措施,充分利用非关键工作的总时差,合理调配人力、物力和资金等资源。
增加对关键工作的投入,以便缩短关键工作的持续时间,实现工期缩短。
运筹学网络计划技术

自由时差或单时差FF:
◦ 单代号:FFi=min{ESj}-EFi ◦ 双代号:FFij=min{ESjk}-EFij
48
工作A的TF
工作 A
工作A紧后工作B 工作A的TF
工作A的FF 工作A紧后工作C
总时差为零的工作单时差一定为零,总时差不为零 自由时差也可能是零
49
图上作业法 ◦ 单代号 ◦ 双代号 ◦ 绘制时标网络进度求 时间参数 表上作业法 i
37
工序名 称
紧前工 作
工作时 间
工序名 称
紧前工 作
工作时 间
工序名 称
紧前工 作
工作时 间
A
B C D
-
A A A
60
14 20 30
G
H I J
BC
EF F
7
12 60
M
N O P
JK
IL N M
5
15 2 7
DG 10
E
F
A
A
21
10
K
L
H
JK
25
10
Q
OP
5
38
B A
G M
C
J
P
D E L O H I K N Q
21
A
B Finish
Start
C
D
E
22
优点:
◦ 工序之间关系明确 ◦ 易于绘制 ◦ 国外常用软件采用
缺点:
◦ 无法带时标 ◦ 不够直观,所以国内工程师习惯双代号
23
基本概念:
◦ 以结点表示事件,即一项活动的开始或结束 ◦ 以箭线表示一项活动 ◦ 箭首和箭尾事件:一项工作的开始通常称为箭尾事件; 一项工作的结束通常称为箭首事件。
管理运筹学讲义:网络计划

资源分级
02
03
资源租赁与购买
Hale Waihona Puke 根据资源的重要性和稀缺性,对 资源进行分级管理,优先满足关 键资源的供给。
在项目资源不足时,考虑租赁或 购买外部资源,以满足项目需求。
调整关键路径
压缩关键路径
通过优化关键路径上的工作,缩短项目总工 期。
增加人力与物力
在关键路径上增加资源投入,提高工作效率。
任务并行化
通过合理安排任务顺序,使非关键路径上的 工作与关键路径上的工作并行进行。
THANKS FOR WATCHING
感谢您的观看
确定活动之间的逻辑关系
根据确定的活动先后关系,确定各个活动之间的逻辑关系,如并行关系、串行关系等。
确定活动的持续时间
根据历史数据、经验或实际情况,为每个活动分配合理的持续时间。
绘制网络图
使用合适的绘图工具
选择合适的绘图工具,如Visio、 Draw.io等,用于绘制网络图。
绘制网络图
根据确定的活动和关系,绘制出项目 的网络图,清晰地展示各个活动之间 的关系和顺序。
优化项目进度
进度计划优化
根据项目目标和资源状况,制定合理的进度计划,确 保项目按时完成。
进度控制
通过监控项目进度,及时发现偏差并采取措施进行调 整,确保项目按计划进行。
风险管理
识别项目中的潜在风险,制定应对措施,降低进度延 误的风险。
05 网络计划的评价与控制
评价网络计划的可行性
资源可行性
评估项目所需资源是否充足,是否符合 实际资源条件,避免资源浪费和短缺。
成本控制
制定项目成本预算,监控项目成本,及时发现和解决成本超支问题,确保项目成本控制 在预算范围内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双代号网络计划
本工作 紧前工作
双代号网络图是以箭线及其两端节点 的编号表示工作的网络图 紧后工作
三要素:箭线、节点、线路 ③
①
② ④
⑤
紧后工作
⑥
注 1):实箭线:消耗资源和时间的施工过程 2):虚箭线:既不消耗资源又不消耗时间只表 示一定的逻辑关系 3):箭杆的长度不表示时间的长短 4) :节点编号顺序从小到大,严禁重复使用
正常 工序 1-2 1-3* 2-4 3-4* 3-5 4-6* 时间 (日) 24 30 22 26 24 18 费用 (元) 5000 9000 4000 10000 8000 5400
最短 时间 (日) 16 18 18 24 20 18 费用 (元) 7000 10200 4800 10300 9000 5400
相差 時间 (日) 8 12 4 2 4 0 费用 (元) 2000 1200 800 300 1000 0
费用率 (元/日) 250 100 200 150 250 —
5-6
18
6400
10
6800
8
400
50
* 者为关键工作
2015-3-17 运筹学 20
通过计算得出此网络计划的工期22目,关键线路为 1→3→4→6。压缩工期必须以关键工作为对象,同時要选 择费用率最低的工作。从上表可以看出,最低费用率的关键 工作为1-3.
CC-CN DN-DC
CN
α N 工期 DC DN
2015-3-17
运筹学
17
通过费用率可以看出哪项工作在缩短工期時花费最低, 需要時即优先加快此项工作。 从成本的观点来分析问题,目的就是使整个项目的总成 本最低。具体需要解决的问题有以下几方面: (1)在规定工期的条件下,求出项目的最低成本; (2)如果需要进一步缩短工期,则应考虑如何使所增加的 成本最小; (3)要求以最低成本完成整个项目计划时,如何确定它的 最优工期; (4)如果可以增加一定数量的费用来缩短项目工期,它可 以比原计划缩短多少天。
最晚开始时间-最早开始时间 最晚结束时间-最早结束时间
表示各项工作在不影响紧后工作最早开始时间的前提下, 本工作可以利用的机动时间。 FF i—j=Tp- ES i—n-D i—j (最后的工作) = Tp- EF i—n FF i—j=ES j—k-ES i—j-D i—j(中间工作) 或 = ES j—k -EF i—j
2015-3-17
运筹学
8
2.双代号网络计划时间参数计算法 按工作参数计算: ES i—j LF i—j TF i—j LS i—j EF i—j FF i—j
最早开 始时间 最早结 束时间 最晚开 始时间
最晚结 束时间
工作名称
i
持续时间
j
工作总 时差 工作自 由时差
计算顺序: D i—j ES i—j EF i—j Tc LF i—j LS i—j TF i—j FF i—j
网络计划
网络计划是以箭线和节点组成的网状图来表示 项目进度的计划。网络计划的优点是把项目过程中的 有关工作组成了一个有机整体,因而能全面明确地反 映出各工作之间的相互制约和相互依赖关系。它可以 进行各种时间参数的计算,能在活动繁多、错综复杂 的计划中找出影响工程项目进度的关键工作,便于管 理人员集中精力抓住项目实施中的主要矛盾,保证进 度目标的完成。还可以利用网络计划反映出来的时差, 更好地配备各种资源,达到节省人力、物力和降低成 本的目的。
关键线路: 自始至终全部由关键工作组成的线路或线路上 总的工作持续时间最长的线路应为关键线路
2015-3-17
运筹学
13
时间参数计算:
ETj=max{ETi +D i—j}
LTi=min{ LTj-D i—j}
LFi,j =min{LFj,k-Dj,k} LSi,j=LFi,j-Di,j
ES i—j LS i—j TF i—j EF i—j LF i—j FF i—j
2015-3-17
运筹学
23
2
24
20
4
18
26
1
18
6 3
18 24
5
总工期缩短到62日后在网络 图中仍然是两条关键线路: ①1→2→4→6;② 1→3→4→6
i
j
-------- D i—j -------- ETi -------- LTi -------- ES i—j
工作最早结束时间earliest finish time 工作最迟开始时间 latest star time 工作最迟结束时间 latest finish time i—j工作的自由时差 i—j工作的总时差
2015-3-17 运筹学
-------- EF i—j -------- LS i—j ------- LF i—j -------- FF i—j -------- TF i—j
4
节点参数与工作参数之间的关系: ETi= ES i—j ; LF i—j = LTj
• 节点的最早时间 tE(1)=0 tE(j)=max{tE(i)+t(i,j)} • 节点的最迟时间 tL(n)=总工期或tE(n) tL(j)=min{tL(j)-t(i,j)}
1、工期与费用的优化 工期与费用是两个相互关联的要素,因为缩短工期,就 要加快进度,或采取一些措施,这样就会增加费用。同样, 项目费用的降低,也会影响项目的进度和工期。而项目的综 合管理就是将两个要素进行集成管理。 项目的成本是由直接费(材料费、人工费、机械设备费 等)和间接费(管理人员的工资、办公费、房屋租金等)构 成。直接费随工期的缩短而增加,因为工期越压缩则增加的 额外费用越多; 间接费与工期成正比关系,即工期越长则花的费用也 越多。这两种费用与工期的关系可用下图表示。
2015-3-17
运筹学
18
2
24
22
4
18
26
1网络计划,已知用于该项目的直接成本 为47800元,间接成本为18000元,该项目原订74日完成, 现要缩短工期,每缩短一天,间接费用可以节省330元,试 求出工期较短而成本最少的最优方案。箭线下的数字为正 常持续时间,括弧内为最短持续时间。相关数据见下表。 1→3→4→6 为关键线路。 运筹学 2015-3-17 19
D1
D2
16
工作的时间与费用曲线有多种形式,但单一的连续直线 型是一种近似求法,己被广泛采用。把正常时间点N与加快 时间点C直接连成一条直线,直线中间各点代表N、C之间 的工期所需相应的费用。对不同的工作,它的直接费的增 加情况也是不一样的,可用单位時间内的费用增加率 △C(即赶工成本斜率)来表示。若正常实施方案点N的正常 時间以DN表示,相应的正常费用为CN,缩短后的加快施工 方案点C,它的加快時间为DC,相应费用为CC,这样就可 以算出费用率△C: 费用 C CC △C=
2015-3-17 运筹学 7
需要明确的几个工期概念: 计算工期(Tc):根据时间参数计算得到的工期。 Tc= max{EF i-n} 要求工期: Tr 是任务委托人所提出的指令性工期,
计划工期(Tp):按要求工期和计算工期确定的作为
实施目标的工期 当已规定了要求工期时: Tp≤ Tr 当未规定要求工期时: Tp = Tc
由上表可知,工作2-3最短时间可压缩为12天,但是重 新计算网络图时间参数时发现工期为62,所以实际只缩短了 10天。总工期为64天。此时增加直接费用=100×10=1000元。 总工期缩短到64日后,在网络图中出现了两条关键线路 (下图):1→2→4→6;②1→3→4→6;
2015-3-17
运筹学
2015-3-17
运筹学
5
• 工作的最早可能开工时间与最早可能结束 的时间 tES(1,j)=0 tES(i,j)=max{tES(k,i)+t(k,i)} tES(i,j)=tES(i,j)+t(i,j) • 工作的最迟可能开工时间与最迟可能结束 的时间 tLF(i,n)=总完工期 tLS(i,j)=min{tLS(j,k)-t(i,j)} tLF(i,j)=tLS(i,j)+t(i,j)
2015-3-17 运筹学 9
h
i
j
1) ES i—j :工作i—j最早开始时间
0(起始工作) ES i—j = ES h—i + D h—i (有一个紧前工作) max{ES h—i + Dh—i }(多个紧前工作) 顺着箭头相加,逢箭头相碰的节点取最大值 (2)EF i—j:工作i—j最早结束时间 EF i—j=ES i—j+D i—j (持续时间) 整个计算工期: Tc= max{EF i—n }
2015-3-17 运筹学 15
• 由于工程项目总成本是直接费与间接费之和, 所以工程项目总成本曲线上,有一个成本最低 点P1,就是费用最低的最优方案,它对应的工 期D1就是最优工期。如果知道了规定工期D2, 也可以很容易地找到与之相对应的总成本P2。
成本 P2 P1
总成本
直接费用
间接费用 工期
2015-3-17 运筹学
21
2
24
22
4
18
26
1
20
6 3
18 24
5
总工期缩短到64日后在网络 图中出现了两条关键线路: ①1→2→4→6;② 1→3→4→6
2015-3-17 运筹学 22
可以继续缩短工期,可是由于有两条关键路线,所以必须对 两条关键路线同时缩短,有这么几种方案: 1)在(1,3)和(1,2)上同时缩短一天,需费用 =100+250=350 2)在(1,3)和(2,4)上同时缩短一天,需费用 =100+200=300 3)在(3,4)和(1,2)上同时缩短一天,需费用 =150+250=400 4)在(3,4)和(2,4)上同时缩短一天,需费用 =150+200=350 可以看出方案2缩短一天增加的直接费用最少,而(1,3) 最多可以缩短2天, (2,4)可缩短4天,取小者。此时增 加直接费用为300×2=600元。
