有限元分析用的材料属性表
一种重卡车架轻量化结构设计及有限元分析

作者简介:严国祥(1982-),男,山西运城人,本科,工程师,主要从事商用物流车、专用汽车的轻量化结构设计工作。
收稿日期:2021-10-18一种重卡车架轻量化结构设计及有限元分析严国祥,薛士博,王雪飞,蒋岩(辽宁忠旺集团有限公司,辽阳111003)摘要:介绍一种基于有限元分析的钢铝混合重卡车架的结构设计:车架材料主要是500L 大梁钢及6×××系铝合金挤压型材,由左右两支钢制纵梁、若干铝合金横梁组成主要受力框架。
纵梁采用原主机厂设计结构样式,横梁断面设计成抗弯刚度和连接性较好的工字型,各零部件之间通过铆钉或高强螺栓连接。
设计过程中通过有限元分析模拟了满载状态下的侧向工况和对扭工况,并重点分析了平衡悬架连接处的结构强度。
经过反复分析、结构优化,车架各处应力均低于材料屈服强度,抗弯和抗扭刚度与原钢车架相当。
对比结果表明,相比同类钢制车架,铝合金车架可减重40%。
关键词:铝合金;卡车;车架;有限元分析;轻量化中图分类号:TG146.21文献标识码:A文章编号:1005-4898(2022)01-0046-04doi:10.3969/j.issn.1005-4898.2022.01.100前言随着我国经济的快速发展,电商、快递业呈爆发式增长,货物运输量剧增,导致商用物流车需求加大,物流运输行业竞争加剧。
为控制成本,增加货运量,各物流企业对车辆的性能、油耗、载质量利用率要求越来越高,而解决上述问题的最佳方案莫过于减重。
轻量化设计对传统燃油汽车而言可显著降低油耗;对新能源汽车则可增加续航能力;对于商用物流车最明显的优势是多拉货物,空载时降低油耗,从而在相同运费情况下增加收益,显著提升竞争力。
车架材料主要是500L 大梁钢及6×××系铝合金挤压型材,是负责承载整车上部载荷的核心部件[1-2]。
因此,在车架轻量化设计时就要充分考虑其强度。
目前钢制车架的纵梁、横梁普遍采用高强钢板折弯成型,再铆接而成。
hyperworks有限元仿真-第9章_材料与属性信息

IX材料与属性信息本章包含“Practical Finiite Elemen t Analysis”一书中的材料。
同时Sascha Beuermann修订并添加附加材料。
9.1 胡克定律与两个常数这里有个常识,就是对于不同的材料,施加相同的力(也就是相同的应力)会得到不同的应变。
对多种材料进行一个简单的拉伸试验,在小位移情况下,应力(单位面积上的力)与应变(单位长度上的伸缩率)之间会存在线性相关性。
s = F/Ae = DL/Ls ~ e a s = Ee其中,常数E与材料相关。
此方程即为胡克定律(Robert Hooke, 1635-1703),是线弹性特性的材料方程。
E为弹性模量或杨氏模量,在线弹性范围内是正应力-应变曲线的斜率,定义为正应力/正应变,单位为:N/mm2。
可以在拉伸试验中看到另一个现象,即不仅在沿力的方向有会长,而且侧向会出现收缩。
μ的物理解释引用了尺寸为1x1x1mm的立方体,泊松比0.30的意味着,如果立方体伸长了1mm,侧向将收缩0.3mm。
金属的泊松比在0.25到0.35之间,泊松比的最大可能值为0.5(橡胶)。
还有一个材料参数G——刚性模量,代表在线弹性范围内剪切应力-应变曲线的斜率。
定义为剪切应力/剪切应变。
单位为e.g. N/mm2。
E,G和μ的相互关系见如下方程:E = 2 G (1+ u)线性静态计算仅需要两个独立的材料常数(比如E和μ)。
其他的分析需要附加的数据,比如重力、离心载荷、动态分析(材料密度r = m/V,单位体积上的质量,比如g/cm3)以及温度感应应力或应变(热膨胀系数a = e/DT = Dl/lDT,单位温度单位长度的膨胀或收缩,比如1/K)。
对于钢材,r = 7.89 •10-9 t/mm3 且a = 1.2 •10-5 1/K, 对铝, r = 2.7 •10-9 t/mm3 且a = 2.4 •10-5 1/K。
9.2 广义胡克定律方程及其36个常量胡克定律以σ = E * ε而熟知(见章节3.1)。
(完整版)有限元分析用的材料属性表
Cr4Mo4V# CrWMn 20CrMnMo 40CrMnMo 20CrMnTi 30CrMnTi 20CrMnSi 40CrMnSiMoV 5Cr21Mn9Ni2N 5Cr21Mn9Ni12N 20CrNiMo 20CrNi2MoA 2Cr12NiMoWV 28CrNiMoV# 30Cr2Ni4MoV# 40CrNiMo 40CrNiMoA 45CrNiMoV 45CrNiMoVA 10Cr2Mo1# 10Cr9Mo1VNb# 10CrMo910# 12Cr1MoV 12Cr1MoVTiB# 12Cr3MoVSiTiB# 12CrNi3 12Cr2Ni4 12Cr2Ni4H 12Cr2Ni4HA 12Cr18Ni9# 12Cr11MoV# 12Cr12Mo#
9Cr2Mo#
Cr12MoV
1.08E+11 2.10E+11 2.23E+11 2.10E+11 2.10E+11 2.10E+11 2.11E+11 2.11E+11 2.15E+11 2.06E+11 2.06E+11 2.06E+11 2.06E+11 2.06E+11 2.00E+11 2.07E+11 2.06E+11 2.11E+11 2.06E+11 2.06E+11 2.12E+11 2.10E+11 2.10E+11 2.11E+11 2.11E+11 2.20E+11 2.11E+11 2.13E+11 2.12E+11 2.25E+11 2.36E+11 2.18E+11
去毛刺机刀片的有限元分析

去毛刺机刀片的有限元分析王会刚(唐山学院河北省智能装备数字化设计及过程仿真重点实验室,河北唐山063000)0引言去毛刺机是板坯连铸工艺中的重要组成部分,提高去毛刺效率是保障铸坯合格率和板卷质量的必要手段之一[1],去毛刺刀片更是保证去毛刺质量和效率的关键所在[2]。
本文主要利用数值模拟方法,对去毛刺刀片与板坯接触面积、刀具角度、刀片材料等进行全面分析,分析结果对降低刀片损耗、提高刀片寿命有重要的指导作用。
1去毛刺机及其刀片常见的去毛刺机有刮刀移动式去毛刺机,铸坯移动式去毛刺机和离心锤刀式去毛刺机[3]。
本文的分析基于离心锤刀式去毛刺机,如图1所示。
离心锤刀式去毛刺机工作时,电动机通过万向联轴器带动去毛刺机的辊轴高速旋转,锤刀刀片在离心力的作用下高速转动并与轴线垂直,板坯进入遮住光栅,旋转的锤刀上升与板坯接触,此时板坯切口处的毛刺就在高速旋转的锤刀刀片打击下被切除。
该种去毛刺机常用的刀具旋转时速度可达到900r/min [4],刀具上各质点都具有很大的向心加速度,因此刀具受到较大离心惯性力的作用。
将锤刀刀片的尾部简化为方形,并不会造成较大的误差。
在刀具离心惯性力计算中,首先假设刀具的质量是均匀的,且刀具下端的外圆和内孔的圆心是重合的,把刀具的整个质量向质心简化。
根据质心求解公式和对称性,得:y =0;z =S y ∑2i =1A i=A 1z 1+A 2z 2A 1+A 2=A 1z 1+Sy 2A 1+A 2;A 1=60×110=6600mm 2;A 2=π×302÷2=1413.7mm 2;d A 2=y d z ;Sy 2=A ∫z d A 2=-2-300∫z (900-z 2)0.5d z =-18000mm 2;z =(40×60×80-18000)/(68×80+1413.7)=28.00mm 。
式中:S ji 为i 部分对j 轴的静距;A i 为i 部分的面积;y i i 部分形心的y 坐标;z i 为i 部分形心的z 坐标;y 为质心y 坐标;z 为质心z 坐标。
有限元分析

彭彭(沈阳化工大学机械工程学院,辽宁沈阳110142)1 研究的目的和意义2 建立桥梁检测车检测臂模型本次设计是对桥梁检测车检测臂进行静力和动力分析。
在分析过程中用到的所有数据及参数均参考有关规范。
钢桁架(steel truss )用钢材制造的桁架工业与民用建筑的屋盖结构吊车梁、桥梁和水工闸门等,常用钢桁架作为主要承重构件。
各式塔架,如桅杆塔、电视塔和输电线路塔等,常用三面、四面或多面平面桁架组成的空间钢桁架。
本文中采用四面桁架[4]。
检测臂为平行弦杆结构全长10米,上弦杆和下弦杆长度均为1米,截面均为直径10cm圆截面,如图2-1、2-2。
图2-1桥梁检测车工作臂结构示意图本文研究的是整个工作臂结构中的水平部分,这部分是带有伸缩功能的臂架结构,是工作臂中主要的承重部分。
图2-2检测臂平面图图2-3 检测臂立体图2.2单元介绍2.2.1 BEAM188单元描述BEAM188 —三维线性有限应变梁单元单元描述:BEAM188单元适合于分析从细长到中等粗短的梁结构。
该单元基于铁木辛哥梁结构理论,并考虑了剪切变形的影响[5]。
BEAM188是三维线性2节点梁单元,每个节点有六或七个自由度,自由度个数取决于KEYOPT(1)的值。
当KEYOPT(1)=0(缺省)时,每个节点有六个自由度:节点坐标系的x、y、z 方向的平动和绕x、y、z轴的转动。
当KEYOPT(1)=1时,每个节点有七个自由度,这时引入了第七个自由度(横截面的翘曲)。
本单元非常适合于线性、大角度转动和/或非线性大应变问题。
当NLGEOM打开(ON)时,BEAM188缺省考虑应力刚化效应。
应力刚化选项使本单元能分析弯曲、横向及扭转稳定性问题。
下面是BEAM188单元的示意图图2-4 BEAM188单元的示意图2.2.2 输入数据BEAM188 输入数据该单元的几何形状、节点位置、坐标体系如图“BEAM Geometry”所示,BEAM188由整体坐标系的节点i和j定义。
传热问题有限元分析

【问题描述】本例对覆铜板模型进行稳态传热以及热应力分析,图I所示的是铜带以及基板的俯视图,铜带和基板之间由很薄的胶层连接,可以认为二者之间为刚性连接,这样的模型不包含胶层,只有长10mm的铜带(横截面2mm×0.1mm)和同样长10mm的基板(横截面2mm×0.2mm)。
材料性能参数如表1所示,有限元分析模型为实体——实体单元,单元大小0.05mm,边界条件为基板下表面温度为100℃,铜带上表面温度为20℃,通过二者进行传热。
图I 铜带与基板的俯视图表1 材料性能参数名称弹性模量泊松比各向同性导热系数基板 3.5GPa 0.4 300W/(m·℃)铜带110GPa 0.34 401W/(m·℃)【要求】在ANSYS Workbench软件平台上,对该铜板及基板模型进行传热分析以及热应力分析。
1.分析系统选择(1)运行ANSYS Workbench,进入工作界面,首先设置模型单位。
在菜单栏中找到Units下拉菜单,依次选择Units>Metric(kg,m,s,℃,A,N,V)命令。
(2)在左侧工具箱【Toolbox】下方“分析系统”【Analysis Systems】中双击“稳态热分析”【Steady-State Thermal】系统,此时在右侧的“项目流程”【Project Schematic】中会出现该分析系统共7个单元格。
相关界面如图1所示。
图1 Workbench中设置稳态热分析系统(3)拖动左侧工具箱中“分析系统”【Analysis Systems】中的“静力分析”【Static Structural】系统进到稳态热分析系统的【Solution】单元格中,为之后热应力分析做准备。
完成后的相关界面如图2所示。
图2 热应力分析流程图2.输入材料属性(1)在右侧窗口的分析系统A中双击工程材料【Engineering Data】单元格,进入工程数据窗口。
第1章UGNX有限元分析入门–基础实例
选择材料
单击【创建】
第44页,共64页。
单击【确定】
4)定义网格属性
单击工具栏中的【网格收集器(俗称为:网格属性定义)】图标,弹出【网格捕集器】对话框
选择物理属性
单击【确定】
第45页,共64页。
5)划分网格
单击工具栏中的【3D四面体网格】图标,弹出【3D四面体网格】对话框
设置相关参数
网格划分后示意图
o 双击【后处理导航器】下【应力-单元节点的】的【最大主应力】子节点:
【最大主应力】位移 云图;【Minimum】 及【Maximum】值
第23页,共64页。
3)新建注释
o 在工具栏上单击【新建注释】图标,弹出【注释】对话框:
显示任意一个单元上节 点的应力值大小
第24页,共64页。
4)后处理视图
输入名称及 参数
单击【新建材料】
第10页,共64页。
单击【确定】
2)创建物理属性
单击工具栏中的【物理属性】图标,弹出【物理属性表管理器】对话框
选择材料
单击【创建】
第11页,共64页。
单击【确定】
3)网格属性定义
单击工具栏中的【网格收集器(俗称为:网格属性定义)】图标,弹出【网格捕集器】对话框
第49页,共64页。
有限元分析用的材料属性表zy
可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁
灰铸铁 灰铸铁 灰铸铁 灰铸铁 灰铸铁 灰铸铁
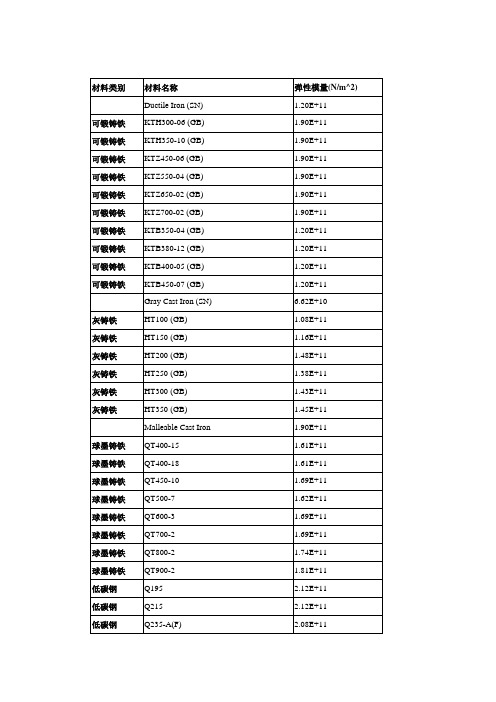
材料名称 Ductile Iron (SN) KTH300-06 (GB) KTH350-10 (GB) KTZ450-06 (GB) KTZ550-04 (GB) KTZ650-02 (GB) KTZ700-02 (GB) KTB350-04 (GB) KTB380-12 (GB) KTB400-05 (GB) KTB450-07 (GB) Gray Cast Iron (SN) HT100 (GB) HT150 (GB) HT200 (GB) HT250 (GB) HT300 (GB) HT350 (GB)
常用工程材料属性( 弹性模量(N/m^2) 1.20E+11 1.90E+11 1.90E+11 1.90E+11 1.90E+11 1.90E+11 1.90E+11 1.20E+11 1.20E+11 1.20E+11 1.20E+11 6.62E+10 1.08E+11 1.16E+11 1.48E+11 1.38E+11 1.43E+11 1.45E+11
碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 铸钢 铸钢 铸钢 合金结构钢 合金结构钢 合金结构钢 合金结构钢
35Mn 45Mn 60Mn 65Mn 70Mn T2 T3 T7 T8 T8Mn T9 T10 ZG230-450 (GB) ZG20SiMn (GB) ZG40Cr (GB) Q295 Q345 Q390 Q420
(完整word版)有限元分析大作业报告要点
有限元分析大作业报告试题1:一、问题描述及数学建模图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图所示。
二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模(1)设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences 为Structural(2)选择单元类型:三节点常应变单元选择的类型是Solid Quad 4 node182;六节点三角形单元选择的类型是Solid Quad 8 node183。
因研究的问题为平面应变问题,故对Element behavior(K3)设置为plane strain。
(3)定义材料参数:弹性模量E=2.1e11,泊松比σ=0.3(4)建几何模型:生成特征点;生成坝体截面(5)网格化分:划分网格时,拾取lineAB和lineBC,设定input NDIV 为15;拾取lineAC,设定input NDIV 为20,选择网格划分方式为Tri+Mapped,最后得到600个单元。
(6)模型施加约束:约束采用的是对底面BC 全约束。
大坝所受载荷形式为Pressure ,作用在AB 面上,分析时施加在L AB 上,方向水平向右,载荷大小沿L AB 由小到大均匀分布。
以B 为坐标原点,BA 方向为纵轴y ,则沿着y 方向的受力大小可表示为:}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 (1) 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图(2)六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图①最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;②结果显示三节点和六节点单元分析出来的最大应力值相差较大,原因可能是B点产生了虚假应力,造成了最大应力值的不准确性。
solidworks有限元分析 (2)
Solidworks有限元分析介绍Solidworks有限元分析(Finite Element Analysis,简称FEA)是一种用于模拟和分析物体结构行为的方法。
它可以帮助工程师们更好地了解产品的性能、强度和耐久性,从而优化设计并减少开发成本。
本文将介绍Solidworks有限元分析的基本概念、步骤和应用场景,并提供一些实际案例来说明其实际应用。
有限元分析的基本概念有限元分析是一种将复杂结构离散化为多个小元素(也称为有限元)的方法,然后对每个小元素进行计算并将其整合到整个结构中的解析技术。
它基于物体受力平衡原理和材料力学行为,利用数值方法求解一系列线性或非线性方程,从而得出结构的应力、变形和振动等特性。
在Solidworks中,用户可以通过插件或内置功能进行有限元分析。
用户需要先导入或创建结构的CAD模型,然后将其转换为有限元模型。
然后,用户可以定义加载条件、约束条件和材料属性等,进行分析并获取结果。
有限元分析的步骤有限元分析通常需要以下步骤:1.导入或创建CAD模型:用户可以通过Solidworks的CAD工具导入现有模型,或使用其设计功能创建新的模型。
2.网格划分:将结构离散化为多个小元素,通常是三角形或四边形的网格。
Solidworks可以自动进行网格划分,也可以手动调整网格密度。
3.定义边界条件:用户需要定义加载条件和约束条件。
加载条件可以是力、压力、温度等,约束条件可以是固定支撑、固定位移等。
4.定义材料属性:用户需要指定每个小元素的材料属性,如杨氏模量、泊松比等。
Solidworks提供了常见材料的数据库,用户可以选择合适的材料。
5.运行分析:用户可以定义分析类型和求解器选项,然后运行有限元分析。
Solidworks会根据用户的设置计算结构的应力、变形和振动等特性。
6.结果分析:分析完成后,用户可以通过Solidworks提供的结果查看工具,如色标图、图表和动画等来分析结果。
用户可以根据结果进行优化设计或验证设计的准确性。
