北京理工大学考研几何光学知识点
几何光学知识点

几何光学知识点Geometry optics, also known as geometrical optics, is a branch of optics that focuses on the behavior of light in terms of rays. 几何光学,也称为几何光学,是光学的一个分支,侧重于光的行为方面的射线。
In this field, light is considered to travel in straight lines and interact with various optical elements such as lenses and mirrors. 在这个领域中,认为光在直线上传播,并与各种光学元件如透镜和镜子相互作用。
Geometry optics is grounded in the principle that light reflects and refracts according to the laws of physics. 几何光学建立在光按照物理定律反射和折射的原则上。
Understanding the principles of geometry optics is essential for designing optical systems and devices for applicationsin areas such as imaging, lighting, and telecommunications. 理解几何光学的原则对于设计用于成像、照明和电信等领域的光学系统和设备至关重要。
One fundamental concept in geometry optics is the point source model, which assumes that light originates from a single point and travels in straight lines. 几何光学中的一个基本概念是点光源模型,假定光源自一个点并以直线传播。
几何光学物理光学知识点

几何光学物理光学知识点光学是研究光的传播、反射、折射、干涉和衍射现象的学科。
几何光学是光学的一个分支,主要研究光的传播直线性质和光的反射、折射的基本规律。
以下是几何光学的一些重要的知识点。
1.光的传播直线性质:光的传播遵循直线传播定律,即光在一种介质中以直线传播,称为光的直线传播性质。
2.光的反射定律:光在光滑表面上发生反射时,入射角等于反射角。
3. 光的折射定律:光从一种介质进入另一种介质时,入射角、折射角和两种介质的折射率之间满足折射定律,即n1*sin(θ1)=n2*sin(θ2),其中n1和n2分别为两种介质的折射率,θ1和θ2分别为入射角和折射角。
4.球面镜和薄透镜的成像公式:对于球面镜,成像公式为1/f=1/v+1/u,其中f为焦距,v为像距,u为物距。
对于薄透镜,成像公式为1/f=1/v-1/u。
5.凸凹透镜成像规律:凸透镜成像规律是物体距离凸透镜距离为f的位置,像无论在哪里都在凸透镜的反面,正立,放大,属于放大系统。
凹透镜成像规律是物体距离凹透镜越远,像越近,倒立,缩小,属于缩小系统。
6.光的干涉现象:光的干涉是指两束或多束光波叠加形成明暗相间的干涉条纹。
干涉分为相干光的干涉和非相干光的干涉,其中相干光干涉又分为同一光源光的干涉和不同光源光的干涉。
7.杨氏双缝干涉实验:是杨振宁做的关于光的干涉实验,实验证明了光的波动性。
8.杨氏实验的解释:杨氏双缝干涉实验的解释是光波从两个缝中通过后分别传播到屏幕上的不同位置,根据光的相位差和干涉条件,形成干涉条纹。
9.光的衍射现象:光的衍射是指光波通过一个小孔或物体边缘时,发生弯曲和扩散的现象。
根据衍射的级数,分为一级衍射、二级衍射、多级衍射。
10.衍射光栅:是利用衍射现象进行光学分析和测量的重要工具。
光栅是一种周期性结构,通过多级衍射产生许多衍射光束,形成明暗相间的衍射条纹。
11.真实像和虚像:根据物体和像的位置关系,成像可以分为真实像和虚像。
北京理工大学应用光学大全李林

v1 v2
n1,2
应用光学讲稿
SinI1 υ1
=
n = 1, 2
SinI2 υ2
第二种介质对第一种介质折射率等于第一种介质中的 光速与第二种介质中的光速之比。
折射率的物理意义
折射率与光速之间的关系
应用光学讲稿
sin I1 sin I2
v1 v2
n1,2
二、相对折射率与绝对折射率
1、相对折射率:
当几何光学不能解释某些光学现象,例如干涉 、衍射时,再采用物理光学的原理
应用光学讲稿
光线与波面之间的关系 • 波面:波动在某一瞬间到达的各点组成的面
t + Δt 时刻 t 时刻 A
应用光学讲稿
光线是波面的法线 波面是所有光线的垂直曲面 同心光束:由一点发出或交于一点的光束;
对应的波面为球面
应用光学讲稿
,折射角
N B
I1
R1
O I2
C N
应用光学讲稿
入射面:入射光线和法线所构成的平面
反射定律:反射光线位在入射面内; 反射角等于入射角 I1=R1。
折射定律:折射光线位在入射面内; 入射角正弦和折射角正弦之比,对两种一 定介质来说是一个和入射角无关的常数 。 Sin I1
Sin I2 = n1, 2
由
n Sin I1
Sin I2
=
1, 2
n2
n 1, 2 =
n1
有
Sin I1 Sin I2
n2
=
n1
或 n1 Sin I1 = n2 Sin I2
应用光学讲稿
课堂练习:判断光线如何折射
I1 空气 n=1 水 n=1.33
I2
I1 玻璃 n=1.5 空气 n=1
考研光学知识点梳理

考研光学知识点梳理光学是物理学的重要分支,研究光的传播规律和光与物质的相互作用。
在考研中,光学是一个重要的考点,需要掌握的知识点非常多。
本文将对考研光学知识进行梳理,帮助考生更好地准备考试。
1. 几何光学1.1 光的直线传播光在均匀介质中传播沿直线传播,光线的传播方向与光线的传播速度方向相同,光线的传播路径是直线。
1.2 光的反射定律光线从一个介质到另一个介质的界面上发生反射时,入射光线、反射光线和法线都在同一平面上。
1.3 光的折射定律光线从一个介质传播到另一个介质中发生折射时,入射光线、折射光线和法线都在同一平面上,入射角和折射角之间满足折射定律。
1.4 球面镜球面镜是一种由曲面组成的镜子,根据曲面形状可以分为凸面镜和凹面镜。
凸面镜和凹面镜分别具有不同的成像性质,需要掌握其成像规律。
1.5 透镜透镜是一种能够使光经过折射聚焦的光学元件,根据透镜形状可以分为凸透镜和凹透镜。
透镜也具有不同的成像性质,需要了解其成像规律。
2. 物理光学2.1 光的干涉光的干涉是指两束或多束光波相遇时相互作用的现象。
干涉分为干涉条纹、杨氏双缝干涉和牛顿环干涉等。
2.2 光的衍射光的衍射是指光通过有缝隙或物体边缘时发生偏斜并扩展的现象。
衍射分为单缝衍射、双缝衍射、光栅衍射等。
2.3 光的偏振光的偏振是指光中的电场矢量在空间中只沿一个方向振动的现象。
根据偏振方向的不同,光的偏振可以分为线偏振、圆偏振和椭偏振。
2.4 光的色散光的色散是指光在透明介质中传播时,不同波长的光产生不同的折射现象。
根据色散的原因,色散可以分为色散棱镜和色散光纤等。
3. 光的量子性3.1 光的波粒二象性光既表现出波动性,又表现出粒子性。
光的波粒二象性是量子力学的基本概念之一。
3.2 光的能量和频率光的能量与其频率有关,高频率的光具有更高的能量。
光的能量可以用普朗克公式来描述。
3.3 光的波长和波速光的波长和波速是光的基本特性,不同波长的光在介质中传播时速度不同。
光学几何光学知识点总结

光学几何光学知识点总结光学几何光学是研究光传播的基本规律和现象的一门学科,它通过几何光学原理来描述光的传播路径和成像规律。
在这篇文章中,我们将总结光学几何光学的核心知识点,帮助读者加深对光学几何光学的理解。
1. 光传播的直线特性光学几何光学的基本假设之一是光在均匀介质中直线传播。
根据光的直线传播特性,我们可以得出光传播的两大基本规律:直线传播定律和逆向规律。
直线传播定律指出,光在均匀介质中传播的路径是直线。
这意味着当光通过一块透明介质时,光线的传播路径是直线,除非发生折射或反射。
逆向规律指出,光线的传播方向与光线的路径相反。
这意味着当光线反射或折射时,其传播方向会发生变化,但光线总是沿着路径的反方向传播。
2. 折射定律和反射定律折射定律和反射定律是光学几何光学中最重要的定律之一。
折射定律描述了光在两种不同介质之间传播时的路径变化规律。
它指出,光线在通过两种介质的交界面时,入射角和折射角之间的正弦比等于两种介质的折射率之比。
反射定律描述了光线从一种介质到同种介质的传播过程中的路径变化规律。
它指出,入射角和反射角之间的角度相等。
这两个定律为解释光在透明介质之间传播和反射的现象提供了重要的理论基础。
3. 成像规律成像规律是光学几何光学的核心内容之一,它用来描述光线经过光学系统(如透镜和反射面)后的成像规律。
对于薄透镜而言,成像规律可以用薄透镜公式来描述。
薄透镜公式指出,当光线通过一个薄透镜时,入射光线与透镜光轴的乘积等于出射光线与透镜光轴的乘积。
对于反射面而言,成像规律可以用镜面成像公式来描述。
镜面成像公式指出,当光线经过反射面时,入射角和出射角之间的角度关系与光的传播路径相对应。
这些成像规律帮助我们理解光在透镜和反射面上的成像过程,从而应用于光学仪器和光学系统的设计和优化。
4. 光的光程差和相干性光程差是光学几何光学中的重要概念之一。
它表示光线经过不同路径传播所经历的光程的差异。
光程差在干涉和衍射现象中起着关键作用。
几何光学基本知识
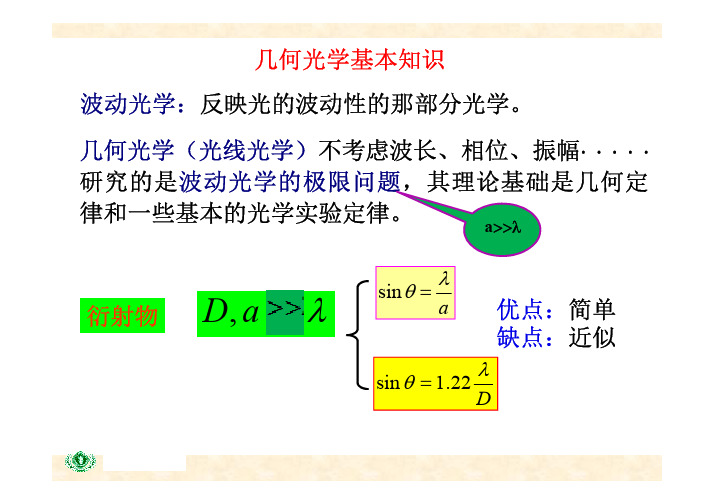
λ基本的光学实验定律包括:光在均匀介质中的直线传播定律;光通过两种介质界面时的反射定律和折射定律; 光的独立传播定律和光路可逆定律。
成立的条件:几何系统的尺度远大于光波波长;介质是各向同性的。
3.光线:光能量的传播方向的几何线表示光的传播方向2.光波面:光波相位相等各点构成的面。
一、光波面与光线1.光源:发光物体统称为光源点光源扩展光源线光源面光源光线1.理想模型:忽略衍射效应2.均匀各向同性介质:直线3.非均匀介质:曲线光线垂直于光波面平面波球面波(发散光)球面波(会聚光)二、费马原理(Fermat principle)费马原理:光在指定的两点间传播,实际的光程总是一极值。
极小值三、光学系统与成像概念1、光学系统:透镜、反射镜等成像元件2、单心(同心)光束物点为顶点的发散光束,其波面为球面物点为顶点的发散光束光点3、物像关系与物点相联系的同心光束,经光学系统仍是同心光束经过光学系统仍是单心光束4、物空间(物方)与像空间(像方)物空间入射光束所在的空间像空间出射光束所在的空间注意!不是用物、像位置所在的空间来定义物、像空间的!物空间与像空间的含义四、物、像的虚实实物:相对于光学系统,入射光束是发散的(a)虚像:相对于光学系统,出射光束是发散的(b)实像:相对于光学系统,出射光束是会聚的(c)虚物:相对于光学系统,入射光束是会聚的(d)a)实物成实像b)实物成虚像c)虚物成实像d)虚物成虚像五、完善成像条件1()k A A ′=常数★等光程性,物像间任意两点光路的光程相等。
★波面一致,球面波仍然为球面波★光束一致,同心光束仍然为同心光束。
几何光学知识点总结2

几何光学1.单球面成像公式说明:①适用范围:近轴光线②n 1λ射光线所在媒质折射率,n 2折射光线所 在媒质折射率③符号规则:实物(像)取正,虚物(像)取负;入射光线对着凸面r 取正2、单球面折射系统的焦度、焦点、焦距(1)焦度((focal power ) φ——反映系统折光本领r n n p n p n 1221-='+rn n 12-=φ单位:屈光度D (r 单位为 m )(2)焦距:(3)焦距和焦度的关系3.共轴球面系统采用顺次成像法4.薄透镜:分类凸透镜、凹透镜度1001=D r n n n f 1211-=r n n n f 1222-=r n n 12-=φr n n n f 1211-=r n n n f 1222-=11f n =φ22f n =如果组成透镜的材料折射率大于镜外介质的折射率,凸透镜是会聚透镜;否则是发散透镜。
成像公式:)11)(('21000r r n n p n p n --=+)11('112100r r n n n p p --=+f n 0=φ在空气中f1=φ6.薄透镜A.薄透镜的成像与单个透镜成像没有区别,可以用对每一个透镜依次成像的方法解决。
B.空气中密接的薄透镜组21ΦΦΦ+=21111f f f +=7、眼的调节瞳孔改变:球面像差,光通量晶状体r变:焦度改变r调节有一定限度:近点:眼睛处于最大调节状态能看清的物体与眼睛之间的距离。
正常眼:10-12cm远点:眼睛不调节时,能看清的最远处物体与眼睛之间的距离,正常眼:∞近视眼远点变近明视距离:适当照明,不易疲劳,最适宜距离 25 cm8.视角:从物体上两点发出的光到眼节点(光心)所张的角。
影响因素:物体大小物体与眼睛之间的距离意义:视角决定了视网膜上像的大小。
9.视力—眼的分辨本领:国家标准对数视力表国际标准视力表10.眼的屈光不正及矫正θ'-=lg 5L θ'=1视力11.放大镜放大镜的角放大率:12.显微镜:a.放大率b.显微镜的最小分辨距离; 如何提高显微镜的分辨本领?(1)减小照射光波的波长紫外光代替可见光,分辨本领提高一倍。
北京理工大学考研光学系统中成像光束和光阑知识点

一、1. 光阑光学系统中,限制成像光束口径和成像范围的孔或框称为光阑1) 孔径光阑:限制进入光学系统成像光束口径大小的光阑;2) 视场光阑:限制光学系统成像范围的光阑;2. 渐晕和渐晕系数1) 渐晕:由于轴外斜光束宽度小于轴上点光束宽度,引起的相平面轴外部分比相平面中心暗的现象;(这里的轴外和轴上点是指的无穷远点)2) 线渐晕系数:轴上点成像光束宽度D ,视场角为ω的斜光束在子午截面内的光线宽度为D ω,那么D ω和D 之比就是线渐晕系数,用D K 表示;3) 面渐晕系数:轴外光束截面面积和轴上光束截面面积之比,用S K 表示。
3. 入瞳和出瞳、出瞳距离和眼点距离在没有渐晕的情况下,孔径光阑在系统物空间的像称为入瞳,在像空间的像称为出瞳,分别限制入射光束孔径D 和出射光束孔径D ’的大小。
入瞳和出瞳对于光学系统成物像共轭关系。
在没有渐晕情况下,轴外光束中心光线(主光线)必然通过孔径光阑中心。
即物方入射光线中心光线通过入瞳中心,像方出射光线通过出瞳中心。
出瞳位置距离系统最后一面顶点的距离称为出瞳距离。
用'z l 表示,'z l 决定出射光束的位置。
系统存在渐晕时,边缘市场成像光束中心光线不再通过入瞳中心,孔径光阑中心和出瞳中心,这是把边缘视场出射光束中心光线和光轴的交点称为眼点,眼点到系统最后一面的距离称为眼点距离,用'z L 表示。
二、选择望远系统成像光束位置的基本原则1. 首先根据系统光学特性('',D f f )的要求,对轴上点边缘光线进行光路计算,确定轴上点边缘光线在系统中每个光学元件或光阑上的口径,这些轴向光束口径是为保证光学系统光学特性,系统中各光学元件所必须的最小口径。
2. 所说的确定光束成像位置,是指选择轴外点的成像光束的位置,成像光束的位置不同,直接影响各光学零件的实际口径。
在保证光学系统光学特性的条件下,能使系统中各光学零件的口径比较均匀的成像光束的位置,是最佳的成像光束的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.光线的概念能够传输能量的几何线二.几何光学基本定律直线传播和折射、反射定律,马吕斯定律,费尔马原理三种表达形式三.全反射现象和光路可逆定理四.几何光学应用范围五.光学系统的有关概念(重要)光学系统:根据需要改变光线传播方向以满足使用要求的光学零件组合;共轴光学系统:有同一对称轴线的光学系统;非共轴光学系统:有同一对称轴线的光学系统;球面光学系统:构成系统的零件表面均为球面的光学系统;非球面光学系统:含有非球面的光学系统;共轴球面光学系统:光学零件表面为球面,且球心排列在同一直线上的光学系统;目前广泛使用的大多是共轴球面系统和平面镜棱镜系统的组合。
六.透镜组成光学系统最基本的元件,主要作用是成像。
按面形划分:球面透镜和非球面透镜;按使光线折转的作用来分:会聚透镜(正透镜)和发散透镜(负透镜);f>;会聚透镜特点:中心厚边缘薄,焦距'0f<;发散透镜特点:中心薄边缘厚,焦距'0七.成像的有关概念由一点A发出的光线经光学系统后聚交或近似聚交在一点'A,则A点为物点,'A点为物点A通过光学系统所成的像点。
物像的虚实:光线延长线的交点是虚的,实际光线的交点是实的。
发散的物,汇聚的像是实的;汇聚的物,发散的像是虚的;物点像点的区分:入射光线交点是物点,出射光线交点是像点。
实物空间:光学系统第一个曲面以前的空间;虚物空间:光学系统第一个曲面以后的空间;实像空间:光学系统最后一个曲面以后的空间;虚像空间:光学系统最后一个曲面以前的空间;物空间折射率:实际入射光线所在空间介质的折射率;像空间折射率:实际出射光线所在空间介质的折射率;八.理想像和理想光学系统理想像点:由同一物点A发出的全部光线,通过光学系统后任然相交于唯一像点'A,A为物点A的理想像点;则称'理想像:在物像空间符合“点对应点,直线对应直线,平面对应平面”关系的像称为理想像;理想光学系统:指能成理想像的光学系统,即在物像空间均为均匀透明介质的条件下,物像空间符合“点对应点,直线对应直线,平面对应平面”关系的光学系统。
理想像和理想光学系统的作用:实际光学系统所成像和理想像的差异可以描述光学系统的品质;理想像的位置和大小可以代表一个质量好的实际光学系统成像的位置和大小。
共轴理想光学系统的成像性质:1. 位于光轴上的物点,其对应像点也一定在光轴上;2. 位于光轴某一截面内的物点,其对应像点也一定在此平面内;3. 过光轴任意截面(这个截面是哪个?)内的成像性质都相同,故可用一个过光轴的界面内的成像性质代表一个光学系统的成像性质; 4. 垂直光轴的物平面的共轭像面也一定垂直于光轴;5. 垂直于光轴的同一平面内的物所成像,几何形状与物相似;6. 一个共轴理想光学系统,若已知两对共轭面位置和放大率;或者一对共轭面位置和放大率,和轴上两对共轭点的位置,就可以确定一切共轭像点就可以根据已知共轭面和共轭点确定;第二章近轴球面系统的物像关系近轴光学主要是解决共轴球面系统的物像关系问题,即根据已知光学系统的结构参数(半径r ,折射率n 、'n ,厚度或者间隔d ),由给定的物平面位置(l )和物的大小(y ),求像平面的位置('l )和像的大小('y )。
基本方法:根据几何光学基本定理,找出由物体上的某一物点出发的一系列光线通过光学系统以后的出射光线的位置,由这些出射光线与光轴和像面的交点决定像的位置和大小。
一. 实际光路计算公式给定光学系统结构参数r 、n 、'n 、d ,由入射光线坐标(L ,U ),求出相应出射光线的坐标('L ,'U )。
相关公式为:''sin sin ,sin sin L r nI U I I r n-=='''''sin ,sin r I U U I I L r U =+-=+转面公式''2121,U U L L d ==-对于具有任意个折射球面的共轴球面系统,可连续应用以上公式,就可由入射光线坐标求得出射光线坐标。
上述公式计算的是实际光线在光学系统中走过的路线,由同一个物点发出的不同光线(L 相同,U 不同),用其计算的到的出射光线并不相交于一点('L 不同),但当入射光线的U 角度较小的时候,出射光线的'L 变化不大,也就是说,靠近光轴的光线,对应的出射光线聚交效果比较好。
所以,对近轴范围内的光线的成像性质有必要进一步研究。
二. 近轴光路计算公式图2-2靠近光轴的光线(近轴光线),其角度U 和I 都比较小,这个时候就可以用角度的正弦值sin U 和sin I 近似代替相应角度,由此可以得到近轴光路计算公式:'',L r ni u i i r n-==''''',i u u i i l r r u=+-=+转面公式''21211,u u l l d ==-以h l u=,''hl u =带入并消去中间变量,得到另一种形式的近轴光学计算公式'''(n n)h n u nu r-=- 转面公式'21u u =,'2111h h d u =-对于具有任意折射球面的光学系统,应连续应用上述公式,可由入射光线坐标(),l u 或()h,u ,求出最后一面的出射光线坐标()'',l u 或()'h,u 。
适用于已知光学系统结构参数r 、n 、'n 、d ,由给定近轴入射光线坐标,求出射光线坐标。
以上公式计算结果'l 与i 、u 无关,即同一物点发射出的不同方向的入射光线,利用近轴光学计算公式求出的出射光线都交于同一点,与中间变量u 、'u 、i 、'i 无关。
正因为近轴光学计算公式的计算结果与中间变量无关,不妨消去这些无关变量,就得到了近轴光学基本公式:'''n n n n l l r--= 单个球面物像位置关系'''y nl y n lβ==单个球面物像大小关系转面公式'21121,l l d y y =-=近轴光学基本公式是近轴光学计算公式的简化形式,建立了物像之间的直接联系,两种形式的公式的公式适用范围和得到的结果是完全一致的。
三. 理想光学系统的物像关系式前面的公式,必须逐面计算,才能得到整个光学系统的物像关系。
实际上,为了更直观的表述一个光学系统的物像关系,可以引入垂轴放大率1β=的一对共轭面,即物(像)方主平面H ('H ),以及两个基点F (物方焦点)和'F (像方焦点)。
用一对主平面和两个焦点表示一个光学系统的成像性质,进而导出理性光学系统的物像关系式。
根据物像位置起点的不同,理想光学系统的物像关系式可分为高斯公式和牛顿公式。
对公式的说明:a) 只有系统的焦距'f 知道了之后,才能使用。
只知道系统的结构参数时,可以利用近轴光路计算公式,计算一条平行光轴入射的光线(1,0h h u ==),根据入射高度1h 和出射光线与光轴夹角'k u 可求出焦距'f ,根据出射光在最后一面上的投射高度'k h 和'k u 求出焦点位置'k l :''1',kk k kh h f l u u == 由此确定了像方焦点和像方主平面的位置,同理可求出物方焦点和物方主平面的位置。
b) 牛顿公式和高斯公式的计算结果应该是一样的,实际应用中应当根据已知物像面的坐标是以什么形式给出的,当然可以根据转换公式''',x l f x l f =-=-改变已知坐标的形式。
c) 牛顿公式和高斯公式是整个理想光学系统物像位置和大小的直接关系公式,知道焦距就可以求解任意平面的位置和对应的放大率,反过来也可以根据物像位置确定系统的焦距。
四. 其他常用公式1. 物像空间不变式实际光学系统在近轴范围内成像时,对任意一个物像空间有:'''nuy n u y =由此可得垂轴放大率的另一种表达形式:'''y nu y n uβ==非近轴情况下,扩展到整个空间就得到理想光学系统物像空间不变式:'''tan tan ny U n y U =无限远物(像)的理想像(物)高公式(很重要)''tan y f ω=-无限远物像高公式''tan y f ω=无限远像对应物高公式当一个光学系统物(或像)位于无限远时,可用以上公式确定系统的视场光阑大小,分划板的分划线,以及确定视场、焦距、视场光阑口径之间的关系。
2. 组合系统焦距公式两个光学系统主面之间的间隔为d ,位于同一种介质中,组合系统焦距:'''''12121111d f f f f f f=+-=- 组合系统焦点位置:'''1212,f f f f f f ==-∆∆'''1122,F F f f f f x x ==-∆∆其中,'12d f f ∆=-+表示第一个系统像方焦点到第二个系统物方焦点的距离。
当组合系统物空间介质的折射率为1n ,两系统之间的折射率为2n ,像空间的折射率为3n 时,组合系统焦距为:33321'''''1212n n n d n n f f f f f f=+-=-在求解组合系统成像问题的时候,可利用上述公式首先确定组合系统焦点和主面的位置,然后就可以利用牛顿公式或者高斯公式求解物像之间的关系了!3. 理想光学系统的光路计算公式组合系统光路计算公式:''''tan tan h n U n U n f -= 过渡公式:''212111,tan U U h h d U ==-对于近轴光线,光路计算公式:''''n n u nu h f-=过渡公式:以上公式可用于理想光学系统或者实际光学系统近轴光线的光路计算问题。
要想求得组合系统的焦距,途径有二,其一,利用组合系统焦距公式;其二,应用以上光路计算公式,计算一条平行于光轴入射的光线,坐标11,tan 0h h U ==,得到出射光线的两个坐标',tan k k h U ,那么组合系统焦距为:'1'tan k h f U =反向计算同样一条光线就可以得到物方焦距。
