脚手架坠落事故树分析
高处坠落事故树分析

高处坠落事故的成因分析装置检维修、建筑施工等都存在高处作业,由于作业环境复杂多变,手工操作劳动强度大,同时也存在多工种交叉作业危险因素多,极易发生事故。
发生事故不但给企业造成严重的经济损失,同时又会造成家庭的不幸和悲痛,影响企业的声誉,制约企业的生存和发展,甚至会影响社会的稳定。
为此,高处作业造成的伤亡事故进行较为科学的分析,从中找出事故的成因及对策是非常迫切和必要的。
1、高处坠落事故的成因的分析(1)导致高处坠落事故的十种方式A、“四口、五临边”防护设施不齐全而坠落。
B、脚手架搭设不规范、防护设施不全、脚手板材质或铺设不符合要求而坠落。
c 、拆除脚手架、塔吊、施工升降机、物料提升机时坠落。
D、起重吊装时坠落。
E、梯子上作业时坠落。
F、轻质板断裂导致坠落。
G、吊篮架、提升架、挂架坠落或失稳而坠落。
H、倒塌脚手架、模板支撑架、塔吊时坠落。
I、提升机吊篮乘人断绳或施工升降机梯笼坠落而坠落。
J、随楼板坍塌而坠落。
(2)高处坠落事故的主要原因分析下面运用安全系统工程的事故树分析法(即FTA法),对高处坠落事故做以定性分析,如图一所示。
图1 高处坠落事故事故树分析图从以上事故树分析中可以看出,发生高处坠落事故的主要原因是2.1人的方面2.2管理人员的违章指挥会造成事故。
2.3监护人的失职、各项管理制度未得到落实,本可避免的事故就会发生。
2.4操作者本人的违章作业、违反劳动纪律和安全技术知识的缺乏,会造成大量的事故。
2.5物的方面2.6没有防护或防护设施有缺陷,留下重大事故隐患。
2.7施工设施的安全度不满足,易发生多人伤亡事故。
根据事故统计分析,可能坠落高度一般在25米以下,尤其是15米以下,占所分析事故的96%以上。
同时,必须重视亚高处(2米以下)作业个体防护措施的落实。
3、高处坠落事故的防治对策和建议3.1对策3.1.1安全生产的第一责任人必须提高对安全生产重要性的认识,树立以人为本的观念,认真贯彻《安全生产法》和《建设工程安全生产管理条例》,加大对安全生产的投入,设置安全管理机构、配备专职安全管理人员,使安全生产的各项措施落到实处。
关于脚手架高处坠落事故分析与处理

关于脚手架高处坠落事故分析与处理一、事故经过8月28日,由某建筑公司承建的宿舍楼主体己封顶,当天上午瓦工于某某等3人站在宿舍楼3单元6楼两阳台中间搭设的毛竹脚手架上浇筑阳台混凝土,由于没有专门搭设卸料平台,吊运的混凝土只好卸在该脚手架上临时铺设的钢模板上。
8时49分左右,当第三料斗混凝土卸在钢模上,瓦丁于某某上前清理料斗时,脚手架右侧内立杆突然断裂,钢模板滑落,于某某随钢模板坠落到地面,脑部和内脏严重受伤,施工现场管理人员急忙将他送往医院,但经抢救无效死亡。
这起事故造成直接经济损失9.5万元。
二、在脚手架上发生高处坠落事故的主要原因分析1、作业人员安全意识淡薄,自我保护能力差,冒险违章作业。
一是架子工从事脚手架搭设与拆除时,未按规定正确佩带安全帽和安全带。
许多作业人员自恃“艺高人胆大”,嫌麻烦,认为不戴安全帽或不系安全带,只要小心一些就不会出事,由此导致的高处坠落事故时有发生。
二是作业人员危险意识差,对可能遇到或发生的危险估计不足,对施工现场存在的安全防护不到位等问题不能及时发现。
2、脚手架搭设不符合规范要求。
建设部行业标准《建筑施工扣件式钢管脚手架安全技术规范》(JGJ130-2001)已经于2001年6月1日起正式实施。
该规范属于强制性标准,在脚手架的设计计算、搭设与拆除、架体结构等方面提出了许多新的要求。
但在部分施工现场,脚手架搭设不规范的现象仍比较普遍,一是脚手架操作层防护不规范;二是密目网、水平兜网系结不牢固,未按规定设置随层兜网和层间网;三是脚手板设置不规范;四是悬挑架等设置不规范,由此导致了多起职工伤亡事故的发生。
3、脚手架材质不符合要求,使用前未进行必要的检验检测;4、脚手架搭设与拆除方案不全面,安全技术交底无针对性。
项目部重视施工现场、忽视安全管理资料的现象比较普遍,应当编制专项安全技术方案的专项施工工程,如脚手架搭设与拆除、基坑支护、模板工程、临时用电、塔机拆装等,不编制施工方案,或者不结合施工现场实际情况,照抄标准、规范,应付检查。
高处坠落事故树分析

安全系统工程课时设计(高处坠落事故树分析)姓名:班级:学号:学院:建工学院指导老师:2014年12月24日目录摘要 (3)1.建筑施工高处坠落事故 (4)1.1.高处坠落的常见类型 (4)1.2.高处坠落的原因 (4)1.3.高处坠落的危害 (5)2.建筑施工高处坠落事故树的建立 (5)2.1.事故树分析的定义 (5)2.2事故树分析图使用的符号说明 (5)2.3.事故树分析步骤 (7)2.4. 建筑施工高处坠落事故树的建立 (8)3. 建筑施工高处坠落事故树的分析 (8)3. 1.最小割集的求解 (8)3. 2.最小径集的求解 (9)3. 3 求顶事件发生的概率 (10)3.4结构重要度的求解 (11)3.5各基本事件概率重要度分析 (11)3. 6各基本事件的临界重要度系数 (12)4.结果分析 (13)5.结论 (16)参考文献 (16)摘要:建筑业是危险性较大的行业,也是事故发生较多的行业之一,“高处坠落、物体打击、机械伤害、触电、坍塌”这五大伤害严重威胁着建筑企业职工的健康和生命安全。
而高处坠落又居建筑施工“五大伤害”之首,事故发生率极高,约占各类事故总数的60%以上,危险性极大。
因此,分析和掌握高处坠落事故的原因和预防对策,对防止高处坠落事故的发生,降低建筑业伤亡事故有着重大的意义。
关键词:建筑事故;高处坠落;预防对策。
前言:每年高空坠落事故高达到75000起,而80%以上是死亡事故。
因此,建筑施工中对高空作业的管理是安全管理的重中之重,本文通过事故树分析法(FTA)进行高空坠落事故分析,意在不仅找出造成事故的直接原因,而且也能深入揭示事故的潜在危险因素,对事故原因进行定性分析,找出易造成事故的危险因素,通过加强对高空作业中涉及的设施、人员、环境等方面的管理,建立建全各种规章制度,并在施工中确保各项规章制度能得到有效执行,避免建筑施工高空坠落事故的发生。
1.建筑施工高处坠落事故1.1.高处坠落的常见类型:1)洞口临边作业的坠落;2)脚手架上坠落;3)卸料平台的坠落;4)悬空高处作业坠落;5)轻质板材断裂导致坠落;6)拆除工程中发生的坠落;7)登高过程中坠落;8)梯子上作业坠落;9)屋面檐口边作业坠落;10) 其他高处坠落。
高处坠落事故树绘制m1m2x1

高处坠落事故树绘制m1m2x1摘要:1.高处坠落事故概述2.树绘制M1、M2、X1的含义3.如何利用树绘制分析高处坠落事故4.案例解析5.预防高处坠落事故的措施6.总结正文:近年来,高处坠落事故在我国频发,给人民生命安全带来严重威胁。
为了更好地分析高处坠落事故的原因和规律,本文将采用树绘制方法进行深入剖析,以期为高处坠落事故的防范提供有益参考。
一、高处坠落事故概述高处坠落事故是指在高处作业过程中,因各种原因导致人员坠落受伤或死亡的意外事件。
事故原因多样,包括作业环境不安全、个人防护不到位、施工设备故障等。
高处坠落事故具有突发性、意外性和严重性等特点,往往给受害者家庭和社会带来巨大的伤痛。
二、树绘制M1、M2、X1的含义为了更直观地展现高处坠落事故的成因,我们可以运用树绘制方法对其进行分解。
在此,我们选取M1、M2、X1三个要素作为分析重点。
1.M1:事故直接原因。
包括作业人员失足、设备故障、材料破损等。
2.M2:事故间接原因。
包括安全管理不到位、教育培训不足、应急预案不完善等。
3.X1:事故根本原因。
涉及企业文化建设、政策法规执行、领导层重视程度等方面。
三、如何利用树绘制分析高处坠落事故1.收集事故相关信息,包括事故发生时间、地点、当事人背景等。
2.依据事故原因分类,将M1、M2、X1细化为更具体的子因素。
3.利用树绘制工具,自上而下逐级展开,形成层次清晰的树状结构。
4.分析各因素之间的逻辑关系,找出事故发生的根本原因。
四、案例解析以某企业高处坠落事故为例,通过树绘制分析,我们发现事故根本原因是企业安全管理不严格,导致现场安全隐患重重。
在此基础上,针对M1、M2、X1三个要素采取相应措施,有效降低了高处坠落事故的发生概率。
五、预防高处坠落事故的措施1.加强安全管理,严格执行安全规程和法规。
2.提高作业人员的安全意识和技能水平,开展针对性培训。
3.完善应急预案,提高事故应对能力。
4.落实企业安全生产文化建设,提高全员安全意识。
安全事故树
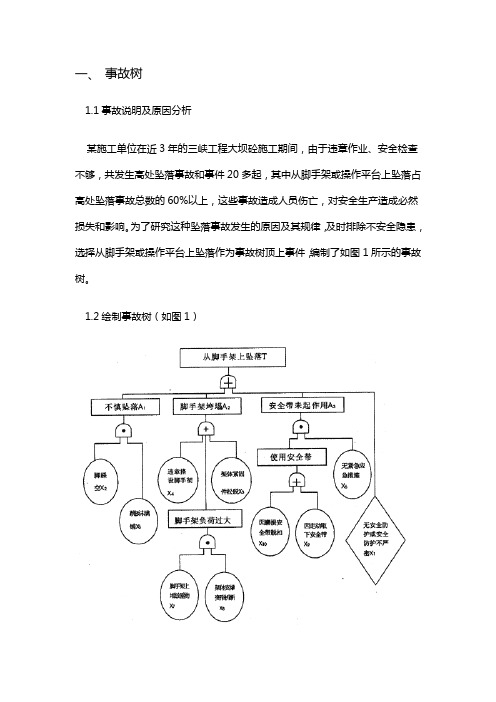
一、事故树1.1事故说明及原因分析某施工单位在近3年的三峡工程大坝砼施工期间,由于违章作业、安全检查不够,共发生高处坠落事故和事件20多起,其中从脚手架或操作平台上坠落占高处坠落事故总数的60%以上,这些事故造成人员伤亡,对安全生产造成必然损失和影响。
为了研究这种坠落事故发生的原因及其规律,及时排除不安全隐患,选择从脚手架或操作平台上坠落作为事故树顶上事件,编制了如图1所示的事故树。
1.2绘制事故树(如图1)图1 脚手架坠落事故树二、定性分析2.1等效事故树(如图)图2 等效事故树2.2最小割集该事故的最小割集:E1=X1,E2=X4,E3=X5,E4=X2X3,E5=X7X8,E6=X6X9,E7=X6X10,由图2可见,发生顶上事件的途径有7种。
2.3最小径集该事故树的最小径集:3结构重要度排序按照事故树及最小割集表示的等效事故树分析,X1,X4,X5最重要,处于一样地位;X6次之,X二、X3和X7、X八、X九、X10处于同等地位,最不重要。
因此,各大体事件的结构重要顺序为:I1=I4=I5>I6>I2=I3=I7=I8=I9=I10三、定量分析3.1 各大体事件发生的概率统计按照某单位1999年7月至2021年12月发生的从脚手架或操作平台上坠落事件统计,估算各大体事件发生的概率为:无安全防护或安全防护不周密(X1),q1=0.27次/月;脚踩空(X2),q2=0.17次/月;脚手架未满铺(X3),q3=0.3次/月;违章搭设脚手架(X4),q4=0.2次/月;脚手架牢固件松脱(X5),q5=0.13次/月;无安全紧急应急办法(X6),q6=0.33次/月;脚手架上堆放重物(X7),q7=0.2次/月;支撑变形折断(X8),q8=0.1次/月;安全带因走动而取下(X9),q9=0.5次/月;因磨损安全带脱扣(X10),q10=0.2次/月。
3.2 顶上事件发生的概率用近似法计算顶上事件的发生概率:q=q1+q4+q5+q2q3+q7q8+q6q9+q6q10=0.902(次/月)由此可见,该事故树顶上事件T的发生概率在该施工单位每个月接近1起,必需采取办法加以改良。
事故树分析法在脚手架坍塌事故中的应用
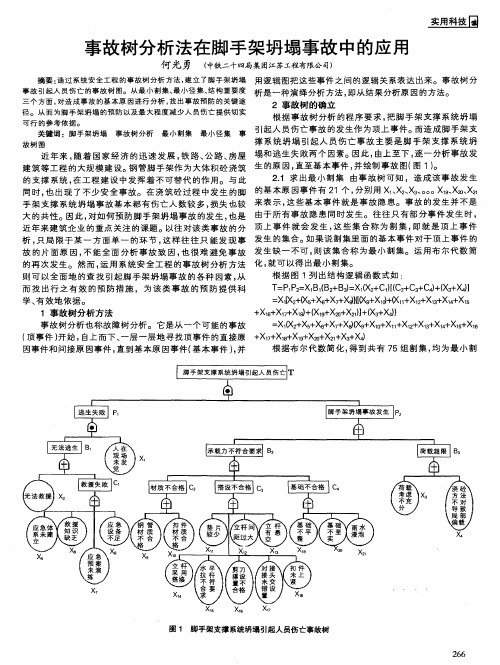
关 键 词 :脚 手 架 坍 塌 事 故 树 分析
故 树 图
最小割集
最 小 径 集 事 引起 人 员伤 亡事故 的发生作 为顶上 事件。而造 成脚 手 架支
撑 系 统坍 塌 引起 人 员伤 亡 事 故 主要 是 脚 手 架 支撑 系统 坍
由上 至下 , 一 分析 事故 发 逐 近 年来 , 随着 国 家经 济 的 迅速 发 展 , 路 、 路 、 铁 公 房屋 塌和 逃 生失败 两 个 因素。因 此 , 直 并 图 。 建 筑 等工 程 的大规 模建 设 。 管脚 手架作 为大体 积砼 浇筑 生 的原 因 , 至基 本事 件 , 绘制 事 故 图( 1) 钢 21 求 出最 小割 集 由事故 树 可 知 ,造 成该 事 故发 生 . 的支 撑 系统 , 工程 建 设 中发 挥着 不 可替 代 的作 用。 与 此 在 1个 , 分别 用 X 、 2x 、 0 X 、 z ,x 、 30 0 X 扣 X 同时 , 出现 了不 少安 全事 故 。在 浇筑 砼 过程 中发生 的脚 的基 本原 因事件 有 2 也 来表 示 , 些基 本 事件 就是 事故 隐 患。 事故 的发生 并不 是 这 手 架 支撑 系 统坍 塌 事故 基 本都 有伤 亡 人数 较 多 , 失 也较 损 大 的 共性 。因此 , 对如何 预 防脚 手架 坍塌 事故 的发生 , 也是 由于 所 有事 故 隐患 同 时发 生。往 往 只 有部 分事 件发 生 时 , 顶上 事件 就 会发 生 , 些集 合 称 为 割集 , 这 即就 是 顶 上 事 件 近 年来 建筑 企 业 的重点 关注 的课 题。以往 对该 类 事故 的分 析 , 局 限于 某 一 方 面 单一 的环 节 , 样 往 往 只 能发 现 事 发生 的集 合。如 果说 割集里 面 的基本 事件 对于 顶上 事件 的 只 这 则该 集合 称 为最 小 割集 。运 用布 尔代 数 简 故 的片 面原 因 , 能 全面 分析 事 故致 因 , 很 难 避免 事 故 发生 缺 一不 可 , 不 也 就 的再 次发 生。 然 而 , 运用 系统 安 全工 程 的事 故 树 分析 方法 化 , 可 以得 出最 小割 集。 根据 图 1列 出结 构 逻辑 函数 式如 : 则 可 以全 面地 的查 找 引起脚 手 架坍 塌 事故 的各 种 因素 , 从 T 12 X B( 2 B )X (2 C)C + 3 C) (3 X) =PP= 1 1 + 3 1 + 1(2 C + 4 X+ 4 B = X 【 + 】 而 找 出行 之 有效 的预 防 措施 , 为该 类 事故 的预 防提 供 科 XI2c5X + 7 ×)c9X C ◇” X 2X3 X4 X5 1 +》+ 6 X+ E )+ 1+ ( + 1 1 1 1 X ( 】( Ⅱ ) + + + 学 、 效地 依据 。 有
建筑爬架事故分析

2
脚手架上施工人员高 处坠落事故中,“架 上作业安全检查缺失 ”是主要原因,“脚手 架安全防护构件未按 规定搭设(错搭、漏 搭)”、“脚手架安全 防护构件被拆卸”其 次。
3
脚手架倾覆、坍塌事 故中,“脚手架材料 进场未组织检验”、“ 脚手架搭设架子工未 进行技术交底”、“脚 手架搭设后未织验收 ”是主要原因;脚手架 材料缺陷,是造成脚 手架倾覆坍塌的次要 原因
建筑施工脚手架安全 事故分析
11
目录
一、简
介 二、手架安全事故分类 三、脚手架事故原因分析 四、脚手架事故树分析 五、灰色关联分析法在脚手架事故中的应用 六、前景展望
2
一、简介
近年来我国建筑施工脚手架安全事故频发, 不论是脚手架整体或局部失稳造成的倾覆、 坍塌,还是脚手架搭拆及架上作业人员的 高处坠落,均造成严重的伤亡事故。脚手 架安全事故的原因复杂多样,对脚手架施 工安全风险进行辨识和分析,是进行脚手 架安全风险预控,预防或减少安全事故的 重要前提。
西安法门寺工程模板坍塌事故
2008年3月13日。西安法 门寺一期工程正圣门东A 区高大厅堂梁板楼盖,支 模高度达20.5 m,采用扣 件式钢管支架,没有设臵 垂直和水平剪刀撑,在浇 筑至板中间部位时,突然 发生坍塌,正在作业的十 几名工人,瞬间如自由落 体般地被摔坠至地面,造 成3人死亡、6人受伤
2010年1月份脚手架事故统计
1、2010年1月3日,昆明机场高架桥东引桥上,水泥浇注时巨大的在建桥体 轰然塌毁,事故导致施工工人7人死亡,8人重伤,26人轻伤。 2、2010年1月12日,安徽省芜湖市芜湖华强文化科技产业园配送中心建设工 地,在混凝土浇筑过程中发生坍塌事故,15名工人被埋,共造成8人死亡,7 人受伤。 3、2010年1月12日,在贵州省黔南州福泉市的利森水泥厂工地上,搭设完毕 的脚手架突然倒塌,造成8人死亡,2人受伤。 4、2010年1月16日,在浦东新区芳甸路梅花路口的证大喜玛拉雅艺术中心工 地,在搭设电梯井道施工脚手架脚手架突然发生坍塌施工人员,3名施工人员 被脚手架埋压。 5、2010年1月21日,浙江嘉兴市南湖区大桥八里村沪杭高铁工地上,一座井 字架突然倒塌,正在上面施工的3名工人掉落被埋。 6、2010年1月25日,浙江省宁波市海曙区中山立交桥往西200米左右一拆迁 施工搭建的脚手架发生坍塌事故,砸中了刚好路过的2辆机动车、4辆电瓶车、 2辆自行车和几位行人。 等等~~
关于脚手架高处坠落事故分析与处理.docx

关于脚手架高处坠落事故分析与处理一、事故经过8月28日,由某建筑公司承建的宿舍楼主体己封顶,当天上午瓦工于某某等3人站在宿舍楼3单元6楼两阳台中间搭设的毛竹脚手架上浇筑阳台混凝土,由于没有专门搭设卸料平台,吊运的混凝土只好卸在该脚手架上临时铺设的钢模板上。
8时49分左右,当第三料斗混凝土卸在钢模上,瓦丁于某某上前清理料斗时,脚手架右侧内立杆突然断裂,钢模板滑落,于某某随钢模板坠落到地面,脑部和内脏严重受伤,施工现场管理人员急忙将他送往医院,但经抢救无效死亡。
这起事故造成直接经济损失9.5万元。
二、在脚手架上发生高处坠落事故的主要原因分析1、作业人员安全意识淡薄,自我保护能力差,冒险违章作业。
一是架子工从事脚手架搭设与拆除时,未按规定正确佩带安全帽和安全带。
许多作业人员自恃“艺高人胆大”,嫌麻烦,认为不戴安全帽或不系安全带,只要小心一些就不会出事,由此导致的高处坠落事故时有发生。
二是作业人员危险意识差,对可能遇到或发生的危险估计不足,对施工现场存在的安全防护不到位等问题不能及时发现。
2、脚手架搭设不符合规范要求。
建设部行业标准《建筑施工扣件式钢管脚手架安全技术规范》(JGJ130-2001)已经于2001年6月1日起正式实施。
该规范属于强制性标准,在脚手架的设计计算、搭设与拆除、架体结构等方面提出了许多新的要求。
但在部分施工现场,脚手架搭设不规范的现象仍比较普遍,一是脚手架操作层防护不规范;二是密目网、水平兜网系结不牢固,未按规定设置随层兜网和层间网;三是脚手板设置不规范;四是悬挑架等设置不规范,由此导致了多起职工伤亡事故的发生。
3、脚手架材质不符合要求,使用前未进行必要的检验检测;4、脚手架搭设与拆除方案不全面,安全技术交底无针对性。
项目部重视施工现场、忽视安全管理资料的现象比较普遍,应当编制专项安全技术方案的专项施工工程,如脚手架搭设与拆除、基坑支护、模板工程、临时用电、塔机拆装等,不编制施工方案,或者不结合施工现场实际情况,照抄标准、规范,应付检查。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
脚手架坠落事故树计算四川成都 江光平制作 某施工单位近 3 年在水库大坝工程施工期间,由于违章作业、安 全检查不够,共发生高处坠落事故和事件 20 多起,其中从脚手架或 操作平台上坠落占高处坠落事故总数的 60%以上,这些事故造成财产 损失、人员伤亡,对安全生产构成负面影响。
为了探索这种坠落事故 发生的原因及其规律,及时排除安全隐患,确定使用事故树分析方法 寻找事故致因因素,采用有针对性的对策措施,提高安全生产管理效 能。
经事故分析和危险辨识,选择以作业人员从脚手架(或操作平台) 上坠落作为事故树顶上事件,编制了以下事故树图。
T 脚手架坠 落伤亡事故+A1 安全防护设施不严密·A2 脚手架垮塌·A3 安全带未起作用·X1 脚 踏 空坠落X2 无防护网保护X3 搭 建 B1 负荷过大质量差+X4 无 检 查制度B2 未使用 安全带+X2 无防护 网保护X5 堆 放 物超重X6 支 撑 物折断X7 安 全 带脱钩X8 走 动 取下安全带1.计算事故树最小割集(1)使用行列方法进行事故树定性分析,计算该事故树的最小割集。
A1 A2 A3X1 X2 X3 B1 X4 B2 X2X1 X2 X3 X5 X4X6 X7 X2 X8X1 X2 X3 X5 X4 X3 X6 X4 X7 X2 X8 X2(2)使用布尔代数式计算最小割集T = A1 + A2 +A3 = X1X2 + X3B1X4 + B2X2 = X1X2 + X3X4(X5 + X6) + (X7 + X8)X2 = X1X2 + X3X4X5 + X3X4X6 + X7X2 + X8X2 得到该事故树的最小割集 5 个:K1 = {X1,X2};K2 = {X3,X4,X5};K3 = {X3,X4,X6}; K4 = {X7,X2}; K5 = {X8,X2} (3)绘制用最小割集表示的事故树等效图T +K1·X1 X2K2K3··X3 X4 X5 X3 X4 X6K4·X7 X2K5·X8 X22.计算事故树最小径集 (1)将事故树转为成功树T′·A′1A′2A′3+++X′X′X′B′1 X′B′2 X′··X′ X′X′ X′(2)计算成功树的最小割集(事故树最小径集) T′ = A1′A2′A3′=(X1′+ X2′)(X3′+B1′+X4′)(B2′+X2′)=(X1′+X2′)(X3′+X5′+X6′+X4′)(X7′ X8′+X2′)= ( X1′ X7′ X8′+X1′ X2′+X2′ X7′ X8′+X2′ ) (X3′+X5′+X6′+X4′) =(X1′ X7′ X8′+X2′+X2′ X7′ X8′)(X3′+X5′+X6′+X4′)=(X1′ X3′ X7′ X8′+X2′ X3′+X2′ X3′ X7′ X8′)+(X1′ X5′ X7′ X8′+X5′ X2′+X2′ X5′ X7′ X8′)+(X1′ X6′ X7′ X8′+X2′ X6′+X2′ X6′X7′ X8′) +(X1′ X4′ X7′ X8′+X2′ X4′+X2′ X4′ X7′ X8′)= X1′ X3′ X7′ X8′+X2′ X3′+X1′ X5′ X7′ X8′+X2′ X5′+X1′ X6′ X7′ X8′+X2′ X6′+X1′ X4′ X7′ X8′+X2′ X4′ 得到 8 个最小径集:P1={X1,X3,X7,X8};P2={X2,X3};P3={X1,X5,X7,X8};P4={X2,X5};P5={X1,X6,X7,X8};P6={X2,X6}; P7={X1,X4,X7,X8};P8={X2,X4} 3.计算基本事件发生概率和顶上事件发生概率(1)确定基本事件发生概率根据该施工单位近 3 年来的事故统计数据,参考《安全评价》教材 P491 表 20-2、20-3,P493 表 20-4、20-5、20-6 的取值范围,我们令该事故树各基本事件的发生概率为:X1=q1= X5=q5=X2=q2= X3=q3= X4=q4= X6=q6= X7=q7= X8=q8=(2)计算顶上事件发生概率 因最小割集数少于最小径集数,所以选择最小割集首项近似法进 行顶上事件发生概率的计算。
即下列公式kP(T ) q1 qi r 1 XiEr1r s k XiErk (1)k1qir 1XiEr解:k qi F1r 1 XiEr(每个割集基本事件概率积的累积相加) qi F2 (每个割集之间的乘积的累积相加)1r sk XiEr EsP(T)= F1 – F25 得:F1 q8=q1q2 + q3q4q5 + q3q4q6 + q2q7 + q2q8r 1 Xikr=×+××+××+×+×== ×10-2 F2 q8 =q1q2q3q4q5 + q1q2q3q4q6 + q1q2q7 + q1q2q81r sk Xikr ks+q3q4q5q6 + q3q4q5q2q7 + q3q4q5q2q8 + q3q4q6q2q7+q3q4q6q2q8 + q2q7q8 == ×10-2P(T) = F1 – F2 = ×10-2 – ×10-2 = ×10-2该事故树顶上事件的发生概率为。
4.基本事件重要度分析(1)基本事件结构重要度分析①采用最小割集判断法判断结果:根据事故树的 5 个最小割集:K1 = {X1,X2};K2 = {X3,X4,X5}; K3 = {X3,X4,X6}; K4 = {X7,X2};K5 = {X8,X2}。
在三个低阶割集中出现三次,其结构重要度最大;,X7,X8 在低阶割集中分别出现一次,其结构重要度相等,但低于 X2; ,X4 在高阶割集中分别出现 2 次,结构重要度相等,但比只出现一次的 X5,X6 结构重要度大; ,X6 结构重要度相等。
由此得到最小割集判断法的基本事件结构重要度排序为:IΦ(2)>IΦ(1)= IΦ(7)= IΦ(8)>IΦ(3)= IΦ(4)>IΦ(5)=IΦ(6)②采用割集近似判别公式I (i)Ki1 2n1,XK 计算结果:(基本事件在割集中出现次数为指数减 1 的倒数的累积相加)IΦ(1)=1 2211 2;IΦ(2)=1 2211 2211 2213 2;IΦ(3)=1 2311 2312 41 2;IΦ(4)=1 2311 2312 41 2;IΦ(5)=1 2311 4;IΦ(6)=1 2311 4;IΦ(7)=1 2211;2IΦ(8)=1 2211 2割集近似判别公式计算的基本事件结构重要度排序为:IΦ(2)>IΦ(1)= IΦ(7)= IΦ(8) = IΦ(3)= IΦ(4)>IΦ(5)=IΦ(6)③采用基本事件的割集重要系数进行近似判断: 根据公式Ik(i)1 kk r 11 mr ( Xi (i=1,2,…,n) Er)解:已知该事故树的 5 个割集是:K1 = {X1,X2};K2 = {X3,X4,X5}; K3 = {X3,X4,X6}; K4 = {X7,X2};K5 = {X8,X2}。
则 m1=2,m2=3, m3=3, m4=2, m5=2. (基本事件在割集中的数量的倒数与割集倒数的乘积)得:Ik(1) = (1/m2 )1/k= 3/30 同理 :(k=5)Ik(2) = (1/m2+1/m2+1/m2)1/k= 9/30Ik(3) = (1/m3 +1/m3)1/k= 4/30 Ik(4) = (1/m3+1/m3)1/k= 4/30 Ik(5) = (1/m3)1/k= 2/30Ik(6) = (1/m3)1/k= 2/30 Ik(7) = (1/m2)1/k= 3/30 Ik(8) = (1/m2)1/k= 3/30得到基本事件的割集重要系数排序为:IΦ(2)>IΦ(1)= IΦ(7)= IΦ(8)>IΦ(3)= IΦ(4)>IΦ(5)=IΦ(6) (2)基本事件概率重要度分析根据基本事件概率重要度计算公式Ig(i)P(T qi)得:P(T ) Ig (1) q1 = q2 – q2q3q4q5 – q2q3q4q6 – q2q7 – q2q8– q3q4q5q6 + q2q3q4q5q6q7q8 =Ig (2)P(T ) q2=q1+q7+q8–q1q3q4q5–q1q3q4q6–q1q7–q1q8 – q3q4q5q6 – q3q4q5q7 – q3q4q6q7 – q3q4q6q8 – q7q8+ q1q3q4q5q6q7q8 =Ig (3) P(T ) q3=q4q5+q4q6–q1q2q4q5–q1q2q4q6–q1q2q7Ig (4) P(T )– q1q2q8 – q4q5q6 – q2q4q5q7 – q2q4q5q8 – q2q4q6q7 –q2q4q6q8 – q2q7q8 +q1q2q4q5q6q7q8 == q3q5+q3q6 – q1q2q3q5 – q1q2q3q6 – q1q2q7– q1q2q8 – q3q5q6 – q2q3q5q7 – q2q3q5q8 – q2q3q6q7 –q2q3q6q8 – q2q7q8 + q1q2q3q5q6q7q8 =Ig(5)P(T ) q5=q3q4–q1q2q3q4–q1q2q7–q1q2q8–q3q4q6 – q2q3q4q7 – q2q3q4q8 – q2q7q8 + q1q2q3q4q6q7q8 =Ig(6)P(T q6)=q3q4–q1q2q3q4–q1q2q7–q1q2q8–q3q4q5 –q3q4q2q7 – q3q4q2q8 – q2q7q8 + q1q2q3q4q5q7q8 =Ig (7)P(T ) q7=q2–q1q2–q3q4q5q6–q3q4q5q2–q3q4q6q2 – q2q8 + q1q2q3q4q5q6q8 =Ig (8)P(T ) q8=q2–q1q2–q2q7–q3q4q5q6–q3q4q6q2+q1q2q3q4q5q6q7 =得到该事故树基本事件概率重要度系数的排序为:Ig(2)>Ig(1)>Ig(7)>Ig(8)>Ig(4)>Ig(3)>Ig(6)>Ig(5)(3)基本事件敏感度系数分析根据偏导数变换公式 得:1ng CIg (i) 1ngqiCI g(1)q1 gIg(1)=×≈CI g(2)q2 gIg (2)=×≈CIg (3)q3 gIg(3)=×≈CI g(4)q4 gIg (4)=×≈CIg (5)q5 gIg (5)=×≈CI g(6)q6 gIg (6)=×≈CI g(7)q7 gIg (7)=×≈CIg (8)q8 gIg(8)=×≈得到按临界重要系数大小的排序:CIg(2) > CIg(1) > CIg(7) > CIg(4) > CIg(3) > CIg(8) > CIg(6) > CIg(5)分析演示:1.本事故树最小割集共 5 个,分别是:K1 = {X1,X2};K2 = {X3,X4,X5};K3 = {X3,X4,X6}; K4 = {X7,X2};K5 = {X8,X2}2.本事故树基本事件结构重要度分析结果:IΦ(2)>IΦ(1)= IΦ(7)= IΦ(8) = IΦ(3)= IΦ(4)>IΦ(5)=IΦ(6) 3.本事故树基本事件概率重要度分析结果:Ig(2)>Ig(1)>Ig(7)>Ig(8)>Ig(4)>Ig(3)>Ig(6)>Ig(5) 4.本事故树基本事件临界重要系数分析结果CIg(2) > CIg(1) > CIg(7) > CIg(4) > CIg(3) > CIg(8) > CIg(6) >CIg(5) 5.本事故树顶上事件的发生概率为。
